Optimizing Thermal Performance of Mini Heat Exchangers: An Experimental Analysis Using a Full Factorial Design
Abstract
:1. Introduction
2. Development of Experimental Apparatus: Prototype for a Mini Heat Exchanger
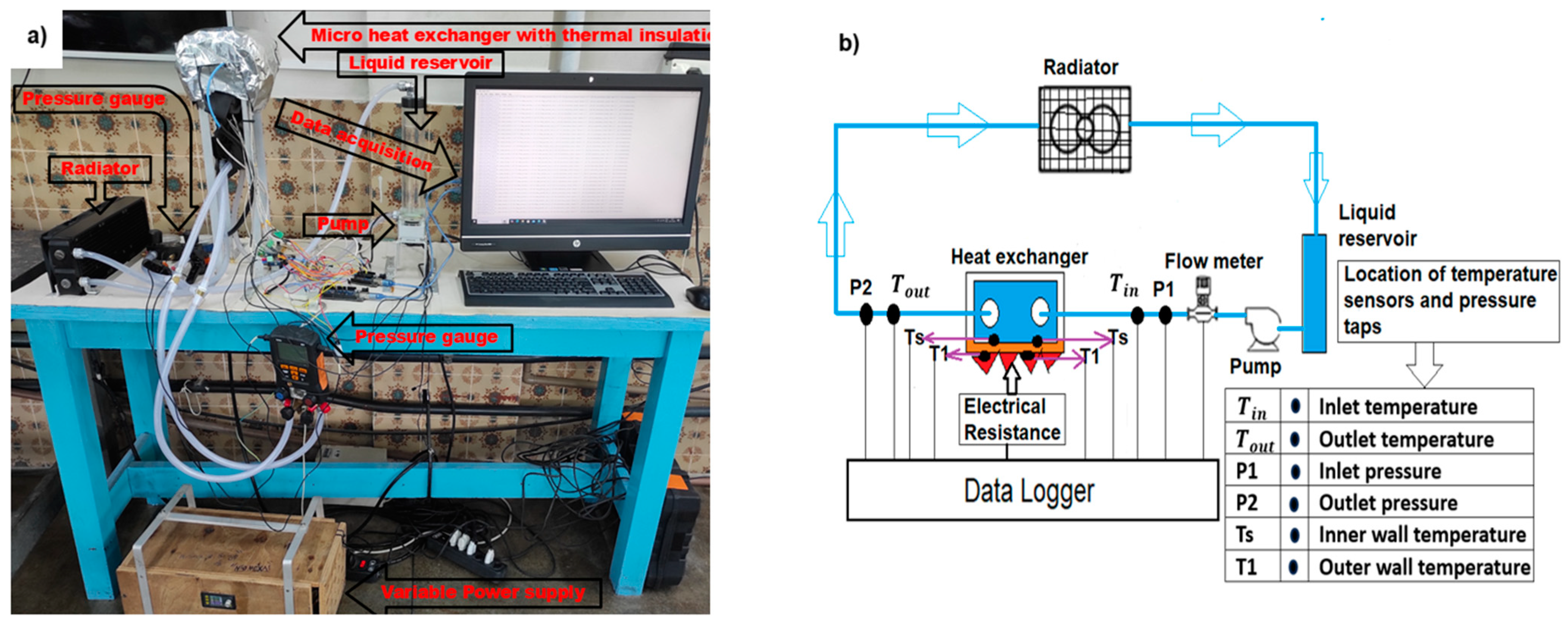
2.1. Description of the Experimental Apparatus
2.2. Sensors and Instruments
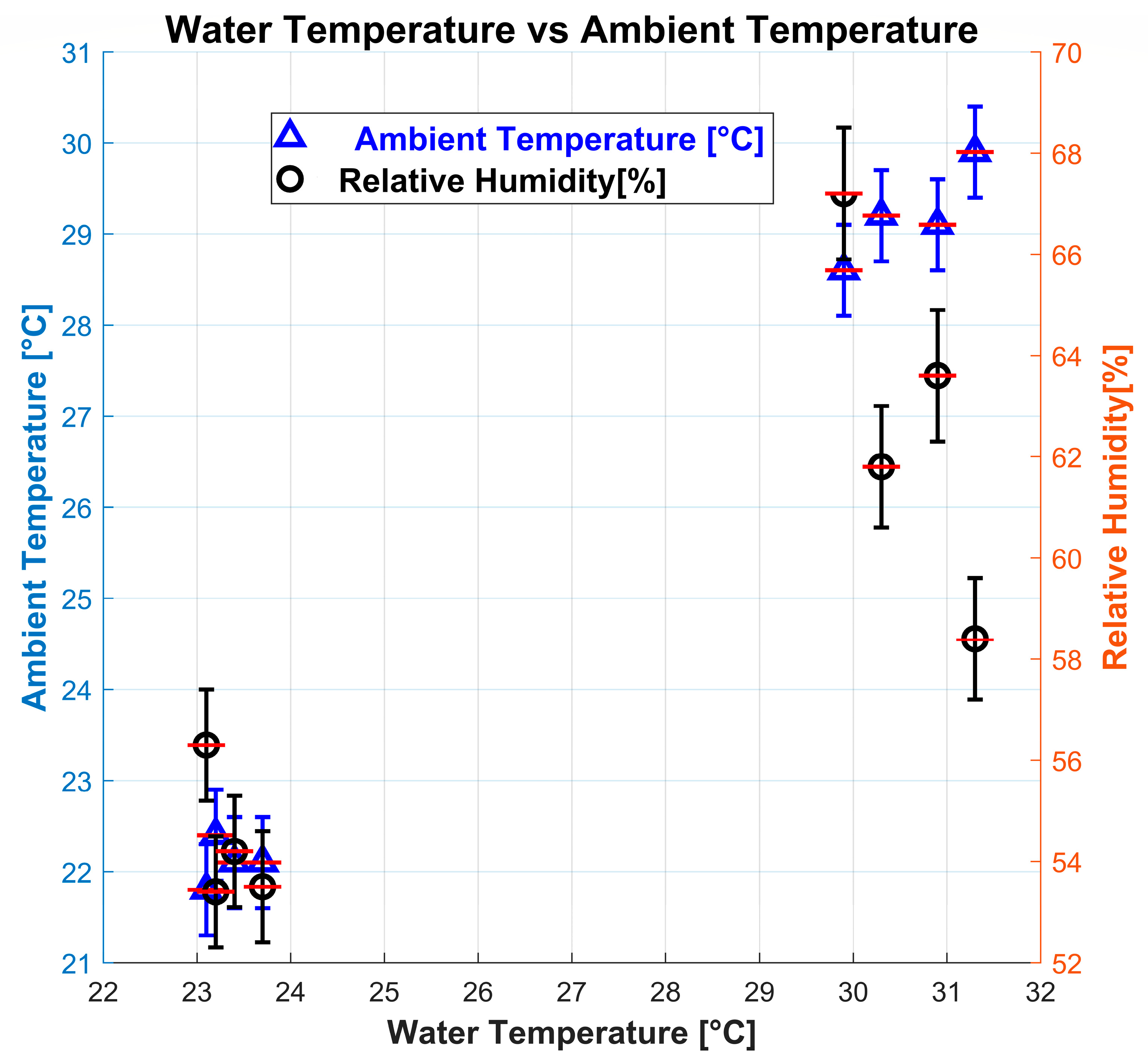
2.3. Calibration and Uncertainty Analysis
2.4. Data Acquisition System
3. Experimental Methodology
- Energy balance based on the first law of thermodynamics;
- One-dimensional heat conduction;
- Constant properties, such as thermal conductivity;
- Negligible thermal radiation;
- Negligible heat loss;
- No internal heat generation;
- A uniform convection coefficient;
- Steady-state conditions;
- Fluid incompressible and Newtonian;
- No-slip condition.
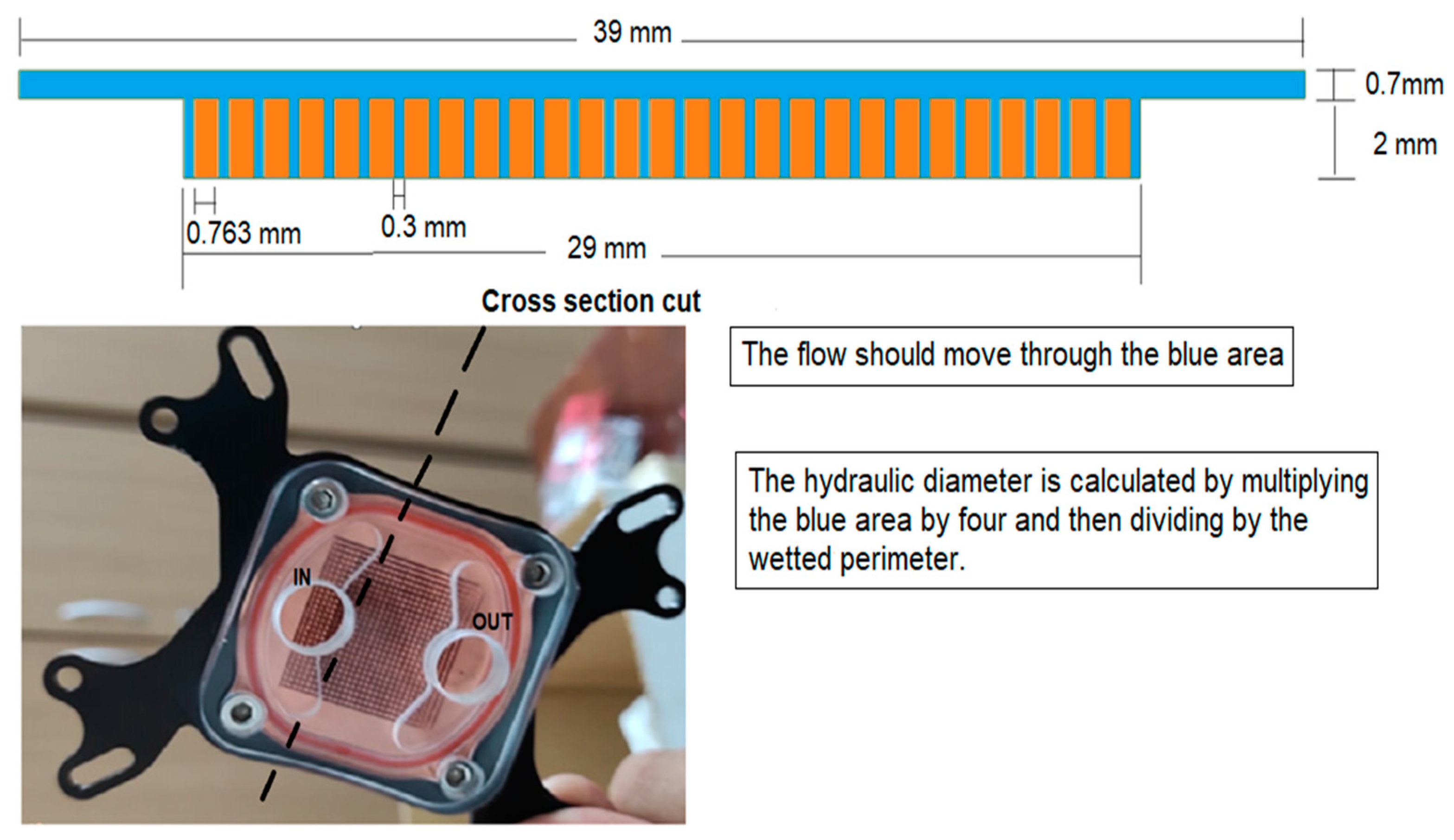
- Transitional channel: 0.1 µm < Dh < 10 µm;
- Microchannel: 10 µm < Dh < 200 µm;
- Minichannel: 200 µm < Dh < 3 mm;
- Conventional channel: Dh > 3 mm.
Basic Principles in FFD Building
4. Analysis and Discussion of Results
4.1. Full 23 Factorial Analysis
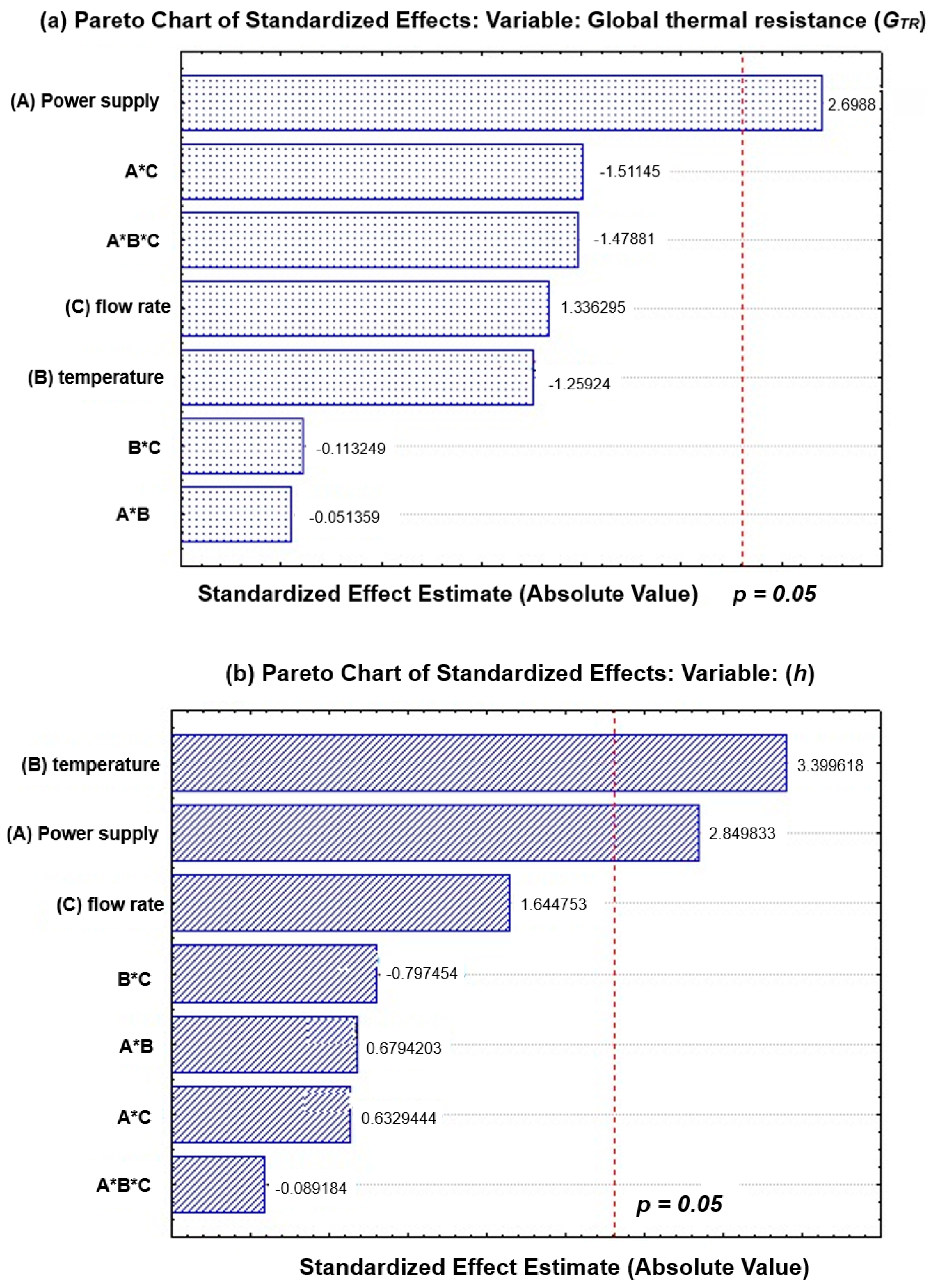
4.2. Interpretation of the Effects
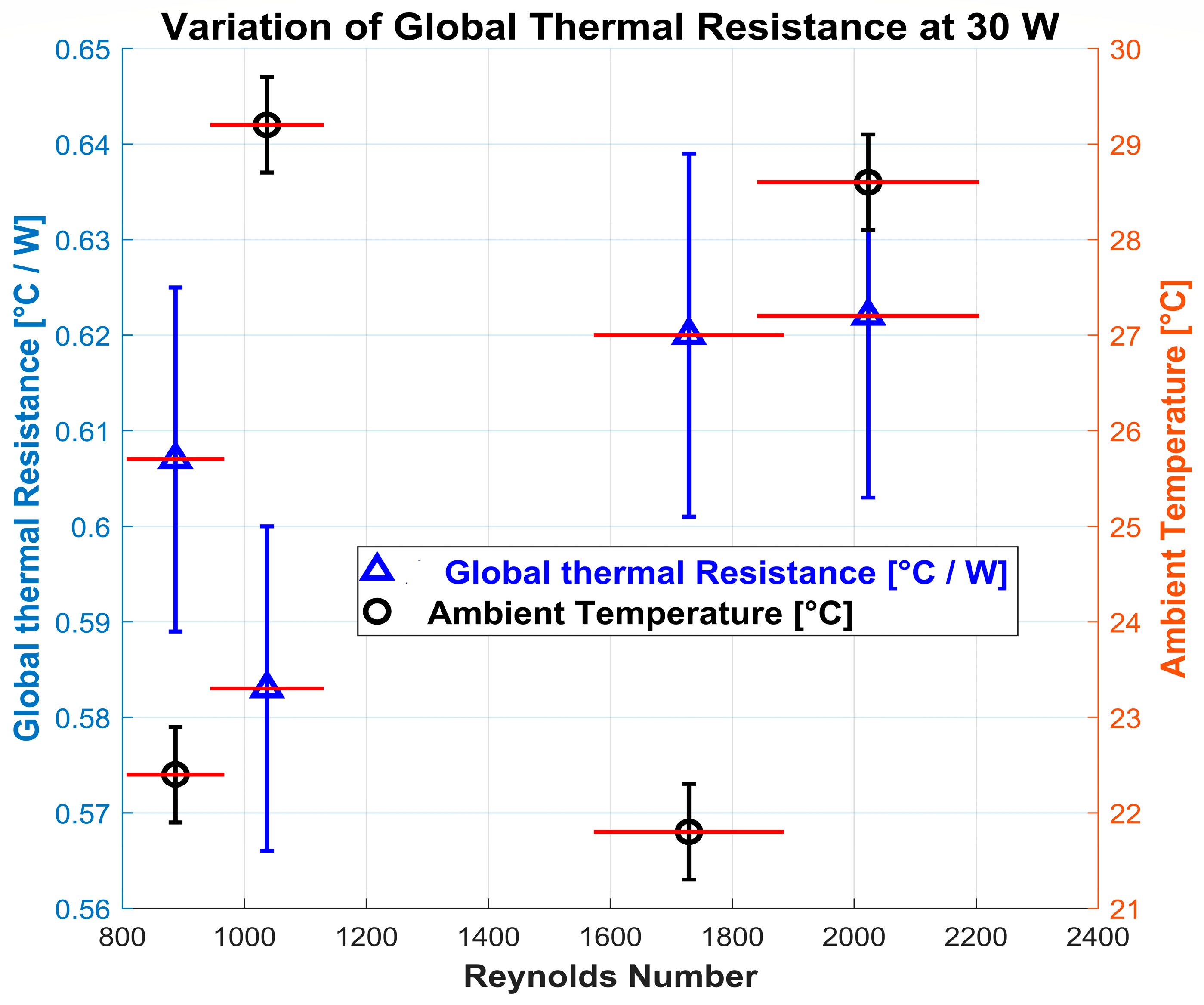
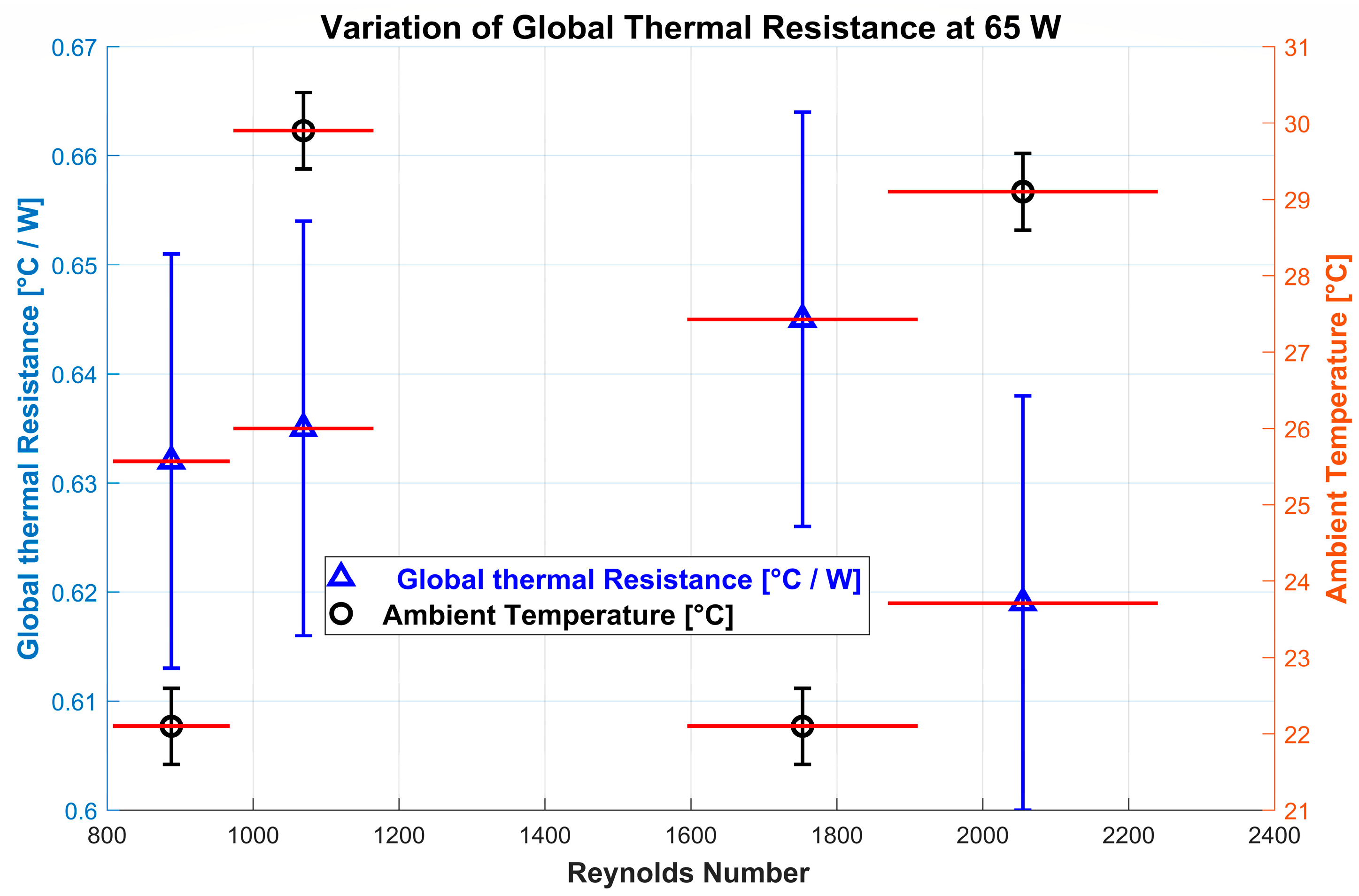
4.2.1. Global Thermal Resistance (GTR)
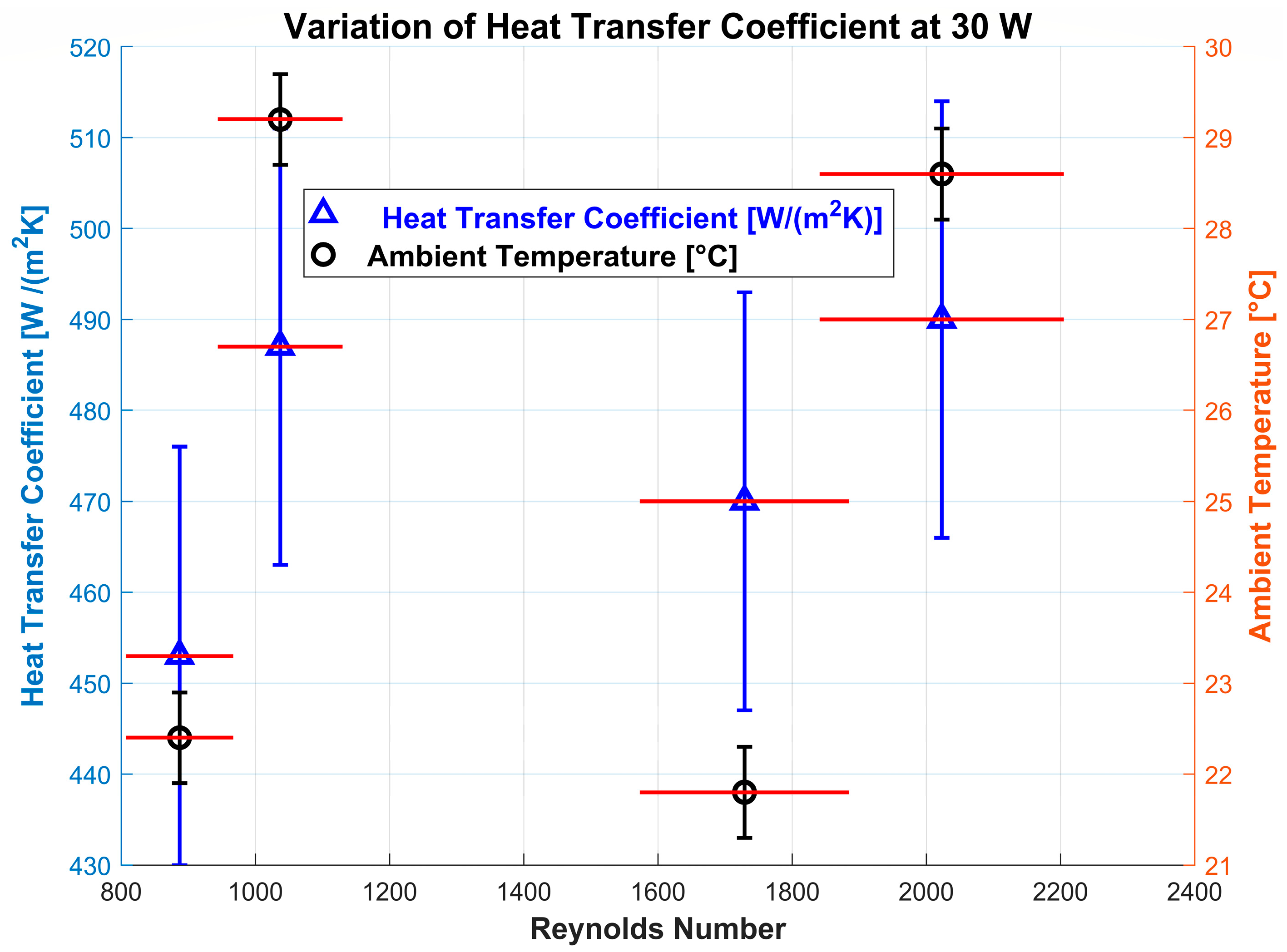
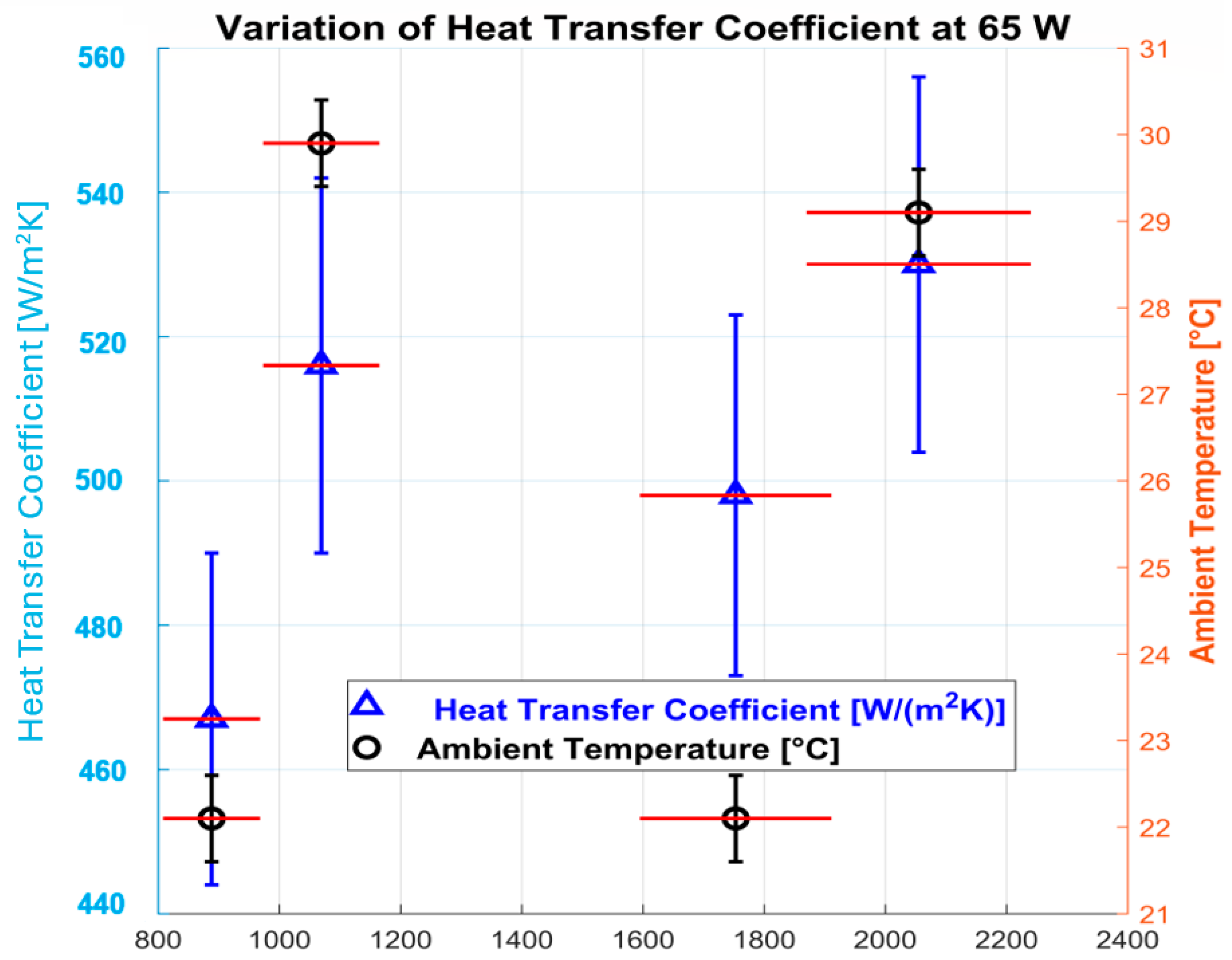
4.2.2. Heat Transfer Coefficient (h)
4.2.3. Comparison of Optimal Conditions
4.2.4. Mini Heat Exchanger Performance
4.3. Critical Considerations on the Dissipation Phenomenon in the Prototype
4.4. Advances in Heat Transfer Through Micro/Minichannels for Cooling Integrated Circuits: Emerging Phenomena and Experimental Challenges
5. Conclusions
- ✓
- The minimization of global thermal resistance was achieved with the reduced power (30 W), high ambient temperature (29 °C), and low volumetric flow rate (2.50 L/min).
- ✓
- The maximization of the heat transfer coefficient was obtained at high power (65 W), high ambient temperature (29 °C), and a high volumetric flow rate (5 L/min).
- ✓
- The methodology developed, which included the assembly of a prototype and detailed statistical analysis, establishes a reference standard for future studies. However, it is recommended that other temperature, power, and flow ranges be investigated to validate the results in different contexts and potentially optimize refrigeration systems.
- ✓
- These findings highlight the importance of striking a balance between thermal performance and energy efficiency, which is a critical factor for optimizing the functionality of miniaturized devices such as high-thermal-density electronic processors.
- ✓
- Optimized configurations such as the use of modified surfaces or nanostructures represent promising opportunities for future improvements to mitigate the increase in GTR.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Q | Heat transfer rate | [W] |
| Heat transfer rate by electrical resistance | [W] | |
| Thermal conductivity | [W/(m·K)] | |
| Thermal conductivity of the tin solder | [W/(m·K)] | |
| Heat transfer coefficient | [W/(m2·K)] | |
| Water inlet temperature | [°C] | |
| Water outlet temperature | [°C] | |
| Water temperature | [°C] | |
| Inner wall temperature | [°C] | |
| Adjusted temperature difference | [°C] | |
| Outer wall temperature | [°C] | |
| T | Temperature | [°C] |
| Global thermal resistance | [°C/W] | |
| Hydraulic diameter | [m] | |
| Average velocity | [m/s] | |
| Cross-sectional area | [m2] | |
| P | Wetted perimeter | [m] |
| µm | Micron | [µm] |
| A | Heat transfer area | [m2] |
| Greek Letters | ||
| ρ | Fluid density | [kg/m3] |
| µ | Dynamic viscosity | [kg/m·s] |
| Acronyms of statistical and experimental methods | ||
| OFAT | One-Factor-at-a-Time | |
| A, B, C | Statistical analysis factor indices | |
| FFD | Full factorial design | |
| Seffects | Standard error of the effect | |
| TDP | Thermal Design Power | |
| NTC | Negative Temperature Coefficient | |
| CPU | Central Processing Unit | |
| Kexpa | Coverage Factor for Expanded Uncertainty | |
| RPM | Revolutions Per Minute | |
| ( | Main effect | |
| df | Design matrix | |
| N | Number of experimental runs | |
| U | Uncertainty | |
| k | Number of model parameters | |
| p | Confidence interval | |
| Re | Reynolds number | |
Appendix A
References
- Gore, S.S.; Dhoble, A.S. Server processor heat sink analysis and modifications to improve its thermal performance. Mater. Today Proc. 2023, 82, 208–216. [Google Scholar] [CrossRef]
- Hu, Z.; Cui, M.; Wu, X. Real-Time Temperature Prediction of Power Devices Using an Improved Thermal Equivalent Circuit Model and Application in Power Electronics. Micromachines 2024, 15, 63. [Google Scholar] [CrossRef]
- Song, H.; Jeong, S.H.; Park, C.H.; Kim, M.J.; Kim, H.; Heo, J.H.; Lee, J.H. A multifaceted heat-switching nanofiller: Design of heat dissipation–insulation switching materials above a critical temperature. Chem. Eng. J. 2024, 497, 154406. [Google Scholar] [CrossRef]
- Liu, K.; Lin, Z.; Han, B.; Hong, M.; Cao, T. Simultaneously realizing thermal and electromagnetic cloaking by multi-physical null medium. Opto-Electron. Adv. 2024, 7, 230027. [Google Scholar] [CrossRef]
- Nair, V.; Baby, A.; Anoop, M.B.; Indrajith, S.; Murali, M.; Nair, M.B. A comprehensive review of air-cooled heat sinks for thermal management of electronic devices. Int. Commun. Heat Mass Transf. 2024, 159, 108055. [Google Scholar] [CrossRef]
- Wang, Q.; Tao, J.; Cui, Z.; Zhang, T.; Chen, G. Passive enhanced heat transfer, hotspot management and temperature uniformity enhancement of electronic devices by micro heat sinks: A review. Int. J. Heat Fluid Flow 2024, 107, 109368. [Google Scholar] [CrossRef]
- Zhang, J.; Zou, Z.; Fu, C. A Review of the Complex Flow and Heat Transfer Characteristics in Microchannels. Micromachines 2023, 14, 1451. [Google Scholar] [CrossRef]
- Dutkowski, K.; Kruzel, M.; Rokosz, K. Review of the State-of-the-Art Uses of Minimal Surfaces in Heat Transfer. Energies 2022, 15, 7994. [Google Scholar] [CrossRef]
- Yu, H.; Li, T.; Zeng, X.; He, T.; Mao, N. A Critical Review on Geometric Improvements for Heat Transfer Augmentation of Microchannels. Energies 2022, 15, 9474. [Google Scholar] [CrossRef]
- Maddah, H.; Aghayari, R.; Mirzaee, M.; Ahmadi, M.H.; Sadeghzadeh, M.; Chamkha, A.J. Factorial experimental design for the thermal performance of a double pipe heat exchanger using Al2O3-TiO2 hybrid nanofluid. Int. Commun. Heat Mass Transf. 2018, 97, 92–102. [Google Scholar] [CrossRef]
- Karakaya, H.; Deviren, H. Experimental Heat Transfer Analysis of a New Turbulator in a Concentric Heat Exchanger Tube: A Full Factorial Design Approach. ASME. J. Therm. Sci. Eng. Appl. 2024, 16, 37–48. [Google Scholar] [CrossRef]
- Pordanjani, A.H.; Vahedi, S.M.; Aghakhani, S.; Afrand, M.; Mahian, O.; Wang, L.P. Multivariate optimization and sensitivity analyses of relevant parameters on efficiency of scraped surface heat exchanger. Appl. Therm. Eng. 2020, 178, 115445. [Google Scholar] [CrossRef]
- de Medeiros, A.O.; da Paz, J.A.; Sales, A.; Navarro, M.; de Menezes, F.D.; Vilar, M. Statistical design analysis of isophorone electrocatalytic hydrogenation: The use of cyclodextrins as inverse phase transfer catalysts. J. Incl. Phenom. Macrocycl. Chem. 2017, 87, 13–20. [Google Scholar] [CrossRef]
- da Paz, J.A.; de Menezes, F.D.; Selva, T.M.G.; Navarro, M.; da Costa, J.Â.P.; da Silva, R.D.; Villa, A.A.O.; Vilar, M. Sonoelectrochemical hydrogenation of safrole: A reactor design, statistical analysis and computational fluid dynamic approach. Ultrason. Sonochem. 2020, 63, 104949. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Dai, Y.; Sun, P.; Meng, S. Interaction-based feature selection using Factorial Design. Neurocomputing 2018, 281, 47–54. [Google Scholar] [CrossRef]
- Em, S. Exploring Experimental Research: Methodologies, Designs, and Applications Across Disciplines. SSRN Electron. J. 2024, 1–9. [Google Scholar] [CrossRef]
- Gürkan, E.H.; Tibet, Y.; Çoruh, S. Application of full factorial design method for optimization of heavy metal release from lead smelting slag. Sustainability 2021, 13, 4890. [Google Scholar] [CrossRef]
- Mihăilescu, M.; Negrea, A.; Ciopec, M.; Negrea, P.; Duțeanu, N.; Grozav, I.; Svera, P.; Vancea, C.; Bărbulescu, A.; Dumitriu, C. Ștefan Full factorial design for gold recovery from industrial solutions. Toxics 2021, 9, 111. [Google Scholar] [CrossRef]
- Chen, T.; Qi, C.; Tang, J.; Wang, G.; Yan, Y. Numerical and experimental study on optimization of CPU system cooled by nanofluids. Case Stud. Therm. Eng. 2021, 24, 100848. [Google Scholar] [CrossRef]
- Li, W.; Cheng, S.; Yi, Z.; Zhang, H.; Song, Q.; Hao, Z.; Sun, T.; Wu, P.; Zeng, Q.; Raza, R. Advanced optical reinforcement materials based on three-dimensional four-way weaving structure and metasurface technology. Appl. Phys. Lett. 2025, 126, 033503. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Attarzadeh-Niaki, S.H.; Duwig, C. Multi-objective optimization of TPMS-based heat exchangers for low-temperature waste heat recovery. Appl. Therm. Eng. 2022, 212, 118448. [Google Scholar] [CrossRef]
- Sui, Z.; Sui, Y.; Wu, W. Multi-objective optimization of a microchannel membrane-based absorber with inclined grooves based on CFD and machine learning. Energy 2022, 240, 122809. [Google Scholar] [CrossRef]
- Huang, S.; Zhao, J.; Gong, L.; Duan, X. Thermal performance and structure optimization for slotted microchannel heat sink. Appl. Therm. Eng. 2017, 115, 1266–1276. [Google Scholar] [CrossRef]
- Yang, S.; Li, J.; Cao, B.; Wu, Z.; Sheng, K. Investigation of Z-type manifold microchannel cooling for ultra-high heat flux dissipation in power electronic devices. Int. J. Heat Mass Transf. 2024, 218, 124792. [Google Scholar] [CrossRef]
- Gao, S.; Li, P.; Shen, H. Heat dissipation analysis on the designed inner-outer circulation impingement double-layer microchannel heat sinks with chamfers in power electronic cooling system. Int. Commun. Heat Mass Transf. 2024, 159, 108305. [Google Scholar] [CrossRef]
- Cao, B.; Li, J.; Wu, Z.; Sheng, K. Flow boiling in novel radial microchannels for cooling of electronic devices and modules of annular temperature distribution. Int. J. Heat Mass Transf. 2025, 239, 126555. [Google Scholar] [CrossRef]
- Hu, C.; Yang, X.; Ma, Z.; Ma, X.; Feng, Y.; Wei, J. Research on heat transfer and flow distribution of parallel-configured microchannel heat sinks for arrayed chip heat dissipation. Appl. Therm. Eng. 2024, 255, 124003. [Google Scholar] [CrossRef]
- Su, L.; Duan, Z.; He, B.; Ma, H.; Ding, G. Laminar flow and heat transfer in the entrance region of elliptical minichannels. Int. J. Heat Mass Transf. 2019, 145, 118717. [Google Scholar] [CrossRef]
- Wang, Y. Numerical investigation of heat transfer enhancement in mini-channels with modified surface protrusions. Int. J. Heat Fluid Flow 2025, 113, 109766. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Arya, A.; Hormozi, F.; Nikkhah, V. On the convective thermal performance of a CPU cooler working with liquid gallium and CuO/water nanofluid: A comparative study. Appl. Therm. Eng. 2017, 112, 1373–1381. [Google Scholar] [CrossRef]
- Haywood, A.M.; Sherbeck, J.; Phelan, P.; Varsamopoulos, G.; Gupta, S.K.S. The relationship among CPU utilization, temperature, and thermal power for waste heat utilization. Energy Convers. Manag. 2015, 95, 297–303. [Google Scholar] [CrossRef]
- Tan, S.O.; Demirel, H. Performance and cooling efficiency of thermoelectric modules on server central processing unit and Northbridge. Comput. Electr. Eng. 2015, 46, 46–55. [Google Scholar] [CrossRef]
- AMD Ryzen. Série AMD RyzenTM AM4 com Disponibilidade Estendida. 2025. Available online: https://www.amd.com/en/products/embedded/ryzen/ryzen-extended-availability.html (accessed on 16 December 2024).
- Yang, K.S.; Jeng, Y.R.; Huang, C.M.; Wang, C.C. Heat transfer and flow pattern characteristics for HFE-7100 within microchannel heat sinks. Heat Transf. Eng. 2011, 32, 697–704. [Google Scholar] [CrossRef]
- Lee, Y.J.; Singh, P.K.; Lee, P.S. Fluid flow and heat transfer investigations on enhanced microchannel heat sink using oblique fins with parametric study. Int. J. Heat Mass Transf. 2015, 81, 325–336. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, Y.; Hu, J.; Fan, X.; Luo, Z.; Liu, Y.; Liu, L. Efficient Representation and Optimization of TPMS-Based Porous Structures for 3D Heat Dissipation. CAD Comput. Aided Des. 2022, 142, 103123. [Google Scholar] [CrossRef]
- Ghani, I.A.; Kamaruzaman, N.; Sidik, N.A.C. Heat transfer augmentation in a microchannel heat sink with sinusoidal cavities and rectangular ribs. Int. J. Heat Mass Transf. 2017, 108, 1969–1981. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Grande, W.J. Evolution of microchannel flow passages-thermohydraulic performance and fabrication technology. Heat Transf. Eng. 2003, 24, 3–17. [Google Scholar] [CrossRef]
- Narendran, G.; Gnanasekaran, N.; Perumal, D.A. Thermodynamic irreversibility and conjugate effects of integrated microchannel cooling device using TiO2 nanofluid. Heat Mass Transf. 2020, 56, 489–505. [Google Scholar] [CrossRef]
- StatSoft. STATISTICA (Data Analysis Software System), Version 6. Available online: http://www.statsoft.com (accessed on 16 January 2024).
- Manikandan, S.P.; Dharmakkan, N.; Sumana, N. Heat transfer studies of Al2O3/water-ethylene glycol nanofluid using factorial design analysis. Chem. Ind. Chem. Eng. Q. 2022, 28, 95–101. [Google Scholar] [CrossRef]
- Jankowski, D.; Wiwatowski, K.; Żebrowski, M.; Pilch-Wróbel, A.; Bednarkiewicz, A.; Maćkowski, S.; Piątkowski, D. Luminescent Nanocrystal Probes for Monitoring Temperature and Thermal Energy Dissipation of Electrical Microcircuit. Nanomaterials 2024, 14, 1985. [Google Scholar] [CrossRef]
- Ding, S.C.; Fan, J.F.; He, D.Y.; Cai, L.F.; Zeng, X.L.; Ren, L.L.; Du, G.P.; Zeng, X.L.; Sun, R. High thermal conductivity and remarkable damping composite gels as thermal interface materials for heat dissipation of chip. Chip 2022, 1, 100013. [Google Scholar] [CrossRef]
- Hajialibabaei, M.; Saghir, M.Z.; Dincer, I.; Bicer, Y. Optimization of heat dissipation in novel design wavy channel heat sinks for better performance. Energy 2024, 297, 131155. [Google Scholar] [CrossRef]
- Lima, C.C.X.S.; Ochoa, A.A.V.; da Costa, J.A.P.; de Menezes, F.D.; Alves, J.V.P.; Ferreira, J.M.G.A.; Azevedo, C.C.A.; Michima, P.S.A.; Leite, G.N.P. Experimental and Computational Fluid Dynamic—CFD Analysis Simulation of Heat Transfer Using Graphene Nanoplatelets GNP/Water in the Double Tube Heat Exchanger. Processes 2023, 11, 2735. [Google Scholar] [CrossRef]
- Beck, J.; Palmer, M.; Inman, K.; Wohld, J.; Cummings, M.; Fulmer, R.; Scherer, B.; Vafaei, S. Heat Transfer Enhancement in the Microscale: Optimization of Fluid Flow. Nanomaterials 2022, 12, 3628. [Google Scholar] [CrossRef]
- Pan, Y.H.; Zhao, R.; Fan, X.H.; Nian, Y.L.; Cheng, W.L. Study on the effect of varying channel aspect ratio on heat transfer performance of manifold microchannel heat sink. Int. J. Heat Mass Transf. 2020, 163, 120461. [Google Scholar] [CrossRef]
- Patel, N.; Mehta, H.B. Experimental investigations on a variable channel width double layered minichannel heat sink. Int. J. Heat Mass Transf. 2021, 165, 120633. [Google Scholar] [CrossRef]
- Sikirica, A.; Grbčić, L.; Kranjčević, L. Machine learning based surrogate models for microchannel heat sink optimization. Appl. Therm. Eng. 2023, 222, 119917. [Google Scholar] [CrossRef]
- Ao, L.; Ramiere, A. Through-chip microchannels for three-dimensional integrated circuits cooling. Therm. Sci. Eng. Prog. 2024, 47, 102333. [Google Scholar] [CrossRef]
- Zhuang, X.; Xie, Y.; Li, X.; Yue, S.; Wang, H.; Wang, H. Experimental investigation on flow boiling of HFE-7100 in a microchannel with pin fin array. Appl. Therm. Eng. 2023, 225, 120180. [Google Scholar] [CrossRef]
- Harris, M.; Wu, H.; Zhang, W.; Angelopoulou, A. Overview of recent trends in microchannels for heat transfer and thermal management applications. Chem. Eng. Process. Process Intensif. 2022, 181, 109155. [Google Scholar] [CrossRef]
- Abdulack, S.A. Heat transfer in cylindrical geometry: An interdisciplinary approach to a real problem. Rev. Bras. Ensino Fís. 2024, 46, e20240258. [Google Scholar] [CrossRef]




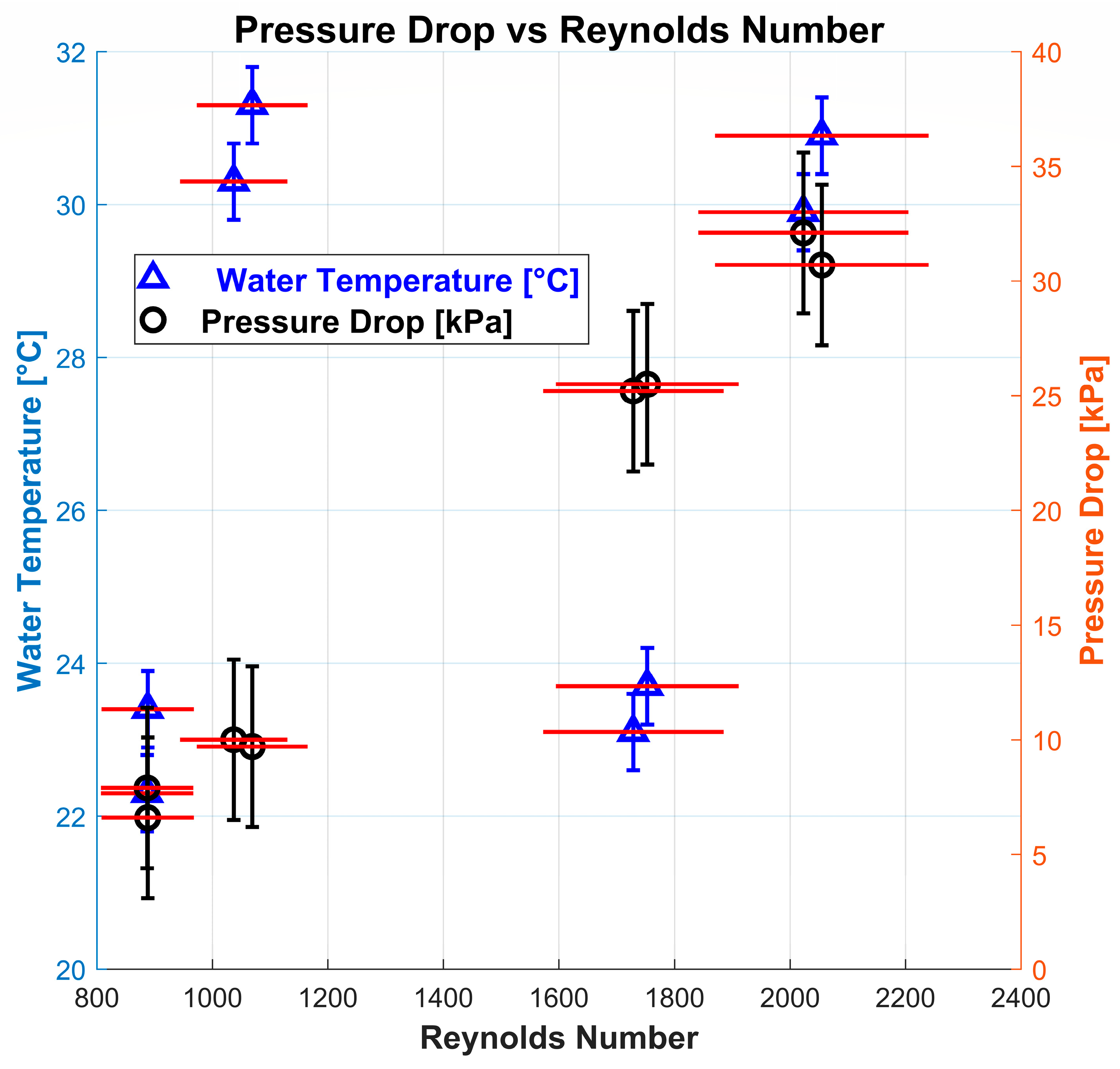
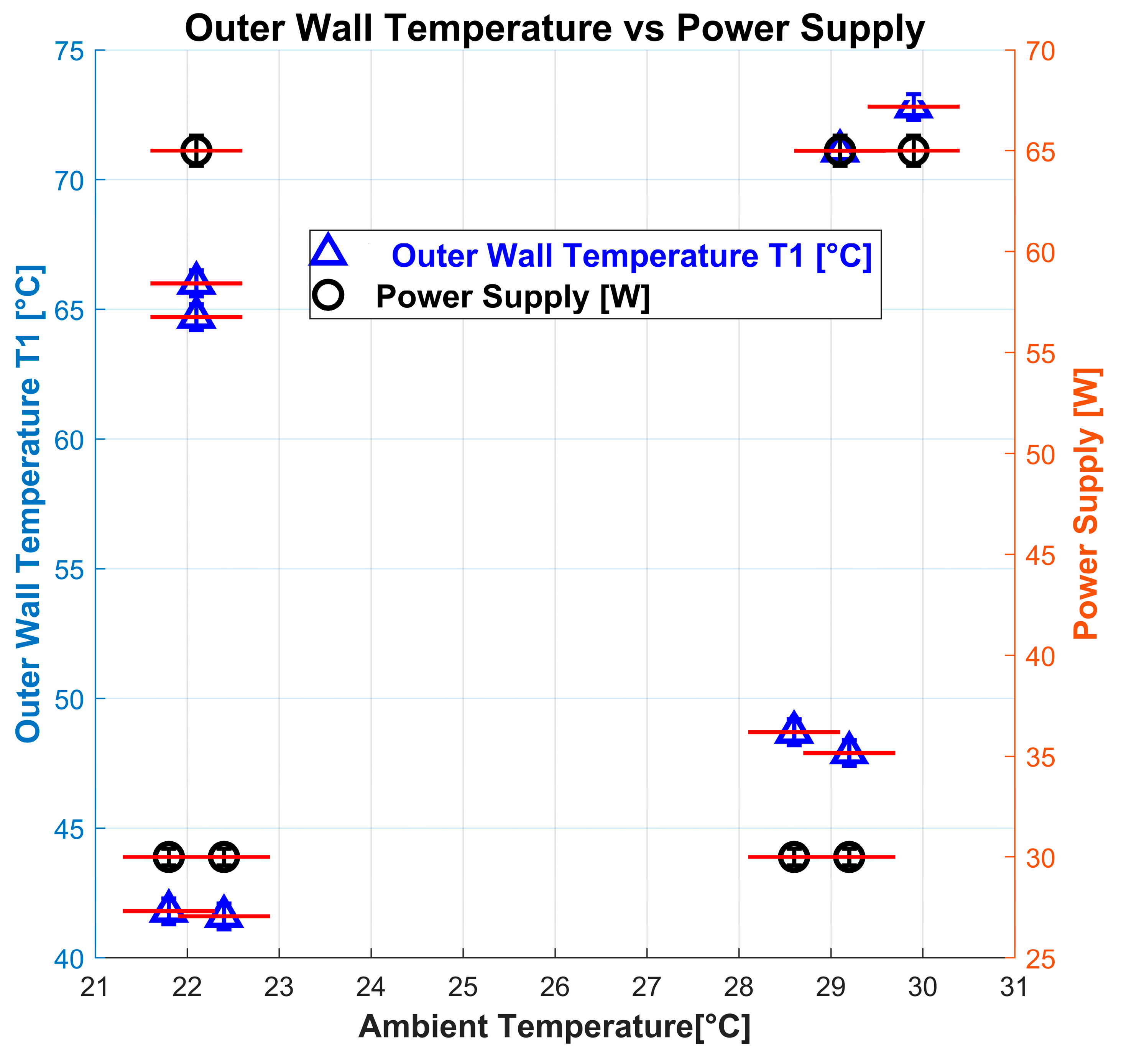
| Variable | Range |
|---|---|
| Input Voltage | 6 V to 60 V |
| Output Voltage | 0 V to 50 V |
| Output Current | 0 A to 20 A |
| Output Power | 0 W to 1000 W |
| Output Voltage Resolution | 0.01 V |
| Output Current Resolution | 0.01 A |
| Output Voltage Accuracy | ±(0.50% + 1 digit) |
| Output Current Accuracy | ±(0.50% + 2 digits) |
| Variable | Value |
|---|---|
| The Uncertainty in the Electrical Resistance Power at 30 W | ±0.42 W |
| The Uncertainty in the Electrical Resistance Power at 65 W | ±0.75 W |
| Global Thermal Resistance Uncertainty [°C·W−1] | ± 3.00% |
| Uncertainty of the Coefficient Heat Transfer [W·m−2·°C−1] | ±5.00% |
| Flow Rate Uncertainty [L/min] | ±5.00% |
| Ambient Temperature Uncertainty | ±0.50 °C |
| Pressure Uncertainty | ±3.50 kPa |
| Water Temperature Uncertainty | ±0.20 °C |
| Uncertainty in the Temperature of the Heat Exchanger Wall | ±0.50 °C |
| Uncertainty in Relative Humidity | ±2.00% |
| Reynolds number uncertainty | ±9.00% |
| Factors | (−) | (+) |
|---|---|---|
| (A) Power supply (W) | 30 | 65 |
| (B) Ambient temperature (°C) | 22 | 29 |
| (C) Flow rate (L·min−1) | 2.50 | 5 |
| Entry | A | B | C | GTR (×10−3 °C·W−1) | Average (×10−3 °C·W−1) |
| 1 | − | − | − | 612.656 (12)|600.602 (8) | 606.629 |
| 2 | + | − | − | 628.971 (7)|635.748 (9) | 632.359 |
| 3 | − | + | − | 565.282 (6)|600.387 (5) | 582.834 |
| 4 | + | + | − | 630.052 (11)|639.872 (4) | 634.962 |
| 5 | − | − | + | 619.678 (14)|620.989 (10) | 620.334 |
| 6 | + | − | + | 633.525 (13)|657.396 (15) | 645.460 |
| 7 | − | + | + | 597.390 (2)|646.193 (16) | 621.791 |
| 8 | + | + | + | 602.825 (1)|634.419 (3) | 618.622 |
| Entry | A | B | C | h (W·m−2·°C−1) | Average (W·m−2·°C−1) |
| 1 | − | − | − | 448.706 (12)|457.082 (8) | 452.894 |
| 2 | + | − | − | 469.972 (7)|464.326 (9) | 467.149 |
| 3 | − | + | − | 481.976 (6)|491.303 (5) | 486.639 |
| 4 | + | + | − | 484.207 (11)|547.843 (4) | 516.025 |
| 5 | − | − | + | 487.272 (14)|452.377 (10) | 469.824 |
| 6 | + | − | + | 490.357 (13)|506.233 (15) | 498.295 |
| 7 | − | + | + | 492.418 (2)|486.836 (16) | 489.627 |
| 8 | + | + | + | 540.450 (1)|518.984 (3) | 529.717 |
| Entry (yi) | A | B | C | AB | AC | BC | ABC | GTR (×10−3 °C·W−1) | h (W·m−2·°C−1) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | − | − | − | + | + | + | − | 606.629 | 452.894 |
| 2 | + | − | − | − | − | + | + | 632.359 | 467.149 |
| 3 | − | + | − | − | + | − | + | 582.834 | 486.639 |
| 4 | + | + | − | + | − | − | − | 634.962 | 516.025 |
| 5 | − | − | + | + | − | − | + | 620.334 | 469.824 |
| 6 | + | − | + | − | + | − | − | 645.460 | 498.295 |
| 7 | − | + | + | − | − | + | − | 621.791 | 489.627 |
| 8 | + | + | + | + | + | + | + | 618.622 | 529.717 |
| Entry | Global Average * | GTR (×10−3 ± ×10−3 (°C·W−1)) | h (W·m−2·°C−1) |
|---|---|---|---|
| 620.374 ± 4.6 | 448.771 ± 4.9 | ||
| Main effects | |||
| 1 | A (Power supply) | 24.954 ± 9.2 | 28.050 ± 9.8 |
| 2 | B (Temperature) | −11.643 ± 9.2 | 33.462 ± 9.8 |
| 3 | C (Flow rate) | 12.356 ± 9.2 | 16.189 ± 9.8 |
| Two-factor interactions | |||
| 4 | A*B | −0.475 ± 9.2 | 6.687 ± 9.8 |
| 5 | A*C | −13.975 ± 9.2 | 6.229 ± 9.8 |
| 6 | B*C | −1.047 ± 9.2 | −7.849 ± 9.8 |
| Three-factor interactions | |||
| 7 | A*B*C | −13.673 ± 9.3 | −0.878 ± 9.8 |
| Variables | Level | Heat Transfer Coefficient (h) | Statistically Relevant |
| Volumetric flow | High | Increase | No |
| Ambient temperature | High | Increase | Yes |
| Power supply | High | Increase | Yes |
| Variables | Level | Global Thermal Resistance (GTR) | Statistically Relevant |
| Volumetric flow | Low | Decrease | No |
| Ambient temperature | High | Decrease | No |
| Power supply | Low | Decrease | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franco, S.d.S.; Lima, Á.A.S.; Ochoa, A.A.V.; da Costa, J.Â.P.; Leite, G.d.N.P.; Vilar, M.; Ferraz, K.A.; Michima, P.S.A. Optimizing Thermal Performance of Mini Heat Exchangers: An Experimental Analysis Using a Full Factorial Design. Appl. Sci. 2025, 15, 4052. https://doi.org/10.3390/app15074052
Franco SdS, Lima ÁAS, Ochoa AAV, da Costa JÂP, Leite GdNP, Vilar M, Ferraz KA, Michima PSA. Optimizing Thermal Performance of Mini Heat Exchangers: An Experimental Analysis Using a Full Factorial Design. Applied Sciences. 2025; 15(7):4052. https://doi.org/10.3390/app15074052
Chicago/Turabian StyleFranco, Sergio da Silva, Álvaro Augusto Soares Lima, Alvaro Antonio Villa Ochoa, José Ângelo Peixoto da Costa, Gustavo de Novaes Pires Leite, Márcio Vilar, Kilvio Alessandro Ferraz, and Paula Suemy Arruda Michima. 2025. "Optimizing Thermal Performance of Mini Heat Exchangers: An Experimental Analysis Using a Full Factorial Design" Applied Sciences 15, no. 7: 4052. https://doi.org/10.3390/app15074052
APA StyleFranco, S. d. S., Lima, Á. A. S., Ochoa, A. A. V., da Costa, J. Â. P., Leite, G. d. N. P., Vilar, M., Ferraz, K. A., & Michima, P. S. A. (2025). Optimizing Thermal Performance of Mini Heat Exchangers: An Experimental Analysis Using a Full Factorial Design. Applied Sciences, 15(7), 4052. https://doi.org/10.3390/app15074052








