Emergency Evacuation Capacity Evaluation of High-Speed Railway Stations Based on Pythagorean Fuzzy Three-Way Decision Models
Abstract
:1. Introduction
2. Related Work
2.1. Emergency Evacuation Evaluation of Stations
2.2. Three-Way Decisions
3. Methodology
3.1. Pythagorean Fuzzy Rough Approximation Construction
3.2. Emergency Evacuation Capacity Evaluation Process
4. Case Study
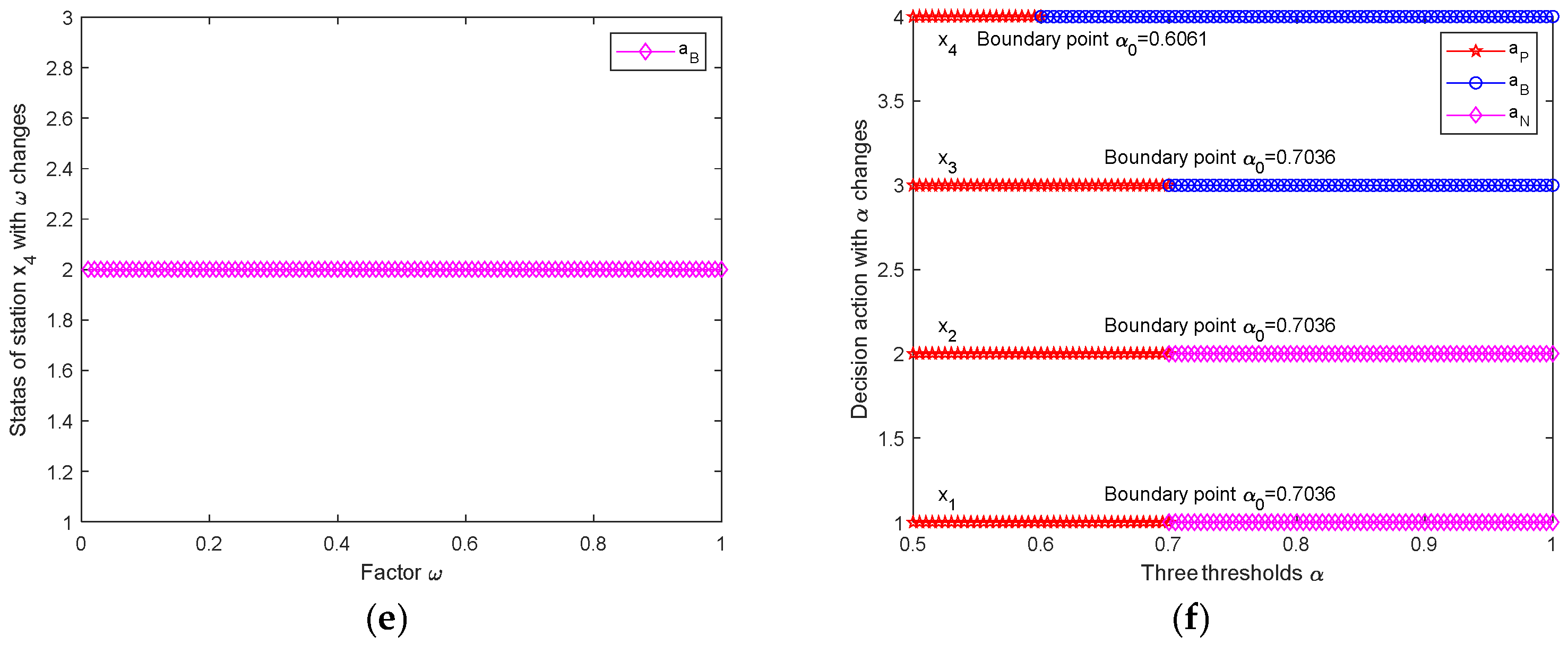
4.1. Result Analysis
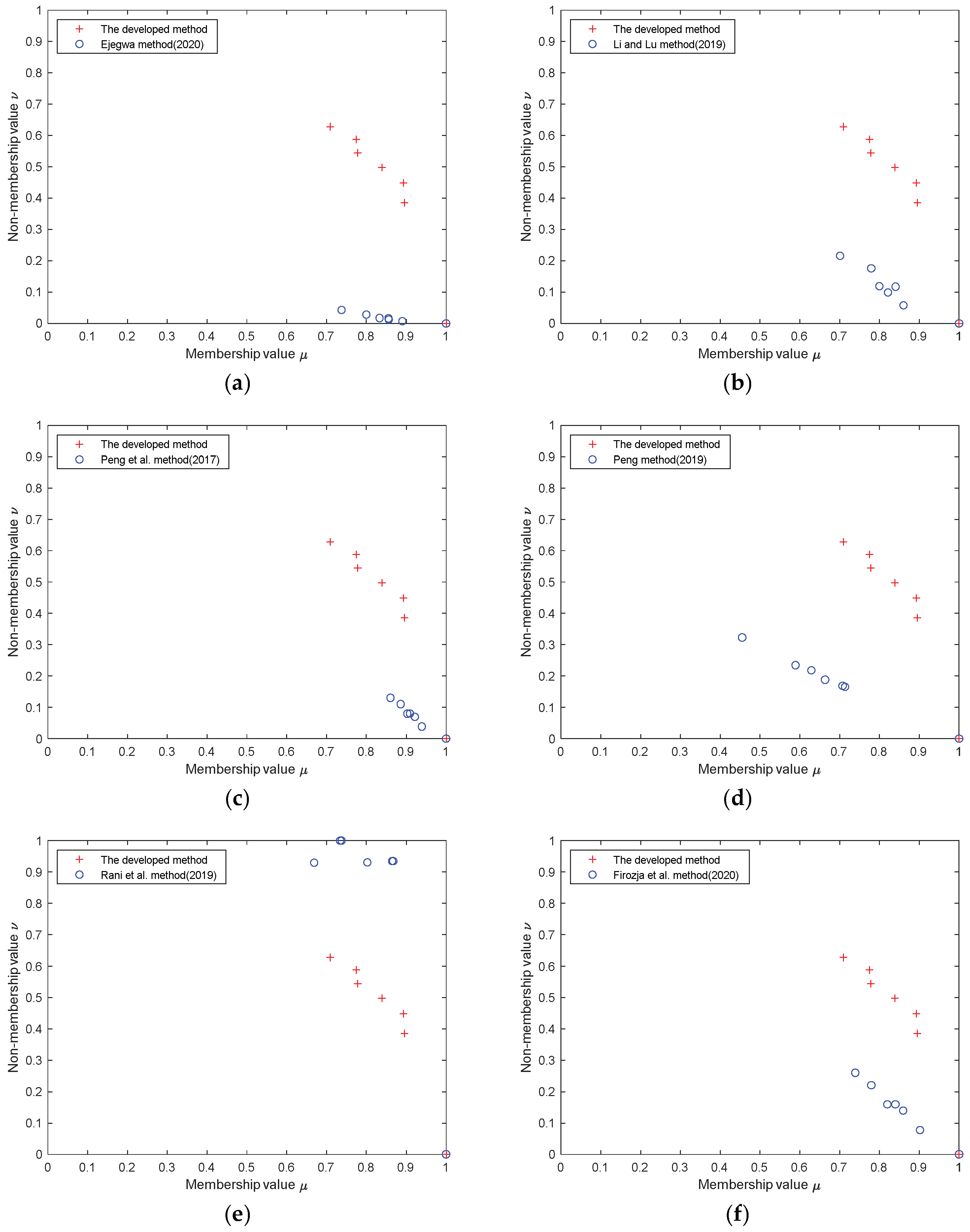
4.2. Comparison Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Salarian, A.H.; Mashhadizadeh, A.; Bagheri, M. Simulating passenger evacuation in railway station under fire emergency using safe zone approach. Transp. Res. Rec. 2020, 2674, 806–812. [Google Scholar] [CrossRef]
- Zhang, Z.; Yao, X.; Xing, Z.; Zhou, X. Understanding fire combustion characteristics and available safe egress time in underground metro trains: A simulation approach. Chaos Solitons Fractals 2024, 187, 115434. [Google Scholar] [CrossRef]
- Zhang, Z.; Yao, X.; Xing, Z.; Zhou, X. Simulation on passenger evacuation of metro train fire in the tunnel. Chaos Solitons Fractals 2024, 187, 115429. [Google Scholar] [CrossRef]
- Hassannayebi, E.; Memarpour, M.; Mardani, S.; Shakibayifar, M.; Bakhshayeshi, I.; Espahbod, S. A hybrid simulation model of passenger emergency evacuation under disruption scenarios: A case study of a large transfer railway station. J. Simul. 2020, 14, 204–228. [Google Scholar] [CrossRef]
- Wan, J.; Sui, J.; Yu, H. Research on evacuation in the subway station in China based on the Combined Social Force Model. Phys. A Stat. Mech. Its Appl. 2014, 394, 33–46. [Google Scholar] [CrossRef]
- Zhou, R.; Cui, Y.; Wang, Y.; Jiang, J. A modified social force model with different categories of pedestrians for subway station evacuation. Tunn. Undergr. Space Technol. 2021, 110, 103837. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, J.; Zhong, M.; Hua, F.; Sui, J. Evacuation effect analysis of guidance strategies on subway station based on modified cellular automata model. Saf. Sci. 2023, 168, 106309. [Google Scholar] [CrossRef]
- Wu, Y.; Kang, J.; Mu, J. Assessment and simulation of evacuation in large railway stations. Build. Simul. 2021, 14, 1553–1566. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, D.; You, Q.; Kang, J.; Shi, M.; Lang, X. Evaluation of emergency evacuation capacity of urban metro stations based on combined weights and TOPSIS-GRA method in intuitive fuzzy environment. Int. J. Disaster Risk Reduct. 2023, 95, 103864. [Google Scholar] [CrossRef]
- Chen, J.; Liu, C.; Meng, Y.; Zhong, M. Multi-Dimensional evacuation risk evaluation in standard subway station. Saf. Sci. 2021, 142, 105392. [Google Scholar] [CrossRef]
- Edrisi, A.; Lahoorpoor, B.; Lovreglio, R. Simulating metro station evacuation using three agent-based exit choice models. Case Stud. Transp. Policy 2021, 9, 1261–1272. [Google Scholar]
- Zhang, Z.; Zhao, X.; Qin, Y.; Si, H.; Zhou, L. Interval type-2 fuzzy TOPSIS approach with utility theory for subway station operational risk evaluation. J. Ambient. Intell. Humaniz. Comput. 2022, 13, 1–15. [Google Scholar]
- Zhang, Z.; Guo, J.; Zhang, H.; Zhou, L.; Wang, M. Product selection based on sentiment analysis of online reviews: An intuitionistic fuzzy TODIM method. Complex Intell. Syst. 2022, 8, 3349–3362. [Google Scholar]
- Yao, Y. Three-way decisions with probabilistic rough sets. Inf. Sci. 2010, 180, 341–353. [Google Scholar]
- Yao, Y. The superiority of three-way decisions in probabilistic rough set models. Inf. Sci. 2011, 181, 1080–1096. [Google Scholar]
- Ma, W.; Lei, W.; Sun, B. Three-way group decisions under hesitant fuzzy linguistic environment for green supplier selection. Kybernetes 2020, 49, 2919–2945. [Google Scholar] [CrossRef]
- Lei, W.; Ma, W.; Sun, B. Multigranulation behavioral three-way group decisions under hesitant fuzzy linguistic environment. Inf. Sci. 2020, 537, 91–115. [Google Scholar]
- He, J.; Zhang, H.; Zhang, Z.; Zhang, J. Probabilistic linguistic three-way multi-attibute decision making for hidden property evaluation of judgment debtor. J. Math. 2021, 2021, 9941200. [Google Scholar]
- Liang, D.; Liu, D. A novel risk decision making based on decision-theoretic rough sets under hesitant fuzzy information. IEEE Trans. Fuzzy Syst. 2014, 23, 237–247. [Google Scholar] [CrossRef]
- Liang, D.; Pedrycz, W.; Liu, D.; Hu, P. Three-way decisions based on decision-theoretic rough sets under linguistic assessment with the aid of group decision making. Appl. Soft Comput. 2015, 29, 256–269. [Google Scholar]
- Liang, D.; Liu, D. Systematic studies on three-way decisions with interval-valued decision-theoretic rough sets. Inf. Sci. 2014, 276, 186–203. [Google Scholar] [CrossRef]
- Zhang, C.; Li, D.; Liang, J. Multi-granularity three-way decisions with adjustable hesitant fuzzy linguistic multigranulation decision-theoretic rough sets over two universes. Inf. Sci. 2020, 507, 665–683. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, H.; Zhou, L. Zero-carbon measure prioritization for sustainable freight transport using interval 2 tuple linguistic decision approaches. Appl. Soft Comput. 2023, 132, 109864. [Google Scholar] [CrossRef]
- Sun, B.; Ma, W.; Li, B.; Li, X. Three-way decisions approach to multiple attribute group decision making with linguistic information-based decision-theoretic rough fuzzy set. Int. J. Approx. Reason. 2018, 93, 424–442. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, D.; Tsang, E.C. Generalized dominance rough set models for the dominance intuitionistic fuzzy information systems. Inf. Sci. 2017, 378, 1–25. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, Q. Three-way decisions with decision-theoretic rough sets based on Pythagorean fuzzy covering. Soft Comput. 2020, 24, 18671–18688. [Google Scholar] [CrossRef]
- Zhang, S.P.; Sun, P.; Mi, J.S.; Feng, T. Belief function of Pythagorean fuzzy rough approximation space and its applications. Int. J. Approx. Reason. 2020, 119, 58–80. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, H.; Zhou, L.; Qin, Y.; Jia, L. Incomplete pythagorean fuzzy preference relation for subway station safety management during COVID-19 pandemic. Expert Syst. Appl. 2023, 216, 119445. [Google Scholar] [CrossRef]
- Mandal, P.; Ranadive, A.S. Decision-theoretic rough sets under Pythagorean fuzzy information. Int. J. Intell. Syst. 2018, 33, 818–835. [Google Scholar] [CrossRef]
- Liang, D.; Xu, Z.; Liu, D.; Wu, Y. Method for three-way decisions using ideal TOPSIS solutions at Pythagorean fuzzy information. Inf. Sci. 2018, 435, 282–295. [Google Scholar] [CrossRef]
- Zhang, S.P.; Sun, P.; Mi, J.S.; Feng, T. Three-way Decision Models of Cognitive Computing in Pythagorean Fuzzy Environments. Cogn. Comput. 2021, 14, 2153–2168. [Google Scholar]
- Wei, W.; Liang, J. Information fusion in rough set theory: An overview. Inf. Fusion 2019, 48, 107–118. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Pardasani, K.R.; Mardani, A.; Liao, H.; Streimikiene, D. A novel VIKOR approach based on entropy and divergence measures of Pythagorean fuzzy sets to evaluate renewable energy technologies in India. J. Clean. Prod. 2019, 238, 117936. [Google Scholar]
- Peng, X.; Yuan, H.; Yang, Y. Pythagorean fuzzy information measures and their applications. Int. J. Intell. Syst. 2017, 32, 991–1029. [Google Scholar] [CrossRef]
- Li, Z.; Lu, M. Some novel similarity and distance measures of pythagorean fuzzy sets and their applications. J. Intell. Fuzzy Syst. 2019, 37, 1781–1799. [Google Scholar]
- Firozja, M.A.; Agheli, B.; Jamkhaneh, E.B. A new similarity measure for Pythagorean fuzzy sets. Complex Intell. Syst. 2020, 6, 67–74. [Google Scholar]
- Li, P.; Wu, J.M.; Zhu, J.J. Stochastic multi-criteria decision-making methods based on new intuitionistic fuzzy distance. Syst. Eng.—Theory Pract. 2014, 36, 1517–1524. [Google Scholar]
- Zhang, X. A novel approach based on similarity measure for Pythagorean fuzzy multiple criteria group decision making. Int. J. Intell. Syst. 2016, 31, 593–611. [Google Scholar]
- Ejegwa, P.A. Distance and similarity measures for Pythagorean fuzzy sets. Granul. Comput. 2020, 5, 225–238. [Google Scholar]
- Peng, X. New similarity measure and distance measure for Pythagorean fuzzy set. Complex Intell. Syst. 2019, 5, 101–111. [Google Scholar] [CrossRef]

| Optimistic | Pessimistic | Neutral | ||||
|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | Cd | |
|---|---|---|---|---|---|---|
| x1 | (,) | (,) | (,) | (,) | (,) | (,) |
| x2 | (,) | (,) | (,) | (,) | (,) | (, ) |
| x3 | (,) | (,) | (,) | (,) | (,) | (,) |
| x4 | (,) | (,) | (,) | (,) | (,) | (,) |
| aP | (,) | (,) |
| aB | (,) | (,) |
| aN | (,) | (, ) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Hong, S. Emergency Evacuation Capacity Evaluation of High-Speed Railway Stations Based on Pythagorean Fuzzy Three-Way Decision Models. Appl. Sci. 2025, 15, 4087. https://doi.org/10.3390/app15084087
Wu S, Hong S. Emergency Evacuation Capacity Evaluation of High-Speed Railway Stations Based on Pythagorean Fuzzy Three-Way Decision Models. Applied Sciences. 2025; 15(8):4087. https://doi.org/10.3390/app15084087
Chicago/Turabian StyleWu, Shang, and Shaozhi Hong. 2025. "Emergency Evacuation Capacity Evaluation of High-Speed Railway Stations Based on Pythagorean Fuzzy Three-Way Decision Models" Applied Sciences 15, no. 8: 4087. https://doi.org/10.3390/app15084087
APA StyleWu, S., & Hong, S. (2025). Emergency Evacuation Capacity Evaluation of High-Speed Railway Stations Based on Pythagorean Fuzzy Three-Way Decision Models. Applied Sciences, 15(8), 4087. https://doi.org/10.3390/app15084087






