An Unsupervised Hybrid Approach for Detection of Damage with Autoencoder and One-Class Support Vector Machine
Abstract
1. Introduction
- Many studies use raw vibration signals as inputs to AE models. However, raw vibration data are high-dimensional and complex due to noise contamination, high-frequency content, and abrupt waveform variations [41]. These characteristics complicate feature extraction in unsupervised learning due to the lack of labeled guidance.
- The discrete nature of raw vibration data or their low-level features can degrade training efficiency and fitting accuracy [42]. To address this, deep AE architectures are often employed; however, they introduce a large number of parameters requiring optimization, which increases computational cost and the risk of overfitting.
- Many unsupervised learning-based methods rely on manually defined damage thresholds based on reconstruction loss. This subjectivity can lead to inconsistent damage detection outcomes.
- Most studies focus on detecting damage and assessing its severity in a comparative manner but do not explicitly address spatial localization, limiting their practical application in SHM.
- While many damage detection methods are validated solely through numerical examples, experimental validation on physical structures remains limited.
- The proposed methodology utilizes local TFs derived directly from response measurements in the frequency domain, reducing the computational burden associated with time-domain data. Additionally, it eliminates the need for preprocessing steps such as natural frequency and mode shape extraction, along with the errors introduced by frequency-domain feature selection.
- The proposed framework integrates an AE with an OC-SVM, requiring only baseline-state training data for damage detection. This eliminates the need for labeled datasets and supervised learning, making the approach suitable for monitoring civil engineering structures where damage-state data are either unavailable or difficult to obtain.
- A novel damage index is proposed, enabling the spatial localization of damage within the resolution of the sensor network.
- The methodology is validated using experimental data from a scaled model of an arch bridge, demonstrating its applicability in real-world scenarios beyond numerical simulations.
2. Research Methodology
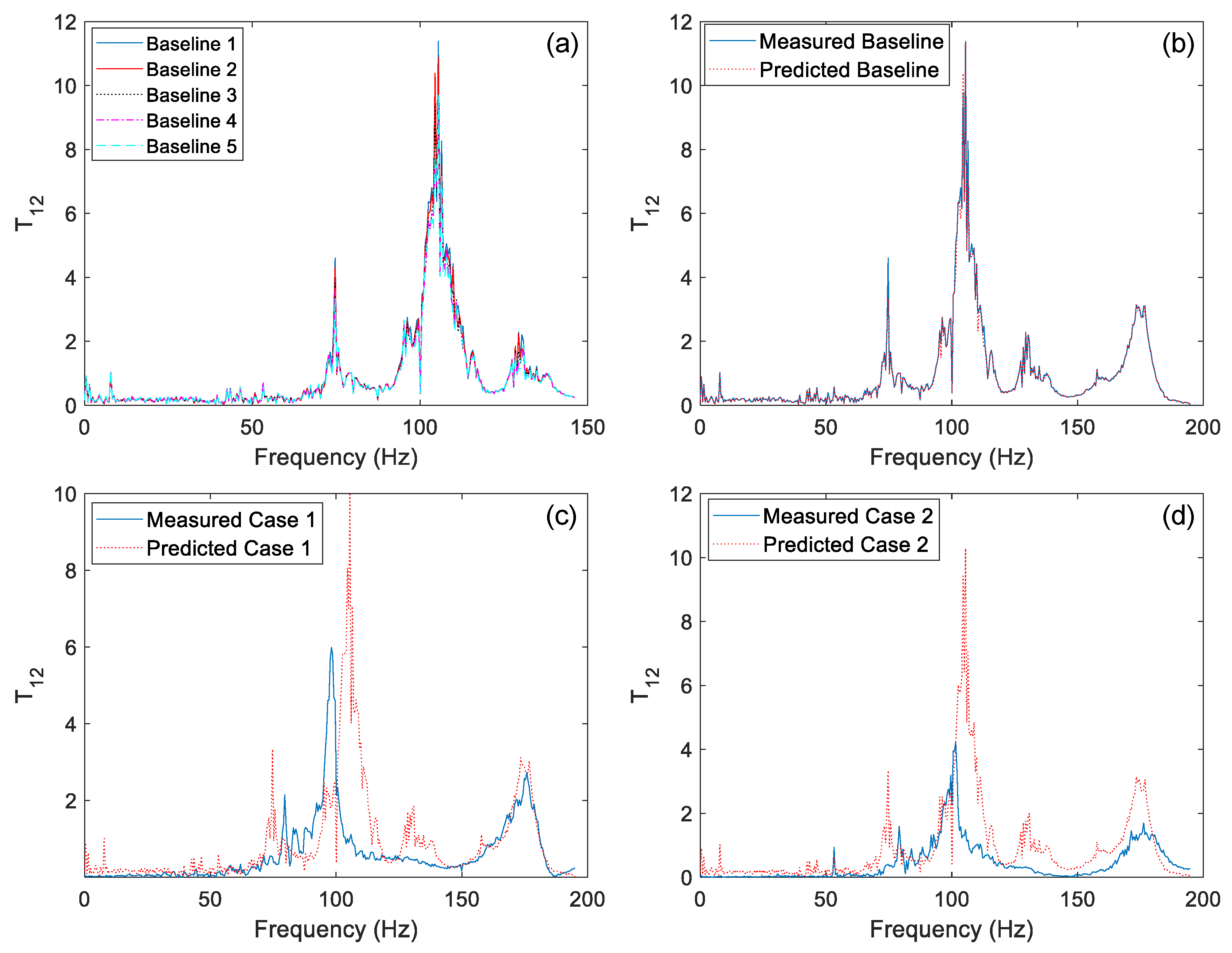
2.1. Transmissibility as Damage Sensitive Feature
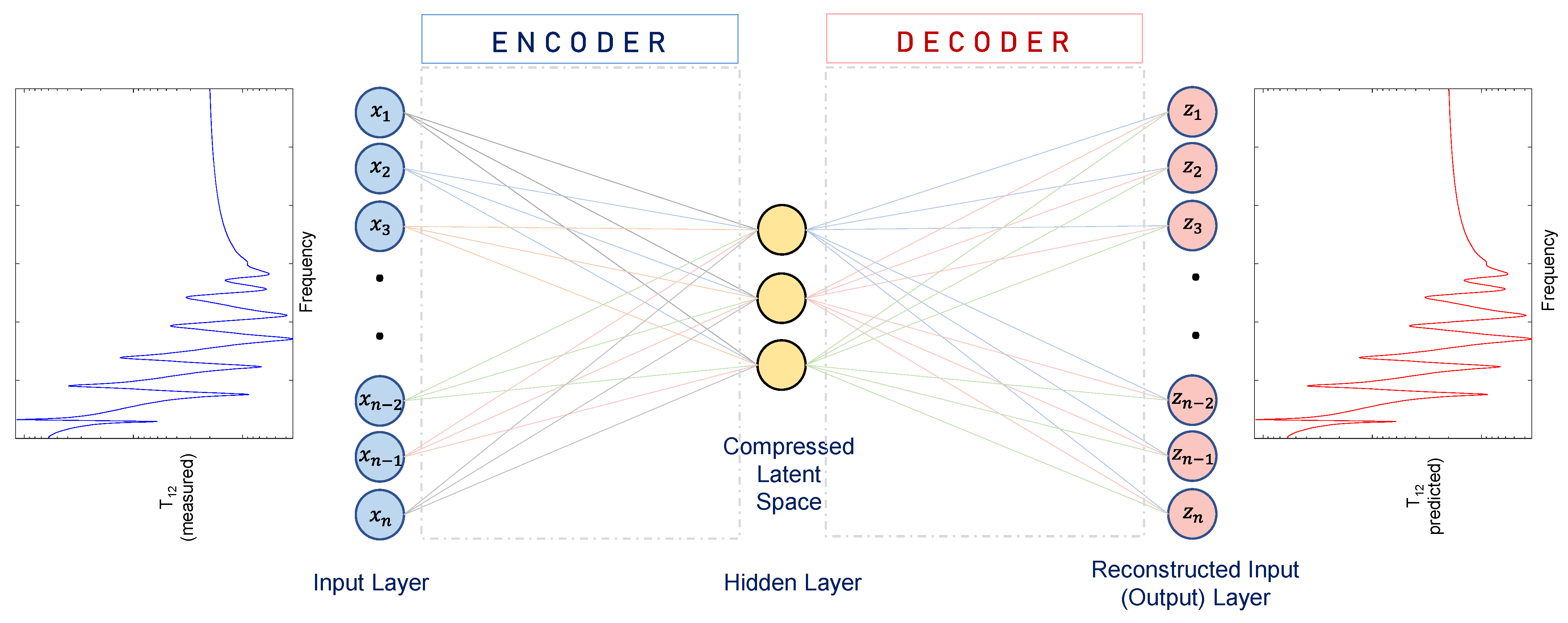
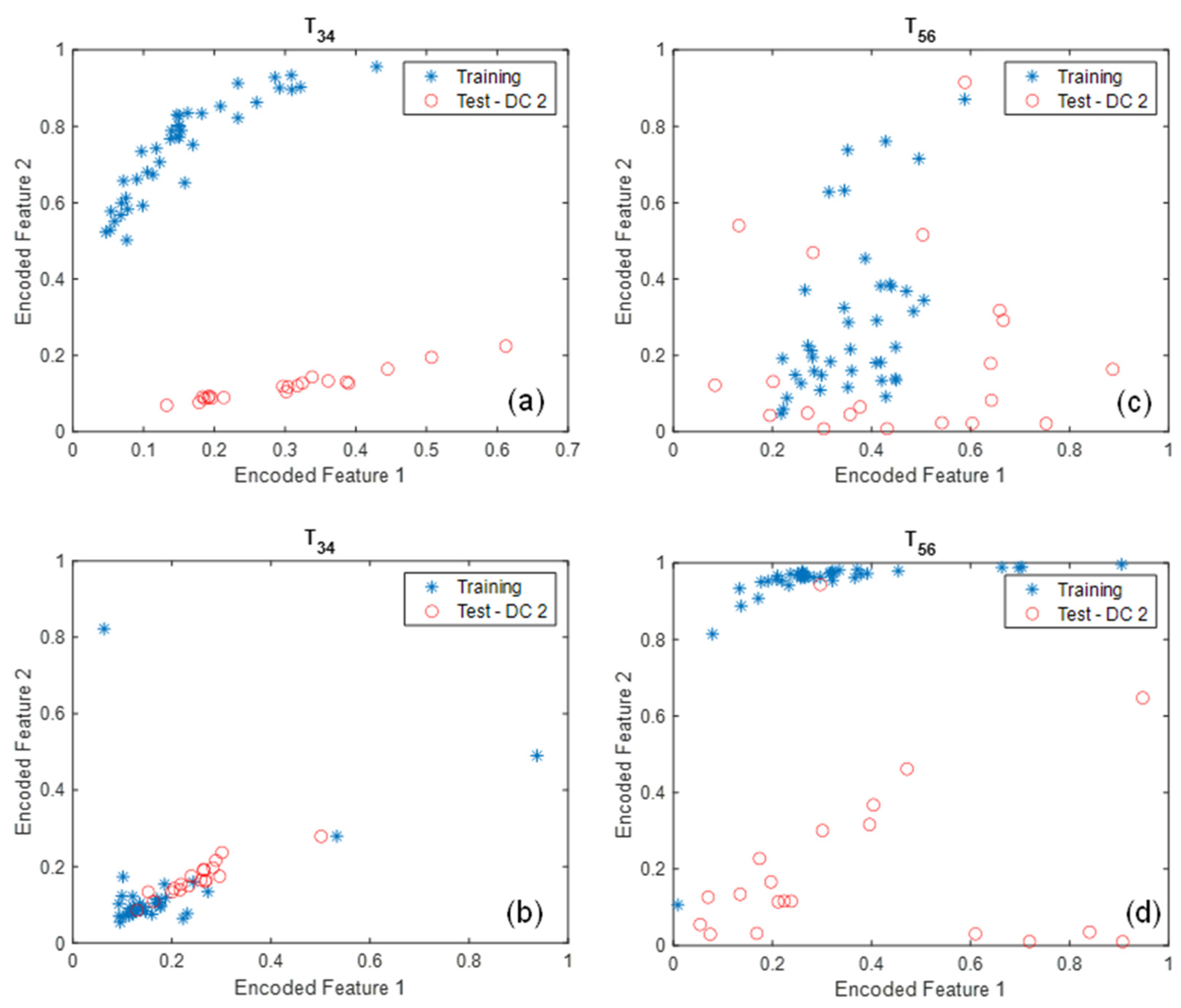
2.2. Autoencoder Architecture
2.3. One-Class Support Vector Machine (OC-SVM)
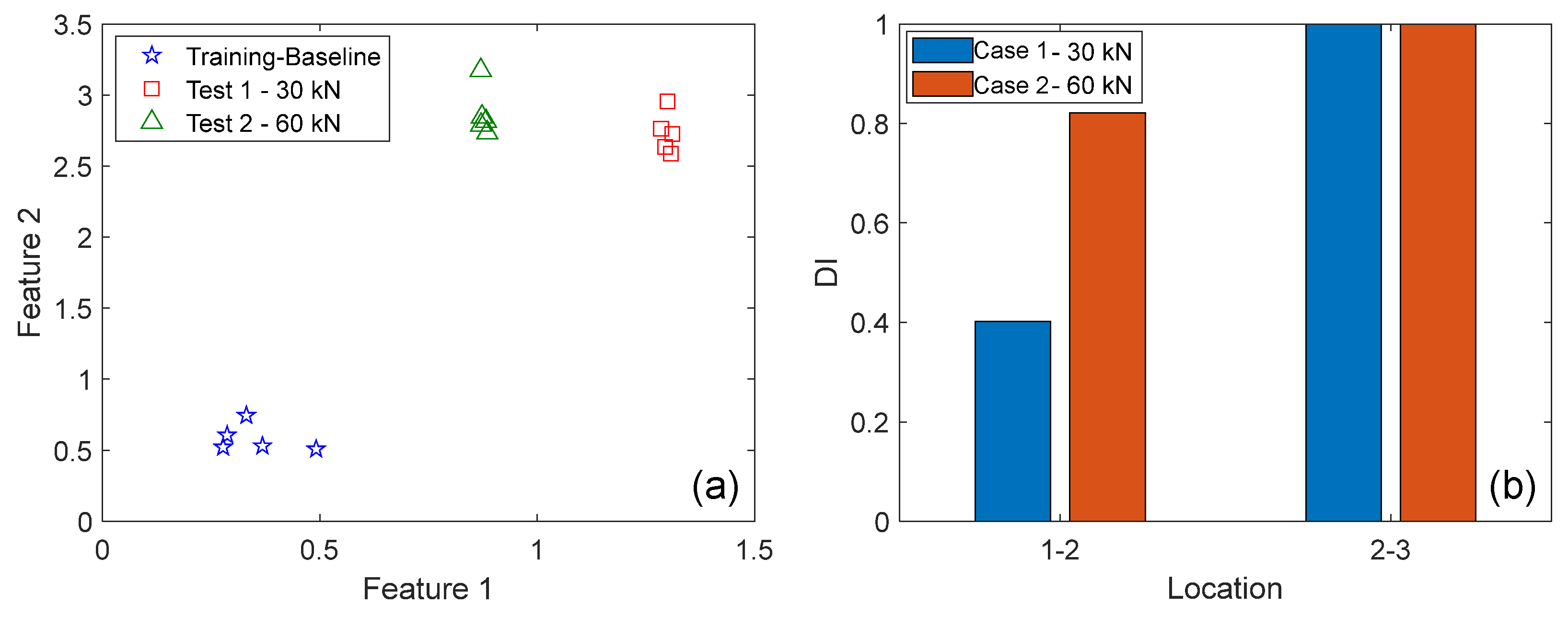
2.4. Damage Localization
3. Performance Evaluation
3.1. Simulation Study
3.2. Experimental Study: Masonry Arch Bridge Model
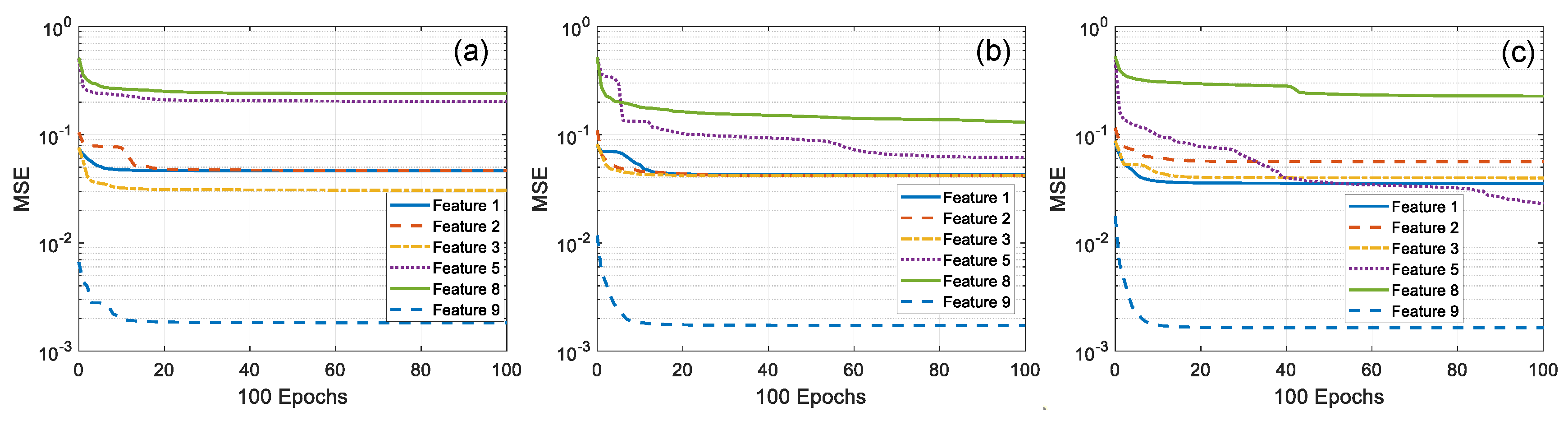
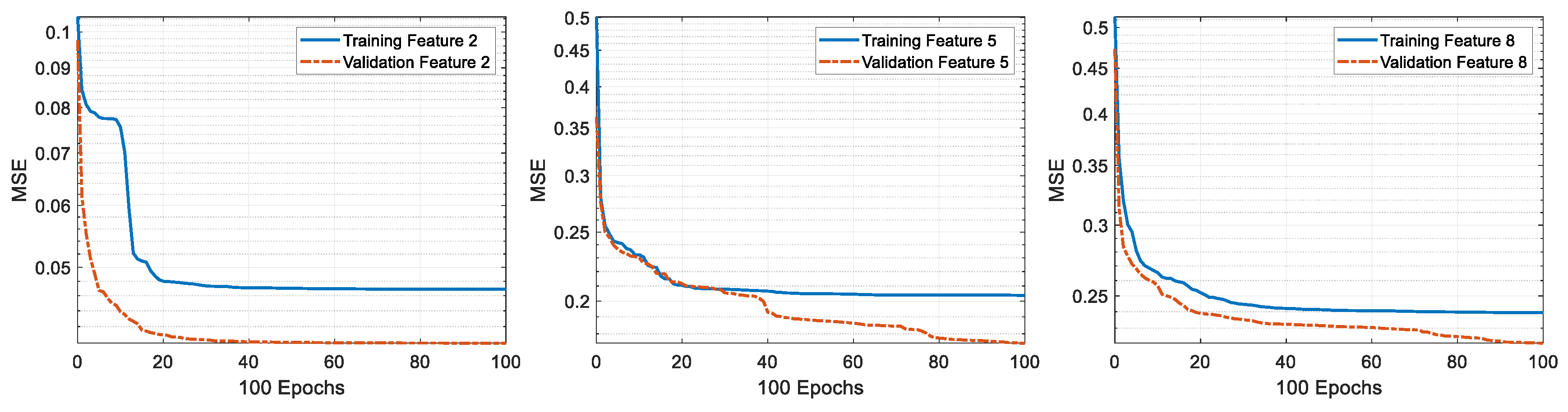
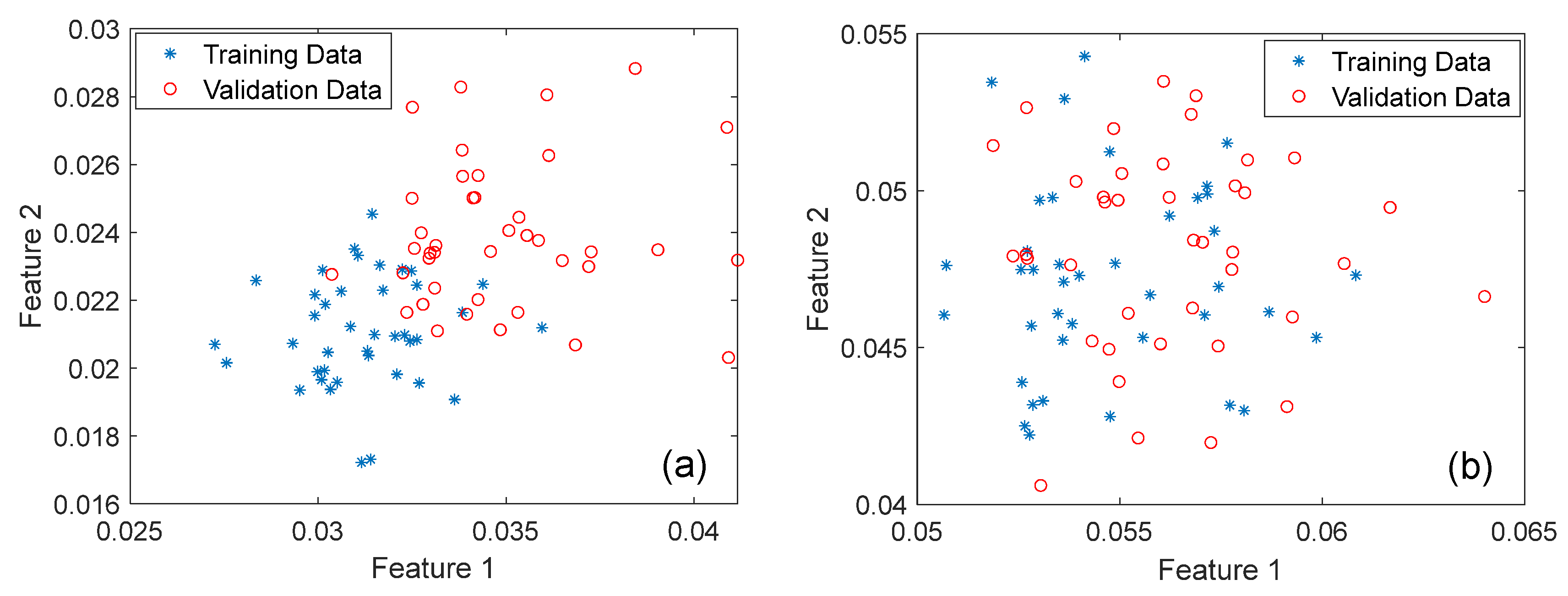
4. Discussion on Noise Effects, Model Selection, and Feature Sensitivity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SHM | Structural health monitoring |
| ANN | Artificial neural network |
| TF | Transmissibility function |
| OC-SVM | One-class support vector machine |
| PCA | Principal component analysis |
| MSE | Mean squared error |
| AE | Autoencoder |
| DSF | Damage sensitive feature |
References
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A Review of Vibration-Based Damage Detection in Civil Structures: From Traditional Methods to Machine Learning and Deep Learning Applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar]
- Rafiei, M.H.; Adeli, H. A Novel Unsupervised Deep Learning Model for Global and Local Health Condition Assessment of Structures. Eng. Struct. 2018, 156, 598–607. [Google Scholar]
- Entezami, A.; Shariatmadar, H.; Karamodin, A. Data-Driven Damage Diagnosis under Environmental and Operational Variability by Novel Statistical Pattern Recognition Methods. Struct. Health Monit. 2019, 18, 1416–1443. [Google Scholar]
- Zhang, H.; Gül, M.; Kostić, B. Eliminating Temperature Effects in Damage Detection for Civil Infrastructure Using Time Series Analysis and Autoassociative Neural Networks. J. Aerosp. Eng. 2019, 32, 04019001. [Google Scholar]
- Sarmadi, H.; Karamodin, A. A Novel Anomaly Detection Method Based on Adaptive Mahalanobis-Squared Distance and One-Class kNN Rule for Structural Health Monitoring under Environmental Effects. Mech. Syst. Signal Process. 2020, 140, 106495. [Google Scholar]
- Wang, Z.; Cha, Y.J. Unsupervised Machine and Deep Learning Methods for Structural Damage Detection: A Comparative Study. Eng. Rep. 2022, 7, e12551. [Google Scholar]
- Soofi, Y.J.; Bitaraf, M. Output-Only Entropy-Based Damage Detection Using Transmissibility Function. J. Civ. Struct. Health Monit. 2022, 12, 191–205. [Google Scholar]
- Liu, L.; Zhang, X.; Lei, Y. Data-Driven Identification of Structural Damage under Unknown Seismic Excitations Using the Energy Integrals of Strain Signals Transformed from Transmissibility Functions. J. Sound Vib. 2023, 546, 117490. [Google Scholar]
- Bank, D.; Koenigstein, N.; Giryes, R. Autoencoders. In Machine Learning for Data Science Handbook: Data Mining and Knowledge Discovery Handbook; Springer: Cham, Switzerland, 2023; pp. 353–374. [Google Scholar]
- Berahmand, K.; Daneshfar, F.; Salehi, E.S.; Li, Y.; Xu, Y. AEs and Their Applications in Machine Learning: A Survey. Artif. Intell. Rev. 2024, 57, 28. [Google Scholar]
- Pathirage, C.S.N.; Li, J.; Li, L.; Hao, H.; Liu, W.; Ni, P. Structural Damage Identification Based on AE Neural Networks and Deep Learning. Eng. Struct. 2018, 172, 13–28. [Google Scholar]
- Anaissi, A.; Zandavi, S.M. Multi-Objective AE for Fault Detection and Diagnosis in Higher-Order Data. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Lee, K.; Jeong, S.; Sim, S.H.; Shin, D.H. A Novelty Detection Approach for Tendons of Prestressed Concrete Bridges Based on a Convolutional AE and Acceleration Data. Sensors 2019, 19, 1633. [Google Scholar] [PubMed]
- Ma, X.; Lin, Y.; Nie, Z.; Ma, H. Structural Damage Identification Based on Unsupervised Feature-Extraction via Variational AE. Measurement 2020, 160, 107811. [Google Scholar]
- Yan, X.; Liu, Y.; Jia, M. Health Condition Identification for Rolling Bearing Using a Multi-Domain Indicator-Based Optimized Stacked Denoising AE. Struct. Health Monit. 2020, 19, 1602–1626. [Google Scholar]
- Rastin, Z.; Ghodrati Amiri, G.; Darvishan, E. Unsupervised Structural Damage Detection Technique Based on a Deep Convolutional AE. Shock Vib. 2021, 2021, 6658575. [Google Scholar]
- Wang, Z.; Cha, Y.J. Unsupervised Deep Learning Approach Using a Deep AE with a One-Class Support Vector Machine to Detect Damage. Struct. Health Monit. 2021, 20, 406–425. [Google Scholar]
- Lee, K.; Jeong, S.; Sim, S.H.; Shin, D.H. Field Experiment on a PSC-I Bridge for Convolutional AE-Based Damage Detection. Struct. Health Monit. 2021, 20, 1627–1643. [Google Scholar]
- Jiang, K.; Han, Q.; Du, X.; Ni, P. A Decentralized Unsupervised Structural Condition Diagnosis Approach Using Deep AEs. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 711–732. [Google Scholar]
- Silva, M.F.; Santos, A.; Santos, R.; Figueiredo, E.; Costa, J.C.W.A. Damage-sensitive feature extraction with stacked AEs for unsupervised damage detection. Struct. Control Health Monit. 2021, 28, e2714. [Google Scholar]
- Shang, Z.; Sun, L.; Xia, Y.; Zhang, W. Vibration-based damage detection for bridges by deep convolutional denoising AE. Struct. Health Monit. 2021, 20, 1880–1903. [Google Scholar]
- Zhang, Y.; Xie, X.; Li, H.; Zhou, B. An unsupervised tunnel damage identification method based on convolutional variational auto-encoder and wavelet packet analysis. Sensors 2022, 22, 2412. [Google Scholar] [CrossRef]
- Spínola Neto, M.; Finotti, R.; Barbosa, F.; Cury, A. Structural Damage Identification Using AEs: A Comparative Study. Buildings 2024, 14, 2014. [Google Scholar]
- Römgens, N.; Abbassi, A.; Jonscher, C.; Grießmann, T.; Rolfes, R. On using AEs with non-standardized time series data for damage localization. Eng. Struct. 2024, 303, 117570. [Google Scholar]
- Li, Z.; Lin, W.; Zhang, Y. Real-time drive-by bridge damage detection using deep auto-encoder. Structures 2023, 47, 1167–1181. [Google Scholar]
- Li, L.; Morgantini, M.; Betti, R. Structural damage assessment through a new generalized AE with features in the quefrency domain. Mech. Syst. Signal Process. 2023, 184, 109713. [Google Scholar] [CrossRef]
- Lin, J.; Ma, H. Structural damage detection based on the correlation of variational AE neural networks using limited sensors. Sensors 2024, 24, 2616. [Google Scholar]
- Li, S.; Cao, Y.; Gdoutos, E.E.; Tao, M.; Alkayem, N.F.; Avci, O.; Cao, M. Intelligent framework for unsupervised damage detection in bridges using deep convolutional AE with wavelet transmissibility pattern spectra. Mech. Syst. Signal Process. 2024, 220, 111653. [Google Scholar]
- Resende, L.V.; Finotti, R.P.; Barbosa, F.S.; Cury, A.A. Structural damage detection with autoencoding neural networks. In Proceedings of the XLIII Ibero-Latin American Congress on Computational Methods in Engineering, Foz do Iguacu, Brazil, 21–25 November 2022; Volume 4, p. 4. [Google Scholar]
- Nicoletti, V.; Quarchioni, S.; Amico, L.; Gara, F. Assessment of different optimal sensor placement methods for dynamic monitoring of civil structures and infrastructures. Struct. Infrastruct. Eng. 2024, 1–16. [Google Scholar] [CrossRef]
- Mendler, A.; Döhler, M.; Ventura, C.E. Sensor placement with optimal damage detectability for statistical damage detection. Mech. Syst. Signal Process. 2022, 170, 108767. [Google Scholar]
- Wang, Y.; Chen, Y.; Yao, Y.; Ou, J. Advancements in Optimal Sensor Placement for Enhanced Structural Health Monitoring: Current Insights and Future Prospects. Buildings 2023, 13, 3129. [Google Scholar] [CrossRef]
- Sun, Z.; Mahmoodian, M.; Sidiq, A.; Jayasinghe, S.; Shahrivar, F.; Setunge, S. Optimal Sensor Placement for Structural Health Monitoring: A Comprehensive Review. J. Sens. Actuator Netw. 2025, 14, 22. [Google Scholar] [CrossRef]
- Chesné, S.; Deraemaeker, A. Damage localization using transmissibility functions: A critical review. Mech. Syst. Signal Process. 2013, 38, 569–588. [Google Scholar] [CrossRef]
- Li, J.; Hao, H.; Lo, J.V. Structural damage identification with power spectral density transmissibility: Numerical and experimental studies. Smart Struct. Syst. 2015, 15, 15–40. [Google Scholar] [CrossRef]
- Zhu, D.; Yi, X.; Wang, Y. A local excitation and measurement approach for decentralized damage detection using transmissibility functions. Struct. Control Health Monit. 2016, 23, 487–502. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Maia, N.M.; Abdel Wahab, M. Damage detection using transmissibility compressed by principal component analysis enhanced with distance measure. J. Vib. Control 2018, 24, 2001–2019. [Google Scholar] [CrossRef]
- Yan, W.J.; Zhao, M.Y.; Sun, Q.; Ren, W.X. Transmissibility-based system identification for structural health monitoring: Fundamentals, approaches, and applications. Mech. Syst. Signal Process. 2019, 117, 453–482. [Google Scholar] [CrossRef]
- Liu, T.; Xu, H.; Ragulskis, M.; Cao, M.; Ostachowicz, W. A data-driven damage identification framework based on transmissibility function datasets and one-dimensional convolutional neural networks: Verification on a structural health monitoring benchmark structure. Sensors 2020, 20, 1059. [Google Scholar] [CrossRef]
- Lei, Y.; Zhang, Y.; Mi, J.; Liu, W.; Liu, L. Detecting structural damage under unknown seismic excitation by deep convolutional neural network with wavelet-based transmissibility data. Struct. Health Monit. 2021, 20, 1583–1596. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Salar, M.; De Michele, C.; Arslan, A.N. A novel data-driven method for structural health monitoring under ambient vibration and high-dimensional features by robust multidimensional scaling. Struct. Health Monit. 2021, 20, 2758–2777. [Google Scholar] [CrossRef]
- Ozdagli, A.I.; Koutsoukos, X. Machine learning-based novelty detection using modal analysis. Comput. Aided Civ. Inf. Eng. 2019, 34, 1119–1140. [Google Scholar] [CrossRef]
- Maia, N.M.M.; Urgueira, A.P.V.; Almeida, R.A.B. An overview of the transmissibility concept and its application to structural damage detection. In Topics in Modal Analysis I, Volume 5, Conference Proceedings of the Society for Experimental Mechanics Series; Allemang, R., De Clerck, J., Niezrecki, C., Blough, J., Eds.; Springer: New York, NY, USA, 2012; pp. 317–330. [Google Scholar] [CrossRef]
- Hejazi, M.; Singh, Y.P. One-class support vector machines approach to anomaly detection. Appl. Artif. Intell. 2013, 27, 351–366. [Google Scholar] [CrossRef]
- Schölkopf, B.; Williamson, R.C.; Smola, A.; Shawe-Taylor, J.; Platt, J. Support vector method for novelty detection. In Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2000; pp. 582–588. [Google Scholar]
- Mentese, V.G.; Gunes, O.; Celik, O.C.; Gunes, B.; Avsin, A.; Yaz, M. Experimental collapse investigation and nonlinear modeling of a single-span stone masonry arch bridge. Eng. Fail. Anal. 2023, 152, 107520. [Google Scholar] [CrossRef]





| Natural Frequency (Hz) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | Mode 7 | Mode 8 | Mode 9 | Mode 10 | |
| Baseline | 1.45 | 3.75 | 6.07 | 8.22 | 10.08 | 11.96 | 13.24 | 14.40 | 15.05 | 16.25 |
| D. Case 1 | 1.42 | 3.67 | 6.03 | 8.20 | 10.07 | 11.71 | 13.02 | 14.17 | 15.02 | 16.25 |
| D. Case 2 | 1.42 | 3.72 | 6.07 | 8.08 | 9.88 | 11.89 | 13.18 | 13.99 | 14.98 | 16.24 |
| D. Case 3 | 1.43 | 3.75 | 6.00 | 8.02 | 10.08 | 11.63 | 13.17 | 14.21 | 14.92 | 16.23 |
| D. Case 4 | 1.43 | 3.73 | 5.94 | 8.22 | 9.84 | 11.96 | 12.97 | 14.40 | 14.83 | 16.15 |
| D. Case 5 | 1.43 | 3.70 | 6.02 | 8.12 | 10.06 | 11.76 | 13.18 | 14.26 | 14.87 | 15.95 |
| D. Case 6 | 1.44 | 3.68 | 6.07 | 8.08 | 9.92 | 11.96 | 13.04 | 14.30 | 15.05 | 15.80 |
| D. Case 7 | 1.44 | 3.68 | 6.00 | 8.21 | 9.92 | 11.76 | 13.07 | 14.40 | 14.87 | 15.96 |
| D. Case 8 | 1.45 | 3.70 | 5.89 | 8.11 | 10.03 | 11.96 | 13.15 | 14.17 | 14.80 | 16.15 |
| D. Case 9 | 1.45 | 3.73 | 5.98 | 8.10 | 9.91 | 11.80 | 12.95 | 14.23 | 14.90 | 16.21 |
| Percent change (%) | ||||||||||
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | Mode 7 | Mode 8 | Mode 9 | Mode 10 | |
| D. Case 1 | 2.44 | 2.07 | 0.74 | 0.24 | 0.09 | 2.06 | 1.60 | 1.61 | 0.21 | 0.01 |
| D. Case 2 | 2.18 | 0.82 | 0.02 | 1.72 | 1.98 | 0.55 | 0.43 | 2.84 | 0.49 | 0.03 |
| D. Case 3 | 1.80 | 0.02 | 1.25 | 2.45 | 0.02 | 2.71 | 0.49 | 1.32 | 0.85 | 0.13 |
| D. Case 4 | 1.68 | 0.57 | 2.25 | 0.01 | 2.42 | 0.00 | 2.04 | 0.00 | 1.45 | 0.62 |
| D. Case 5 | 1.27 | 1.45 | 0.85 | 1.21 | 0.22 | 1.66 | 0.40 | 0.97 | 1.20 | 1.86 |
| D. Case 6 | 0.84 | 2.00 | 0.02 | 1.67 | 1.63 | 0.00 | 1.45 | 0.66 | 0.00 | 2.78 |
| D. Case 7 | 0.46 | 1.86 | 1.27 | 0.05 | 1.58 | 1.64 | 1.22 | 0.01 | 1.21 | 1.77 |
| D. Case 8 | 0.24 | 1.45 | 3.10 | 1.29 | 0.48 | 0.00 | 0.65 | 1.57 | 1.67 | 0.62 |
| D. Case 9 | 0.06 | 0.45 | 1.55 | 1.40 | 1.70 | 1.36 | 2.20 | 1.13 | 1.01 | 0.21 |
| PCA | AE | |||||||
|---|---|---|---|---|---|---|---|---|
| Predicted Healthy | Predicted Damaged | Total | Metric: Recall (%) | Predicted Healthy | Predicted Damaged | Total | Metric: Recall (%) | |
| True Healthy | 18 | 22 | 40 | 45 | 38 | 2 | 40 | 95 |
| True Damaged | 0 | 180 | 180 | 100 | 0 | 180 | 180 | 100 |
| Predictions | 18 | 202 | 220 | 38 | 182 | 220 | ||
| Metric (%) | Precision: 100.0 | Precision: 89.1 | Accuracy: 90.0 | Precision: 100.0 | Precision: 98.9 | Accuracy: 99.1 | ||
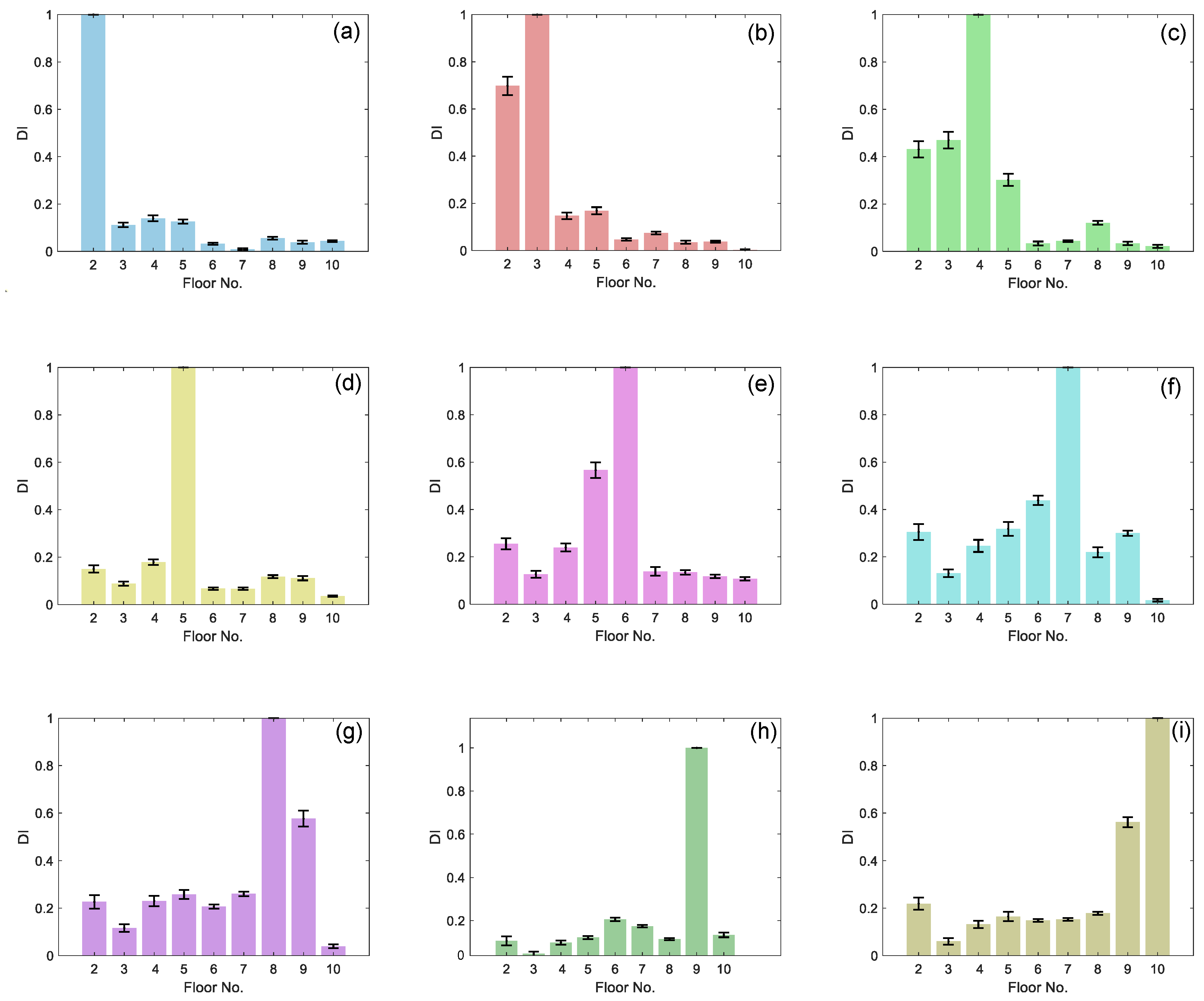
| Damage Scenario | Damaged Floor | Predicted Damage Location PCA | Predicted Damage Location AE | ||
|---|---|---|---|---|---|
| Accuracy | Accuracy | ||||
| D. Case 1 | 2 | 2 (☑) | 20/20 | 2 (☑) | 20/20 |
| D. Case 2 | 3 | 4 (⊠) | 0/20 | 3 (☑) | 20/20 |
| D. Case 3 | 4 | 5 (⊠) | 0/20 | 4 (☑) | 20/20 |
| D. Case 4 | 5 | 5 (☑) | 20/20 | 5 (☑) | 20/20 |
| D. Case 5 | 6 | 7 (⊠) | 0/20 | 6 (☑) | 20/20 |
| D. Case 6 | 7 | 8 (⊠) | 0/20 | 7 (☑) | 20/20 |
| D. Case 7 | 8 | 9 (⊠) | 0/20 | 8 (☑) | 20/20 |
| D. Case 8 | 9 | 9 (☑) | 20/20 | 9 (☑) | 20/20 |
| D. Case 9 | 10 | 10 (☑) | 20/20 | 10 (☑) | 20/20 |
| PCA | AE | ||||||
|---|---|---|---|---|---|---|---|
| Predicted | Predicted | ||||||
| Healthy | Damaged | Total | Healthy | Damaged | Total | ||
| True | Healthy | 70% | 30% | 40 | 75% | 25% | 40 |
| Damage Case 1 | 35% | 65% | 20 | 5% | 95% | 20 | |
| Damage Case 2 | 20% | 80% | 20 | 5% | 95% | 20 | |
| Damage Case 3 | 100% | 0% | 20 | 5% | 95% | 20 | |
| Damage Case 4 | 65% | 35% | 20 | 5% | 95% | 20 | |
| Damage Case 5 | 50% | 50% | 20 | 45% | 55% | 20 | |
| Damage Case 6 | 75% | 25% | 20 | 5% | 95% | 20 | |
| Damage Case 7 | 60% | 40% | 20 | 15% | 85% | 20 | |
| Damage Case 8 | 10% | 90% | 20 | 5% | 95% | 20 | |
| Damage Case 9 | 5% | 95% | 20 | 0% | 100% | 20 | |
| iForest Predicted | OC-SVM Predicted | ||||
|---|---|---|---|---|---|
| Healthy | Damaged | Healthy | Damaged | ||
| True | Healthy | 95% | 5% | 75% | 25% |
| Damage Case 1 | 5% | 95% | 5% | 95% | |
| Damage Case 2 | 10% | 90% | 5% | 95% | |
| Damage Case 3 | 30% | 70% | 5% | 95% | |
| Damage Case 4 | 55% | 45% | 5% | 95% | |
| Damage Case 5 | 75% | 25% | 45% | 55% | |
| Damage Case 6 | 75% | 25% | 5% | 95% | |
| Damage Case 7 | 75% | 25% | 15% | 85% | |
| Damage Case 8 | 55% | 45% | 5% | 95% | |
| Damage Case 9 | 0% | 100% | 0% | 100% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunes, B.; Gunes, O. An Unsupervised Hybrid Approach for Detection of Damage with Autoencoder and One-Class Support Vector Machine. Appl. Sci. 2025, 15, 4098. https://doi.org/10.3390/app15084098
Gunes B, Gunes O. An Unsupervised Hybrid Approach for Detection of Damage with Autoencoder and One-Class Support Vector Machine. Applied Sciences. 2025; 15(8):4098. https://doi.org/10.3390/app15084098
Chicago/Turabian StyleGunes, Burcu, and Oguz Gunes. 2025. "An Unsupervised Hybrid Approach for Detection of Damage with Autoencoder and One-Class Support Vector Machine" Applied Sciences 15, no. 8: 4098. https://doi.org/10.3390/app15084098
APA StyleGunes, B., & Gunes, O. (2025). An Unsupervised Hybrid Approach for Detection of Damage with Autoencoder and One-Class Support Vector Machine. Applied Sciences, 15(8), 4098. https://doi.org/10.3390/app15084098








