Analyzing Transportation Network Vulnerability to Critical-Link Attacks Through Topology Changes and Traffic Volume Assessment
Abstract
:1. Introduction
- The proposed method identifies the network vulnerability under worst-case scenarios by targeting critical components derived from network topological parameters. To systematically characterize network performance changes under critical-link attacks, this study employs the complementary cumulative distribution function (CCDF) to analyze the empirical distribution of each topological parameter. The CCDF, which has been rarely utilized in previous studies, provides a novel approach for assessing transportation network performance.
- This study proposes a straightforward modeling framework that uses topological parameters to assess the impact of critical-link attacks on traffic flow changes through multiple linear regression. To analyze traffic flow changes under disruptions, this study integrates critical-link attacks into the model and uses the CCDF to assess the network’s response to each attack. The findings reveal that disruptions to certain road segments cause significantly greater reductions in traffic volume than other critical-link attacks.
- The proposed method was applied to a road network in Sri Lanka’s CMC area, serving as a case study to demonstrate its effectiveness in assessing network vulnerability and identifying critical links that influence traffic flow changes and explore pre- and post-disaster transportation planning. This analysis provides valuable insights, particularly within an Asian context. This study also highlights key findings and policy implications relevant to other Asian cities with similar characteristics, extending its applicability beyond Colombo to urban transportation planning in comparable settings.
2. Analytical Framework
2.1. Topological Parameters and Their Characteristics
2.1.1. Street Connectivity (SC)
2.1.2. Betweenness Centrality (BC)
2.1.3. Closeness Centrality (CC)
2.1.4. Eigenvector Centrality (EC)
2.2. Topological Transformation of Geometric Transportation Network
2.3. Critical-Link Attack Method
3. Materials and Methodology
3.1. Data Description and Sources
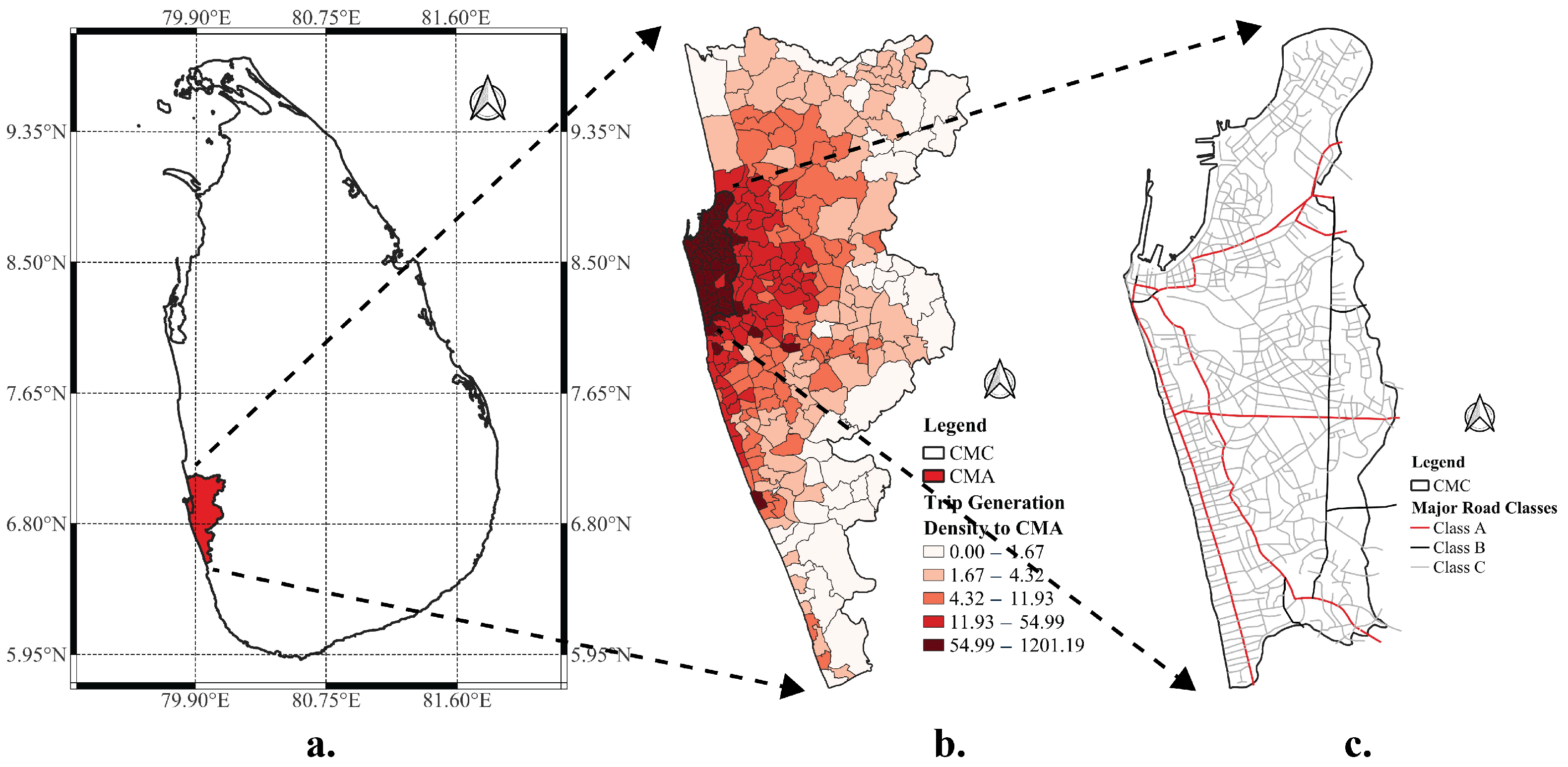
3.2. Case Study Area
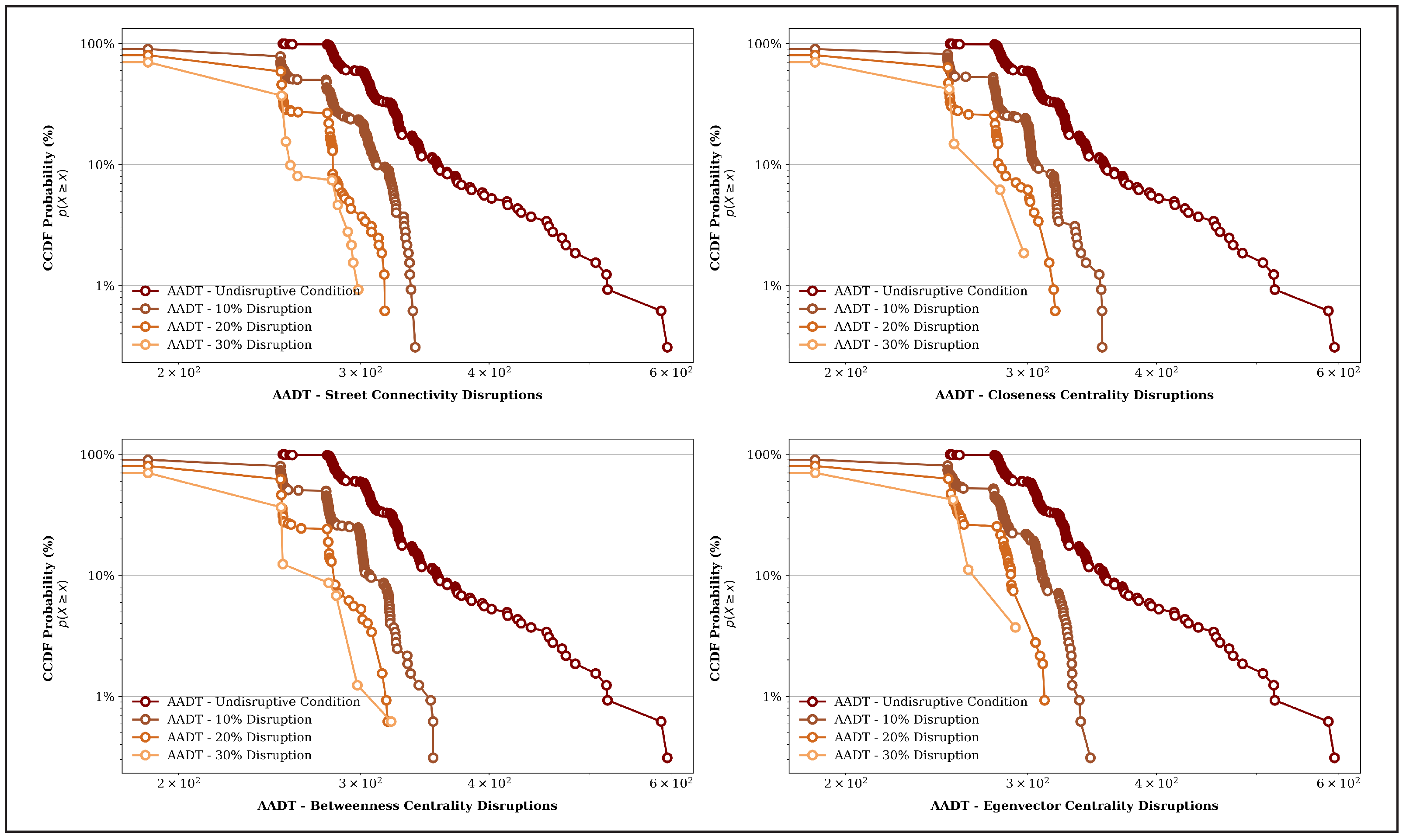
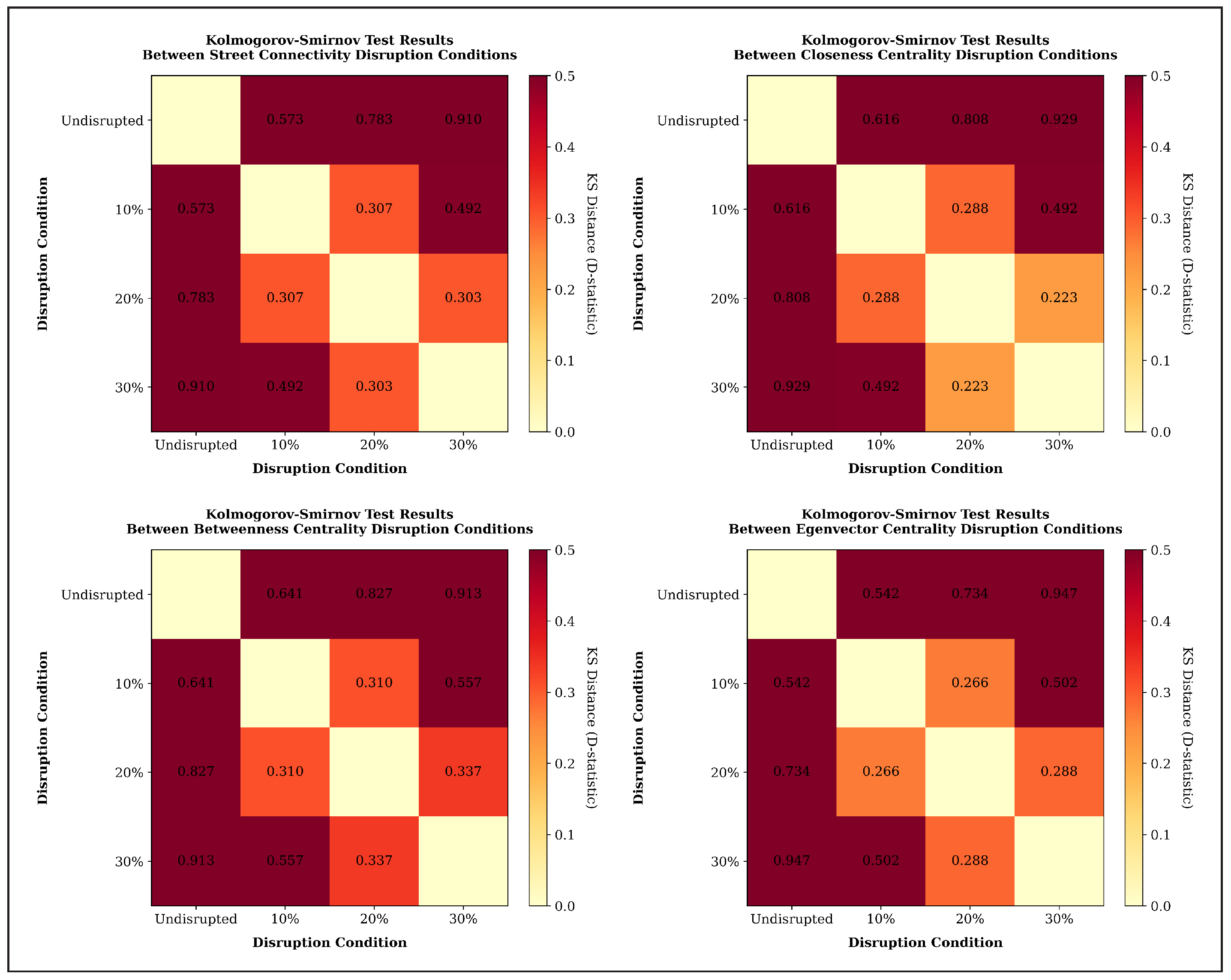
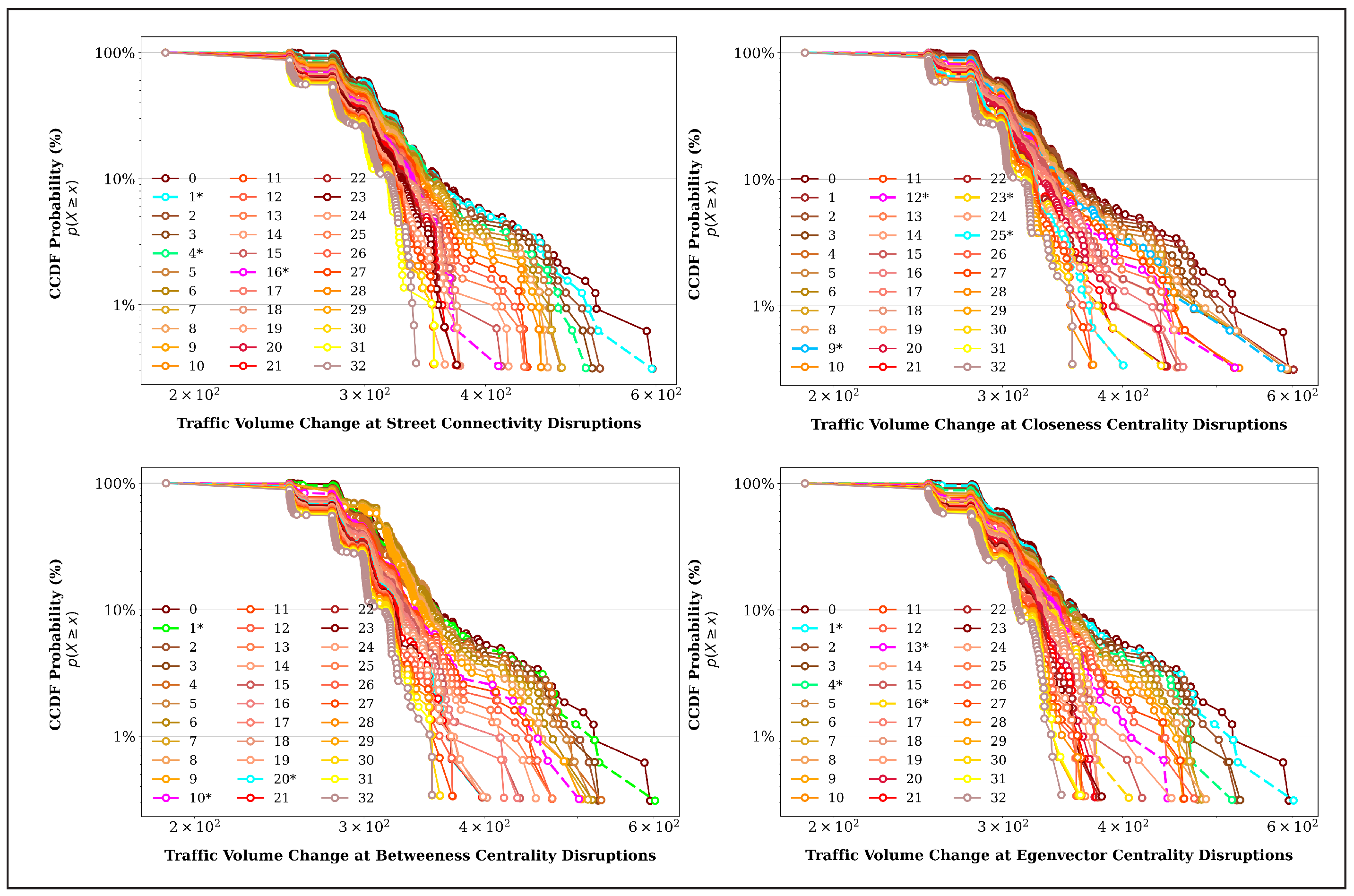
3.3. Applying CCDF to Assess Transportation Network Performance
3.4. Development of a Modeling Framework to Estimate Traffic Volume
4. Analysis and Discussion
4.1. Identifying the Network Performance Changes Under Critical-Link Attacks
4.2. Capture the Traffic Flow Change Under the Critical-Link Attacks
5. Conclusions and Future Work
Limitations and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCDF | Complementary Cumulative Distribution Function; |
| CDF | Cumulative Distribution Function; |
| CMC | Colombo Municipal Council; |
| UE | User Equilibrium; |
| SC | Street Connectivity; |
| BC | Betweenness Centrality; |
| CC | Closeness Centrality; |
| EC | Eigenvector Centrality; |
| TS | Total Segment; |
| AS | Attacked Segment; |
| CMA | Colombo Metropolitan Area; |
| GDP | Gross Domestic Product; |
| JICA | Japan International Cooperation Agency; |
| DS | Divisional Secretariat; |
| SLSD | Survey Department of Sri Lanka; |
| AADT | Annual Average Daily Traffic; |
| CDF | Cumulative Distribution Function; |
| VIF | Variance Inflation Factor; |
| MAPE | Mean Absolute Percentage Error. |
References
- Taylor, M.A.; D’Este, G.M. Transport network vulnerability: A method for diagnosis of critical locations in transport infrastructure systems. In Critical Infrastructure: Reliability and Vulnerability; Springer: Berlin/Heidelberg, Germany, 2007; pp. 9–30. [Google Scholar] [CrossRef]
- Bell, M.G.; Kanturska, U.; Schmöcker, J.D.; Fonzone, A. Attacker–defender models and road network vulnerability. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2008, 366, 1893–1906. [Google Scholar] [CrossRef] [PubMed]
- Derrible, S.; Kennedy, C. The complexity and robustness of metro networks. Phys. Stat. Mech. Its Appl. 2010, 389, 3678–3691. [Google Scholar] [CrossRef]
- Taylor, M. Vulnerability Analysis for Transportation Networks; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar] [CrossRef]
- Mattsson, L.G.; Jenelius, E. Vulnerability and resilience of transport systems—A discussion of recent research. Transp. Res. Part Policy Pract. 2015, 81, 16–34. [Google Scholar] [CrossRef]
- Starita, S.; Scaparra, M.P. Assessing road network vulnerability: A user equilibrium interdiction model. J. Oper. Res. Soc. 2021, 72, 1648–1663. [Google Scholar] [CrossRef]
- Wisetjindawat, W.; Wilson, R.E.; Bullock, S.; De Villafranca, A.E.M. Modeling the impact of spatial correlations of road failures on travel times during adverse weather conditions. Transp. Res. Rec. 2019, 2673, 157–168. [Google Scholar] [CrossRef]
- Casali, Y.; Heinimann, H.R. A topological characterization of flooding impacts on the Zurich road network. PLoS ONE 2019, 14, e0220338. [Google Scholar] [CrossRef]
- Kermanshah, A.; Derrible, S. A geographical and multi-criteria vulnerability assessment of transportation networks against extreme earthquakes. Reliab. Eng. Syst. Saf. 2016, 153, 39–49. [Google Scholar] [CrossRef]
- Postance, B.; Hillier, J.; Dijkstra, T.; Dixon, N. Extending natural hazard impacts: An assessment of landslide disruptions on a national road transportation network. Environ. Res. Lett. 2017, 12, 014010. [Google Scholar] [CrossRef]
- Wisetjindawat, W.; Kermanshah, A.; Derrible, S.; Fujita, M. Stochastic modeling of road system performance during multihazard events: Flash floods and earthquakes. J. Infrastruct. Syst. 2017, 23, 04017031. [Google Scholar] [CrossRef]
- Lu, Q.C.; Peng, Z.R.; Zhang, J. Identification and prioritization of critical transportation infrastructure: Case study of coastal flooding. J. Transp. Eng. 2015, 141, 04014082. [Google Scholar] [CrossRef]
- Abenayake, C.; Jayasinghe, A.; Kalpana, H.N.; Wijegunarathna, E.E.; Mahanama, P. An innovative approach to assess the impact of urban flooding: Modeling transportation system failure due to urban flooding. Appl. Geogr. 2022, 147, 102772. [Google Scholar] [CrossRef]
- Jenelius, E.; Mattsson, L.G. Road network vulnerability analysis of area-covering disruptions: A grid-based approach with case study. Transp. Res. Part Policy Pract. 2012, 46, 746–760. [Google Scholar] [CrossRef]
- Hosseini Nourzad, S.H.; Pradhan, A. Vulnerability of infrastructure systems: Macroscopic analysis of critical disruptions on road networks. J. Infrastruct. Syst. 2016, 22, 04015014. [Google Scholar] [CrossRef]
- Jenelius, E.; Mattsson, L.G. Road network vulnerability analysis: Conceptualization, implementation and application. Comput. Environ. Urban Syst. 2015, 49, 136–147. [Google Scholar] [CrossRef]
- Jenelius, E.; Petersen, T.; Mattsson, L.G. Importance and exposure in road network vulnerability analysis. Transp. Res. Part Policy Pract. 2006, 40, 537–560. [Google Scholar] [CrossRef]
- Gao, L.; Liu, X.; Liu, Y.; Wang, P.; Deng, M.; Zhu, Q.; Li, H. Measuring road network topology vulnerability by Ricci curvature. Phys. Stat. Mech. Its Appl. 2019, 527, 121071. [Google Scholar] [CrossRef]
- Hackl, J.; Adey, B.T. Estimation of traffic flow changes using networks in networks approaches. Appl. Netw. Sci. 2019, 4, 28. [Google Scholar] [CrossRef]
- Lin, C.; Yu, Y.; Wu, D.; Gong, B. Traffic flow catastrophe border identification for urban high-density area based on cusp catastrophe theory: A case study under sudden fire disaster. Appl. Sci. 2020, 10, 3197. [Google Scholar] [CrossRef]
- Jiang, B.; Huang, J.T. A new approach to detecting and designing living structure of urban environments. Comput. Environ. Urban Syst. 2021, 88, 101646. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, J. Characteristics, Impacts and trends of urban transportation. Encyclopedia 2022, 2, 1168–1182. [Google Scholar] [CrossRef]
- Wan, C.; Yang, Z.; Zhang, D.; Yan, X.; Fan, S. Resilience in transportation systems: A systematic review and future directions. Transp. Rev. 2018, 38, 479–498. [Google Scholar] [CrossRef]
- Pucher, J. The urban Transport Crisis in Emerging Economies; Taylor & Francis: Oxfordshire, UK, 2018. [Google Scholar] [CrossRef]
- Tsiotas, D.; Polyzos, S. The topology of urban road networks and its role to urban mobility. Transp. Res. Procedia 2017, 24, 482–490. [Google Scholar] [CrossRef]
- Chen, M.; Wu, F.; Yin, M.; Xu, J. Impact of road network topology on public transportation development. Wirel. Commun. Mob. Comput. 2021, 2021, 6209592. [Google Scholar] [CrossRef]
- Tu, Y.; Yang, C.; Chen, X. Road network topology vulnerability analysis and application. Proc. Inst. Civ. Eng. Transp. 2013, 166, 95–104. [Google Scholar] [CrossRef]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- Jiang, B.; Zhao, S.; Yin, J. Self-organized natural roads for predicting traffic flow: A sensitivity study. J. Stat. Mech. Theory Exp. 2008, 2008, P07008. [Google Scholar] [CrossRef]
- Porta, S.; Crucitti, P.; Latora, V. The network analysis of urban streets: A primal approach. Environ. Plan. Plan. Des. 2006, 33, 705–725. [Google Scholar] [CrossRef]
- Lowry, M. Spatial interpolation of traffic counts based on origin–destination centrality. J. Transp. Geogr. 2014, 36, 98–105. [Google Scholar] [CrossRef]
- Lin, J.; Ban, Y. Complex network topology of transportation systems. Transp. Rev. 2013, 33, 658–685. [Google Scholar] [CrossRef]
- Boeing, G. Street network models and indicators for every urban area in the world. Geogr. Anal. 2022, 54, 519–535. [Google Scholar] [CrossRef]
- Hillier, B. Space is the Machine: A Configurational Theory of Architecture; Space Syntax: London, UK, 2007. [Google Scholar]
- Jiang, B.; Liu, C. Street-based topological representations and analyses for predicting traffic flow in GIS. Int. J. Geogr. Inf. Sci. 2009, 23, 1119–1137. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar] [CrossRef]
- Porta, S.; Latora, V.; Wang, F.; Rueda, S.; Strano, E.; Scellato, S.; Cardillo, A.; Belli, E.; Cardenas, F.; Cormenzana, B.; et al. Street centrality and the location of economic activities in Barcelona. Urban Stud. 2012, 49, 1471–1488. [Google Scholar] [CrossRef]
- Turner, A. From axial to road-centre lines: A new representation for space syntax and a new model of route choice for transport network analysis. Environ. Plan. Plan. Des. 2007, 34, 539–555. [Google Scholar] [CrossRef]
- Solá, L.; Romance, M.; Criado, R.; Flores, J.; García del Amo, A.; Boccaletti, S. Eigenvector centrality of nodes in multiplex networks. Chaos Interdiscip. J. Nonlinear Sci. 2013, 23, 033131. [Google Scholar] [CrossRef] [PubMed]
- Freeman, L.C. Visualizing social networks. J. Soc. Struct. 2000, 1, 4. [Google Scholar]
- Jiang, B.; Claramunt, C. Topological analysis of urban street networks. Environ. Plan. Plan. Des. 2004, 31, 151–162. [Google Scholar] [CrossRef]
- Thomson, R.C. Bending the axial line: Smoothly continuous road centre-line segments as. In Proceedings of the 4th International Space Syntax Symposium, London, UK, 17–19 June 2003; Citeseer: Pensilvania, PA, USA, 2004. [Google Scholar]
- Jiang, B.; Claramunt, C.; Klarqvist, B. Integration of space syntax into GIS for modelling urban spaces. Int. J. Appl. Earth Obs. Geoinf. 2000, 2, 161–171. [Google Scholar] [CrossRef]
- Ma, D.; Omer, I.; Osaragi, T.; Sandberg, M.; Jiang, B. Why topology matters in predicting human activities. Environ. Plan. Urban Anal. City Sci. 2019, 46, 1297–1313. [Google Scholar] [CrossRef]
- Lämmer, S.; Gehlsen, B.; Helbing, D. Scaling laws in the spatial structure of urban road networks. Phys. Stat. Mech. Its Appl. 2006, 363, 89–95. [Google Scholar] [CrossRef]
- JICA. Urban Transport System Development Project for Colombo Metropolitan Region and Suburbs—Final Report; Technical Report; JICA: Tokyo, Japan, 2014. [Google Scholar]
- Malalgoda, C.; Amaratunga, D. A disaster resilient built environment in urban cities: The need to empower local governments. Int. J. Disaster Resil. Built Environ. 2015, 6, 102–116. [Google Scholar] [CrossRef]
- Hewawasam, V.; Matsui, K. Equitable resilience in flood prone urban areas in Sri Lanka: A case study in Colombo Divisional Secretariat Division. Glob. Environ. Chang. 2020, 62, 102091. [Google Scholar] [CrossRef]
- Patankar, A.M. Colombo: Exposure, Vulnerability, and Ability to Respond to Floods; World Bank Policy Research Working Paper WPS8084; World Bank Group: Washington, DC, USA, 2017. [Google Scholar] [CrossRef]
- Yi, J.; Zhang, H.; Liu, H.; Zhong, G.; Li, G. Flight delay classification prediction based on stacking algorithm. J. Adv. Transp. 2021, 2021, 4292778. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Kyriazos, T.; Poga, M. Dealing with multicollinearity in factor analysis: The problem, detections, and solutions. Open J. Stat. 2023, 13, 404–424. [Google Scholar] [CrossRef]
- Shrestha, N. Detecting multicollinearity in regression analysis. Am. J. Appl. Math. Stat. 2020, 8, 39–42. [Google Scholar] [CrossRef]
- Jayasinghe, A.; Sano, K.; Abenayake, C.C.; Mahanama, P. A novel approach to model traffic on road segments of large-scale urban road networks. MethodsX 2019, 6, 1147–1163. [Google Scholar] [CrossRef] [PubMed]
- Mitra, S.; Washington, S. On the significance of omitted variables in intersection crash modeling. Accid. Anal. Prev. 2012, 49, 439–448. [Google Scholar] [CrossRef]
- Shankar, V.; Mannering, F. Modeling the endogeneity of lane-mean speeds and lane-speed deviations: A structural equations approach. Transp. Res. Part Policy Pract. 1998, 32, 311–322. [Google Scholar] [CrossRef]
- Alstott, J.; Bullmore, E.; Plenz, D. powerlaw: A Python package for analysis of heavy-tailed distributions. PLoS ONE 2014, 9, e85777. [Google Scholar] [CrossRef]

| Specifications | Correlations—AADT and Explanatory Variables | Presence of Multicollinearity | Coefficient Value | |
|---|---|---|---|---|
| Tolerance | VIF | |||
| b (SC) | 0.817 ** | 0.338 | 2.955 | 64.220, |
| c (BC) | 0.790 ** | 0.349 | 2.867 | 51.935, |
| d (EC) | 0.665 ** | 0.619 | 1.614 | 31.295, |
| a (Constant) | 186.873, | |||
| Goodness-of-Fit Assessment | |||||
|---|---|---|---|---|---|
| Calibration (80% of the Sample) | Validation (20% of the Sample | ||||
| N | Adjusted | MAPE | N | Adjusted | MAPE |
| 510 | 0.747 | 0.375 | 128 | 0.768 | 0.361 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ldchn, K.; Kato, T.; Sano, K. Analyzing Transportation Network Vulnerability to Critical-Link Attacks Through Topology Changes and Traffic Volume Assessment. Appl. Sci. 2025, 15, 4099. https://doi.org/10.3390/app15084099
Ldchn K, Kato T, Sano K. Analyzing Transportation Network Vulnerability to Critical-Link Attacks Through Topology Changes and Traffic Volume Assessment. Applied Sciences. 2025; 15(8):4099. https://doi.org/10.3390/app15084099
Chicago/Turabian StyleLdchn, Kalpana, Teppei Kato, and Kazushi Sano. 2025. "Analyzing Transportation Network Vulnerability to Critical-Link Attacks Through Topology Changes and Traffic Volume Assessment" Applied Sciences 15, no. 8: 4099. https://doi.org/10.3390/app15084099
APA StyleLdchn, K., Kato, T., & Sano, K. (2025). Analyzing Transportation Network Vulnerability to Critical-Link Attacks Through Topology Changes and Traffic Volume Assessment. Applied Sciences, 15(8), 4099. https://doi.org/10.3390/app15084099







