Algorithm for Extraction of Reflection Waves in Single-Well Imaging Based on MC-ConvTasNet
Abstract
:1. Introduction
2. Theory and Method
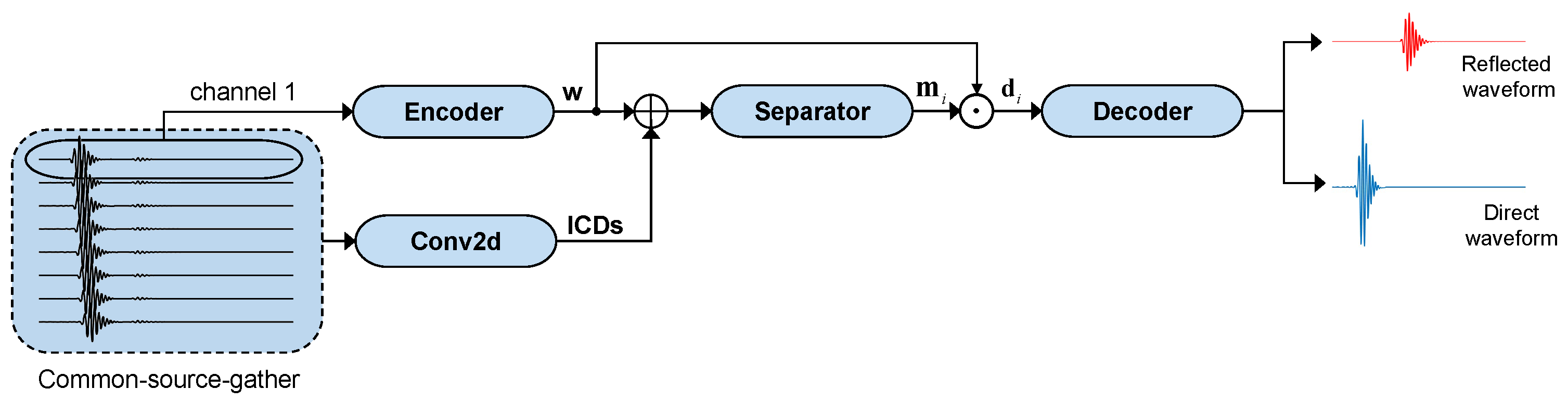
2.1. Network Model
2.2. Network Architecture
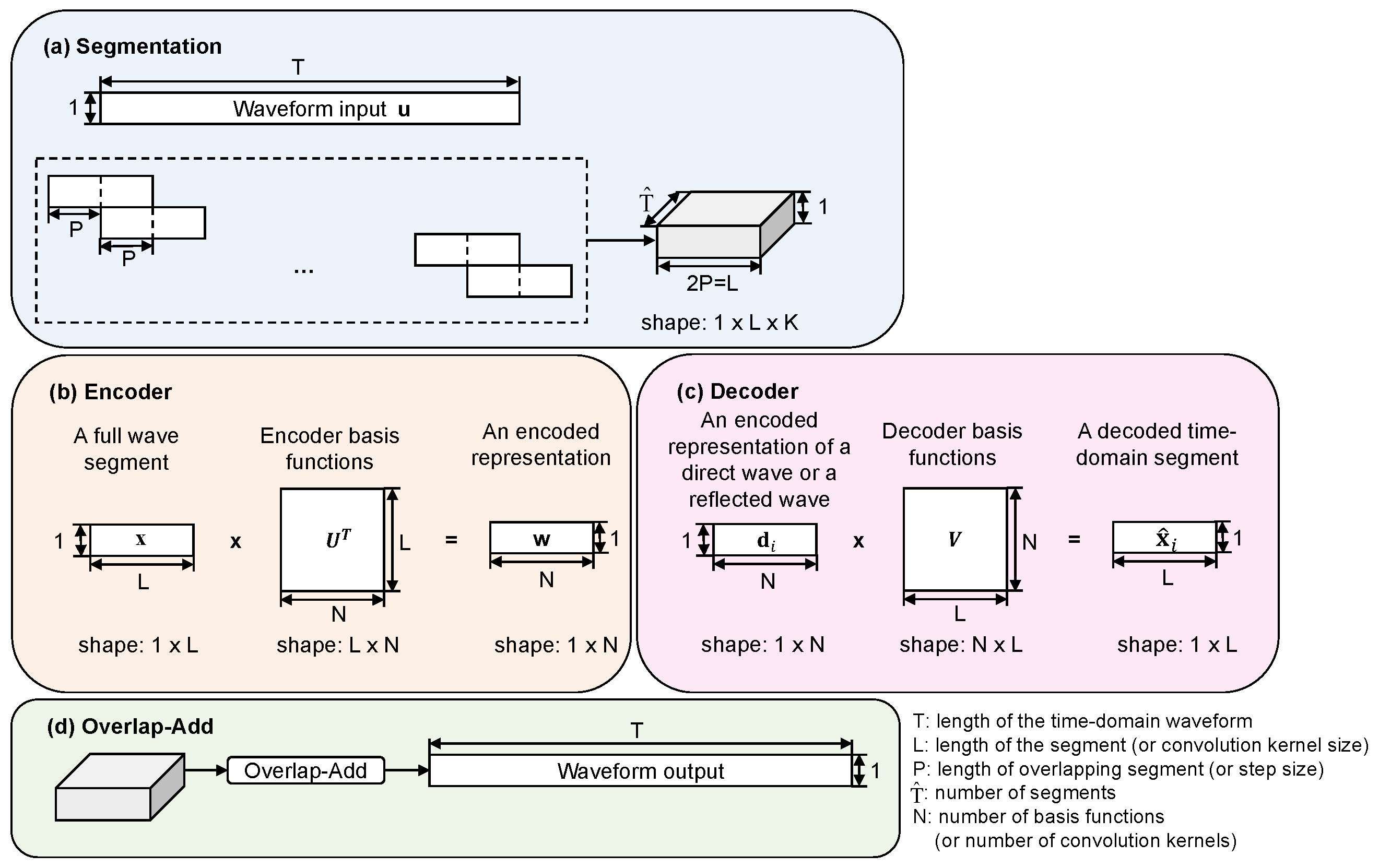
2.2.1. Encoder
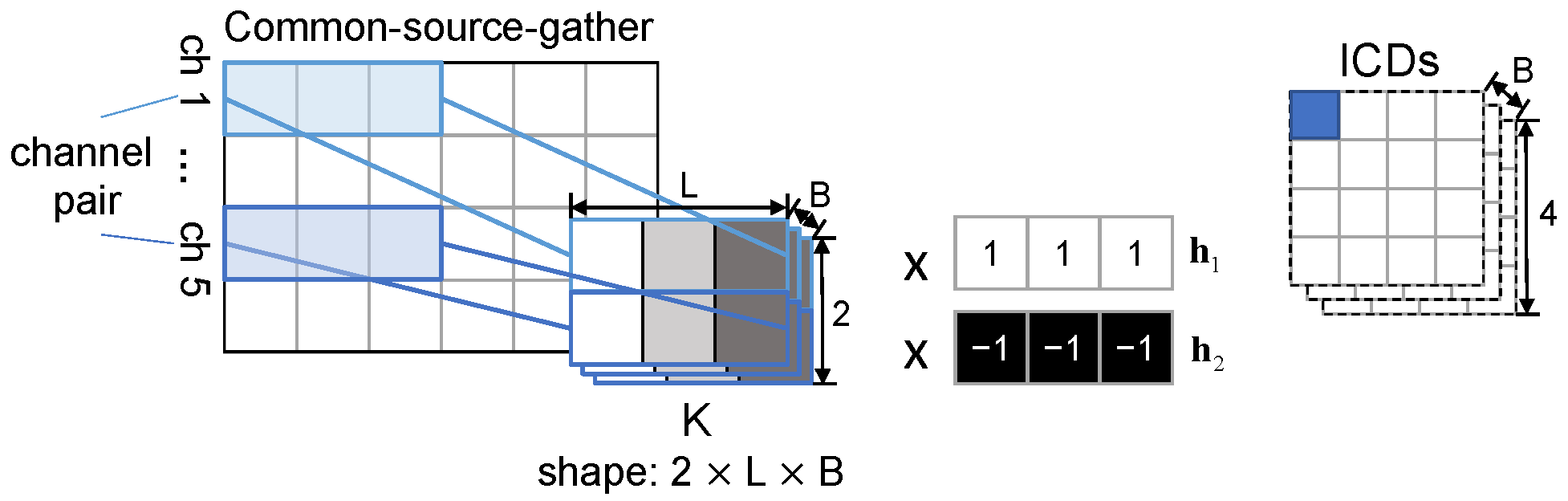
2.2.2. Conv2d (Spatial Feature Extraction)
2.2.3. Separation
2.2.4. Decoder
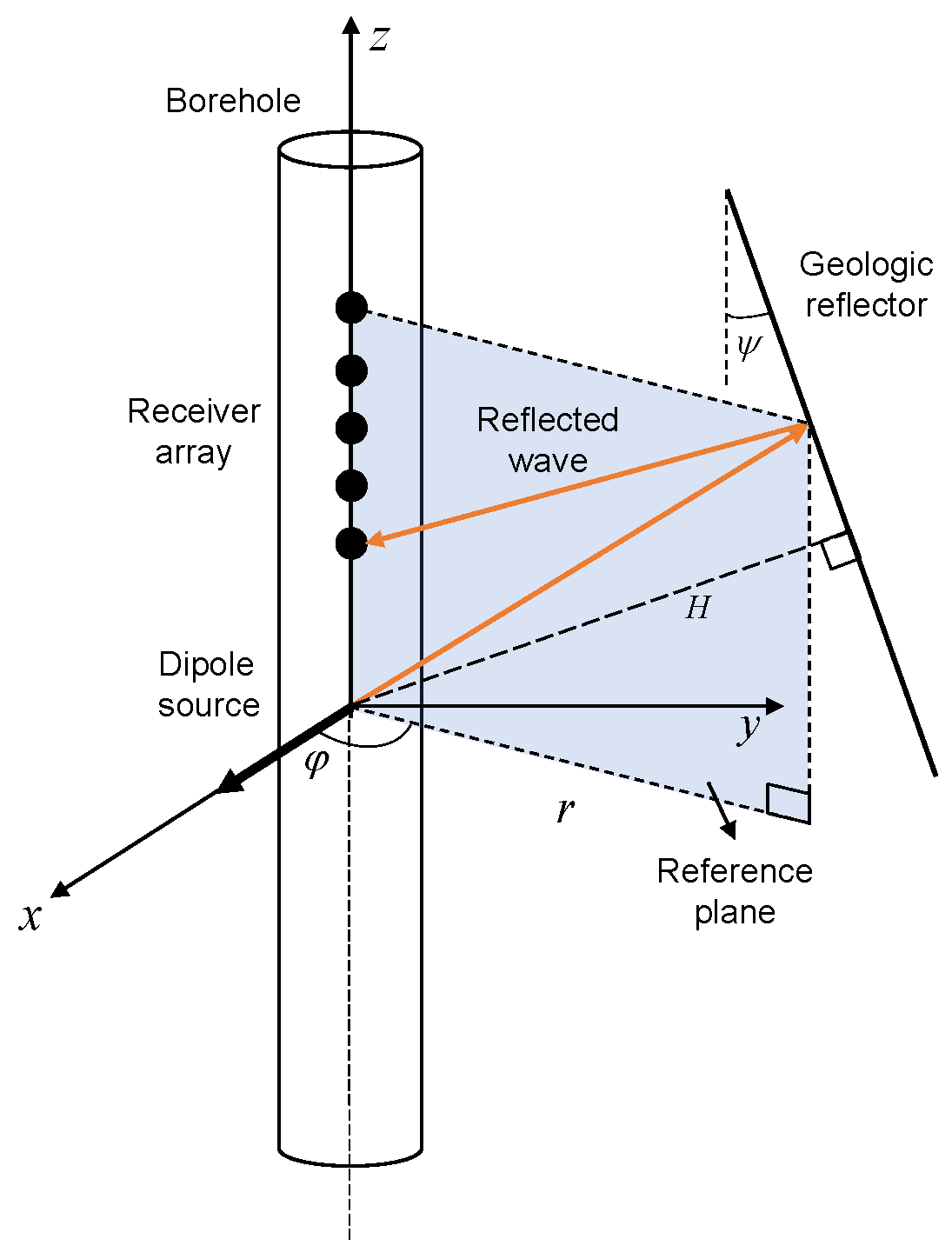
2.3. Dataset
2.4. Loss Function and Training Details
3. Results
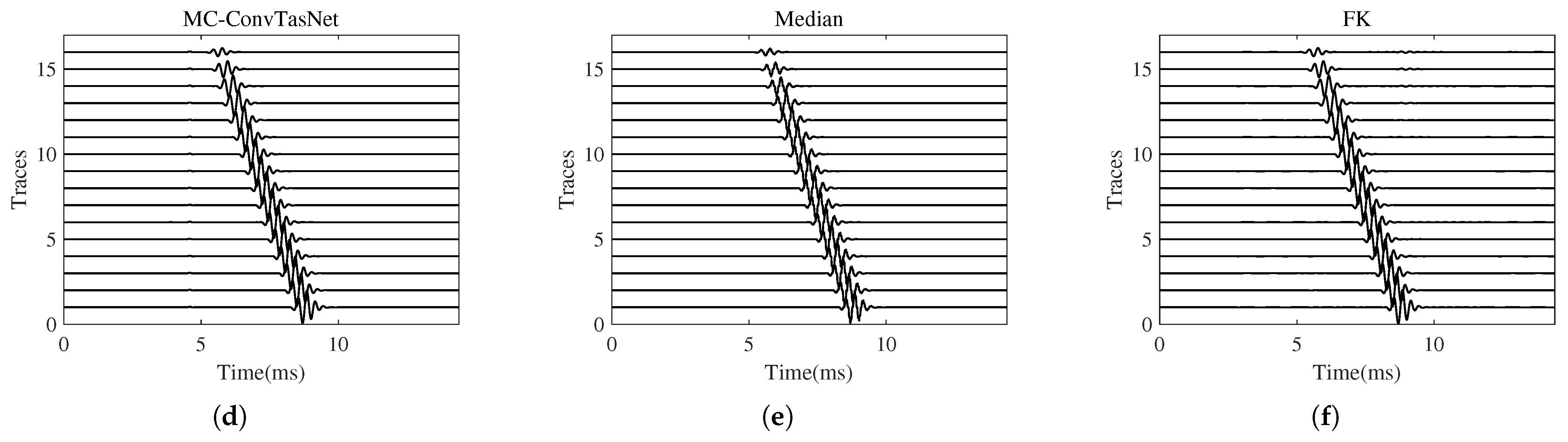
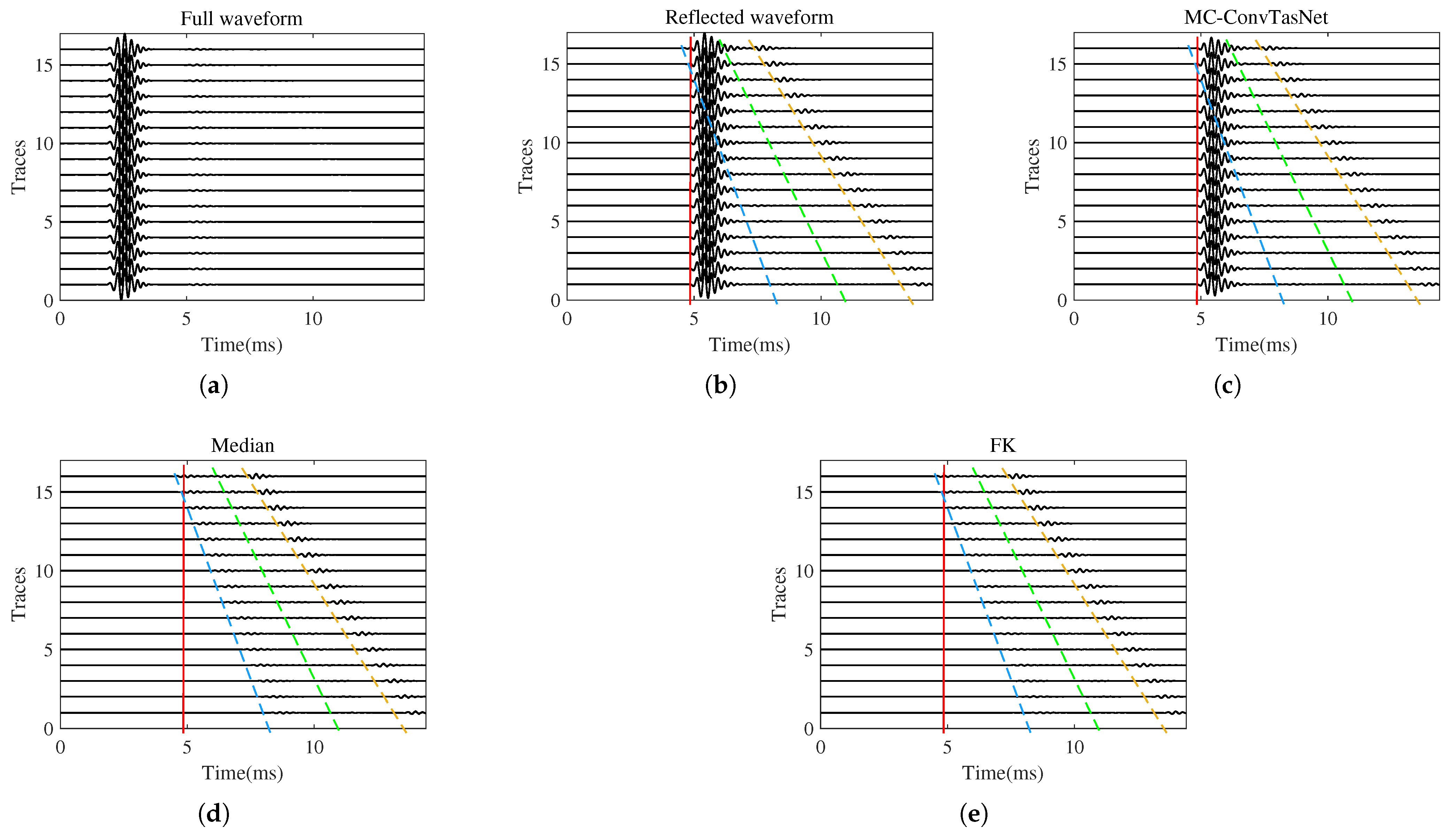
3.1. Wave Separation for the Hard-to-Hard Single-Interface Model
3.2. Wave Separation for the Soft-to-Hard Single-Interface Model
3.3. Wave Separation for the Double-Interface Model
3.3.1. COG Signals
3.3.2. CSG Signals
3.4. Wave Separation for Noisy Data
3.5. Wave Separation for Field Logging Data
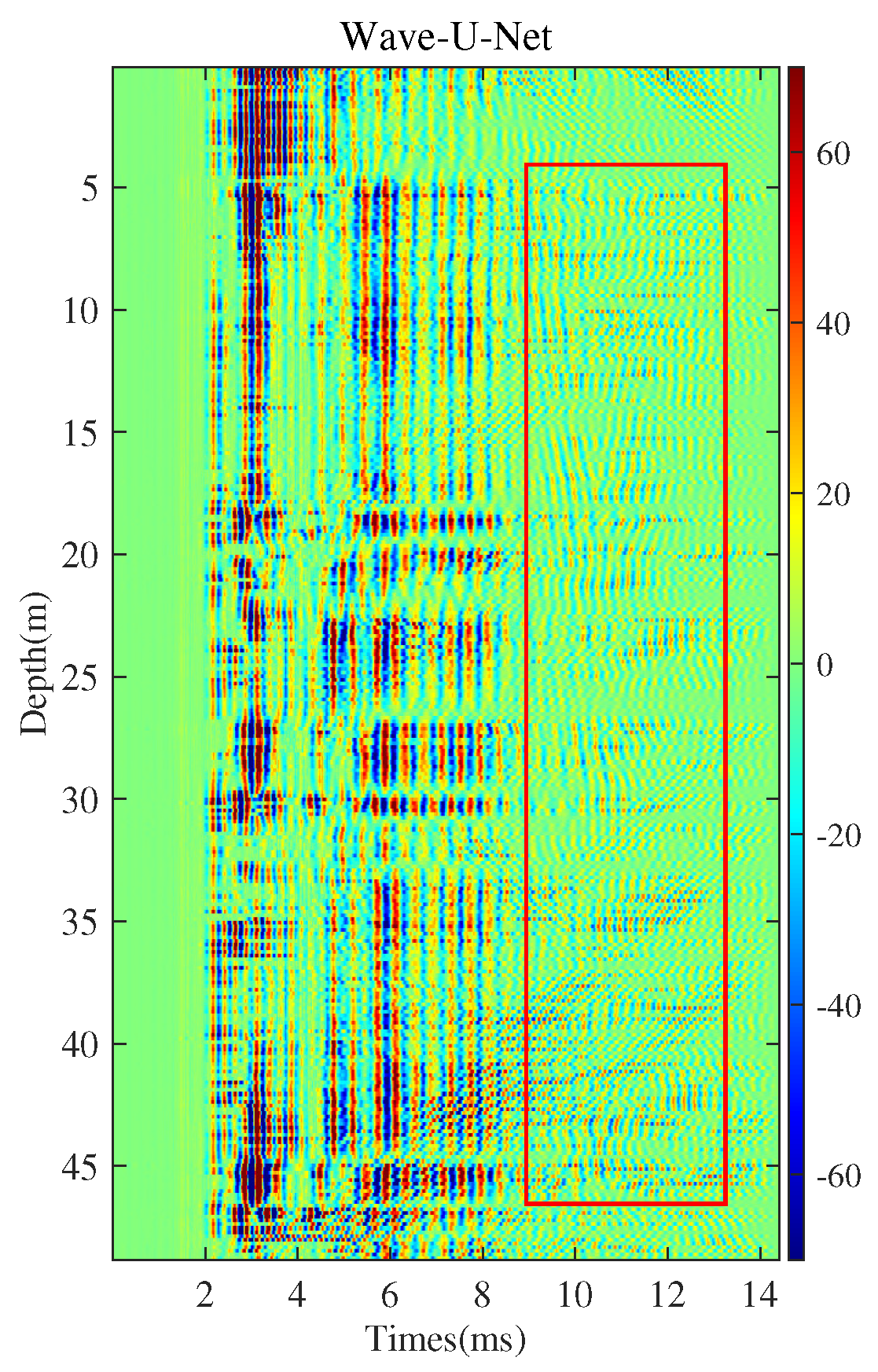
3.6. Comparison of the Wave Separation Capabilities of MC-ConvTasNet and Wave-U-Net
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MC-ConvTasNet | Multi-channel convolutional time-domain audio separation network |
| CSG | Common-source gather |
| CRG | Common-receiver gather |
| COG | Linear dichroism |
| Conv-TasNet | Convolutional time-domain audio separation network |
| ICD | Inter-channel convolution difference |
| Conv2d | Two-dimensional convolution |
Appendix A. Expressions for Direct and Reflected Waves
References
- Tang, X. Imaging near-borehole structure using directional acoustic-wave measurement. Geophysics 2004, 69, 1378–1386. [Google Scholar] [CrossRef]
- Esmersoy, C.; Chang, C.; Kane, M.; Coates, R.; Tichelaar, B.; Quint, E. Acoustic imaging of reservoir structure from a horizontal well. Lead. Edge 1998, 17, 940–946. [Google Scholar] [CrossRef]
- Hu, H.; Xu, J.; Wang, Z. Analytical Simulation of the Waves Reflected From a Distant Slanted Interface Outside a Borehole. In Proceedings of the 2019 13th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Shijiazhuang, China, 1–4 November 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Xu, J.; Hu, H.; Liu, Q.H. Combination of FDTD with Analytical Methods for Simulating Elastic Scattering of 3-D Objects Outside a Fluid-Filled Borehole. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5325–5334. [Google Scholar] [CrossRef]
- Gao, Y.; Hu, H.; Xu, J. Elastic Reverse Time Migration Method for Single-Well Imaging and Elimination of Azimuthal Ambiguity With a Combined Receiver System. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5921215. [Google Scholar] [CrossRef]
- Borland, W.; Holderson, J.; Rougha, H.; Sultan, A.; Chakravorty, S.; Al-Raisi, M. Integration of Microelectrical and Sonic Reflection Imaging Around the Borehole-Offshore UAE. In Proceedings of the IPTC International Petroleum Technology Conference, Doha, Qatar, 11 November 2005; p. IPTC-11021. [Google Scholar] [CrossRef]
- Hirabayashi, N.; Leaney, W.S. Wavefield separation for borehole acoustic reflection survey using parametric decomposition and waveform inversion. Geophysics 2019, 84, D151–D159. [Google Scholar] [CrossRef]
- Tang, X.M.; Zheng, Y.; Patterson, D. Processing array acoustic-logging data to image near-borehole geologic structures. Geophysics 2007, 72, E87–E97. [Google Scholar] [CrossRef]
- Hornby, B.E. Imaging of near-borehole structure using full-waveform sonic data. Geophysics 1989, 54, 747–757. [Google Scholar] [CrossRef]
- Li, C.; Yue, W. High-resolution Radon transforms for improved dipole acoustic imaging. Geophys. Prospect. 2017, 65, 467–484. [Google Scholar] [CrossRef]
- Li, J.; Innanen, K.A.; Tao, G. Extraction of reflected events from sonic-log waveforms using the Karhunen-Loève transform. Geophysics 2017, 82, D265–D277. [Google Scholar] [CrossRef]
- Chen, J.; Yue, W.; Li, C.; Zeng, F. Extracting Reflected Waves From Acoustic Logging Data Based on the Shearlet Transform. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1688–1692. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, H.; Fang, Z.; Xu, D.; Qi, X.; Yu, Y. Weak Reflection Extraction in Borehole Acoustic Reflection Imaging Using an Unsupervised Machine Learning Method. In Proceedings of the SPWLA Annual Logging Symposium, Rio de Janeiro, Brazil, 18–22 May 2024; SPWLA: Houston, TX, USA, 2024. [Google Scholar]
- Li, Y.; Zhou, R.; Tang, X.M.; Jackson, J.; Patterson, D. Single-Well Imaging with Acoustic Reflection Survey at Mounds, Oklahoma, USA. In Proceedings of the 64th EAGE Conference & Exhibition, Florence, Italy, 27–30 May 2002. [Google Scholar] [CrossRef]
- Gannot, S.; Vincent, E.; Golan, S.M.; Ozerov, A. A Consolidated Perspective on Multimicrophone Speech Enhancement and Source Separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 692–730. [Google Scholar] [CrossRef]
- Hershey, J.R.; Chen, Z.; Le Roux, J.; Watanabe, S. Deep clustering: Discriminative embeddings for segmentation and separation. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 31–35. [Google Scholar] [CrossRef]
- Jansson, A.; Humphrey, E.J.; Montecchio, N.; Bittner, R.M.; Kumar, A.; Weyde, T. Singing Voice Separation with Deep U-Net Convolutional Networks. In Proceedings of the International Society for Music Information Retrieval Conference, Suzhou, China, 23–27 October 2017. [Google Scholar]
- Kolbaek, M.; Yu, D.; Tan, Z.; Jensen, J.H. Multitalker Speech Separation With Utterance-Level Permutation Invariant Training of Deep Recurrent Neural Networks. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 1901–1913. [Google Scholar] [CrossRef]
- Wang, D.; Chen, J. Supervised Speech Separation Based on Deep Learning: An Overview. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 1702–1726. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Mesgarani, N. TasNet: Time-Domain Audio Separation Network for Real-Time, Single-Channel Speech Separation. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 696–700. [Google Scholar]
- Stoller, D.; Ewert, S.; Dixon, S. Wave-U-Net: A Multi-Scale Neural Network for End-to-End Audio Source Separation. arXiv 2018, arXiv:1806.03185. [Google Scholar]
- Luo, Y.; Mesgarani, N. Conv-TasNet: Surpassing Ideal Time–Frequency Magnitude Masking for Speech Separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 1256–1266. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Wang, H.; Shi, S. A deep learning workflow for weak reflection extraction in pitch-catch measurements in the cased hole. Geophysics 2023, 88, D147–D157. [Google Scholar] [CrossRef]
- Gu, R.; Zhang, S.X.; Chen, L.; Xu, Y.; Yu, M.; Su, D.; Zou, Y.; Yu, D. Enhancing End-to-End Multi-Channel Speech Separation Via Spatial Feature Learning. In Proceedings of the ICASSP 2020–2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 7319–7323. [Google Scholar] [CrossRef]
- Grumiaux, P.A.; Kitić, S.; Girin, L.; Guerin, A. A survey of sound source localization with deep learning methods. J. Acoust. Soc. Am. 2022, 152, 107–151. [Google Scholar] [CrossRef]
- Kurkjian, A.L.; Chang, S.K. Acoustic multipole sources in fluid-filled boreholes. Geophysics 1986, 51, 148–163. [Google Scholar] [CrossRef]
- Tsang, L.; Rader, D. Numerical evaluation of the transient acoustic waveform due to a point source in a fluid-filled borehole. Geophysics 1979, 44, 1706–1720. [Google Scholar] [CrossRef]
- Xu, J.; Hu, H. Solutions of P-SV and SV-P waves in single-well imaging through reciprocity relations. Geophysics 2020, 85, D245–D259. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Z.; Yoshioka, T. Dual-Path RNN: Efficient Long Sequence Modeling for Time-Domain Single-Channel Speech Separation. In Proceedings of the ICASSP 2020–2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 46–50. [Google Scholar] [CrossRef]
- Tang, X.M.; Cao, J.J.; Wei, Z.T. Shear-wave radiation, reception, and reciprocity of a borehole dipole source: With application to modeling of shear-wave reflection survey. Geophysics 2014, 79, T43–T50. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology: Theory and Methods, 2nd ed.; University Science Books: Melville, NY, USA, 2002; pp. 128–149,209–215. [Google Scholar]
- Wang, Z.; Hu, H.; Yang, Y. Reciprocity relations for the elastodynamic fields generated by multipole sources in a fluid–solid configuration. Geophys. J. Int. 2015, 203, 883–892. [Google Scholar] [CrossRef]
- Xu, J.; Hu, H.; Wang, Z. Asymptotic solution to a 3D dipole single-well imaging system with combined monopole and dipole receivers with an application in elimination of azimuth ambiguity. Geophysics 2019, 84, D191–D207. [Google Scholar] [CrossRef]
- Castagna, J.P.; Batzle, M.L.; Eastwood, R.L. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks. Geophysics 1985, 50, 571–581. [Google Scholar] [CrossRef]
- Li, Q. Velocity regularities of p and s-waves in formations. Oil Geophys. Prospect. (China) 1992, 27, 5519369. [Google Scholar]
- Ma, Z.; Xie, J. Relationship among conpressional wave, shear wave velocities and density in rocks. Prog. Geophys. 2005, 20, 905–910. [Google Scholar]
- Kolbæk, M.; Tan, Z.; Jensen, S.H.; Jensen, J.H. On Loss Functions for Supervised Monaural Time-Domain Speech Enhancement. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 28, 825–838. [Google Scholar] [CrossRef]
- Roux, J.L.; Wisdom, S.; Erdogan, H.; Hershey, J.R. SDR—Half-baked or Well Done? In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 626–630. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Gazdag, J.; Sguazzero, P. Migration of seismic data by phase shift plus interpolation. Geophysics 1984, 49, 124–131. [Google Scholar] [CrossRef]
- Sridhar, K.; Cutler, R.; Saabas, A.; Parnamaa, T.; Loide, M.; Gamper, H.; Braun, S.; Aichner, R.; Srinivasan, S. ICASSP 2021 Acoustic Echo Cancellation Challenge: Datasets, Testing Framework, and Results. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 151–155. [Google Scholar] [CrossRef]
- Zhu, W.; Mousavi, S.M.; Beroza, G.C. Chapter Four—Seismic signal augmentation to improve generalization of deep neural networks. In Machine Learning in Geosciences; Advances in Geophysics; Moseley, B., Krischer, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Volume 61, pp. 151–177. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, Z.; Liu, S. Improving Performance of Seismic Fault Detection by Fine-Tuning the Convolutional Neural Network Pre-Trained with Synthetic Samples. Energies 2021, 14, 3650. [Google Scholar] [CrossRef]

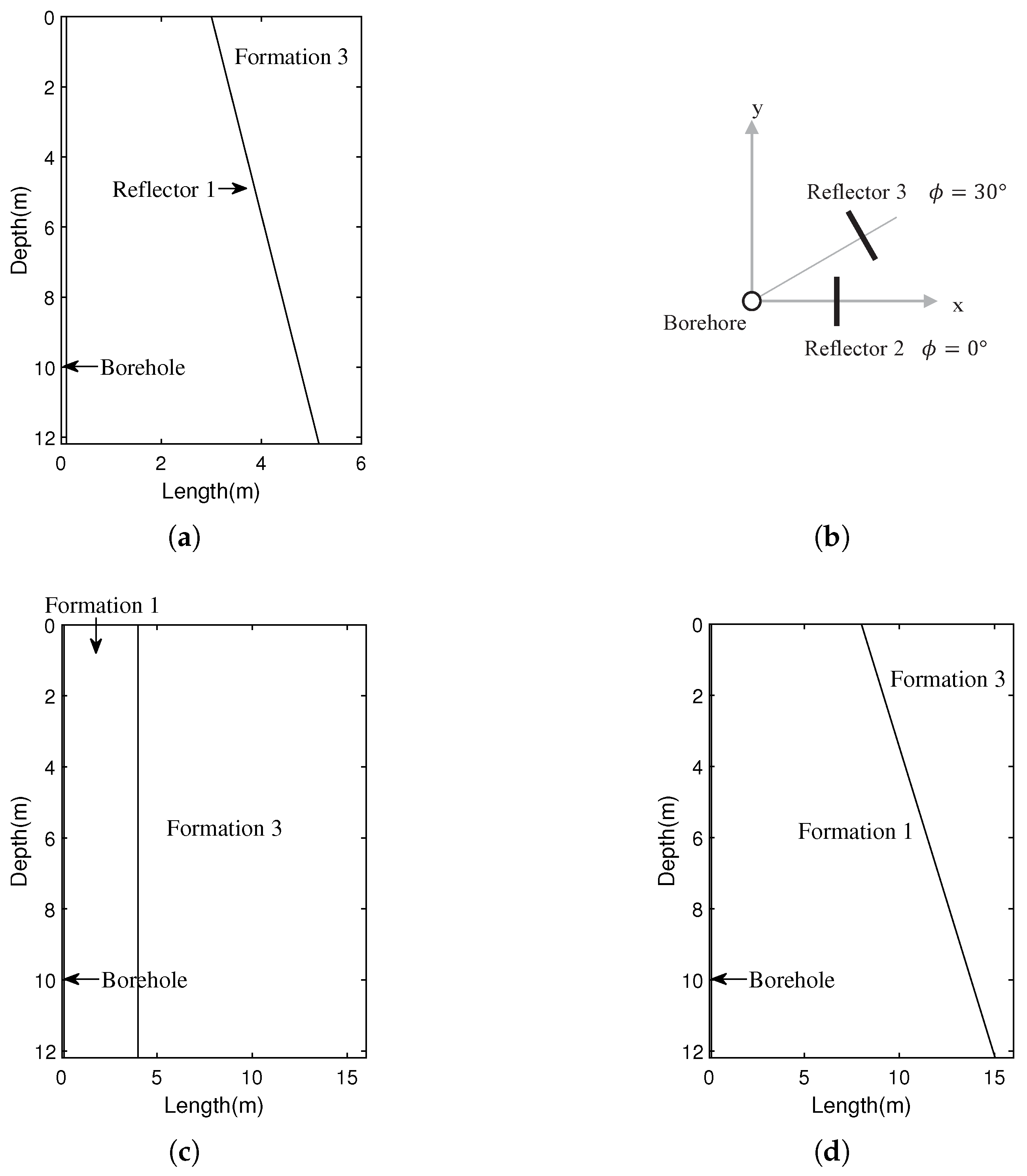
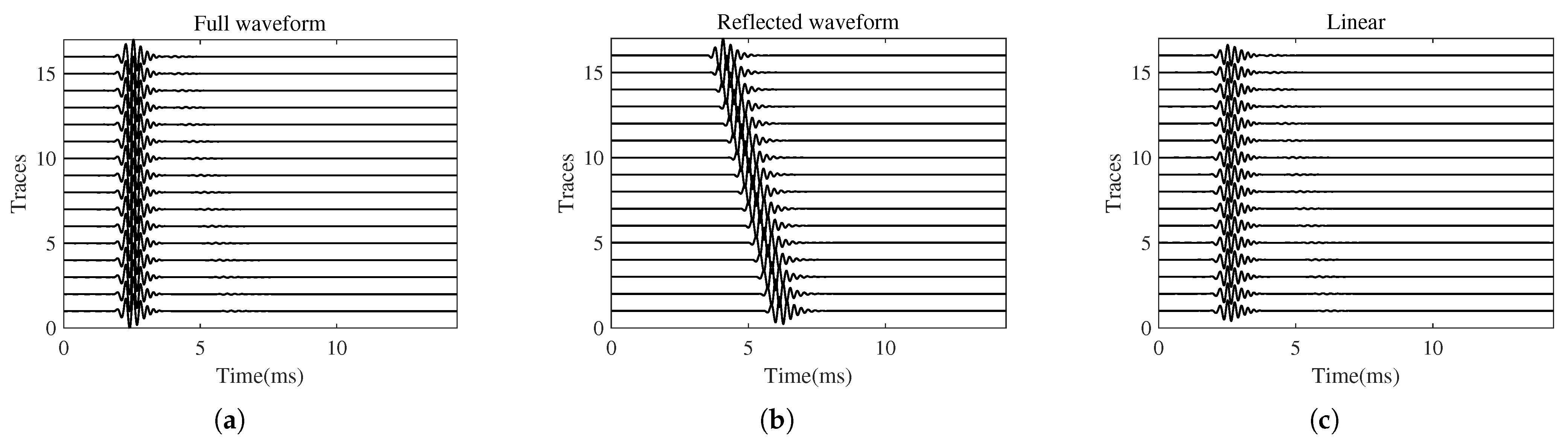
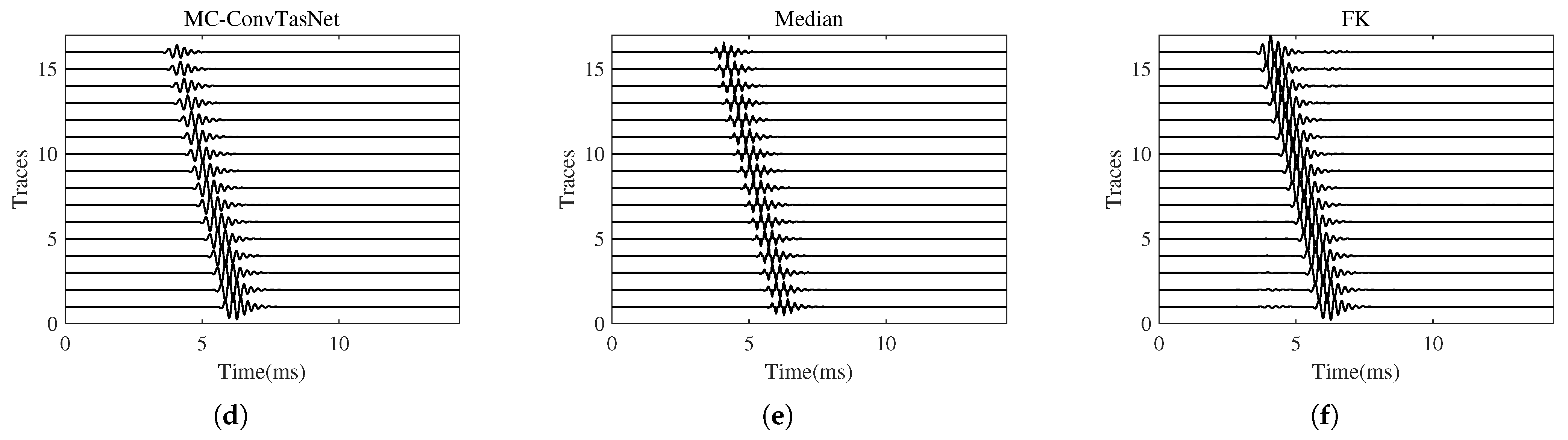
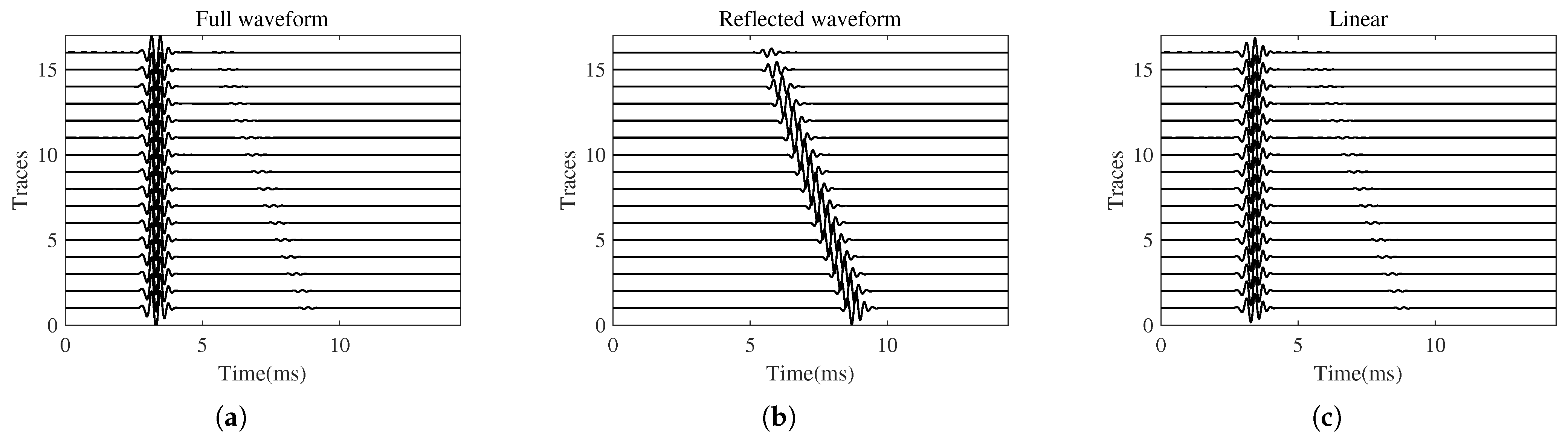




| Geometry Properties | Lower Limit | Upper Limit | Step Size |
|---|---|---|---|
| Distance (m) | 3 | 13 | 1 |
| Dip angle (°) | −70 | 70 | 10 |
| Azimuth angle (°) | 0 | 90 | 45 |
| Formation Parameters | Lower Limit | Upper Limit |
|---|---|---|
| P-velocity (m/s) | 2595 | 5080 |
| S-velocity (m/s) | 1170 | 3200 |
| Density () | 1743 | 2702 |
| Model | P-Velocity (m/s) | S-Velocity (m/s) | Density () |
|---|---|---|---|
| Fluid | 1500 | - | 1000 |
| Formation 1 | 3000 | 1800 | 2000 |
| Formation 2 | 2200 | 1200 | 2000 |
| Formation 3 | 4500 | 2400 | 2650 |
| Model | (dB) | |||
|---|---|---|---|---|
| MC-ConvTasNet | Median Filter | Parameter Estimation | F-K Filter | |
| 1 | 34.7 | 6.8 | −24.9 | 27.9 |
| 2 | 33.4 | 12.4 | −25.7 | 30.6 |
| 3 | 32.3 | −19.1 | −25.0 | −19.5 |
| Model | (dB) | |||
|---|---|---|---|---|
| MC-ConvTasNet | Median Filter | Parameter Estimation | F-K Filter | |
| 1 | 0.044 | 0.077 | 2.080 | 0.006 |
| 2 | 0.010 | 0.030 | 1.893 | 0.003 |
| 3 | 0.028 | 0.133 | 2.146 | 0.133 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.; Xu, J.; Hu, H. Algorithm for Extraction of Reflection Waves in Single-Well Imaging Based on MC-ConvTasNet. Appl. Sci. 2025, 15, 4189. https://doi.org/10.3390/app15084189
Lin W, Xu J, Hu H. Algorithm for Extraction of Reflection Waves in Single-Well Imaging Based on MC-ConvTasNet. Applied Sciences. 2025; 15(8):4189. https://doi.org/10.3390/app15084189
Chicago/Turabian StyleLin, Wanting, Jiaqi Xu, and Hengshan Hu. 2025. "Algorithm for Extraction of Reflection Waves in Single-Well Imaging Based on MC-ConvTasNet" Applied Sciences 15, no. 8: 4189. https://doi.org/10.3390/app15084189
APA StyleLin, W., Xu, J., & Hu, H. (2025). Algorithm for Extraction of Reflection Waves in Single-Well Imaging Based on MC-ConvTasNet. Applied Sciences, 15(8), 4189. https://doi.org/10.3390/app15084189






