Hybrid Compensation Method for Non-Uniform Creep Difference and Hysteresis Nonlinearity of Piezoelectric-Actuated Machine Tools Under S-Shaped Curve Trajectory
Abstract
1. Introduction
2. Background and Driving Principles
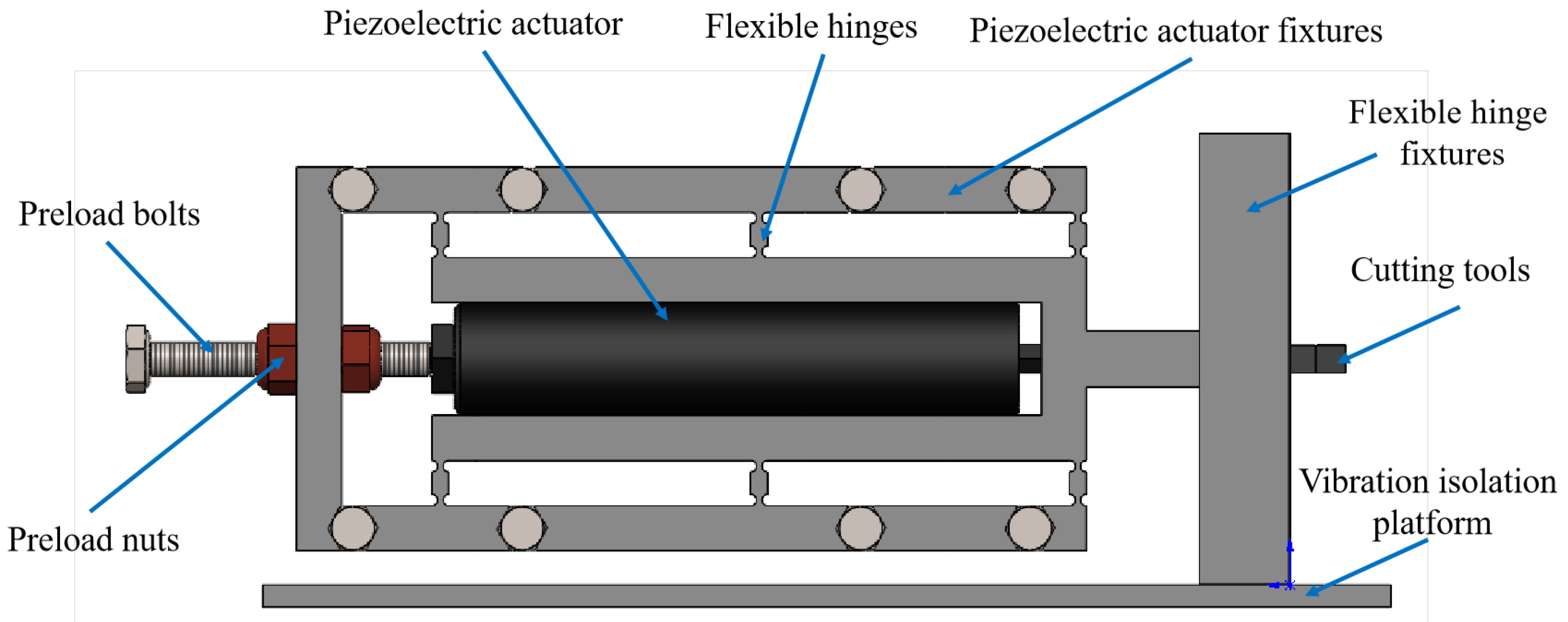
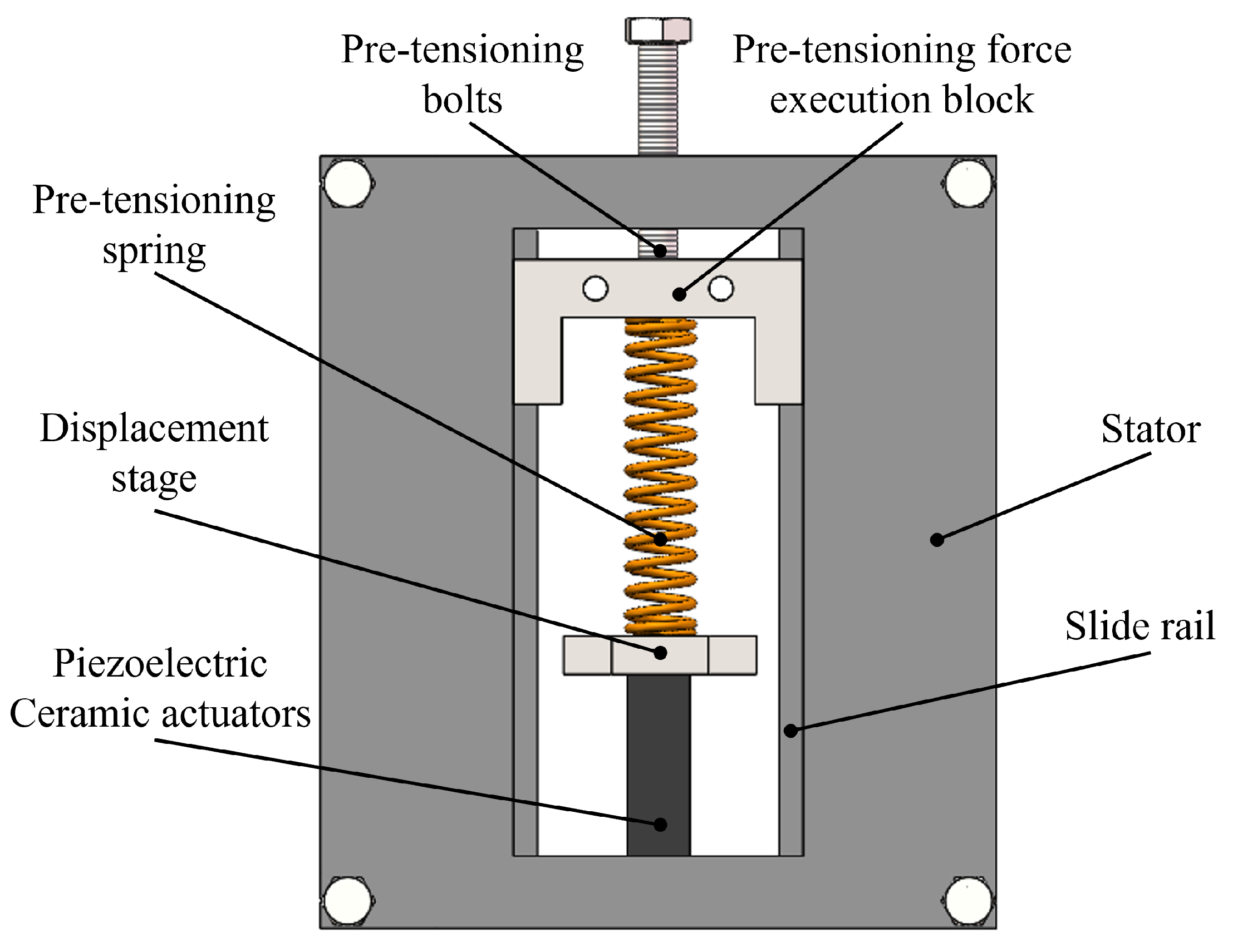
2.1. Structure of Typical PAMTs
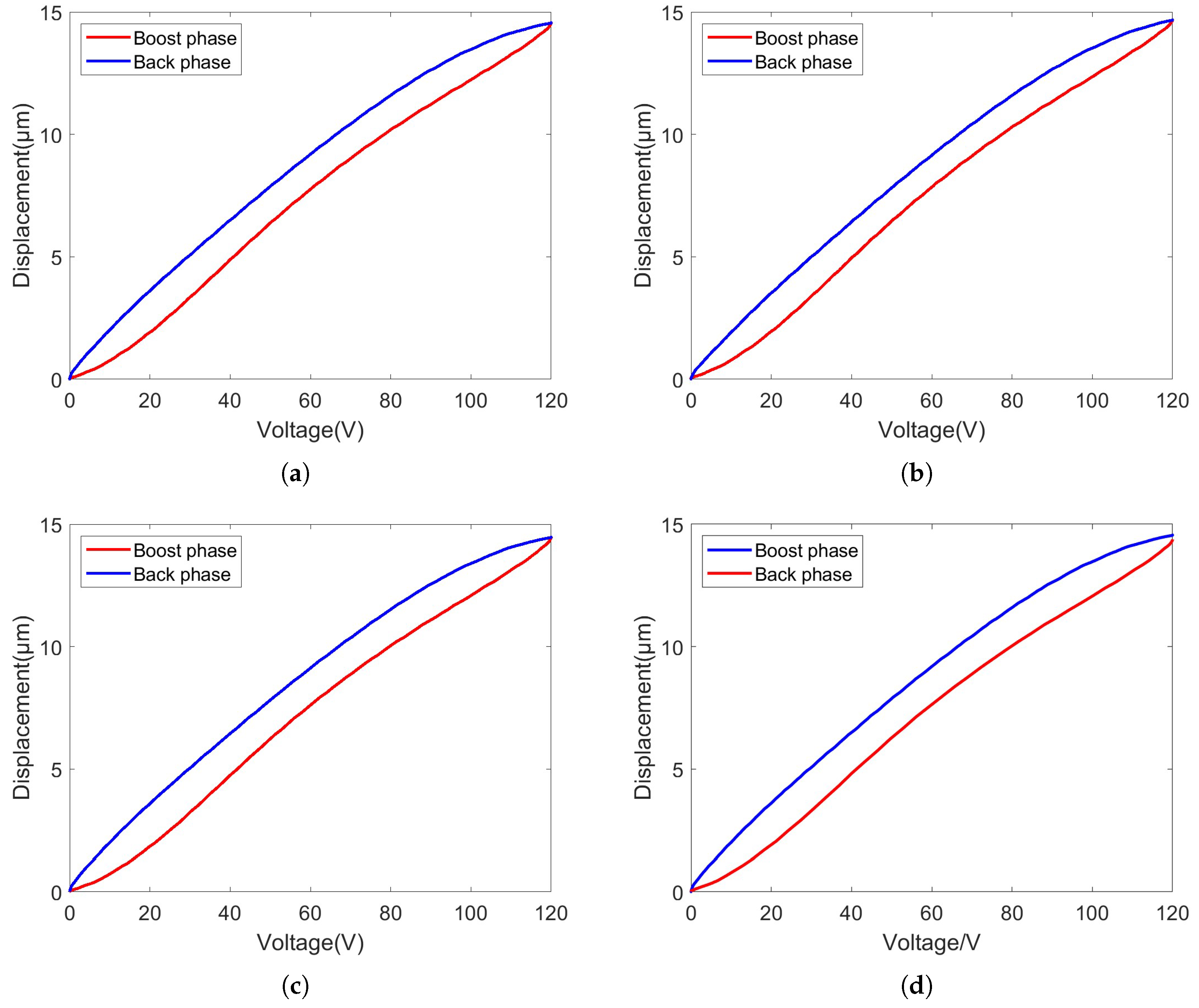
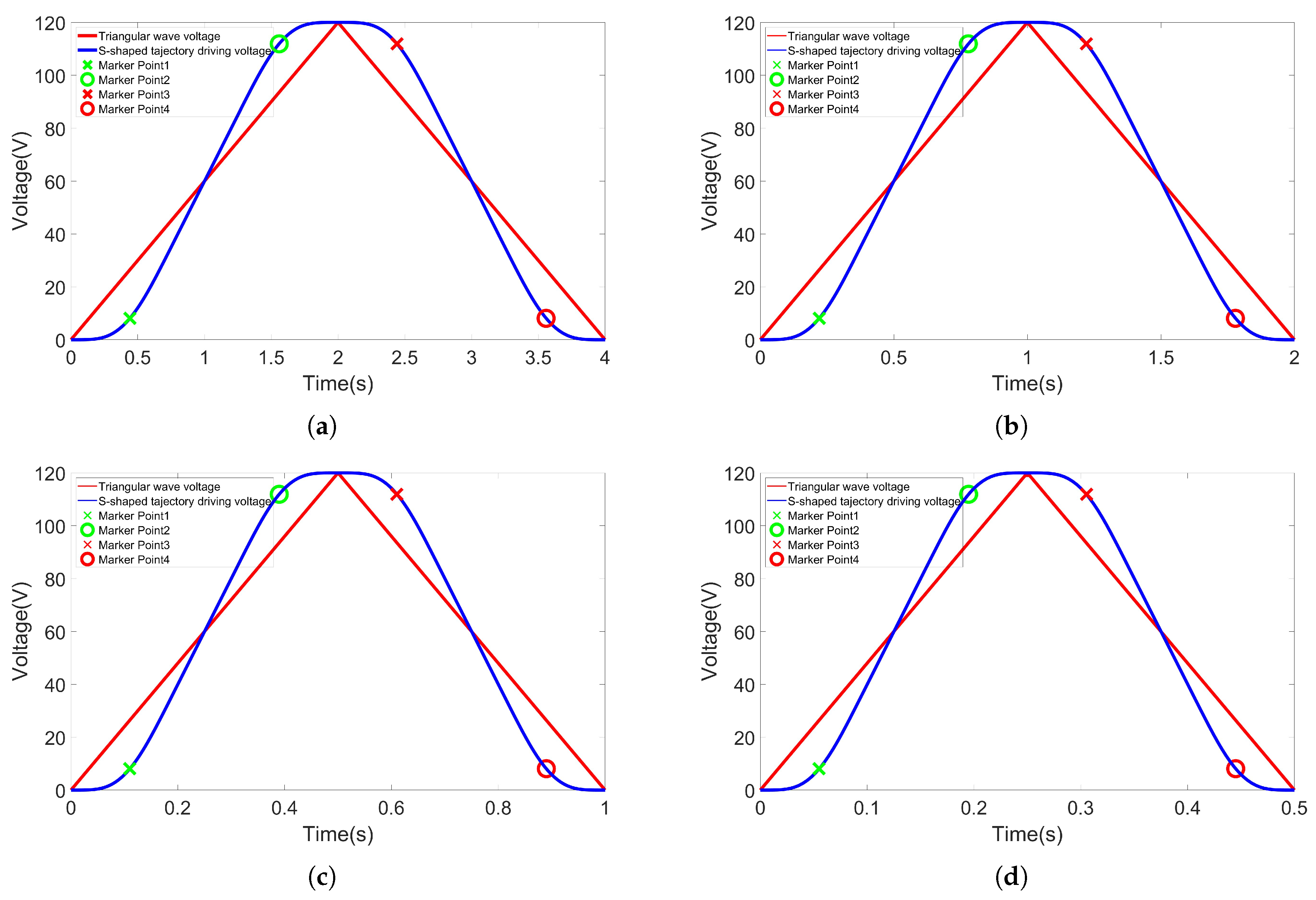
2.2. Analysis of Nonlinear Characteristics of Piezoelectric Actuators Under S-Shaped Trajectory Driving Voltage
3. Feedforward Control Considering Non-Uniform Creep Difference and Hysteresis Nonlinearity
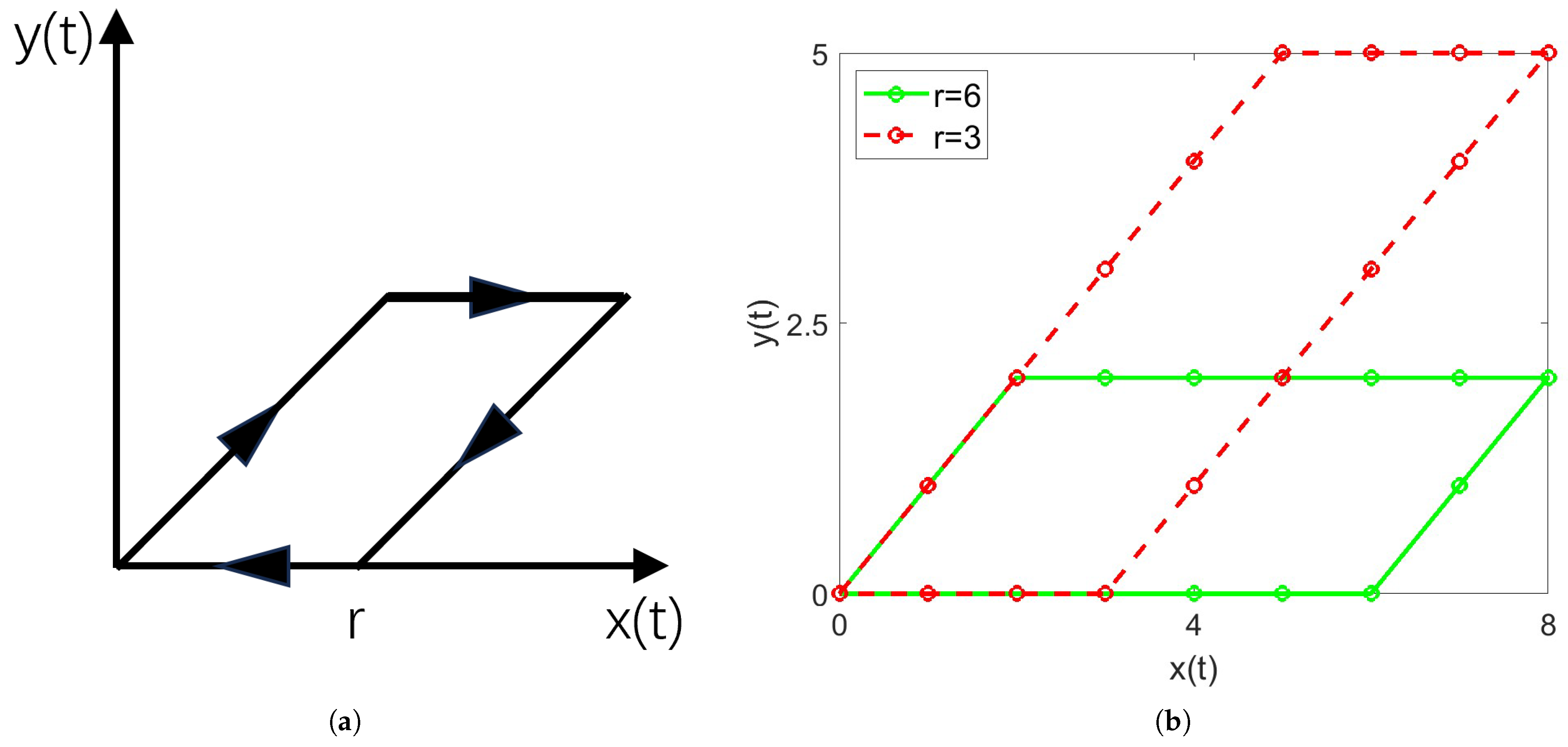
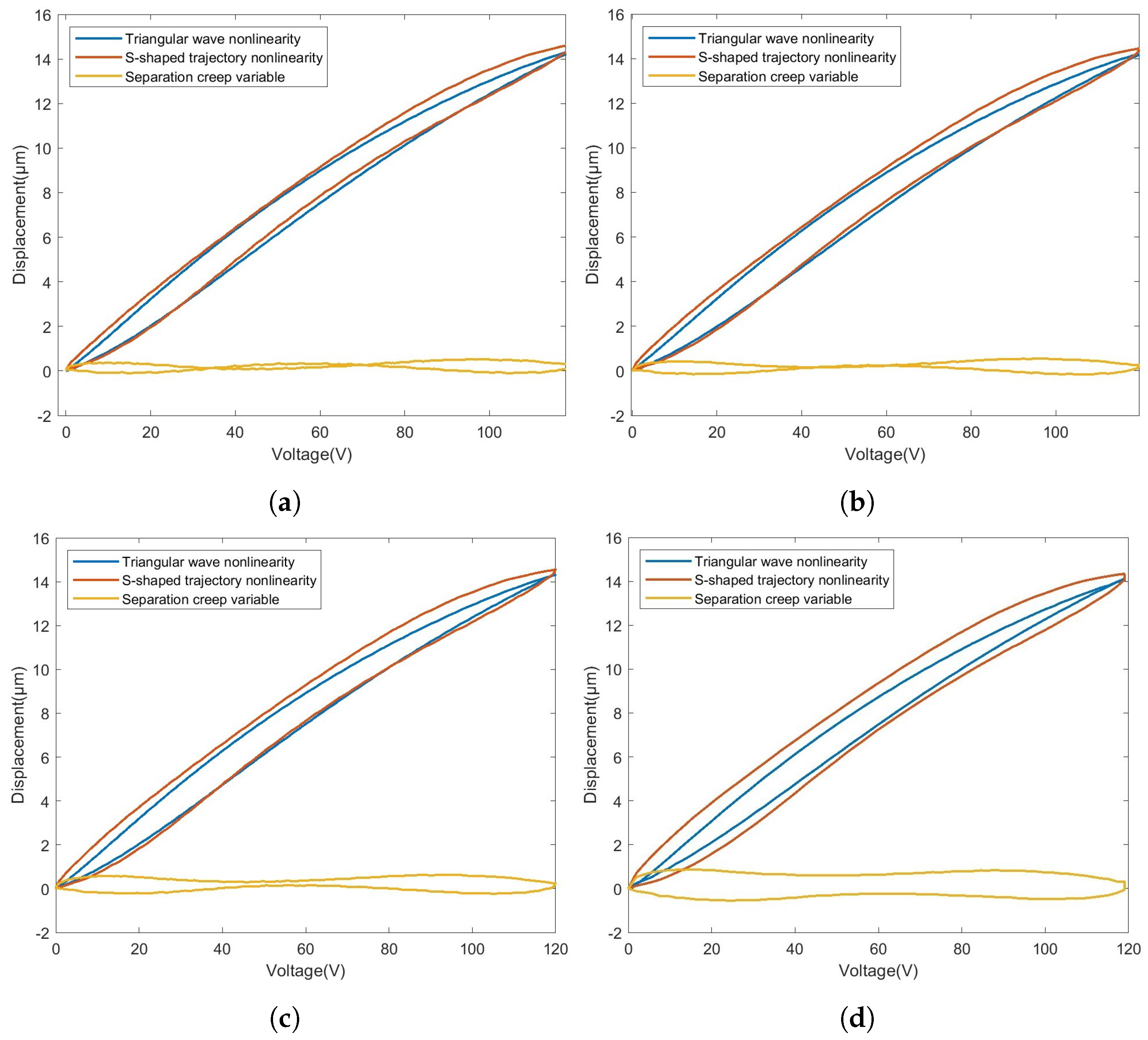
3.1. NCD Mechanism Analysis and Separation Basis
3.2. Module Function Introduction
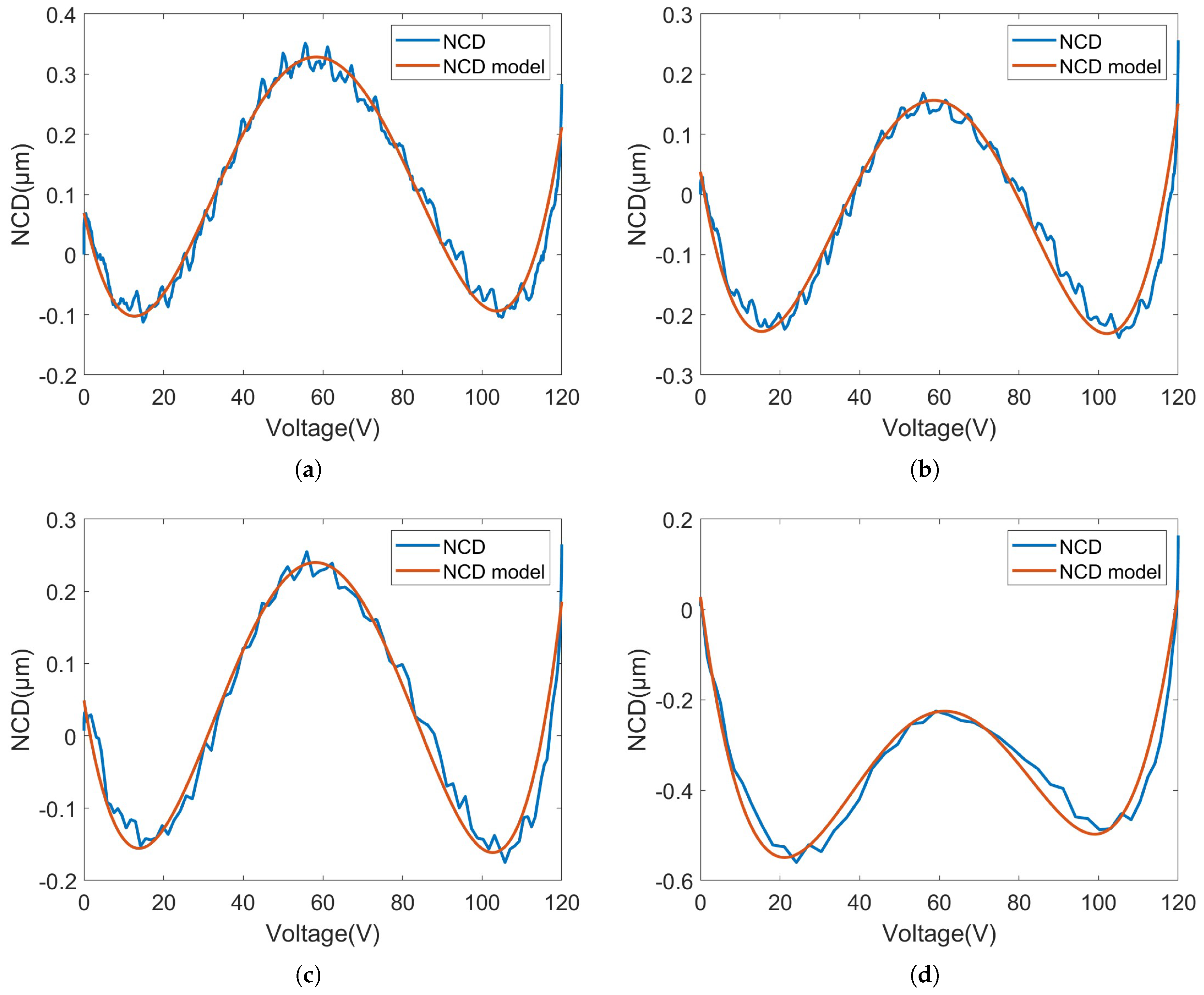
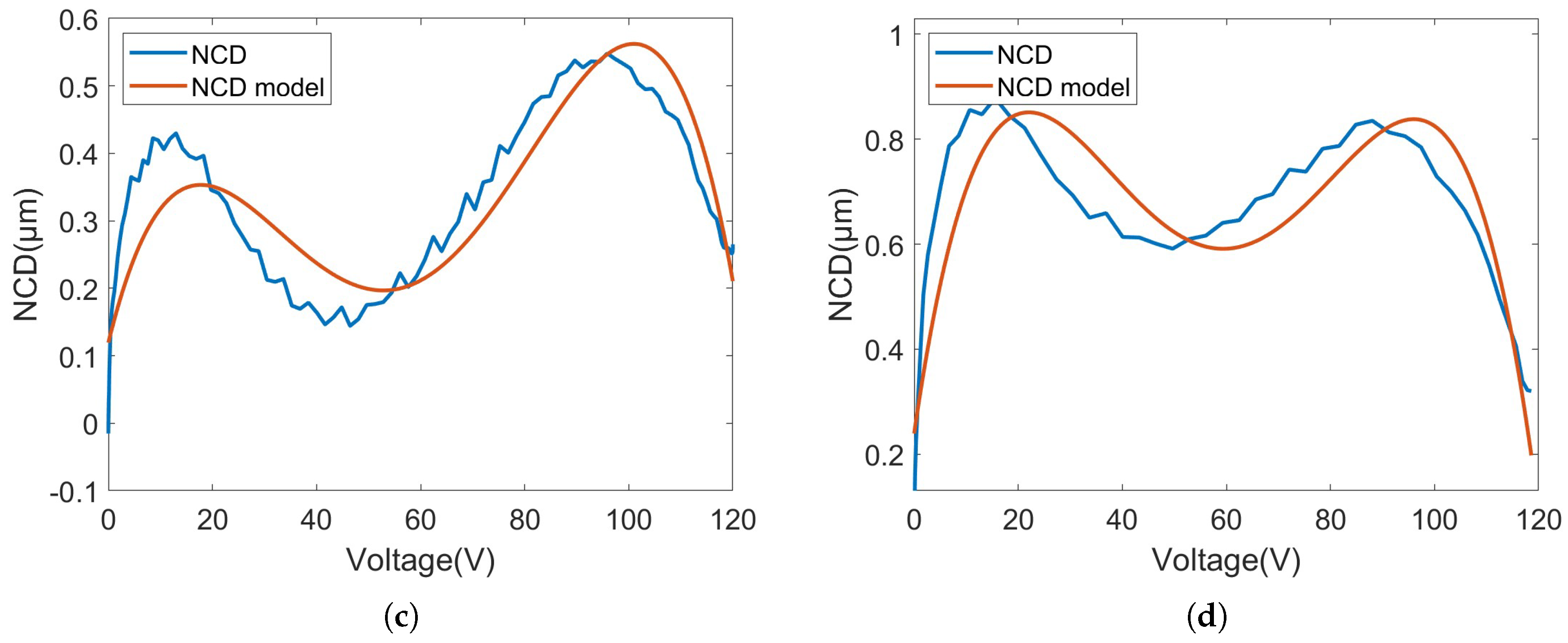
3.2.1. NCD Processor
3.2.2. NCD Model
3.2.3. Clockwise Operator and Clockwise Operator Model
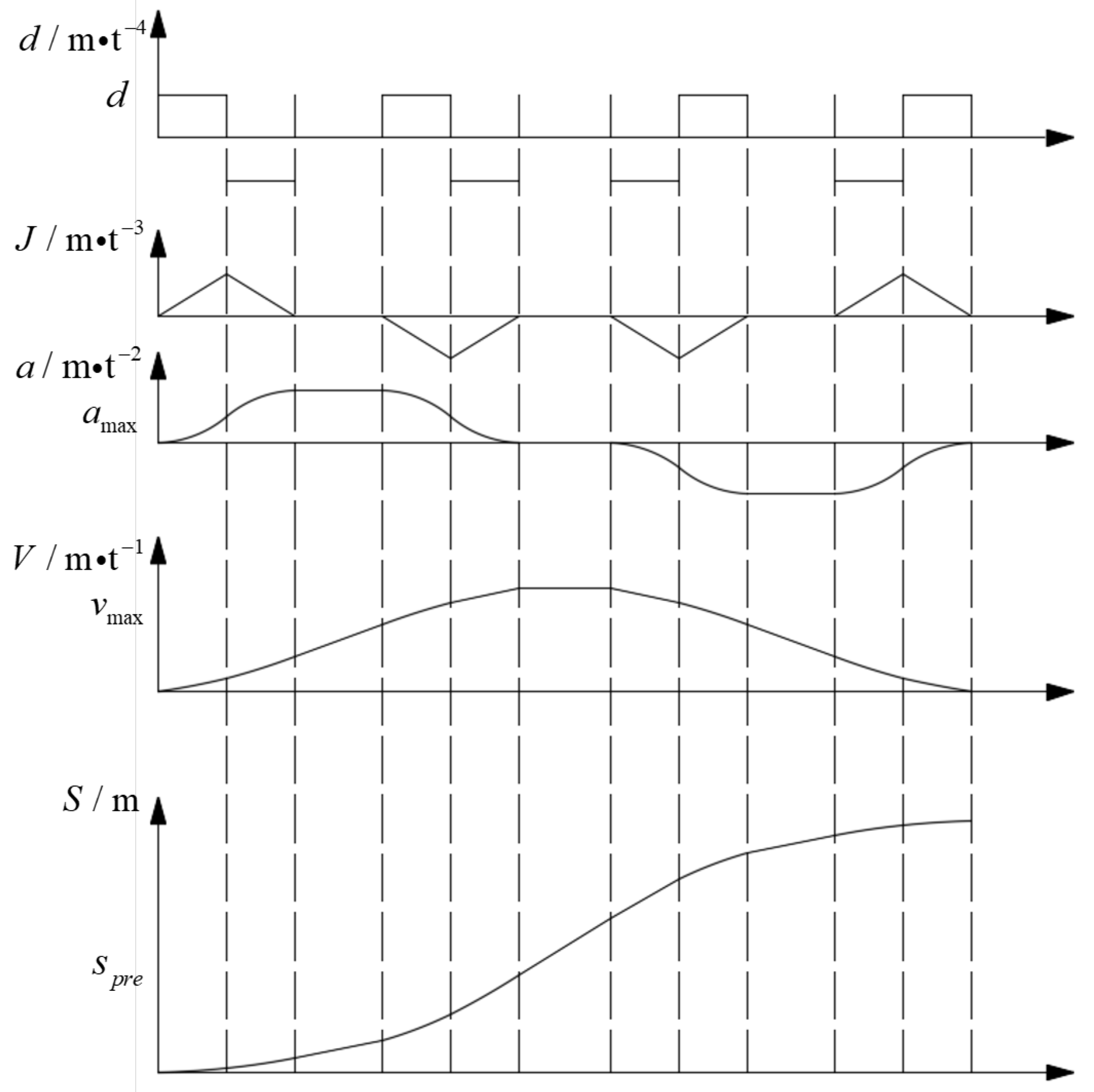
3.3. Hybrid Control Strategy Combining Nonlinear Compensation and Trajectory Shaping
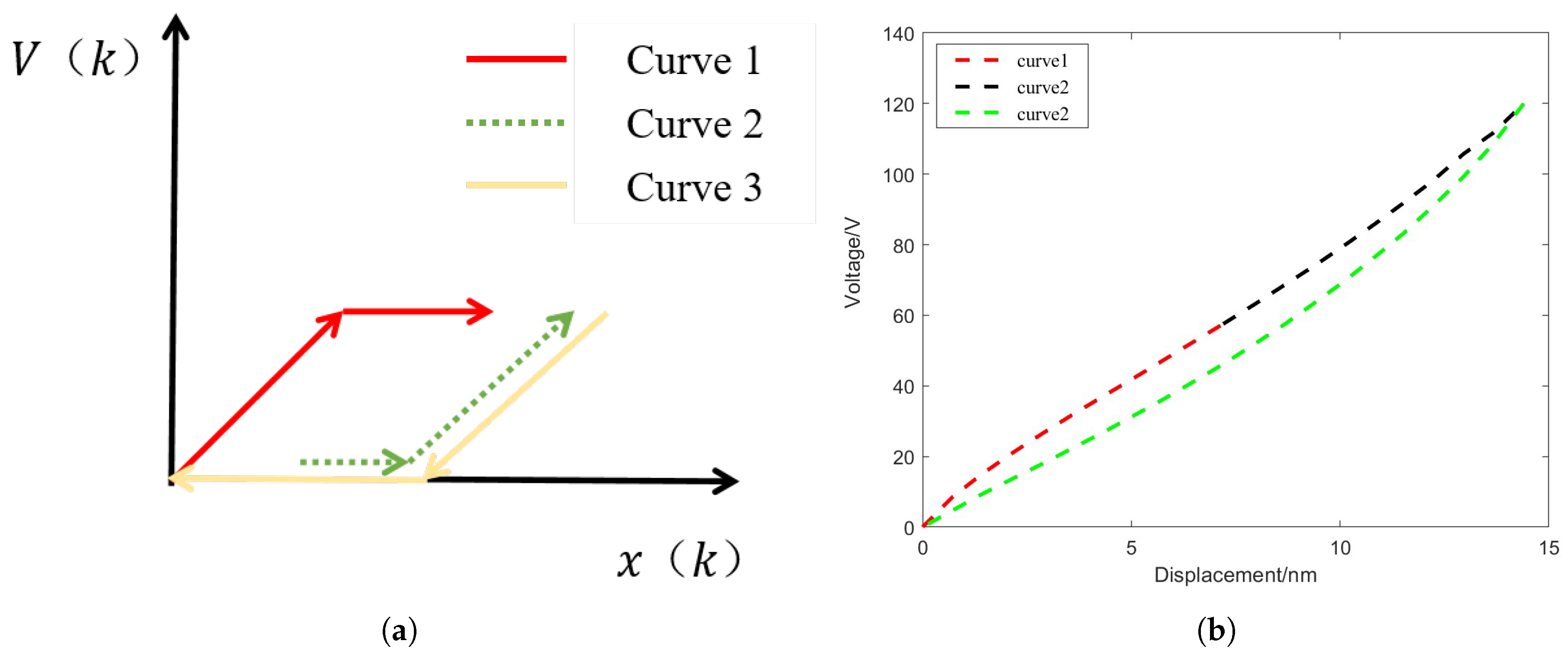
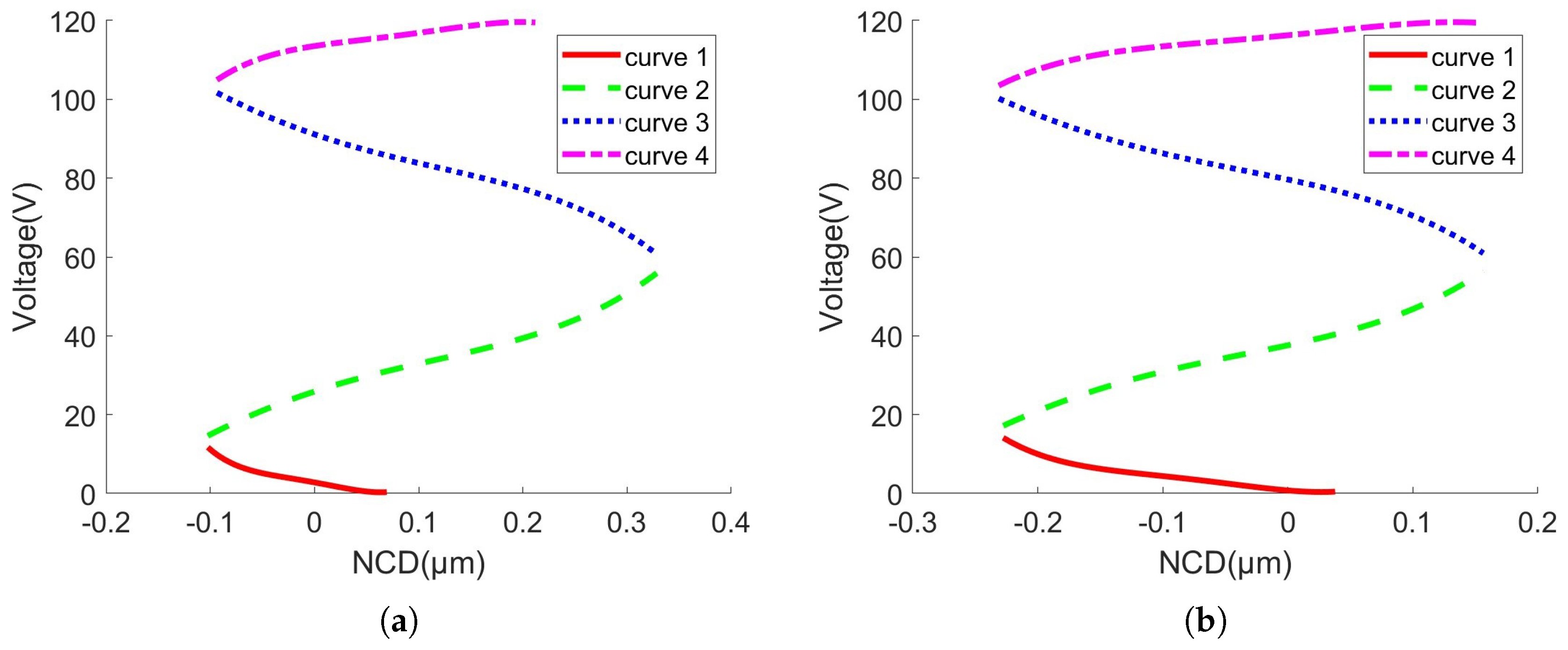
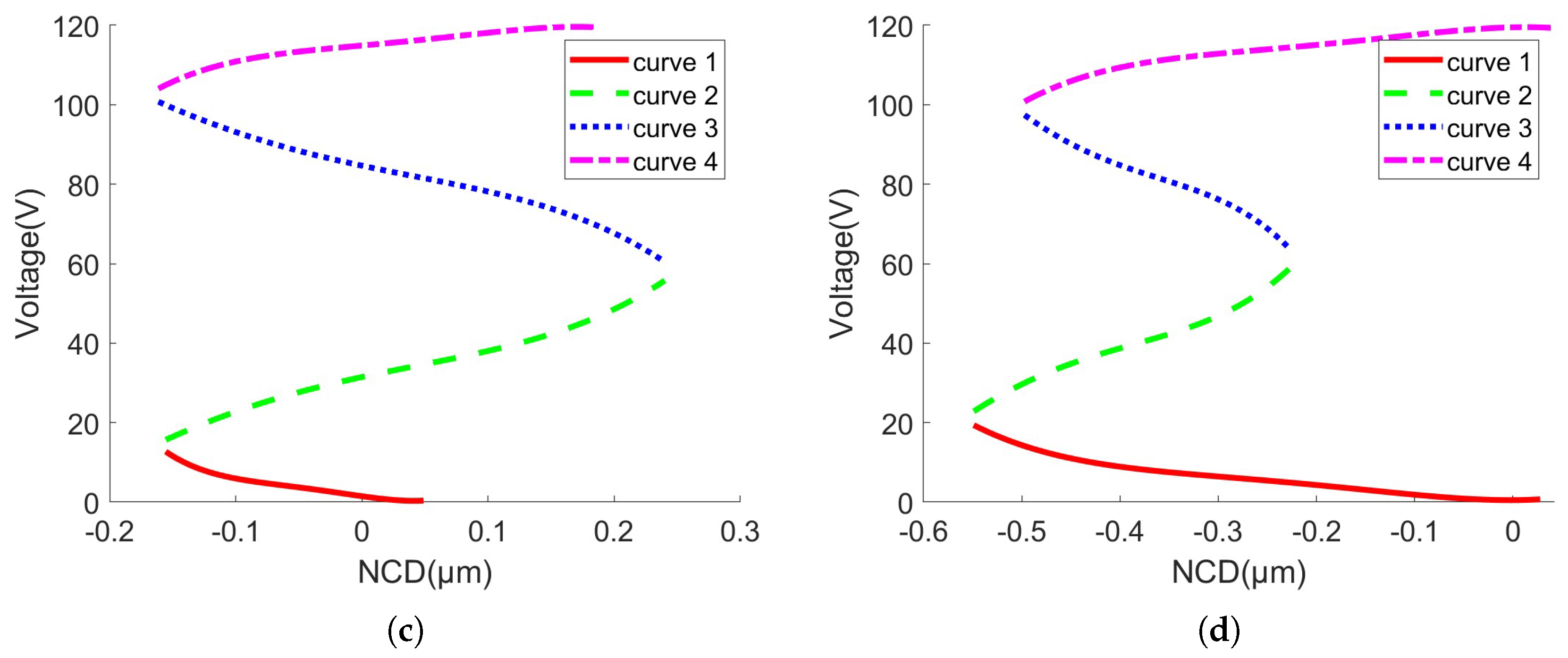
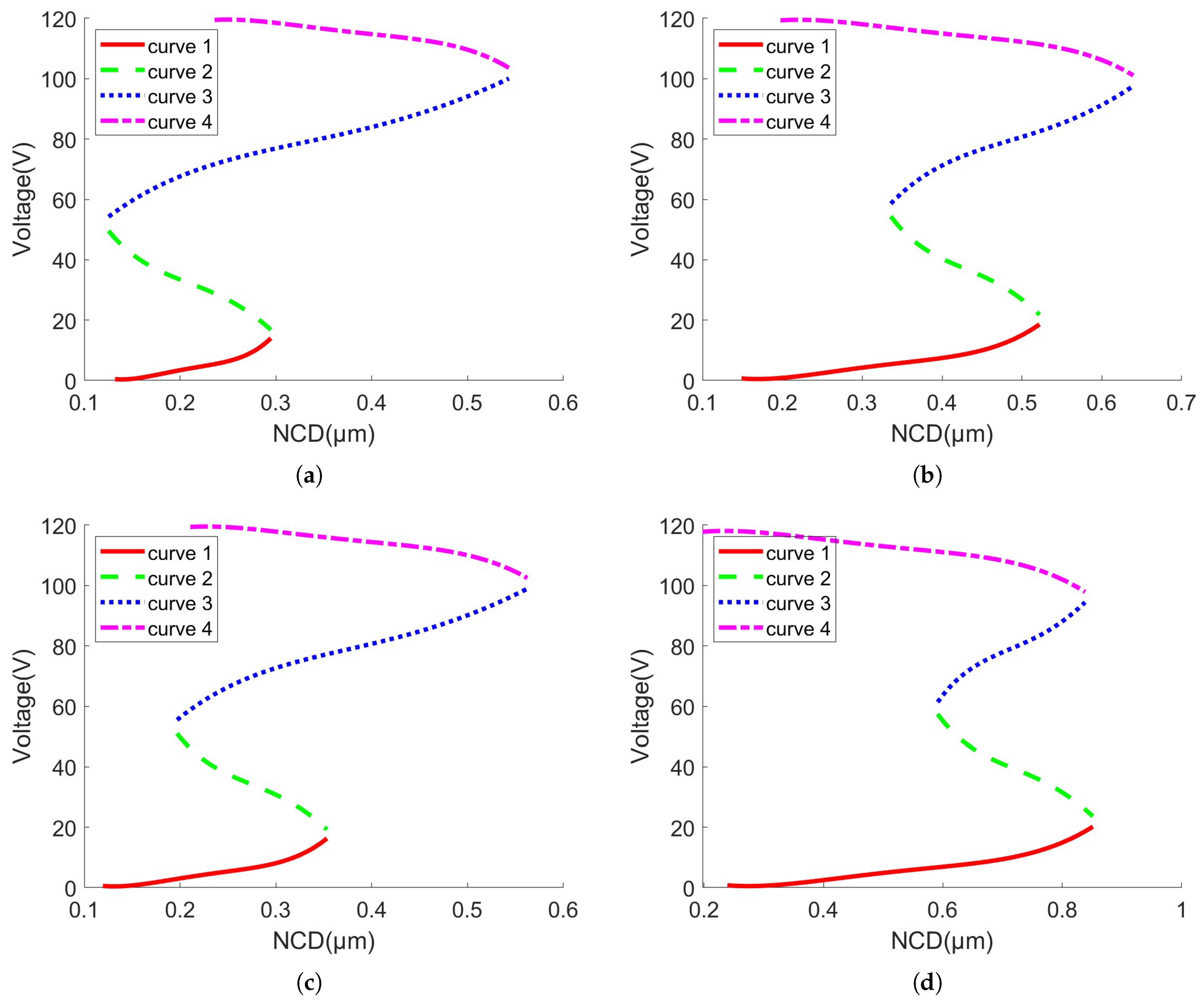
- First Segment (Rising Curve from Zero Displacement to the Inflection Point);The inflection point is determined based on the fuzzy selection of voltage rate. When the voltage rises from 0 to the minimum rate, the relationship between voltage and displacement is described by a unilateral operator, as shown by curve 1 in Figure 7a.
- Second Segment (Rising Curve from the Inflection Point to the Maximum Displacement);In this segment, the relationship between voltage and displacement is described by another unilateral operator, as shown by curve 2 in Figure 7a. During the displacement increase, the voltage rate also increases, which exhibits a trend opposite to the falling unilateral process of the clockwise operator. Therefore, a reverse falling unilateral clockwise operator is used for special modeling in this segment.
- Third Segment (Falling Curve from Maximum Displacement to Zero Displacement).
4. Experiments and Discussion
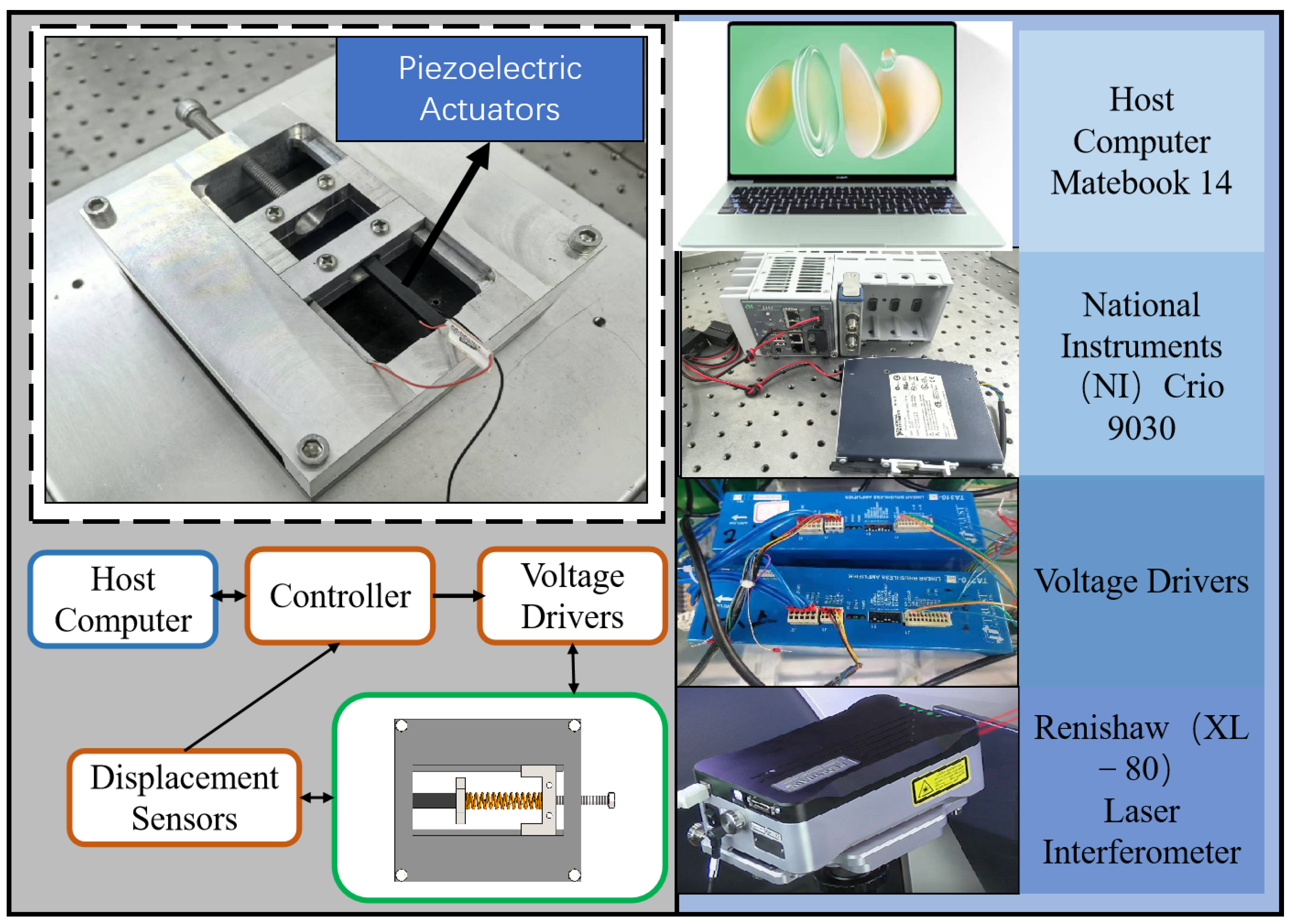
4.1. Experimental Setup
4.2. Separation Results from Model Identification Results
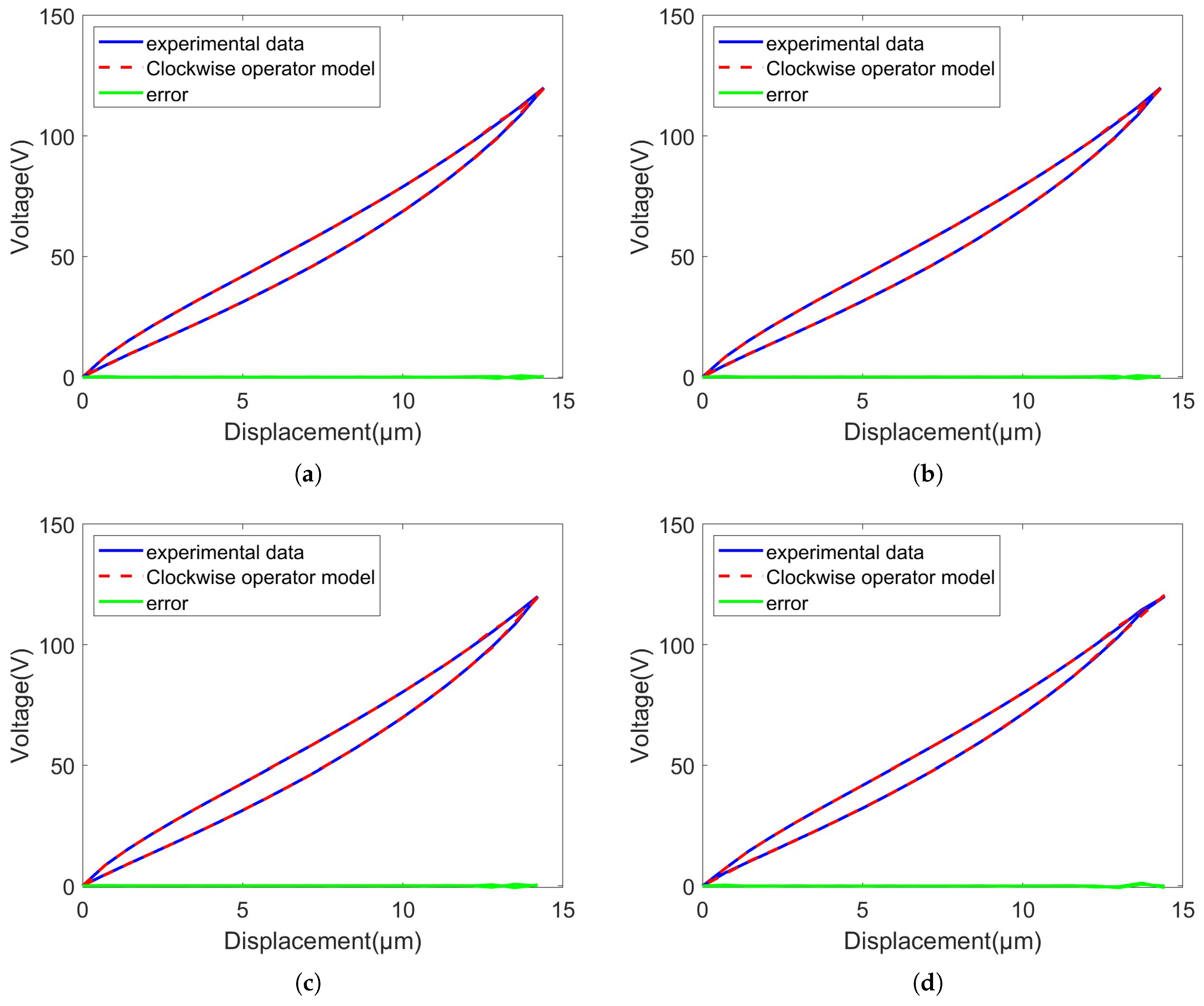
4.3. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Frequency | The First Paragraph | The Second Paragraph | The Third Paragraph |
|---|---|---|---|
| 0.25 Hz | 0.61 | 0.71 | 1.42 |
| 1.22 | 1.42 | 2.84 | |
| 1.83 | 2.13 | 4.26 | |
| 2.44 | 2.84 | 5.68 | |
| 3.05 | 3.55 | 7.10 | |
| 3.66 | 4.26 | 8.52 | |
| 4.27 | 4.97 | 9.94 | |
| 4.88 | 5.68 | 11.36 | |
| 5.49 | 6.39 | 12.78 | |
| 0.5 Hz | 0.61 | 0.71 | 1.42 |
| 1.22 | 1.42 | 2.84 | |
| 1.83 | 2.13 | 4.26 | |
| 2.44 | 2.84 | 5.68 | |
| 3.05 | 3.55 | 7.10 | |
| 3.66 | 4.26 | 8.52 | |
| 4.27 | 4.97 | 9.94 | |
| 4.88 | 5.68 | 11.36 | |
| 5.49 | 6.39 | 12.78 | |
| 1 Hz | 0.61 | 0.71 | 1.42 |
| 1.22 | 1.42 | 2.84 | |
| 1.83 | 2.13 | 4.26 | |
| 2.44 | 2.84 | 5.68 | |
| 3.05 | 3.55 | 7.10 | |
| 3.66 | 4.26 | 8.52 | |
| 4.27 | 4.97 | 9.94 | |
| 4.88 | 5.68 | 11.36 | |
| 5.49 | 6.39 | 12.78 | |
| 2 Hz | 0.61 | 0.71 | 1.42 |
| 1.22 | 1.42 | 2.84 | |
| 1.83 | 2.13 | 4.26 | |
| 2.44 | 2.84 | 5.68 | |
| 3.05 | 3.55 | 7.10 | |
| 3.66 | 4.26 | 8.52 | |
| 4.27 | 4.97 | 9.94 | |
| 4.88 | 5.68 | 11.36 | |
| 5.49 | 6.39 | 12.78 |
| Frequency | The First Paragraph | The Second Paragraph | The Third Paragraph |
|---|---|---|---|
| 0.25 Hz | 0.61 | 0.71 | 1.42 |
| 1.22 | 1.42 | 2.84 | |
| 1.83 | 2.13 | 4.26 | |
| 2.44 | 2.84 | 5.68 | |
| 3.05 | 3.55 | 7.10 | |
| 3.66 | 4.26 | 8.52 | |
| 4.27 | 4.97 | 9.94 | |
| 4.88 | 5.68 | 11.36 | |
| 5.49 | 6.39 | 12.78 | |
| 0.25 Hz | 7.99 | 8.34 | 6.57 |
| −5.13 | 2.06 | −0.64 | |
| 14.03 | −1.38 | 0.17 | |
| −21.51 | −0.35 | 0.38 | |
| 19.18 | −0.33 | 0.41 | |
| −9.38 | −0.30 | 0.72 | |
| 2.65 | −0.43 | 0.80 | |
| 0.56 | 0.07 | 1.07 | |
| −0.85 | −0.37 | 1.08 | |
| 4.34 | 0.69 | 3.71 | |
| 0.5 Hz | 8.02 | 8.39 | 6.65 |
| −5.29 | 1.98 | −0.71 | |
| 15.01 | −1.36 | 0.25 | |
| −24.19 | 0.30 | 0.33 | |
| 23.15 | −0.37 | 0.44 | |
| −12.54 | −0.29 | 0.73 | |
| 4.00 | −0.35 | 0.82 | |
| 0.15 | −0.01 | 1.06 | |
| −0.19 | −0.34 | 1.24 | |
| 3.54 | 0.67 | 3.59 | |
| 1 Hz | 8.15 | 8.45 | 6.40 |
| −5.99 | 1.90 | −0.40 | |
| 18.05 | −1.20 | 0.23 | |
| −30.75 | −0.55 | 0.41 | |
| 31.38 | −0.16 | 0.41 | |
| −18.76 | −0.35 | 0.72 | |
| 6.79 | −0.26 | 0.84 | |
| −0.48 | −0.21 | 1.04 | |
| −0.06 | −0.12 | 1.39 | |
| 3.76 | 0.65 | 3.62 | |
| 2 Hz | 8.05 | 8.32 | 7.08 |
| −4.58 | 2.48 | −1.14 | |
| 12.43 | −1.52 | 0.33 | |
| −18.64 | −0.36 | 0.38 | |
| 16.28 | −0.33 | 0.53 | |
| 0.62 | |||
| 2.36 | 0.94 | ||
| −0.12 | 0.80 | ||
| 1.58 | 2.39 | ||
| 0.69 | 0.60 | −0.13 |
References
- Zhang, F.; Zhang, C.; Zhang, L.; Cheng, R.; Li, R.; Pan, Q.; Huang, Q. Hysteresis segmentation modeling and experiment of piezoelectric ceramic actuator. IEEE Sens. J. 2022, 4, 21153–21162. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Y.; Zhao, Z.; Li, D. Fractional-order control for nano-positioning of piezoelectric actuators. Int. J. Mod. Phys. B 2022, 7, 2250134. [Google Scholar] [CrossRef]
- Li, C.X.; Gu, G.Y.; Yang, M.J.; Zhu, L.M. High-speed tracking of a nanopositioning stage using modified repetitive control. IEEE Trans. Autom. Sci. Eng. 2015, 5, 1467–1477. [Google Scholar] [CrossRef]
- Zhao, D.; Zhu, Z.; Huang, P.; Guo, P.; Zhu, L.; Zhu, Z. Development of a piezoelectrically actuated dual-stage fast tool servo. Mech. Syst. Signal Process. 2020, 144, 106873. [Google Scholar] [CrossRef]
- Liu, Y.T. Recent development of piezoelectric fast tool servo (FTS) for precision machining. Int. J. Precis. Eng. Manuf. 2024, 25, 851–874. [Google Scholar] [CrossRef]
- Xu, A.; Gu, Q.; Yu, H. Mechanism of controllable force generated by coupling inverse effect of piezoelectricity and magnetostriction. Int. J. Precis. Eng. Manuf. Green Technol. 2021, 144, 1297–1307. [Google Scholar] [CrossRef]
- Malayath, G.; Mote, R.G. A review of cutting tools for ultra-precision machining. Mach. Sci. Technol. 2022, 26, 923–976. [Google Scholar]
- Liu, H.; Lai, X.; Wu, W. Time-optimal and jerk-continuous trajectory planning for robot manipulators with kinematic constraints. Robot. Comput. Integr. Manuf. 2013, 29, 309–317. [Google Scholar] [CrossRef]
- Han, C.J.; Song, K.R.; Rim, U.R. An asymmetric S-curve trajectory planning based on an improved jerk profile. Robotica 2024, 42, 2184–2208. [Google Scholar] [CrossRef]
- Mahale, B.; Kumar, N.; De, A.; Pandey, R.; Ranjan, R. A comparative study of energy harvesting performance of polymer-piezoceramic composites fabricated with different piezoceramic constituents. Int. J. Energy Res. 2020, 9, 2694–2708. [Google Scholar] [CrossRef]
- Tao, H.; Wu, J. New poling method for piezoelectric ceramics. J. Mater. Chem. C 2017, 5, 1601–1606. [Google Scholar] [CrossRef]
- Gu, G.Y.; Zhu, L.M.; Su, C.Y.; Ding, H.; Fatikow, S. Modeling and control of piezo-actuated nanopositioning stages: A survey. IEEE Trans. Autom. Sci. Eng. 2014, 13, 313–332. [Google Scholar] [CrossRef]
- Kanchan, M.; Santhya, M.; Bhat, R.; Naik, N. Application of modeling and control approaches of piezoelectric actuators: A review. Technologies 2023, 11, 155. [Google Scholar] [CrossRef]
- Li, P.Z.; Wang, X.D.; Zhao, L.; Zhang, D.F.; Guo, K. Dynamic linear modeling, identification and precise control of a walking piezo-actuated stage. Mech. Syst. Signal Process. 2019, 128, 141–152. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Al Saaideh, M.; Tan, X. The Prandtl–Ishlinskii hysteresis model: Fundamentals of the model and its inverse compensator [Lecture Notes]. IEEE Control Syst. Mag. 2023, 43, 66–84. [Google Scholar] [CrossRef]
- Baziyad, A.G.; Ahmad, I.; Salamah, Y.B. Precision Motion Control of a Piezoelectric Actuator via a Modified Preisach Hysteresis Model and Two-Degree-of-Freedom H-Infinity Robust Control. Micromachines 2023, 6, 1208. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Su, L.; Chen, S. Improved PI hysteresis model with one-sided dead-zone operator for soft joint actuator. Sens. Actuators A Phys. 2022, 12, 114072. [Google Scholar] [CrossRef]
- Yang, L.; Wang, Q.; Xiao, Y.; Li, Z. Hysteresis modeling of piezoelectric actuators based on a TS fuzzy model. Electronics 2022, 11, 2786. [Google Scholar] [CrossRef]
- Garra, R.; Mainardi, F.; Spada, G. A generalization of the Lomnitz logarithmic creep law via Hadamard fractional calculus. Chaos Solitons Fractals 2017, 102, 333–338. [Google Scholar] [CrossRef]
- Dogruer, C.U.; Yıldırım, B. Multiple Model Switching Control of Linear Time-Invariant Systems. Chaos Solitons Fractals 2024, 49, 10961–10975. [Google Scholar] [CrossRef]
- Liu, Y.; Shan, J.; Qi, N. Creep modeling and identification for piezoelectric actuators based on fractional-order system. Mechatronics 2013, 49, 840–847. [Google Scholar] [CrossRef]
- Jung, H.; Shim, J.Y.; Gweon, D.G. New open-loop actuating method of piezoelectric actuators for removing hysteresis and creep. Rev. Sci. Instrum. 2000, 71, 3436–3440. [Google Scholar] [CrossRef]
- Nie, Z.; Cui, Y.; Huang, J.; Wang, Y.; Chen, T. Precision open-loop control of piezoelectric actuator. J. Intell. Mater. Syst. Struct. 2022, 33, 1198–1214. [Google Scholar] [CrossRef]
- Ru, C.; Sun, L. Hysteresis and creep compensation for piezoelectric actuator in open-loop operation. Sens. Actuators A Phys. 2005, 122, 124–130. [Google Scholar]
- Krejci, P.; Kuhnen, K. Inverse control of systems with hysteresis and creep. IEE Proc. Control Theory Appl. 2001, 148, 185–192. [Google Scholar] [CrossRef]
- Kuhnen, K.; Janocha, H. Operator-based compensation of hysteresis, creep and force-dependence of piezoelectric stack actuators. IFAC Proc. Vol. 2000, 33, 407–412. [Google Scholar] [CrossRef]
- Mokaberi, B.; Requicha, A.A.G. Compensation of scanner creep and hysteresis for AFM nanomanipulation. IEEE Trans. Autom. Sci. Eng. 2008, 5, 197–206. [Google Scholar] [CrossRef]
- Yang, Q.; Jagannathan, S. Creep and hysteresis compensation for nanomanipulation using atomic force microscope. Asian J. Control 2009, 11, 182–187. [Google Scholar] [CrossRef]
- Huang, L.C.; Fu, C.M. Spontaneous polarization and dielectric relaxation dynamics of two novel diastereomeric ferroelectric liquid crystals. Acta Phys. Pol. A 2016, 129, 97–102. [Google Scholar] [CrossRef]
- Kang, H.; Shu, F.; Li, Z.; Yang, X. Modeling of bonding piezoelectric stack using conductive adhesive with metal-coated polymer fillers. Mech. Syst. Signal Process. 2023, 194, 110138. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, P.Y.; Shi, H.T.; Guo, J. Fault detection method based on improved dynamic partial least square method. J. Shenyang Jianzhu Univ. Sci. 2024, 40, 167–178. [Google Scholar]




| Nonlinear Factors | Solution | Advantage | Limitation |
|---|---|---|---|
| Hysteresis | Improved Preisach hysteresis model [16]
Improved Prandtl–Ishlinskii (PI) model [17] TS fuzzy model [18] | They address the asymmetric features and dead zone issues in hysteresis characteristics. | Only consider the nonlinear effect of hysteresis on piezoelectric actuators, without taking into account creep characteristics |
| Creep | Logarithmic creep models [19] Linear time-invariant (LTI) creep models [20] Fractional-order models [21] | The models are simple and easy to implement, suitable for open-loop control. | Poor dynamic adaptability; reliance on empirical parameters |
| Hysteresis + Creep | A feedforward controller based on the LTI creep model and hysteresis operator [22] The nonlinear effects of hysteresis and creep [23] A compensator combining the PI model and LTI model [24] | They provide a more comprehensive description of nonlinearity (such as operator superposition, adaptive combination). | Complex calculations and insufficient real-time performance; most of them did not consider strong coupling effects |
| Technical Indicators | Numeric Value | Unit |
|---|---|---|
| Stiffness | 24.5 | µm/N |
| Maximum displacement | 45 ± 1 | µm |
| Displacement loss ratio | 18.3% ± 0.6 | |
| Hinge minimum width d | 1 | mm |
| Hinge cutout radius R | 2 | mm |
| Span length L | 22 | mm |
| Spring recovery force | 1344 | N |
| Piezo minimum preload | 968 | N |
| Natural frequencies | 858.8 | Hz |
| Frequency | |||||
|---|---|---|---|---|---|
| 0.25 Hz | 9.9565 | −2.3243 | 0.0016 | −0.0305 | 0.0694 |
| 0.5 Hz | 1.1026 | −2.5842 | 0.0019 | −0.0403 | 0.0385 |
| 1 Hz | 1.0219 | −2.3784 | 0.0017 | −0.0336 | 0.0489 |
| 2 Hz | 1.2875 | −3.1169 | 0.0024 | −0.0661 | 0.0279 |
| Frequency | |||||
|---|---|---|---|---|---|
| 0.25 Hz | 1.7520 | −0.0012 | 0.0249 | 0.1321 | |
| 0.5 Hz | 2.3277 | −0.0017 | 0.0449 | 0.1484 | |
| 1 Hz | 1.8969 | −0.0013 | 0.0314 | 0.1194 | |
| 2 Hz | 2.2908 | −0.0023 | 0.0661 | 0.2259 |
| 0.25 Hz | 0.5 Hz | 1 Hz | 2 Hz | |
|---|---|---|---|---|
| MRE | 3.89% | 4.89% | 5.48% | 4.78% |
| MMSE | 0.11% | 0.12% | 0.15% | 0.28% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, D.; Qin, Z.; Yang, Y.; Yu, X.; Li, C. Hybrid Compensation Method for Non-Uniform Creep Difference and Hysteresis Nonlinearity of Piezoelectric-Actuated Machine Tools Under S-Shaped Curve Trajectory. Appl. Sci. 2025, 15, 4207. https://doi.org/10.3390/app15084207
An D, Qin Z, Yang Y, Yu X, Li C. Hybrid Compensation Method for Non-Uniform Creep Difference and Hysteresis Nonlinearity of Piezoelectric-Actuated Machine Tools Under S-Shaped Curve Trajectory. Applied Sciences. 2025; 15(8):4207. https://doi.org/10.3390/app15084207
Chicago/Turabian StyleAn, Dong, Zicheng Qin, Yixiao Yang, Xiaoyang Yu, and Chaofeng Li. 2025. "Hybrid Compensation Method for Non-Uniform Creep Difference and Hysteresis Nonlinearity of Piezoelectric-Actuated Machine Tools Under S-Shaped Curve Trajectory" Applied Sciences 15, no. 8: 4207. https://doi.org/10.3390/app15084207
APA StyleAn, D., Qin, Z., Yang, Y., Yu, X., & Li, C. (2025). Hybrid Compensation Method for Non-Uniform Creep Difference and Hysteresis Nonlinearity of Piezoelectric-Actuated Machine Tools Under S-Shaped Curve Trajectory. Applied Sciences, 15(8), 4207. https://doi.org/10.3390/app15084207







