Experimental and Numerical Investigation of Vibration-Suppression Efficacy in Spring Pendulum Pounding-Tuned Mass Damper
Abstract
1. Introduction
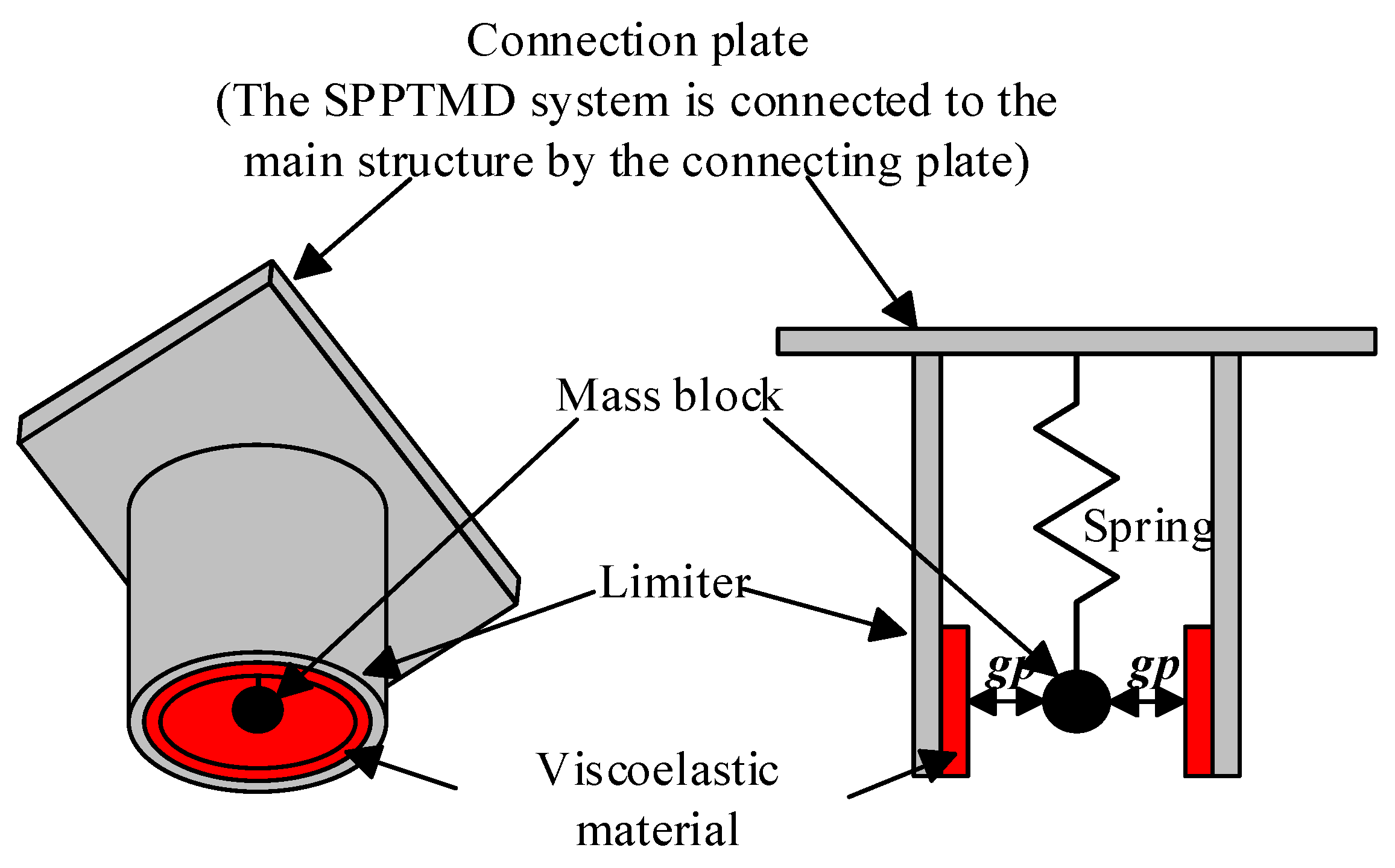
2. Mechanism of SPPTMD and Numerical Model of Structure–SPPTMD System
2.1. Mechanism of the SP
2.2. Mechanism of the SPPTMD
2.3. Numerical Model of the Structure–SPPTMD System
3. Experimental Model and Setups
4. Experimental Results
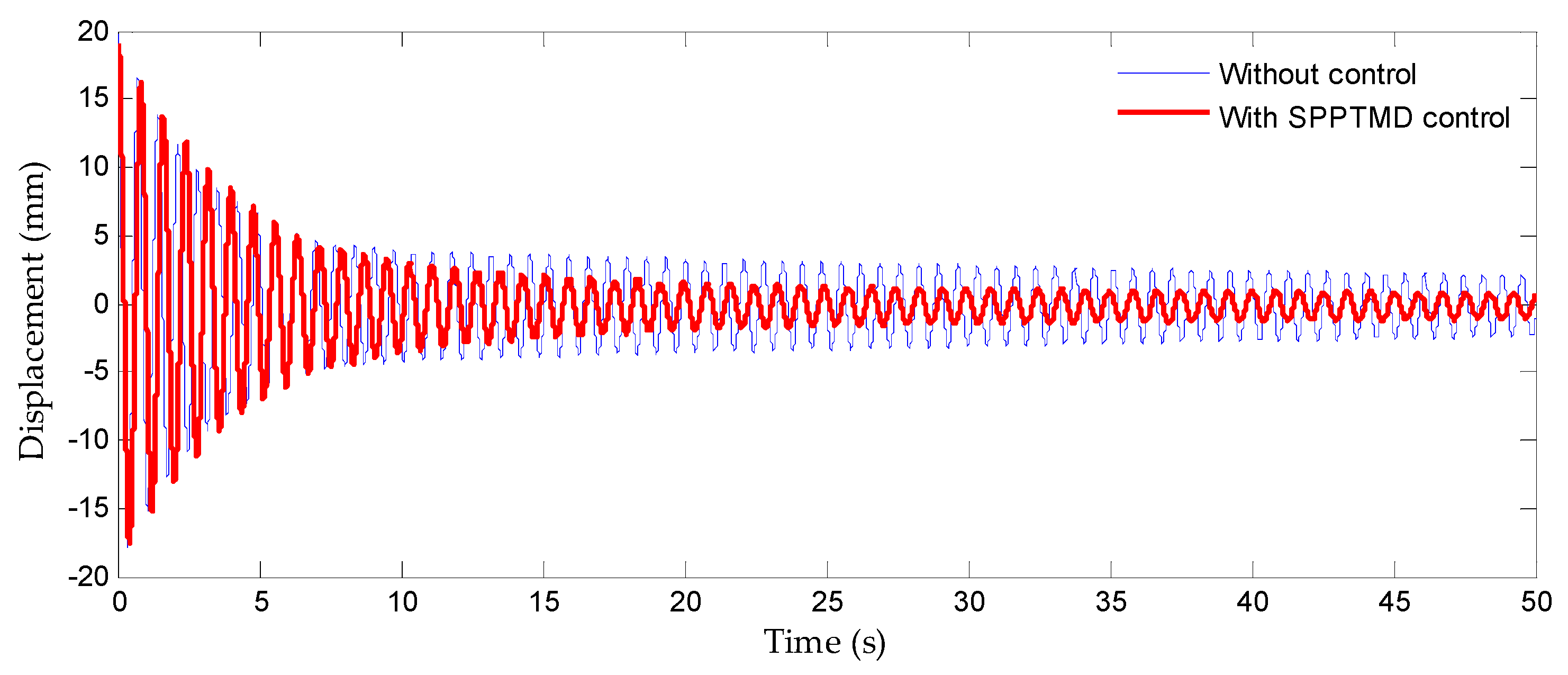
4.1. Free Vibration Case
4.2. Resonant Vibration Case
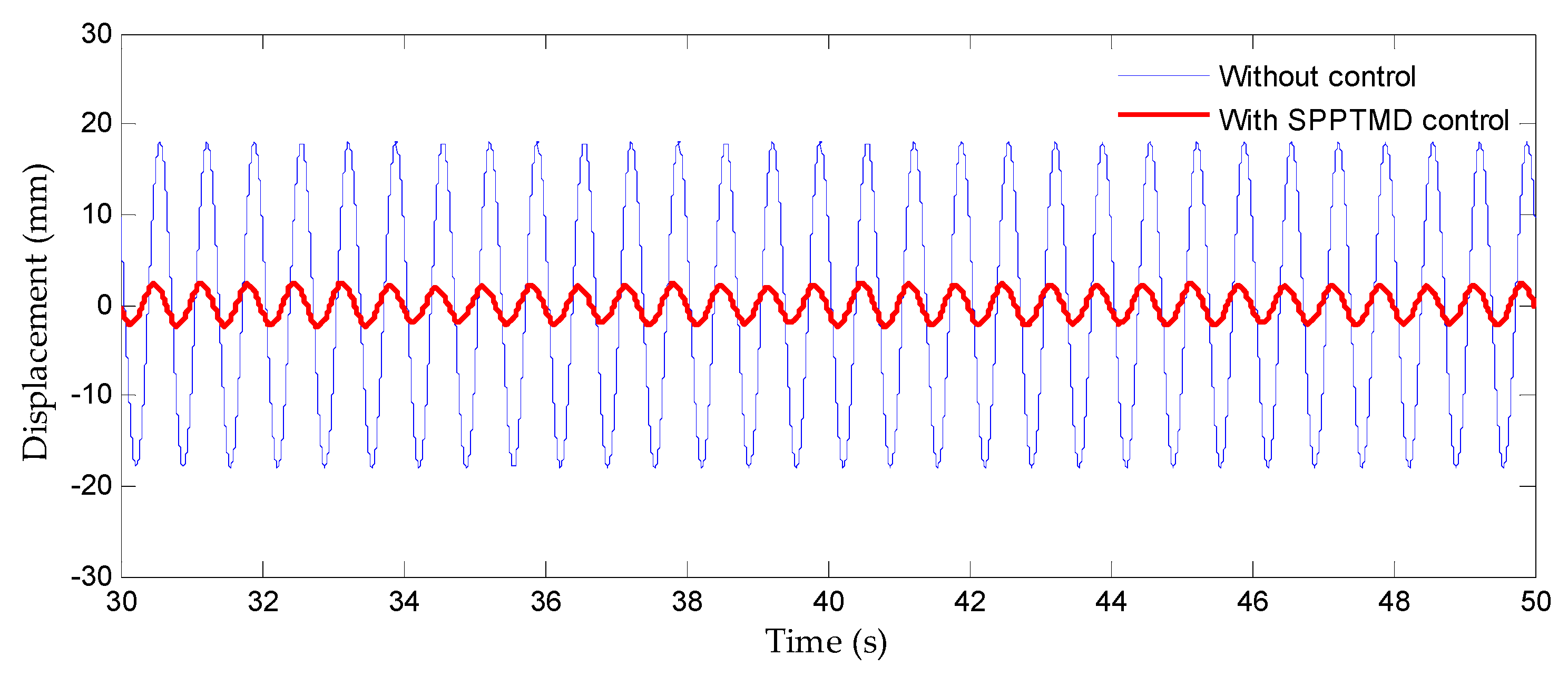
4.3. Forced Vibration Response Under Variable Excitation Frequencies
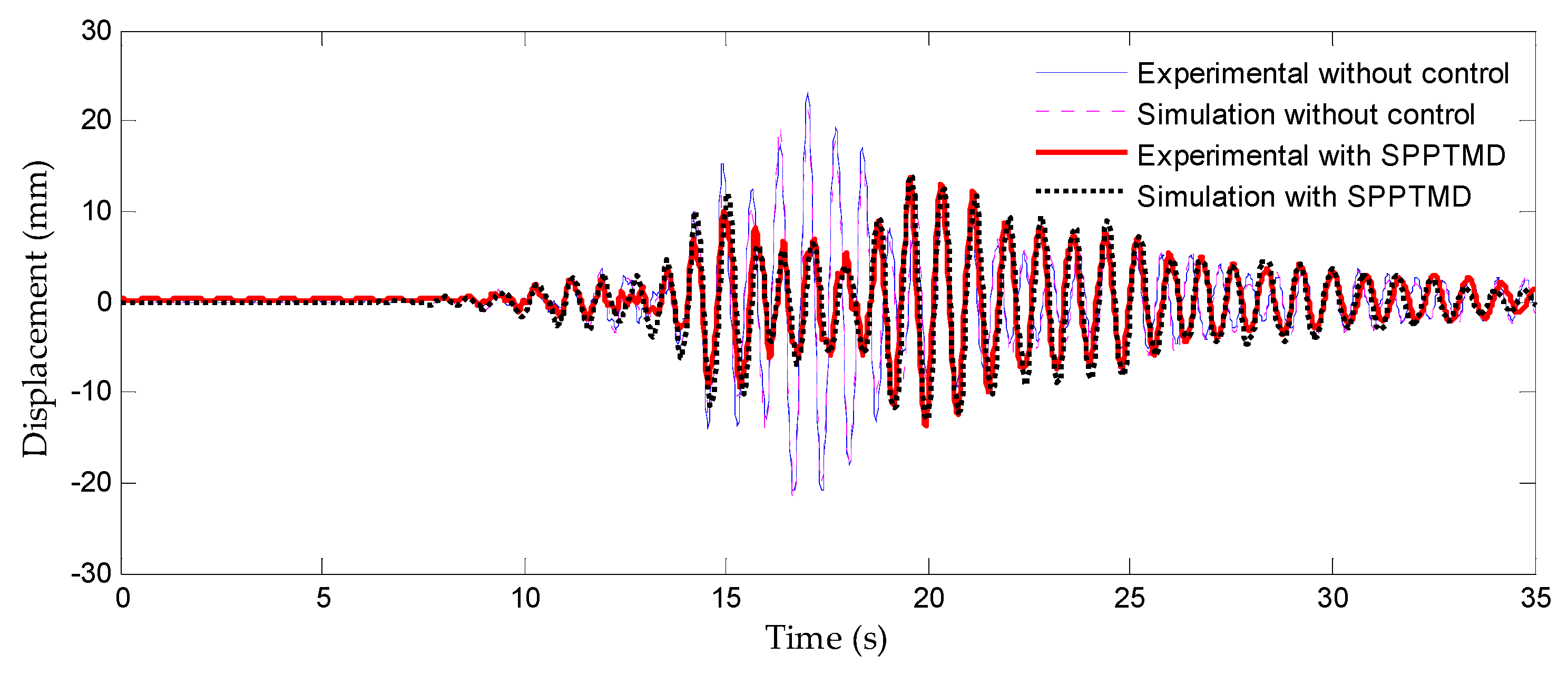
4.4. Earthquake Excitation Case
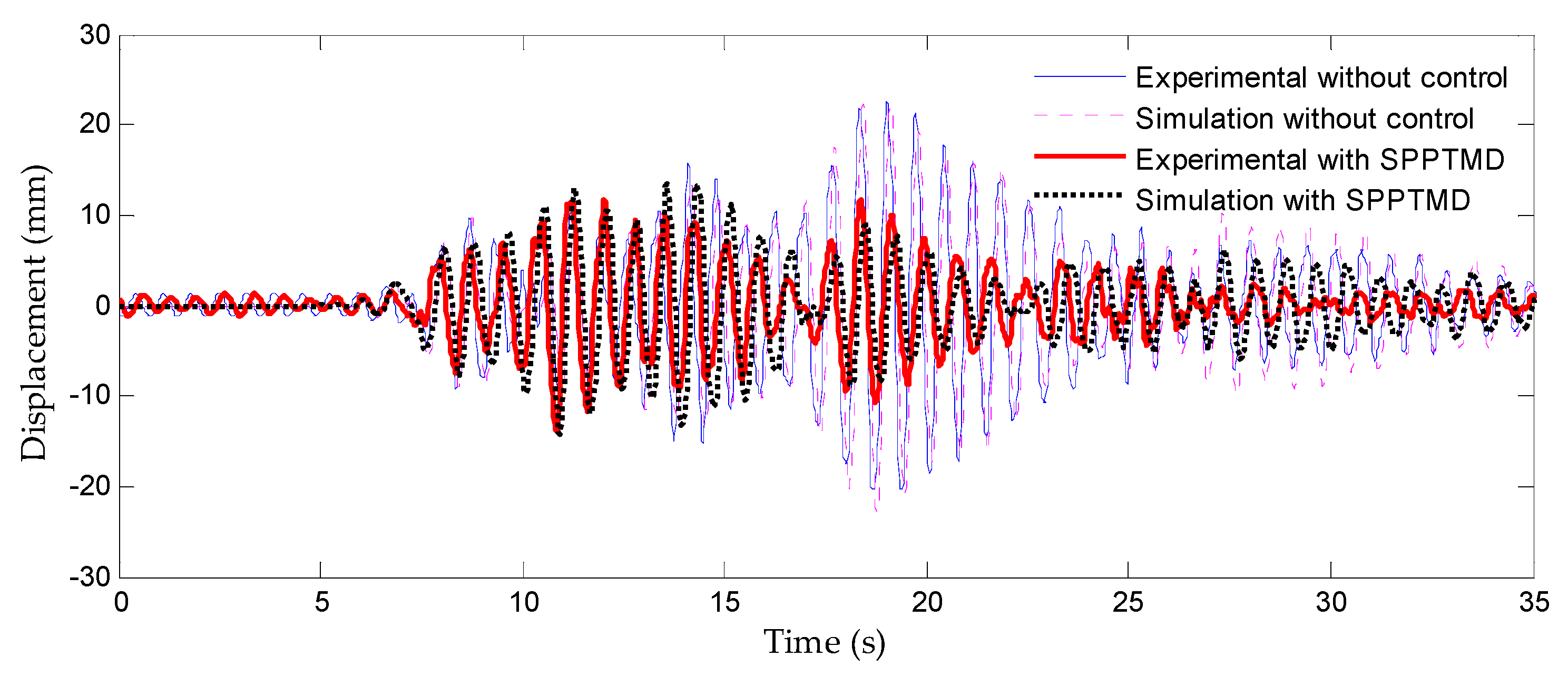
4.4.1. Vibration-Suppression Effectiveness
4.4.2. Validation of Numerical Model
5. Conclusions
- (1)
- The proposed SPPTMD demonstrated high vibration-reduction efficiency in experimental tests on the two-story frame structure, significantly shortening the structural settling time when implemented while achieving 86.13% displacement mitigation under resonant conditions;
- (2)
- The displacement vibration-reduction rate of SPPTMD consistently remained above 33% across forced vibration tests, with excitation frequencies ranging from 1.5 Hz to 2.9 Hz. These findings conclusively demonstrate that the SPPTMD maintains pronounced vibration-reduction effects on the structure regardless of variations in external excitation frequencies while exhibiting robust performance across all tested operational conditions;
- (3)
- The experimental data demonstrate that the SPPTMD effectively mitigates structural displacement responses under seismic loading, achieving a peak vibration-reduction rate of 60.25% and an RMS reduction rate of 58.35%, with all results indicating that the vibration control capability of the SPPTMD increases when the ground is softer;
- (4)
- A comparative analysis of displacement response data obtained from shake-table testing and numerical simulations revealed close agreement in displacement time–history curves, demonstrating that the implemented impact force model and equations of motion accurately capture the dynamic behavior of the SPPTMD–structure coupled system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yadav, D.; Sahoo, D.R. Validation of hysteretic behavior and prediction of energy dissipation potential of aluminium shear yielding devices. Int. J. Mech. Sci. 2021, 194, 106204. [Google Scholar] [CrossRef]
- Azandariani, M.G.; Abdolmaleki, H.; Azandariani, A.G. Numerical and analytical investigation of cyclic behavior of steel ring dampers (srds). Thin-Walled Struct. 2020, 151, 106751. [Google Scholar] [CrossRef]
- Aliakbari, F.; Garivani, S.; Aghakouchak, A.A. An energy based method for seismic design of frame structures equipped with metallic yielding dampers considering uniform inter-story drift concept. Eng. Struct. 2020, 205, 110114. [Google Scholar] [CrossRef]
- Kumar, S.; Chakraborty, S.K. Reduction of seismic vibration in multistorey structures retrofitted with nonlinear viscous dampers using mode summation method. Appl. Math. Model. 2020, 86, 294–310. [Google Scholar] [CrossRef]
- Idels, O.; Lavan, O. Optimization-based seismic design of steel moment-resisting frames with nonlinear viscous dampers. Struct. Control Health Monit. 2021, 28, e2655. [Google Scholar] [CrossRef]
- Vaezi, M.; Pourzangbar, A.; Fadavi, M.; Mousavi, S.M.; Sabbahfar, P.; Brocchini, M. Effects of stiffness and configuration of brace-viscous damper systems on the response mitigation of offshore jacket platforms. Appl. Ocean Res. 2021, 107, 102482. [Google Scholar] [CrossRef]
- Jarrahi, H.; Asadi, A.; Khatibinia, M.; Etedali, S. Optimal design of rotational friction dampers for improving seismic performance of inelastic structures. J. Build. Eng. 2020, 27, 100960. [Google Scholar] [CrossRef]
- Lupini, A.; Shim, J.; Epureanu, B.I. Experimental and Computational Study of a Tuned Damper with Frictional Contacts. AIAA J. 2020, 58, 3607–3613. [Google Scholar] [CrossRef]
- Jaisee, S.; Yue, F.; Ooi, Y.H. A state-of-the-art review on passive friction dampers and their applications. Eng. Struct. 2021, 235, 112022. [Google Scholar] [CrossRef]
- Zafarani, M.M.; Halabian, A.M. A new supervisory adaptive strategy for the control of hysteretic multi-story irregular buildings equipped with MR-dampers. Eng. Struct. 2020, 217, 110786. [Google Scholar] [CrossRef]
- Lozoya-Santos, J.D.J.; Tudon-Martinez, J.C.; Morales-Menendez, R.; Sename, O.; Spaggiari, A.; Ramírez-Mendoza, R. A General Modeling Approach for Shock Absorbers: 2 DoF MR Damper Case Study. Front. Mater. 2021, 7, 590328. [Google Scholar] [CrossRef]
- Sapiński, B.; Orkisz, P.; Jastrzębski, Ł. Experimental Analysis of Power Flows in the Regenerative Vibration Reduction System with a Magnetorheological Damper. Energies 2021, 14, 848. [Google Scholar] [CrossRef]
- Tian, L.; Li, W.F.; Wang, Z.L. Study on suspended mass pendulums for vibration control of transmission tower under seismic excitation. Adv. Mater. Res. 2012, 446–449, 3323–3327. [Google Scholar] [CrossRef]
- Huang, C.; Huo, L.S.; Gao, H.G.; Li, H.N. Control performance of suspended mass pendulum with the consideration of out-of-plane vibrations. Struct. Control Health Monit. 2018, 25, e2217. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, K.; Mercan, O.; Chen, H.; Tan, P. Experimental and numerical studies on the optimal design of tuned mass dampers for vibration control of high-rise structures. Eng. Struct. 2020, 211, 110486. [Google Scholar] [CrossRef]
- Raze, G.; Kerschen, G. H∞ optimization of multiple tuned mass dampers for multimodal vibration control. Comput. Struct. 2021, 248, 106485. [Google Scholar] [CrossRef]
- Masri, S. Theory of the dynamic vibration neutralizer with motion-limiting stops. J. Appl. Mech. 1972, 39, 563–568. [Google Scholar] [CrossRef]
- Masri, S.F.; Caffrey, J.P. Response of Pounding Dynamic Vibration Neutralizer Under Harmonic and Random Excitation. J. Appl. Mech. 2019, 86, 021003. [Google Scholar] [CrossRef]
- Li, S.; Sun, L.; Kong, F. Vibration Control Performance Analysis and Shake-Table Test of a Pounding Tuned Rotary Mass Damper under the Earthquake. Shock Vib. 2019, 2019, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.-C.; Kong, X.-R.; Yang, Z.-X.; Zhang, H.-L. Targeted energy transfer and parameter design of a nonlinear vibration absorber. J. Vib. Eng. 2011, 24, 111–117. [Google Scholar]
- Zhang, P.; Ren, L.; Li, H.; Jia, Z.; Jiang, T. Control of wind-induced vibration of transmission tower-line system by using a spring pendulum. Math. Probl. Eng. 2015, 2015, 671632. [Google Scholar] [CrossRef]
- Tan, J.; Jiang, J.; Liu, M.; Feng, Q.; Zhang, P.; Ho, S.C.M. Implementation of Shape Memory Alloy Sponge as Energy Dissipating Material on Pounding Tuned Mass Damper: An Experimental Investigation. Appl. Sci. 2019, 9, 1079. [Google Scholar] [CrossRef]
- Tian, L.; Zhou, M.; Qiu, C.; Pan, H.; Rong, K. Seismic response control of transmission tower-line system using SMA-based TMD. Struct. Eng. Mech. 2020, 74, 129–143. [Google Scholar]
- Tiwari, N.D.; Gogoi, A.; Hazra, B.; Wang, Q. A shape memory alloy-tuned mass damper inerter system for passive control of linked-SDOF structural systems under seismic excitation. J. Sound Vib. 2021, 494, 115893. [Google Scholar] [CrossRef]
- Zhang, P.; Song, G.; Li, H.-N.; Lin, Y.-X. Seismic control of power transmission tower using pounding TMD. J. Eng. Mech. 2013, 139, 1395–1406. [Google Scholar] [CrossRef]
- Wang, W.; Hua, X.; Wang, X.; Chen, Z.; Song, G. Numerical modeling and experimental study on a novel pounding tuned mass damper. J. Vib. Control 2018, 24, 4023–4036. [Google Scholar] [CrossRef]
- Collette, F.S. A combined tuned absorber and pendulum impact damper under random excitation. J. Sound Vib. 1998, 216, 199–213. [Google Scholar] [CrossRef]
- Li, H.; Zhang, P.; Song, G.; Patil, D.; Mo, Y. Robustness study of the pounding tuned mass damper for vibration control of subsea jumpers. Smart Mater. Struct. 2015, 24, 095001. [Google Scholar] [CrossRef]
- Song, G.; Zhang, P.; Li, L.; Singla, M.; Patil, D.; Li, H.; Mo, Y. Vibration control of a pipeline structure using pounding tuned mass damper. J. Eng. Mech. 2016, 142, 04016031. [Google Scholar] [CrossRef]
- Yang, W.; Yang, S.; Zhang, Z.; Wang, N.; Song, G. Experimental study on damping performance of a pounding tuned mass damper to vibration suppression of vortex-induced vibration. Ocean. Eng. 2022, 249, 110860. [Google Scholar] [CrossRef]
- Lin, W.; Song, G.; Chen, S. PTMD Control on a Benchmark TV Tower under Earthquake and Wind Load Excitations. Appl. Sci. 2017, 7, 425. [Google Scholar] [CrossRef]
- Fu, X.; Li, H.N.; Li, J.X.; Zhang, P. A pounding spacer damper and its application on transmission line subjected to fluctuating wind load. Struct. Control Health Monit. 2017, 24, e1950. [Google Scholar] [CrossRef]
- Yin, X.; Liu, Y.; Song, G.; Mo, Y. Suppression of bridge vibration induced by moving vehicles using pounding tuned mass dampers. J. Bridge Eng. 2018, 23, 04018047. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Hua, X.; Song, G.; Chen, Z. Vibration control of vortex-induced vibrations of a bridge deck by a single-side pounding tuned mass damper. Eng. Struct. 2018, 173, 61–75. [Google Scholar] [CrossRef]
- Lin, W.; Lin, Y.; Song, G.; Li, J. Multiple Pounding Tuned Mass Damper (MPTMD) control on benchmark tower subjected to earthquake excitations. Earthq. Struct 2016, 11, 1123–1141. [Google Scholar] [CrossRef]
- Yin, X.; Song, G.; Liu, Y. Vibration suppression of wind/traffic/bridge coupled system using multiple pounding tuned mass dampers (MPTMD). Sensors 2019, 19, 1133. [Google Scholar] [CrossRef]
- Tan, J.; Ho, M.; Chun, S.; Zhang, P.; Jiang, J. Experimental Study on Vibration Control of Suspended Piping System by Single-Sided Pounding Tuned Mass Damper. Appl. Sci. 2019, 9, 285. [Google Scholar] [CrossRef]
- Liu, M.; Yang, W.; Chen, W.; Li, H. Experimental investigation on multi-mode vortex-induced vibration control of stay cable installed with pounding tuned mass dampers. Smart Struct. Syst. 2019, 23, 579–587. [Google Scholar]
- Tian, L.; Rong, K.; Bi, K.; Zhang, P. A Bidirectional Pounding Tuned Mass Damper and its Application to Transmission Tower-Line Systems under Seismic Excitations. Int. J. Struct. Stab. Dyn. 2019, 19, 25. [Google Scholar] [CrossRef]
- Ghasemi, M.R.; Shabakhty, N.; Enferadi, M.H. Vibration control of offshore jacket platforms through shape memory alloy pounding tuned mass damper (SMA-PTMD). Ocean Eng. 2019, 191, 106348. [Google Scholar] [CrossRef]
- Zhao, N.; Huang, G.; Liu, R.; Zhang, P.; Lu, C.; Song, G. Novel Hidden Pounding Tuned Mass Damper for Vibration Control of a Cantilevered Traffic Signal Structure. J. Eng. Mech. 2020, 146, 04020005. [Google Scholar] [CrossRef]
- Duan, Y.; Wang, W.; Zhang, P.; Huo, L.; Song, G. New Type of Pounding Tuned Mass Damper for Confined Space. J. Aerosp. Eng. 2020, 33, 04020023. [Google Scholar] [CrossRef]
- Wang, W.; Hua, X.; Chen, Z.; Wang, X.; Song, G. Modeling, simulation, and validation of a pendulum-pounding tuned mass damper for vibration control. Struct. Control Health Monit. 2019, 26, e2326. [Google Scholar] [CrossRef]
- Wang, W.; Yang, Z.; Hua, X.; Chen, Z.; Wang, X.; Song, G. Evaluation of a pendulum pounding tuned mass damper for seismic control of structures. Eng. Struct. 2021, 228, 111554. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.; Yuan, D.; Xu, Z. An improved state space model for parts of nonlinear oscillation systems and its numerical method. Chin. J. Appl. Mech. 2002, 112, 116–167. [Google Scholar] [CrossRef]
- Yang, Z.; Xia, Q.; Liu, S. The spring pendulum under different controlled parameters. Coll. Phys. 2011, 5, 23–26+42. [Google Scholar]
- Gitterman, M. Spring pendulum: Parametric excitation vs an external force. Phys. A Stat. Mech. Its Appl. 2010, 389, 3101–3108. [Google Scholar] [CrossRef]
- De Sousa, M.; Marcus, F.; Caldas, I.; Viana, R. Energy distribution in intrinsically coupled systems: The spring pendulum paradigm. Phys. A Stat. Mech. Its Appl. 2018, 509, 1110–1119. [Google Scholar] [CrossRef]
- van der Weele, J.P.; de Kleine, E. The order—Chaos—Order sequence in the spring pendulum. Phys. A Stat. Mech. Its Appl. 1996, 228, 245–272. [Google Scholar] [CrossRef][Green Version]
- Chandra, M. Spring Pendulum: A Nonlinear Paradigm. SSRN 2018. [Google Scholar] [CrossRef]
- Wang, Q.; Li, H.-N.; Zhang, P. Vibration Control of a High-Rise Slender Structure with a Spring Pendulum Pounding Tuned Mass Damper. Actuators 2021, 10, 44. [Google Scholar] [CrossRef]







| Vibration-Reduction Ratio | Excitation Frequency | |||||||
|---|---|---|---|---|---|---|---|---|
| 1.5 Hz | 1.7 Hz | 1.9 Hz | 2.1 Hz | 2.3 Hz | 2.5 Hz | 2.7 Hz | 2.9 Hz | |
| Peak (%) | 86.13 | 62.73 | 52.68 | 42.94 | 44.38 | 38.64 | 37.59 | 33.87 |
| RMS (%) | 87.88 | 63.12 | 55.29 | 47.92 | 42.85 | 35.69 | 33.71 | 31.89 |
| Class | ID | Earthquake | Event Date | Station |
|---|---|---|---|---|
| I | EQ1 (experiment + simulation) | Northridge | 1994 | Lake Hughes |
| EQ2 (simulation) | Duzce Turkey | 1999 | Lamont | |
| EQ3 (simulation) | Chi-Chi | 1999 | ILA050 | |
| II | EQ4 (experiment + simulation) | Kern County, | 1952 | Taft |
| EQ5 (simulation) | Morgan Hill | 1984 | Foster City | |
| EQ6 (simulation) | Landers | 1992 | Desert Hot Springs | |
| III | EQ7 (experiment + simulation) | Imperial Valley | 1940 | El Centro |
| EQ8 (simulation) | Borrego | 1942 | El Centro | |
| EQ9 (simulation) | Coyote Lake | 1979 | Gilroy | |
| IV | EQ10 (experiment + simulation) | Loma Prieta | 1989 | APEEL 2 |
| EQ11 (simulation) | Kobe | 1995 | Kobe University | |
| EQ12 (simulation) | Iwate | 2008 | HKD161 |
| Class | ID | (%) | (%) | Average | |
|---|---|---|---|---|---|
| (%) | |||||
| I | EQ1 | 44.83 | 30.81 | 42.90 | 36.06 |
| EQ2 | 36.92 | 49.80 | |||
| EQ3 | 46.94 | 27.56 | |||
| II | EQ4 | 38.66 | 42.22 | 44.06 | 36.60 |
| EQ5 | 41.53 | 19.81 | |||
| EQ6 | 52.00 | 47.78 | |||
| III | EQ7 | 47.08 | 55.93 | 45.15 | 44.45 |
| EQ8 | 43.20 | 24.71 | |||
| EQ9 | 45.18 | 52.70 | |||
| IV | EQ10 | 38.60 | 55.19 | 50.27 | 56.78 |
| EQ11 | 51.97 | 56.79 | |||
| EQ12 | 60.25 | 58.35 | |||
| ID | Type | Peak Value | |
|---|---|---|---|
| No Ctrl | SPPTMD | ||
| EQ1 | Experimental (mm) | 23.17 | 13.68 |
| Simulation (mm) | 21.92 | 13.97 | |
| Error (%) | 5.36 | −2.07 | |
| EQ2 | Experimental (mm) | 22.67 | 13.91 |
| Simulation (mm) | 22.93 | 14.34 | |
| Error (%) | −1.18 | −3.04 | |
| EQ3 | Experimental (mm) | 16.87 | 9.96 |
| Simulation (mm) | 17.33 | 10.21 | |
| Error (%) | −2.72 | −2.49 | |
| EQ4 | Experimental (mm) | 21.40 | 13.13 |
| Simulation (mm) | 21.62 | 14.44 | |
| Error (%) | −1.00 | −9.99 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zhang, L.; Li, H.; Guo, X. Experimental and Numerical Investigation of Vibration-Suppression Efficacy in Spring Pendulum Pounding-Tuned Mass Damper. Appl. Sci. 2025, 15, 4297. https://doi.org/10.3390/app15084297
Wang Q, Zhang L, Li H, Guo X. Experimental and Numerical Investigation of Vibration-Suppression Efficacy in Spring Pendulum Pounding-Tuned Mass Damper. Applied Sciences. 2025; 15(8):4297. https://doi.org/10.3390/app15084297
Chicago/Turabian StyleWang, Qi, Lipeng Zhang, Hongnan Li, and Xin Guo. 2025. "Experimental and Numerical Investigation of Vibration-Suppression Efficacy in Spring Pendulum Pounding-Tuned Mass Damper" Applied Sciences 15, no. 8: 4297. https://doi.org/10.3390/app15084297
APA StyleWang, Q., Zhang, L., Li, H., & Guo, X. (2025). Experimental and Numerical Investigation of Vibration-Suppression Efficacy in Spring Pendulum Pounding-Tuned Mass Damper. Applied Sciences, 15(8), 4297. https://doi.org/10.3390/app15084297









