Cold Wave Recognition and Wind Power Forecasting Technology Considering Sample Scarcity and Meteorological Periodicity Characteristics
Abstract
:1. Introduction
- Proposed cold wave recognition criterion: By considering regional meteorological changes and wind turbine operation characteristics, a cold wave discriminant criterion is proposed. This criterion can accurately identify cold-wave conditions in the region, especially with regard to the duration of the cold wave, providing hour-level accuracy.
- Improved U-Net classification model: Building on the U-Net model, a multi-modal classification method is proposed to optimize the model for the seasonal characteristics of cold waves. The improved model not only accurately forecasts the occurrence time of cold waves but also enhances the recognition accuracy of small-sample cold wave events using cold wave samples generated by an adversarial network.
- Construction of wind power combination forecasting model for cold-wave conditions: By combining cold wave recognition results with the Ns-Transformer model, a combined forecasting model for wind power is developed. This model effectively improves the accuracy of day-ahead wind power forecasting during cold conditions and offers a new solution for power forecasting under extreme weather events.
2. Analysis of the Impact of Cold Wave Events on Wind Power Output
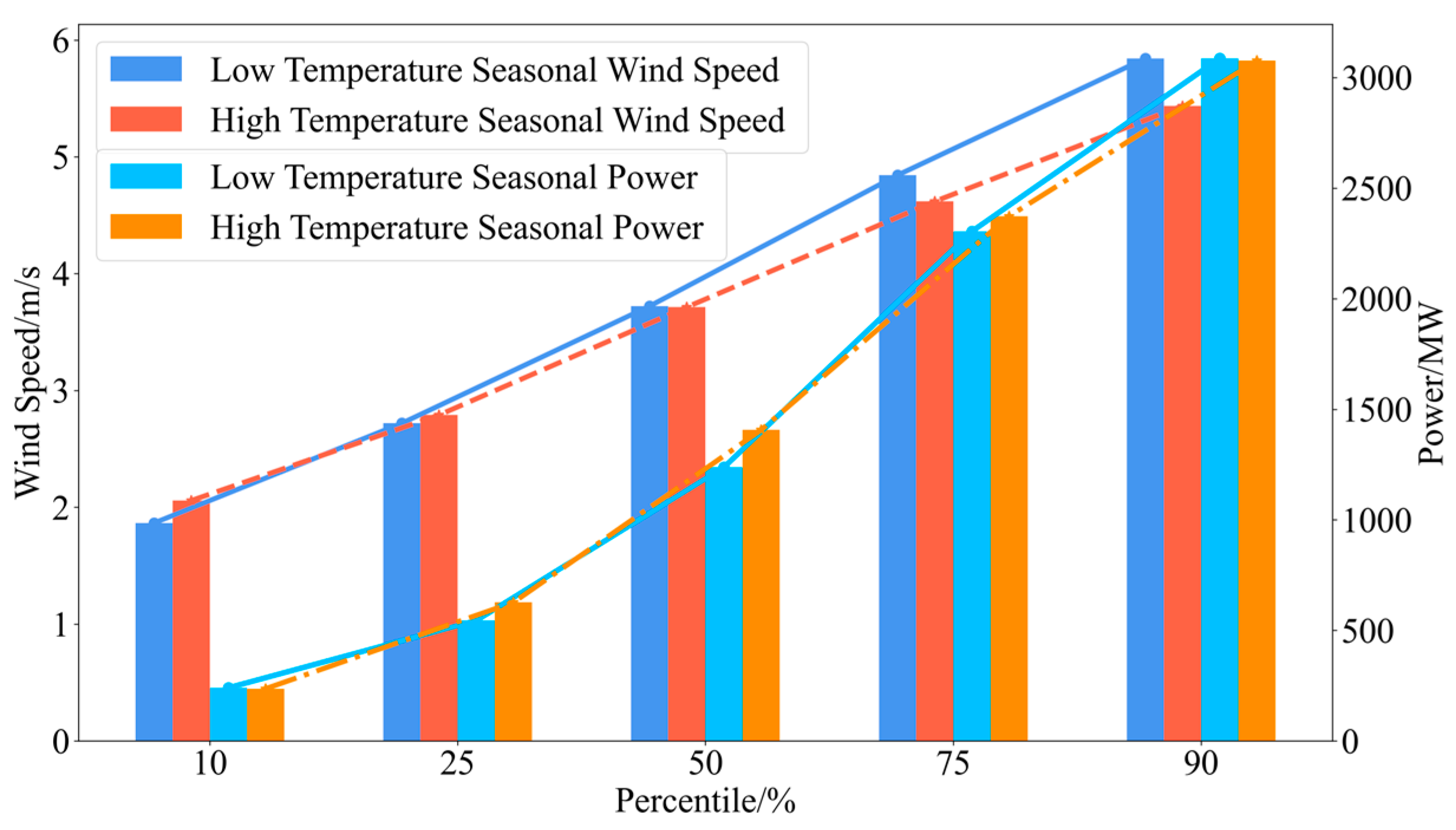
2.1. Influence of Temperature on Wind Power Output
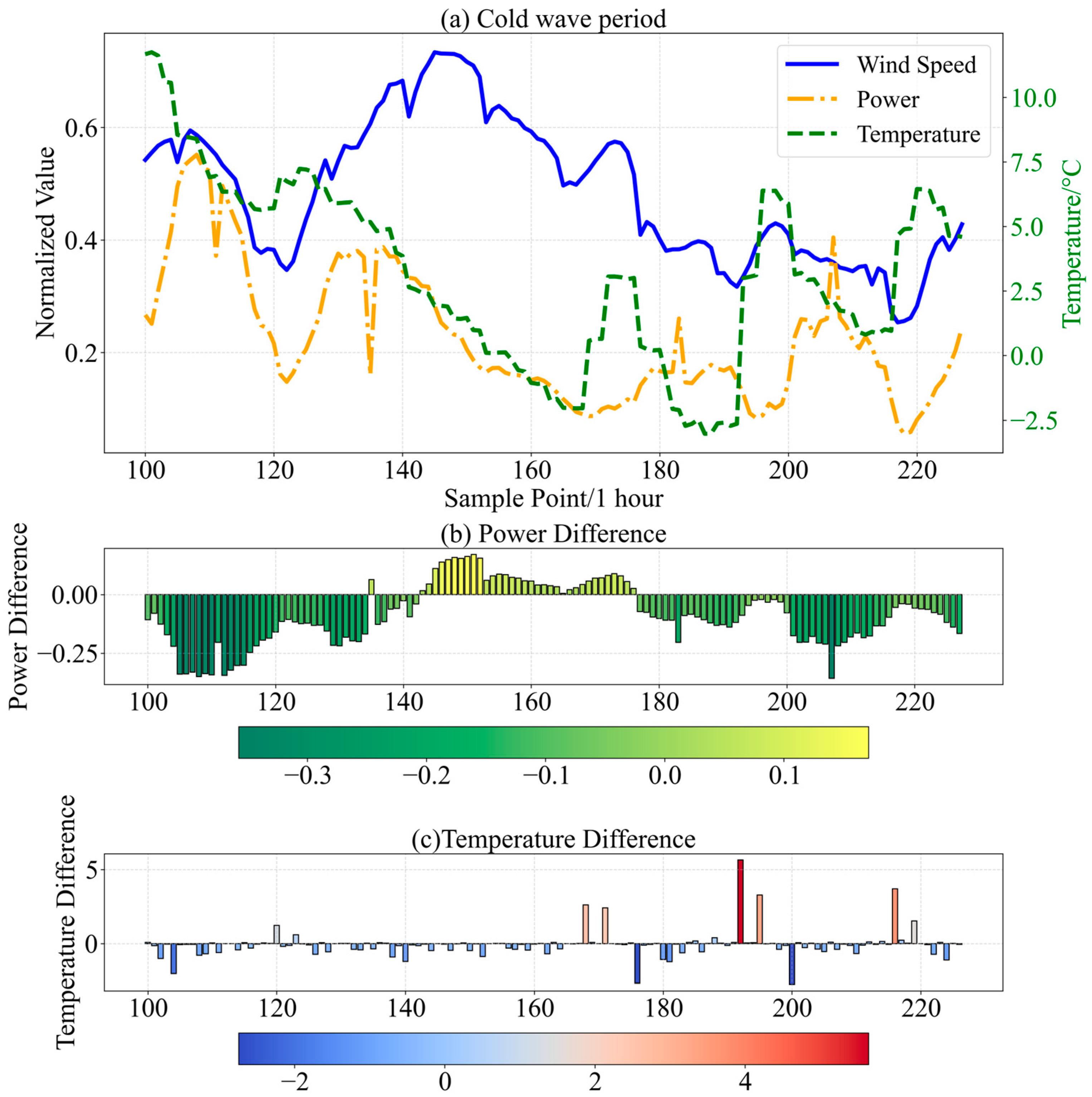
2.2. Influence of Cold Wave Events on Wind Power Output
2.3. Cold Wave Event Criteria
2.3.1. Cold Wave Event Meteorology Criteria
2.3.2. Comprehensive Judgment Conditions Based on Cold Wave Events Judgment and Wind Power Deviation
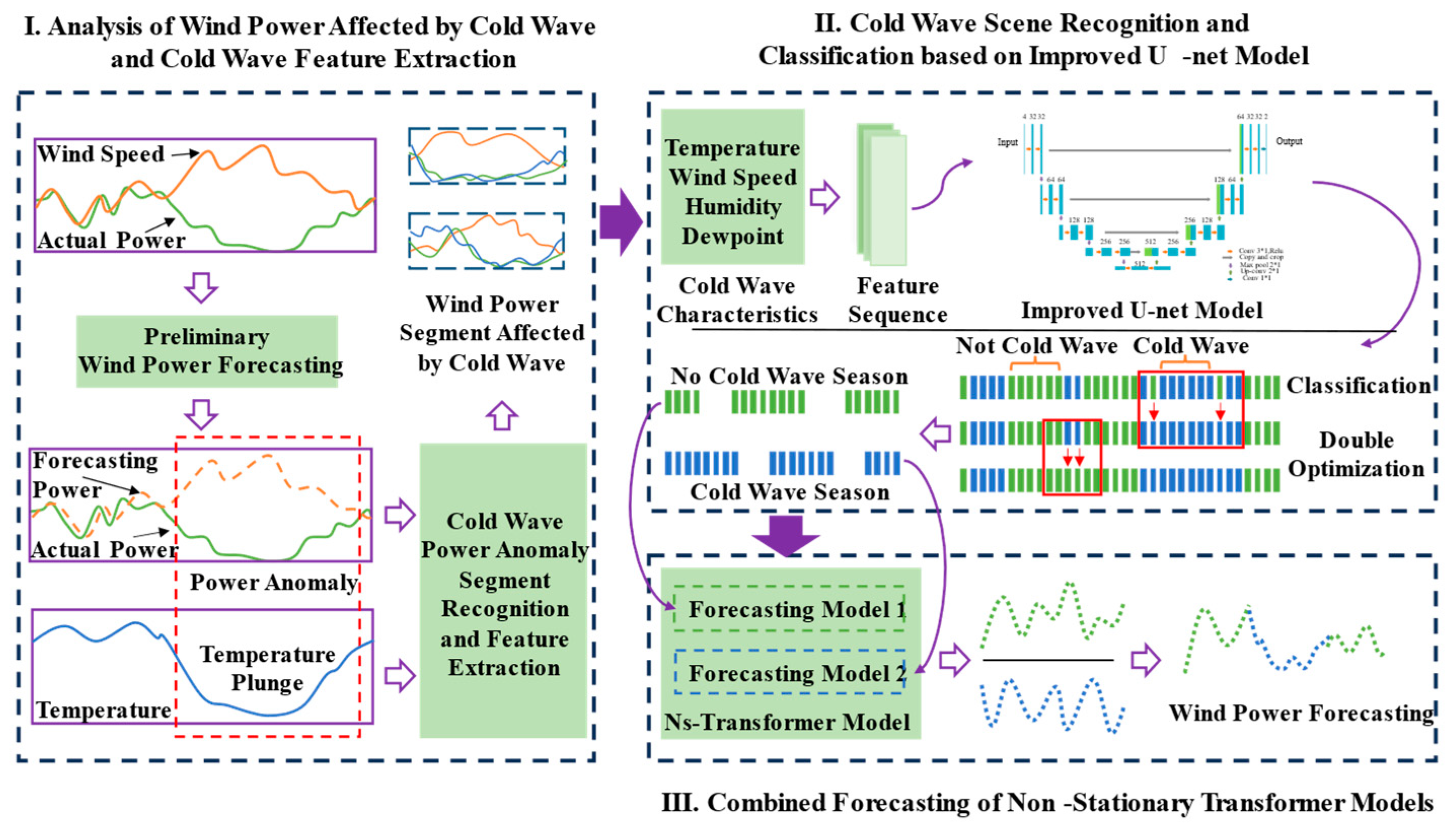
3. The Method Presented in This Paper
3.1. Cold Wave Recognition Process
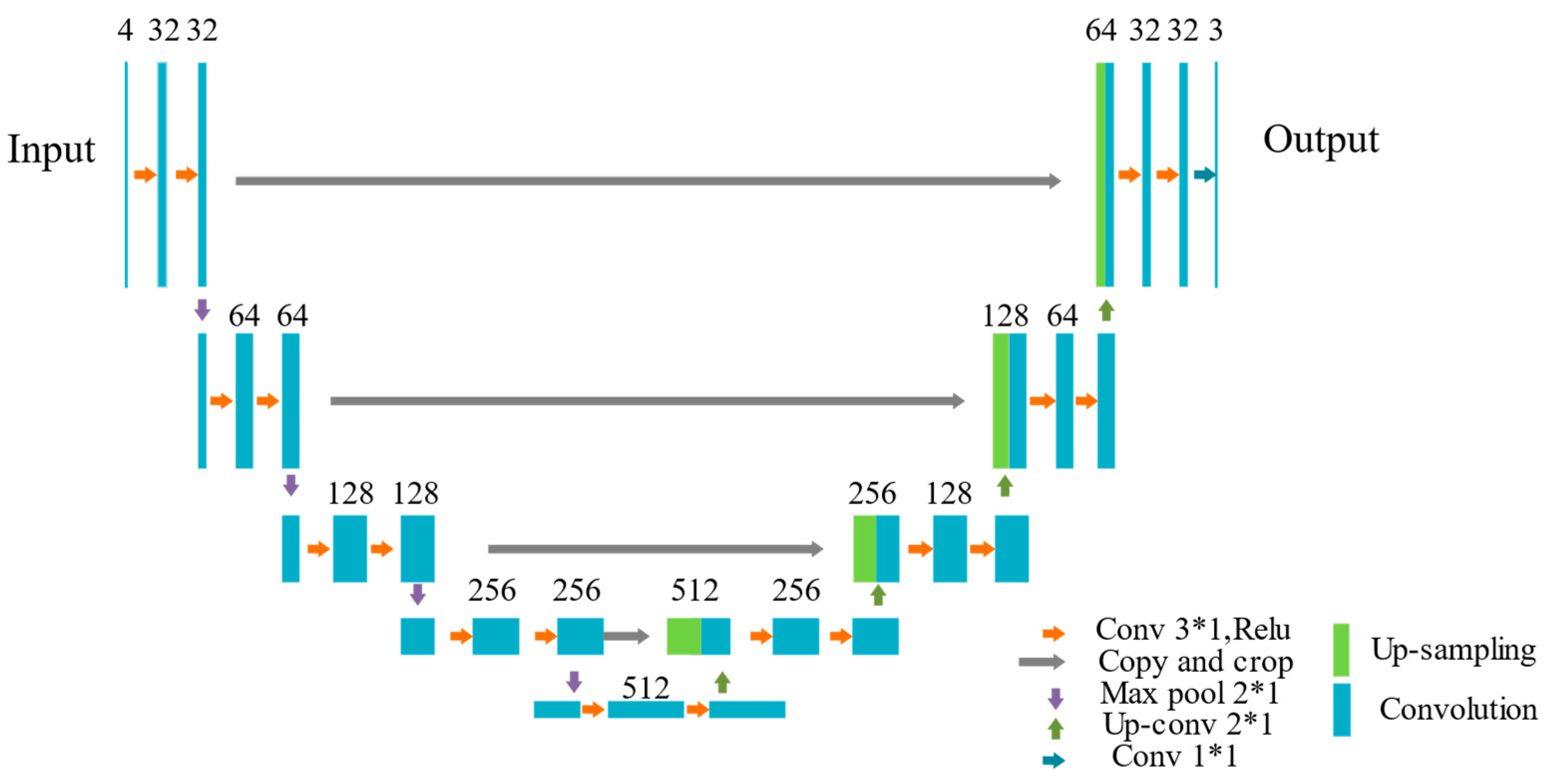
3.1.1. Cold Wave Weather Recognition Model Based on Improved U-Net
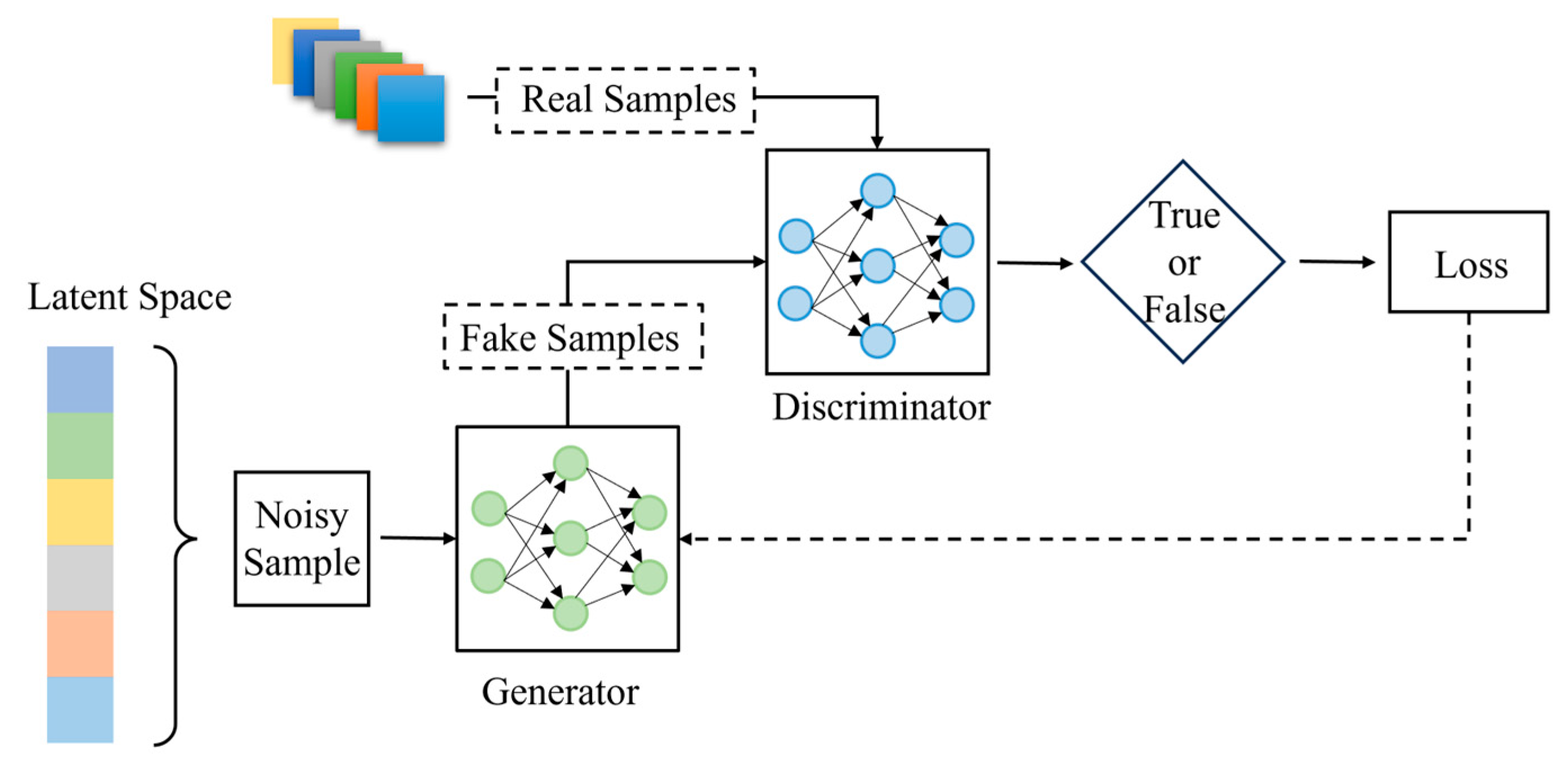
3.1.2. Cold Wave Recognition Under Small Sample Conditions
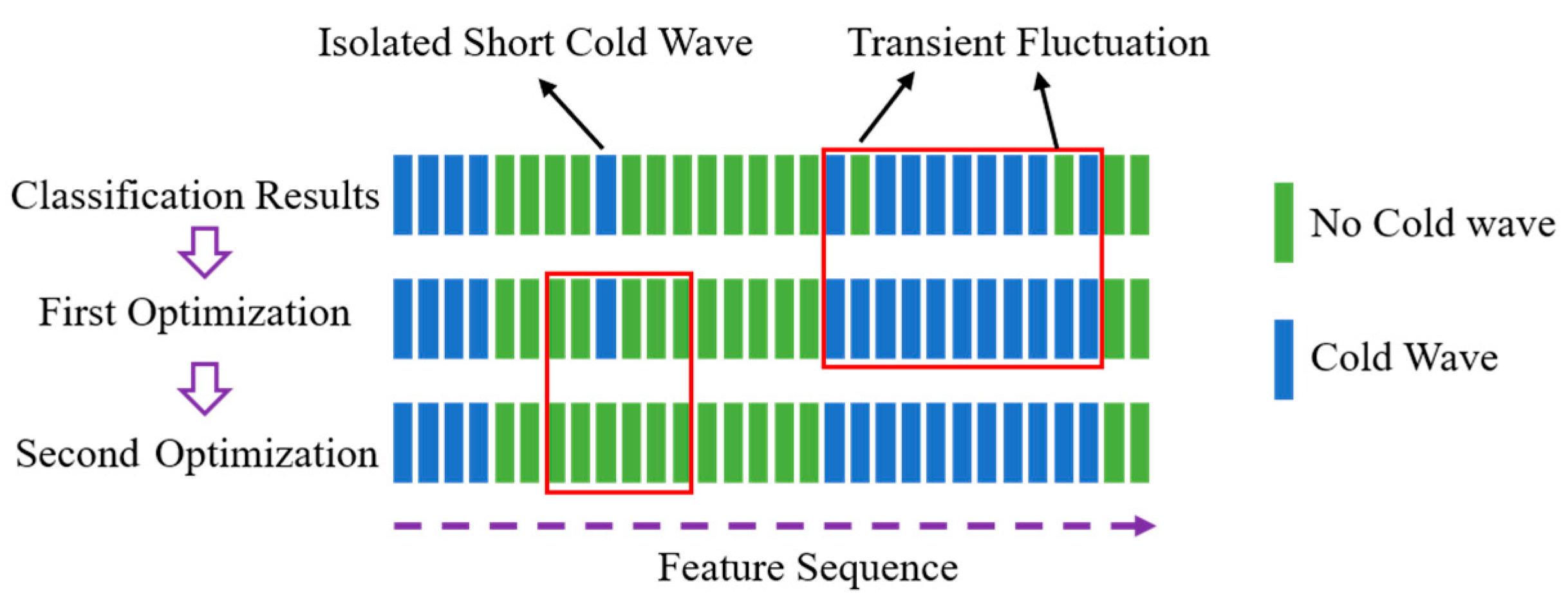
3.1.3. Classification Optimization Approach Based on Continuous Cold Wave Events
- Transient fluctuations within a long cold wave: In the case of a prolonged cold wave, the temperature may temporarily rise, but the wind turbine continues to be affected by the cold wave.
- Isolated short-term cold wave: This refers to a brief cold wave event that appears sporadically in a time series that has not experienced a cold wave for a long period. These short-duration cold waves have a relatively small impact on wind power and can be treated as normal weather conditions.
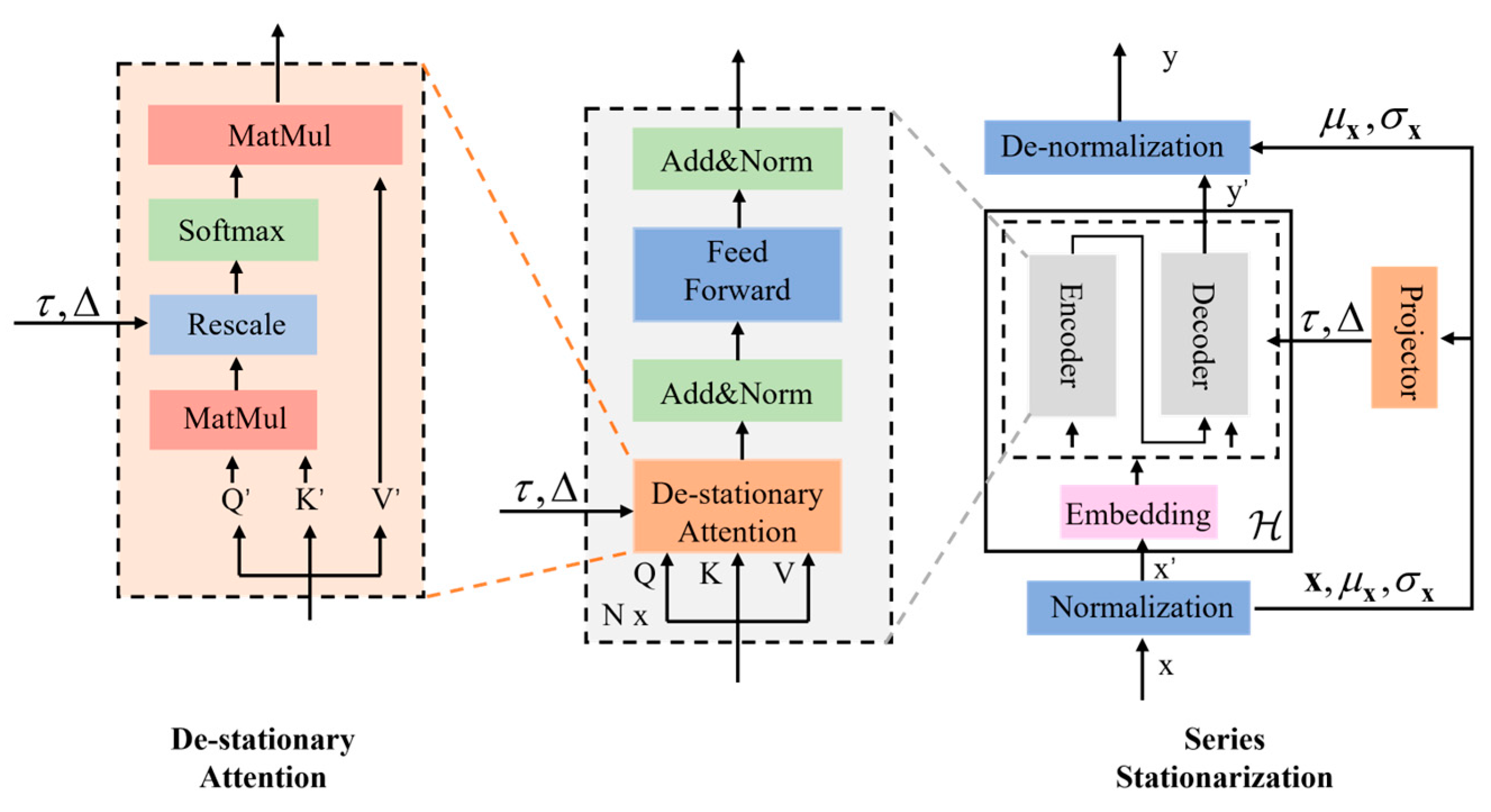
3.2. Wind Power Forecasting During Cold Wave Events
4. Case Study
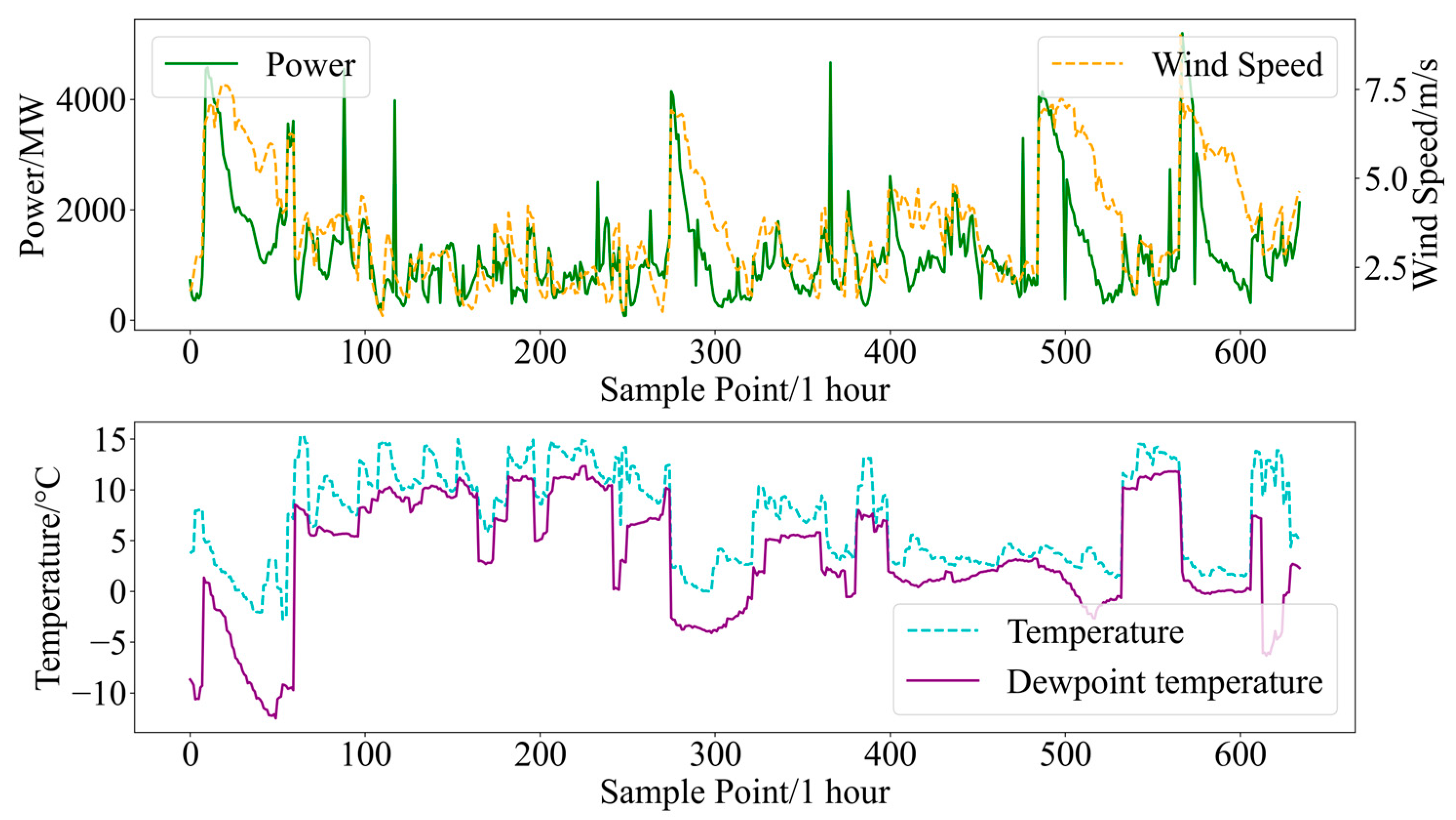
4.1. Data Presentation and Analysis
4.1.1. Data Presentation and Evaluation Metrics
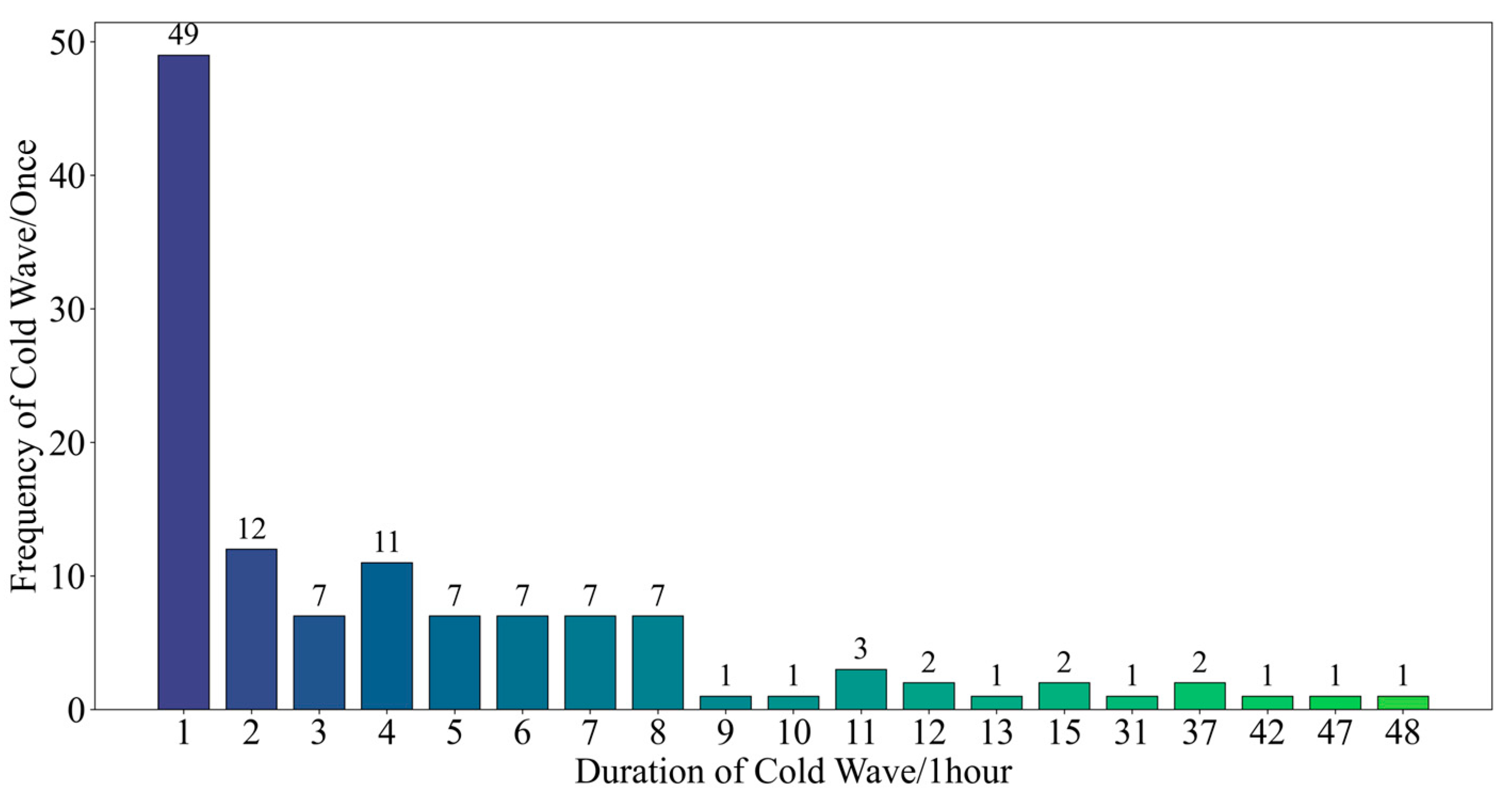
4.1.2. Analysis of Cold Wave Weather Characteristics
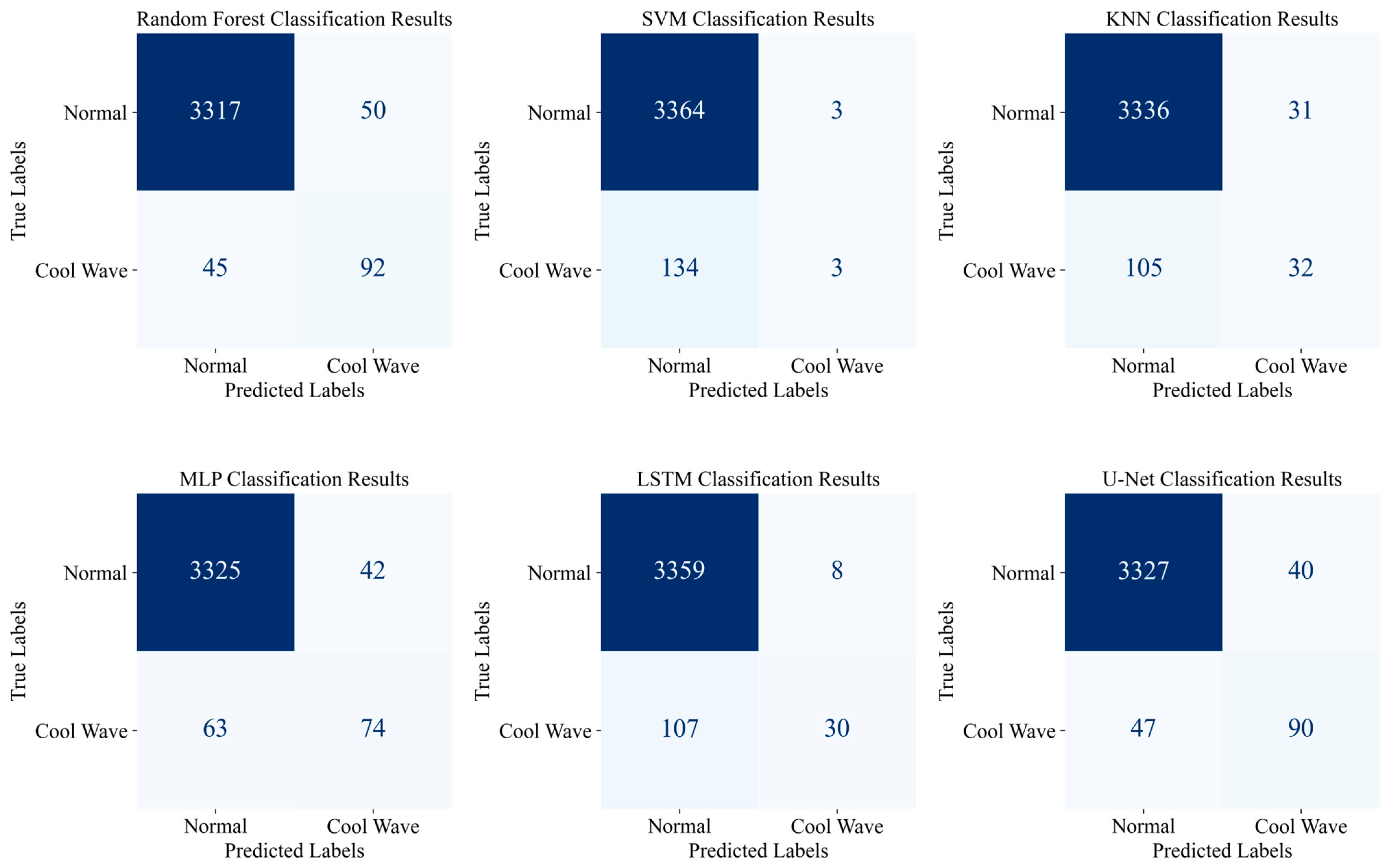
4.2. Recognition Result
4.2.1. Cold Wave Weather Identification Under Small Sample Conditions
4.2.2. Cold Wave Weather Recognition Under GAN Sample Generation
4.3. Wind Power Forecasting Results
4.3.1. Comparison of Power Forecasting Results of Different Models
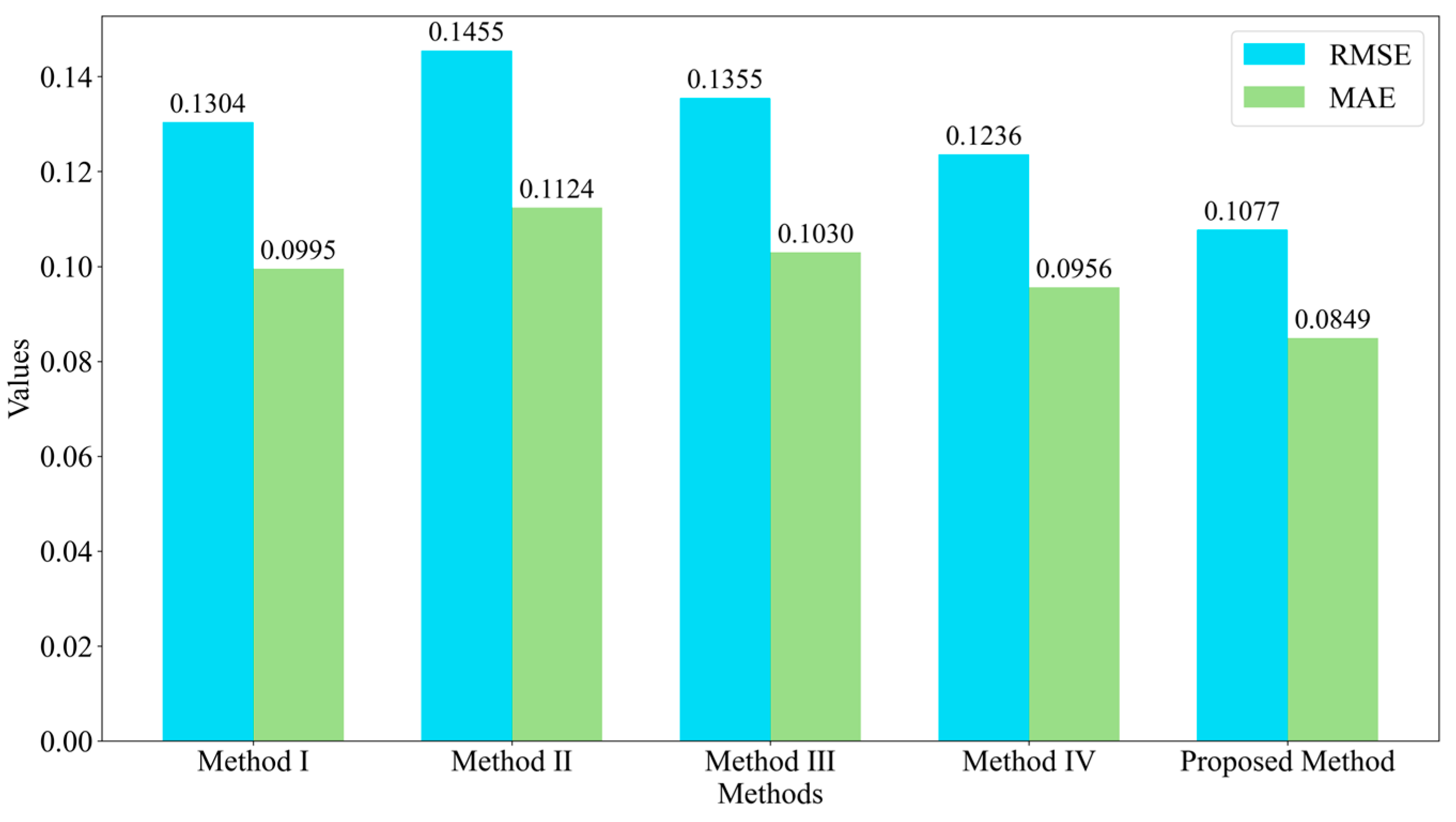
4.3.2. Ablation Experiments for the Forecasting Method
5. Discussion
- Starting with the impact of cold wave weather on wind power, this paper establishes the discriminant criteria for cold wave events and extracts key features through an in-depth analysis of historical data, providing a basis for subsequent cold wave events recognition.
- Aiming to address the recognition problem of small-sample cold wave events, an improved multi-modal U-Net classification model is proposed. Cold wave events samples generated by this model are added to the training set, significantly enhancing the classification model’s ability to recognize cold wave events. The model utilizes future NWP to accurately forecast the occurrence of cold waves, providing an effective early warning for the power system to handle extreme weather events.
- Based on cold wave recognition, this paper establishes distinct wind power forecasting models for the cold-wave and non-cold-wave seasons, respectively. Compared with the experimental results of different classification models, the Ns-Transformer model demonstrates superior wind power forecasting accuracy under cold-wave conditions.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NWP | Numerical Weather Prediction |
| GAN | Generative Adversarial Network |
| Ns-Transformer | Non-Stationary Transformer |
| EMD | Empirical Mode Decomposition |
| GA | Genetic Algorithms |
| PSO | Particle Swarm Optimization |
| WRF | Weather Research and Forecasting |
| GFS | Global Forecast System |
| KNN | K-Nearest Neighbors |
| MLP | Multilayer Perceptron |
| SVM | Support Vector Machine |
| LSTM | Long Short-Term Memory |
| BP | Back Propagation |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
References
- Yang, M.; Wang, D.; Zhang, W.; Yv, X. A centralized power prediction method for large-scale wind power clusters based on dynamic graph neural network. Energy 2024, 310, 133210. [Google Scholar] [CrossRef]
- National Energy Administration. 2024 National Power Industry Statistics; National Energy Administration: Beijing, China, 2024. [Google Scholar]
- Xue, Y.; Lei, X.; Xue, F.; Yu, C.; Dong, Z.; Wen, F.; Ju, P. A Review on Impacts of Wind Power Uncertainties on Power Systems. Proc. CSEE 2014, 34, 5029–5040. [Google Scholar] [CrossRef]
- Serrano-Notivoli, R.; Lemus-Canovas, M.; Barrao, S.; Sarricolea, P.; Meseguer-Ruiz, O.; Tejedor, E. Heat and Cold Waves in Mainland Spain: Origins, Characteristics, and Trends. Weather Clim. Extrem. 2022, 37, 100471. [Google Scholar] [CrossRef]
- Zhao, H.; Lin, S.; Qu, Y.; Yang, A.; Chang, J. Reliability Evaluation of Wind Turbine Competitive Failure Considering Extreme Weather Impact Process. Electr. Power Autom. Equip. 2024, 44, 40–47. [Google Scholar]
- Perera, A.T.D.; Nik, V.M.; Chen, D.; Scartezzini, J.; Hong, T. Quantifying the Impacts of Climate Change and Extreme Climate Events on Energy Systems. Nat. Energy 2020, 5, 150–159. [Google Scholar] [CrossRef]
- Hang, G.; Zhong, H.; Tan, Z.; Cheng, T.; Xia, Q.; Kang, C. Texas Electric Power Crisis of 2021 Warns of a New Blackout Mechanism. CSEE J. Power Energy Syst. 2022, 8, 1–9. [Google Scholar]
- Yu, G.Z.; Liu, L.; Tang, B.; Wang, S.Y.; Chung, C.Y. Ultra-Short-Term Wind Power Subsection Forecasting Method Based on Extreme Weather. IEEE Trans. Power Syst. 2023, 38, 5045–5056. [Google Scholar] [CrossRef]
- Yang, M.; Huang, Y.; Xu, C.; Liu, C.; Dai, B. Review of Several Key Processes in Wind Power Forecasting: Mathematical Formulations, Scientific Problems, and Logical Relations. Appl. Energy 2025, 377, 124361. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, J.; Qiao, J.; Shi, M.; Wang, C. Application and Prospect of Artificial Intelligence Technology in Renewable Energy Forecasting. Proc. CSEE 2023, 43, 3027–3048. [Google Scholar] [CrossRef]
- Yang, M.; Li, X.; Fan, F.; Wang, B.; Su, X.; Ma, C. Two-stage day-ahead multi-step prediction of wind power considering time-series information interaction. Energy 2024, 312, 133580. [Google Scholar] [CrossRef]
- Wang, Y.; Pei, L.; Li, W.; Zhao, Y.; Shan, Y. Short-term wind power prediction method based on multivariate signal decomposition and RIME optimization algorithm. Expert Syst. Appl. 2025, 259, 125376. [Google Scholar] [CrossRef]
- Yang, M.; Guo, Y.; Wang, B.; Wang, Z.; Chai, R. A Day-ahead Wind Speed Correction Method: Enhancing Wind Speed Forecasting Accuracy Using a Strategy Combining Dynamic Feature Weighting with Multi-Source Information and Dynamic Matching with Improved Similarity Function. Expert Syst. Appl. 2025, 263, 125724. [Google Scholar] [CrossRef]
- Saoud, L.S.; Al-Marzouqi, H.; Deriche, M. Wind Speed Forecasting Using the Stationary Wavelet Transform and Quaternion Adaptive-gradient Methods. IEEE Access 2021, 9, 127356–127367. [Google Scholar] [CrossRef]
- Zou, F.; Fu, W.; Fang, P.; Xiong, D.; Wang, R. A Hybrid Model Based on Multi-Stage Principal Component Extraction, GRU Network, and KELM For Multi-Step Short-Term Wind Speed Forecasting. IEEE Access 2020, 8, 222931–222943. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Muneeb, M. A Novel Genetic LSTM Model for Wind Power Forecast. Energy 2021, 223, 120069. [Google Scholar] [CrossRef]
- Viet, D.T.; Phuong, V.V.; Duong, M.Q.; Tran, Q.T. Models for Short-Term Wind Power Forecasting Based on Improved Artificial Neural Network Using Particle Swarm Optimization and Genetic Algorithms. Energies 2020, 13, 2873. [Google Scholar] [CrossRef]
- Peng, X.; Wang, H.; Lang, J. EALSTM-QR: Interval Wind-power Prediction Model Based on Numerical Weather Prediction and Deep Learning. Energy 2021, 220, 119692. [Google Scholar] [CrossRef]
- Chang, Y.; Yang, H.; Chen, Y.; Zhou, M.; Yang, H.; Wang, Y.; Zhang, Y. A Hybrid Model for Long-term Wind Power Forecasting Utilizing NWP Subsequence Correction and Multi-Scale Deep Learning Regression Methods. IEEE Trans. Sustain. Energy 2023, 15, 263–275. [Google Scholar] [CrossRef]
- Yang, M.; Guo, Y.; Huang, Y. Wind Power Ultra-short-term Forecasting Method Based on NWP Wind Speed Correction and Double Clustering Division of Transitional Weather Process. Energy 2023, 282, 128947. [Google Scholar] [CrossRef]
- Yu, G.; Lu, L.; Tang, B.; Wang, S.; Dong, Q. Research on Ultra-short-term Subsection Forecasting Method of Offshore Wind Power Considering Transitional Weather. Proc. CSEE 2022, 42, 4859–4871. [Google Scholar] [CrossRef]
- Sideratos, G.; Hatziargyriou, N.D. Wind Power Forecasting Focused on Extreme Power System Events. IEEE Trans. Sustain. Energy 2012, 3, 445–454. [Google Scholar] [CrossRef]
- Zhang, J.; Fu, H. An Integrated Modeling Strategy for Wind Power Forecasting Based on Dynamic Meteorological Visualization. IEEE Access 2024, 12, 69423–69433. [Google Scholar] [CrossRef]
- Lu, X.; Dong, C.; Wang, Z.; Jiang, J.; Wang, B.; Li, B. Research on Short-term Wind Power Forecasting Technology Under Low Temperature and Cold Wave Weather. Power Syst. Technol. 2024, 48, 4833–4843. [Google Scholar] [CrossRef]
- Ye, L.; Li, Y.; Pei, M.; Li, Z.; Xu, X.J.; Lu, J. Combined Approach for Short-term Wind Power Forecasting Under Cold Weather With Small Sample. Proc. CSEE 2023, 43, 543–555. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Takahashi, Y.; Hayashi, Y. Alerting to Rare Large-scale Ramp Events in Wind Power Generation. IEEE Trans. Sustain. Energy 2019, 10, 55–65. [Google Scholar] [CrossRef]
- Yang, M.; Guo, Y.; Huang, T.; Zhang, W. Power Forecasting Considering NWP Wind Speed Error Tolerability: A Strategy to Improve the Accuracy of Short-term Wind Power Forecasting Under Wind Speed Offset Scenarios. Appl. Energy 2025, 377, 124720. [Google Scholar] [CrossRef]
- Wei, Z.; Liu, Y.; Shen, X.; Liu, J. Ultra-short-term Power Generation Modeling and Prediction for Small Hydropower in Data-scarce Areas Based on Sample Data Transfer Learning. Proc. CSEE 2022, 43, 1–17. [Google Scholar]
- Peng, X.; Yang, Z.; Li, Y.; Wang, B.; Che, J. Short-Term Wind Power Forecasting Based on Stacked Denoised Auto-encoder Deep Learning and Multi-evel Transfer Learning. Wind Energy 2023, 26, 1066–1081. [Google Scholar] [CrossRef]
- Chen, H.; Birkelund, Y.; Zhang, Q. Data-augmented Sequential Deep Learning for Wind Power Forecasting. Energy Convers. Manag. 2021, 248, 114790. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Liu, L. Physics-informed Reinforcement Learning for Probabilistic Wind Power Forecasting Under Extreme Events. Appl. Energy 2024, 376, 124068. [Google Scholar] [CrossRef]
- Yang, M.; Guo, Y.; Fan, F. Ultra-short-term prediction of wind farm cluster power based on embedded graph structure learning with spatiotemporal information gain. IEEE Trans. Sustain. Energy 2025, 16, 308–322. [Google Scholar] [CrossRef]
- Feng, M.; Qin, Y.; Lu, C. An Objective Recognition Method for Wintertime Cold Fronts in Eurasia. Adv. Atmos. Sci. 2021, 38, 1695–1705. [Google Scholar] [CrossRef]
- Grochowicz, A.; van Greevenbroek, K.; Bloomfield, H. Using power system modelling outputs to identify weather-induced extreme events in highly renewable systems. Environ. Res. Lett. 2024, 19. [Google Scholar] [CrossRef]
- Li, Y.; Chen, F.; Yan, J.; Ge, C.; Han, S.; Liu, Y. Adaptive Short-term Wind Power Forecasting for Extreme Weather Based on Transfer Learning and AutoEncoder. Autom. Electr. Power Syst. 2025, 1–13. [Google Scholar]
- Li, F.; Liu, D.; Sun, K.; Hong, S.; Peng, F.; Zhang, C.; Tao, T.; Qin, B. Stochastic and Extreme Scenario Generation of Wind Power and Supply–demand Balance Analysis Considering Wind Power-temperature Correlation. Electronics 2024, 13, 2100. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Wang, Y. Road Extraction by Deep Residual U-Net. IEEE Geosci. Remote Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef]
- Wang, K.; Gou, C.; Duan, Y.; Lin, Y.; Zheng, X.; Wang, F.Y. Generative Adversarial Networks: Introduction and Outlook. IEEE/CAA J. Autom. Sin. 2017, 4, 588–598. [Google Scholar] [CrossRef]
- Zhu, G.; Jia, W.; Cheng, L.; Xiang, L.; Hu, A. A Non-stationary Transformer Model for Power Forecasting with Dynamic Data Distillation and Wake Effect Correction Suitable for Large Wind Farms. Energy Convers. Manag. 2025, 324, 119292. [Google Scholar] [CrossRef]





| Literature | Time Scale | Preprocessing Methods | Model | Cold Wave Identification | Limitations |
|---|---|---|---|---|---|
| Wang, et al. [12] | Short-term | MEMD | BiLSTM | × | |
| Peng, et al. [18] | Short-term | None | EALSTM-QR | × | |
| Yu, et al. [21] | Short-term | MASM | LightGBM-GRU | × | |
| Zhang, et al. [23] | Short-term | K-means | UMAP-IVMD-ILSTM | ✓ | Missing scene discrimination criteria |
| Lu, et al. [24] | Short-term | HMM | CNN-LSTM | ✓ | Limited to extreme fan cutter cases |
| Ye, et al. [25] | Short-term | TimeGAN | XGBoost- Transformer | ✓ | Inadequate accuracy validation |
| Liu, et al. [31] | Short-term | RL | DDPG | ✓ | No recognition protocol |
| Layer Type | Input Channels | Output Channels | Kernel Size | Activation | Operation |
|---|---|---|---|---|---|
| Input Layer | 4 | 32 | |||
| Lower Sampling 1 | 32 | 64 | 3 × 1 | ReLU | Conv 3 × 1 |
| Lower Sampling 2 | 64 | 128 | 3 × 1 | ReLU | Conv 3 × 1 |
| Lower Sampling 3 | 128 | 256 | 3 × 1 | ReLU | Conv 3 × 1 |
| Lower Sampling 4 | 256 | 512 | 3 × 1 | ReLU | Conv 3 × 1 |
| Upper Sampling 1 | 256 | 512 | 2 × 1 | ReLU | Conv 2 × 1 |
| Upper Sampling 2 | 512 | 128 | 2 × 1 | ReLU | Conv 2 × 1 |
| Upper Sampling 3 | 128 | 64 | 2 × 1 | ReLU | Conv 2 × 1 |
| Upper Sampling 4 | 64 | 2 | 1 × 1 | Softmax | Conv 1 × 1 |
| Bottleneck | 256 | 512 | 3 × 1 | ReLU | Conv 3 × 1 |
| Type | Training Set | Test Set |
|---|---|---|
| Cold wave occurs | January–February, November–December 2021 | November–December 2022 |
| No Cold wave occurs | March–October 2021 | September–October 2022 |
| Model | Accuracy | Precision | Recall | F1 |
|---|---|---|---|---|
| Random Forest | 0.9729 | 0.9734 | 0.6175 | 0.9731 |
| SVM | 0.9609 | 0.9436 | 0.0219 | 0.9434 |
| KNN | 0.9612 | 0.9514 | 0.2336 | 0.9542 |
| MLP | 0.9672 | 0.9611 | 0.5401 | 0.9620 |
| LSTM | 0.9706 | 0.9665 | 0.2189 | 0.9674 |
| U-Net | 0.9775 | 0.9789 | 0.6569 | 0.9780 |
| Model | Accuracy | Precision | Recall | F1 |
|---|---|---|---|---|
| Random Forest | 0.9863 | 0.8069 | 0.8540 | 0.8300 |
| SVM | 0.9823 | 0.8100 | 0.7153 | 0.7600 |
| KNN | 0.9899 | 0.8500 | 0.9051 | 0.8700 |
| MLP | 0.9926 | 0.8936 | 0.9198 | 0.9000 |
| LSTM | 0.9951 | 0.9412 | 0.9344 | 0.9300 |
| U-Net | 0.9971 | 0.9568 | 0.9731 | 0.9600 |
| Cold Wave Season | Non-Cold Wave Season | |||
|---|---|---|---|---|
| Model | RMSE | MAE | RMSE | MAE |
| LSTM | 0.1642 | 0.1144 | 0.1244 | 0.0935 |
| Random Forest | 0.1635 | 0.1189 | 0.1302 | 0.1042 |
| BP | 0.1558 | 0.1100 | 0.1579 | 0.1229 |
| Transformer | 0.1121 | 0.0854 | 0.0881 | 0.0785 |
| Proposed Method | 0.1077 | 0.0849 | 0.0842 | 0.0692 |
| Method | Model | Cold Wave Characteristics | Data Generation | Continuity Correction |
|---|---|---|---|---|
| Method I | Transformer | ✓ | ✓ | ✓ |
| Method II | Ns-Transformer | |||
| Method III | ✓ | |||
| Method IV | ✓ | ✓ | ||
| Proposed Method | ✓ | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Chai, R.; Sun, Y.; Jiang, Y.; Sun, D. Cold Wave Recognition and Wind Power Forecasting Technology Considering Sample Scarcity and Meteorological Periodicity Characteristics. Appl. Sci. 2025, 15, 4312. https://doi.org/10.3390/app15084312
Liang Z, Chai R, Sun Y, Jiang Y, Sun D. Cold Wave Recognition and Wind Power Forecasting Technology Considering Sample Scarcity and Meteorological Periodicity Characteristics. Applied Sciences. 2025; 15(8):4312. https://doi.org/10.3390/app15084312
Chicago/Turabian StyleLiang, Zhifeng, Rongfan Chai, Yupeng Sun, Yue Jiang, and Dayan Sun. 2025. "Cold Wave Recognition and Wind Power Forecasting Technology Considering Sample Scarcity and Meteorological Periodicity Characteristics" Applied Sciences 15, no. 8: 4312. https://doi.org/10.3390/app15084312
APA StyleLiang, Z., Chai, R., Sun, Y., Jiang, Y., & Sun, D. (2025). Cold Wave Recognition and Wind Power Forecasting Technology Considering Sample Scarcity and Meteorological Periodicity Characteristics. Applied Sciences, 15(8), 4312. https://doi.org/10.3390/app15084312






