Improved FraSegNet-Based Rock Nodule Identification Method and Application
Abstract
:1. Introduction
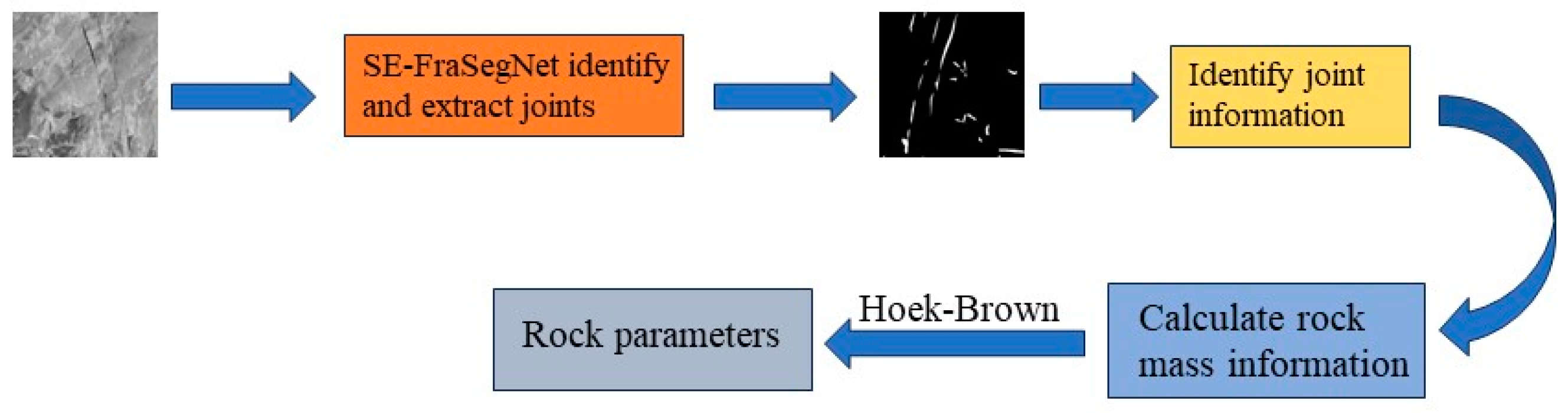
2. Improved FraSegNet Algorithm
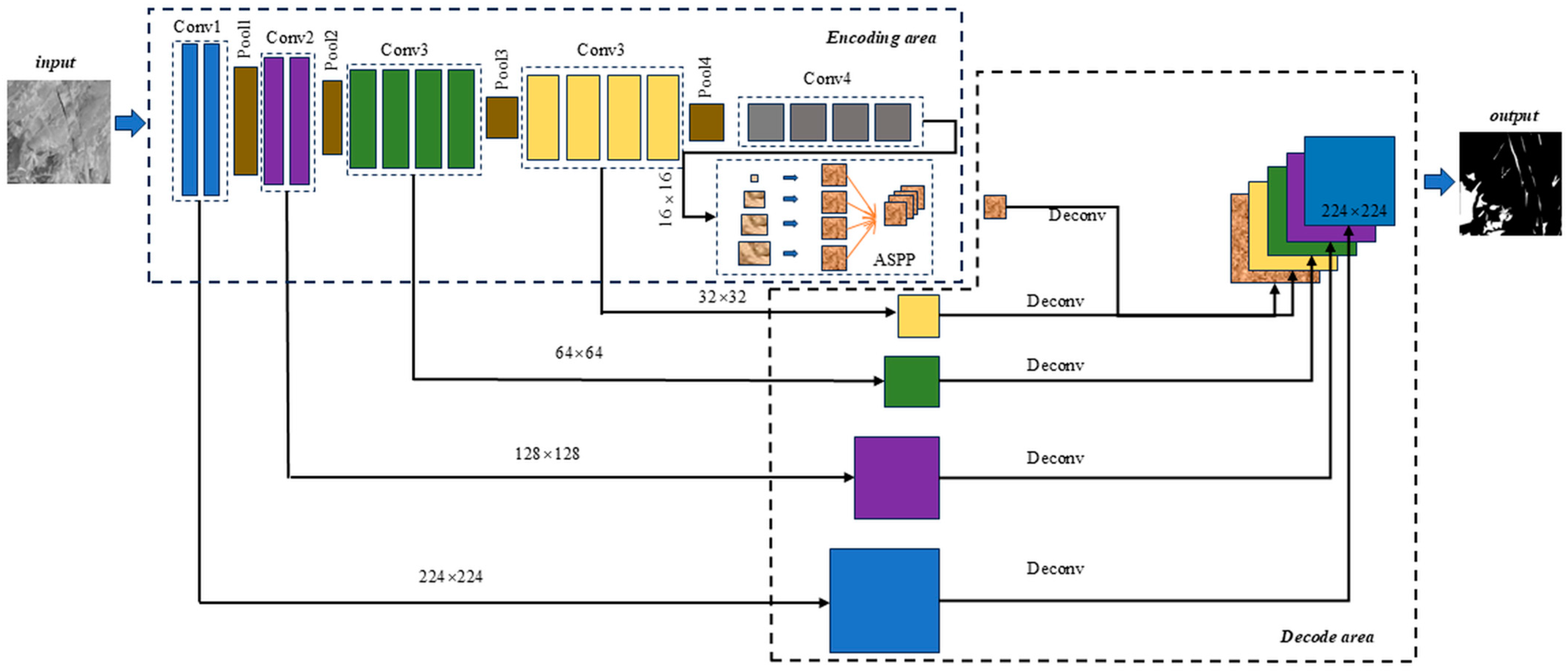
2.1. FraSegNet Algorithm
- (1)
- The input image is a 224 × 224 grayscale rock image with nodal fissure information. The image is preprocessed and normalized before being input into the model.
- (2)
- The encoder extracts multi-scale features from the image using several convolution and pooling layers. The process includes the following steps:Conv1 and Pool1: After extracting the base texture features, the output size is reduced to 128 × 128 after the pooling operation.Conv2 and Pool2: Deeper features are then extracted to capture the local properties of the nodes, giving an output size of 64 × 64.Conv3 and Pool3: Higher-level features, like the overall shape and distribution of nodules, are then extracted, resulting in an output size of 32 × 32.Conv4 and ASPP: At the final layer of the encoder, a 16 × 16 feature map is created by combining multi-scale context using a void space pyramid pooling module (ASPP).
- (3)
- The decoder gradually upsamples the feature map and combines it with the encoder’s features using jump connections. This process helps restore the spatial resolution of the segmentation result. The decoder’s procedure is as follows:Deconv1: The feature map is upsampled from 16 × 16 to 32 × 32 and combined with the matching 32 × 32 feature maps from the encoder layers.Deconv2: The feature map is upsampled from 32 × 32 to 64 × 64 and combined with the matching 64 × 64 feature maps from the encoder.Deconv3: The feature map is upsampled from 64 × 64 to 128 × 128 and combined with the matching 128 × 128 feature maps from the encoder.Deconv4: The feature map is upsampled from 128 × 128 to 224 × 224, and the initial layer feature maps from the encoder are combined to preserve more edge details. Finally, the decoder creates a binary segmentation map, matching the size of the input image, using a 1 × 1 convolution. This map shows the locations of the nodules.
- (4)
- The segmentation results are output at the pixel level. Each pixel is classified as either a nodal region (target) in white or a non-nodal region (background) in black.
2.2. Model Optimization
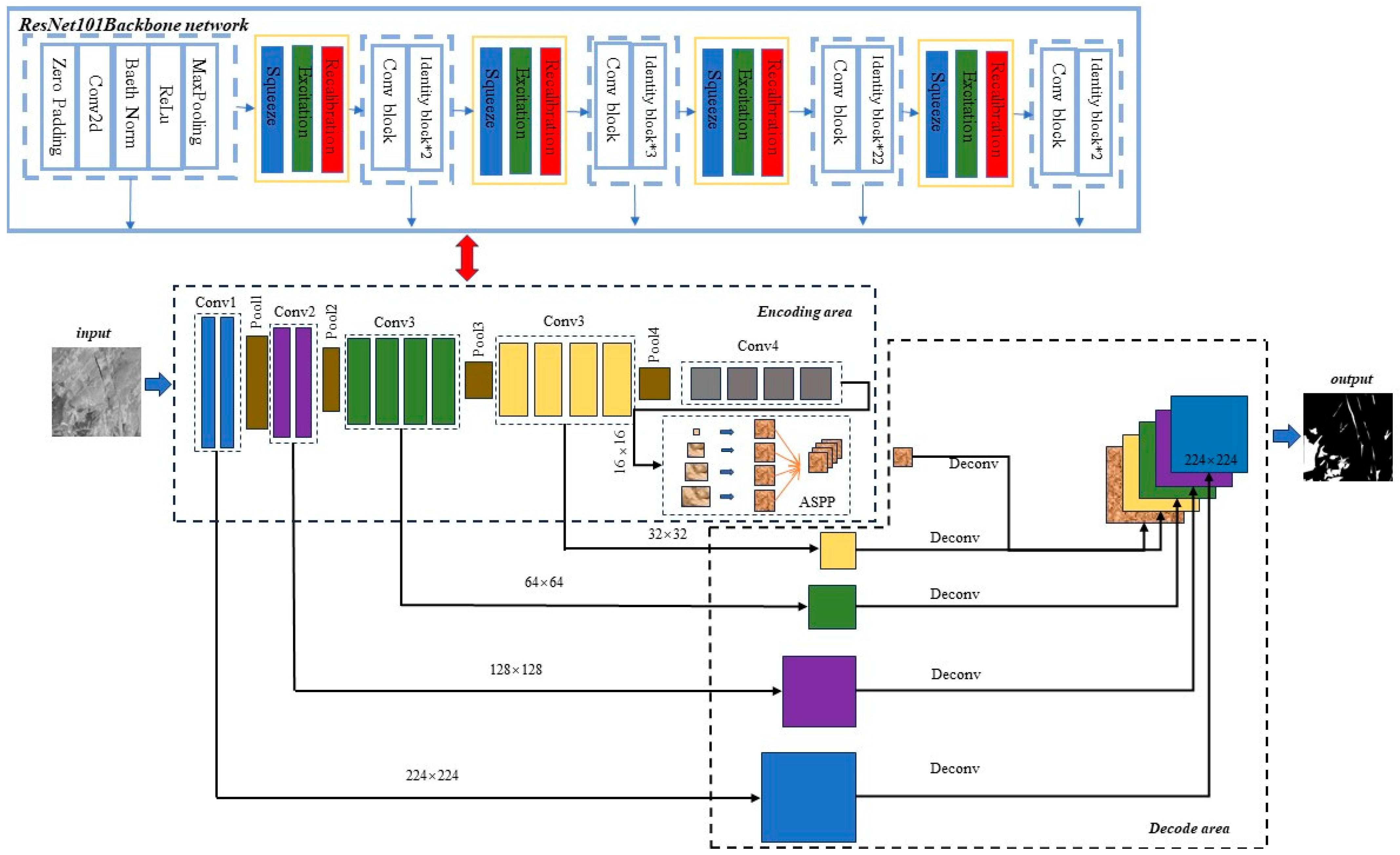
2.2.1. ResNet101 Backbone Network
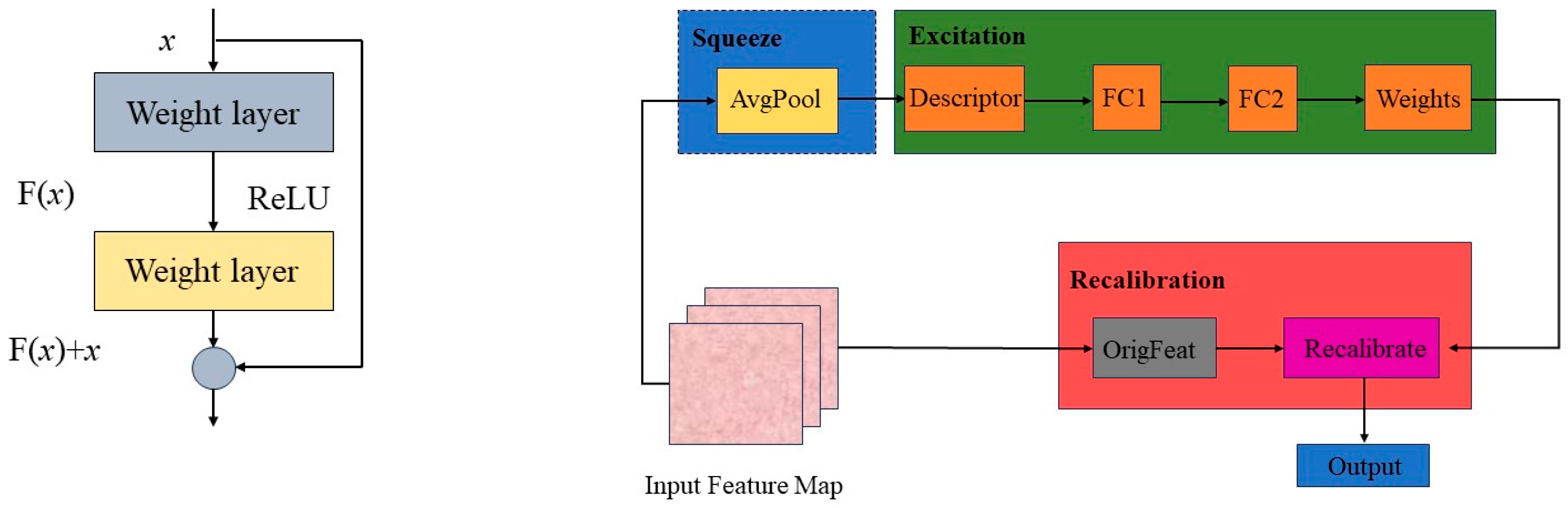
2.2.2. Introduction of the SE Attention Mechanism
2.2.3. Dynamic Learning Rate Strategy
- ηt is the current learning rate;
- ηmax and ηmin are the maximum and minimum learning rates;
- t is the current training iteration;
- T is the total number of iterations.
3. Evaluation Methods
3.1. Image Segmentation Evaluation Metrics
- (1)
- IoU (Intersection over Union): This metric measures the overlap between the predicted and ground truth regions. It is defined as follows:
- (2)
- Dice Coefficient: This metric measures the similarity between the predicted segmentation and the ground truth, and is defined as follows:
- True Positive (TP): The number of pixels correctly predicted as the target class.
- False Positive (FP): The number of pixels incorrectly predicted as the target class (background predicted as the target class).
- False Negative (FN): The number of pixels incorrectly predicted as background (target class predicted as background).
- True Negative (TN): The number of pixels correctly predicted as the background class.
3.2. Rock Mass Parameter Evaluation Metrics
Correlation Analysis of Nodal Cleavage Parameters Rock Mass Parameters
3.3. Barton–Bandis Parameter Mapping
3.3.1. Parameter Mapping Formula
- (1)
- Density: Density decreases as fracture density increases, and this is shown by the following equation:
- ρ: The density of the fractured rock mass (kg/m3).
- ρ0: The density of the intact rock (kg/m3), i.e., the original rock without fractures.
- D: The fracture density, typically defined as the total length of fractures per unit area (m/m2).
- α: The density decay coefficient quantifies the effect of fracture density on the overall rock mass density.
- (2)
- The formula for the cohesion (C) of a fractured rock mass, considering fracture density and area, is usually written as follows:
- C: The cohesion of the fractured rock mass (in MPa).
- C0: The cohesion of the intact rock (in MPa).
- A: The fracture area (in m2), representing the total area of fractures in a given volume or unit area of rock.
- D: The fracture density (in m/m2), defined as the total length of fractures per unit area.
- k: The weakening coefficient quantifies the reduction in cohesion caused by the presence of fractures.
- JCS: The peak normal stress on the fracture surface, related to the fracture’s resistance to shear along the fracture plane (in MPa).
- (3)
- The formula for the friction angle (φ) of a fractured rock mass, affected by the fracture dip angle (θ), is usually written as follows:
- Φ: The friction angle of the fractured rock mass.
- Φ0: The initial friction angle of the intact rock.
- JRC: The Joint Roughness Coefficient represents the roughness of the fracture surface.
- σn: The normal stress on the fracture surface (in MPa).
- θ: The dip angle of the fracture relative to the horizontal (in degrees).
- kΦ: The influence coefficient accounts for the effect of fracture characteristics (such as roughness and orientation) on the friction angle.
- (4)
- The formula for the elastic modulus (E) of a fractured rock mass, considering fracture density (D) and fracture width (W), is usually written as follows:
- E: The elastic modulus of the fractured rock mass.
- E0: The elastic modulus of the intact rock.
- D: The fracture density, usually expressed as the total length of fractures per unit area (fracture length density).
- W: The average fracture width.
- Wc: The critical width of the fractures at which they close and the elastic modulus returns to that of the intact rock.
- kE: The elastic modulus attenuation coefficient represents the rate at which the elastic modulus decreases as the fracture density increases.
- (5)
- Shear modulus and bulk modulus are calculated using the elastic modulus and Poisson’s ratio of the rock mass:
- (6)
- Tensile Strength: The increase in fracture density and width reduces the tensile strength:
- σt: the tensile strength of the rock mass with fractures.
- σt0: the tensile strength of the intact rock mass.
- Kt: the attenuation coefficient.
- ν0: the Poisson’s ratio of the intact rock mass (without fractures).
- β: the attenuation coefficient of Poisson’s ratio.
- UCS: Uniaxial compressive strength of the intact rock.
- R: Fracture strength degradation factor influenced by weathering.
3.3.2. Obtaining the Attenuation Coefficients
3.4. Hoek–Brown Criterion Parameter Transformation
3.4.1. Hoek–Brown Model Parameter Calculation
- Jd: Joint density;
- Js: Joint Spacing.
- σ1: Maximum principal stress;
- σ3: Minimum principal stress (confining pressure);
- σc: Uniaxial compressive strength of the intact rock;
- mb: Rock mass strength parameter, representing the shear characteristics of the rock mass;
- s: Rock mass integrity parameter;
- a: Empirical parameter, describing the nonlinear behavior of the rock mass.
- mi: Rock material constant, determined experimentally;
- D: Disturbance factor, reflecting the degree of engineering disturbance to the rock mass.
3.4.2. Conversion from Rock Parameters to Rock Mass Parameters
- ρrock: Rock density;
- φ: Porosity.
- D: Disturbance parameter, this article takes 0.9.
- GSI: The Geological Strength Index is used to assess the quality of the rock mass.
- k: Empirical parameter is related to the rock type and joint characteristics.
- σc: Compressive strength of the intact rock.
4. Reliability Analysis
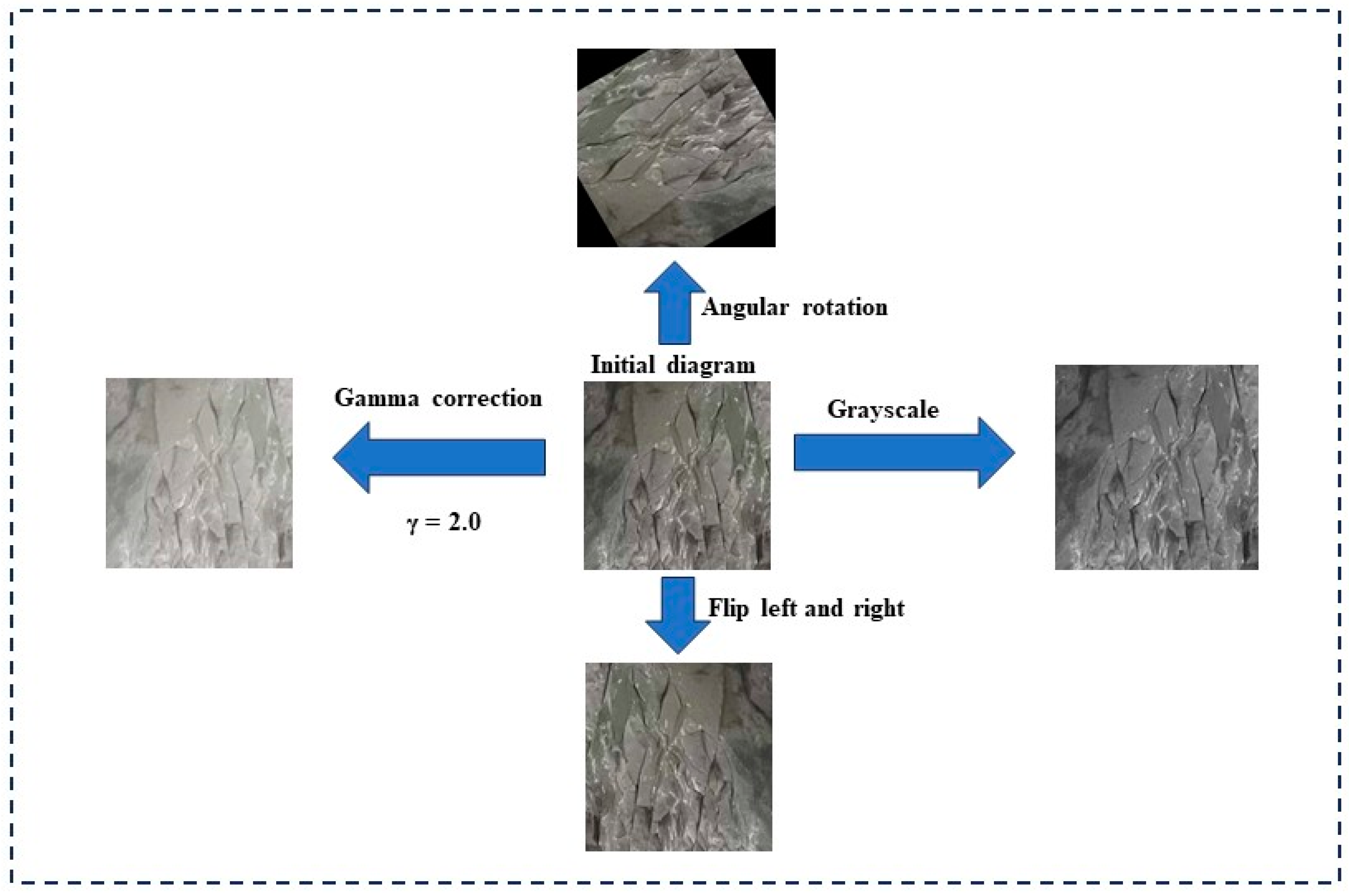
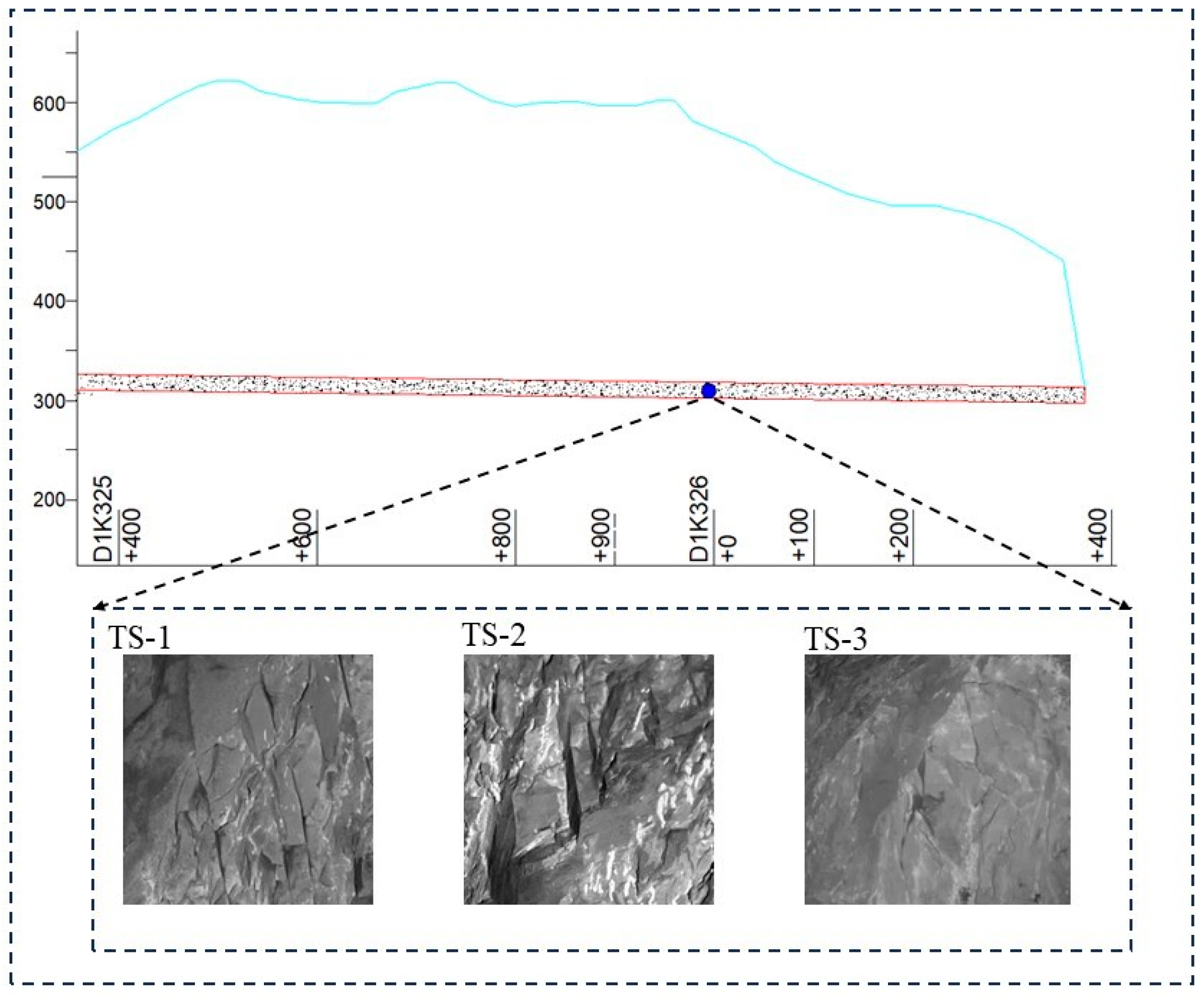
4.1. Dataset Creation
4.2. Performance Analysis Before and After Optimization
5. Experimental Results and Analysis
5.1. Data Analysis
5.2. Evaluation
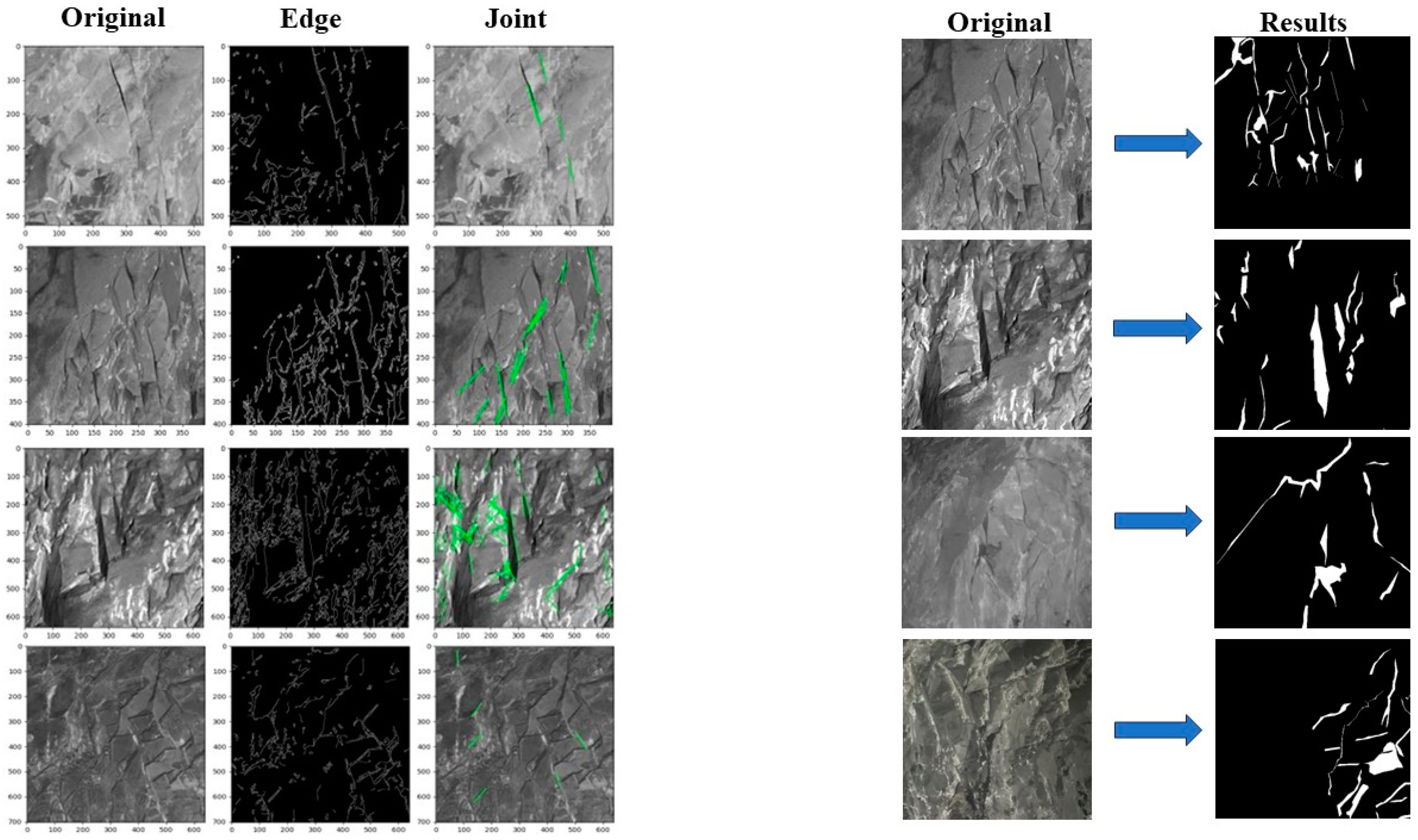
5.2.1. Image Segmentation Evaluation
5.2.2. Rock Mass Parameter Characterization Evaluation
6. Conclusions
- (1)
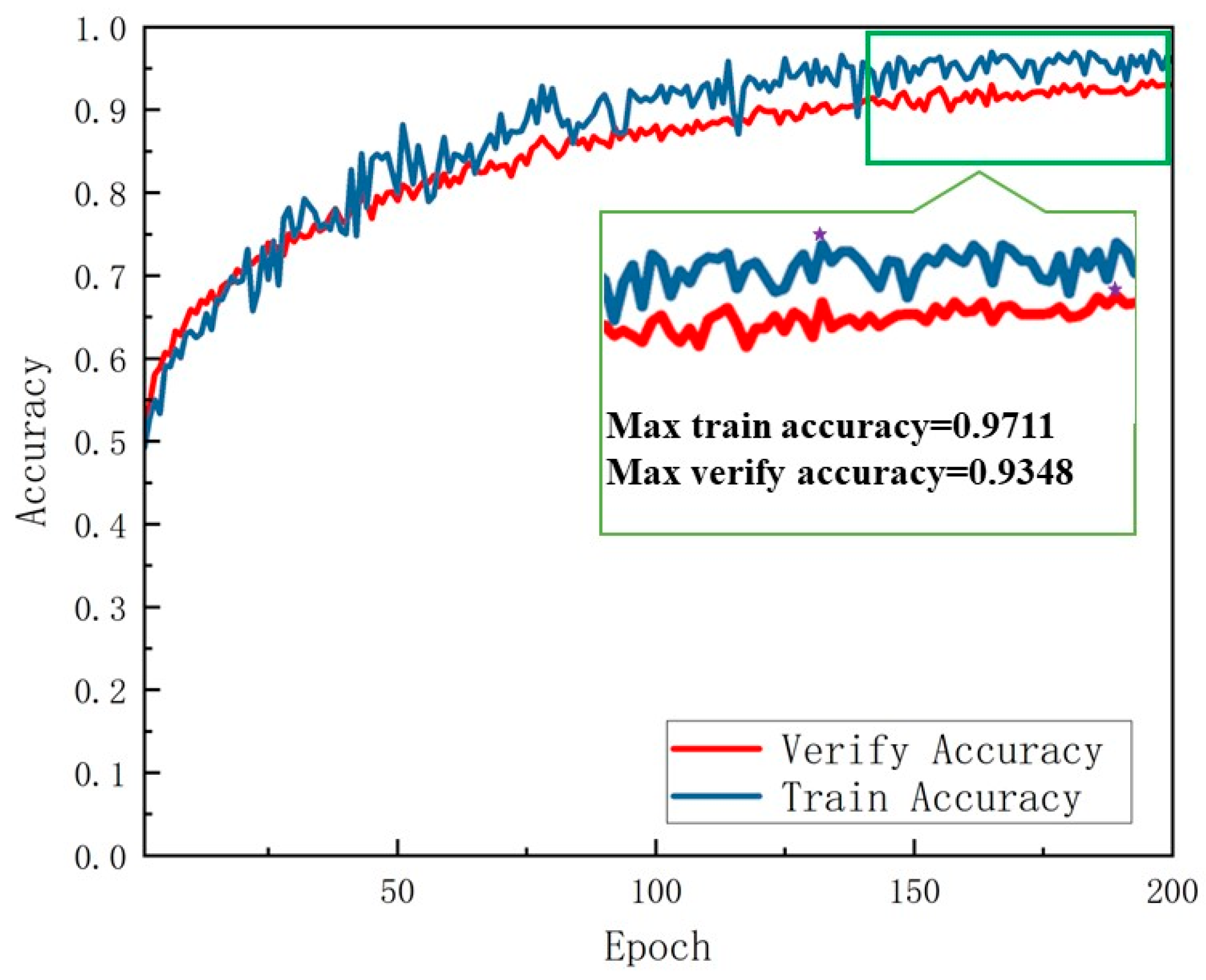
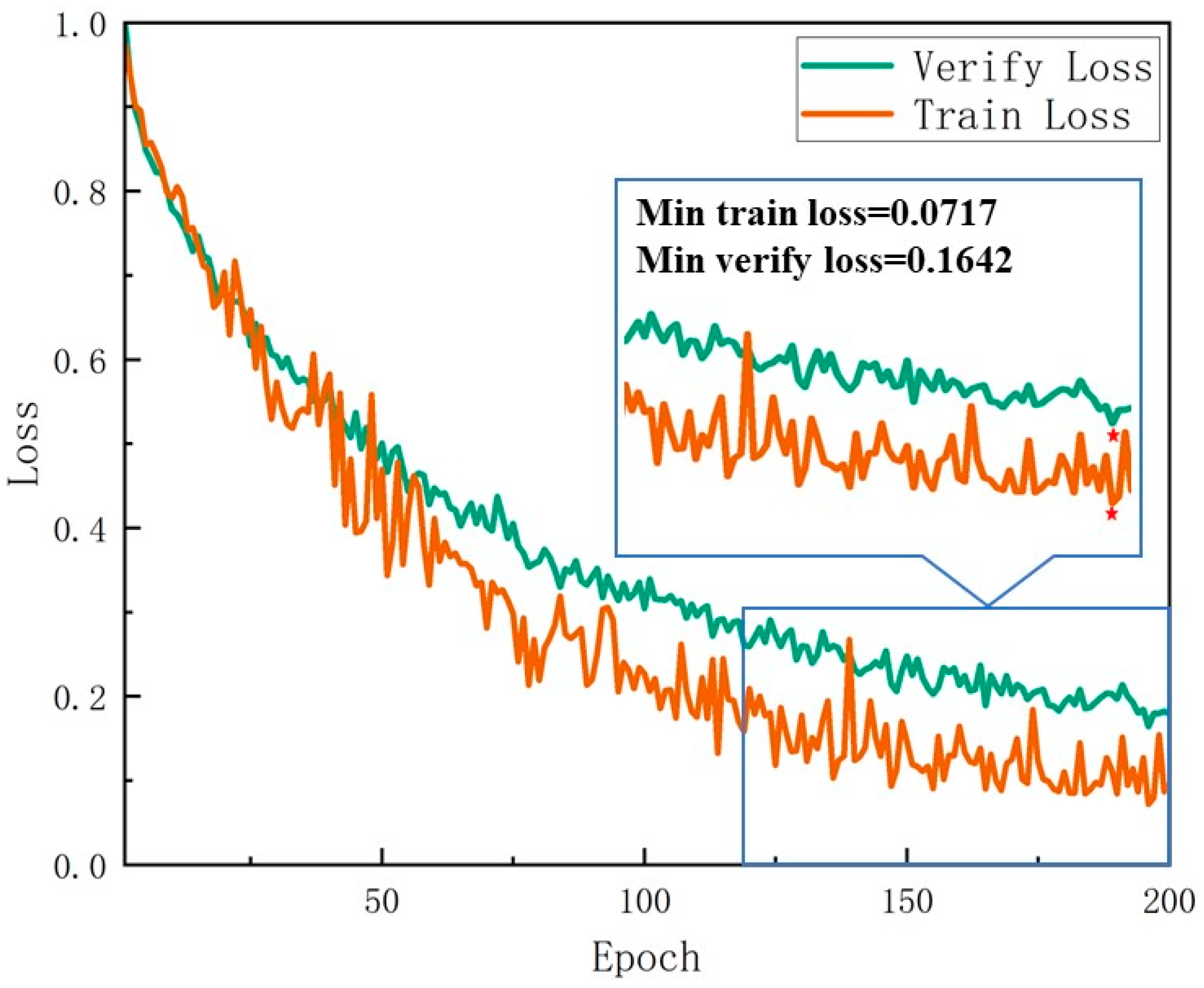
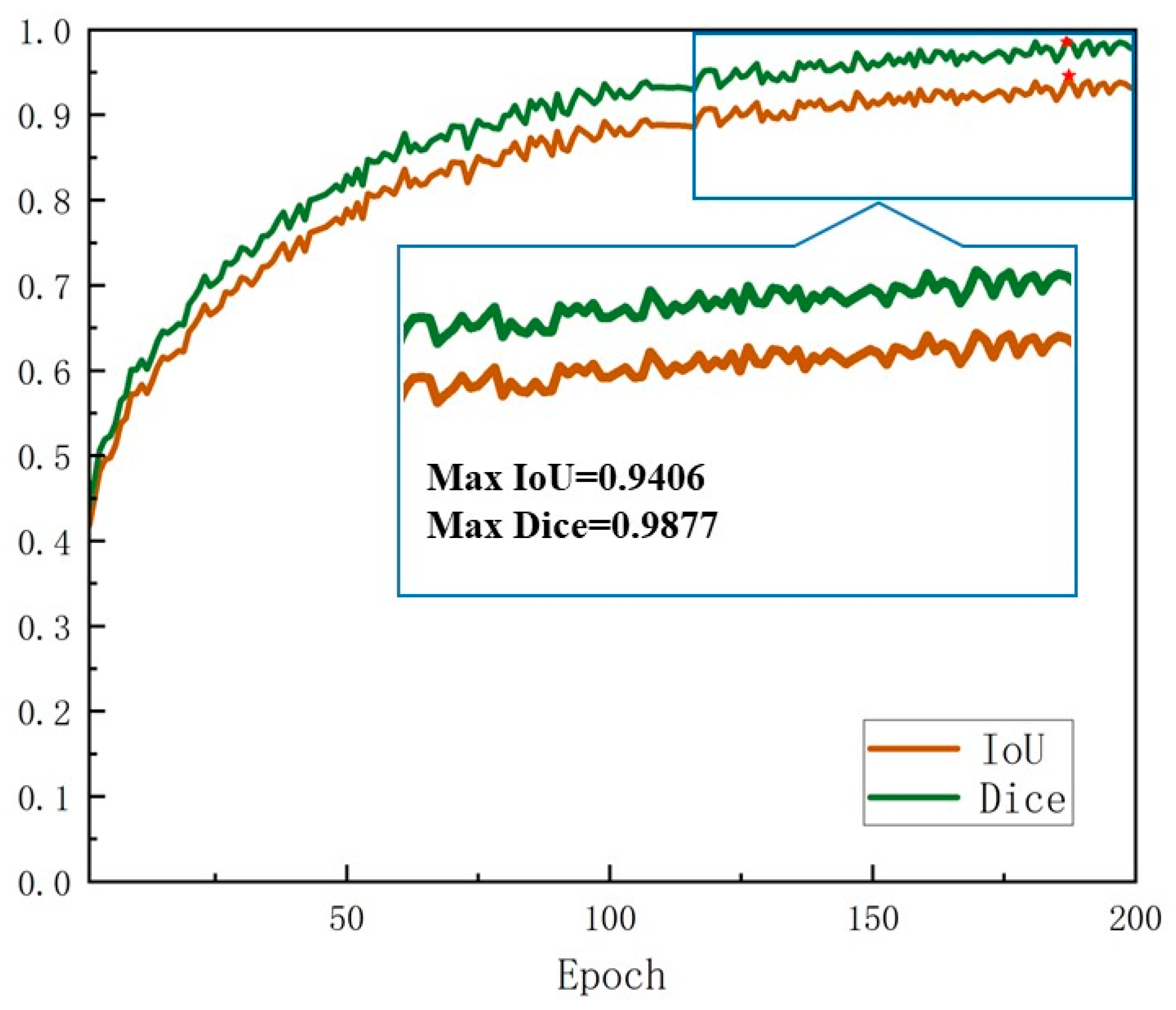
- By incorporating the ResNet101 backbone, the SE attention mechanism, and a dynamic learning rate strategy, the optimized FraSegNet network enhances its feature extraction capabilities. This improvement is particularly beneficial for handling complex backgrounds and fine-grained targets. The experimental results show that the network achieves a training accuracy of 0.9711 and a minimum loss rate of 0.0717, with validation accuracy reaching 0.9348 and a minimum loss rate of 0.1642. The IoU and Dice coefficients for the automatic segmentation of nodal fissures stabilize at 0.94 and 0.98, respectively, demonstrating a notable enhancement in capturing fissure edge details compared to traditional segmentation methods. Additionally, the model excels in recognizing joints in tunnel surrounding rocks, with the confusion matrix and Grad-CAM visualization further validating its superior classification performance and ability to accurately assess dense joint areas.
- (2)
- By combining the Barton–Bandis fracture parameter mapping with the Hoek–Brown strength criterion, this study establishes a clear relationship between the nodal features extracted by FraSegNet and the mechanical parameters of rock bodies. This integration provides reliable data support for future engineering applications, offering improvements in joint segmentation accuracy and a more precise reflection of rock body mechanical properties compared to traditional methods.
- (3)
- The proposed method was successfully tested in the Huayingshan Tunnel, validating its applicability and efficiency under complex geological conditions. It enhances the accuracy of rock joint and fissure identification, providing a reliable foundation for rock engineering design, stability analysis, and safety assessments. This approach holds significant value for both theoretical research and practical engineering applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, P.; An, J.; Shi, S.S.; Hu, J.; Wu, W.T.; Yan, Z.Q. Research on tunnel block collapse instability characteristics and support optimization design based on multi-scale modeling method of nodular rock body. J. Rock Mech. Eng. 2025, 1–15. [Google Scholar]
- Abbas, N.; Li, K.G.; Fissha, Y.; Khatti, J.; Geberegergis, M.B.; Cheepurupalli, N.R.; Taiwo, B.O.; Gebrehiwot, Z.; Kide, Y.; Chandrahas, N.S. Reliability analysis of support strategies in tunnel construction: Insights from geomechanical analysis of jointed rock masses. Results Earth Sci. 2024, 2, 100044. [Google Scholar] [CrossRef]
- Ge, C.H.; Li, P.F.; Zhang, M.J.; Li, Z. Eccentric load bearing performance of high bolt screw (HBS) active joints for prestressed internal supports in the subway excavation. Structures 2024, 70, 107876. [Google Scholar] [CrossRef]
- Yan, J.; Chen, J.; Zhang, Y.; Liu, Y.; Zhao, X.; Xue, J.; Zhu, C.; Mehmood, Q.; Wang, Q. Semi-automatic extraction of dangerous rock blocks from jointed rock exposures based on a discontinuity trace map. Comput. Geotech. 2023, 156, 105265. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, K.; Liu, W.; Xie, J. A novel DIC-based methodology for crack identification in a jointed rock mass. Mater. Des. 2023, 230, 111944. [Google Scholar] [CrossRef]
- Priest, S.D.; Hudson, J.A. Discontinuity spacing in rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1976, 13, 135–148. [Google Scholar] [CrossRef]
- Zhang, L.; Einstein, H.H. Estimating the intensity of rock discontinuities. Int. J. Rock Mech. Min. Sci. 2000, 37, 819–837. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, J.; Chen, Q.; Chen, J.; Zhu, C.; Li, H. Automatic interpretation of geometric information of discontinuities and its influence on the stability of highly-jointed rock slopes. J. Rock Mech. Geotech. Eng. 2024. [Google Scholar] [CrossRef]
- He, P.; Yan, Z.; Wang, G.; Shi, S.; Zheng, C. Research on the multi-scale DFN-DEM equivalent modeling method for jointed rock masses and the collapse law of block structures. Tunn. Undergr. Space Technol. 2025, 157, 106316. [Google Scholar] [CrossRef]
- Ge, Y.; Yuan, S.; Chen, K.; Tang, H. Estimation of rock joint roughness using binocular stereo vision. Measurement 2024, 234, 114881. [Google Scholar] [CrossRef]
- Monteiro, B.A.A.; Canguçu, G.L.; Jorge, L.M.S.; Vareto, R.H.; Oliveira, B.S.; Silva, T.H.; Lima, L.A.; Machado, A.M.C.; Schwartz, W.R.; Vaz-de-Melo, P.O.S. Literature review on deep learning for the segmentation of seismic images. Earth-Sci. Rev. 2024, 258, 104955. [Google Scholar]
- Zhao, S.; Shadabfar, M.; Zhang, D.; Chen, J.; Huang, H. Deep learning-based classification and instance segmentation of leakage-area and scaling images of shield tunnel linings. Struct. Control. Health Monit. 2021, 1, e2732. [Google Scholar] [CrossRef]
- Cui, X.; Yan, E.C. A clustering algorithm based on differential evolution for the identification of rock discontinuity sets. Int. J. Rock Mech. Min. Sci. 2020, 126, 104181. [Google Scholar] [CrossRef]
- Lemy, F.; Hadjigeorgiou, J. Discontinuity trace map construction using photographs of rock exposures. Int. J. Rock Mech. Min. Sci. 2003, 40, 903–917. [Google Scholar] [CrossRef]
- Zou, Q.; Cao, Y.; Li, Q.; Mao, Q.; Wang, S. CrackTree: Automatic crack detection from pavement images. Pattern Recognit. Lett. 2012, 33, 227–238. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Navab, N., Hornegger, J., Wells, W.M., Frangi, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Bordehore, J.L.; Riquelme, A.; Cano, M.; Tomás, R. Comparing manual and remote sensing field discontinuity collection used in kinematic stability assessment of failed rock slopes. Int. J. Rock Mech. Min. Sci. 2017, 97, 24–32. [Google Scholar] [CrossRef]
- Huang, H.; Zhao, S.; Zhang, D.; Chen, J. Deep learning-based instance segmentation of cracks from shield tunnel lining images. Struct. Infrastruct. Eng. 2020, 1, 1–14. [Google Scholar] [CrossRef]
- Xu, H.; Su, X.; Wang, Y.; Cai, H.; Cui, K.; Chen, X. Automatic bridge crack detection using a convolutional neural network. Appl. Sci. 2019, 9, 2867. [Google Scholar] [CrossRef]
- Dias, L.O.; Bom, C.R.; Faria, E.L.; Valentín, M.B.; Correia, M.D.; De Albuquerque, M.P.; De Albuquerque, M.P.; Coelho, J.M. Automatic detection of fractures and breakout patterns in acoustic borehole image logs using fast-region convolutional neural networks. J. Pet. Sci. Eng. 2020, 191, 107099. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J.; Li, Y. Segmentation and quantitative analysis of geological fracture: A deep transfer learning approach based on borehole televiewer image. Arab. J. Geosci. 2022, 15, 300. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, G.; Xiao, L.; Liang, Z.; Zhang, J.; Zhang, X.; Zhang, Z.; Zhou, J.; Li, G. Automatic fracture segmentation and detection from image logging using Mask R-CNN. In Proceedings of the SPWLA 63rd Annual Logging Symposium, Stavanger, Norway, 11–15 June 2022. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 28th IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Alghalandis, Y.F. ADFNE: Open source software for discrete fracture network engineering, two and three-dimensional applications. Comput. Geosci. 2017, 102, 1–11. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, M.; Huang, H.; Zhang, D.; Peng, Z. Automated extraction and evaluation of fracture trace maps from rock tunnel face images via deep learning. Int. J. Rock Mech. Min. Sci. 2021, 142, 104745. [Google Scholar] [CrossRef]
- Bandis, S.; Lumsden, A.C.; Barton, N.R. Experimental studies of scale effects on the shear behavior of rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 1–21. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, C.; Cheng, X.; Zuo, S.; Jiao, K. A method for seismic stability analysis of jointed rock slopes using Barton-Bandis failure criterion. Int. J. Rock Mech. Min. Sci. 2020, 136, 104487. [Google Scholar] [CrossRef]
- Zhao, L.-H.; Zuo, S.; Li, L.; Lin, Y.-L.; Zhang, Y.-B. System reliability analysis of plane slide rock slope using Barton-Bandis failure criterion. Int. J. Rock Mech. Min. Sci. 2016, 88, 1–11. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Empirical strength criterion for rock masses. J. Geotech. Geoenviron. Eng. 1980, 106, 1013–1035. [Google Scholar] [CrossRef]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Hu, Y.; Sun, Z.; Ji, J. Pseudo-dynamic stability analysis of 3D rock slopes considering tensile strength-modified Hoek–Brown failure criterion: Seismic UBLA implementations. Eng. Geol. 2024, 343, 107786. [Google Scholar] [CrossRef]
- Taylor, J.R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements, 2nd ed.; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]





| Fracture Surface Roughness | JRC Range |
|---|---|
| Very Smooth | 0–2 |
| Slightly Rough | 4–8 |
| Significantly Rough | 10–20 |
| Extremely Rough | >20 |
| Fracture Surface Condition | R-Value Range |
|---|---|
| No Weathering | 0.7–1.0 |
| Slight Weathering | 0.4–0.6 |
| Moderate Weathering | 0.2–0.4 |
| Severe Weathering | 0.1–0.2 |
| Sample | Density (g/cm3) | Cohesion (MPa) | Friction Angle (°) | Elastic Modulus (GPa) | Shear Modulus (GPa) | Bulk Modulus (GPa) | Tensile Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|---|
| Intact Rock Sample | 2.81 | 7.84 | 42.37 | 72.15 | 33.21 | 85.43 | 12.33 | 0.27 |
| Sample No. | Fracture Density | Fracture Length (m) | Fracture Width (m) | Fracture Dip Angle (°) | Fracture Area (m2) |
|---|---|---|---|---|---|
| 1 | 1.25 | 4.18 | 0.48 | 27.42 | 5.51 |
| 2 | 2.4 | 1.14 | 0.8 | 8.79 | 1.93 |
| 3 | 1.96 | 0.99 | 0.24 | 61.58 | 9.7 |
| 4 | 1.7 | 1 | 0.54 | 39.61 | 7.77 |
| 5 | 0.81 | 1.59 | 0.61 | 10.98 | 9.4 |
| 6 | 0.8 | 2.67 | 0.09 | 44.57 | 8.96 |
| 7 | 0.62 | 2.22 | 0.63 | 3.09 | 6.02 |
| 8 | 2.23 | 1.53 | 0.21 | 81.84 | 9.23 |
| 9 | 1.7 | 3.1 | 0.11 | 23.29 | 0.98 |
| 10 | 1.92 | 0.78 | 0.95 | 59.63 | 2.04 |
| 11 | 0.54 | 1.53 | 0.97 | 28.05 | 0.55 |
| Sample No. | JCS/MPa | JRC | σn/MPa | Wc/cm |
|---|---|---|---|---|
| 1 | 65 | 15 | 6 | 0.23 |
| 2 | 67 | 16 | 6 | 0.24 |
| 3 | 62 | 13 | 5 | 0.22 |
| 4 | 74 | 15 | 6 | 0.25 |
| 5 | 68 | 15 | 7 | 0.24 |
| 6 | 69 | 15 | 7 | 0.24 |
| 7 | 74 | 13 | 8 | 0.26 |
| 8 | 65 | 17 | 6 | 0.25 |
| 9 | 67 | 16 | 6 | 0.24 |
| 10 | 63 | 19 | 5 | 0.23 |
| 11 | 66 | 17 | 6 | 0.23 |
| Sample No. | Density (g/cm3) | Cohesion (MPa) | Friction Angle (°) | Elastic Modulus (GPa) | Shear Modulus (GPa) | Bulk Modulus (GPa) | Tensile Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|---|
| 1 | 2.39 | 1.02 | 26.22 | 38.98 | 11.47 | 82.67 | 2.1 | 0.26 |
| 2 | 2.27 | 4.26 | 26.5 | 32.79 | 5.85 | 82.21 | 4 | 0.21 |
| 3 | 2.76 | 3.83 | 34.59 | 6.65 | 13.72 | 38.62 | 9.5 | 0.25 |
| 4 | 2.36 | 3.92 | 32.75 | 12.01 | 8.97 | 19.9 | 3.9 | 0.26 |
| 5 | 2.28 | 4.09 | 37.74 | 7.04 | 31.4 | 30.51 | 5.7 | 0.21 |
| 6 | 2.54 | 1.3 | 29.44 | 46.37 | 32.9 | 48.44 | 7.3 | 0.26 |
| 7 | 2.14 | 2.43 | 22.39 | 25.43 | 26.44 | 83.62 | 4.3 | 0.25 |
| 8 | 2.72 | 1.46 | 34.26 | 38.06 | 32.24 | 83.47 | 9.7 | 0.25 |
| 9 | 2.07 | 4.45 | 35.22 | 63.99 | 32.74 | 10.63 | 9.7 | 0.23 |
| 10 | 2.74 | 3.49 | 31.23 | 21.2 | 9.9 | 55.97 | 3.3 | 0.21 |
| 11 | 2.77 | 2.32 | 35.42 | 31.67 | 29.02 | 47.57 | 5.5 | 0.22 |
| Density | 0.125 |
| Cohesion | 0.622 |
| Friction Angle | 0.258 |
| Elastic Modulus | 0.591 |
| Tensile Strength | 0.521 |
| Poisson’s Ratio | 0.121 |
| Training Set | Test Set | Validation Set | |
|---|---|---|---|
| Original Images | 700 | 200 | 100 |
| Labels | 700 | 200 | 100 |
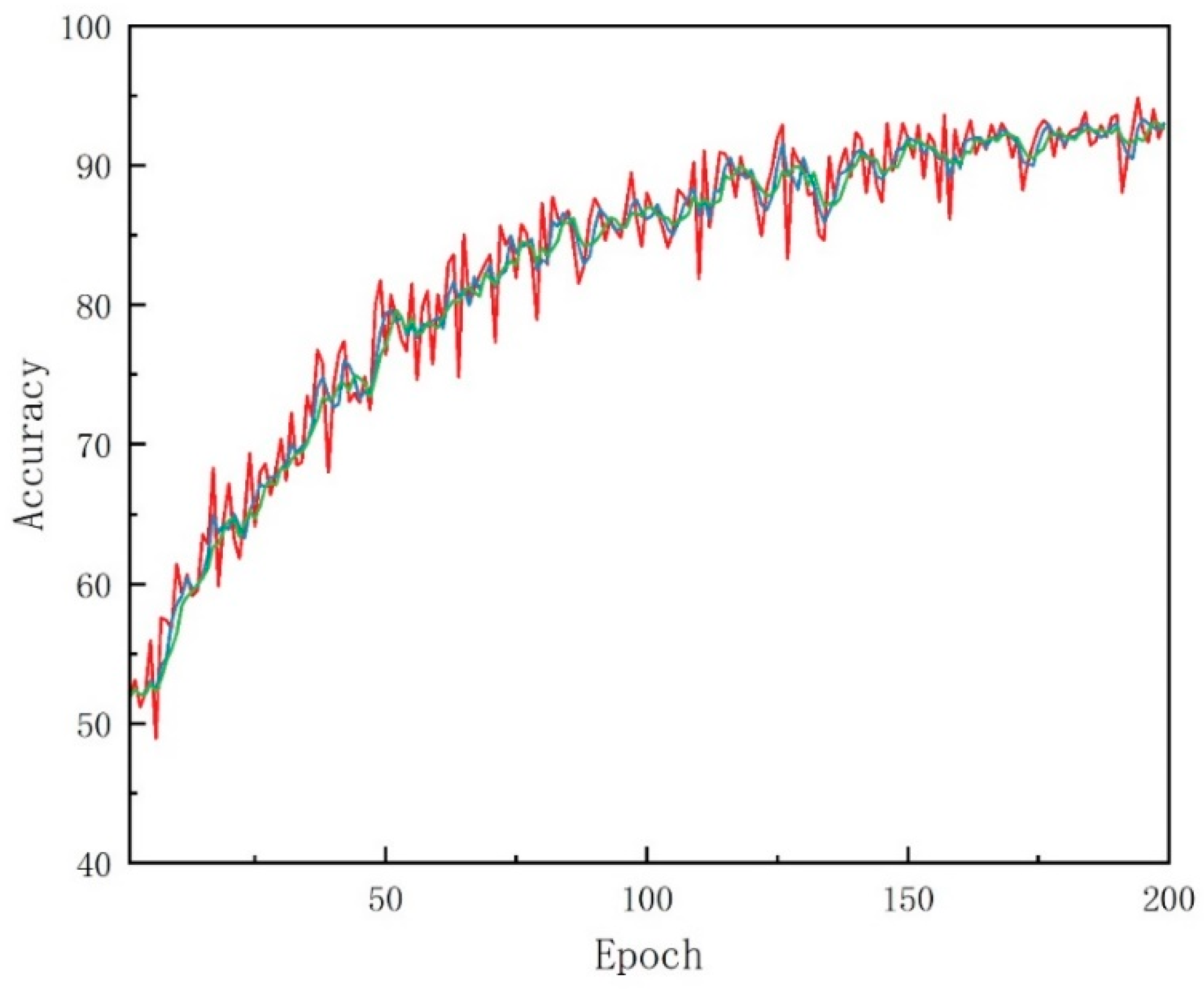
| Performance Metric | Pre-Optimization Model | Post-Optimization Model | Improvement |
|---|---|---|---|
| Accuracy | 90.21% | 93.25% | +3.32% |
| Training Time | 37 h | 26 h | −42.3% |
| Testing Speed | 2 images/s | 4 images/s | −50% |
| Robustness | Slight Decrease | More Stable | Improvement |
| Stability | High Fluctuations | Low Fluctuations | Improvement |
| Original Image | Pre-Optimization Model | Post-Optimization Model | |
|---|---|---|---|
| Increased Brightness |  |  |  |
| Decreased Brightness |  |  |  |
| Strong Noise Interference |  |  |  |
| Weak Noise Interference |  |  |  |
| Rock Sample | Joint Length (m) | Joint Width (m) | Joint Dip Angle (°) | Joint Density | Joint Area (m2) |
|---|---|---|---|---|---|
| TS-1 | 14.17 | 1.5 | 44.32 | 0.005 | 7.08 |
| TS-2 | 6.22 | 0.65 | 22.28 | 0.002 | 3.11 |
| TS-3 | 10.96 | 0.75 | 32.11 | 0.004 | 5.48 |
| Rock Mass | Density (kg/m3) | Cohesion (MPa) | Friction Angle (°) | Elastic Modulus (GPa) | Shear Modulus (GPa) | Bulk Modulus (GPa) | Tensile Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|---|
| TS-1 | 2451 | 8.96 | 39.66 | 27.29 | 10.46 | 18.23 | 1.27 | 0.21 |
| TS-2 | 2482 | 4.05 | 32.42 | 12.46 | 4.83 | 8.33 | 0.67 | 0.2 |
| TS-3 | 2467 | 6.9 | 31.56 | 21.37 | 8.26 | 14.26 | 0.67 | 0.2 |
| Rock Mass | Density (kg/m3) | Cohesion (MPa) | Friction Angle (°) | Elastic Modulus (GPa) | Shear Modulus (GPa) | Bulk Modulus (GPa) | Tensile Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|---|
| TS-1 | 2445 | 17.6 | 39.43 | 54.63 | 21.01 | 36.42 | 2.4 | 0.21 |
| TS-2 | 2478 | 8.06 | 37.23 | 24.83 | 9.55 | 16.55 | 1.12 | 0.2 |
| TS-3 | 2462 | 13.75 | 31.79 | 42.6 | 16.38 | 28.4 | 1.27 | 0.2 |
| Rock Mass | Density (kg/m3) | Cohesion (MPa) | Friction Angle (°) | Elastic Modulus (GPa) | Shear Modulus (GPa) | Bulk Modulus (GPa) | Tensile Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|---|
| TS-1 | 2445 | 8.8 | 39.65 | 27.32 | 10.51 | 18.21 | 1.2 | 0.21 |
| TS-2 | 2478 | 4.03 | 32.35 | 12.42 | 4.78 | 8.28 | 0.66 | 0.2 |
| TS-3 | 2462 | 6.88 | 31.82 | 21.3 | 8.19 | 14.2 | 0.64 | 0.2 |
| TS-1 Barton–Bandis | TS-1 Hoek–Brown | TS-2 Barton–Bandis | TS-2 Hoek–Brown | TS-3 Barton–Bandis | TS-3 Hoek–Brown | |
|---|---|---|---|---|---|---|
| Density | 2451 | 2445 | 2482 | 2478 | 2467 | 2462 |
| Cohesion | 8.96 | 8.8 | 4.05 | 4.03 | 6.9 | 6.88 |
| Friction Angle | 39.66 | 39.43 | 32.42 | 32.35 | 31.56 | 31.79 |
| Elastic Modulus | 27.29 | 27.32 | 12.46 | 12.42 | 21.37 | 21.3 |
| Shear Modulus | 10.46 | 10.51 | 4.83 | 4.78 | 8.26 | 8.19 |
| Bulk Modulus | 18.23 | 18.21 | 8.33 | 8.28 | 14.26 | 14.2 |
| Tensile Strength | 1.27 | 1.2 | 0.67 | 0.66 | 0.67 | 0.64 |
| Poisson’s Ratio | 0.21 | 0.21 | 0.2 | 0.2 | 0.2 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, G.; Li, Q.; Yao, X.; Zhou, H. Improved FraSegNet-Based Rock Nodule Identification Method and Application. Appl. Sci. 2025, 15, 4314. https://doi.org/10.3390/app15084314
Zhang Y, Zhang G, Li Q, Yao X, Zhou H. Improved FraSegNet-Based Rock Nodule Identification Method and Application. Applied Sciences. 2025; 15(8):4314. https://doi.org/10.3390/app15084314
Chicago/Turabian StyleZhang, Yanbo, Guanghan Zhang, Qun Li, Xulong Yao, and Hao Zhou. 2025. "Improved FraSegNet-Based Rock Nodule Identification Method and Application" Applied Sciences 15, no. 8: 4314. https://doi.org/10.3390/app15084314
APA StyleZhang, Y., Zhang, G., Li, Q., Yao, X., & Zhou, H. (2025). Improved FraSegNet-Based Rock Nodule Identification Method and Application. Applied Sciences, 15(8), 4314. https://doi.org/10.3390/app15084314







