Matching and Control Optimisation of Variable-Geometry Turbochargers for Hydrogen Fuel Cell Systems
Abstract
1. Introduction
2. Materials and Methods
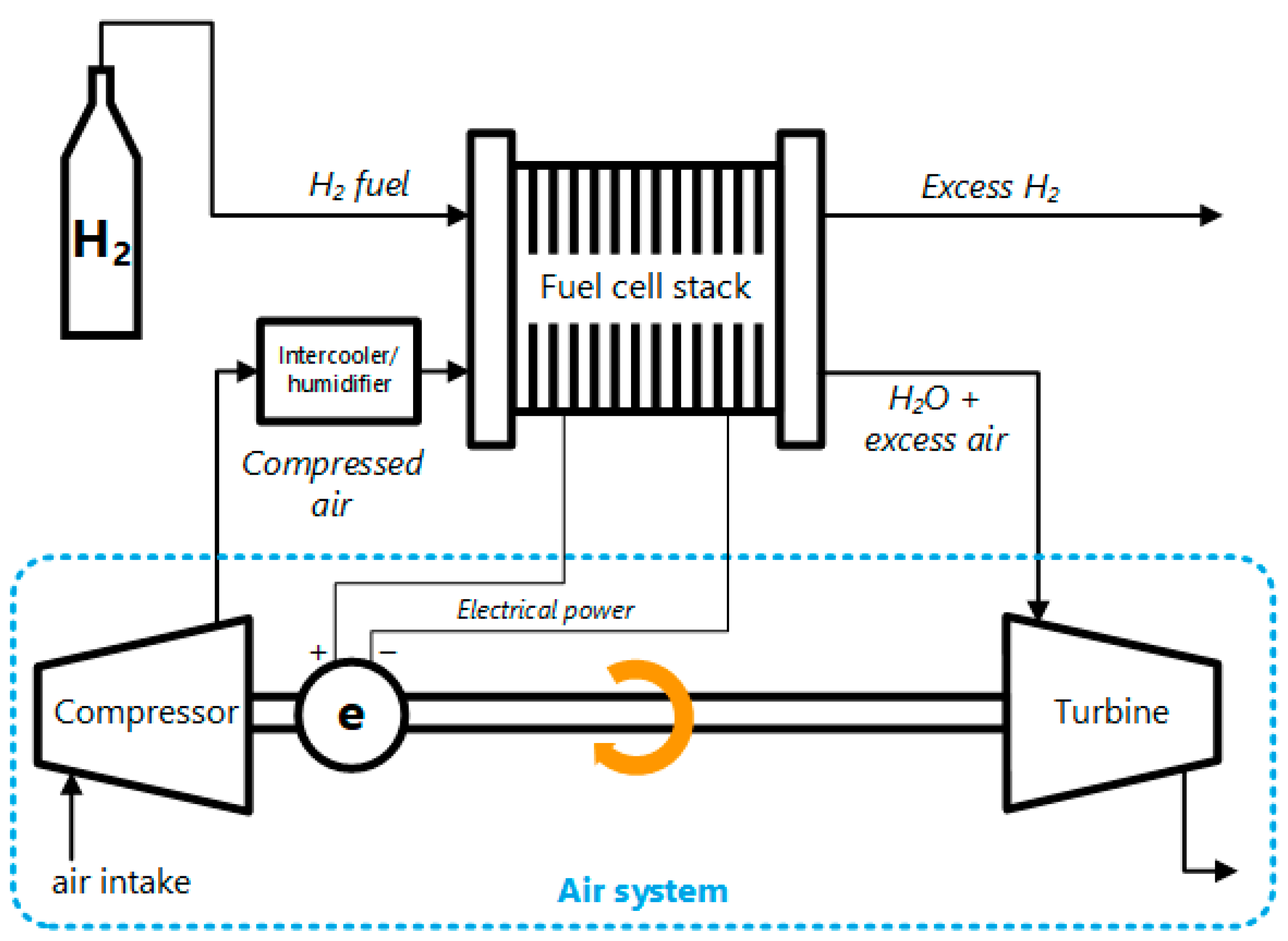
2.1. Fuel Cell Air Path Matching Tool (FCMT)
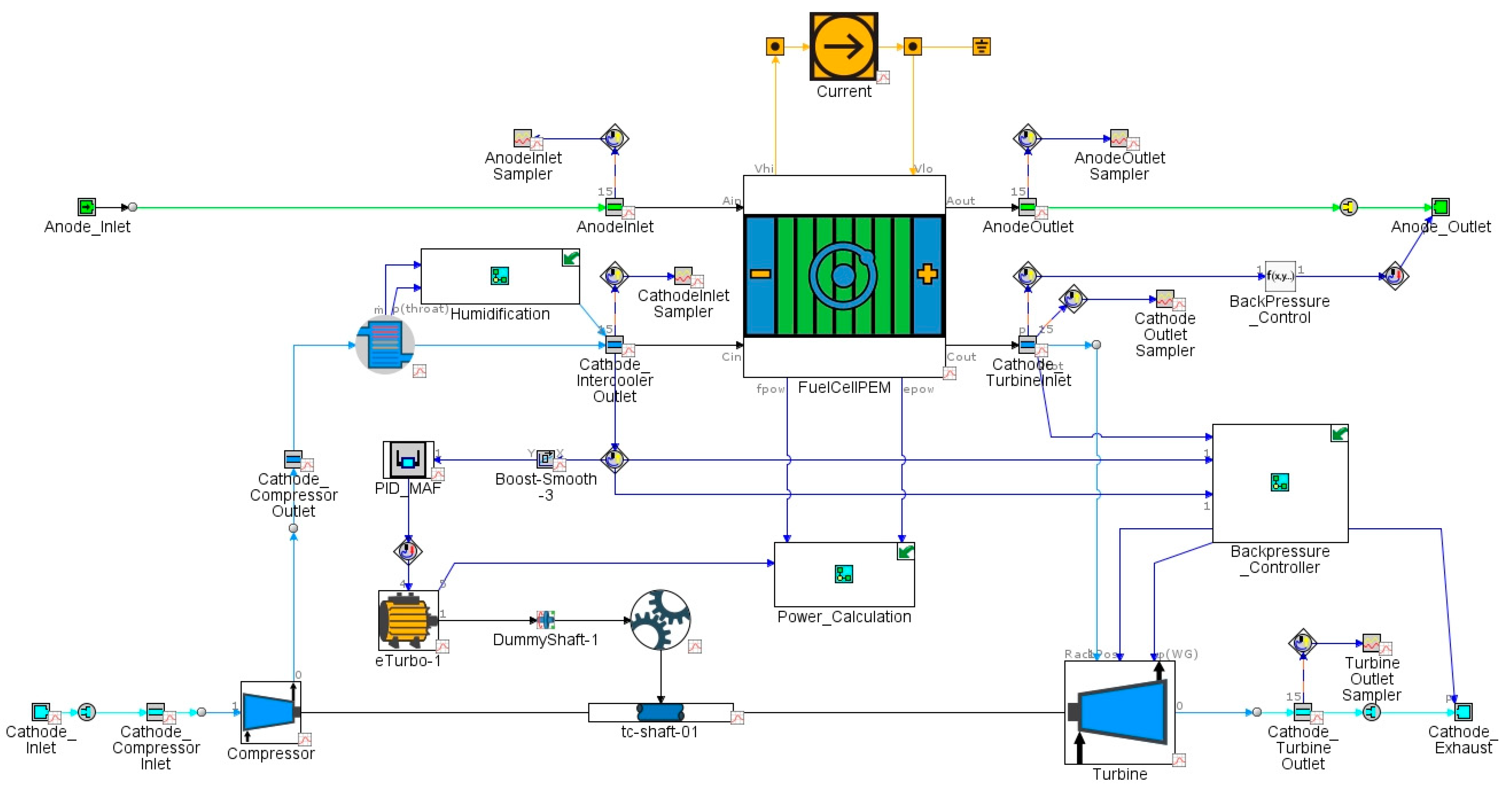
2.2. One-Dimensional System Model
Operating Point Optimisation
3. Results
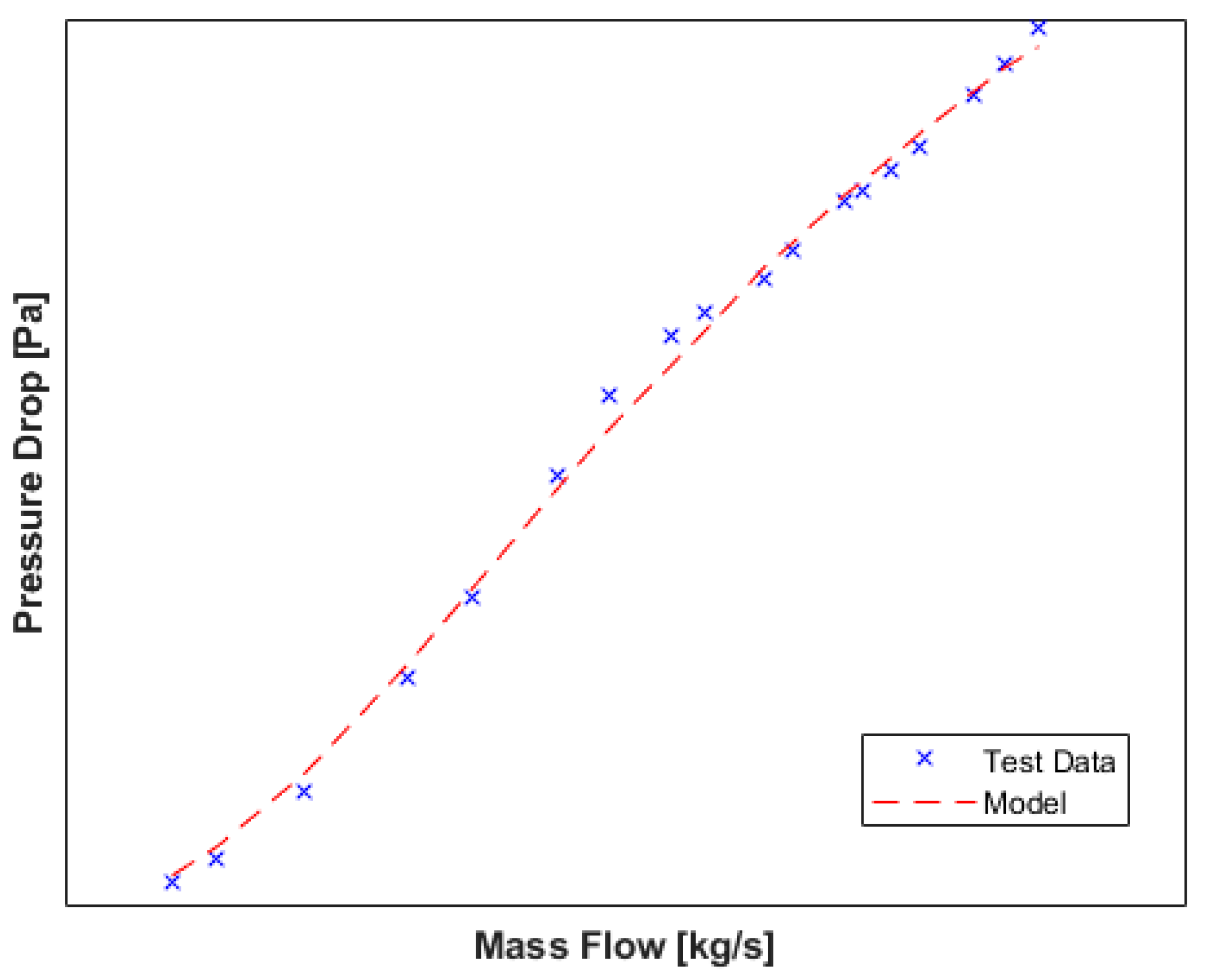
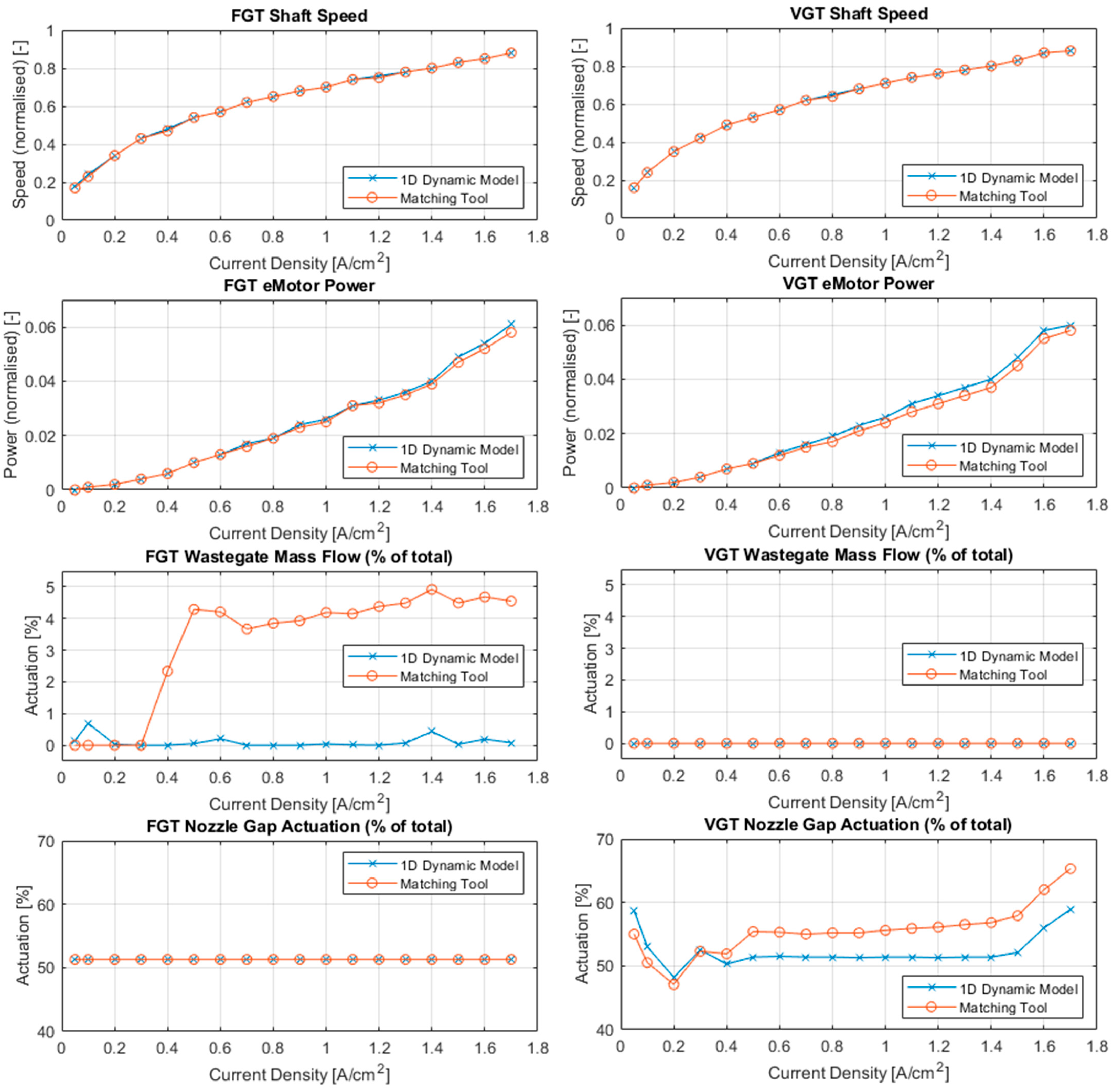
3.1. One-Dimensional Modelling
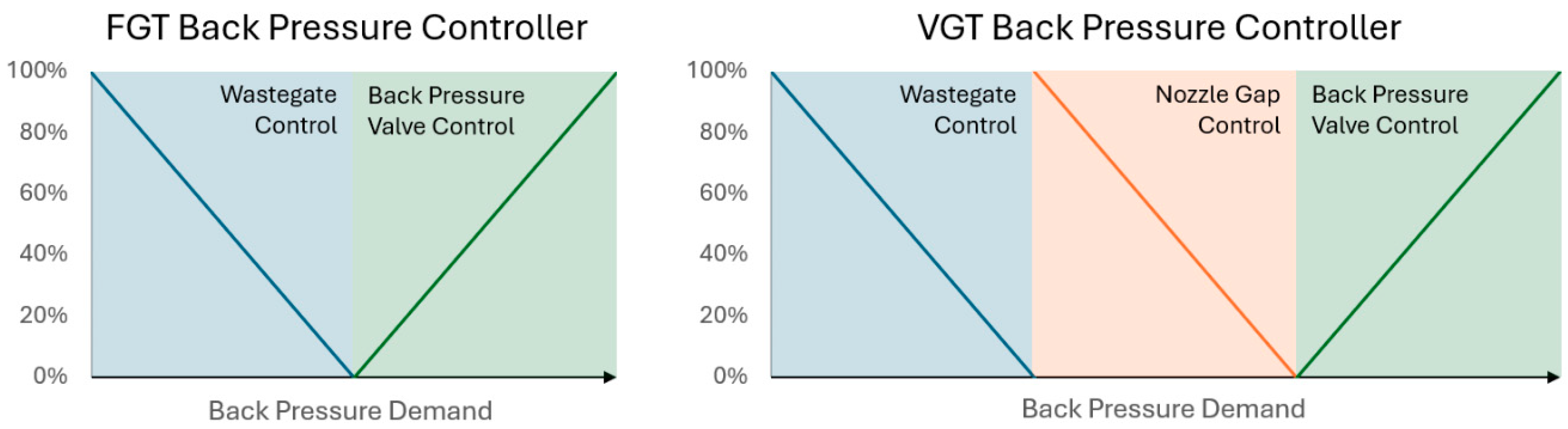
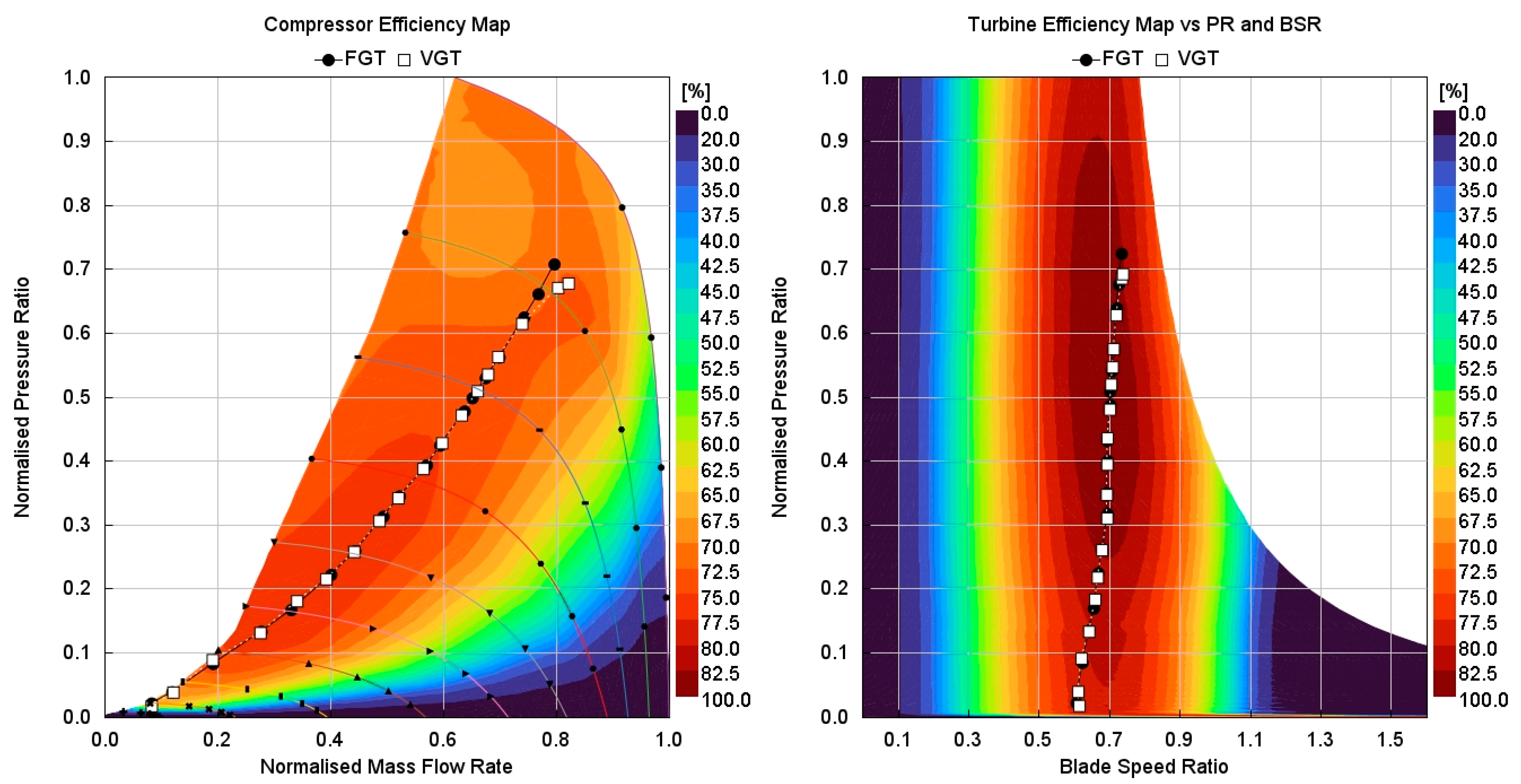
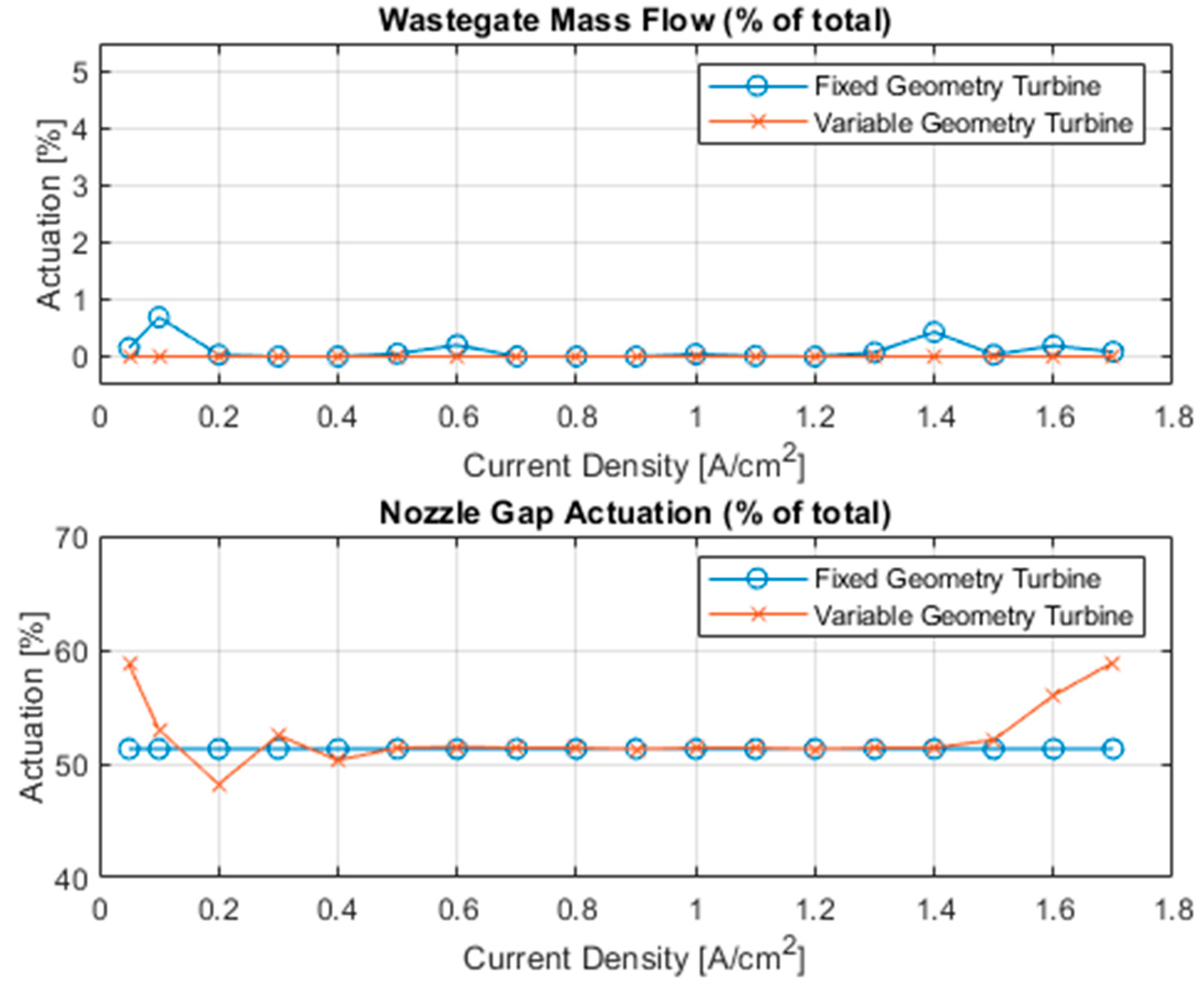
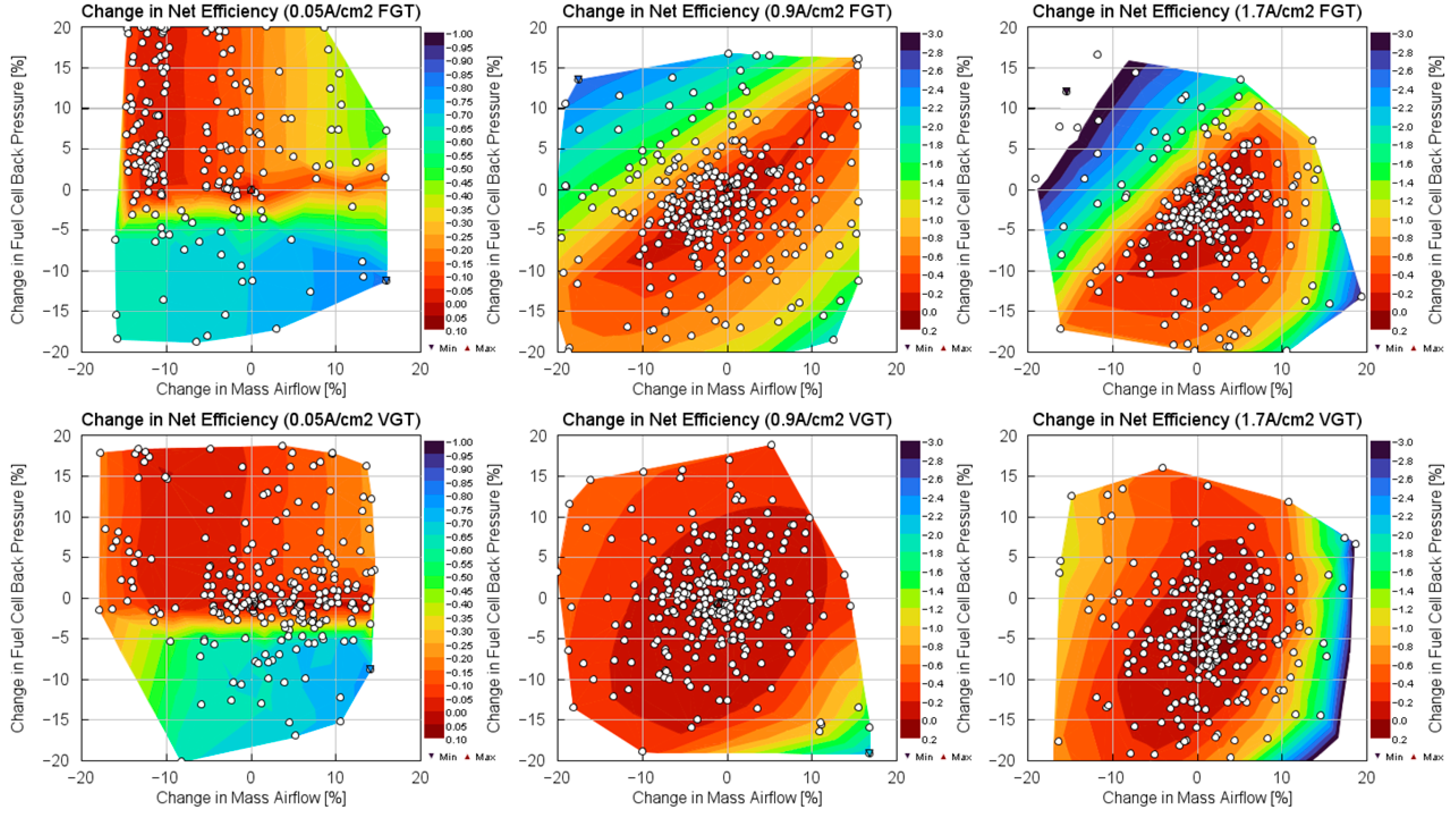
3.2. Optimisation of Turbine Operating Points
3.3. Matching Tool Results
4. Discussion
5. Conclusions, Limitations, and Future Work
- Optimising the mass air flow and pressure to ensure that both the FGT and VGT were able to operate at their maximum system efficiency across the range of current densities.
- Ensuring that both the FGT and VGT are appropriately sized for the application.
- Using an identical map, representing the VGT ‘flush gap’, for the FGT, essentially isolating the ‘variable’ aspect of the VGT.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| A-GA | Accelerated Genetic Algorithm |
| BPV | Back Pressure Valve |
| CFD | Computational Fluid Dynamics |
| EGR | Exhaust Gas Recirculation |
| EM | Electric Motor |
| FCEV | Fuel Cell Electric Vehicle |
| FCS | Fuel Cell System |
| FGT | Fixed Geometry Turbocharger |
| FCMT | Fuel Cell Matching Tool |
| GT | GT-Suite 1D System Modelling Software (Gamma Technologies) |
| ICE | Internal Combustion Engine |
| MT | Matching Tool |
| N | Angular Velocity |
| NSGA | Non-Dominated Sorting Genetic Algorithm |
| OER | Oxygen Excess Ratio |
| OP | Operating Point |
| PEMFC | Proton Exchange Membrane Fuel Cell |
| SAE | Society of Automotive Engineers |
| VGT | Variable-Geometry Turbocharger |
| WG | Wastegate |
| Nomenclature | |
| AC | Active cell area |
| cmp | Compressor |
| cp | Specific heat capacity at constant pressure |
| elec | Electrical |
| F | Faraday constant |
| FC | Fuel cell |
| i | Current density |
| in | At inlet |
| isn | Isentropic |
| J | Cost of each turbine in selection algorithm |
| k | Orifice area and discharge coefficient (summarised) |
| ki | Weight of an operating point (turbine selection algorithm) |
| LHV | Lower heating value (of hydrogen) |
| Mass flow rate | |
| mch | Mechanical |
| MH2 | Molar mass of hydrogen |
| MO2 | Molar mass of oxygen |
| nC | Number of cells |
| out | At outlet |
| p | Pressure |
| P | Power |
| REO | Oxygen excess ratio |
| T | Temperature |
| trb | Turbine |
| Greek Characters | |
| Δ | Change in |
| γ | Ratio of specific heats |
| η | Efficiency |
| λ,air | of air (subscript) |
| λ,H2 | of hydrogen (subscript) |
| λ,O2 | of oxygen (subscript) |
| π | Pressure ratio |
| ρ | Density |
| Torque | |
References
- Miller, A.; Hess, K.; Barnes, D.; Erickson, T. System design of a large fuel cell hybrid locomotive. J. Power Sources 2007, 173, 935–942. [Google Scholar] [CrossRef]
- Dall’armi, C.; Pivetta, D.; Taccani, R. Hybrid PEM Fuel Cell Power Plants Fuelled by Hydrogen for Improving Sustainability in Shipping: State of the Art and Review on Active Projects. Energies 2023, 16, 2022. [Google Scholar] [CrossRef]
- Frey, A.C.; Bosak, D.; Stonham, J.; Sangan, C.M.; Pountney, O.J. Liquid Cooling of Fuel Cell Powered Aircraft: The Effect of Coolants on Thermal Management. J. Eng. Gas Turbines Power 2024, 146, 111021. [Google Scholar] [CrossRef]
- Quan, R.; Li, Z.; Liu, P.; Li, Y.; Chang, Y.; Yan, H. Minimum hydrogen consumption-based energy management strategy for hybrid fuel cell unmanned aerial vehicles using direction prediction optimal foraging algorithm. Fuel Cells 2023, 23, 221–236. [Google Scholar] [CrossRef]
- Mancino, A.N.; Menale, C.; Vellucci, F.; Pasquali, M.; Bubbico, R. PEM Fuel Cell Applications in Road Transport. Energies 2023, 16, 6129. [Google Scholar] [CrossRef]
- Corbo, P.; Migliardini, F.; Veneri, O. Experimental analysis and management issues of a hydrogen fuel cell system for stationary and mobile application. Energy Convers. Manag. 2007, 48, 2365–2374. [Google Scholar] [CrossRef]
- Elgowainy, A. Electric, Hybrid, and Fuel Cell Vehicles; Springer: New York, NY, USA, 2021; Available online: http://www.springer.com/series/15436 (accessed on 27 March 2025).
- Atilhan, S.; Park, S.; El-Halwagi, M.M.; Atilhan, M.; Moore, M.; Nielsen, R.B. Green hydrogen as an alternative fuel for the shipping industry. Curr. Opin. Chem. Eng. 2021, 31, 100668. [Google Scholar] [CrossRef]
- Heid, B.; Martens, C.; Wilthaner, M. Unlocking Hydrogen’s Power for Long-Haul Freight Transport; McKinsey: New York, NY, USA, 2022. [Google Scholar]
- Blunier, B.; Miraoui, A. Proton exchange membrane fuel cell air management in automotive applications. J. Fuel Cell Sci. Technol. 2010, 7, 041007. [Google Scholar] [CrossRef]
- Kim, D.K.; Seo, J.H.; Kim, S.; Lee, M.K.; Nam, K.Y.; Song, H.H.; Kim, M.S. Efficiency improvement of a PEMFC system by applying a turbocharger. Int. J. Hydrogen Energy 2014, 39, 20139–20150. [Google Scholar] [CrossRef]
- Yu, W.; Sichuan, X.; Ni, H. Air Compressors for Fuel Cell Vehicles: An Systematic Review. SAE Int. J. Altern. Powertrains 2015, 4, 115–122. [Google Scholar] [CrossRef]
- Kerviel, A.; Pesyridis, A.; Mohammed, A.; Chalet, D. An evaluation of turbocharging and supercharging options for high-efficiency Fuel Cell Electric Vehicles. Appl. Sci. 2018, 8, 2474. [Google Scholar] [CrossRef]
- Wiartalla, A.; Pischinger, S.; Bornscheuer, W.; Fieweger, K.; Ogrzewalla, J. Compressor Expander Units for Fuel Cell Systems. In Fuel Cell Power for Transportation; SAE International: Detroit, MI, USA, 2000. [Google Scholar]
- Zhang, Y.; Xu, S.; Lin, C. Performance improvement of fuel cell systems based on turbine design and supercharging system matching. Appl. Therm. Eng. 2020, 180, 115806. [Google Scholar] [CrossRef]
- Hou, J.; Yang, M.; Ke, C.; Zhang, J. Control logics and strategies for air supply in PEM fuel cell engines. Appl. Energy 2020, 269, 115059. [Google Scholar] [CrossRef]
- Ahmadi, N.; Dadvand, A.; Rezazadeh, S.; Mirzaee, I. Analysis of the operating pressure and GDL geometrical configuration effect on PEM fuel cell performance. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 2311–2325. [Google Scholar] [CrossRef]
- Qin, Y.; Du, Q.; Fan, M.; Chang, Y.; Yin, Y. Study on the operating pressure effect on the performance of a proton exchange membrane fuel cell power system. Energy Convers. Manag. 2017, 142, 357–365. [Google Scholar] [CrossRef]
- Amirinejad, M.; Rowshanzamir, S.; Eikani, M.H. Effects of operating parameters on performance of a proton exchange membrane fuel cell. J. Power Sources 2006, 161, 872–875. [Google Scholar] [CrossRef]
- Hu, D.; Liu, J.; Yi, F.; Yang, Q.; Zhou, J. Enhancing heat dissipation to improve efficiency of two-stage electric air compressor for fuel cell vehicle. Energy Convers. Manag. 2022, 251, 115007. [Google Scholar] [CrossRef]
- Milburn, S.M.; Cronin, J.J.; Cohen, B.M. A Variable Displacement Compressor/Expander for Vehicular Fuel Cell Air Management. In Future Transportation Technology Conference; SAE: Vancouver, BC, USA, 1995. [Google Scholar]
- Zhao, D.; Xu, L.; Huangfu, Y.; Dou, M.; Liu, J. Semi-physical modeling and control of a centrifugal compressor for the air feeding of a PEM fuel cell. Energy Convers. Manag. 2017, 154, 380–386. [Google Scholar] [CrossRef]
- Menze, M.; Schoedel, M.; Seume, J.R. Numerical Investigation of a Radial Turbine with Variable Nozzle Geometry for Fuel Cell Systems in Automotive Applications. In Proceedings of the 14th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Gdansk, Poland, 12–16 April 2021; Available online: www.euroturbo.eu (accessed on 27 March 2025).
- Martinez-Boggio, S.; Di Blasio, D.; Fletcher, T.; Burke, R.; García, A.; Monsalve-Serrano, J. Optimization of the air loop system in a hydrogen fuel cell for vehicle application. Energy Convers. Manag. 2023, 283I, 116911. [Google Scholar] [CrossRef]
- Ahsan, N.; Al Rashid, A.; Zaidi, A.A.; Imran, R.; Qadir, S.A. Performance analysis of hydrogen fuel cell with two-stage turbo compressor for automotive applications. Energy Rep. 2021, 7, 2635–2646. [Google Scholar] [CrossRef]
- Zhang, Y.; Bao, P.; Wan, Y.; Xu, S. Modeling and analysis of air supply system of polymer electrolyte membrane fuel cell system. Energy Procedia 2017, 142, 1053–1058. [Google Scholar] [CrossRef]
- Filsinger, D.; Kuwata, G.; Ikeya, N. Tailored Centrifugal Turbomachinery for Electric Fuel Cell Turbocharger. Int. J. Rotating Mach. 2021, 2021, 3972387. [Google Scholar] [CrossRef]
- Bao, C.; Ouyang, M.; Yi, B. Modeling and optimization of the air system in polymer exchange membrane fuel cell systems. J. Power Sources 2006, 156, 232–243. [Google Scholar] [CrossRef]
- Kulp, G.W.; Gurski, S.; Nelson, D.J. PEM Fuel Cell Air Management Efficiency at Part Load. In Future Car Congress; SAE International: Pittsburgh, PA, USA, 2002. [Google Scholar]
- Cunningham, J.M.; Hoffman, M.A.; Eggert, A.R.; Friedman, D.J. The Implications of Using an Expander (Turbine) in and Air System of a PEM Fuel Cell Engine. In Proceedings of the 17 International Electric Vehicle Symposium and Exposition: Driving New Visions, Montreal, QC, Canada, 15–18 October 2000. [Google Scholar]
- Saidur, R.; Rezaei, M.; Muzammil, W.K.; Hassan, M.H.; Paria, S.; Hasanuzzaman, M. Technologies to recover exhaust heat from internal combustion engines. Renew. Sustain. Energy Rev. 2012, 16, 5649–5659. [Google Scholar] [CrossRef]
- Feneley, A.J.; Pesiridis, A.; Andwari, A.M. Variable Geometry Turbocharger Technologies for Exhaust Energy Recovery and Boosting—A Review. Renew. Sustain. Energy Rev. 2017, 71, 959–975. [Google Scholar] [CrossRef]
- Liu, J.; Wang, H.; Zheng, Z.; Zou, Z.; Yao, M. Effects of Different Turbocharging Systems on Performance in a HD Diesel Engine with Different Emission Control Technical Routes. In SAE Technical Papers; SAE International: Pittsburgh, PA, USA, 2016. [Google Scholar] [CrossRef]
- Cheong, J.; Cho, S.; Kim, C. Effect of Variable Geometry Turbocharger on HSDI Diesel Engine. In Proceedings of the Seoul 2000 FISITA World Automotive Congress, Seoul, Republic of Korea, 12–15 June 2000. [Google Scholar]
- Schoedel, M.; Menze, M.; Seume, J.R. Experimentally validated extension of the operating range of an electrically driven turbocharger for fuel cell applications. Machines 2021, 9, 331. [Google Scholar] [CrossRef]
- Taylor, A.H.; Naik, P.; Nibler, S.; Al-Hasan, N. Optimization of Variable Geometry Turbine Electric Turbocharger for a Heavy Duty, On-Highway Fuel Cell. In Proceedings of the ASME Turbo Expo 2023: Turbomachinery Technical Conference and Exposition, Boston, MA, USA, 26–30 June 2023; Available online: http://asmedigitalcollection.asme.org/GT/proceedings-pdf/GT2023/87110/V13DT34A004/7046079/v13dt34a004-gt2023-101224.pdf?casa_token=FjiX3e16VWgAAAAA:KMKCtwnJLFUXUvmZcjJnEMDQR1cBmRSsWz1gPDPBIKR_y6fO82Bypeds6iHX6fGbuNDVhBA (accessed on 27 March 2025).
- Piqueras, P.; de la Morena, J.; Sanchis, E.J.; Lalangui, J.A. Potential of Proton-Exchange Membrane Fuel-Cell System with On-Board O2-Enriched Air Generation. Appl. Sci. 2024, 14, 836. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Y.; Liu, G.; Yang, Q.; Li, L.; Gao, Z. Air and hydrogen supply systems and equipment for PEM fuel cells: A review. Int. J. Green Energy 2021, 19, 331–348. [Google Scholar] [CrossRef]
- Wang, C.; Xing, Z.; Sun, S.; Chen, W.; He, Z. Experimental study on the performance of oil-free twin-screw expanders for recovering energy in fuel cell systems. Appl. Therm. Eng. 2020, 165, 114613. [Google Scholar] [CrossRef]
- Baines, N.C. Fundamentals of Turbocharging; Concepts NREC: White River Junction, VT, USA, 2005. [Google Scholar]
- J922_201106; Turbocharger Nomenclature and Terminology. SAE International Recommended Practice: Pittsburgh, PA, USA, 2011. [CrossRef]
- J1826_202204; Turbocharger Gas Stand Test Code. SAE International Technical Standard: Pittsburgh, PA, USA, 2022. [CrossRef]
- Wittmann, T.; Lück, S.; Bode, C.; Friedrichs, J. On the Impact of Condensation and Liquid Water on the Radial Turbine of a Fuel Cell Turbocharger. Machines 2022, 10, 1053. [Google Scholar] [CrossRef]
- Mao, H.; Tang, X.; Liu, J.; Xu, S. Numerical investigation of the non-equilibrium condensation inside a fuel cell turbine with variable geometry. Int. J. Heat Mass Transf. 2023, 217, 124710. [Google Scholar] [CrossRef]



| Reference | Low/Part Load Sys. Eff. Improvement | High Load Sys. Eff. Improvement | Compressor Power Offset by Turbine |
|---|---|---|---|
| Martinez-Boggio et al., 2023 [24] | +1% | +8% | Up to 60% |
| Ahsan et al., 2021 [25] | +6% (approx.) across the operating range. | 43.1–47.9% (approx.) | |
| Filsinger et al., 2021 [27] | 9–39.3% | ||
| Kerviel et al., 2018 [13] | +3.3% (WLTP avg.) vs. single-stage compressor +1.6% (WLTP avg.) vs. two-stage compressor | 45.8% on average | |
| Zhang et al., 2017 [26] | +6.9% (approx.) | 25–44.7% (approx.) | |
| Bao et al., 2006 [28] | +3% (approx.) vs. single-stage compressor +1% (approx.) vs. two-stage compressor | ||
| Kulp et al., 2002 [29] | +1% (approx.) | +5% (approx.) | |
| Cunningham et al., 2000 [30] | “Largely unchanged” | +4% (approx.) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smith, M.L.; Fritot, A.; Di Blasio, D.; Burke, R.; Fletcher, T. Matching and Control Optimisation of Variable-Geometry Turbochargers for Hydrogen Fuel Cell Systems. Appl. Sci. 2025, 15, 4387. https://doi.org/10.3390/app15084387
Smith ML, Fritot A, Di Blasio D, Burke R, Fletcher T. Matching and Control Optimisation of Variable-Geometry Turbochargers for Hydrogen Fuel Cell Systems. Applied Sciences. 2025; 15(8):4387. https://doi.org/10.3390/app15084387
Chicago/Turabian StyleSmith, Matt L., Alexander Fritot, Davide Di Blasio, Richard Burke, and Tom Fletcher. 2025. "Matching and Control Optimisation of Variable-Geometry Turbochargers for Hydrogen Fuel Cell Systems" Applied Sciences 15, no. 8: 4387. https://doi.org/10.3390/app15084387
APA StyleSmith, M. L., Fritot, A., Di Blasio, D., Burke, R., & Fletcher, T. (2025). Matching and Control Optimisation of Variable-Geometry Turbochargers for Hydrogen Fuel Cell Systems. Applied Sciences, 15(8), 4387. https://doi.org/10.3390/app15084387








