Surface Roughness and Its Role in Flotation Behavior, Wettability, and Bubble–Particle Interactions: A Systematic Review
Abstract
1. Introduction
2. Measurement and Roughening Methods
2.1. Measurement Methods
2.2. Roughening Methods
2.2.1. Grinding Method
2.2.2. Laboratory Test Methods
3. Flotation Behavior
4. Wettability
4.1. Wettability Model for Rough Surface
4.2. The Effect of Surface Roughness on Wettability
5. Bubble–Particle Interaction
5.1. Bubble–Particle Attachment
5.2. Bubble–Particle Interaction Force
5.3. Bubble–Particle Interaction Energy
6. Conclusions and Perspectives
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, X.; Zhang, Q. Role of surface roughness in the wettability, surface energy and flotation kinetics of calcite. Powder Technol. 2020, 371, 55–63. [Google Scholar] [CrossRef]
- Li, Z.; Rao, F.; Corona-Arroyo, M.A.; Bedolla-Jacuinde, A.; Song, S. Comminution effect on surface roughness and flotation behavior of malachite particles. Miner. Eng. 2019, 132, 1–7. [Google Scholar] [CrossRef]
- Zhu, Z.; Fu, Y.; Yin, W.; Sun, H.; Chen, K.; Tang, Y.; Yang, B. Role of surface roughness in the magnesite flotation and its mechanism. Particuology 2022, 62, 63–70. [Google Scholar] [CrossRef]
- Elleuch, R.; Elleuch, K.; Ben Abdelounis, H.; Zahouani, H. Surface roughness effect on friction behaviour of elastomeric material. Mater. Sci. Eng. A 2007, 465, 8–12. [Google Scholar] [CrossRef]
- He, C.L.; Zong, W.J.; Zhang, J.J. Influencing factors and theoretical modeling methods of surface roughness in turning process: State-of-the-art. Int. J. Mach. Tools Manuf. 2018, 129, 15–26. [Google Scholar] [CrossRef]
- Zhang, S.J.; To, S.; Wang, S.J.; Zhu, Z.W. A review of surface roughness generation in ultra-precision machining. Int. J. Mach. Tools Manuf. 2015, 91, 76–95. [Google Scholar] [CrossRef]
- Vencl, A.; Ivanović, L.; Stojanović, B.; Zadorozhnaya, E.; Miladinović, S.; Svoboda, P. Surface texturing for tribological applications: A review. Proc. Eng. Sci. 2019, 1, 227–239. [Google Scholar] [CrossRef]
- Korbel, C.; Filippova, I.V.; Filippov, L.O. Froth flotation of lithium micas—A review. Miner. Eng. 2023, 192, 107986. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, C.; Sun, W.; Gao, Y.; Kowalczuk, P.B. Froth flotation of fluorite: A review. Adv. Colloid Interface Sci. 2021, 290, 102382. [Google Scholar] [CrossRef]
- Wan Nafi, A.; Taseidifar, M. Removal of hazardous ions from aqueous solutions: Current methods, with a focus on green ion flotation. J. Environ. Manag. 2022, 319, 115666. [Google Scholar] [CrossRef]
- Saththasivam, J.; Loganathan, K.; Sarp, S. An overview of oil–water separation using gas flotation systems. Chemosphere 2016, 144, 671–680. [Google Scholar] [CrossRef]
- Deliyanni, E.A.; Kyzas, G.Z.; Matis, K.A. Various flotation techniques for metal ions removal. J. Mol. Liq. 2017, 225, 260–264. [Google Scholar] [CrossRef]
- Vashisth, S.; Bennington, C.P.J.; Grace, J.R.; Kerekes, R.J. Column Flotation Deinking: State-of-the-art and opportunities. Resour. Conserv. Recycl. 2011, 55, 1154–1177. [Google Scholar] [CrossRef]
- Costa, C.A.; Rubio, J. Deinking flotation: Influence of calcium soap and surface-active substances. Miner. Eng. 2005, 18, 59–64. [Google Scholar] [CrossRef]
- Li, W.; Ma, Y.; Feng, X.; Alheshibri, M.; Bu, X.; Ma, G.; Ni, M.; Li, Q.; Liu, A.; Niu, X. Optimization of an oil recovery process from oily sludge using a combined technique of froth flotation and centrifugal treatment. J. Clean. Prod. 2023, 400, 136752. [Google Scholar] [CrossRef]
- Ramaswamy, B.; Kar, D.D.; De, S. A study on recovery of oil from sludge containing oil using froth flotation. J. Environ. Manag. 2007, 85, 150–154. [Google Scholar] [CrossRef]
- Kökkılıç, O.; Mohammadi-Jam, S.; Chu, P.; Marion, C.; Yang, Y.; Waters, K.E. Separation of plastic wastes using froth flotation—An overview. Adv. Colloid Interface Sci. 2022, 308, 102769. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Wang, C. Surface modification and selective flotation of waste plastics for effective recycling—A review. Sep. Purif. Technol. 2019, 226, 75–94. [Google Scholar] [CrossRef]
- Mennik, F.; Dinç, N.İ.; Burat, F. Selective recovery of metals from spent mobile phone lithium-ion batteries through froth flotation followed by magnetic separation procedure. Results Eng. 2023, 17, 100868. [Google Scholar] [CrossRef]
- Verdugo, L.; Zhang, L.; Etschmann, B.; Bruckard, W.; Menacho, J.; Hoadley, A. Effect of lithium ion on the separation of electrode materials in spent lithium ion batteries using froth flotation. Sep. Purif. Technol. 2023, 311, 123241. [Google Scholar] [CrossRef]
- Xing, Y.; Gui, X.; Pan, L.; Pinchasik, B.-E.; Cao, Y.; Liu, J.; Kappl, M.; Butt, H.-J. Recent experimental advances for understanding bubble-particle attachment in flotation. Adv. Colloid Interface Sci. 2017, 246, 105–132. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, A.; Evans, G. Attachment interaction between air bubbles and particles in froth flotation. Exp. Therm. Fluid Sci. 2004, 28, 381–385. [Google Scholar] [CrossRef]
- Li, C.; Zhang, H. Surface nanobubbles and their roles in flotation of fine particles–A review. J. Ind. Eng. Chem. 2022, 106, 37–51. [Google Scholar] [CrossRef]
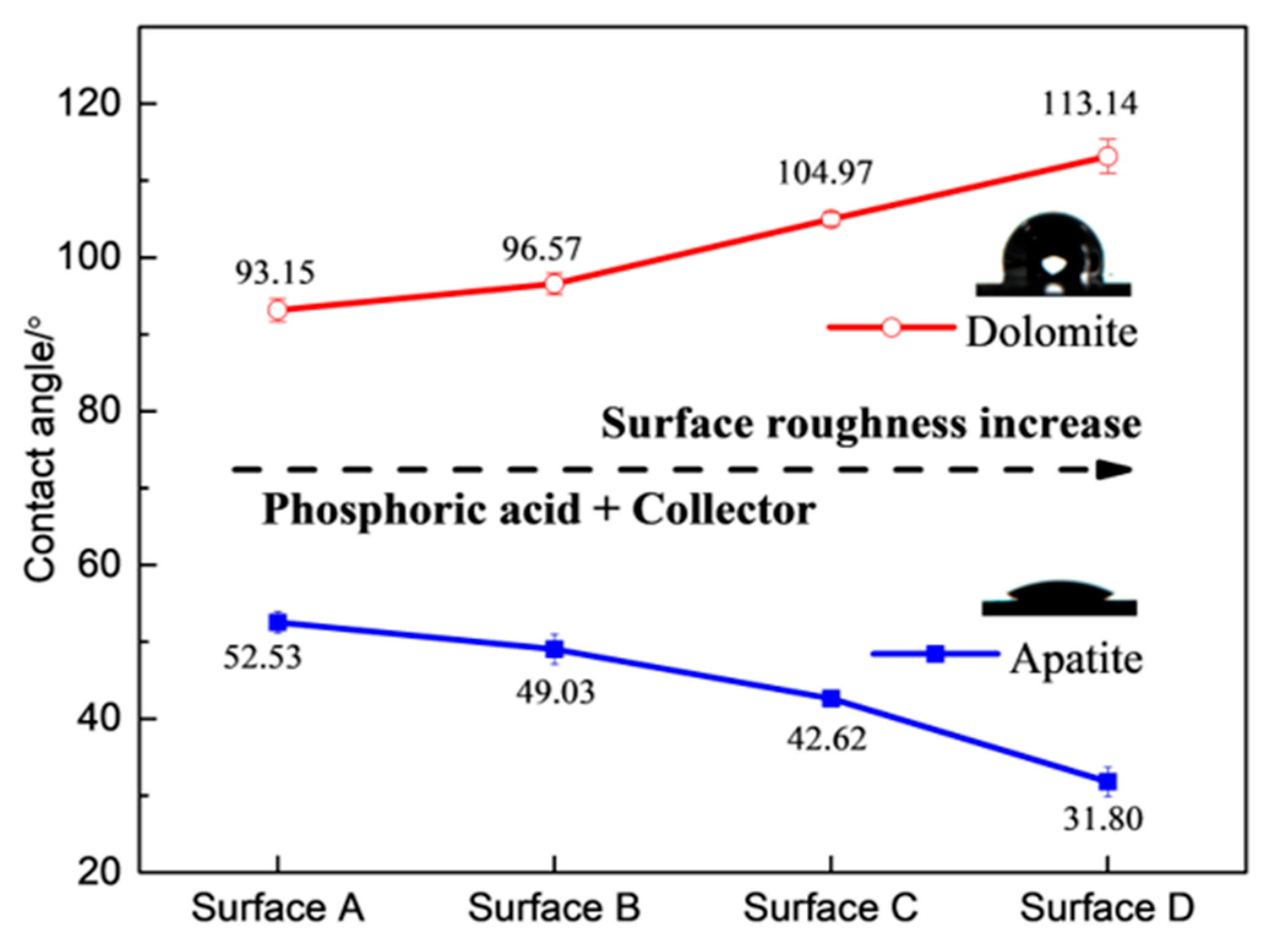
- Wang, X.; Zhang, Q. Insight into the Influence of Surface Roughness on the Wettability of Apatite and Dolomite. Minerals 2020, 10, 114. [Google Scholar] [CrossRef]
- Guven, O.; Karakas, F.; Kodrazi, N.; Çelik, M.S. Dependence of morphology on anionic flotation of alumina. Int. J. Miner. Process. 2016, 156, 69–74. [Google Scholar] [CrossRef]
- Xie, L.; Wang, J.; Lu, Q.; Hu, W.; Yang, D.; Qiao, C.; Peng, X.; Peng, Q.; Wang, T.; Sun, W.; et al. Surface interaction mechanisms in mineral flotation: Fundamentals, measurements, and perspectives. Adv. Colloid Interface Sci. 2021, 295, 102491. [Google Scholar] [CrossRef] [PubMed]
- Yin, W.; Zhu, Z.; Yang, B.; Fu, Y.; Yao, J. Contribution of particle shape and surface roughness on the flotation behavior of low-ash coking coal. Energy Sources Part A Recovery Util. Environ. Eff. 2019, 41, 636–644. [Google Scholar] [CrossRef]
- Busscher, H.J.; van Pelt, A.W.J.; de Boer, P.; de Jong, H.P.; Arends, J. The effect of surface roughening of polymers on measured contact angles of liquids. Colloids Surf. 1984, 9, 319–331. [Google Scholar] [CrossRef]
- Guven, O.; Ozdemir, O.; CELIK, M. Contribution of roughness and shape factors on flotation of glass beads. In Proceedings of the IMPC, Sundsvall, Sweden, 27–29 May 2024. [Google Scholar]
- Guo, Z.; Yang, J.; Wang, Y. An investigation of continuous interaction process between air bubble and various roughness coal surfaces using microbalance. Physicochem. Probl. Miner. Process. 2020, 56, 11–23. [Google Scholar]
- Uysal, T.; Guven, O.; Ozdemir, O.; Karaagaclioglu, I.; Tunç, B.; Çelik, M. Contribution of particle morphology on flotation and aggregation of sphalerite particles. Miner. Eng. 2021, 165, 106860. [Google Scholar] [CrossRef]
- Ulusoy, U. Physical attributes of particles and their roles on wetting and flotation. Chap 2008, 9, 213–230. [Google Scholar]
- Ulusoy, U.; Yekeler, M. Correlation of the surface roughness of some industrial minerals with their wettability parameters. Chem. Eng. Process. Process Intensif. 2005, 44, 555–563. [Google Scholar] [CrossRef]
- Ulusoy, U.; Yekeler, M.; Hiçyılmaz, C. Determination of the shape, morphological and wettability properties of quartz and their correlations. Miner. Eng. 2003, 16, 951–964. [Google Scholar] [CrossRef]
- Hassas, B.V.; Caliskan, H.; Guven, O.; Karakas, F.; Cinar, M.; Celik, M.S. Effect of roughness and shape factor on flotation characteristics of glass beads. Colloids Surf. A Physicochem. Eng. Asp. 2016, 492, 88–99. [Google Scholar] [CrossRef]
- Karakas, F.; Hassas, B.V. Effect of surface roughness on interaction of particles in flotation. Physicochem. Probl. Miner. Process. 2016, 52, 18–34. [Google Scholar]
- Zhu, Z.; Wang, D.; Yang, B.; Yin, W.; Ardakani, M.S.; Yao, J.; Drelich, J.W. Effect of nano-sized roughness on the flotation of magnesite particles and particle-bubble interactions. Miner. Eng. 2020, 151, 106340. [Google Scholar] [CrossRef]
- Tong, Z.; Liu, L.; Yuan, Z.; Liu, J.; Lu, J.; Li, L. The effect of comminution on surface roughness and wettability of graphite particles and their relation with flotation. Miner. Eng. 2021, 169, 106959. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, Z.; Yin, W.; Yang, B.; Zhang, N.; Qu, J.; Chen, S.; Chang, J.; Yu, Y.; Liu, L. Effect of surface roughness on the flotation separation of hematite from fine quartz. J. Ind. Eng. Chem. 2022, 109, 431–441. [Google Scholar] [CrossRef]
- Zhu, Z.; Yin, W.; Han, H.; Cao, S.; Yang, B.; Wang, D. Investigation on the influence of surface roughness on magnetite flotation from the view of both particle-particle and bubble-particle interactions. Colloids Surf. A Physicochem. Eng. Asp. 2020, 595, 124681. [Google Scholar] [CrossRef]
- Zhu, Z.; Yin, W.; Wang, D.; Sun, H.; Chen, K.; Yang, B. The role of surface roughness in the wettability and floatability of quartz particles. Appl. Surf. Sci. 2020, 527, 146799. [Google Scholar] [CrossRef]
- Guven, O.; Kaymakoğlu, B.; Ehsani, A.; Hassanzadeh, A.; Sivrikaya, O. Effects of grinding time on morphology and collectorless flotation of coal particles. Powder Technol. 2022, 399, 117010. [Google Scholar] [CrossRef]
- Xing, Y.; Xu, M.; Gui, X.; Cao, Y.; Babel, B.; Rudolph, M.; Weber, S.; Kappl, M.; Butt, H.-J. The application of atomic force microscopy in mineral flotation. Adv. Colloid Interface Sci. 2018, 256, 373–392. [Google Scholar] [CrossRef]
- Rezai, B.; Rahimi, M.; Aslani, M.; Eslamian, A.; Dehghani, F. Relationship between surface roughness of minerals and their flotation kinetics. In Proceedings of the XI International Mineral Processing and Technology Congress, Brisbane, Australia, 6–10 September 2010; p. 238. [Google Scholar]
- Rahimi, M.; Dehghani, F.; Rezai, B.; Aslani, M.R. Influence of the roughness and shape of quartz particles on their flotation kinetics. Int. J. Miner. Metall. Mater. 2012, 19, 284–289. [Google Scholar] [CrossRef]
- Hicyilmaz, C.; Ulusoy, U.; Bilgen, S.; Yekeler, M. Flotation responses to the morphological properties of particles measured with three-dimensional approach. Int. J. Miner. Process. 2005, 75, 229–236. [Google Scholar] [CrossRef]
- Rahimi, M.; Aslani, M.; Rezai, B. Influence of surface roughness on flotation kinetics of quartz. J. Cent. South. Univ. 2012, 19, 1206–1211. [Google Scholar] [CrossRef]
- Yekeler, M.; Ulusoy, U. Characterisation of surface roughness and wettability of salt-type minerals: Calcite and barite. Miner. Process. Extr. Metall. 2004, 113, 145–152. [Google Scholar] [CrossRef]
- Ulusoy, U.; Yekeler, M. Variation of critical surface tension for wetting of minerals with roughness determined by Surtronic 3+ instrument. Int. J. Miner. Process. 2004, 74, 61–69. [Google Scholar] [CrossRef]
- Li, C.; Sun, C.-y.; Wang, Y.-l.; Fu, Y.-f.; Xu, P.-y.; Yin, W.-z. Research on new beneficiation process of low-grade magnesite using vertical roller mill. Int. J. Miner. Metall. Mater. 2020, 27, 432–442. [Google Scholar] [CrossRef]
- Guven, O.; Ozdemir, O.; Karaagaclioglu, I.E.; Çelik, M.S. Surface morphologies and floatability of sand-blasted quartz particles. Miner. Eng. 2015, 70, 1–7. [Google Scholar] [CrossRef]
- Drelich, J.; Chibowski, E.; Meng, D.D.; Terpilowski, K. Hydrophilic and superhydrophilic surfaces and materials. Soft Matter 2011, 7, 9804–9828. [Google Scholar] [CrossRef]
- Guven, O.; Çelik, M.S. Interplay of particle shape and surface roughness to reach maximum flotation efficiencies depending on collector concentration. Miner. Process. Extr. Metall. Rev. 2016, 37, 412–417. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, Y.; Ding, S.; Zheng, X.; Xu, M.; Cao, Y.; Gui, X. Effect of surface roughness on the detachment between bubble and glass beads with different contact angles. Powder Technol. 2020, 361, 812–816. [Google Scholar] [CrossRef]
- Zhou, S.; Bu, X.; Wang, X.; Ni, C.; Ma, G.; Sun, Y.; Xie, G.; Bilal, M.; Alheshibri, M.; Hassanzadeh, A.; et al. Effects of surface roughness on the hydrophilic particles-air bubble attachment. J. Mater. Res. Technol. 2022, 18, 3884–3893. [Google Scholar] [CrossRef]
- Xia, W.; Ma, G.; Bu, X.; Peng, Y. Effect of particle shape on bubble-particle attachment angle and flotation behavior of glass beads and fragments. Powder Technol. 2018, 338, 168–172. [Google Scholar] [CrossRef]
- Guven, O.; Celik, M.S.; Drelich, J.W. Flotation of methylated roughened glass particles and analysis of particle–bubble energy barrier. Miner. Eng. 2015, 79, 125–132. [Google Scholar] [CrossRef]
- Wang, D.; Zhu, Z.; Yang, B.; Yin, W.; Drelich, J.W. Nano-scaled roughness effect on air bubble-hydrophilic surface adhesive strength. Colloids Surf. A Physicochem. Eng. Asp. 2020, 603, 125228. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, Z.; Yin, W.; Yang, B.; Qu, J.; Zhang, N.; Chen, S.; Yu, Y.; Chang, J.; Liu, L. Snap-in interactions between water droplets and hematite/quartz surfaces with various roughness after conditioning with soluble starch and DDA using a dynamic microbalance. Miner. Eng. 2022, 177, 107358. [Google Scholar] [CrossRef]
- Xia, W.; Ni, C.; Xie, G. The influence of surface roughness on wettability of natural/gold-coated ultra-low ash coal particles. Powder Technol. 2016, 288, 286–290. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, Y.; Liu, M.; Xu, M.; Guo, F.; Han, H.; Gao, Z.; Cao, Y.; Gui, X. Improving the floatability of coal with varying surface roughness through hypobaric treatment. Powder Technol. 2019, 345, 643–648. [Google Scholar] [CrossRef]
- Ulusoy, U.; Yekeler, M. Floatability of barite particles with different shape and roughness. Indian J. Chem. Technol. 2007, 14, 616–626. [Google Scholar]
- Ulusoy, U.; Hiçyılmaz, C.; Yekeler, M. Role of shape properties of calcite and barite particles on apparent hydrophobicity. Chem. Eng. Process. Process Intensif. 2004, 43, 1047–1053. [Google Scholar] [CrossRef]
- Luo, L.; Xu, L.; Shi, X.; Meng, J.; Liu, R. Microscale insights into the influence of grinding media on spodumene micro-flotation using mixed anionic/cationic collectors. Int. J. Min. Sci. Technol. 2022, 32, 171–179. [Google Scholar] [CrossRef]
- Zhu, G.; Wang, Y.; Liu, X.; Yu, F.; Lu, D. The cleavage and surface properties of wet and dry ground spodumene and their flotation behavior. Appl. Surf. Sci. 2015, 357, 333–339. [Google Scholar] [CrossRef]
- Hicyilmaz, C.; Ulusoy, U.; Bilgen, S.; Yekeler, M.; Akdogan, G. Response of rough and acute surfaces of pyrite with 3-D approach to the flotation. J. Min. Sci. 2006, 42, 393–402. [Google Scholar] [CrossRef]
- Song, L.; He, F.; Sun, C.; Sun, Z. Effects of grinding media on surface properties and flotation behaviour of pyrite. Nonferrous Metals 2007, 1, 30–34. [Google Scholar]
- Cao, Y.; Tong, X.; Xie, X.; Song, Q.; Zhang, W.; Du, Y.; Zhang, S. Effects of grinding media on the flotation performance of cassiterite. Miner. Eng. 2021, 168, 106919. [Google Scholar] [CrossRef]
- Yekeler, M.; Ulusoy, U.; Hiçyılmaz, C. Effect of particle shape and roughness of talc mineral ground by different mills on the wettability and floatability. Powder Technol. 2004, 140, 68–78. [Google Scholar] [CrossRef]
- Wotruba, H.; Hoberg, H.; Schneider, F. Investigation on the separation of microlithe and zircon. The influence of particle shape on floatability. In Proceedings of the Preprints. XVII. International Mineral Processing Congress, Dresden, Germany, 23–28 September 1991; pp. 23–28. [Google Scholar]
- Xu, P.-Y.; Li, J.; Hu, C.; Chen, Z.; Ye, H.-Q.; Yuan, Z.-Q.; Cai, W.-J. Surface property variations in flotation performance of calcite particles under different grinding patterns. J. Cent. South Univ. 2018, 25, 1306–1316. [Google Scholar] [CrossRef]
- Ulusoy, U.; Yekeler, M.; Hicyilmaz, C. Characterization of surface roughness of Calcite by BET and Surtronic 3+ Techniques. In Proceedings of the 18th International Mining Congress and Exhibition of Turkey-IMCET, Antalya, Turkey, 10–13 June 2003. [Google Scholar]
- Zhang, X.; Qin, Y.; Han, Y.; Li, Y.; Gao, P.; Li, G.; Wang, S. A potential ceramic ball grinding medium for optimizing flotation separation of chalcopyrite and pyrite. Powder Technol. 2021, 392, 167–178. [Google Scholar] [CrossRef]
- Chipakwe, V.; Karlkvist, T.; Rosenkranz, J.; Chelgani, S.C. Exploring the effect of a polyacrylic acid-based grinding aid on magnetite-quartz flotation separation. Sep. Purif. Technol. 2023, 305, 122530. [Google Scholar] [CrossRef]
- Chipakwe, V.; Rosenkranz, J.; Semsari, P.; Chelgani, S.C.; Karlkvist, T. A comparative study on the effect of chemical additives on dry grinding of magnetite ore. S. Afr. J. Chem. Eng. 2020, 34, 135–141. [Google Scholar] [CrossRef]
- Feng, D.; Aldrich, C. A comparison of the flotation of ore from the Merensky Reef after wet and dry grinding. Int. J. Miner. Process. 2000, 60, 115–129. [Google Scholar] [CrossRef]
- Ahmed, M.M. Effect of comminution on particle shape and surface roughness and their relation to flotation process. Int. J. Miner. Process. 2010, 94, 180–191. [Google Scholar] [CrossRef]
- Chelgani, S.C.; Parian, M.; Parapari, P.S.; Ghorbani, Y.; Rosenkranz, J. A comparative study on the effects of dry and wet grinding on mineral flotation separation–a review. J. Mater. Res. Technol. 2019, 8, 5004–5011. [Google Scholar] [CrossRef]
- Bu, X.; Chen, Y.; Ma, G.; Sun, Y.; Ni, C.; Xie, G. Differences in dry and wet grinding with a high solid concentration of coking coal using a laboratory conical ball mill: Breakage rate, morphological characterization, and induction time. Adv. Powder Technol. 2019, 30, 2703–2711. [Google Scholar] [CrossRef]
- Guven, O. The effect of shape and roughness on flotation and aggregation of quartz particles. Physicochem. Probl. Miner. Process. 2022, 58, 154021. [Google Scholar] [CrossRef]
- Wang, S.; Fan, H.; He, H.; Tang, L.; Tao, X. Effect of particle shape and roughness on the hydrophobicity of low-rank coal surface. Int. J. Coal Prep. Util. 2018, 40, 876–891. [Google Scholar] [CrossRef]
- Wang, X.H.; Xie, Y. The effect of grinding media and environment on the surface properties and flotation behaviour of sulfide minerals. Miner. Procesing Extr. Metall. Rev. 1990, 7, 49–79. [Google Scholar] [CrossRef]
- Xia, W. Role of surface roughness in the attachment time between air bubble and flat ultra-low-ash coal surface. Int. J. Miner. Process. 2017, 168, 19–24. [Google Scholar] [CrossRef]
- Li, M.; Xing, Y.; Zhu, C.; Liu, Q.; Yang, Z.; Zhang, R.; Zhang, Y.; Xia, Y.; Gui, X. Effect of roughness on wettability and floatability: Based on wetting film drainage between bubbles and solid surfaces. Int. J. Min. Sci. Technol. 2022, 32, 1389–1396. [Google Scholar] [CrossRef]
- Mao, Y.; Xie, G.; Qi, X.; Peng, Y. Effects of ultrasonic pretreatment on particle size and surface topography of lignite and its relationship to flotation response. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 43, 1274–1282. [Google Scholar] [CrossRef]
- Gungoren, C.; Ozdemir, O.; Wang, X.; Ozkan, S.; Miller, J. Effect of ultrasound on bubble-particle interaction in quartz-amine flotation system. Ultrason. Sonochem. 2019, 52, 446–454. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Wang, N.; Yuan, Z.; Zhang, Q.; Li, L.; Wang, Z. The effects of ultrasonic wave on heterogeneous coagulation and flotation separation of pentlandite-serpentine. Miner. Eng. 2022, 188, 107828. [Google Scholar] [CrossRef]
- Azghdi, S.; Barani, K. Effect of microwave treatment on the surface properties of chalcopyrite. Miner. Metall. Process. 2018, 35, 141–147. [Google Scholar] [CrossRef]
- Barani, K.; Azghadi, M.; Azadi, M.; Karrech, A. Influence of microwave treatment on surface roughness, hydrophobicity, and chemical composition of galena. J. Min. Environ. 2019, 10, 787–797. [Google Scholar]
- An, M.; Liao, Y.; Gui, X.; Zhao, Y.; He, Y.; Liu, Z.; Lai, Q. An investigation of coal flotation using nanoparticles as a collector. Int. J. Coal Prep. Util. 2020, 40, 679–690. [Google Scholar] [CrossRef]
- Xia, W.; Li, Y. Role of roughness change on wettability of taixi anthracite coal surface before and after the heating process. Energy Fuels 2016, 30, 281–284. [Google Scholar] [CrossRef]
- Wang, D.; Xu, M.; He, J.; Guo, C. Effects of low-temperature air plasma pretreatment on the surface properties of low-rank coal. Powder Technol. 2018, 340, 227–233. [Google Scholar] [CrossRef]
- Güven, O.; Karakaş, F.; Yaşar, G.; Çelik, M.S. Morphological character of blasted Talc particles on Talc flotation. In Proceedings of the World Congress on Mechanical, Chemical, and Material Engineering (MCM” 15), Barcelona, Spain, 20–21 July 2015. [Google Scholar]
- Behzad, V.H.; Güven, O.; Baştürkcü, E.; Çelik, M.S. Morphological changes of glass bead particles upon an abrasive blasting as characterized by settling and flotation experiments. Physicochem. Probl. Miner. Process. 2021, 57, 156–167. [Google Scholar]
- Güven, O.; Karakaş, F.; Yaşar, G.; Çelik, M.S. Morphological character and floatability of blasted talc particles. Int. J. Min. Mater. Metall. Eng. 2015, 1, 11–15. [Google Scholar]
- Ulusoy, U.; Hicyilmaz; Yekeler, M.; Bilgen; Akdogan, G. Review of Morphological Attributes with the New 3-D Approach: Role of Roughness and Acuteness of Barite and Pyrite Particles on the Floatability. In Proceedings of the XXIV International Mineral Processing Congress, Beijing, China, 24–28 September 2008. [Google Scholar]
- Raghavan, S.; Hsu, L.L. Factors affecting the flotation recovery of molybdenite from porphyry copper ores. Int. J. Miner. Process. 1984, 12, 145–162. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Y.; Gao, P.; Li, Y. Effects of grinding media on grinding products and flotation performance of chalcopyrite. Miner. Eng. 2020, 145, 106070. [Google Scholar] [CrossRef]
- Fahlstrom, P. Autogenous grinding of base metal ores at Boliden Aktiebolag. Canad. Ming Metallurg. Bull. 1974, 67, 128–141. [Google Scholar]
- Forssberg, E.; Zhai, H. Shape and surface properties of the particles liberated by autogenous grinding. Scand. J. Metall. 1985, 14, 25–32. [Google Scholar]
- Ducker, W.A.; Pashley, R.M.; Ninham, B.W. The flotation of quartz using a double-chained cationic surfactant. J. Colloid Interface Sci. 1989, 128, 66–75. [Google Scholar] [CrossRef]
- Verrelli, D.I.; Bruckard, W.J.; Koh, P.T.L.; Schwarz, M.P.; Follink, B. Particle shape effects in flotation. Part 1: Microscale experimental observations. Miner. Eng. 2014, 58, 80–89. [Google Scholar] [CrossRef]
- Çalışkan, H.; Vaziri Hassas, B.; Cinar, M.; Çelik, M. Effect of Roughness and Shape Factor on Flotation Recoveries of Glass Beads. In Proceedings of the XVI Balkan Mineral Processing Congress, Belgrade, Serbia, 17–19 June 2015. [Google Scholar]
- Chau, T.T.; Bruckard, W.J.; Koh, P.T.L.; Nguyen, A.V. A review of factors that affect contact angle and implications for flotation practice. Adv. Colloid Interface Sci. 2009, 150, 106–115. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Gharabaghi, M.; Aghazadeh, S. A review of the role of wetting and spreading phenomena on the flotation practice. Curr. Opin. Colloid Interface Sci. 2014, 19, 266–282. [Google Scholar] [CrossRef]
- Cassie, A.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- Miller, J.; Veeramasuneni, S.; Drelich, J.; Yalamanchili, M.; Yamauchi, G. Effect of roughness as determined by atomic force microscopy on the wetting properties of PTFE thin films. Polym. Eng. Sci. 1996, 36, 1849–1855. [Google Scholar] [CrossRef]
- Gao, L.; McCarthy, T.J. How Wenzel and Cassie were wrong. Langmuir 2007, 23, 3762–3765. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; McCarthy, T.J. An attempt to correct the faulty intuition perpetuated by the Wenzel and Cassie “laws”. Langmuir 2009, 25, 7249–7255. [Google Scholar] [CrossRef] [PubMed]
- Extrand, C.W. Contact angles and hysteresis on surfaces with chemically heterogeneous islands. Langmuir 2003, 19, 3793–3796. [Google Scholar] [CrossRef]
- Johnson, R.E., Jr.; Dettre, R.H.I. Study of an idealized rough surface. In Contact Angle Hysteresis; ACS Publications: Washington, DC, USA, 1964. [Google Scholar]
- Bormashenko, E. Progress in understanding wetting transitions on rough surfaces. Adv. Colloid Interface Sci. 2015, 222, 92–103. [Google Scholar] [CrossRef]
- Onda, T.; Shibuichi, S.; Satoh, N.; Tsujii, K. Super-water-repellent fractal surfaces. Langmuir 1996, 12, 2125–2127. [Google Scholar] [CrossRef]
- Wenzel, R.N. Surface roughness and contact angle. J. Phys. Chem. 1949, 53, 1466–1467. [Google Scholar] [CrossRef]
- Chen, Y.; Xia, W.; Xie, G. Contact angle and induction time of air bubble on flat coal surface of different roughness. Fuel 2018, 222, 35–41. [Google Scholar] [CrossRef]
- Zhu, C.; Li, G.; Xing, Y.; Gui, X. Adhesion forces for water/oil droplet and bubble on coking coal surfaces with different roughness. Int. J. Min. Sci. Technol. 2021, 31, 681–687. [Google Scholar] [CrossRef]
- Li, Q.; Liang, L.; Tan, J.; Xie, G. The influence mechanism of micron surface roughness on slime coating and bubble attachment on coal surface. Miner. Eng. 2022, 189, 107895. [Google Scholar] [CrossRef]
- Ding, L.P. Investigation of Bituminous Coal Hydrophobicity and its Influence on Flotation. Energy Fuels 2009, 23, 5536–5543. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, D.; Yang, B.; Yin, W.; Drelich, J.W. Water droplets and air bubbles at magnesite nano-rough surfaces: Analysis of induction time, adhesion and detachment using a dynamic microbalance. Miner. Eng. 2020, 155, 106449. [Google Scholar] [CrossRef]
- Shibuichi, S.; Onda, T.; Satoh, N.; Tsujii, K. Super water-repellent surfaces resulting from fractal structure. J. Phys. Chem. 1996, 100, 19512–19517. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Cao, Y.; Li, G.; Liao, Y. Influence of surface roughness on contact angle hysteresis and spreading work. Colloid Polym. Sci. 2020, 298, 1107–1112. [Google Scholar] [CrossRef]
- Extrand, C.W.; Kumagai, Y. An experimental study of contact angle hysteresis. J. Colloid Interface Sci. 1997, 191, 378–383. [Google Scholar] [CrossRef]
- Eske, L.D.; Galipeau, D.W. Characterization of SiO2 surface treatments using AFM, contact angles and a novel dewpoint technique. Colloids Surf. A Physicochem. Eng. Asp. 1999, 154, 33–51. [Google Scholar] [CrossRef]
- Dang-Vu, T.; Hupka, J.; Drzymala, J. Impact of roughness on hydrophobicity of particles measured by the Washburn method. Physicochem. Probl. Miner. Process. 2006, 40, 45–52. [Google Scholar]
- Veeramasuneni, S.; Drelich, J.; Miller, J.D.; Yamauchi, G. Hydrophobicity of ion-plated PTFE coatings. Prog. Org. Coat. 1997, 31, 265–270. [Google Scholar] [CrossRef]
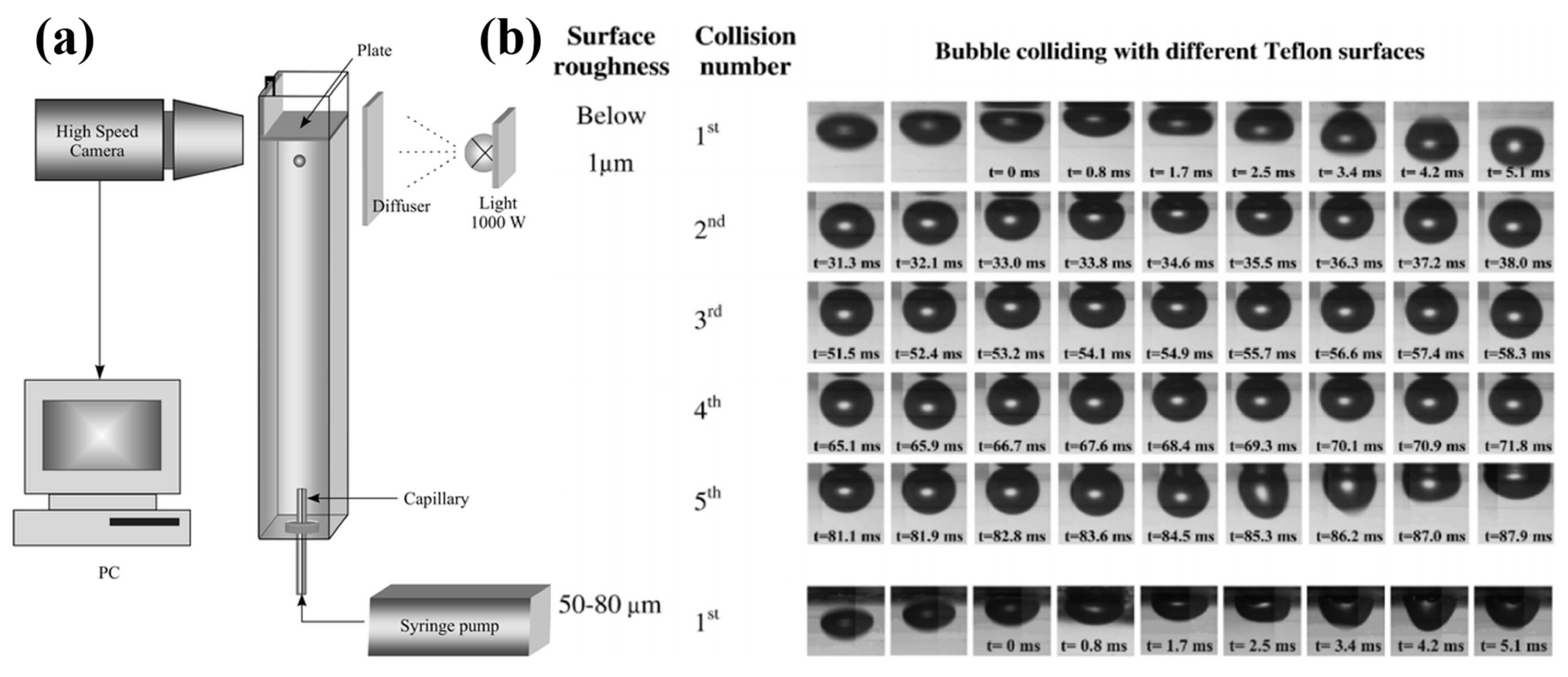
- Krasowska, M.; Malysa, K. Kinetics of bubble collision and attachment to hydrophobic solids: I. Effect of surface roughness. Int. J. Miner. Process. 2007, 81, 205–216. [Google Scholar] [CrossRef]
- Krasowska, M.; Krastev, R.; Rogalski, M.; Malysa, K. Air-facilitated three-phase contact formation at hydrophobic solid surfaces under dynamic conditions. Langmuir 2007, 23, 549–557. [Google Scholar] [CrossRef]
- Extrand, C.W. Criteria for Ultralyophobic Surfaces. Langmuir 2004, 20, 5013–5018. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, A.; Nalaskowski, J.; Miller, J. A study of bubble–particle interaction using atomic force microscopy. Miner. Eng. 2003, 16, 1173–1181. [Google Scholar] [CrossRef]
- Drelich, J.; Miller, J.D.; Good, R.J. The Effect of Drop (Bubble) Size on Advancing and Receding Contact Angles for Heterogeneous and Rough Solid Surfaces as Observed with Sessile-Drop and Captive-Bubble Techniques. J. Colloid Interface Sci. 1996, 179, 37–50. [Google Scholar] [CrossRef]
- Yang, J.; Duan, J.; Fornasiero, D.; Ralston, J. Very Small Bubble Formation at the Solid−Water Interface. J. Phys. Chem. B 2003, 107, 6139–6147. [Google Scholar] [CrossRef]
- Xu, M.; Li, C.; Zhang, H.; Kupka, N.; Peuker, U.A.; Rudolph, M. A contribution to exploring the importance of surface air nucleation in froth flotation–The effects of dissolved air on graphite flotation. Colloids Surf. A Physicochem. Eng. Asp. 2022, 633, 127866. [Google Scholar] [CrossRef]
- Darbha, G.K.; Schäfer, T.; Heberling, F.; Lüttge, A.; Fischer, C. Retention of Latex Colloids on Calcite as a Function of Surface Roughness and Topography. Langmuir 2010, 26, 4743–4752. [Google Scholar] [CrossRef]
- Zheng, R.; Ren, Z.; Gao, H.; Qian, Y. Flotation Behavior of Different Colored Fluorites Using Sodium Oleate as a Collector. Minerals 2017, 7, 159. [Google Scholar] [CrossRef]
- Dai, Z.; Fornasiero, D.; Ralston, J. Particle–bubble collision models—A review. Adv. Colloid Interface Sci. 2000, 85, 231–256. [Google Scholar] [CrossRef]
- Wang, B.; Peng, Y. The effect of saline water on mineral flotation–A critical review. Miner. Eng. 2014, 66, 13–24. [Google Scholar] [CrossRef]
- Muganda, S.; Zanin, M.; Grano, S. Benchmarking flotation performance: Single minerals. Int. J. Miner. Process. 2011, 98, 182–194. [Google Scholar] [CrossRef]
- Kouachi, S.; Hassas, B.V.; Hassanzadeh, A.; Çelik, M.S.; Bouhenguel, M. Effect of negative inertial forces on bubble-particle collision via implementation of Schulze collision efficiency in general flotation rate constant equation. Colloids Surf. A Physicochem. Eng. Asp. 2017, 517, 72–83. [Google Scholar] [CrossRef]
- Derjaguin, B.; Dukhin, S. Theory of flotation of small and medium-size particles. Prog. Surf. Sci. 1993, 43, 241–266. [Google Scholar] [CrossRef]
- Ralston, J.; Fornasiero, D.; Hayes, R. Bubble–particle attachment and detachment in flotation. Int. J. Miner. Process. 1999, 56, 133–164. [Google Scholar] [CrossRef]
- Nguyen, A.V.; Schulze, H.J.; Ralston, J. Elementary steps in particle—Bubble attachment. Int. J. Miner. Process. 1997, 51, 183–195. [Google Scholar] [CrossRef]
- Kowalczuk, P.B.; Zawala, J.; Kosior, D.; Drzymala, J.; Malysa, K. Three-phase contact formation and flotation of highly hydrophobic polytetrafluoroethylene in the presence of increased dose of frothers. Ind. Eng. Chem. Res. 2016, 55, 839–843. [Google Scholar] [CrossRef]
- Schulze, H.J. New theoretical and experimental investigations on stability of bubble/particle aggregates in flotation: A theory on the upper particle size of floatability. Int. J. Miner. Process. 1977, 4, 241–259. [Google Scholar] [CrossRef]
- Basařová, P.; Zawala, J.; Zedníková, M. Interactions between a Small Bubble and a Greater Solid Particle during the Flotation Process. Miner. Process. Extr. Metall. Rev. 2019, 40, 410–426. [Google Scholar] [CrossRef]
- Albijanic, B.; Ozdemir, O.; Nguyen, A.V.; Bradshaw, D. A review of induction and attachment times of wetting thin films between air bubbles and particles and its relevance in the separation of particles by flotation. Adv. Colloid Interface Sci. 2010, 159, 1–21. [Google Scholar] [CrossRef]
- Nguyen, A.V.; Ralston, J.; Schulze, H.J. On modelling of bubble–particle attachment probability in flotation. Int. J. Miner. Process. 1998, 53, 225–249. [Google Scholar] [CrossRef]
- Yoon, R.-H.; Yordan, J.L. Induction time measurements for the quartz—Amine flotation system. J. Colloid Interface Sci. 1991, 141, 374–383. [Google Scholar] [CrossRef]
- Drelich, J.W.; Marmur, A. Meaningful contact angles in flotation systems: Critical analysis and recommendations. Surf. Innov. 2017, 6, 19–30. [Google Scholar] [CrossRef]
- Zawala, J.; Drzymala, J.; Malysa, K. An investigation into the mechanism of the three-phase contact formation at fluorite surface by colliding bubble. Int. J. Miner. Process. 2008, 88, 72–79. [Google Scholar] [CrossRef]
- Szczerkowska, S.; Wiertel-Pochopien, A.; Zawala, J.; Larsen, E.; Kowalczuk, P.B. Kinetics of froth flotation of naturally hydrophobic solids with different shapes. Miner. Eng. 2018, 121, 90–99. [Google Scholar] [CrossRef]
- Kosior, D.; Kowalczuk, P.B.; Zawala, J. Surface roughness in bubble attachment and flotation of highly hydrophobic solids in presence of frother–experiment and simulations. Physicochem. Probl. Miner. Process. 2018, 54, 63–72. [Google Scholar]
- Kosior, D.; Zawala, J.; Krasowska, M.; Malysa, K. Influence of n-octanol and α-terpineol on thin film stability and bubble attachment to hydrophobic surface. Phys. Chem. Chem. Phys. 2013, 15, 2586–2595. [Google Scholar] [CrossRef] [PubMed]
- Kosior, D.; Zawala, J.; Malysa, K. When and how α-terpineol and n-octanol can inhibit the bubble attachment to hydrophobic surfaces. Physicochem. Probl. Miner. Process 2011, 47, 169–182. [Google Scholar]
- Krasowska, M.; Malysa, K. Wetting films in attachment of the colliding bubble. Adv. Colloid Interface Sci. 2007, 134–135, 138–150. [Google Scholar] [CrossRef]
- Krasowska, M.; Terpilowski, K.; Chibowski, E.; Malysa, K. Apparent contact angles and time of the three phase contact formation by the bubble colliding with teflon surfaces of different roughness. Physicochem. Probl. Miner. Process. 2006, 40, 293–306. [Google Scholar]
- Gomez-Flores, A.; Solongo, S.K.; Heyes, G.W.; Ilyas, S.; Kim, H. Bubble−particle interactions with hydrodynamics, XDLVO theory, and surface roughness for flotation in an agitated tank using CFD simulations. Miner. Eng. 2020, 152, 106368. [Google Scholar] [CrossRef]
- Dippenaar, A. The destabilization of froth by solids. I. The mechanism of film rupture. Int. J. Miner. Process. 1982, 9, 1–14. [Google Scholar] [CrossRef]
- Dippenaar, A. The destabilization of froth by solids. II. The rate-determining step. Int. J. Miner. Process. 1982, 9, 15–22. [Google Scholar] [CrossRef]
- Anfruns, J.; Kitchener, J.A. Rate of capture of small particles in flotation. Trans. Inst. Min. Metall. 1977, 86, 9–15. [Google Scholar]
- Brown, S.; Moudgil, B. Influence of nanoscale roughness on surface wettability. Miner. Metall. Process. 2004, 21, 33–35. [Google Scholar] [CrossRef]
- Wang, S.; Guo, J.; Tang, L.; He, H.; Tao, X. Effect of surface roughness of Chinese sub-bituminous coal on the kinetics of three-phase contact formation. Fuel 2018, 216, 531–537. [Google Scholar] [CrossRef]
- Albijanic, B.; Amini, E.; Wightman, E.; Ozdemir, O.; Nguyen, A.V.; Bradshaw, D.J. A relationship between the bubble–particle attachment time and the mineralogy of a copper–sulphide ore. Miner. Eng. 2011, 24, 1335–1339. [Google Scholar] [CrossRef]
- Krasowska, M.; Zawala, J.; Malysa, K. Air at hydrophobic surfaces and kinetics of three phase contact formation. Adv. Colloid Interface Sci. 2009, 147, 155–169. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Sun, L.; Yang, H.; Gui, X.; Schönherr, H.; Kappl, M.; Cao, Y.; Xing, Y. Recent advances for understanding the role of nanobubbles in particles flotation. Adv. Colloid Interface Sci. 2021, 291, 102403. [Google Scholar] [CrossRef]
- Han, S.; You, K.; Kim, K.; Park, J. Measurement of the attachment force between an air bubble and a mineral surface: Relationship between the attachment force and flotation kinetics. Langmuir 2019, 35, 9364–9373. [Google Scholar] [CrossRef]
- Ahmed, M. Fractal Surfaces of Particles and Their Floatability. Ph.D. Thesis, Assiut University, Assiut, Egypt, 1999. [Google Scholar]
- Ahmed, M.; Stechemesser, H.; Mabrouk, S.; Ibrahim, G.; Tarshan, M. Image analysis technique for determination of the size, structure and texture of fine particle profile. In Proceedings of the 6th International Conference on Mining, Petroleum and Metallurgy, Accra, Ghana, 29–31 October 2024; pp. 40–56. [Google Scholar]
- Chipfunhu, D.; Zanin, M.; Grano, S. The dependency of the critical contact angle for flotation on particle size–Modelling the limits of fine particle flotation. Miner. Eng. 2011, 24, 50–57. [Google Scholar] [CrossRef]
- Yoon, R.-H.; Mao, L. Application of extended DLVO theory, IV: Derivation of flotation rate equation from first principles. J. Colloid Interface Sci. 1996, 181, 613–626. [Google Scholar] [CrossRef]
- Nikolaev, A. Flotation kinetic model with respect to particle heterogeneity and roughness. Int. J. Miner. Process. 2016, 155, 74–82. [Google Scholar] [CrossRef]
- Buchmann, M.; Öktem, G.; Rudolph, M.; Boogaart, K.G.v.d. Proposition of a bubble-particle attachment model based on DLVO van der Waals and electric double layer interactions for froth flotation modelling. Physicochem. Probl. Miner. Process. 2022, 58, 154812. [Google Scholar] [CrossRef]
- Hoek, E.M.; Agarwal, G.K. Extended DLVO interactions between spherical particles and rough surfaces. J. Colloid Interface Sci. 2006, 298, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Flores, A.; Bradford, S.A.; Hwang, G.; Heyes, G.W.; Kim, H. Particle–bubble interaction energies for particles with physical and chemical heterogeneities. Miner. Eng. 2020, 155, 106472. [Google Scholar] [CrossRef]
- Drelich, J.W.; Bowen, P.K. Hydrophobic nano-asperities in control of energy barrier during particle–surface interactions. Surf. Innov. 2015, 3, 164–171. [Google Scholar] [CrossRef]
- Drelich, J. Hydrophobic Nano-Asperities of Rough Particles in Control of Energy Barrier During Flotation. In Proceedings of the VIII International Mineral Processing Congress, Quebec City, QC, Canada, 11–15 September 2016. [Google Scholar]
- Drelich, J.W. A simplified analysis of the effect of nano-asperities on particle-bubble interactions. Physicochem. Probl. Miner. Process. 2018, 54, 10–18. [Google Scholar]
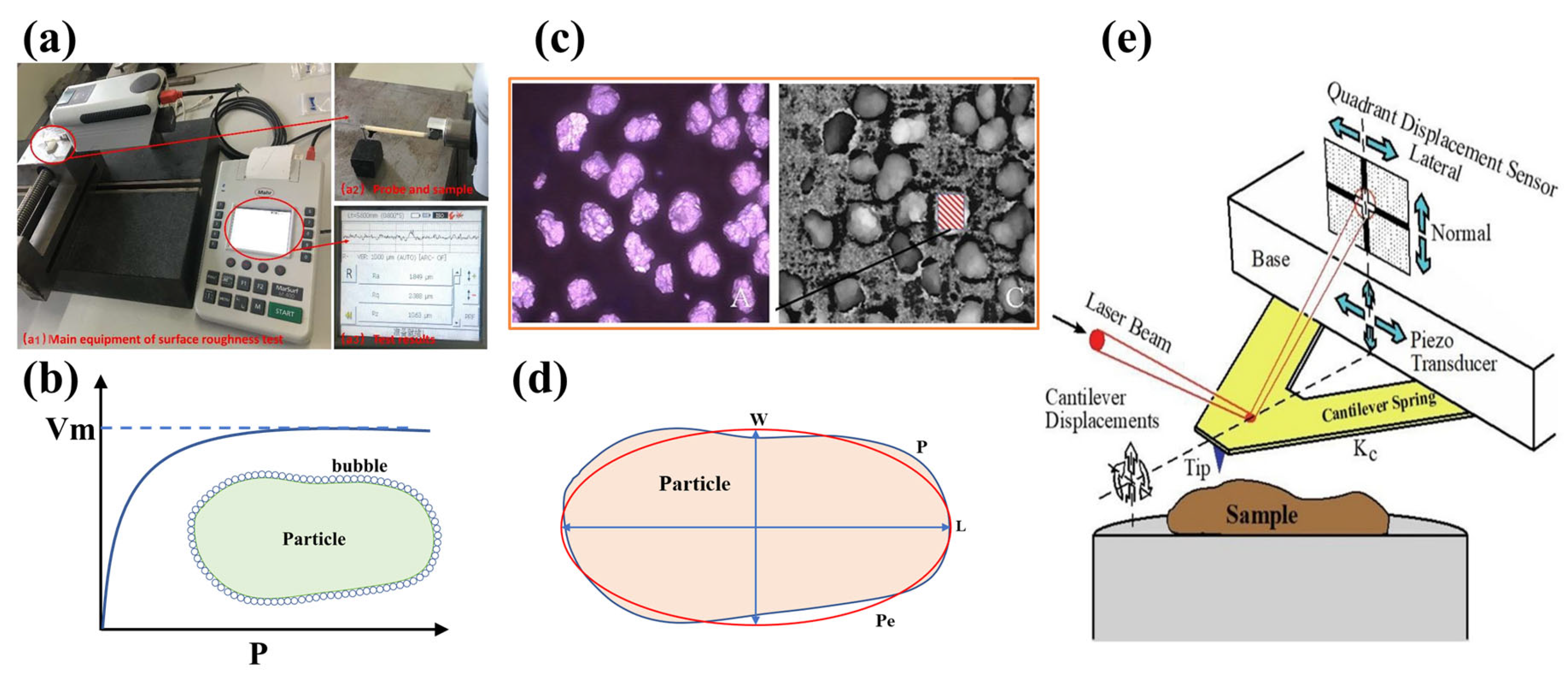
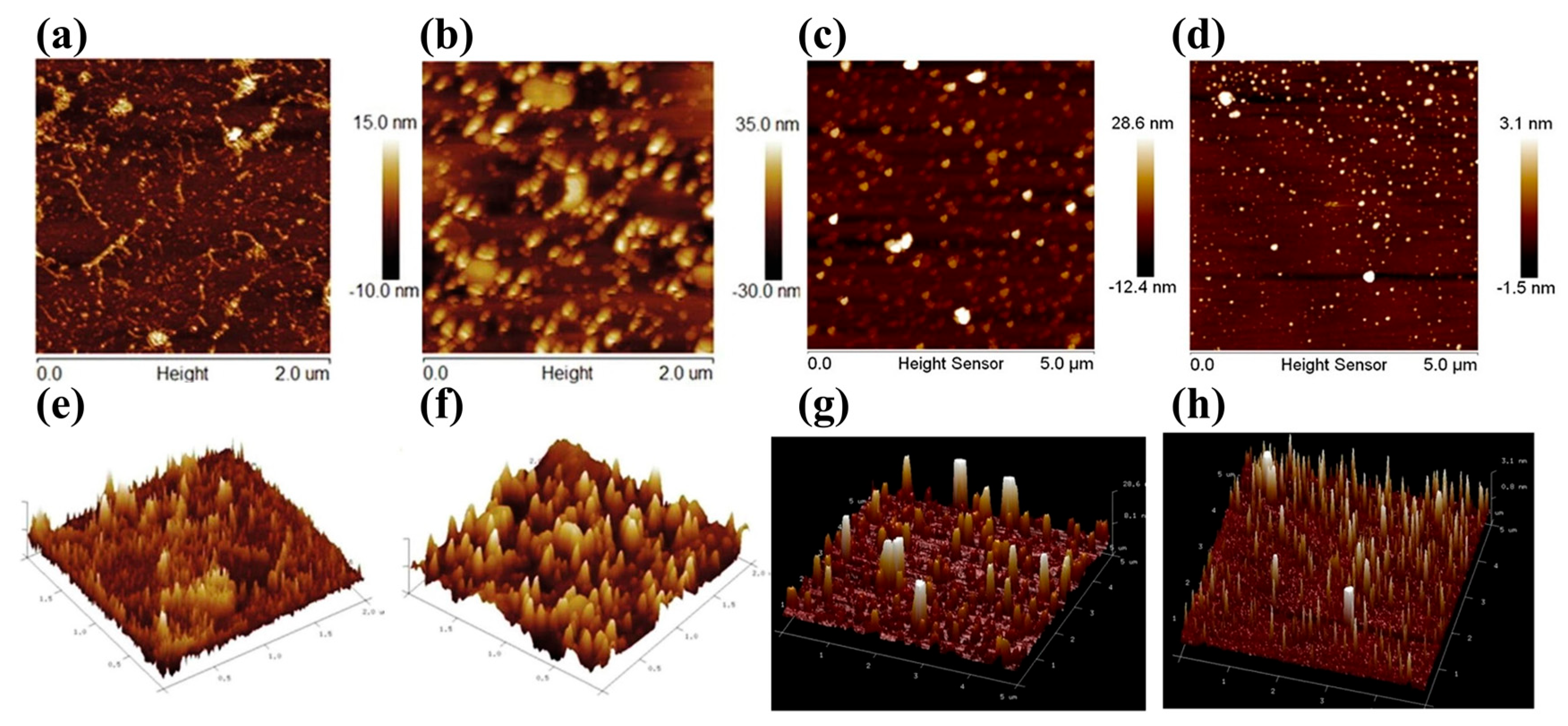



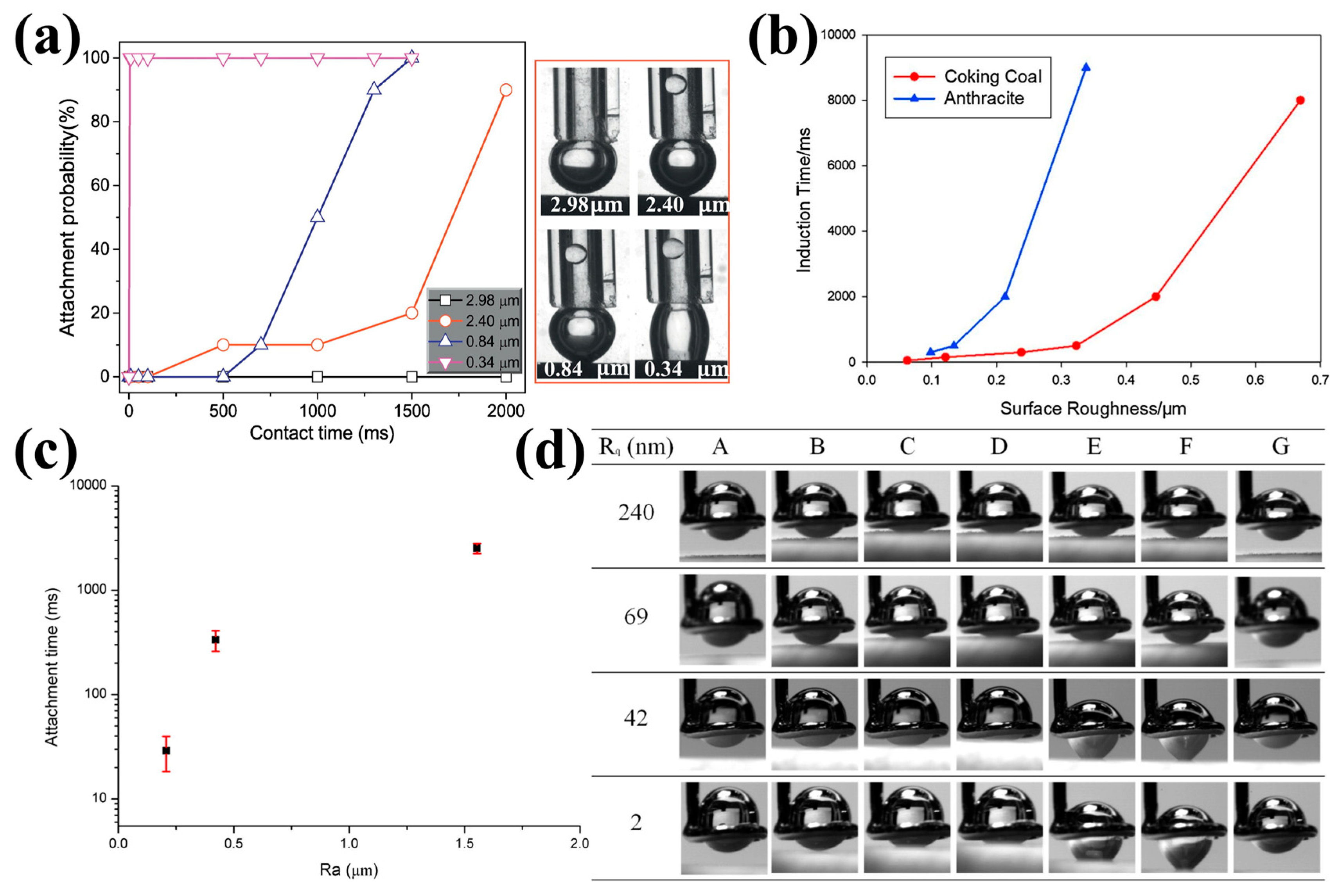
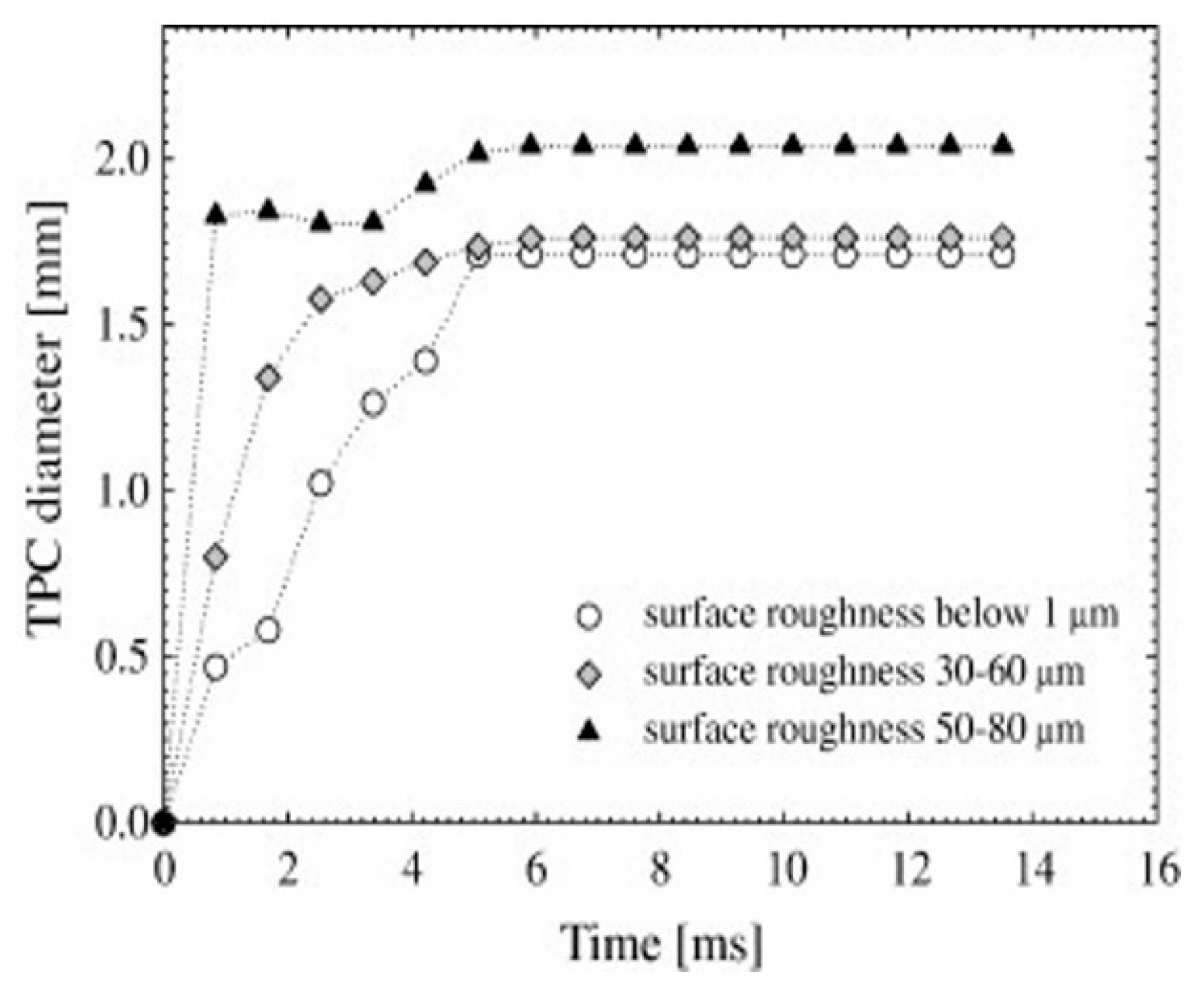

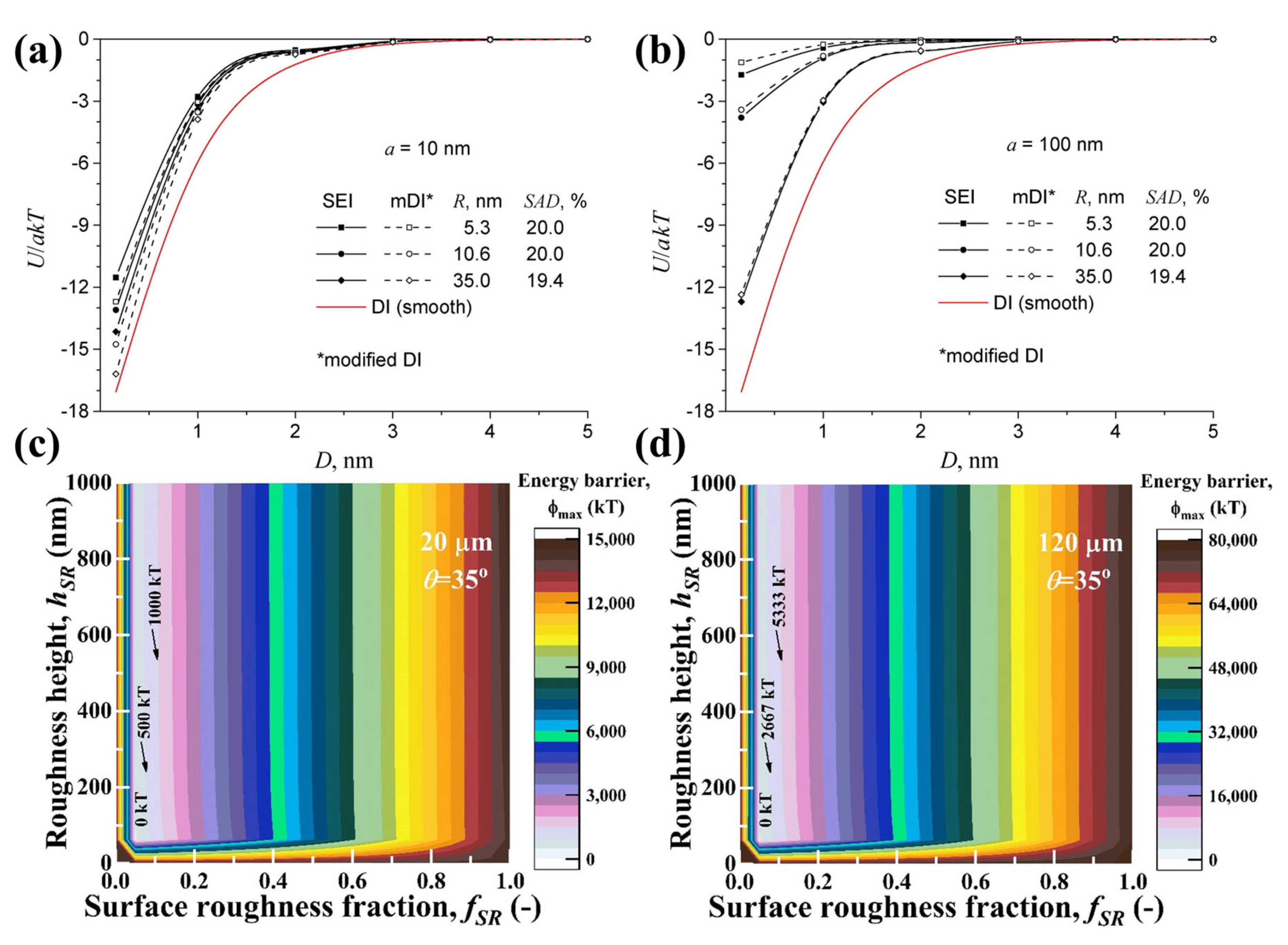

| Methods | Measurement Accuracy |
|---|---|
| AFM | 0.1–100 nm |
| BET | 0.1–100 nm |
| The fitting ellipse method | 0.1 nm–1 μm |
| Surface roughness measurer | 0.01–100 μm |
| Optical profilometer | 1 nm–1 mm |
| Minerals | Methods | Particle Size/μm | Findings |
|---|---|---|---|
| magnetite [40] | AFM | 55–74 | The Ra value for the rod-milled particles was about 28.03 nm and those for the ball-milled ones were 9.47 nm. |
| calcite [1] | BET | 180–250 125–150 75–125 45–75 | The roughness of rod-milled calcites of the same size fraction was about 5% higher than that of ball-milled ones. |
| calcite [71] | AFM | no classification | The particles ground by a high-pressure grinding roller and jaw crusher are the roughest, and those ground by a dry ball mill were rather smooth. |
| quartz [45,47] | BET | 212–250 180–212 125–150 106–125 75–106 | The rod-milled quartz particles had higher surface roughness than the ball-milled ones in all granularity ranges. |
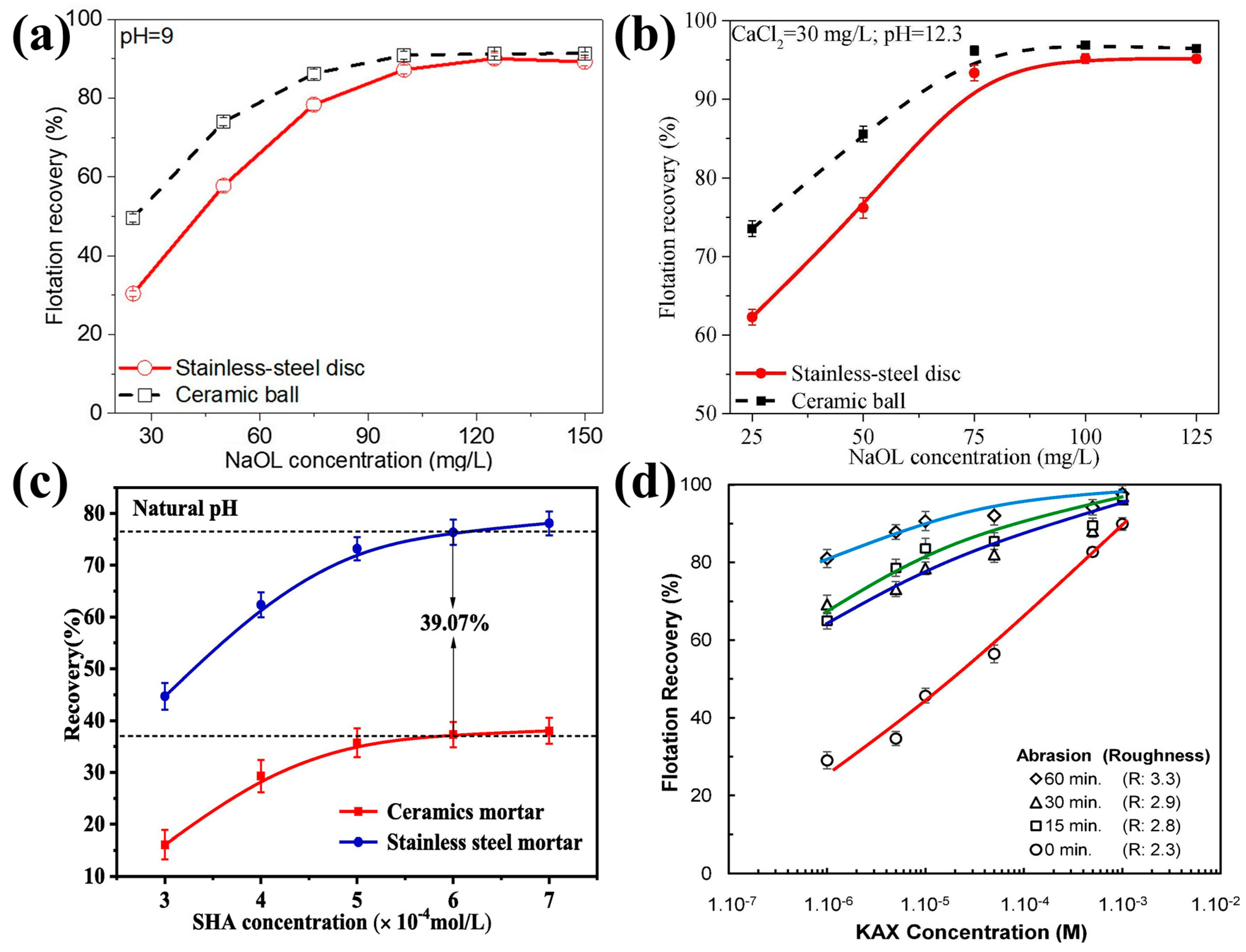
| quartz [41] | AFM | 38–74 | The ceramic ball-milled quartz particles (Ra = 1.16 nm) had a higher surface roughness than that of the stainless steel disk-milled ones (Ra = 0.52 nm). |
| quartz [34] | Surface roughness measurements | 45–250 | The rod-milled quartz particles (Ra = 4.24 μm) exhibited smoother surfaces than the ball-milled (Ra = 4.49 μm) and autogenous-milled (Ra = 4.30 μm) ones. |
| spodumenes [64] | AFM | 38–74 | Compared with the surface of the ball-milled spodumenes (Ra = 0.87 nm), more protrusions were observed on the surface of the rod-milled ones (Ra = 1.14 nm). |
| talc [69] | Surface roughness measurements | 45–250 | The ball-milled (Ra = 0.68 μm) and rod-milled (Ra = 0.55 μm) particles showed a higher and lower surface roughness compared with that of autogenous-milled particles (Ra = 0.66 μm). |
| hematite [39] | AFM | 55–74 | The surface roughness for the ball-milled particles (Ra = 8.5 nm) was larger than that for the rod-milled ones (Ra = 2.1 nm). |
| barite [46] | BET | 104–147 74–104 53–74 44–53 | The autogenous-milled particles showed a lower surface roughness than that of ball-milled ones for all the fractions. |
| magnesite [3,37] | AFM | 38–74 | The ceramic ball-milled magnesite particle surfaces (Ra = 1.59 nm) were rougher than that of the stainless steel-milled ones (Ra = 0.28 nm). |
| pyrite [66] | BET | 104–147 74–104 53–74 44–53 | The surface roughness values for ball-milled pyrite products were lower than all fractions of autogenous-milled pyrite products. |
| magnesite [50] | AFM | no classification | The surface roughness of magnesite particles ground by the vertical roller mill and the ball mill was about 0.19 nm and 0.10 nm, respectively. |
| graphite [38] | AFM | 150–180 | The Ra value of graphite particles produced by the ball mill and high-pressure grinding roller was 0.667 nm and 1.350 nm, respectively. |
| calcite, barite, talc, quartz [32,33] | Surface roughness measurements | 45–250 | The roughest and smoothest product for calcite was the autogenously ground product and rod-milled product, and that for barite was the autogenous-milled and ball-milled ones, whereas for talc and quartz it was the ball-milled and rod-milled products. |
| coal particles [27] | BET | 250–500 | The roughness of the coal particles was 1.1028 for the ball-milled ones, measured by the BET method, and it increased to 1.1134 and 1.1089 upon grinding with the disk mill and jaw crusher. |
| Minerals | Particle Size/μm | Flotation Results |
|---|---|---|
| talc, quartz [51,93,95] | 106–150 75–150 | The talc and quartz particles with a higher angularity and roughness exhibited better floatability. |
| spodumene [64] | 38–74 | The max flotation recovery of spodumene particles increased from 40.3% to 80.7% while increasing the Ra value from 0.87 nm to 1.14 nm. |
| calcite [1] | 180–250 125–150 75–125 45–75 | The calcite particles with rougher surfaces had a larger theoretical ultimate recovery than the smoother ones in all granularity ranges. |
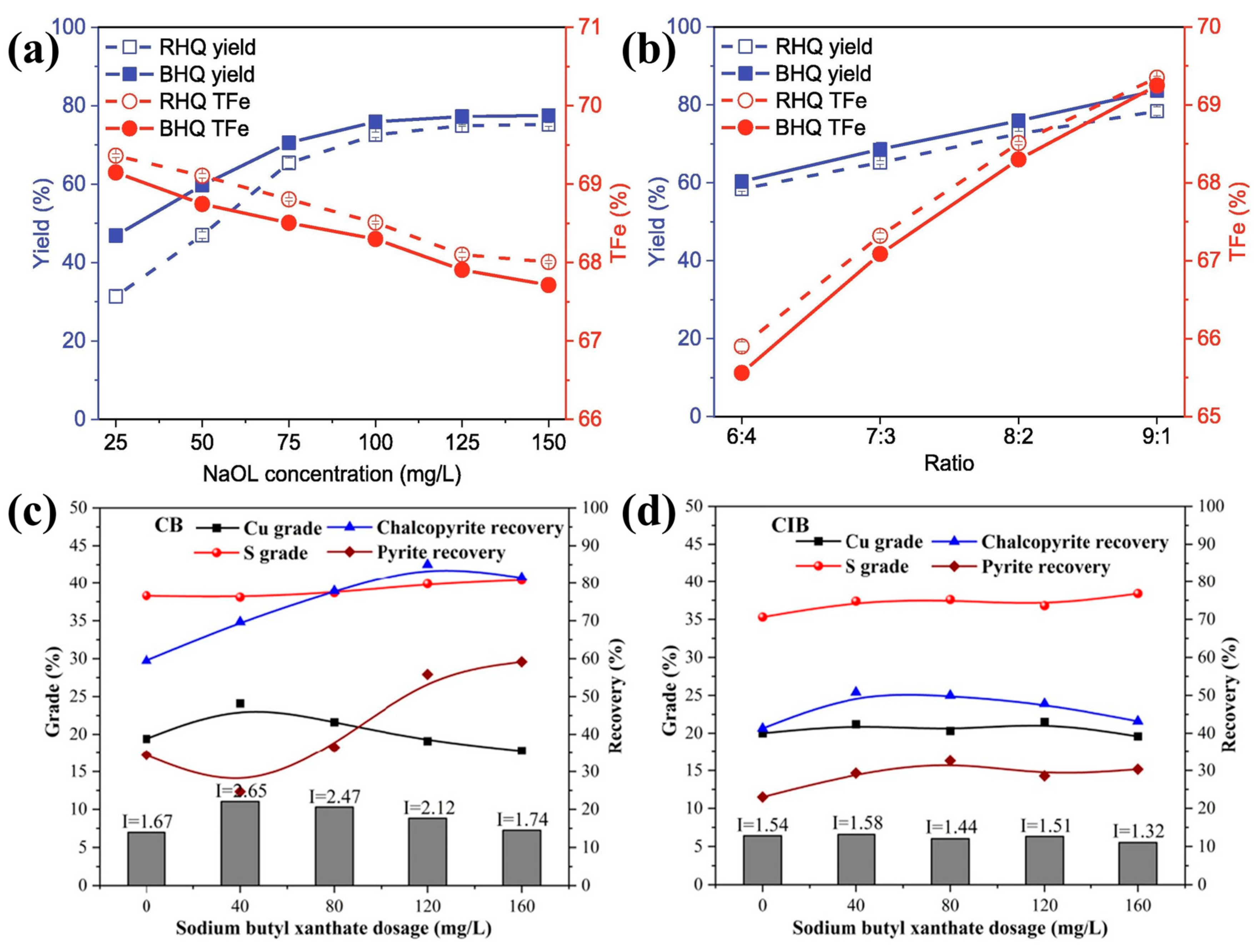
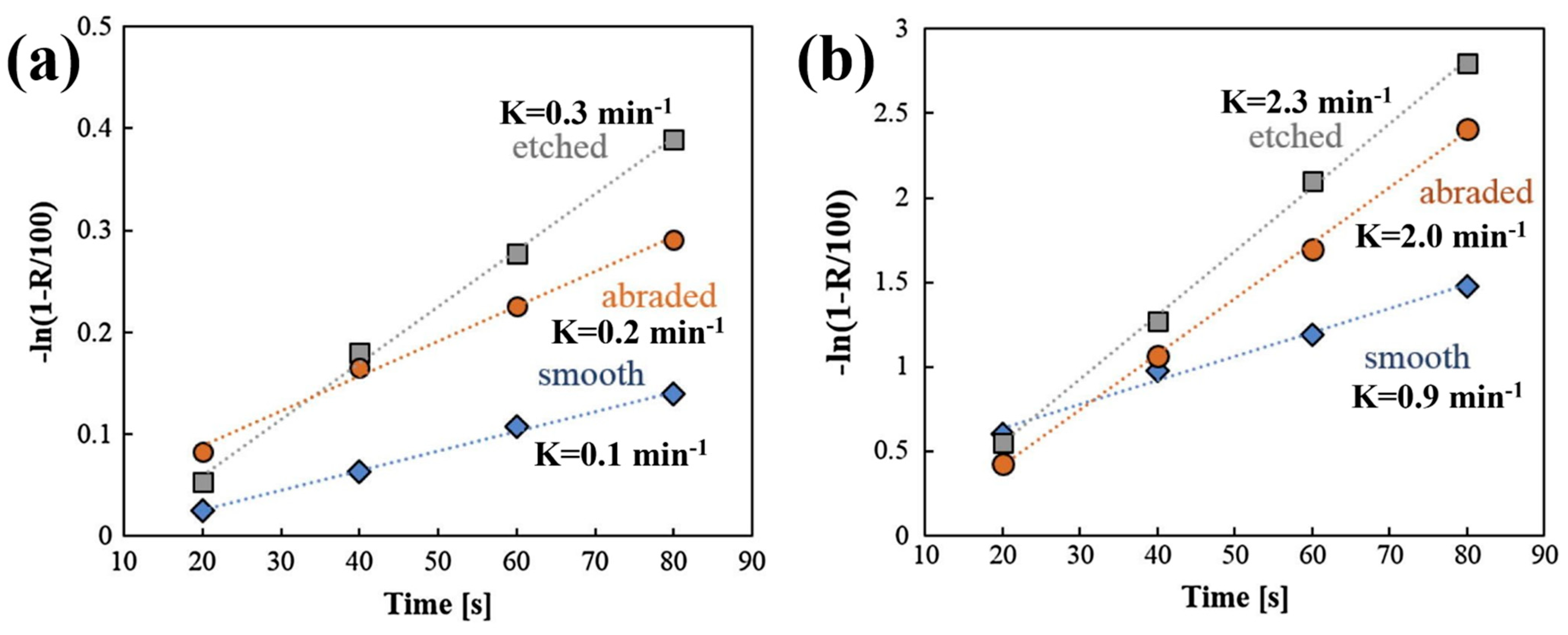
| magnesite, quartz [3,37,41] | 38–74 | The rougher magnesite and quartz particles exhibited a higher flotation recovery in the wide range of selected sodium oleate (NaOL) concentrations and at each pH value, but the effect of surface roughness on flotation was diminished with increasing NaOL concentrations. |
| hematite [39] | 55–74 | The flotation recovery of hematite particles arrived at 88.0% and 75.9% with the NaOL concentration by 125 mg/L when the Ra value was 8.5 nm and 2.1 nm, respectively. |
| graphite [38] | 150–180 | The flotation recovery increased from about 76% to 85% by increasing the Ra value from about 0.667 nm to 1.350 nm in the presence of kerosene, and the difference in flotation recovery was decreased with the increase in kerosene amounts. |
| malachite [2] | 38–75 | The flotation recoveries of rougher malachite were around 12% higher than that of smoother ones. |
| cassiterite [68] | 5–38 | The flotation recovery of rougher cassiterite was 39.07% higher than that of smoother ones. |
| the platinum-bearing sulfide ore [76,77] | about 60% below 74 | The dry-ground samples exhibited relatively rougher surfaces, higher flotation recovery, and faster flotation kinetics than wet-ground products. |
| sphalerite [31] | 38–74 | When increasing the surface roughness values of the abraded particles from 2.3 µm to 3.3 µm, the flotation recoveries increased from 29% to 81% at a low collector concentration of 10−6 M. |
| quartz, calcite, talc, and barite [32,33,62,69,72] | 45–250 | A smoother surface led to an improvement in the floatability of quartz, calcite, talc, and barite; and talc particles that reported to the concentrates were smoother than those that reported to the tailings. |
| barite, pyrite [46,66,96] | 104–147 74–104 53–74 44–53 | The barite and pyrite particles with a lower surface roughness and acuteness had better floatability and better concentrate grades. |
| coking coal [79] | 250–500 125–250 74–125 45–74 | The wet-ground particles were characterized by more irregular shape factors and smoother coal surfaces and, thus, presented higher flotation recoveries compared to the dry-ground ones. |
| molybdenite [97] | 120–200 | The floatability of fine molybdenite particles was significantly reduced due to the creation of very rough surfaces. |
| chalcopyrite [98] | no classification | The flotation recovery of smoother ground chalcopyrite was approximately 16% higher than the rougher ones. |
| spodumene [65] | 75–105 45–75 38–45 23–38 | The flotation recovery of wet-ground spodumene particles with smoother surfaces was higher than that of dry-ground ones with rougher surfaces in all granularity ranges. |
| Findings | References |
|---|---|
| A smoother surface improved the hydrophobicity of talc particles. | [33] |
| The talc particles with a higher roundness and surface roughness caused a decrease in hydrophobicity. | [69] |
| The contact angles of smooth and rough coking coal particles were about 99.10° and 94.83°, respectively, without collector addition. | [79] |
| The advancing contact angle of anthracite coal steadily decreased from 93° to 78° as the Ra value increased from 0.12 µm to 2.51 µm. | [30] |
| The contact angle of the air bubble on coking coal surfaces with a surface roughness of 0.053 μm and 0.648 μm (polished by different sandpapers) was 46° and 23°, respectively. | [116] |
| As the surface roughness of the coking coal particles decreased from 2.79 μm to 0.98 μm and 0.23 μm, the contact angle increased from 66.0° to 75.3° and then to 82.5°. | [117] |
| The contact angle decreased from 59° to 29° when the Ra value of coal particles increased from 2.5 μm to 6.02 μm. | [118] |
| The advancing contact angle of dull coals increased from a range of 20–50° to 30–65° when the surface roughness was reduced through polishing. | [119] |
| The receding contact angle of air bubbles on particles decreased from about 32° to 17° for hematite and from about 30° to 20° for pyrite, when the Rq value of hematite (3 nm) and pyrite (4 nm) increased to about 50 nm and 18 nm. | [58] |
| The advancing contact angle (measured at point F) decreased from about 41° to 29° and then fell below 13° as the Rq value increased from 2 nm to 42 nm and then to 240 nm. | [120] |
| Findings | References |
|---|---|
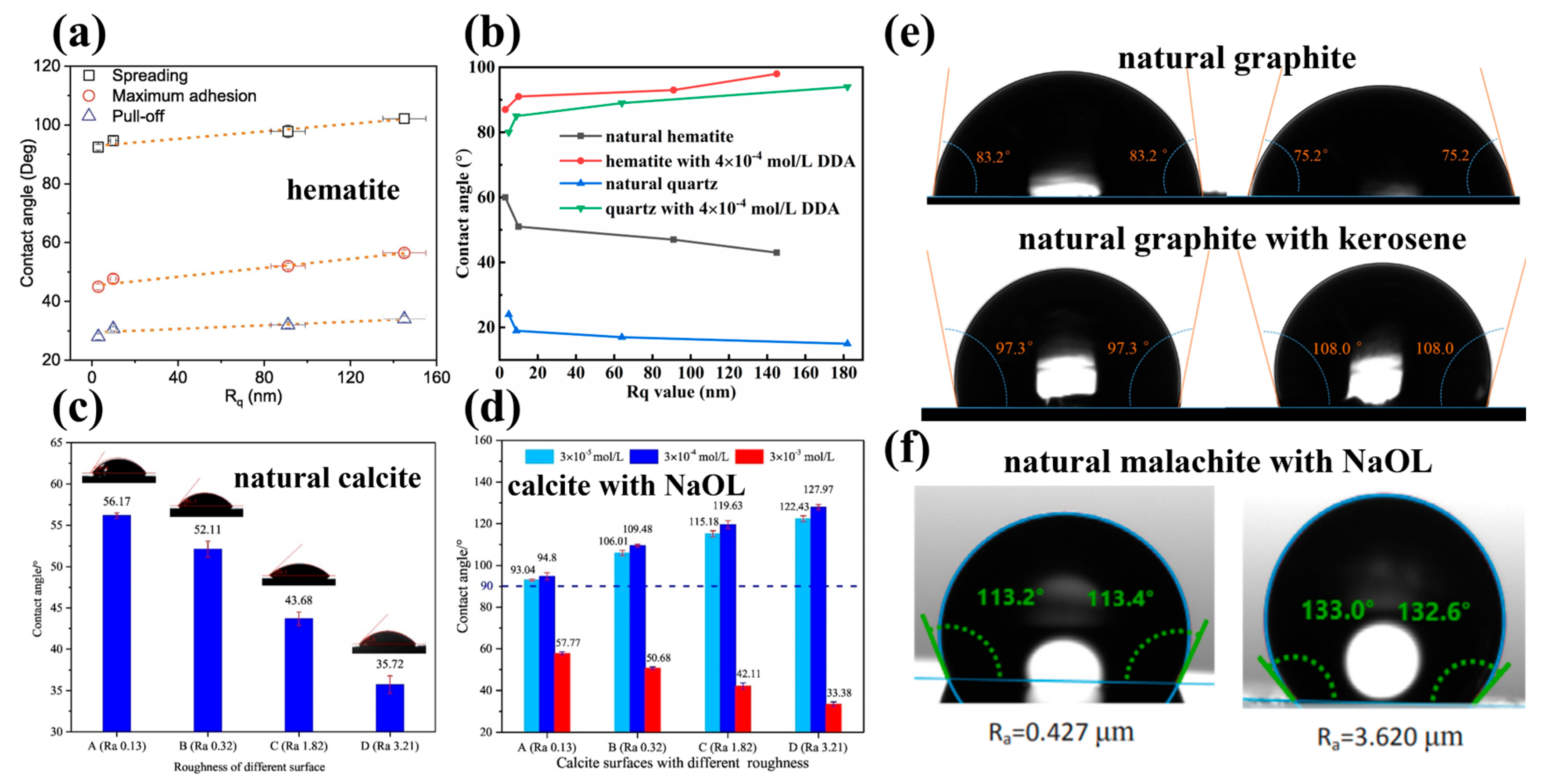
| The angle changed from 97.3° to 108.0° as the Ra value increased from 0.667 nm to 1.350 nm in the presence of kerosene. | [38] |
| The advancing contact angle increased in the presence of a surfactant (HTAB). | [35] |
| The contact angle of the malachite surface increased from 113.3° to 132.8° as the Ra value rose from 0.427 μm to 3.620 μm in the presence of NaOL. | [2] |
| The contact angle could be adjusted by altering the solid roughness and showed that both hydrophobicity and hydrophilicity could be enhanced through roughness. | [121] |
| The contact angle of hematite and quartz surfaces increased from 87° and 80° to 98° and 94° in the presence of dodecyl amine (DDA). | [59] |
| The particles with a nanoscale roughness were more hydrophobic than those with smooth surfaces. | [44] |
| The contact angle of natural calcite increased from 93.07° to 122.43° with the NaOL addition as the Ra value rose from 0.13 nm to 3.21 nm. | [1] |
| The angles increased from 38.08° to 69.81° and then to 81.01° with the hydrophobic treatment, as the Ra value of the glass beads increased from 0.418 μm to 0.846 μm and 1.565 μm, respectively. | [84] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, H.; Sun, W.; Tang, H.; Jiang, F.; Wang, L. Surface Roughness and Its Role in Flotation Behavior, Wettability, and Bubble–Particle Interactions: A Systematic Review. Appl. Sci. 2025, 15, 4557. https://doi.org/10.3390/app15084557
Zeng H, Sun W, Tang H, Jiang F, Wang L. Surface Roughness and Its Role in Flotation Behavior, Wettability, and Bubble–Particle Interactions: A Systematic Review. Applied Sciences. 2025; 15(8):4557. https://doi.org/10.3390/app15084557
Chicago/Turabian StyleZeng, Hua, Wei Sun, Honghu Tang, Feng Jiang, and Li Wang. 2025. "Surface Roughness and Its Role in Flotation Behavior, Wettability, and Bubble–Particle Interactions: A Systematic Review" Applied Sciences 15, no. 8: 4557. https://doi.org/10.3390/app15084557
APA StyleZeng, H., Sun, W., Tang, H., Jiang, F., & Wang, L. (2025). Surface Roughness and Its Role in Flotation Behavior, Wettability, and Bubble–Particle Interactions: A Systematic Review. Applied Sciences, 15(8), 4557. https://doi.org/10.3390/app15084557










