A Blockchain-Based Collaborative Storage Scheme for Roadside Unit Clusters in Social Internet of Vehicles

Abstract

With the gradual application of blockchain technology in the domain of Social Internet of Vehicles (SIoV), the increasing volume of blockchain data has imposed significant storage pressure on roadside units (RSUs). Collaborative storage schemes, which organize RSUs into clusters to jointly store content for vehicles, have been explored. However, existing collaborative storage solutions in IoV primarily focus on caching content and are not well-suited to the deployment constraints of blockchain networks. Building on blockchain’s decentralized characteristics and data integrity mechanisms, this paper proposes a collaborative storage scheme that reduces RSU storage loads while sustaining distributed ledger operations in SIoV. Specifically, the RSU Access Preference-based Spectral Clustering Algorithm (RAPSCA) is proposed to address RSU clustering by analyzing both the RSUs’ access preferences for blockchain data and their resource availability. Subsequently, the Vehicle Service Priority-based Greedy Block Allocation Algorithm (VSPGBAA) is devised for intra-cluster storage allocation, which considers vehicles’ dwell times and block access probabilities to reduce overall access costs. Experimental results indicate that, compared to baseline algorithms, the proposed method achieves a 27.7% reduction in cost and a 3.5-fold decrease in execution time, thereby demonstrating the feasibility of collaborative storage optimization in blockchain-enabled SIoV.

1. Introduction

With the rapid development of the Internet of Things (IoT) technology, a wide variety of smart devices are becoming interconnected. Internet of Vehicles (IoV), a key IoT application in the vehicular domain, integrates vehicles, roadside units (RSUs), and cloud platforms to form a collaborative network for resource sharing. This integration significantly enhances data exchange efficiency and improves the intelligence level of transportation systems. Building upon the foundation of IoV, Social Internet of Vehicles (SIoV) introduces social relationships into vehicular networks, enabling vehicles to interact based on trust relationships and shared interests. This transformation allows vehicles to evolve from passive data transmission nodes into intelligent entities that actively construct and manage social relationship networks. Consequently, SIoV further promotes internal information exchange and resource sharing within the network [1,2,3,4].

Blockchain offers a promising solution for distributed reputation management in SIoV through decentralization, data immutability, and smart contract automation [5,6,7]. In blockchain-enabled SIoV, blockchain serves as a trusted infrastructure that records vehicle interactions through a distributed ledger and consensus mechanisms, ensuring data authenticity and reliability. However, the integration of blockchain introduces additional storage burdens to SIoV systems. Due to the append-only nature and multiple-replica storage mechanism of blockchain, its storage demand continuously increases over time [8]. For RSU nodes with limited and heterogeneous storage resources, this ever-growing demand may become a performance bottleneck, thereby impacting the scalability and operational efficiency of the entire SIoV system [9,10,11].

A feasible approach to addressing storage performance challenges in SIoV is collaborative storage. This method enables blockchain data to be distributed across multiple storage nodes, with each node storing only a portion of the data. When full data access is required, nodes can efficiently retrieve missing blocks through an inter-node data exchange mechanism, thereby reducing the storage burden on individual nodes and enhancing overall resource utilization. Several studies have explored collaborative storage in blockchain, such as leveraging the InterPlanetary File System (IPFS) [12] or employing consistent hashing-based encoding schemes [13] for distributed storage. However, these studies primarily focus on storage balance and fairness, overlooking access costs in the SIoV context. Therefore, designing an optimized collaborative storage scheme tailored for RSUs in blockchain networks is essential to improving the performance and efficiency of SIoV systems.

There are still several challenges in optimizing collaborative storage for RSUs in a blockchain-enabled SIoV system:

• In traditional IoV systems, RSUs operate independently without clustering or collaboration. In blockchain-enabled SIoV, RSUs must collaboratively maintain blockchain integrity despite limited storage resources. The full-node storage model imposes high demands, restricting resource-constrained RSUs from participating in consensus, thereby limiting network scalability. Existing clustering methods, based on geographical location or network topology, overlook vehicles’ block access patterns. Thus, an RSU clustering strategy that integrates blockchain data characteristics while addressing storage constraints is essential for enhancing efficiency and performance.
• In a collaborative storage cluster, block allocation among RSUs directly impacts vehicle access latency and service quality. Existing methods, relying on general content popularity, fail to account for vehicle mobility and block access correlations, leading to higher access costs. Therefore, developing an RSU cluster-based storage allocation scheme tailored to blockchain scenarios is crucial for minimizing vehicle access costs and enhancing system performance.

To overcome these challenges, this paper innovatively proposes a blockchain-based RSU cluster architecture and intra-cluster collaborative storage strategy for SIoV. Spectral clustering is employed to dynamically group RSUs into clusters, which ensures decentralized, adaptive aggregation of RSUs with limited storage resources into cohesive clusters, collaboratively maintaining blockchain integrity. Meanwhile, the collaborative storage strategy enables each RSU to prioritize and store blockchain data autonomously, which ensures low-cost, resource-efficient decisions that align with RSUs’ computational constraints. Specifically, the main contributions of this paper are as follows:

• This paper proposes an RSU cluster architecture for blockchain-enabled SIoV. In traditional blockchain systems, each node maintains a complete copy of the distributed ledger to achieve decentralized trust consensus. However, such a full replication model encounters significant resource constraints in SIoV scenarios. The collaborative storage scheme proposed in this paper leverages RSU clustering strategies and block allocation mechanisms to reduce the storage burden on individual nodes, ensuring that each cluster can still deliver complete blockchain services and thus balancing decentralization with operational efficiency.
• This paper introduces the RSU Access Preference-based Spectral Clustering Algorithm (RAPSCA) to optimize RSU grouping. Unlike traditional methods that rely solely on physical distance or communication cost, RAPSCA incorporates vehicle block access behaviors and storage availability, ensuring more efficient and rational resource allocation for collaborative storage. Additionally, to optimize intra-cluster block allocation, the Vehicle Service Priority-based Greedy Block Allocation Algorithm (VSPGBAA) is designed. This method reduces access latency and improves storage utilization by considering vehicle dwell time, block access probability, and RSU storage availability.
• Extensive experiments evaluate the proposed methods in terms of storage hit rate, access cost, and runtime efficiency. Experimental results indicate that, compared to baseline algorithms, the proposed method achieves a 27.7% reduction in per-vehicle access costs for required blockchain blocks, and a 3.5-fold decrease in average algorithm execution time measured on identical hardware configurations.

2. Related Work

2.1. Blockchain-Enabled IoV System

Blockchain technology has been recognized as a promising solution for addressing trustworthy data sharing in the IoV. Javaid et al. [6] integrated blockchain with public key infrastructure (PKI) to manage vehicle identity information in SIoV, proposing a checkpoint-based dynamic consensus mechanism to achieve trusted vehicle access control. Vishwakarma et al. [14] tackled the high computational and communication overhead in blockchain-enabled IoV by introducing an SDN-based lightweight blockchain security protocol, which modifies the Practical Byzantine Fault Tolerance (PBFT) consensus algorithm [15] to reduce computational and communication costs in secure message propagation. Lin et al. [16] developed a P2P computing resource trading system for IoV, utilizing a two-stage Stackelberg game mechanism to optimize pricing utilities for buyers and sellers under consortium blockchain environments.

The above-mentioned works primarily focus on security and trust management in IoV [6,14,16], often customizing blockchain consensus mechanisms to fit vehicular network scenarios. However, the storage scalability challenges introduced by blockchain in IoV systems remain largely overlooked. For RSUs with limited and heterogeneous storage resources, efficiently managing ever-growing blockchain data while providing low-access-cost services to vehicles remains an open and complex problem. We address blockchain storage allocation in SIoV by proposing a collaborative storage approach based on RSU clustering. By leveraging cooperative storage, our method enhances RSU storage efficiency and optimizes overall network service quality.

2.2. Collaborative Caching in IoV

Several studies have explored collaborative caching as a means of optimizing storage in IoV. Wang et al. [17] proposed a content popularity-based collaborative caching method, utilizing LSTM to predict vehicle user requests and applying reinforcement learning to maximize cache hit rates. Alnagar et al. [18] designed both cooperative and non-cooperative RSU proactive caching schemes, where vehicle mobility patterns were predicted to optimize content allocation, thereby reducing communication delays in vehicular ad hoc networks. Hu et al. [19] considered the limited capacity of RSUs and developed an RSU caching scheme based on a multi-object auction mechanism, aiming to maximize the volume of data downloaded by vehicle users.

While existing studies have proposed effective solutions for collaborative caching in RSU-based IoV scenarios [17,18,19], they primarily consider RSUs as service providers that distribute general-purpose content from third-party providers to improve the user experience of vehicles. These works often focus on enhancing content allocation efficiency through vehicle mobility prediction and content popularity analysis, thereby laying a foundation for storage optimization in IoV. However, they give limited attention to the challenges of collaborative storage in blockchain-based environments. In contrast, our work targets the blockchain-enabled SIoV scenario, where RSUs not only provide services to vehicles but also serve as blockchain network nodes. To preserve the integrity of the distributed ledger, our proposed scheme requires each RSU cluster to collaboratively maintain at least one complete copy of the blockchain, and we optimize the storage strategy accordingly under these stricter network constraints to improve both system efficiency and service quality.

2.3. Blockchain Storage Scalability

The issue of blockchain storage scalability has been widely studied in existing research. Luu et al. [20] proposed sharding in blockchain networks, where each shard is managed by an independent committee responsible for transaction management and storage. While this approach significantly reduces the amount of blockchain data stored on individual nodes, it introduces high processing latency when handling cross-shard transactions, thereby increasing the network consensus cost. Xu et al. [21] proposed pruning the blockchain state, offloading old blocks to the cloud to reduce storage consumption in local networks. Although this method effectively optimizes local storage costs, it compromises blockchain integrity within the local network, making it unsuitable for systems with high backhaul latency. Hassanzadeh-Nazarabadi et al. [13] introduced the LightChain architecture, which employs a distributed hash table (DHT) for distributed blockchain storage allocation, allowing nodes in the network to store only a portion of the blockchain data. However, this approach primarily focuses on load balancing in block distribution and does not optimize access costs resulting from the allocation strategy. Li et al. [12] integrated the InterPlanetary File System (IPFS) into IoT blockchain systems, delegating storage tasks to distributed trusted third parties. However, the introduction of third-party storage raises additional latency issues that remain unresolved. Xu et al. [22] proposed the concept of “consensus unit”, which aggregates multiple different network nodes into one consensus unit, enabling nodes to jointly store and maintain blockchain data.

Although these mentioned studies improve blockchain storage scalability in their respective contexts [12,13,20,21,22], their studies either lack comprehensive modeling tailored to the SIoV scenario or have optimization objectives that differ from the problem we address. Therefore, these solutions cannot be directly applied to the system we propose. The studies by Luu et al. [20] and Xu et al. [21] focus on blockchain data pruning as the core idea. However, the damage to blockchain integrity caused by this approach means that it is only applicable to specific scenarios. The study by Li et al. [12] needs to take into account the credibility and stability of third-party systems. The schemes proposed by Hassanzadeh-Nazarabadi et al. [13] and Xu et al. [22] are similar to collaborative storage architectures, but there is still room for improvement in the detailed strategies for block allocation. In this paper, we design an RSU cluster-based collaborative storage scheme that accounts for blockchain storage demands in SIoV and the mobility characteristics of vehicle users. By employing RSU clustering and a distributed block storage strategy, our approach further improves blockchain storage efficiency while reducing block access costs for vehicle users.

3. System Model

In this section, we present a detailed description of the blockchain-based RSU cluster collaborative storage model in SIoV. Given the limited storage resources of RSUs, we organize them into collaborative storage clusters. Within each cluster, RSU nodes share storage resources to jointly maintain blockchain integrity while providing efficient block data query services for vehicles.

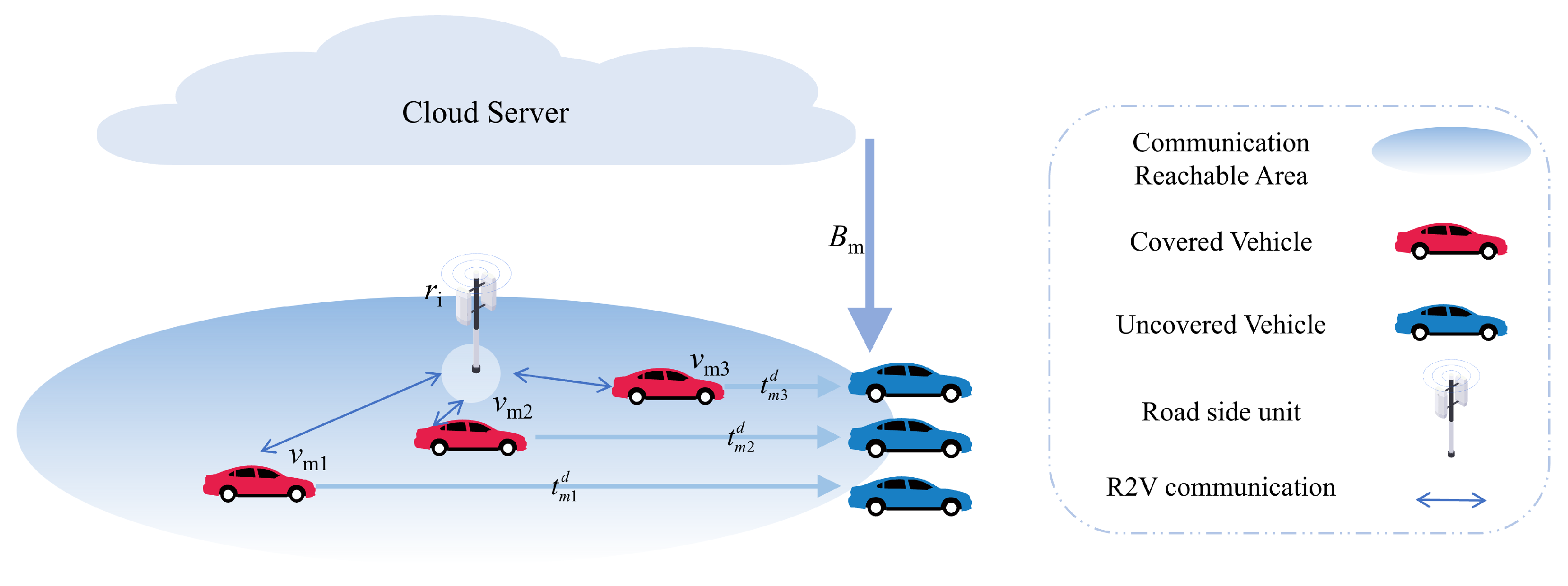
3.1. RSU Cluster Cooperative Storage System Model

In blockchain-enabled social Internet of Vehicles, RSU nodes collect reputation change information generated by vehicles within their service range. This information is encapsulated into blocks as transactions and submitted to the blockchain network through a consensus mechanism for recording. As full nodes in the blockchain network, RSUs are required to store a complete copy of the blockchain data locally to provide services to vehicles. However, as the blockchain network grows over time, the increasing length and volume of blockchain data exceed the storage capacity of individual RSUs, preventing resource-limited RSUs from participating in the blockchain consensus process as full nodes. To address this issue, the model proposed in this paper organizes multiple RSUs into collaborative storage clusters, enabling them to jointly maintain blockchain data integrity. Within each cluster, RSUs store only a portion of the blockchain data while still providing essential services such as reputation queries and transaction verification for vehicles. If an RSU lacks the required block data locally, it can retrieve the missing blocks from other RSUs within the cluster, ensuring service continuity and efficiency.

As shown in Figure 1, the system primarily consists of vehicles, RSUs, a cloud server, and a blockchain network that provides reputation activity recording and authentication for the vehicular social network. Vehicles act as primary users, collecting information about themselves and their surroundings while interacting and communicating with other vehicles or RSUs through built-in communication devices. When multiple vehicles generate activities within the social network, all reputation update information related to the involved vehicles is encapsulated into blocks by RSUs and appended to the blockchain via the consensus network connected to the cloud server. The vehicular network cluster is defined as the set of multiple RSUs and vehicles within a specific region. The set of vehicles participating in social activities is represented as $V=\{v_1,v_2,\cdots ,v_M\}$, the set of RSUs that construct the blockchain network, store blockchain data, and provide services is denoted as $R=\{r_1,r_2,\cdots ,r_N\}$, where the available storage capacity of an RSU $r_i$ is represented as $r{c}_i$. Assuming that the current blockchain state consists of K blocks, the complete blockchain ledger is expressed as $B=\{b_1,b_2,\cdots ,b_K\}$, where the size of block $b_k$ is defined as $s_k$. In the cooperative storage system of the RSU cluster, the RSU cluster is represented as $CLU=\{C_1,C_2,\cdots ,C_L\}$, where each cluster $C_l=\{r_1^l,r_2^l,\cdots ,r_{N_l}^l\}$ consists of multiple RSUs that collectively store all blocks in the blockchain B, and $N_l$ is the number of RSU nodes in cluster $C_l$.

In the system, RSU nodes and cloud nodes act as consensus nodes to construct the blockchain network collaboratively, maintaining consistency and integrity while providing query and verification services to vehicle users. When vehicle users need to obtain data from the blockchain, such as vehicle reputation status and historical reputation change records, they can choose to retrieve this information either from nearby RSU nodes or remote cloud nodes based on their current location. Upon receiving a query request from a vehicle, the RSU or cloud node queries the local or cluster ledger for block data and transmits the complete block information to the vehicle. Meanwhile, all vehicles participating in the SIoV within the cluster store lightweight block header data. Upon retrieving block data from RSU nodes or the cloud nodes, they can independently verify the integrity and authenticity of the data using the locally stored block headers, ensuring data reliability. By leveraging these immutable and tamper-proof reputation profiles recorded in the blockchain, vehicles dynamically establish social relationships such as trust-based collaborations or resource sharing with other entities, thereby enabling decentralized and credibility-driven interactions within the SIoV.

For the block deployment and vehicle access process, taking the system in Figure 1 as an example, we cluster RSUs into three clusters $C_1$, $C_2$, and $C_3$. Assuming that the current blockchain ledger is $B=\{b_1,b_2,\cdots ,b_6\}$, then in addition to being stored as a backup in the cloud, the blockchain data also need to be deployed within the RSU clusters $C_1$, $C_2$, and $C_3$. For cluster $C_1$, which consists of four RSUs $r_1\sim r_4$, unlike traditional full nodes that need to store the entire blockchain, each RSU in the cluster only stores a subset of the blockchain blocks, while storing only block headers for the remaining blocks to support basic verification. The cluster must collaboratively ensure that at least one complete copy of the blockchain data is available within the storage cluster. For the RSU node $r_3$ within the collaborative storage cluster, even if it does not store all blockchain blocks locally, it can still provide services to vehicles through RSU collaboration. Considering RSU $r_3$ within the collaborative storage cluster as shown in Figure 1, it stores the full data of block $b_6$ while only keeping the block headers of the remaining blocks. When vehicle $v_2$ requests the data contained in block $b_2$ from $r_3$, the RSU first checks whether it has stored block $b_2$ locally. Upon detecting the absence of this block, $r_3$ sends a request via the R2R (RSU-to-RSU) link to another RSU within the cluster, $r_2$ which has stored block $b_2$. After retrieving the required block data, $r_3$ transmits it to vehicle $v_2$ via the R2V (RSU-to-Vehicle) link.

Based on the full-node constraints imposed by blockchain, all RSUs within a cluster $C_l$ must collaboratively store at least one complete copy of the blockchain ledger to support verification and consensus functions. Therefore, the total storage capacity of the RSU cluster must satisfy the following condition:

$$\sum _{r_i\in C_l}r{c}_i\ge \eta \sum _{b_k\in B}{s}_k,\eta \ge 1$$

(1)

where $\eta$ is an adjustment factor that ensures the cluster meets the fundamental storage constraints while reserving additional storage capacity to accommodate newly generated blocks within the cluster. A larger $\eta$ value enhances the cluster’s fault tolerance against individual node failures but also increases the overall storage resource requirements, potentially necessitating additional nodes to maintain stable cluster operation. Subject to the constraint in Equation (1), any RSU node within the cluster can selectively store the complete data of certain blocks while retaining only block header information for the remaining blocks. This approach optimizes the utilization of storage resources.

3.2. Block Access Probability Model

In SIoV, when vehicles establish social relationships or engage in information exchange, they typically need to verify each other’s identity and reputation information. In this system, a vehicle’s reputation update information is packaged into blocks by RSUs and becomes part of the blockchain. Due to the random block packaging mechanism in blockchain, a single block may contain reputation update records for multiple vehicles. Similarly, a vehicle’s identity and reputation updates may be stored across different blocks. For a given vehicle, the proportion of its relevant information in each block varies, leading to different access preferences for different blocks during identity and reputation verification. To better account for vehicle access preferences in block deployment, we define the access probability of vehicle $v_m$ to block $b_k$ as $P_{mk}$, which is expressed as follows:

$$P_{mk}=co{r}_{mk}·P_f(b_k,A_k)$$

(2)

where $co{r}_{mk}$ represents the correlation between vehicle $v_m$ and block $b_k$, which is determined by the random block packaging mechanism of the blockchain. When a block contains multiple transactions related to the same vehicle, its correlation with that vehicle is stronger. Consequently, when the vehicle’s reputation information needs to be verified, this block is more likely to be requested. Consider a block $b_k$ that contains $n_l$ transactions, represented as $T{x}^k=\{T{x}_1^k,T{x}_2^k,\cdots ,T{x}_{n_l}^k\}$, where each transaction may involve multiple vehicles. Let $y_m^k$ denote the relevance of a transaction within block $b_k$ to any vehicle in the cluster. If transaction $T{x}_l^k$ is associated with vehicle $v_m$ (i.e., it contains the reputation information of vehicle $v_m$), then $y_{lm}^k=1$. Otherwise, if transaction $T{x}_l^k$ does not involve node $v_m$, then $y_{lm}^k=0$. Thus, the correlation between vehicle $v_m$ with block $b_k$ is defined as follows:

$${cor}_{mk}={\displaystyle \frac{\left|T{x}_l^k\right|y_{lm}^k=1|}{n_l}}$$

(3)

Additionally, $P_f(b_k,A_k)$ represents the baseline query probability based on historical query frequency. Since different blocks exhibit varying access frequencies, with newer blocks generally containing more recent vehicle reputation updates, we incorporate both correlation and access frequency into our analysis. By examining historical social behavior patterns, we estimate block access behavior within the current cycle. Following the definition provided in reference [21], we assume that the query frequency follows an exponential decay pattern. Thus, the baseline query probability for block $b_k$, given its block age $A_k$, is expressed as follows:

$$P_f(b_k,A_k)={[{\int }_0^{A_k}{F}_0\left(b_k\right)e^{-\alpha t}d\left(t\right)]}^{-1}$$

(4)

where $F_0\left(b_k\right)$ denotes the initial query frequency of $b_k$ at the time of block generation, and the block age $A_k$ starts from an initial value of 0 at the time of block creation and gradually increases as new blocks are generated.

3.3. Block Data Transmission Model

Block data retrieval latency is a critical metric in collaborative storage systems, as it reflects the quality of service in the network. In the proposed collaborative storage scheme, vehicles obtain block data from RSUs through two possible transmission links: RSU-to-RSU (R2R) and RSU-to-Vehicle (R2V). Therefore, it is essential to model the latency of both R2R and R2V transmission links.

3.3.1. R2V Transmission Latency

For R2V communication, data transmission between an RSU and a vehicle occurs through wireless propagation. The communication rate between RSU $r_i$ and vehicle $v_m$ is given by [23]:

$$C{R}_{im}=B_{im}{log}_2\left(1+{\displaystyle \frac{p_i{\left|h_{im}\right|}^2}{{\sigma }^2}}\right)$$

(5)

where $B_{im}$ denotes the available spectrum bandwidth of RSU $r_i$, $p_i$ represents the transmit power of $r_i$, $h_{im}$ denotes the channel gain between RSU $r_i$ and $v_m$, and $\sigma$ represents the noise power spectral density.

The transmission latency incurred when RSU $r_j$ transmits a single block $b_k$ of size $s_k$ to vehicle $v_m$ can be expressed as follows:

$$TD(r_i,{\nu }_m,b_k)={\displaystyle \frac{s_k}{C{R}_{im}}}={\displaystyle \frac{s_k}{B_{im}{log}_2\left(1+\frac{p_i{\left|h_{im}\right|}^2}{{\sigma }^2}\right)}}$$

(6)

3.3.2. R2R Transmission Latency

For R2R communication, where RSUs are connected via wired links, the transmission latency incurred when RSU $r_j$ transmits a block $b_k$ of size $s_k$ to RSU $r_i$ can be expressed as follows:

$$TD(r_j,r_i,b_k)={\displaystyle \frac{s_k}{B_{ij}}}$$

(7)

where $B_{ij}$ denotes the available transmission bandwidth between RSU $r_j$ and RSU $r_i$.

4. Problem Formulation

4.1. Block Access Cost

Considering the process in which a vehicle requests access to a block from an RSU within the cluster, we define the decision variable $x_{ik}$, which determines the storage status of a block in an RSU. This variable indicates whether block $b_k$ is stored in RSU $r_i$. The decision variable set for RSU cluster $C_l$ is denoted as $X_l=\left\{x_{ik}\left|r_i\in C_l,b_k\in B\right.\right\}$ which forms an $N_l\times K$ matrix. Here, $x_{ik}=1$ indicates that RSU $r_i$ has stored block $b_k$, while $x_{ik}=0$ indicates that RSU $r_i$ does not store block $b_k$. The block allocation decision table X is maintained by the cloud server and synchronized across all RSUs in the cluster. Additionally, each RSU can update this table based on local real-time network conditions. If a vehicle requests block $b_k$ data from RSU $r_i$ while $x_{ik}=0$ (i.e., RSU $r_i$ does not store the block $b_k$ data), the RSU must query $X_l$ to identify the RSU within the cluster that holds the complete copy of block $b_k$ and has the lowest expected access latency. Let RSU $r_j$ be the selected node that retrieves the block and transmits it to RSU $r_i$, which then forwards the block to the requesting vehicle. Thus, the latency cost for vehicle $v_m$ to obtain block $b_k$ from RSU $r_i$ is defined as follows:

$$T{D}_{mk}=TD(r_i,v_m,b_k)+(1-x_{ik})·TD(r_j,r_i,b_k)$$

(8)

Assuming that the service ranges of RSUs in the system do not overlap, an RSU can transmit block data to a vehicle only when the vehicle is within its coverage area. If the retrieval delay for block data from an RSU exceeds the vehicle’s dwell time within the RSU’s coverage, the vehicle must instead obtain the data from a remote cloud server via a backhaul link, discarding any incomplete data fragments [24]. This process incurs a higher additional access latency cost. We define the set of blocks of interest for vehicle $v_m$ as $B_m=\left\{b_k\left|b_k\in B,P_{mk}>0\right.\right\}$. Let $\Delta C$ denote the cost of a single data access from the cloud server. For a vehicle $v_m$ located within the coverage area of RSU $r_i$, we define the vehicle’s dwell time within vehicle $v_m$’s coverage as $t_m^d$. Given the block set $B_m$, the total block access cost for vehicle $v_m$ is defined as follows:

$$C_m=\left\{\begin{array}{cc}{\displaystyle \sum _{b_k\in B_m}}{TD}_{mk}·P_{mk},& {\displaystyle \sum _{b_k\in B_m}}{TD}_{mk}\le t_m^d\\ \Delta C+{\displaystyle \sum _{b_k\in B_m}}{TD}_{mk}·P_{mk},& {\displaystyle \sum _{b_k\in B_m}}{TD}_{mk}>t_m^d\end{array}\right.$$

(9)

For the overall vehicle access process, the access cost is determined by the following factors:

• The vehicle’s access probability for a block.
• The latency cost for the vehicle to retrieve the block from an RSU.
• Whether the vehicle can obtain all required block data directly from RSUs.

Among these factors, the latency cost for a vehicle to retrieve a block from an RSU is influenced by both the clustering strategy and the block allocation strategy within the cluster. This latency cost directly impacts whether the vehicle needs to retrieve data via the backhaul link from the remote cloud server. Therefore, it is essential to design an effective collaborative storage scheme for RSU clusters to optimize the access cost for vehicles served by the cluster.

4.2. Optimization Objective

The blockchain collaborative storage optimization problem in SIoV is formally defined as follows: The system consists of multiple RSUs with limited available storage resources, where each RSU $r_i$ serves a set of vehicles $V^i$, and the service areas of different RSUs do not overlap. The challenge is to partition RSUs into L cluster $CLU$, and distribute all blocks in the current blockchain ledger B across $N_l$ RSUs within each cluster $C_l$ while respecting the storage constraints of RSUs. The goal is to minimize the total block access cost incurred by all vehicles in the system when performing reputation verification. The optimization objective is formulated as follows:

$$min\sum _{C_l\in CLU}\sum _{r_i\in C_l}\sum _{v_m\in V^i}{C}_m$$

(10)

$$s.t.\sum _{r_i\in C_l}r{c}_i\ge \eta \sum _{b_k\in B}{s}_k,\eta \ge 1$$

(11)

$$\sum _{r_i\in C_l}{x}_{ik}\ge 1,\forall b_k\in B$$

(12)

$$\sum _{b_k\in B}{x}_{ik}·s_k\le r{c}_i,\forall r_i\in C_l$$

(13)

Equation (11) regulates the formation of clusters, ensuring that the total storage capacity of all RSUs within a cluster is at least equal to the total size of the blockchain, thereby guaranteeing that the formed cluster can store a complete copy of the blockchain. Equations (12) and (13) govern the block allocation process within the cluster, ensuring that each block in the blockchain is stored at least once within the cluster to meet the demand of any vehicle served by the RSUs in the cluster, while also ensuring that the number of blocks allocated to a single RSU does not exceed its own storage capacity.

5. Algorithm

This section addresses the proposed problem in two key components: RSU clustering and intra-cluster block allocation. To this end, this paper introduces RAPSCA and VSPGBAA. RAPSCA clusters RSUs into collaborative storage groups based on block access similarity and resource availability, establishing the foundation for VSPGBAA. Operating within these clusters, VSPGBAA optimizes block allocation by considering vehicle dwell time and block access probabilities, ensuring that each RSU stores an optimal subset of blocks. This approach reduces access costs for vehicles while enhancing data retrieval efficiency. Together, these algorithms constitute the blockchain-based RSU cluster collaborative storage scheme, improving data access services in SIoV.

5.1. RSU Clustering

In the proposed system, since RSU nodes have limited available storage resources, it is essential to cluster RSUs to form RSU clusters that can efficiently provide full blockchain query services for vehicles. To achieve effective clustering, it is necessary to consider not only the distance between RSU nodes but also the block access preferences of the vehicles served by each RSU.

Therefore, we propose RAPSCA, which incorporates both spatial relationships and vehicle access behaviors to optimize clustering. Under the collaborative storage architecture, redundant storage of critical block data within clusters is allowed. This strategy ensures that redundant copies can better satisfy the data needs of multiple nodes, thereby improving overall storage efficiency. The pseudocode for RAPSCA is presented in Algorithm 1.

The algorithm consists of six main steps: determining the number of clusters, similarity matrix construction, Laplacian matrix computation, spectral decomposition, feature normalization, and K-means clustering with a minimum capacity constraint. To better illustrate the role of RAPSCA in collaborative storage, we further explain the steps of the algorithm as follows:

• Determining the Number of Clusters: The number of clusters can be determined based on the storage resources of RSU nodes in the system and the storage constraints of individual clusters, as follows:

  $$L=⌊{\displaystyle \frac{{\sum }_{r_i\in R}r{c}_i}{\eta {\sum }_{k=1}^K{s}_k}}⌋$$

  (14)
  Equation (14) ensures that each cluster satisfies the storage resource constraints imposed by blockchain size requirements within the cluster. Simultaneously, it partitions RSU nodes into the maximum feasible number of clusters to optimally preserve the decentralized characteristics of the system.
• Similarity Matrix Construction: As mentioned earlier, due to the random block packaging mechanism in blockchain, a single block may contain reputation update records for any vehicle. Therefore, even if vehicles are distributed across different RSUs and have never had direct social interactions, their reputation updates may still be packaged into the same block. From the packaging results, we can infer that RSUs exhibit certain similarities in their preferences for blocks, even if they serve different sets of vehicles. However, modifying the blockchain packaging mechanism to introduce systematic patterns or preferences could compromise the security and decentralization of the blockchain. Thus, this paper assumes that the block packaging process is random and unpredictable. Instead of modifying the packaging mechanism, we analyze the existing block data and their associated vehicle relationships to determine the similarity in block demand among RSU nodes.
  As previously defined, the set of blocks of interest for vehicle $v_m$ is represented as $B_m$. Since RSU $r_i$ needs to consider the block access probabilities of all vehicles within its coverage area, the set of required blocks for RSU $r_i$ is given by the following:

  $$B_{r_i}=\bigcup _{v_m\in V^i}{B}_m$$

  (15)

  where $V^i$ represents the set of vehicles within the coverage area of RSU $r_i$. Referring to the interest similarity described in reference [25], we define the weight between RSU nodes $r_i$ and $r_j$ based on their block demand similarity. Specifically, the weight is determined by the cosine similarity of their required block sets, multiplied by the Gaussian kernel function of their physical distance $d_{ij}$:

  $$w_{i,j}=s_B(r_i,r_j)={\displaystyle \frac{{∥B_{r_i}\cap B_{r_j}∥}_1}{{∥B_{r_i}∥}_2·{∥B_{r_j}∥}_2}}·GK(r_i,r_j)$$

  (16)

  where ${∥B_{r_i}∥}_2=\sqrt{\left|B_{r_i}\right|}$ represents the number of blocks required by RSU $r_i$, ${∥B_{r_i}\cap B_{r_j}∥}_1$ denotes the number of blocks that RSU $r_i$ and $r_j$ have in common demand, and $GK(r_i,r_j)$ represents the Gaussian kernel function, which quantifies the spatial aggregation of RSU nodes based on their geographical proximity. It is defined as follows:

  $$GK(r_i,r_j)=exp(-d_{ij}^2/{\sigma }^2)$$

  (17)

  where $\sigma$ is a parameter that controls the strength of the distance relationship.
  Based on the above block demand similarity definition, the similarity matrix between nodes can be expressed as follows:

  $$W_{RSU}=\left[\begin{array}{ccc}{w}_{1,1}& \cdots & w_{1,N}\\ ⋮& \ddots & ⋮\\ w_{N,1}& \cdots & w_{N,N}\end{array}\right]$$

  (18)
  At the same time, for each RSU node, its degree can be computed as $d_i={\sum }_{j=1}^N{w}_{i,j}$. Thus, the degree matrix $D_{RSU}$ can be expressed as follows:

  $$D_{RSU}=\left[\begin{array}{ccc}{d}_1& \cdots & \cdots \\ ⋮& \ddots & ⋮\\ \cdots & \cdots & d_N\end{array}\right]$$

  (19)
• Laplacian Matrix Computation: After obtaining the similarity matrix $W_{RSU}$ and the degree matrix $D_{RSU}$, the Laplacian matrix can be expressed as $L_{RSU}=D_{RSU}-W_{RSU}$. At the same time, we perform normalization on the Laplacian matrix, yielding $L_{norm}$:

  $$L_{norm}=D^{-1/2}L{D}^{-1/2}$$

  (20)
• Spectral Decomposition: Perform eigen decomposition on the normalized Laplacian matrix $L_{norm}$ to obtain the eigenvalues $\Lambda =\{{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_N\}$ and the corresponding eigenvectors $U=\{u_1,u_2,\cdots ,u_N\}$. From these, select the smallest L eigenvalues ${\lambda }_1\sim {\lambda }_L$ and construct the matrix $U_L=\{u_1,u_2,\cdots ,u_L\}$ by using their corresponding eigenvectors as column vectors.
• Feature Normalization: Normalize each row of the eigenvector matrix $U_L$ to obtain the final feature matrix F.
• K-means Clustering with Minimum Capacity Constraint: Using each row of the feature matrix F as an input sample, perform K-means clustering with constraints, obtaining the clustering result $CLU$.

Algorithm 1 RSU Access Preference-based Spectral Clustering Algorithm (RAPSCA)

Require: RSU set R, vehicle set $V^i$ within each RSU coverage area Ensure: number of clusters L, RSU Cluster $CLU$   1: $L\leftarrow ⌊{\displaystyle \frac{{\sum }_{r_i\in R}r{c}_i}{\eta {\sum }_{k=1}^K{s}_k}}⌋$   2: for each pair of RSU nodes $r_i$ and $r_j$ do   3:     Compute the Euclidean distance $d_{ij}$ between nodes $r_i$ and $r_j$ based on the location information $\{x_{r_i},y_{r_i}\}$ and $\{x_{r_j},y_{r_j}\}$   4:     Compute the weight $w_{i,j}$ between $r_i$ and $r_j$ based on $B_{r_i}$ and $B_{r_j}$: $w_{i,j}=s_B(r_i,r_j)={\displaystyle \frac{{∥B_{r_i}\cap B_{r_j}∥}_1}{{∥B_{r_i}∥}_2·{∥B_{r_j}∥}_2}}·GK(r_i,r_j)$   5: end for   6: Construct the similarity matrix $W_{RSU}$   7: Compute the node degree $d_i={\sum }_{j=1}^N{w}_{i,j}$ and obtain the degree matrix $D_{RSU}=\left\{d_i\right\}$   8: Compute the Laplacian matrix $L_{RSU}=D_{RSU}-W_{RSU}$   9: Normalize the Laplacian matrix $L_{norm}=D^{-1/2}{LD}^{-1/2}$ 10: Perform eigen decomposition on the normalized Laplacian matrix $L_{norm}$ to obtain eigenvalues $\Lambda =\{{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_N\}$ and corresponding eigenvectors $U=\{u_1,u_2,\cdots ,u_N\}$ 11: Select the smallest L eigenvalues ${\lambda }_1\sim {\lambda }_L$ and form the matrix $U_L=\{u_1,u_2,\cdots ,u_L\}$ with their corresponding eigenvectors as column vectors. 12: Compute $F[i,:]={\displaystyle \frac{U_L[i,:]}{\parallel U_L[i,:]\parallel }}$ to construct the normalized feature matrix F 13: Use K-means clustering with a minimum capacity constraint $S_K=\eta {\displaystyle \sum _{k=1}^K}{s}_k,\eta \ge 1$ to cluster each row of the feature matrix F as an input sample, obtaining clustering results $\left\{C_l\right\}$. 14: $CLU\leftarrow \left\{C_l\right\}$

For the complexity analysis, first, constructing the similarity matrix requires computing the weight relationship between every pair of RSU nodes, resulting in a complexity of $O\left(n^2\right)$. Next, computing the Laplacian matrix involves row-wise normalization, which also has a complexity of $O\left(n^2\right)$. The spectral decomposition has a complexity of $O\left(n^3\right)$, while feature normalization has a complexity of $O\left(nL\right)$. The K-means clustering with minimum capacity constraints has a complexity of $O\left(nLT\right)$, where T represents the number of iterations. Thus, the total time complexity of RAPSCA is $O\left(n^3\right)$.

5.2. Intra-Cluster Block Allocation

In Algorithm 1, the clustering of RSUs into collaborative storage clusters has been completed. Since each RSU cluster must collaboratively store at least one complete copy of the blockchain, it is necessary to determine the specific block allocation within the cluster, i.e., which blocks each RSU in the cluster should store. When addressing the block allocation problem, in addition to considering the block access probabilities of the vehicles served by each RSU, it is also important to take into account the priority of the vehicles being served.

As shown in Figure 2, we consider a vehicle $v_m$ located within the coverage area of RSU $r_i$, with a required block set $B_m$. The states of $v_m$ during the block allocation process can be categorized into three cases:

• State 1: Vehicle $v_{m1}$ has just entered the coverage area of $r_i$ and will remain for a relatively long dwell time $t_{m1}^d$ before leaving.
• State 2: Vehicle $v_{m2}$ has a shorter dwell time $t_{m2}^d$ compared to $t_{m1}^d$.
• State 3: Vehicle $v_{m3}$ is about to leave the coverage area of $r_i$ with a very short dwell time $t_{m3}^d$.

At the same time, different block allocation strategies will result in RSU $r_i$ storing different block sets. The entire block set $B_m$ may be fully deployed in $r_i$, or only a subset of $B_m$ may be stored. When $r_i$ does not fully store all the blocks in $B_m$, it has to request the missing blocks from other RSUs in the cluster, which will introduce additional access latency. Since excessive access latency may force a vehicle to switch to the remote cloud server for data retrieval, resulting in extra access costs, the system must carefully balance the acceptable access latency for vehicles with the expected access latency of the deployment strategy to enhance its effectiveness.

Based on the above scenario, we define ${\tau }_0$ as the transmission delay required to transfer a standard-sized block from an RSU to a vehicle. For a vehicle $v_{m3}$ that is about to leave the RSU coverage area, if $t_{m3}^d<{\tau }_0$, then regardless of whether $r_i$ stores the blocks required by $v_{m3}$, the vehicle will not be able to complete the block access process within the coverage area of $r_i$. Therefore, in this case, the service priority of the RSU for $v_{m3}$ is very low. When $t_m^d>{\tau }_0$, vehicles with smaller dwell times require lower transmission latency, meaning that from the perspective of the RSU, these vehicles should be given higher priority. As a result, the service priority for vehicle $v_{m2}$ is higher than that for $v_{m1}$. Within the coverage area of a single RSU, the service priority of $r_i$ for vehicle $v_m$, denoted as $PR\left(t_m^d\right)$, can be expressed as follows:

$$PR\left(t_m^d\right)=\sigma (t_m^d-{\tau }_0)·\left(1+\mu e^{-\omega (t_m^d-{\tau }_0)}\right)$$

(21)

where $\sigma (t_m^d-{\tau }_0)$ is the Sigmoid function, defined as follows: $\sigma (t_m^d-{\tau }_0)=1/\left(1+e^{-\theta (t_m^d-{\tau }_0)}\right)$. When the vehicle dwell time $t_m^d$ approaches the threshold ${\tau }_0$, the rapid saturation property effectively filters out vehicle requests with extremely short dwell times, thereby preventing resource wastage. Conversely, when $t_m^d>{\tau }_0$, the service priority gradually decreases with increasing dwell time, thus prioritizing vehicles with shorter dwell times. These vehicles not only have a sufficient time window for data transmission but are also more sensitive to latency. The adjustment factor $\mu$ controls the global scaling of the interest value, while $\omega$ determines the smoothness of the exponential decay. Together, these parameters optimize the shape of the priority curve, making it adaptable to various application scenarios.

At the RSU level, the demand of RSU $r_i$ for block $b_k$ can be expressed as follows:

$${\Omega }_{ik}=\sum _{v_m\in V^i}{P}_{mk}·PR\left(t_m^d\right)$$

(22)

Within an RSU cluster, the transmission latency between nearby RSUs are relatively low, meaning that the block allocation strategy for one RSU will impact the storage demand of RSUs within a certain range. Specifically, suppose block $b_k$ is allocated to RSU $r_i$ for storage, i.e., $x_{ik}=1$. Let $C_i^{neighbor}$ represent the set of RSUs within the neighboring region of $r_i$. After the allocation, both $r_i$ and the neighboring RSUs in $C_i^{neighbor}$ will have a reduced demand for the next allocation of block $b_k$ because they can retrieve it from $r_i$ with low latency. The extent of this demand reduction is determined by the physical distance between RSUs. Based on this scenario, we define the block demand function of RSU $r_i$ for $b_k$ as follows:

$$Q(r_i,b_k)=\left\{\begin{array}{cc}{\Omega }_{ik}+{\displaystyle \sum _{r_j\in C_i^{neighbor}}}{\lambda }_{ij}·(1-x_{jk})·{\Omega }_{jk},& x_{ik}=0\\ 0,& x_{ik}=1\end{array}\right.$$

(23)

If $x_{ik}=1$, then RSU $r_i$ has already stored block $b_k$, meaning that no additional storage resources are required for redundant storage of $b_k$. In this case, the block demand function value of $r_i$ for block $b_k$ reduces to 0. If $x_{ik}=0$ and $x_{jk}=0$, it indicates that neither $r_i$ nor its neighboring RSUs have stored block $b_k$. In this case, the block demand function value of $r_i$ for block $b_k$ will increase as the number of neighboring RSUs that require $b_k$ also increases. The parameter ${\lambda }_{ij}$ is a physical weight factor, determined by the distance between RSUs within the cluster:

$${\lambda }_{ij}={\displaystyle \frac{D_l^{max}-D_{ij}}{D_l^{max}}}$$

(24)

where $D_l^{max}$ represents the Euclidean distance between the two most distant RSUs within the cluster.

Based on the above definitions, this paper proposes VSPGBAA. The algorithm first calculates the vehicle service priority in each RSU based on vehicle dwell time and defines the block demand for each RSU. Then, it considers the dynamic changes in RSU block demand during the allocation process. Finally, the algorithm further optimizes the overall access cost by utilizing the remaining available storage space within the cluster. The complete process of the proposed algorithm is presented in Algorithm 2.

The overall process of Algorithm 2 consists of three main steps: Initialization—Greedy Allocation—Cost Optimization. First, in the initialization step, we process the vehicle-related information for each RSU, computing the vehicle service priority and block access probability to determine the block demand of each RSU. Since each RSU cluster must store a complete copy of all blockchain blocks, we ensure this requirement in the greedy allocation step by assigning each block at least once. This guarantees that all RSUs in the cluster can provide complete block data query services for vehicles. During the allocation, blocks are assigned in descending order of demand, prioritizing those with higher demand to achieve a near-optimal allocation that minimizes access cost. After each allocation, we update the impact of the current allocation on neighboring RSUs. Once all blocks have been allocated, the cluster constraint is satisfied, and the remaining storage space can be used for further access cost optimization. In the cost optimization step, we iteratively select the most critical RSU-block pair based on the demand function to perform redundant block allocation. This process is repeated whenever storage space is available, maximizing the utilization of storage resources within the cluster.

Algorithm 2 Vehicle Service Priority-based Greedy Block Allocation Algorithm (VSPGBAA)

Require: The set of all blocks B, an RSU cluster $C_l$, the set of vehicles within the coverage of each RSU $V^i$ Ensure: Block allocation strategy X in the RSU cluster $C_l$   1: for $r_i$ in $C_l$ do   2:    Compute the service priority of each vehicle in $r_i$’s coverage based on its dwell time: $PR\left(t_m^d\right)=\sigma (t_m^d-{\tau }_0)·\left(1+\mu e^{-\omega (t_m^d-{\tau }_0)}\right)$   3:    Compute the block access probability $P_{mk}$ based on the correlation between vehicles and blocks and the baseline query probability, then obtain the block demand of $r_i$: ${\Omega }_{ik}={\displaystyle \sum _{v_m\in V^i}}{P}_{mk}·PR\left(t_m^d\right)$   4: end for   5: Initialize $X=\left\{\varphi \right\}$; that is, the initial allocation state is empty.   6: Sort blocks in descending order based on ${\Omega }_{ik}$ to obtain $B_{sort}$   7: for $b_k$ in $B_{sort}$ do   8:     Select the RSU node $r_i$ with the highest demand function value $Q(r_i,b_k)$ for block $b_k$, where the block size is given by $s_k$   9:     if the node $r_i$’s remaining storage capacity $r{c}_i>s_k$ then 10:      Set $x_{ik}=1$, allocate block $b_k$ to RSU node $r_i$ 11:      Update remaining storage: $r{c}_i\leftarrow r{c}_i-s_k$ 12:      Update the demand function $Q^{*}$ for $r_i$ and and its neighboring RSUs $C_i^{neighbor}$ 13:     else 14:      Select $r_j$ in descending order based on $Q(r_j,b_k)$ and repeat the process until $r{c}_j>s_k$ 15:     end if 16: end for 17: while any RSU node in cluster $C_l$ has remaining available storage capacity $rc>0$ do 18:     Select the RSU node $r_i$ and block $b_k$ with the highest demand function value $Q(r_i,b_k)$ 19:     if the node $r_i$’s remaining storage capacity $r{c}_i>s_k$ then 20:      Set $x_{ik}=1$, allocate block $b_k$ to RSU node $r_i$ 21:      Update remaining storage: $r{c}_i\leftarrow r{c}_i-s_k$ 22:      Update the demand function $Q^{*}$ for $r_i$ and its neighboring RSUs $C_i^{neighbor}$ 23:     end if 24: end while

For the complexity analysis, first, VSPGBAA defines the block demand for each RSU based on the association between the vehicles it serves and the blocks and then sorts the blocks by demand. The complexity of this step is $O(N_l{M}_{i}K+KlogK)$, where $M_i$ is the number of vehicles served by RSU $r_i$, and K is the number of blocks to be allocated. Then, VSPGBAA performs the initial allocation of each block and updates the block demand function of RSU nodes, with a complexity of $O\left(K{N}_l\right)$. Finally, VSPGBAA utilizes the remaining available storage space in the cluster to perform redundant block replication for further access cost optimization, with a complexity of $O\left(K{\overline{N}}_l\right)$, where ${\overline{N}}_l({\overline{N}}_l\ll N_l)$ represents the average number of neighboring RSUs for each RSU. Thus, the overall complexity of VSPGBAA is $O(N_l{M}_{i}K+KlogK)$.

6. Evaluation

In this section, we evaluate the effectiveness and performance of the proposed algorithm through a Python 3.10.16-based simulation of an IoV system with blockchain data. The experiments were conducted on a machine equipped with an Intel i5 processor and 16 GB of RAM, with system initialization based on the data described later in this paper. Each test randomly generates a varying number of RSUs and vehicle devices, and every experiment is executed 20 times to assess the algorithm’s performance. For evaluation metrics, we focus on the storage hit rate of the collaborative storage scheme, the overall access cost for vehicles in the system, and the runtime of the algorithm. Since the proposed strategy can be described as a constraint-based caching scheme, the storage hit rate, similar to the cache hit rate, is defined as the percentage of block access requests completed within the vehicle’s dwell time. A higher storage hit rate indicates that more vehicles can access block data without relying on the backhaul link to the remote cloud server.

6.1. Experimental Setup

We consider a system consisting of multiple RSU nodes and vehicle devices, which are randomly distributed within a specified area. In this system, RSU nodes generate and store blockchain data, while vehicles access these blocks based on their individual demands. Given the heterogeneity of available storage resources among RSUs at a given time, we assume that the available storage capacity of each RSU node follows a normal distribution within the range of $[200,800]$ MB. The communication cost between RSUs depends on their positions and the network topology. RSU nodes can communicate either directly or via multi-hop transmission. Meanwhile, vehicles move within the coverage area of RSUs, request block data, and eventually leave the RSU coverage area after a certain period. The dwell time of a vehicle within an RSU’s coverage area follows a uniform distribution within the range $[0,t^d]$.

Hyperledger Fabric [26] is a permissioned blockchain platform that has been widely adopted in IoT and IoV applications [27,28] due to its robust security features and flexible architecture. We utilize the Hyperledger Fabric consortium blockchain platform to construct the blockchain network, adopting its default parameter constraints. Specifically, the block size is limited to 10 MB, each block can contain a maximum of 10 transactions, and the maximum data size per transaction is 512 KB. We assume that the blockchain network has been running for a certain period, and the existing block sizes follow a uniform distribution within the range $[5,10]$ MB. For each newly created block, its initial query frequency is randomly assigned as $F_0$, while its block age $A_k$ starts from 0 and gradually increases as new blocks are generated.

For the proposed RSU clustering scheme, we choose the following clustering algorithms for comparison based on VSPGBAA as the allocation algorithm:

• Random Clustering: RSU nodes are clustered randomly with their neighboring nodes without considering vehicle access preferences until each cluster satisfies the blockchain storage capacity constraint.
• Single-Cluster Scheme: No preprocessing is applied to RSU nodes. Instead, all RSUs are treated as a single cluster, and block allocation is performed directly within this global cluster. In the subsequent block allocation phase, all methods adopt the VSPGBAA algorithm proposed in this paper.

For the proposed intra-cluster block allocation scheme, we perform clustering based on the RAPSCA algorithm and select the following allocation algorithms for comparison:

• Two-Step Greedy Algorithm (TSGA) [22]: This algorithm considers the impact of the allocation process on total access cost. For each allocation step, it pre-evaluates the change in total query cost after allocation and selects the decision that results in the greatest cost reduction. After each allocation, it iterates over all blocks and RSUs, updating the expected query cost for further decisions.
• Node First Algorithm [29]: This algorithm first selects the RSU that has the highest demand for each block to store its first backup copy. Then, for each RSU, it considers only local demand, sequentially storing the most required blocks until the available storage capacity is fully utilized.
• Random Allocation: This algorithm does not consider RSU block demand but ensures that each block has at least one backup to maintain blockchain ledger integrity within the cluster. After initial placement, blocks are sorted based on their demand, and randomly assigned to RSUs with available storage until all storage resources in the cluster are utilized.

6.2. Performance Evaluation

6.2.1. RSU Clustering Performance Evaluation

To verify the effectiveness of the proposed RAPSCA algorithm, this paper evaluates the vehicle access cost and the algorithm’s impact on the overall block allocation running time under different numbers of RSU nodes, varying blockchain lengths, and different numbers of clusters.

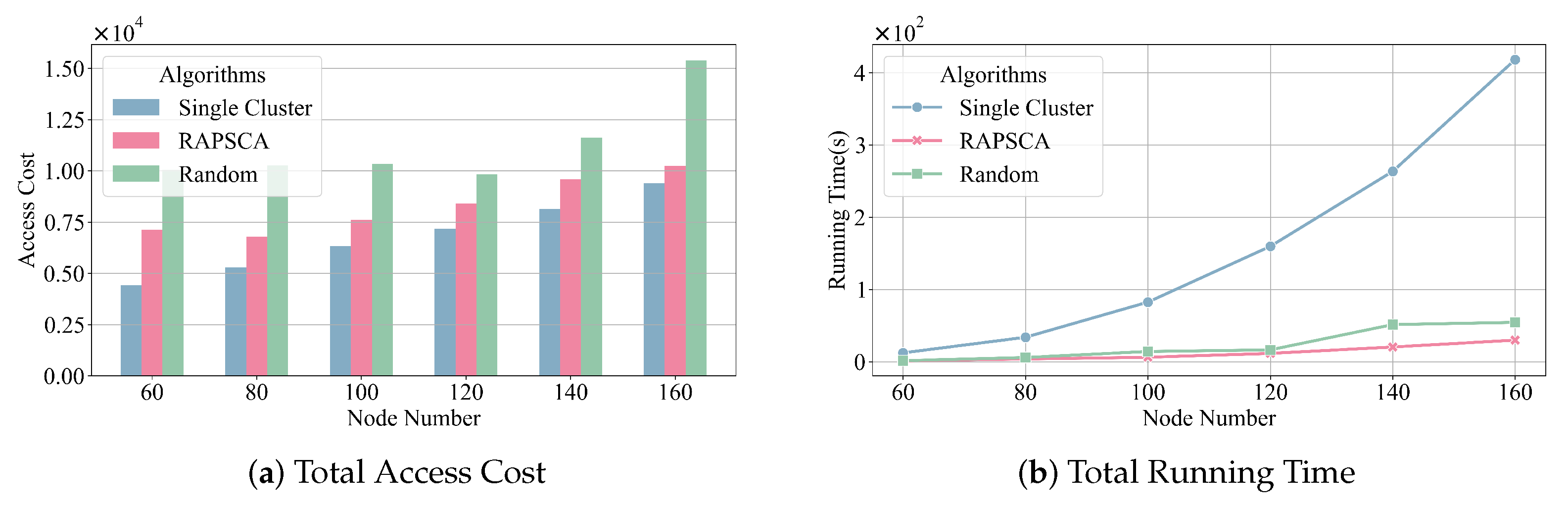
• Impact of the number of RSU nodes on the RSU Clustering Process: As shown in Figure 3a,b, the system is configured with a fixed block count of 200, a vehicle-to-RSU ratio of 10:1, a fixed cluster number of 3, while the number of RSU nodes varies from 60 to 160. As shown in Figure 3a, as the number of nodes increases, the access cost of the RAPSCA algorithm approaches that of the single-cluster scheme and outperforms the adjacent random clustering strategy. The single-cluster scheme is a cooperative storage method commonly adopted in traditional vehicular networks, relying on a fully centralized architecture to achieve globally distributed storage. Although this scheme enables near-optimal block allocation through centralized scheduling, its centralized design contradicts the decentralization principle of blockchain. Experimental results indicate that the RAPSCA algorithm effectively reduces access costs through a multi-cluster coordination mechanism while preserving the decentralized characteristics of blockchain, without causing a significant negative impact on system performance.
  Furthermore, the impact of the algorithm on the execution time of the block allocation process is illustrated in Figure 3b. As the system scales up, the execution time of the block allocation algorithm increases accordingly. In the single-cluster scheme, the complexity of the network topology rises significantly with the growing number of nodes, leading to a substantial increase in the execution time of the block allocation process. In contrast, the cluster partitioning mechanism effectively reduces the solution space, thereby improving the algorithm’s computational efficiency.

• Impact of the number of blocks on the RSU Clustering Process: As shown in Figure 4a,b, the system is configured with 120 RSUs, 1200 vehicles, three clusters, while the block count varies from 100 to 500. As shown in Figure 4a, as the number of stored blocks within a cluster increases, the overall access cost for vehicles in the cluster also rises. This is because, with a fixed number of RSUs and cluster size, the total storage resources of the system remain limited, leading to a reduction in the average number of block copies. Consequently, some RSUs may need to request block data from more distant nodes, increasing access latency. Additionally, as the number of blocks grows, the range of data involved in vehicle queries for historical blocks expands, further elevating access costs. At the same time, the block access cost of RAPSCA is significantly lower than that of the random clustering strategy and comparable to the single-cluster scheme. When the block count is high, the access cost of the single-cluster scheme is slightly lower than RAPSCA. This is because, with fewer block copies available, the number of locations where a single RSU in the RAPSCA scheme can directly access a required block is lower than in the single-cluster mode, resulting in additional data transmission overhead.
  As shown in Figure 4a,b, as the block count increases, RAPSCA maintains relatively low access costs while also improving the overall efficiency of the algorithm. Therefore, this algorithm is well-suited for RSU devices with limited computational and storage resources, demonstrating strong adaptability in large-scale block storage scenarios.

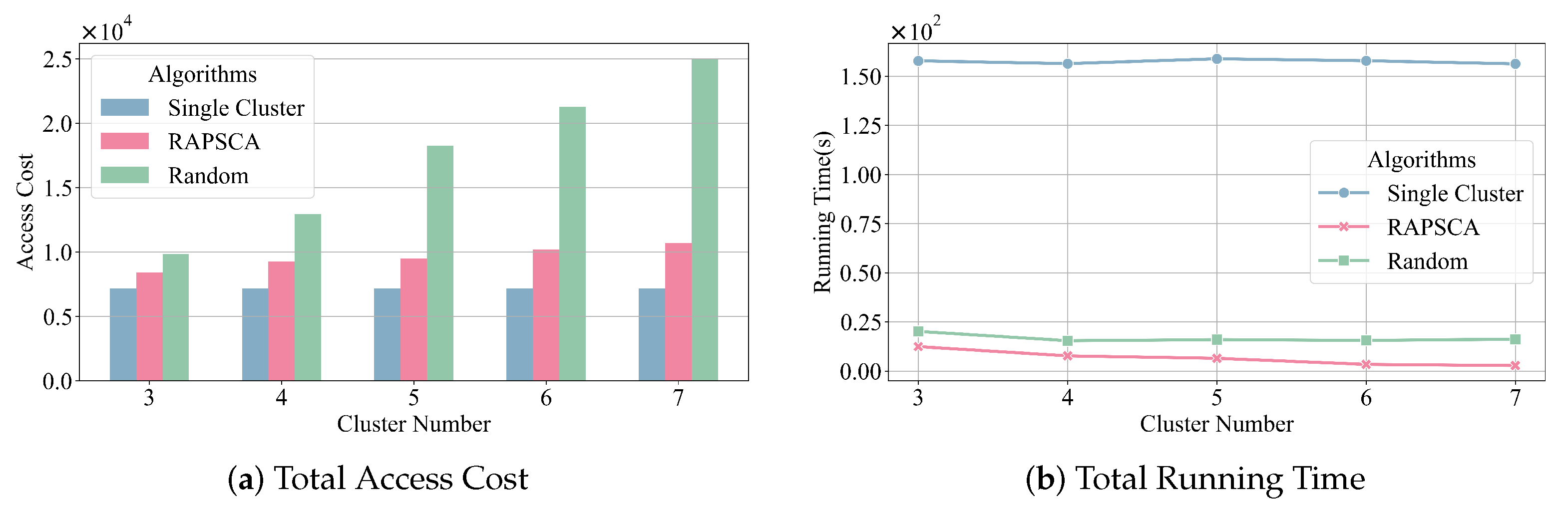
• Impact of the number of clusters on the RSU Clustering Process: As shown in Figure 5a,b, the system is configured with 120 RSUs, 1200 vehicles, and 200 blocks, while the number of clusters varies from 3 to 7. As shown in Figure 5a, the RAPSCA algorithm achieves access costs comparable to the single-cluster scheme, and its access cost remains stable as the number of clusters changes. This indicates that the RAPSCA clustering process does not introduce additional access overhead. When sufficient storage resources are available in the IoV system, a well-designed clustering strategy ensures that the total access cost remains at an optimal level, without imposing extra burdens due to cluster partitioning. However, since strong trust relationships among RSUs are only guaranteed within individual clusters, improper cluster partitioning may disrupt critical communication paths, making it difficult for some RSUs to directly access required blocks. This would increase access latency and significantly raise the overall system access cost. Therefore, a well-structured cluster partitioning strategy not only optimizes storage resource utilization efficiency but also reduces system access overhead, enhancing the overall performance of the SIoV system.
  As shown in Figure 5b, as the number of clusters increases, the number of RSUs per cluster decreases, leading to a reduction in the runtime of the block allocation algorithm. Although increasing the number of clusters improves overall algorithm efficiency, it also reduces the total storage resources within each cluster. Therefore, in practical applications, parameters such as $\eta$ and the number of clusters should be carefully chosen to ensure that clusters are reasonably partitioned while maintaining sufficient storage resources within each cluster.

6.2.2. Intra-Cluster Block Allocation Performance Evaluation

To evaluate the effectiveness of the VSPGBAA algorithm, the experiments compare its storage hit rate, total access cost within the cluster, and algorithm runtime under different numbers of RSU nodes, varying vehicle counts, and different blockchain lengths. The baseline algorithms are introduced in the experiment setup in Section 6.1.

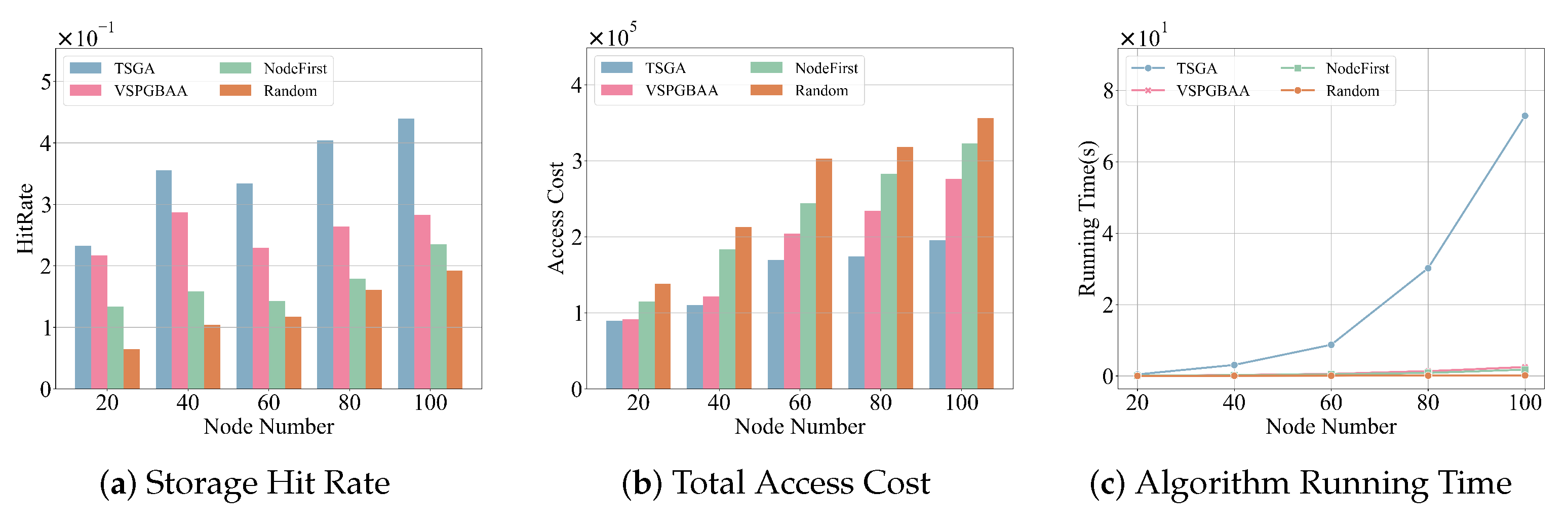
• Impact of the number of RSU nodes on Intra-Cluster Block Allocation: As shown in Figure 6a–c, the system is configured with a fixed block count of 300, a fixed vehicle-to-RSU ratio of 9:1, and a fixed number of three clusters, while the number of RSU nodes varies from 20 to 100. As illustrated in Figure 6a,b, when the number of RSU nodes within a cluster is small, the storage hit rate and total access cost of VSPGBAA are close to those of TSGA. However, as the number of RSUs within the cluster increases, the storage hit rate of VSPGBAA remains stable but is slightly lower than that of TSGA. Specifically, compared to TSGA, VSPGBAA incurs 16.4% higher access cost, and achieves a 36% lower cache hit rate, but significantly improves efficiency with a 16× shorter runtime. Meanwhile, as shown in Figure 6c, the running time of TSGA increases sharply as the number of RSUs in the cluster grows, greatly exceeding that of VSPGBAA, NodeFirst, and the random allocation strategy. This is because TSGA globally updates the entire system state for each block allocation, whereas VSPGBAA only updates the local neighborhood affected by the allocation. As a result, VSPGBAA reduces computational overhead while maintaining competitive performance, making it adaptable to different cluster sizes. Furthermore, compared to NodeFirst, VSPGBAA reduces total access cost by 26.9%, improves the cache hit rate by 34%, but requires 19.5% more runtime. This trade-off highlights VSPGBAA’s ability to balance efficiency and performance, demonstrating its potential in large-scale deployments.

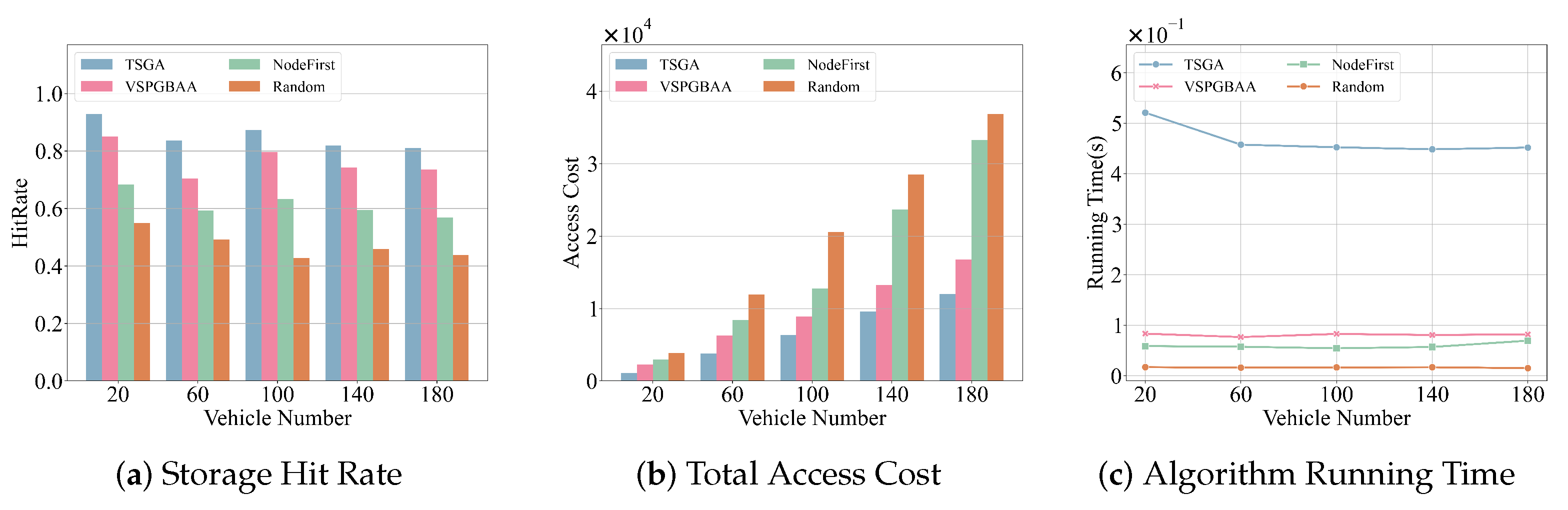
• Impact of the number of vehicles on Intra-Cluster Block Allocation: As shown in Figure 7a–c, the system consists of three clusters, 20 RSUs, and 300 blocks to be allocated, while the total number of vehicles varies from 20 to 180. As illustrated in Figure 7a,b, as the number of vehicles increases, the volume of access requests within the cluster grows, leading to a linear increase in total access cost, while the storage hit rate remains relatively stable. The storage hit rate of VSPGBAA is slightly lower than that of TSGA but significantly outperforms the random and NodeFirst allocation strategies. Specifically, compared to TSGA, VSPGBAA incurs a 32.9% higher access cost, and achieves a 10.6% lower cache hit rate, but compensates with a 6.7× shorter runtime, demonstrating a strong trade-off between efficiency and performance. Meanwhile, as shown in Figure 7c, the runtime of TSGA increases significantly with the number of vehicles, greatly exceeding that of VSPGBAA and NodeFirst. Additionally, compared to NodeFirst, VSPGBAA reduces total access cost by 61.5%, and improves the cache hit rate by 20.2%, but requires 25% more runtime. This highlights VSPGBAA’s ability to handle high-traffic vehicular environments effectively, striking a balance between computational efficiency and system performance.

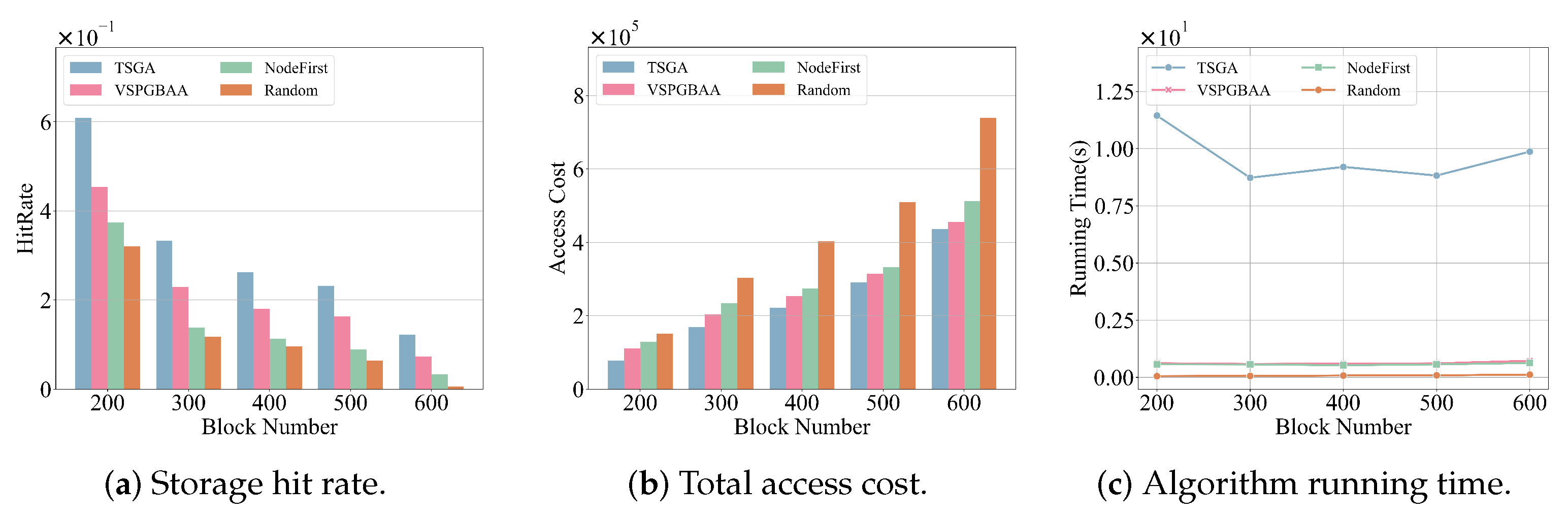
• Impact of the number of blocks on the RSU Clustering Process: As shown in Figure 8a–c, the system consists of three clusters, 60 RSU nodes, and 540 vehicles, while the number of blocks to be allocated varies from 200 to 600. As illustrated in Figure 8a,b, as the number of blocks increases, the storage hit rate declines, while the total access cost gradually rises. This is because the increasing amount of block data reduces the available storage space for redundant copies within the cluster, thereby limiting the effectiveness of access cost optimization. Under different block counts, VSPGBAA maintains a storage hit rate comparable to TSGA and significantly outperforms the random allocation strategy. Specifically, compared to TSGA, VSPGBAA incurs a 14.3% higher access cost, and experiences a 46.5 percentage point lower cache hit rate, but achieves a 14× shorter runtime, demonstrating a strong efficiency advantage. Meanwhile, as shown in Figure 8c, TSGA’s runtime increases significantly with the number of blocks, far exceeding that of VSPGBAA. Additionally, compared to NodeFirst, VSPGBAA reduces total access cost by 11.3%, improves the cache hit rate by 39.1%, but requires 9% more runtime. By effectively balancing storage hit rate, access cost, and computational efficiency, VSPGBAA ensures an optimized storage allocation strategy while significantly enhancing performance.

7. Discussion and Conclusions

In this paper, a blockchain-based RSU cluster collaborative storage scheme was proposed to address the storage scalability issue in blockchain-enabled SIoV. First, we introduced RAPSCA to tackle the RSU clustering problem, where RSUs were grouped into collaborative storage clusters based on block access preference similarity and resource conditions. Then, we designed VSPGBAA, which optimally allocated blocks to RSUs within each cluster by considering both the dwell time of vehicles and their block access probability. The proposed collaborative storage scheme effectively reduced the storage burden on individual RSUs while also optimizing the vehicle access cost introduced by the cluster-based architecture.

Through simulation experiments, the proposed scheme has demonstrated robust optimization performance and high computational efficiency. It is important to acknowledge that the current validation was conducted in a simulation setting. Thus, the lack of real-world IoT device heterogeneity and dynamic network topology variations may limit the direct applicability of the findings. Future work will focus on validating the framework in edge computing environments that incorporate actual vehicular nodes. In addition, the following key research directions are identified for further investigation:

• Dynamic Cluster Adaptation: While the current RSU clustering assumes static networks, practical SIoV requires mechanisms addressing vehicular mobility and load fluctuations. Future research will focus on developing an adaptive cluster reorganization mechanism that dynamically adjusts cluster membership based on real-time monitoring of storage utilization, inter-node latency, and blockchain query patterns.
• Large-Scale Validation in Heterogeneous Edge Environments: The simulation-based evaluation will expand to physical testbeds combining heterogeneous edge devices and intermittent connectivity scenarios. Priority will be given to ultra-dense urban deployments where storage-consensus latency coupling impacts service reliability.
• Storage-Consensus Co-Design: Building upon honest-but-curious assumptions, future research will formalize Byzantine-resilient storage strategies, particularly anti-collusion mechanisms against storage-aware Sybil attacks. This involves co-optimizing Proof-of-Storage parameters with cluster formation criteria to prevent adversarial coalitions without compromising access efficiency.