Experimental and Theoretical Evaluation of Incident Solar Irradiance on Photovoltaic Power Plants Under Real Operating Conditions: Fixed Tilt Angle System vs. Horizontal Single-Axis Tracker
Abstract
:1. Introduction
- (i)
- Sun et al. [25] presented several solar tracking algorithms for a horizontal single-axis tracker. The astronomical solar tracking algorithm obtained more energy than the fixed tilt angle system. In this study, was not used.
- (ii)
- A comparative study of different module mounting systems was the focus of the paper presented by [18]. In this work, 39 locations in the northern hemisphere with latitudes between 6(°) and 60(°) were analysed, as well as different mounting systems, including the horizontal single-axis tracker and the fixed tilt angle system. The horizontal single-axis tracker obtained better results than the fixed tilt angle system (between and ), considering normal tracking mode from sunrise to sunset. Therefore, backtracking mode and static mode were not taken into account.
- (iii)
- Berrian et al. [26] presented a tool that integrates crop modelling with horizontal single-axis trackers. In this tool, the solar tracker is considered to operate all day in normal tracking mode. Therefore, by not considering backtracking mode, the solar trackers shade each other. Furthermore, only horizontal single-axis trackers are analysed, without considering fixed tilt angle systems.
- (iv)
- Ge et al. [27] presented a technical and economic study of photovoltaic systems that used different photovoltaic tracking systems in six regions of different latitudes in China. This study included horizontal single-axis trackers and fixed tilt angle systems. The horizontal single-axis tracker obtained more energy than the fixed tilt angle system. This study did not take into account backtracking mode or .
- (i)
- A theoretical study of the annual, monthly, and daily energy gain of the horizontal single-axis tracker with respect to the fixed tilt angle system, considering various modes of operation of the solar tracker.
- (ii)
- A theoretical study of the hourly incident solar irradiance on the field of a horizontal single-axis tracker and of a fixed tilt angle system, considering various modes of operation of the solar tracker.
- (iii)
- A study under real operating conditions of the annual, monthly, and daily energy gain of the horizontal single-axis tracker with respect to the fixed tilt angle system, considering various modes of operation of the solar tracker.
- (iv)
- A study under real operating conditions of the hourly incident solar irradiance on the field of a horizontal single-axis tracker and a fixed tilt angle system, considering various modes of operation of the solar tracker.
2. Fixed Tilt Angle System vs. Horizontal Single-Axis Tracker
2.1. Technical Considerations for PV Module Mounting Systems
2.1.1. Fixed Tilt Angle System
2.1.2. Horizontal Single-Axis Tracker
2.2. Differences Between PV Module Mounting Systems Under Study
- (i)
- Energy production. The availability of moving parts allows horizontal single-axis trackers to align the field with the sun throughout the day. Therefore, these mounting systems improve energy production compared to fixed tilt angle systems [18]. However, this improvement in production depends on the location of the power plant. Several questions arise with regard to the energy production of horizontal single-axis trackers: Do they obtain energy gain at all times of the year? Do they obtain energy gain throughout the day? These questions will be analysed in this experimental and theoretical study.
- (ii)
- Reliability. Moving parts in a horizontal single-axis tracker complicate the reliability of the system, as they increase the risk of mechanical failure. As fixed tilt angle systems lack moving parts, these systems are very reliable. In contrast, horizontal single-axis trackers are less reliable, as their operating principle is based on the movement of the field. Martin et al. [20] evaluated two power plants equipped with fixed tilt angle systems and one power plant equipped with horizontal single-axis trackers. The study covered several years of operation, concluding that fixed tilt angle systems were more reliable than horizontal single-axis trackers.
- (iii)
- Durability. Fixed tilt angle systems have no mechanical problems, due to the simplicity of their components. In contrast, horizontal single-axis trackers, with moving parts, require more maintenance and have a shorter lifespan.
- (iv)
- Simplicity of installation. Moving parts in a horizontal single-axis tracker complicate installation work. Therefore, fixed tilt angle systems are easier to install than horizontal single-axis trackers.
- (v)
- Maintenance costs. Moving parts in a horizontal single-axis tracker increase maintenance. Therefore, fixed tilt angle systems have lower maintenance costs than horizontal single-axis trackers. There is no standardised method for determining maintenance costs [36]. However, many authors use the report by the National Renewable Energy Laboratory [37] to calculate them; the criteria followed in this report, to calculate the annual maintenance cost, are as follows: (i) of the initial cost for fixed tilt angle systems, and (ii) of the initial cost for horizontal single-axis trackers. Other authors consider that the maintenance costs of horizontal single-axis trackers are double those considered for fixed tilt angle systems [37]. If the maintenance required is minimal, as in the case of fixed tilt angle systems, plants installed in remote locations benefit greatly, as the number of regular checks is reduced.
- (vi)
- Initial costs. The absence of moving parts also influences initial costs, as it facilitates the installation of the mounting system. Fixed tilt angle systems have lower initial costs than horizontal single-axis trackers. Horizontal single-axis trackers are more expensive than fixed tilt angle systems [38]. This feature is a determining factor in smaller-scale installations or projects with limited budgets.
- (vii)
- Vulnerability to extreme environmental factors. According to a report by the United Nations Intergovernmental Panel on Climate Change (), climate change will notably increase wind loads and extreme phenomena [39]. The operational characteristics of the module mounting system make it susceptible to extreme environmental factors (strong winds or heavy snowfall) causing significant damage to power plants [19]. Therefore, horizontal single-axis trackers are more susceptible to this type of damage.
- (viii)
- Limitation of geographical location. It has been demonstrated that the efficiency of fixed tilt angle systems decreases considerably in locations far from the equator [18], as their capacity to capture solar resources is not adequate throughout the year. In contrast, horizontal single-axis trackers are better suited to different latitudes [18], expanding the range of suitable geographical locations.
- (ix)
- Land occupation. A report by Mordon Intelligence [38] indicates that the density of modules per square metre using horizontal single-axis trackers is between and higher than the use of fixed tilt angle systems.
- (x)
- Budgetary considerations. When making a decision about the choice of module mounting system, the initial investment must be weighed against the expected return on investment. Although horizontal single-axis trackers offer higher performance, they also offer higher initial costs. In contrast, fixed tilt angle systems offer the opposite. Therefore, it may happen that the higher initial cost of a project makes it unviable.
- (xi)
- Environmental impact. From the point of view of environmental impact, horizontal single-axis trackers offer greater environmental benefits, as they generate more energy [18].
3. Methodology
3.1. Choice of Solar Irradiance Estimation Model
- (i)
- Determination of .
- (ii)
- Determination of the .
- (iii)
- Determination of the .
- (iv)
- Determination of .
3.2. Theoretical Study
- (i)
- Determination of . As this was a theoretical study, the Hottel model [52] was used to determine the . The Hottel model is a model of clear skies. Hottel proposes Equation (18) to determine the beam horizontal solar irradiance in clear atmospheres [52]:where is the extraterrestrial solar irradiance measured in the plane normal to the Sun’s rays (W/m2), and where is the atmospheric transmittance for beam solar irradiance (); can be calculated using the following equation [52]:where , , and k are empirical constants. If the standard atmosphere has 23 (km) of visibility, they can be calculated using the following equations:where A is the height above sea level of the location (km). For altitudes lower than (km), the empirical constants (, , k) have to be multiplied by their corresponding correction factors (, , ). These correction factors were tabulated for four different types of climate [52].
- (ii)
- Determination of . As this was a theoretical study, the Liu–Jordan model [53] was used to determine the . The Liu–Jordan model is a model of clear skies. Liu and Jordan proposed Equation (23), to determine the diffuse horizontal solar irradiance in clear atmospheres [53]:where is the extraterrestrial solar irradiance measured in the plane normal to the Sun’s rays (W/m2), and where is the atmospheric transmittance for diffuse solar irradiance (); can be calculated using the following equation [53]:
3.3. Study Under Real Operating Conditions
- (i)
- Location of the experimental setup. In order to be able to compare both module mounting systems, it was necessary that the installation location was the same. The experimental setup was installed at the Department of Electrical Engineering of the University of Oviedo (Gijón, Spain) (latitude N, longitude W, elevation 28 (m) above sea level). Gijón is characterised by a temperate oceanic climate typical of Spain’s Atlantic coast, with cool summers and wet and mostly mild winters. The code assigned to Gijón under the Köppen climate classification is .
- (ii)
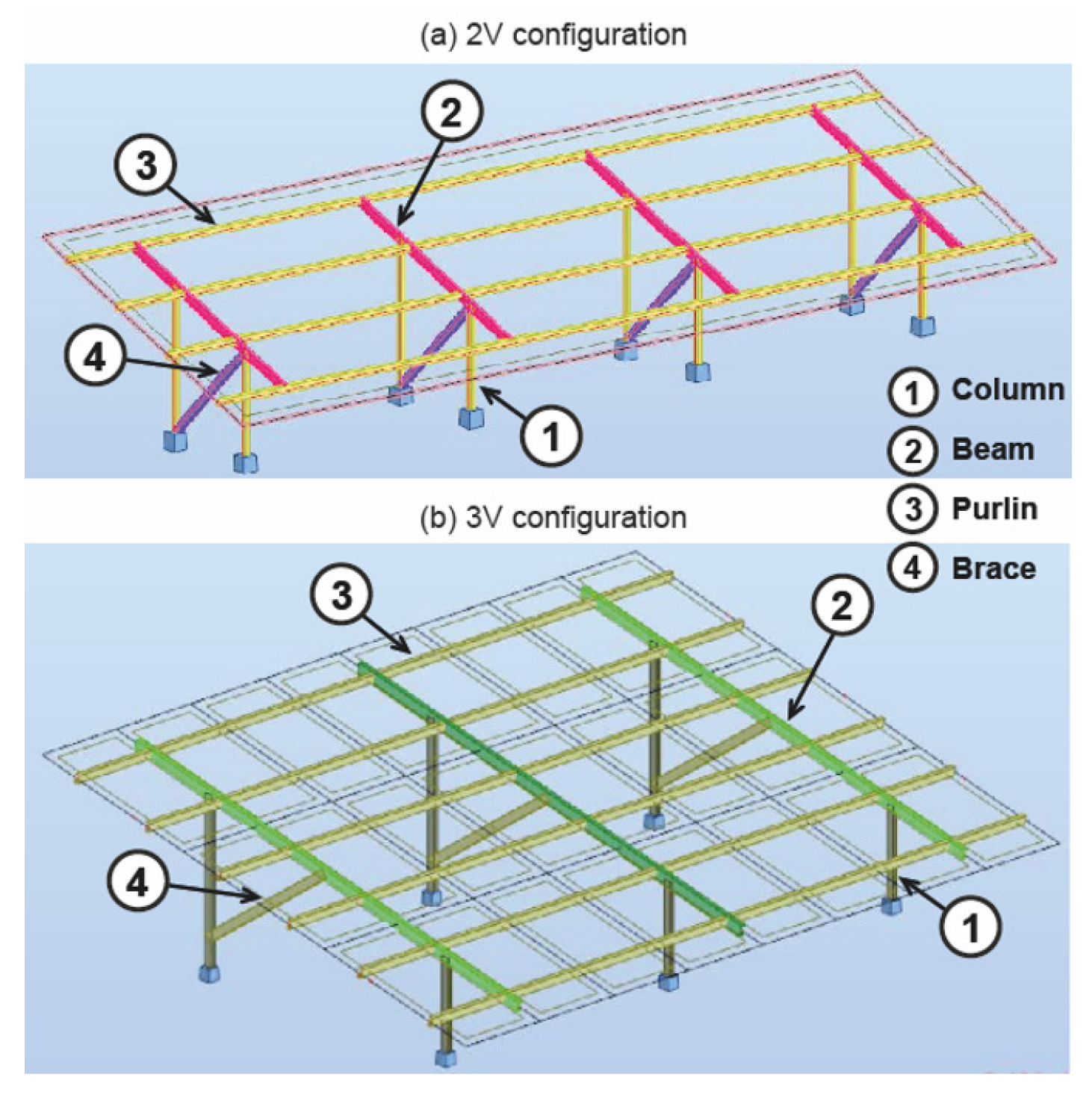
- The ground-mounted power plant. This type of power plant is composed of fixed tilt angle systems (see Figure 5a). The following considerations were taken into account in the design of this plant: (1) the configuration was ; (2) the fixed tilt angle system was south-facing; (3) the field had a tilt angle of (°); this angle is the optimum angle according to the Jacobson equation [18]; (4) the longitudinal spacing for maintenance was 4 (m); (5) the transversal installation distance was (m); (6) the transverse and longitudinal installation distance between the modules was (m), due to the clamps; (7) the module used was the CanadianSolar CS3U-355PB-FG, 355 (Wp).
- (iii)
- The single-axis tracking power plant. This type of power plant is composed of horizontal single-axis trackers (see Figure 5b). The following considerations were taken into account in the design of this plant: (1) the configuration was ; (2) the pitch was (m); (3) the limit of movement was (°); (4) the transversal installation distance was (m); (5) the transverse and longitudinal installation distance between the modules was (m), due to the clamps; (6) the module used was the CanadianSolar CS3U-355PB-FG, 355 (Wp).
- (iv)
- Measuring instruments (see Figure 5c). The measurement system consisted of three pyranometers. The experimental measurements taken were global horizontal solar irradiance (Pyranometer 1), diffuse horizontal solar irradiance (Pyranometer 2), and reflected solar irradiance (Pyranometer 3). Its characteristics were as follows: (a) the same type of pyranometer was used; (b) the pyranometer used was the model manufactured by Kipp & Zonen; (c) the accuracy class was Class A (secondary standard); (d) the pyranometer’s measurement range was 0–4000 (W/m2); (e) the expected daily accuracy was less than . Several sources of error can be associated with any experimental process, such as calibration, precision, methodology of experiments, etc. [54]. These sources of error affect the experimental results [54]. In this study, solar irradiances were measured directly; therefore, the uncertainty of the measurements was defined by the accuracy of the pyranometers [55]. As the uncertainty of the pyranometers was less than , the experimental data can be considered to be highly accurate [55].
- (v)
- Duration of the test campaign. The test campaign was carried out in 2022. The pyranometers measured solar irradiance every second, calculating the average every minute. Data were recorded for one year. During the data collection campaign, no incidents occurred in the horizontal single-axis tracker. Therefore, in our study the reliability of the horizontal single-axis solar tracker was high. It is also true that the wind loads supported by the horizontal single-axis tracker were low. The initial cost of the horizontal single-axis tracker prototype was approximately times higher than the fixed tilt angle system prototype.
3.4. Assessment Indicators for the Comparison of Studies
3.4.1. Annual Energy Gain
3.4.2. Monthly Energy Gain
3.4.3. Daily Energy Gain
4. Results and Discussion
4.1. Module Mounting Systems Under Study
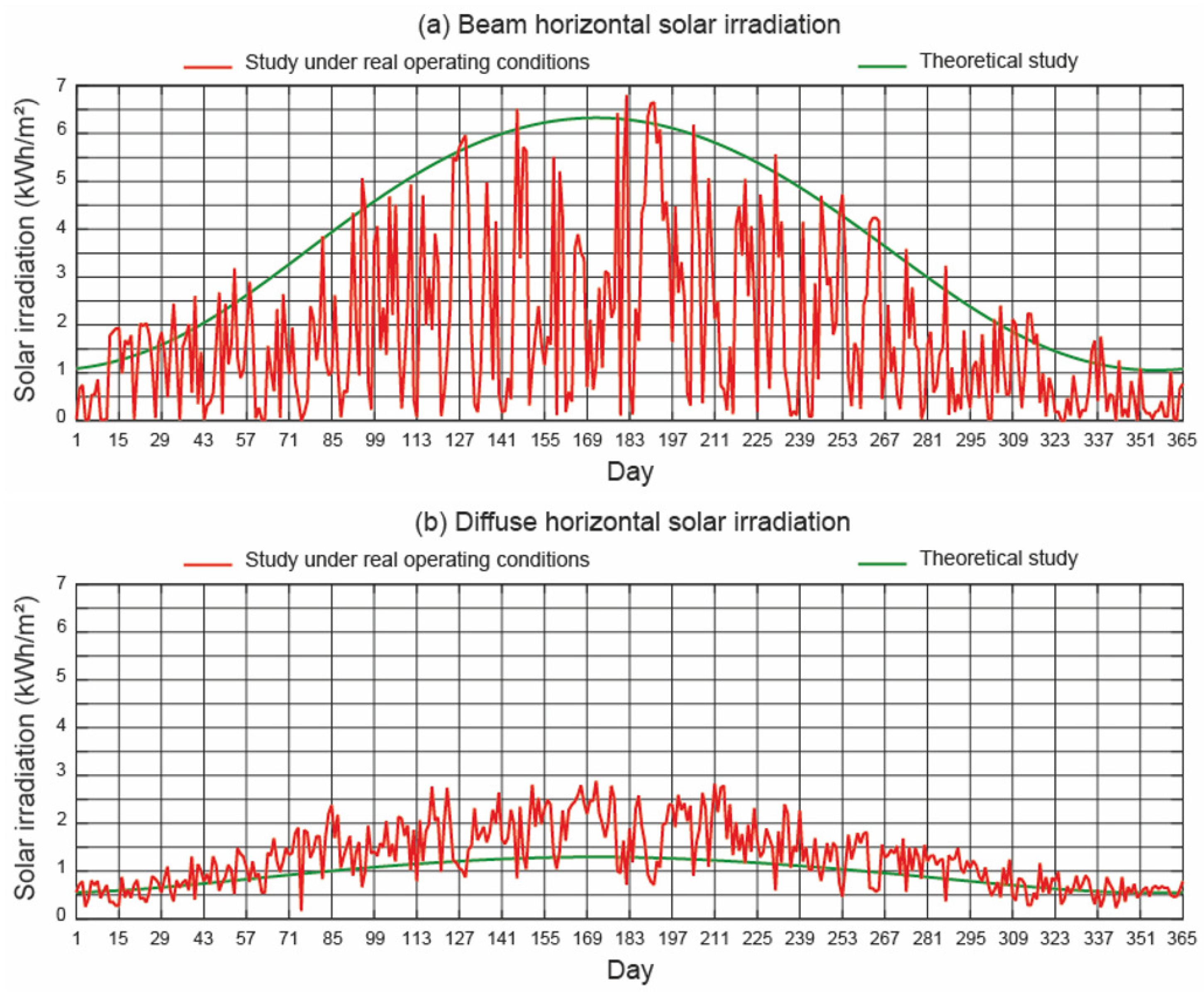
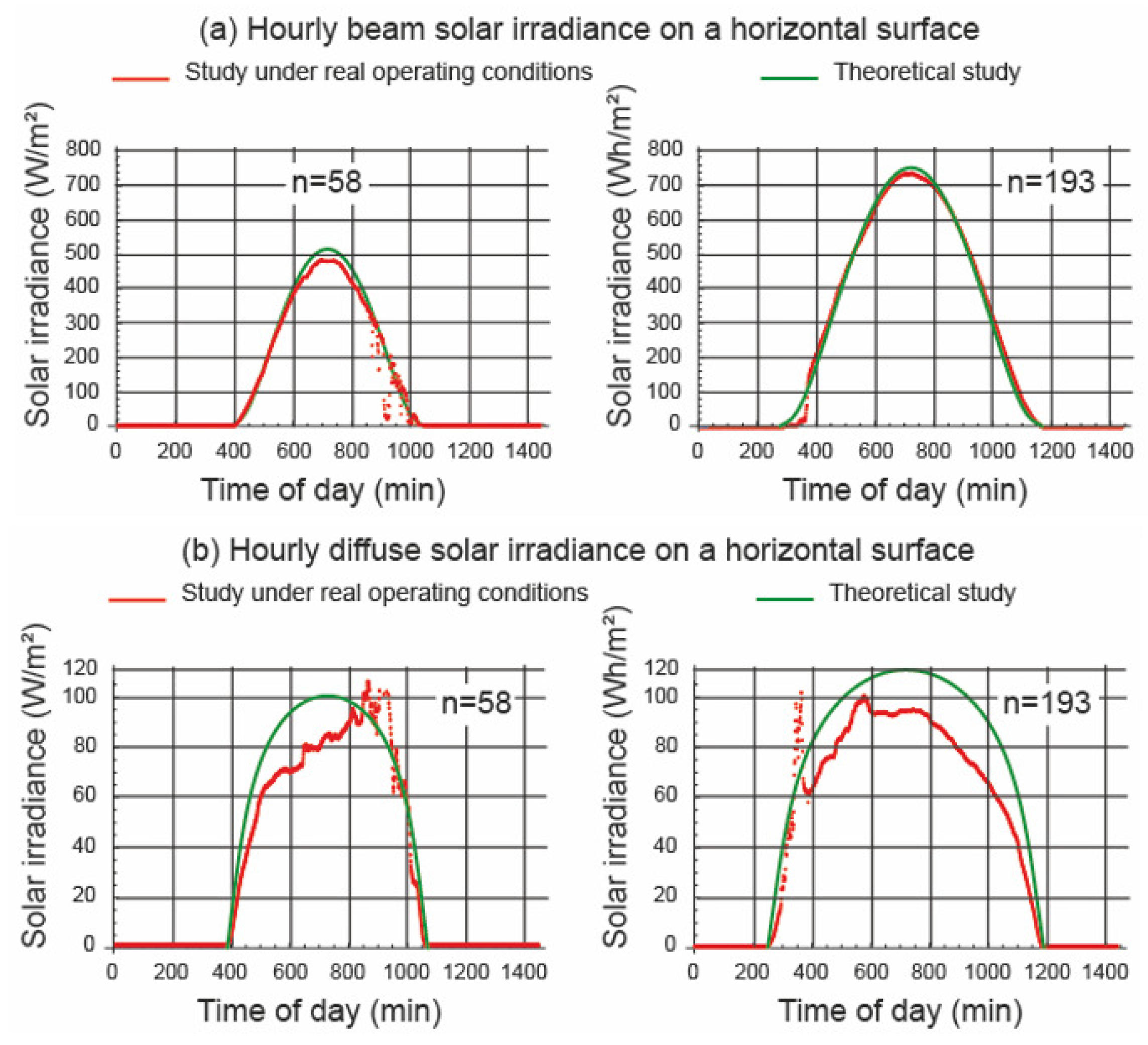
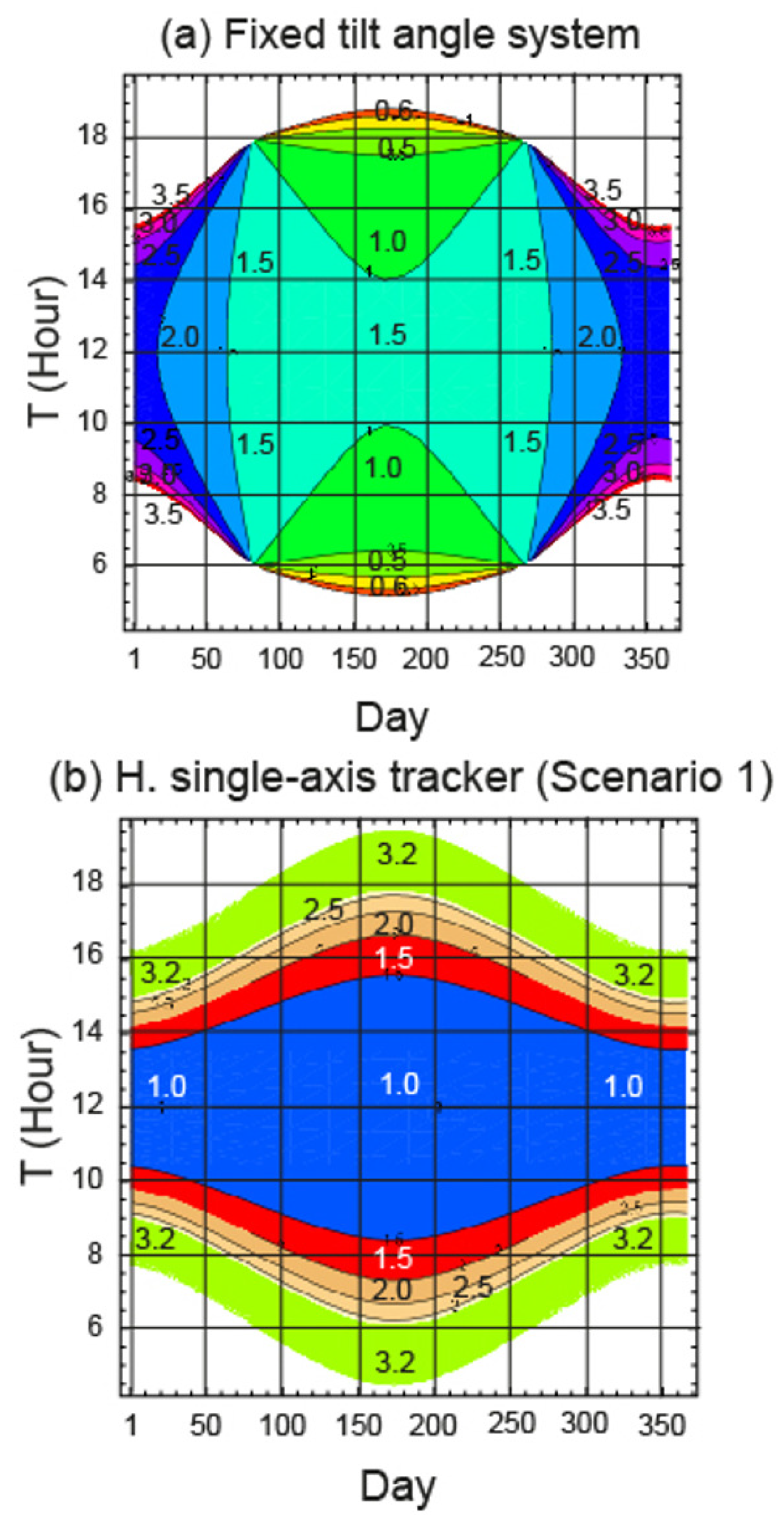
4.2. Solar Irradiation Data
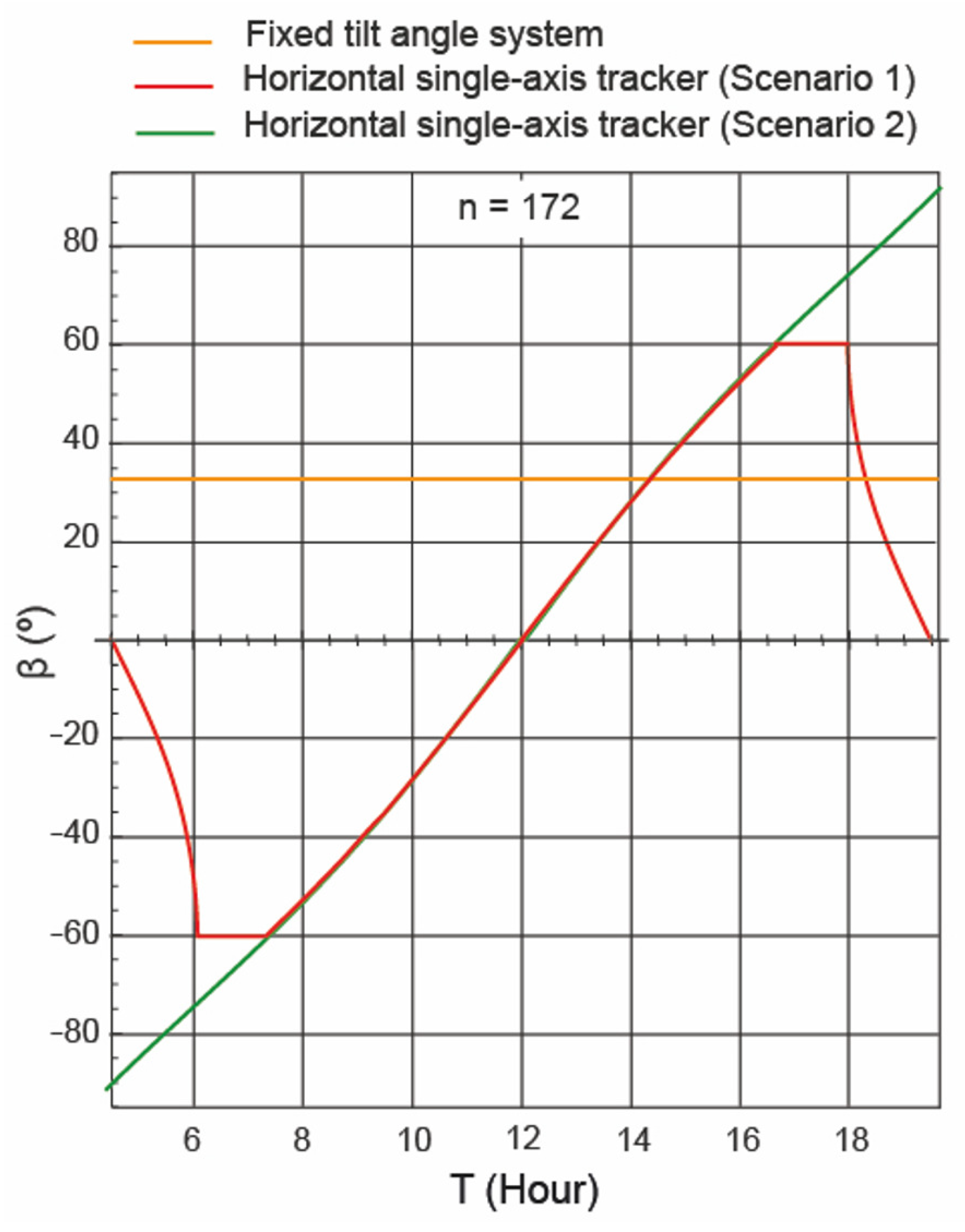
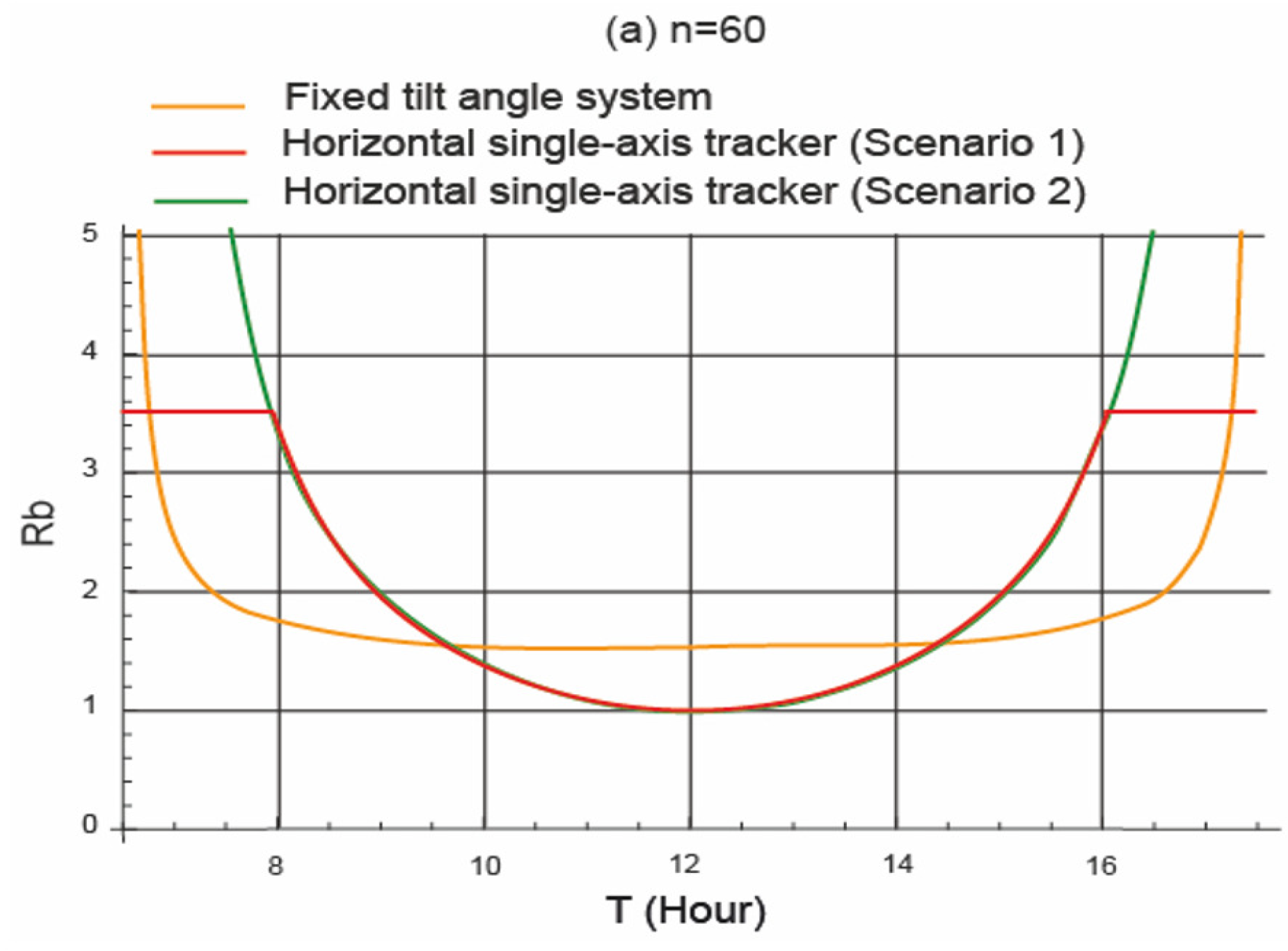
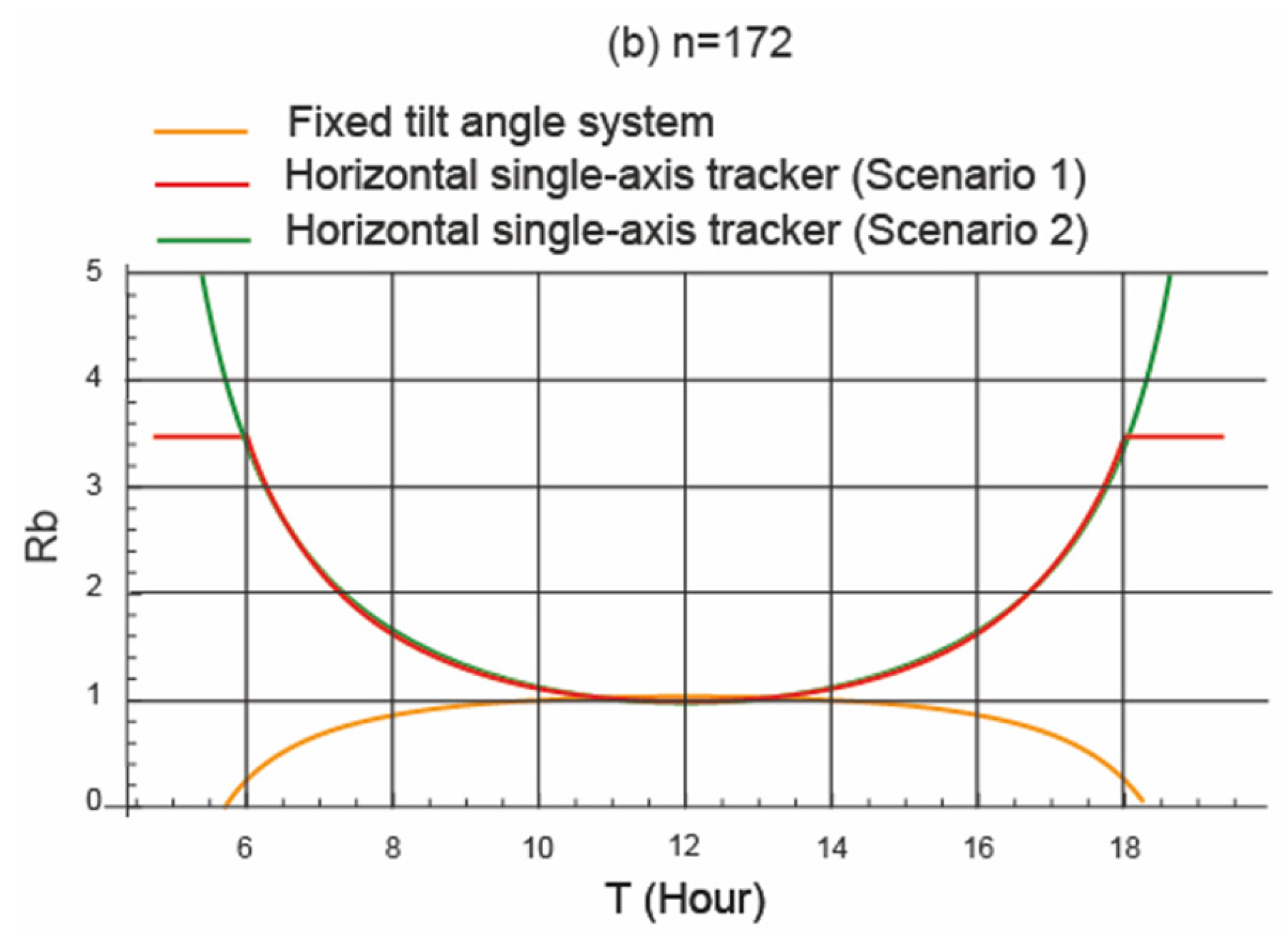
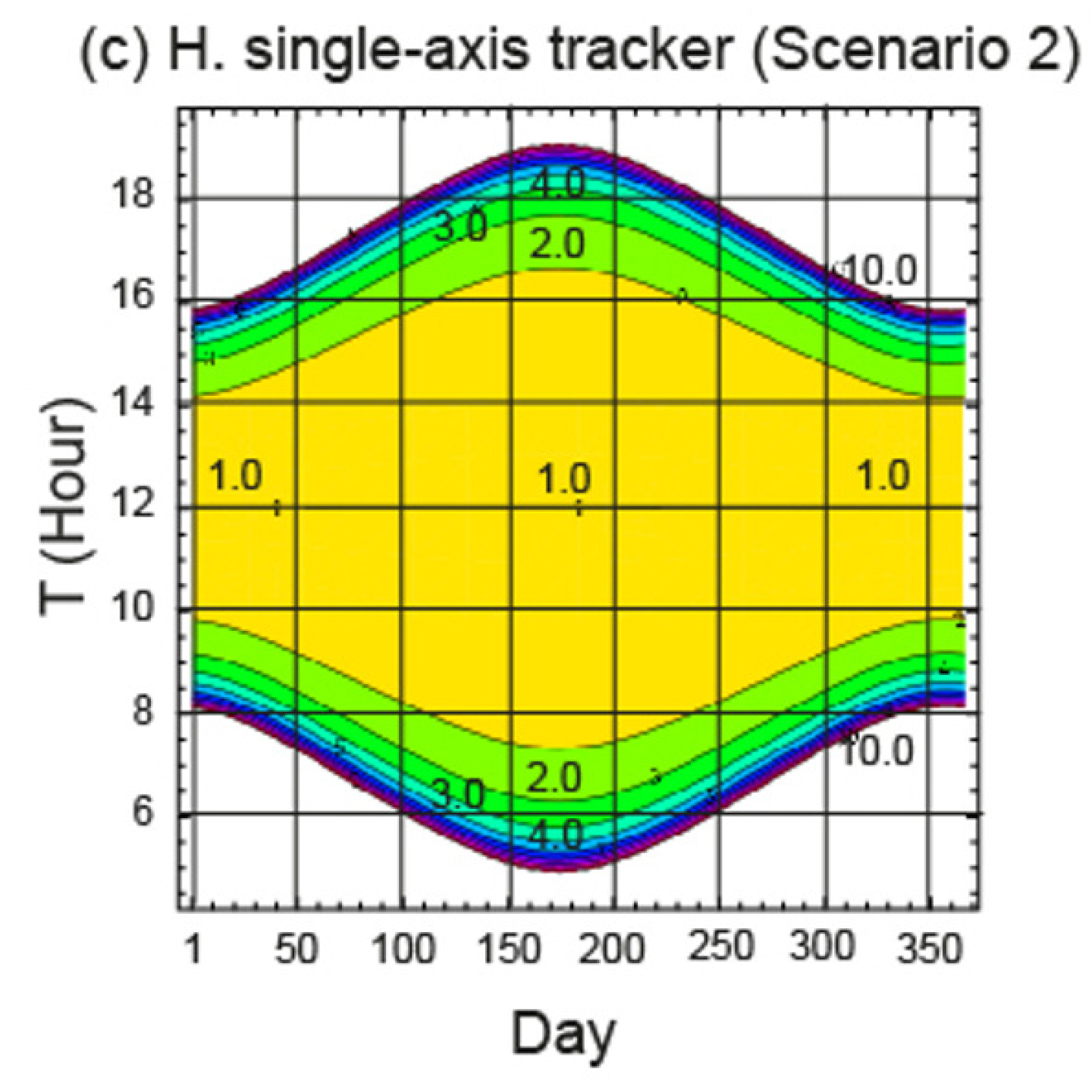
4.3. Analysis of the Angles of Incident Solar Irradiance on the PV Field
4.4. Annual Energy Gain
- (i)
- In Scenario 1, an of approximately was obtained in the theoretical study. This result is in accordance with the results obtained by [56]. In the study under real operating conditions, this parameter decreased to approximately .
- (ii)
- In Scenario 2, an of approximately was obtained in the theoretical study. This result is consistent with the results obtained by [18]. In the study under real operating conditions, this parameter decreased to approximately .
- (iii)
- The best results were obtained in Scenario 2, both in the theoretical study and in the study under real operating conditions. However, Scenario 1 is the one implemented in a power plant. The biggest difference was obtained in the theoretical study, of approximately . In contrast, in the study under real operating conditions, this difference was approximately .
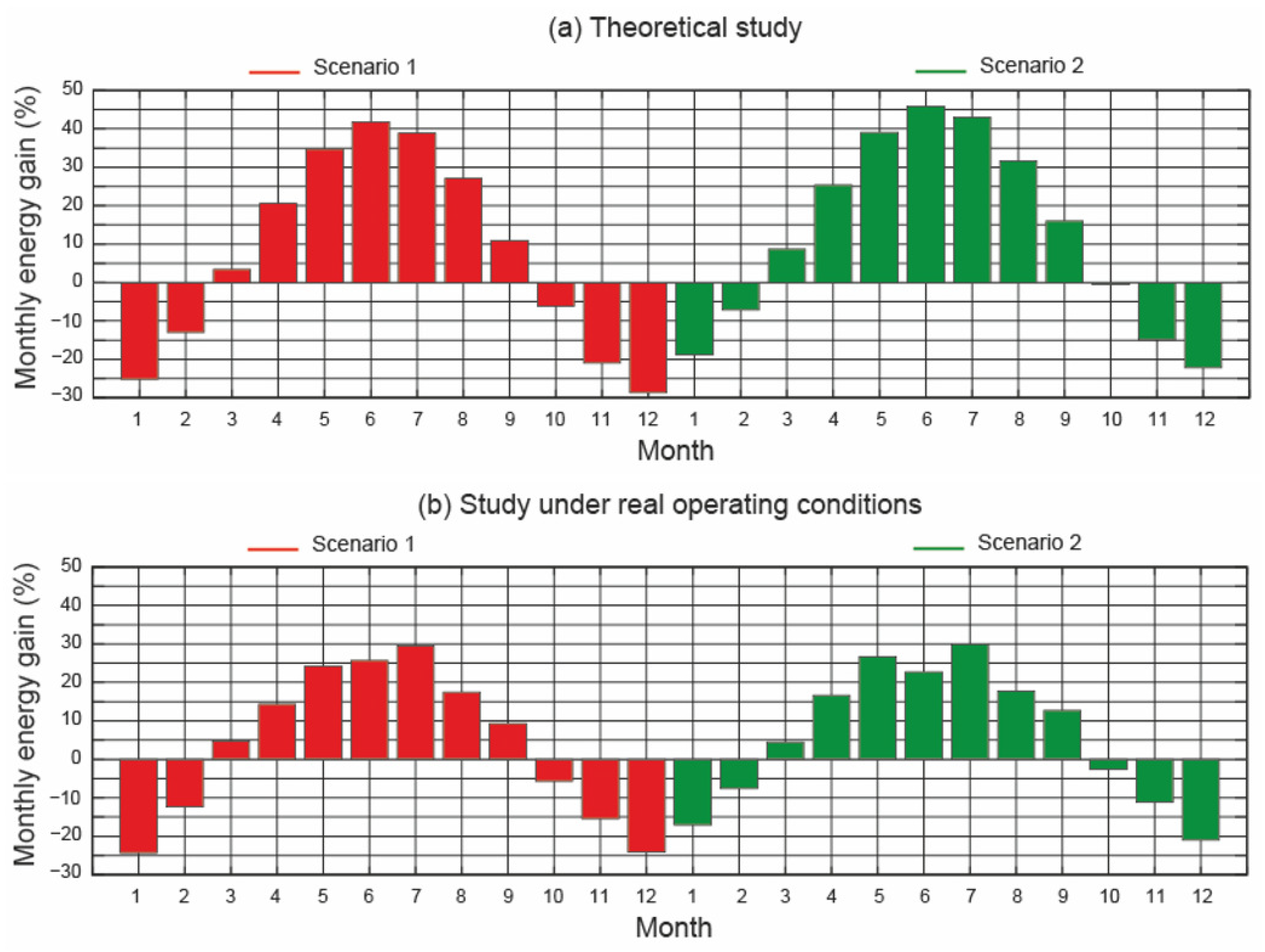
4.5. Monthly Energy Gain
- (i)
- In the months of October, November, December, January, and February, the fixed tilt angle system performed better than the horizontal single-axis tracker, both in the theoretical study and in the study under real operating conditions. In the other months, the horizontal single-axis tracker performed better. Therefore, during the months of greatest incident solar irradiance, the horizontal single-axis tracker performed better. Figure 10, which shows the variation of , explains this trend.
- (ii)
- In the theoretical study, the highest value of was in June and the worst was in December. These results were true in both the scenarios under study. In Scenario 1, these results were approximately and , respectively, and in Scenario 2 they were approximately and , respectively.
- (iii)
- In the study under real operating conditions, the best month was July and the worst month was December. This was true in both the scenarios under study. In Scenario 1, these results were approximately and , respectively, and in Scenario 2, approximately and , respectively.
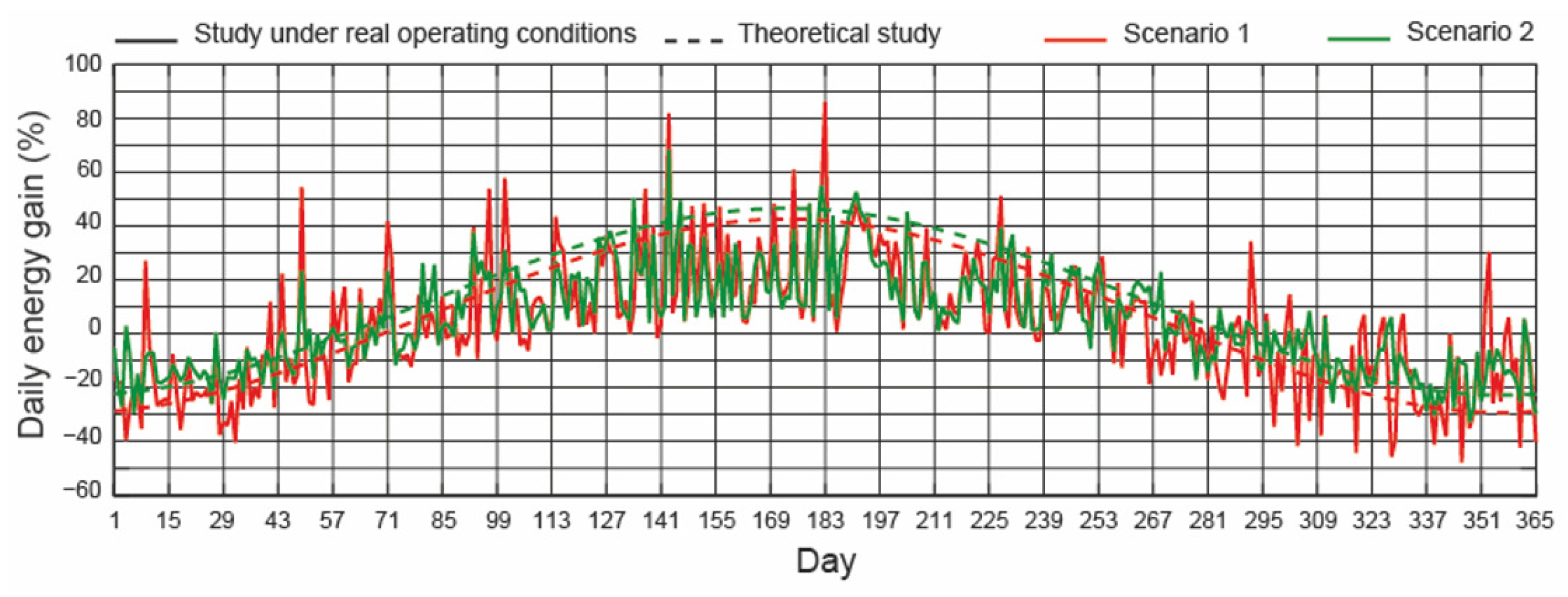
4.6. Daily Energy Gain
- (i)
- In Scenario 1, and considering the theoretical study, on days 1 to 69 and 278 to 365 the fixed tilt angle system performed better than the horizontal single-axis tracker. On the other days, the opposite happened. When Scenario 2 was considered, there was variation on these days: that is to say, on days 1 to 59 and 288 to 365 the fixed tilt angle system performed better than the horizontal single-axis tracker.
- (ii)
- Considering the theoretical study, in Scenario 1 the highest and lowest values were and , respectively, and in Scenario 2 these values were and , respectively.
- (iii)
- Considering the study under real operating conditions, in Scenario 1 the highest and lowest values were and , respectively, and in Scenario 2 these values were and , respectively.
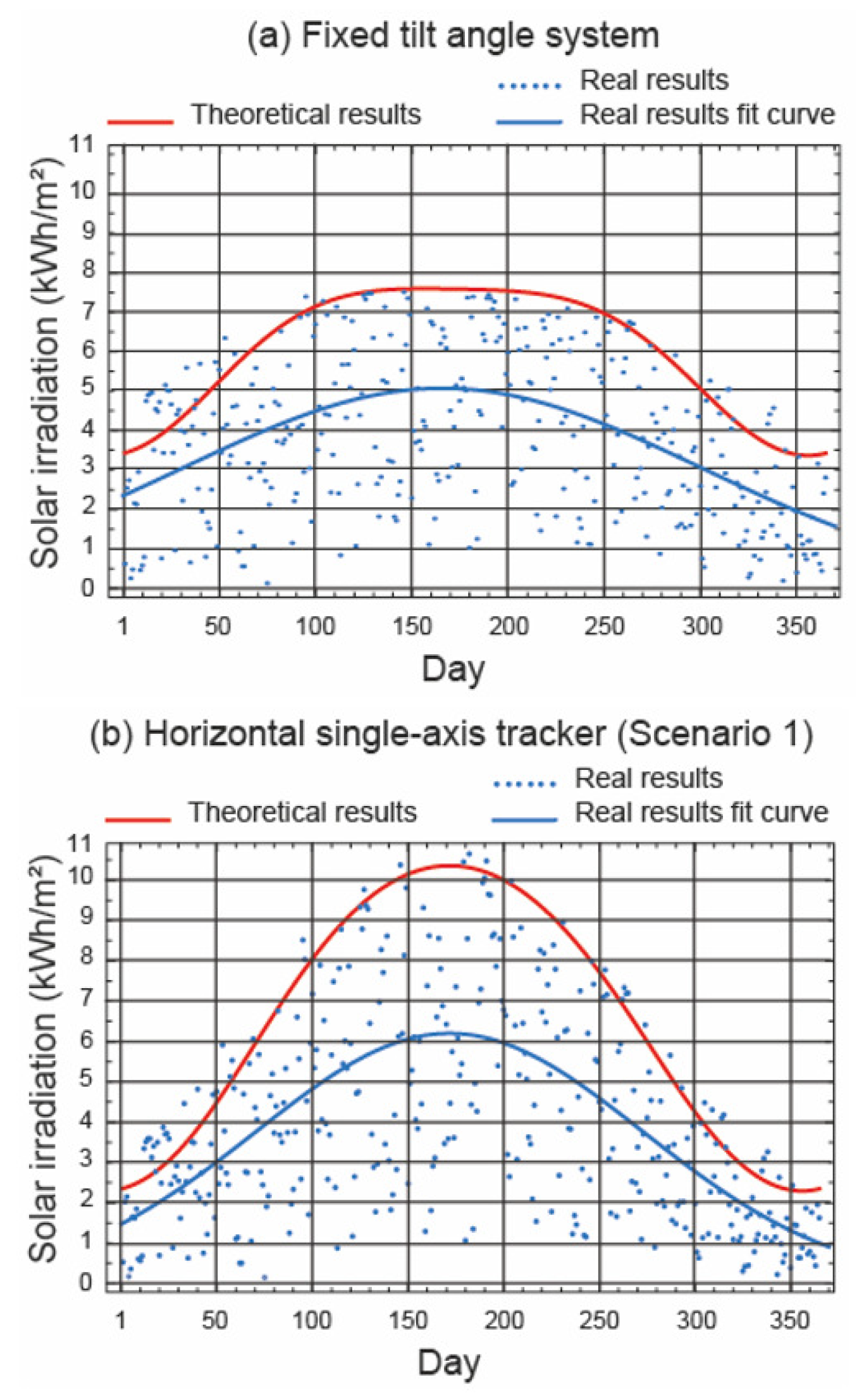
4.7. Regression Analysis Based on the Results of the Experiment
- (i)
- Except in the fixed tilt angle system, the adjustment equations of the other two mounting systems provided very similar results.
- (ii)
- The theoretical study obtained better results than the study under real operating conditions in all three mounting systems.
5. Conclusions
- (i)
- The obtained was approximately and in the theoretical study and in the real study, respectively, in Scenario 1, and approximately and , respectively, in Scenario 2. Scenario 2 obtained higher results than Scenario 1 in all the assessment indicators. But it must be considered that Scenario 1 is the real mode of operation.
- (ii)
- Considering the theoretical study and Scenario 1, the highest value of was in June () and the lowest was in December (). When the study was considered under real operating conditions, the highest result was in July () and the lowest was in December ().
- (iii)
- In scenario 1, on days 70 to 277 the horizontal single-axis tracker performed better. On the other days, the opposite occurred. Taking into account the theoretical study, the highest and lowest values were and , respectively. When the study was considered under real operating conditions, the highest and lowest values were and , respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Annual energy gain (%) | |
| A | Height above sea level of the location (km) |
| , | Empirical constants of the Hottel model (dimensionless) |
| Daily energy gain (%) | |
| Monthly energy gain (%) | |
| Pitch (m) | |
| Klucher coefficient () | |
| Global horizontal solar irradiation (Wh/m2) | |
| Total solar irradiation on a tilted surface (Wh/m2) | |
| Beam horizontal solar irradiance (W/m2) | |
| Diffuse horizontal solar irradiance (W/m2) | |
| Global horizontal solar irradiance (W/m2) | |
| Total solar irradiance on a tilted surface (W/m2) | |
| Normal extraterrestrial solar irradiance (W/m2) | |
| k | Empirical constant of the Hottel model (dimensionless) |
| n | Ordinal of the day (day) |
| Variable geometric factor (dimensionless) | |
| T | Solar time (h) |
| Sunrise solar time (h) | |
| Sunset solar time (h) | |
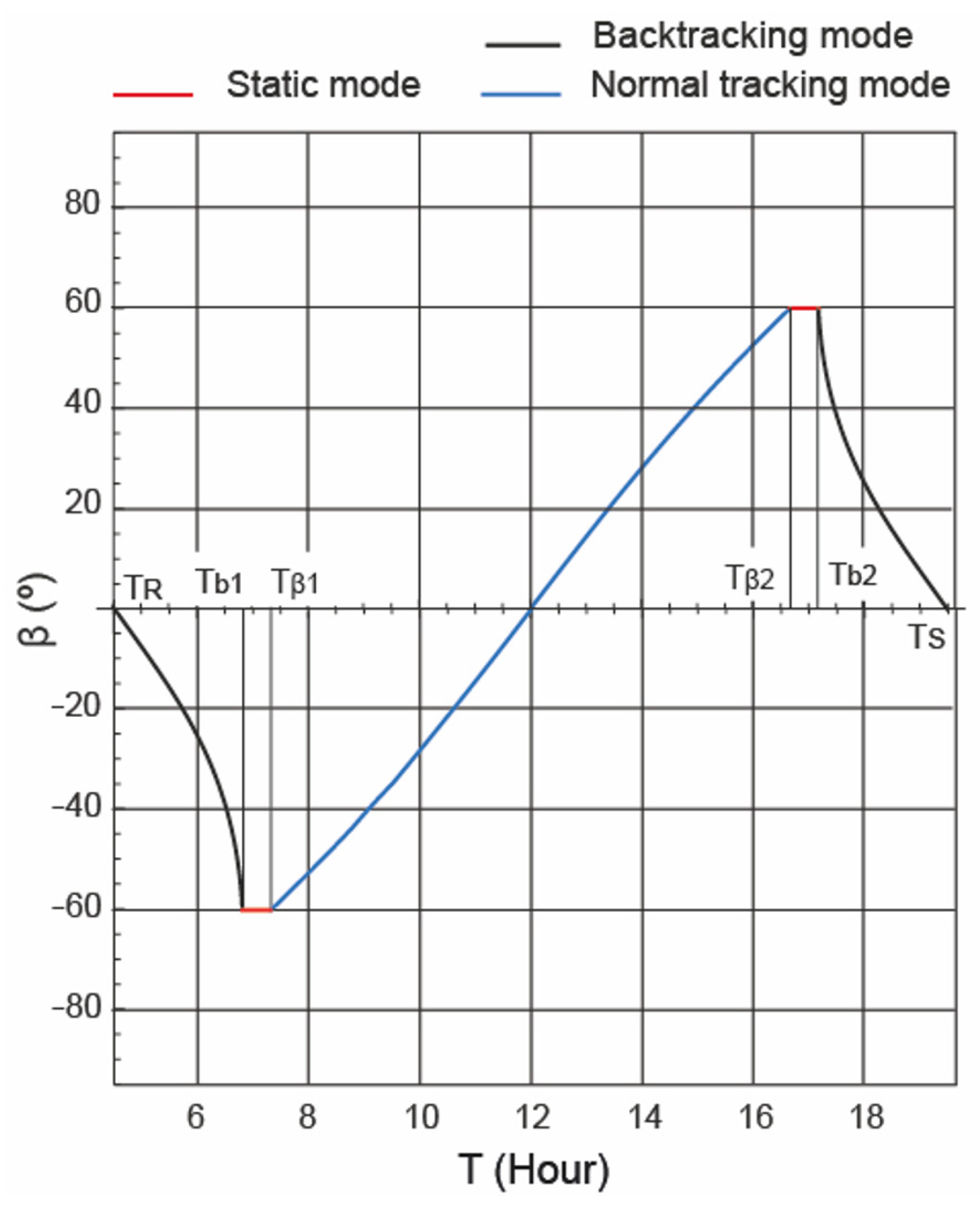
| End of the backtracking mode (h) | |
| Start of the backtracking mode (h) | |
| Start of the normal tracking mode (h) | |
| End of the normal tracking mode (h) | |
| Tilt angle of photovoltaic module (°) | |
| Backtracking angle (°) |
| Limited range of motion angle (°) | |
| Azimuth angle of photovoltaic module (°) | |
| Azimuth of the Sun (°) | |
| Solar declination (°) | |
| Incidence angle (°) | |
| Transversal angle (°) | |
| Zenith angle of the Sun (°) | |
| Latitude angle (°) | |
| Ground reflectance (dimensionless) | |
| Atmospheric transmittance for beam solar irradiance (dimensionless) | |
| Atmospheric transmittance for diffuse solar irradiance (dimensionless) | |
| Hour angle (°) |
Appendix A. Flowchart of the Mathematica Codes Used

References
- IEA. Electricity 2024. Available online: https://iea.blob.core.windows.net/assets/18f3ed24-4b26-4c83-a3d2-8a1be51c8cc8/Electricity2024-Analysisandforecastto2026.pdf (accessed on 20 February 2025).
- IEA. Global Energy and Climate Model 2024. Available online: https://www.iea.org/reports/global-energy-and-climate-model (accessed on 20 February 2025).
- European Union. European Green Deal. 2019. Available online: https://commission.europa.eu/strategy-and-policy/priorities-2019-2024/european-green-deal/delivering-european-green-deal_en (accessed on 20 February 2025).
- European Union. Directive 2018/2001/EC, on the Promotion of the Use of Energy from Renewable Sources; European Union: Brussels, Belgium, 2018. [Google Scholar]
- Statista. Available online: https://www.statista.com/statistics/482733/energy-consumption-worldwide-sector (accessed on 20 February 2025).
- IEA. World Energy Outlook 2023. Available online: https://www.iea.org/reports/world-energy-outlook-2023?language=es (accessed on 20 February 2025).
- Aslam Bhatti, U.; Aslam Bhatti, M.; Tang, H.; Syam, M.S.; Mahrous Awwad, E.; Sharaf, M.; Yasin Ghadi, Y. Global production patterns: Understanding the relationship between greenhouse gas emissions, agriculture greening and climate variability. Environ. Res. 2024, 245, 118049. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Wu, W.; Li, C.; Lu, G.; Ye, D.; Ma, C.; Ren, L.; Li, G. Ecological and environmental effects of global photovoltaic power plants: A meta-analysis. J. Environ. Manag. 2025, 373, 123785. [Google Scholar] [CrossRef] [PubMed]
- Ameur, A.; Berrada, A.; Loudiyi, K.; Aggour, M. Analysis of renewable energy integration into the transmission network. Electr. J. 2019, 32, 106676. [Google Scholar] [CrossRef]
- Weber, P.; Woerman, M. Intermittency or Uncertainty? Impacts of Renewable Energy in Electricity Markets. J. Assoc. Environ. Resour. Econ. 2024, 11, 1351–1385. [Google Scholar] [CrossRef]
- Vindel, J.M.; Trincado, E. Discontinuity in the production rate due to the solar resource intermittency. J. Clean. Prod. 2021, 321, 128976. [Google Scholar] [CrossRef]
- Zhu, H.; Hou, R.; Jiang, T.; Lv, Q. Research on energy storage capacity configuration for PV power plants using uncertainty analysis and its applications. Glob. Energy Interconnect. 2021, 4, 608–618. [Google Scholar] [CrossRef]
- Laugs, G.A.H.; Benders, R.M.J.; Moll, H.C. Balancing responsibilities: Effects of growth of variable renewable energy, storage, and undue grid interaction. Energy Policy 2020, 139, 111203. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M.D. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Qiao, J.; Meng, X.; Zheng, W.; Huang, P.; Xu, T.; Xu, Y. Optimization configuration method of energy storage considering photovoltaic power consumption and source-load uncertainty. IEEE Access 2025, 13, 9401–9412. [Google Scholar] [CrossRef]
- Bin Wali, S.; Hannan, M.A.; Reza, M.S.; Jern Ker, P.; Begum, R.A.; Abd Rahman, M.S.; Mansor, M. Battery storage systems integrated renewable energy sources: A biblio metric analysis towards future directions. J. Energy Storage 2021, 35, 102296. [Google Scholar] [CrossRef]
- Marocco, P.; Ferrero, D.; Gandiglio, M.; Ortiz, M.M.; Sundseth, K.; Lanzini, A.; Santarelli, M. A study of the techno-economic feasibility of H2-based energy storage systems in remote areas. Energy Convers. Manag. 2020, 211, 112768. [Google Scholar] [CrossRef]
- Barbón, A.; Fortuny Ayuso, P.; Bayón, L.; Silva, C.A. A comparative study between racking systems for photovoltaic power systems. Renew. Energy 2021, 180, 424–437. [Google Scholar] [CrossRef]
- Gonvarri Solar Steel. Available online: https://www.gsolarsteel.com/ (accessed on 20 February 2025).
- Martín-Martínez, S.; Cañas-Carretón, M.; Honrubia-Escribano, A.; Gómez-Lázaro, E. Performance evaluation of large solar photovoltaic power plants in Spain. Energy Convers. Manag. 2019, 183, 515–528. [Google Scholar] [CrossRef]
- Future Market Insights, Solar Trackers Market: Solar Trackers Market Analysis by Single-Axis and Dual-Axis for 2023 to 2033. Available online: https://www.futuremarketinsights.com/reports/solar-trackers-market#:~:text=The%20global%20solar%20trackers%20market,to%20\protect\@normalcr\relaxrenewable%20energy%20sources%20grows (accessed on 20 February 2025).
- Mordor Intelligence. Available online: https://www.mordorintelligence.com/industry-reports/solar-tracker-market (accessed on 20 February 2025).
- Barbón, A.; Carreira-Fontao, V.; Bayón, L.; Silva, C.A. Optimal design and cost analysis of single-axis tracking photovoltaic power plants. Renew. Energy 2023, 211, 626–646. [Google Scholar] [CrossRef]
- Barbón, A.; Martínez-Suárez, J.; Bayón, L.; Bayón-Cueli, C. Photovoltaic power plants with horizontal single-axis trackers: Influence of the movement limit on incident solar irradiance. Appl. Sci. 2025, 15, 1175. [Google Scholar] [CrossRef]
- Sun, L.; Bai, J.; Kumar Pachauri, R.; Wang, S. A horizontal single-axis tracking bracket with an adjustable tilt angle and its adaptive real-time tracking system for bifacial PV modules. Renew. Energy 2024, 221, 119762. [Google Scholar] [CrossRef]
- Berrian, D.; Chhapia, G.; Linder, J. Performance of land productivity with single-axis trackers and shade-intolerant crops in agrivoltaic systems. Appl. Energy 2025, 384, 125471. [Google Scholar] [CrossRef]
- Ge, Z.; Xu, Z.; Li, J.; Xu, J.; Xie, J.; Yang, F. Technical-economic evaluation of various photovoltaic tracking systems considering carbon emission trading. Sol. Energy 2024, 271, 112451. [Google Scholar] [CrossRef]
- Anderson, K.S.; Jensen, A.R. Shaded fraction and backtracking in single-axis trackers on rolling terrain. J. Renew. Sustain. Energy 2024, 16, 023504. [Google Scholar] [CrossRef]
- Huang, B.; Huang, J.; Xing, K.; Liao, L.; Xie, P.; Xiao, M.; Zhao, W. Development of a solar-tracking system for horizontal single-axis PV arrays using spatial projection analysis. Energies 2023, 16, 4008. [Google Scholar] [CrossRef]
- Alves Veríssimo, P.H.; Antunes Campos, R.; Vivian Guarnieri, M.; Alves Veríssimo, J.P.; do Nascimento, L.R.; Rüther, R. Area and LCOE considerations in utility-scale, single-axis tracking PV power plant topology optimization. Sol. Energy 2020, 211, 433–445. [Google Scholar] [CrossRef]
- Keiner, D.; Walter, L.; ElSayed, M.; Breyer, C. Impact of backtracking strategies on techno-economics of horizontal single-axis tracking solar photovoltaic power plants. Sol. Energy 2024, 267, 112228. [Google Scholar] [CrossRef]
- Ledesma, J.R.; Lorenzo, E.; Narvarte, L. Single-axis tracking and bifacial gain on sloping terrain. Prog. Photovoltaics Res. Appl. 2024, 33, 309–325. [Google Scholar] [CrossRef]
- Chinchilla, M.; Santos-Martín, D.; Carpintero-Rentería, M.; Lemon, S. Worldwide annual optimum tilt angle model for solar collectors and photovoltaic systems in the absence of site meteorological data. Appl. Energy 2021, 281, 116056. [Google Scholar] [CrossRef]
- Nicolás-Martín, C.; Santos-Martín, D.; Chinchilla-Sánchez, M.; Lemon, S. A global annual optimum tilt angle model for photovoltaic generation to use in the absence of local meteorological data. Renew. Energy 2020, 161, 722–735. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Du, Y. Considerations of photovoltaic system structure design for effective lightning protection. IEEE Trans. Electromagn. Compat. 2020, 62, 1333–1341. [Google Scholar] [CrossRef]
- Talavera, D.L.; Muñoz-Cerón, E.; Ferrer-Rodríguez, J.P.; Pérez-Higueras, P.J. Assessment of cost-competitiveness and profitability of fixed and tracking photovoltaic systems: The case of five specific sites. Renew. Energy 2019, 134, 902–913. [Google Scholar] [CrossRef]
- Abdulla, H.; Sleptchenko, A.; Nayfeh, A. Photovoltaic systems operation and maintenance: A review and future direction. Renew. Sustain. Energy Rev. 2024, 195, 114342. [Google Scholar] [CrossRef]
- Mordor Intelligence. Available online: https://www.mordorintelligence.com/industry-reports/europe-solar-tracker-market (accessed on 20 February 2025).
- IPCC. Available online: https://www.ipcc.ch/ (accessed on 22 March 2025).
- Xu, L.; Long, E.; Wei, J.; Cheng, Z.; Zheng, H. A new approach to determine the optimum tilt angle and orientation of solar collectors in mountainous areas with high altitude. Energy 2021, 237, 121507. [Google Scholar] [CrossRef]
- Lu, N.; Qin, J. Optimization of tilt angle for PV in China with long-term hourly surface solar radiation. Renew. Energy 2024, 229, 120741. [Google Scholar] [CrossRef]
- Mahmoudi, E.; Lucas de Souza Silva, J.; André dos Santos Barros, T. Assessing the performance of physical transposition models in photovoltaic power forecasting: A comprehensive micro and macro accuracy analysis. Energy Convers. Manag. X 2024, 24, 100792. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Kavadias, K.A.; Farahat, A.M. Solar energy received on flat-plate collectors fixed on 2-axis trackers: Effect of ground albedo and clouds. Energies 2024, 17, 3721. [Google Scholar] [CrossRef]
- Akgul, B.A.; Sadettin Ozyazici, M.; Fatih Hasoglu, M. Estimation of the solar radiation intensity on photovoltaic surfaces using anisotropic Models, investigation of influence of tilt angles and solar trackers: A case study for the southeastern of Türkiye. Comput. Electr. Eng. 2024, 118, 109411. [Google Scholar] [CrossRef]
- Villena-Ruiz, R.; Martín-Martínez, S.; Honrubia-Escribano, A.; Javier Ramírez, F.; Gómez-Lázaro, E. Solar PV power plant revamping: Technical and economic analysis of different alternatives for a Spanish case. J. Clean. Prod. 2024, 446, 141439. [Google Scholar] [CrossRef]
- Thaker, J.; Höller, R. Hybrid model for intra-day probabilistic PV power forecast. Renew. Energy 2024, 232, 121057. [Google Scholar] [CrossRef]
- Alam, S.; Qadeer, A.; Afazal, M. Determination of the optimum tilt-angles for solar panels in Indian climates: A new approach. Comput. Electr. Eng. 2024, 119, 109638. [Google Scholar] [CrossRef]
- Silva, M.K.; de Melo, K.B.; Costa, T.S.; Narvez, D.I.; de Bastos Mesquita, D.; Villalva, M.G. Comparative Study of Sky Diffuse Irradiance Models Applied to Photovoltaic Systems. In Proceedings of the 2019 International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019; pp. 1–5. [Google Scholar]
- Serrano-Guerrero, X.; Cantos, E.; Feijoo, J.J.; Barragán-Escandón, A.; Clairand, J.M. Optimal tilt and orientation angles in fixed flat surfaces to maximize the capture of solar insolation: A case study in Ecuador. Appl. Sci. 2021, 11, 4546. [Google Scholar] [CrossRef]
- Barbón, A.; Bayón-Cueli, C.; Bayón, L.; Carreira-Fontao, V. A methodology for an optimal design of ground-mounted photovoltaic power plants. Appl. Energy 2022, 314, 118881. [Google Scholar] [CrossRef]
- Tuomiranta, A.; Alet, P.J.; Ballif, C.; Ghedira, H. Worldwide performance evaluation of ground surface reflectance models. Sol. Energy 2021, 224, 1063–1078. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, J.; Yang, X. Design and performance analysis of a solar tracking system with a novel single-axis tracking structure to maximize energy collection. Appl. Energy 2020, 264, 114647. [Google Scholar] [CrossRef]
- Barbón, A.; Fortuny Ayuso, P.; Bayón, L.; Fernández-Rubiera, J.A. Predicting beam and diffuse horizontal irradiance using Fourier expansions. Renew. Energy 2020, 154, 46–57. [Google Scholar] [CrossRef]
- Habte, A.; Sengupta, M.; Andreas, A.; Jaker, S.; Yang, J.; Reda, I.; Xie, Y. Measured Long-term Solar Irradiance for Climate Studies. In Proceedings of the 2024 IEEE 52nd Photovoltaic Specialist Conference (PVSC), Seattle, WA, USA, 9–14 June 2024; pp. 1267–1269. [Google Scholar]
- Barbón, A.; Carreira-Fontao, V.; Bayón, L.; Spagnuolo, G. Energy, environmental and economic analysis of the influence of the range of movement limit on horizontal single-axis trackers at photovoltaic power plants. J. Clean. Prod. 2025, 489, 144637. [Google Scholar] [CrossRef]
- Solar Feeds. Available online: https://www.solarfeeds.com/mag/what-is-the-difference-between-fixed-and-single-axis-trackers/ (accessed on 20 February 2025).





| Specifications | PV Module Mounting System | ||
|---|---|---|---|
| Fixed Tilt Angle System | Scenario 1 | Scenario 2 | |
| Location | Gijon, (Spain) | Gijon, (Spain) | Gijon, (Spain) |
| Latitude | N | N | N |
| Longitude | W | W | W |
| Altitude (m) | 28.0 | 28.0 | 28.0 |
| Fixed tilt angle (°) | - | - | |
| Tracking type | - | Horiz. single-axis tracker | Horiz. single-axis tracker |
| Type of control | - | Astronomical algorithm | Astronomical algorithm |
| Backtracking mode | - | Yes | No |
| Rotation angle () (°) | - | ||
| Configuration | 2Vx2 | 1Vx8 | 1Vx8 |
| Pitch () (m) | 6.5 | 6.5 | 6.5 |
| Reflectance () | 0.3 | 0.3 | 0.3 |
| Specifications | Theoretical Study | Real Operating Conditions | ||
|---|---|---|---|---|
| (kWh/m2) | Hbh | Hdh | Hbh | Hdh |
| January | 40.61 | 18.72 | 32.49 | 18.71 |
| February | 60.46 | 21.25 | 39.80 | 25.48 |
| March | 107.37 | 29.29 | 34.68 | 43.57 |
| April | 145.29 | 33.44 | 76.77 | 48.20 |
| May | 181.50 | 38.35 | 85.39 | 53.73 |
| June | 188.72 | 38.76 | 71.84 | 63.20 |
| July | 188.63 | 39.16 | 110.49 | 56.94 |
| August | 163.34 | 35.95 | 65.80 | 51.70 |
| September | 120.78 | 30.26 | 68.96 | 38.03 |
| October | 82.16 | 25.66 | 35.47 | 33.40 |
| November | 46.99 | 19.57 | 25.63 | 20.61 |
| December | 33.95 | 17.24 | 15.82 | 17.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbón, A.; Martínez-Suárez, J.; Bayón, L.; Fernández-Rubiera, J.A. Experimental and Theoretical Evaluation of Incident Solar Irradiance on Photovoltaic Power Plants Under Real Operating Conditions: Fixed Tilt Angle System vs. Horizontal Single-Axis Tracker. Appl. Sci. 2025, 15, 4571. https://doi.org/10.3390/app15084571
Barbón A, Martínez-Suárez J, Bayón L, Fernández-Rubiera JA. Experimental and Theoretical Evaluation of Incident Solar Irradiance on Photovoltaic Power Plants Under Real Operating Conditions: Fixed Tilt Angle System vs. Horizontal Single-Axis Tracker. Applied Sciences. 2025; 15(8):4571. https://doi.org/10.3390/app15084571
Chicago/Turabian StyleBarbón, Arsenio, Jaime Martínez-Suárez, Luis Bayón, and José A. Fernández-Rubiera. 2025. "Experimental and Theoretical Evaluation of Incident Solar Irradiance on Photovoltaic Power Plants Under Real Operating Conditions: Fixed Tilt Angle System vs. Horizontal Single-Axis Tracker" Applied Sciences 15, no. 8: 4571. https://doi.org/10.3390/app15084571
APA StyleBarbón, A., Martínez-Suárez, J., Bayón, L., & Fernández-Rubiera, J. A. (2025). Experimental and Theoretical Evaluation of Incident Solar Irradiance on Photovoltaic Power Plants Under Real Operating Conditions: Fixed Tilt Angle System vs. Horizontal Single-Axis Tracker. Applied Sciences, 15(8), 4571. https://doi.org/10.3390/app15084571






