Procedure for the Determination of the Appropriate Protective Foil Size to Reduce Step Voltage Using a FEM Model and Evolutionary Methods
Abstract
Featured Application
Abstract
1. Introduction
- An analysis of the step voltage depending on the width of the used protective foil using an FEM model based on real data from the transmission line pole and the earthing system;
- A new procedure for determining the optimal width of the foil, with the minimum number of time-consuming FEM calculations;
- Determination of the most appropriate function Us = f(fw) among the five selected functions;
- Selection of the most appropriate evolutionary method among DE using three different strategies, TLBO and ABC, to determine the coefficients of the function Us = F(fw);
- Determination of potential differences between the potential above and below the protective foil on the basis of the FEM model, which are important for the selection of the appropriate material.
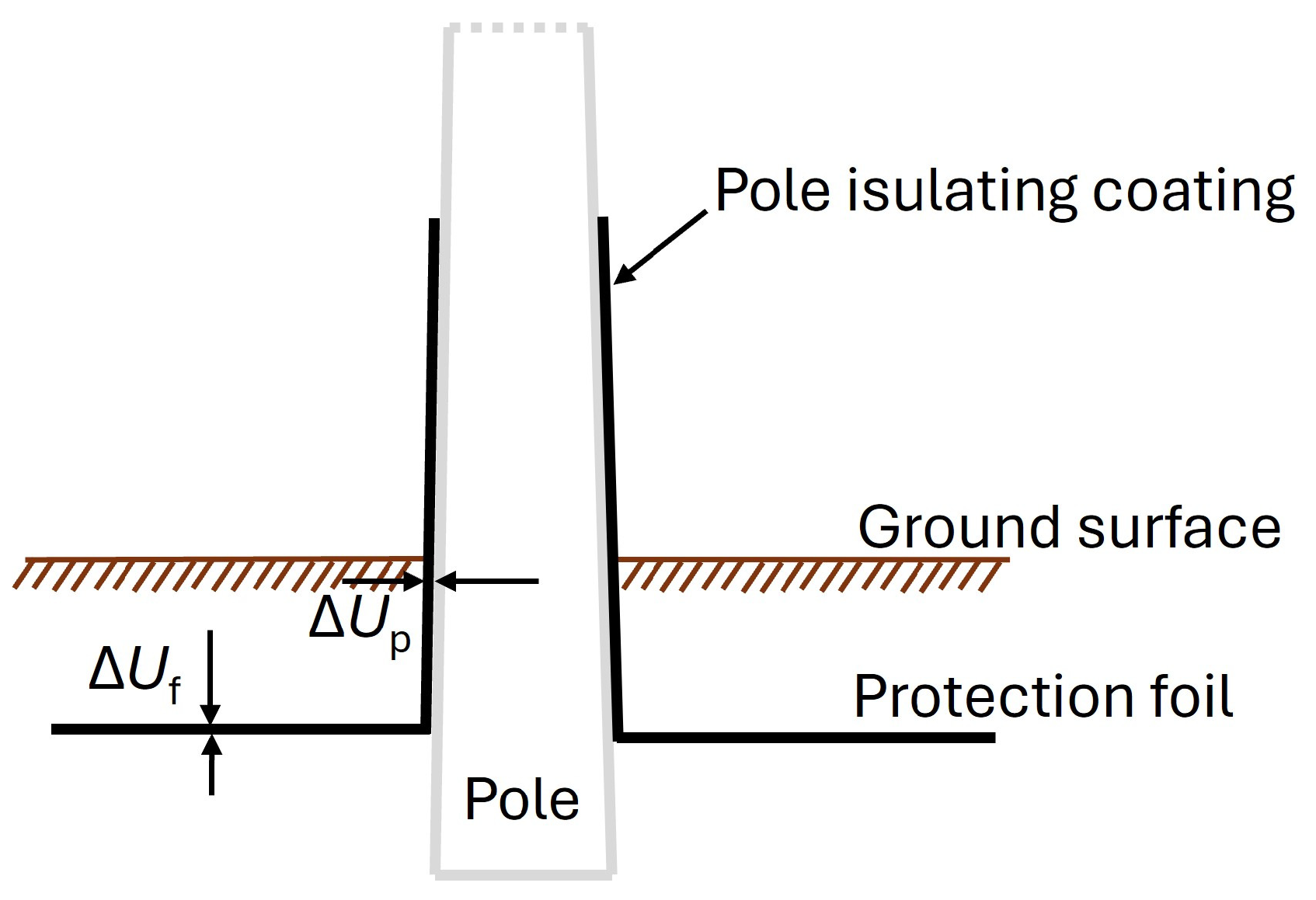
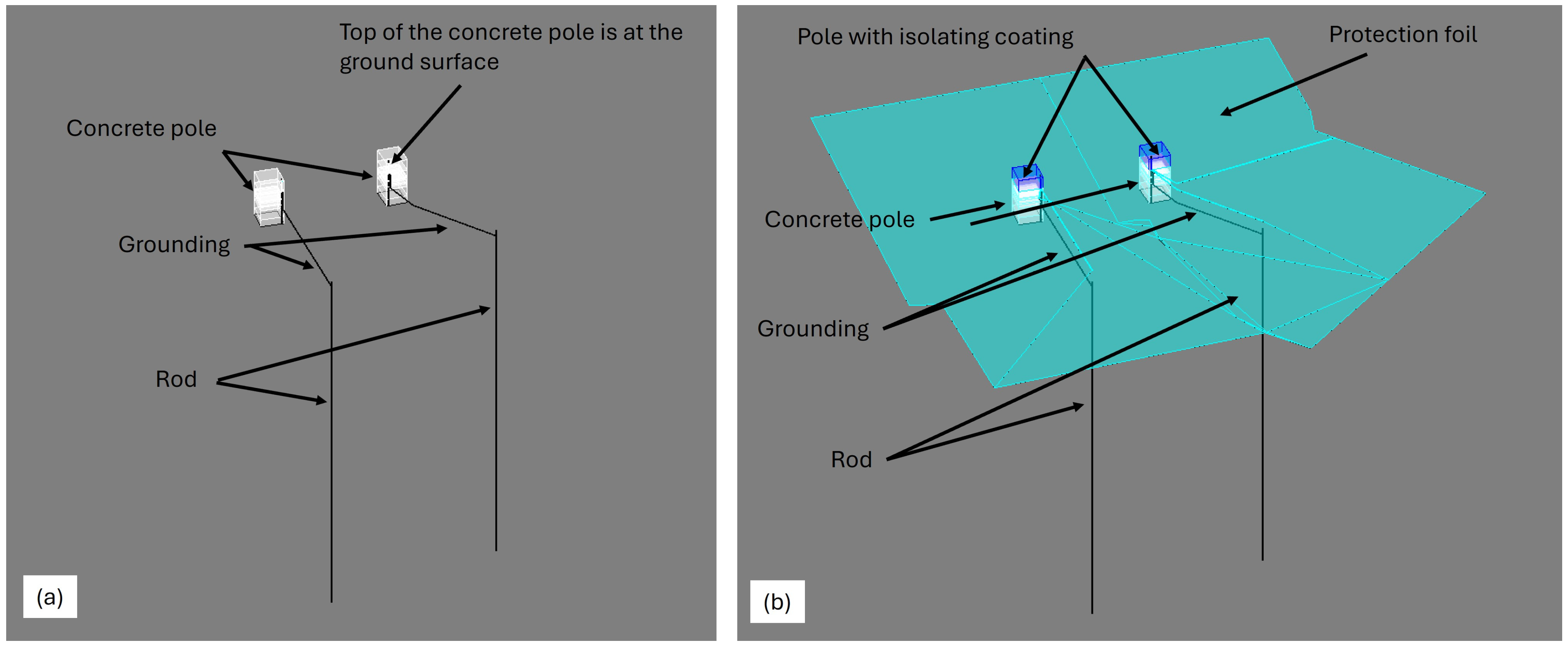
2. Selected Protection with Protective Foil
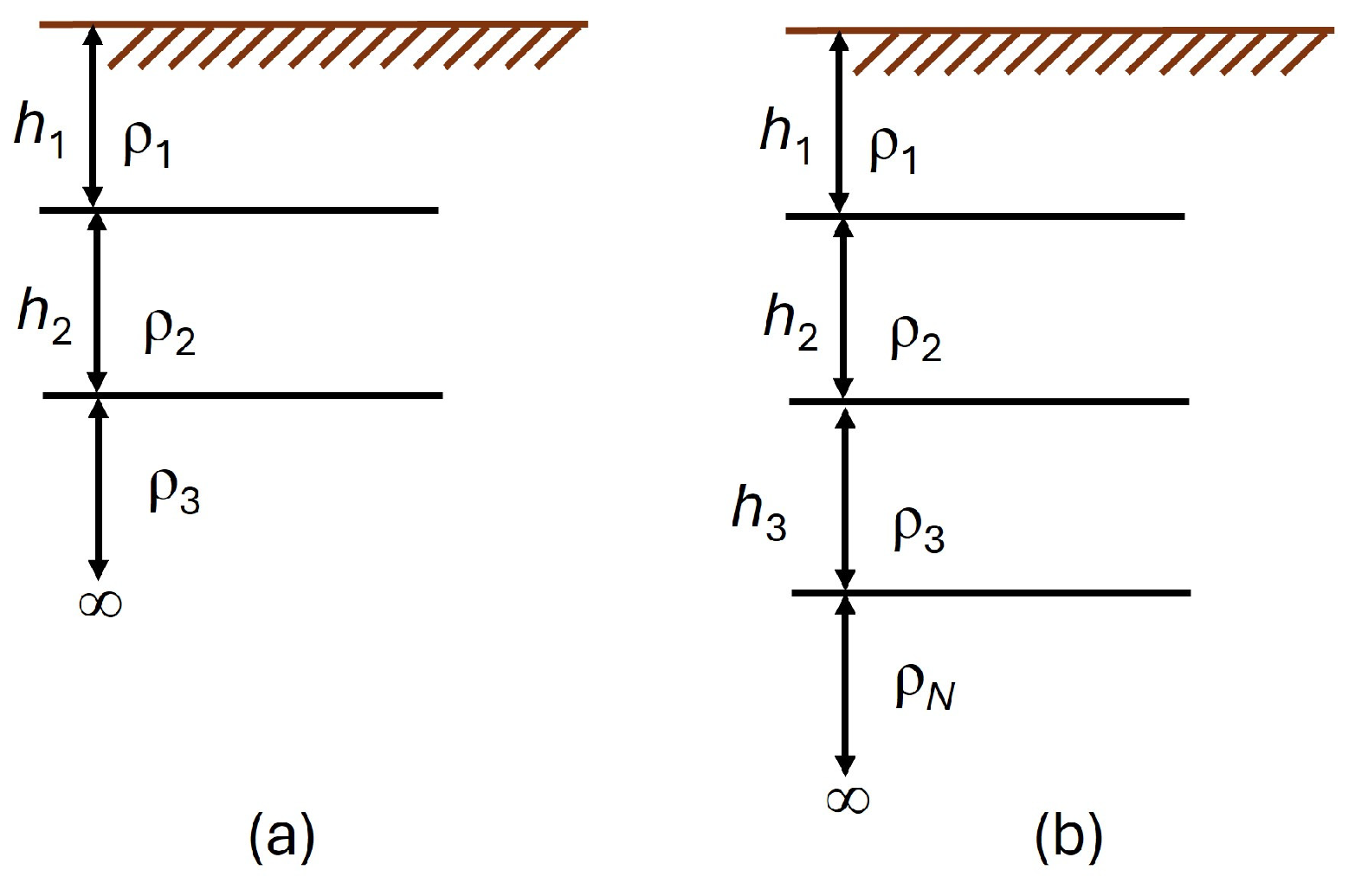
3. Geometry of Test Transmission Poles and Determination of Soil Parameters
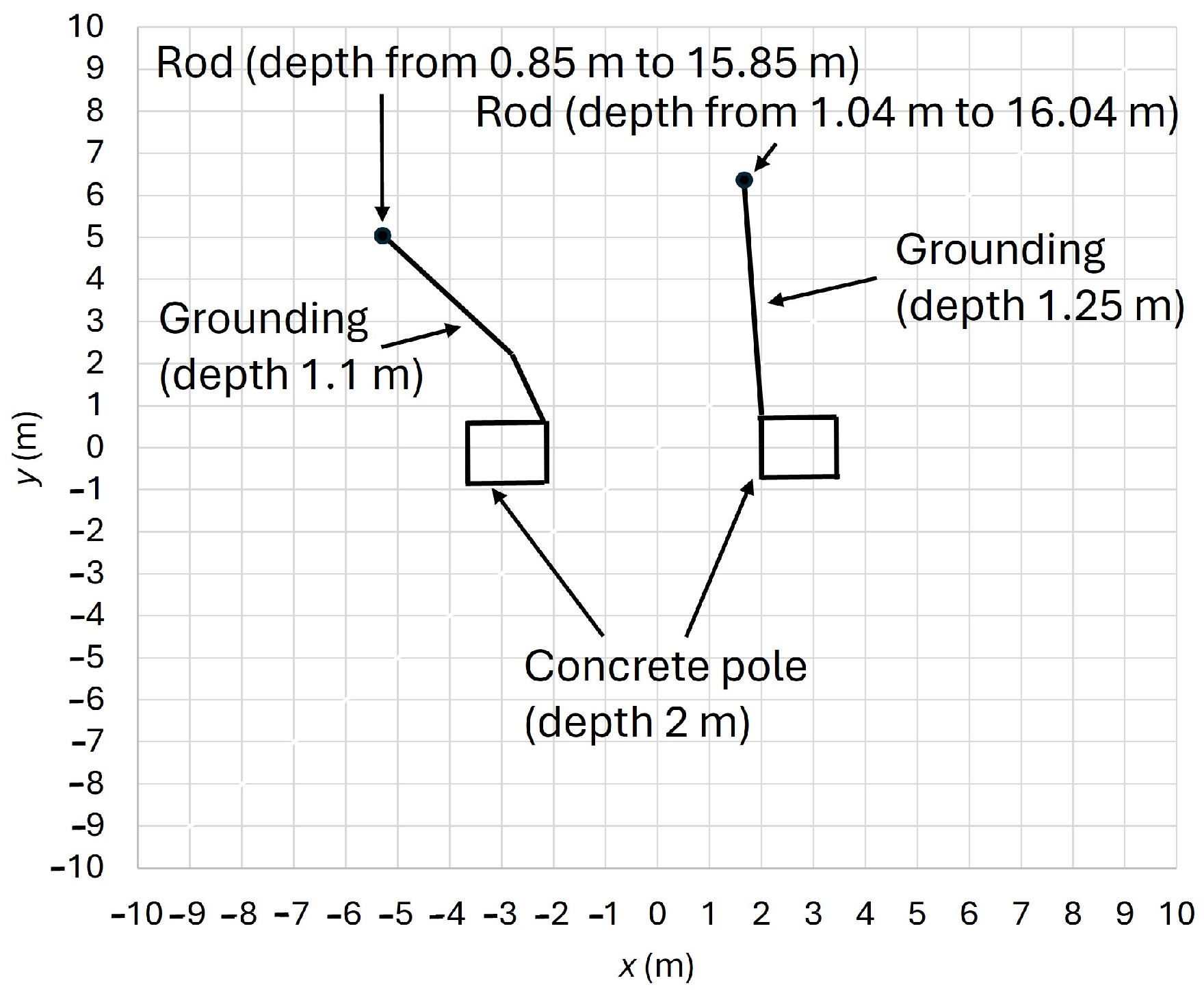
3.1. Transmission Pole TP1
3.2. Transmission Pole TP2
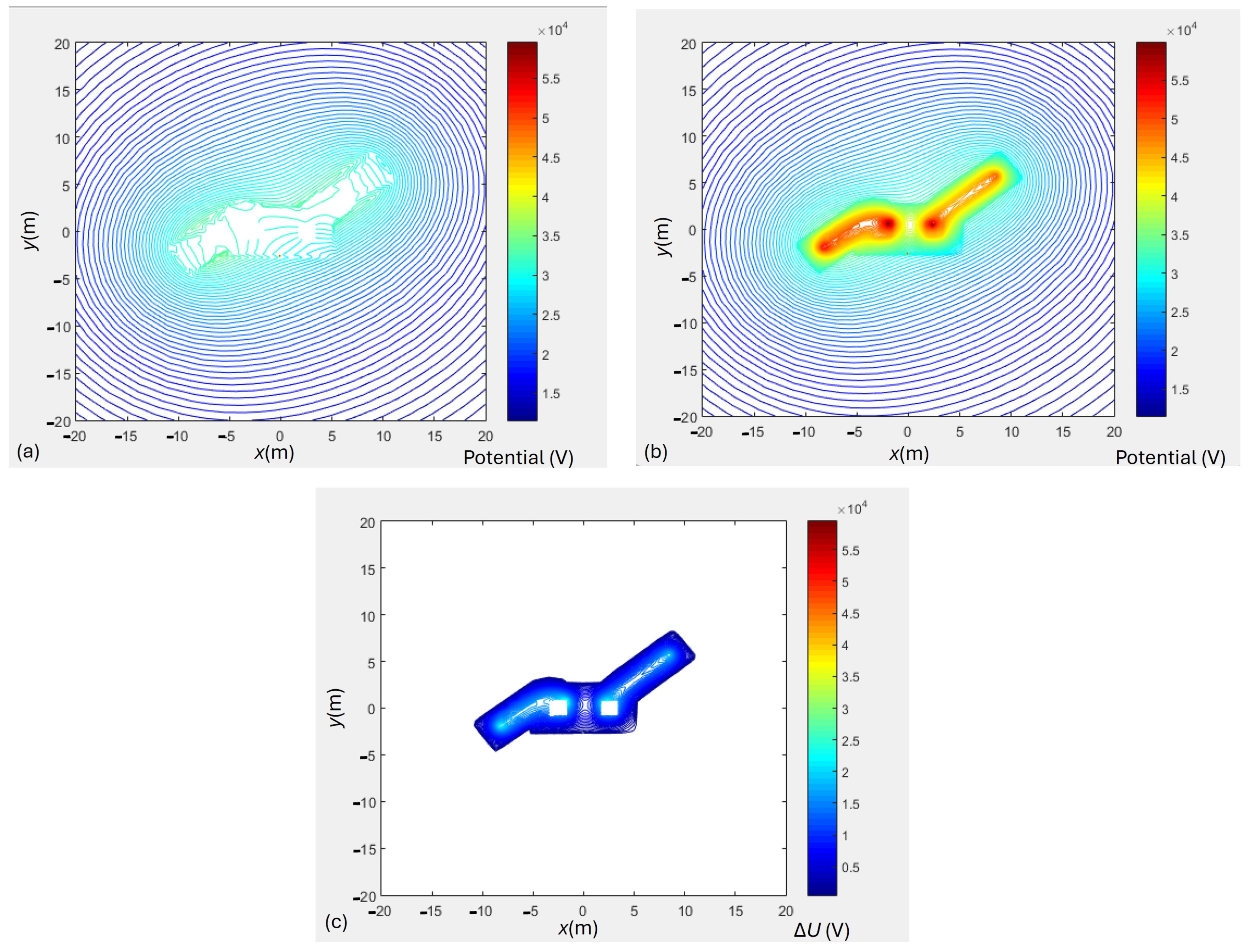
4. The FEM Model
- On the top surface, it is necessary to specify the boundary condition “tangential electric”; that is, the current can flow only along the surface of the earth and not pass from it.
- On the bottom and side surfaces, the Dirichlet boundary condition potential V = 0 was set. The bottom and side surfaces of the model should be spaced sufficiently so as not to affect the distribution of potential in the vicinity of the earthing system. Figure 7 shows that the FEM model is made to a depth of 100 m and has dimensions on an area of 100 × 100 m, so that the edge on which the boundary condition potential V = 0 is placed is sufficiently far from the grounding system.
- A fault current is injected into the grounding system, which we received as information from ELES, d.o.o. It depends on the position of the distribution pole in relation to the other elements of the power system.
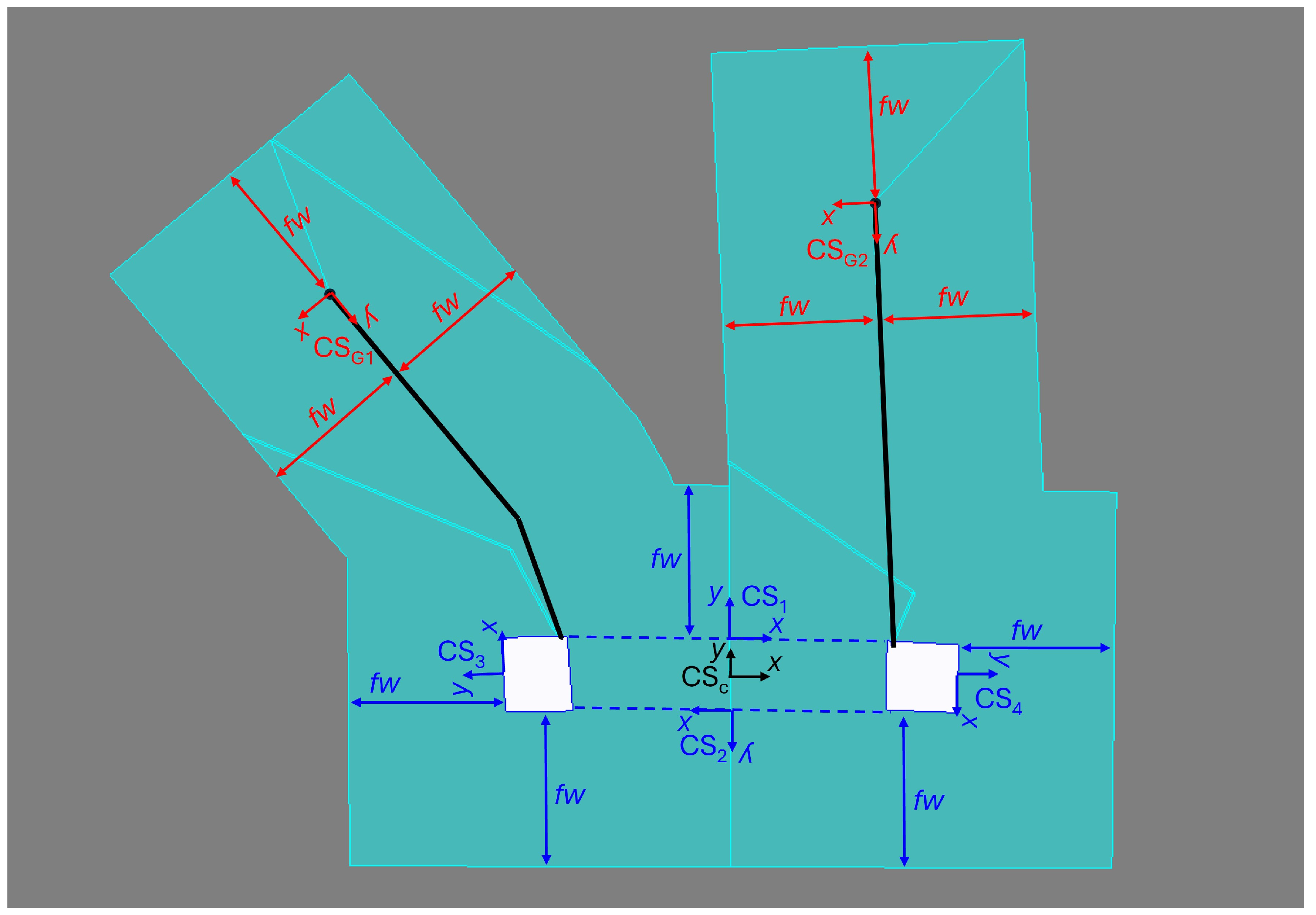
- Coordinate systems CS1, CS2, CS3, and CS4 were used to distance the edge of the foil correctly from the pole legs.
- Coordinate systems CSG1 and CSG2 are of particular importance. They are placed at the end point of the grounding, and their y component points in the direction of the grounding. They were used to distance the foil properly from the ground. The presented position proved to be the best for proper modeling of the size of the foil.
- The CSC coordinate system was used to post-process the results. This coordinate system was used to present the results in the figures in the continuation of the article.
4.1. TP1 FEM Model
4.2. TP2 FEM Model
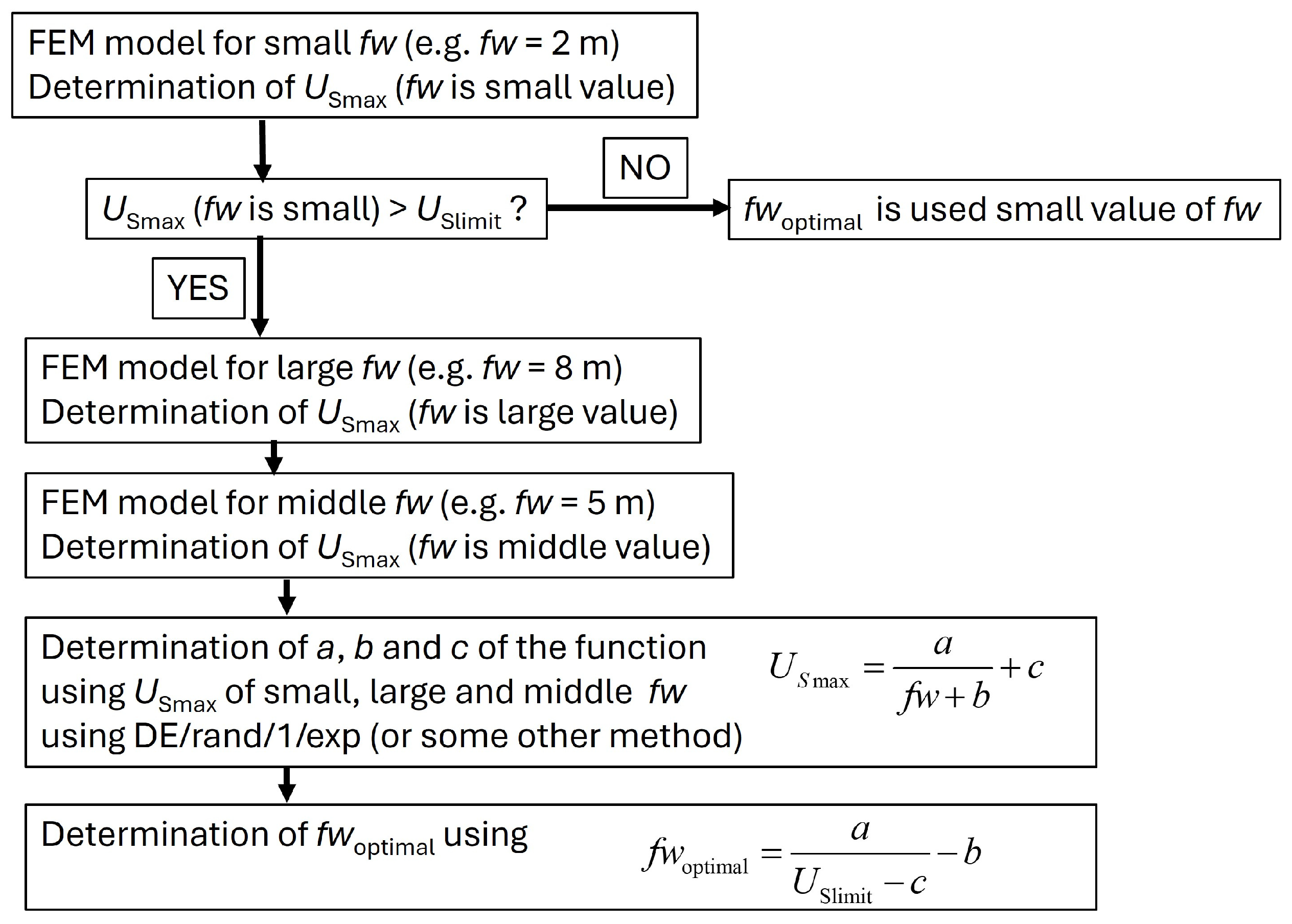
5. Process of Optimal Foil Width Determination and Results
- The soil structure;
- The magnitude of the fault current that causes the potential on the grounded parts;
- It does not depend on the geometry of the problem, because fw stands for the distance from the grounded parts, regardless of their configuration.
- Three FEM calculations are performed and the maximum step voltage (USmax) for each is written depending on the fw used. It is advantageous to specify USmax (fw1 small value), USmax (fw3 large value), and USmax (fw2 value between small and large).
- Based on USmax(fw1), USmax(fw2), and USmax(fw3), three parameters of the function USmax = F(fw) can be defined (three parameters, because we have three known values of USmax for three fw). The rest of the article shows the determination of the corresponding function F based on the choice between five functions.
- From the written function USmax = F(fw), fw is determined by taking into account that USmax is equal to the limit value of the step voltage.
5.1. Results TP1
5.1.1. Determination of the USmax Function Depending on fw
5.1.2. Determination of Parameters a, b, and c
5.1.3. Determination of the Optimal Foil Width for TP1
- It is not possible to determine the parameters of the earth with absolute precision, because we can never know exactly what is hidden under the surface.
- Defining material data such as concrete, rolled steel, etc., can lead to errors due to different concrete structures, corrosion affecting rolled steel, etc.
- The finite element method is a numerical method dependent on input data, and its accuracy is limited.
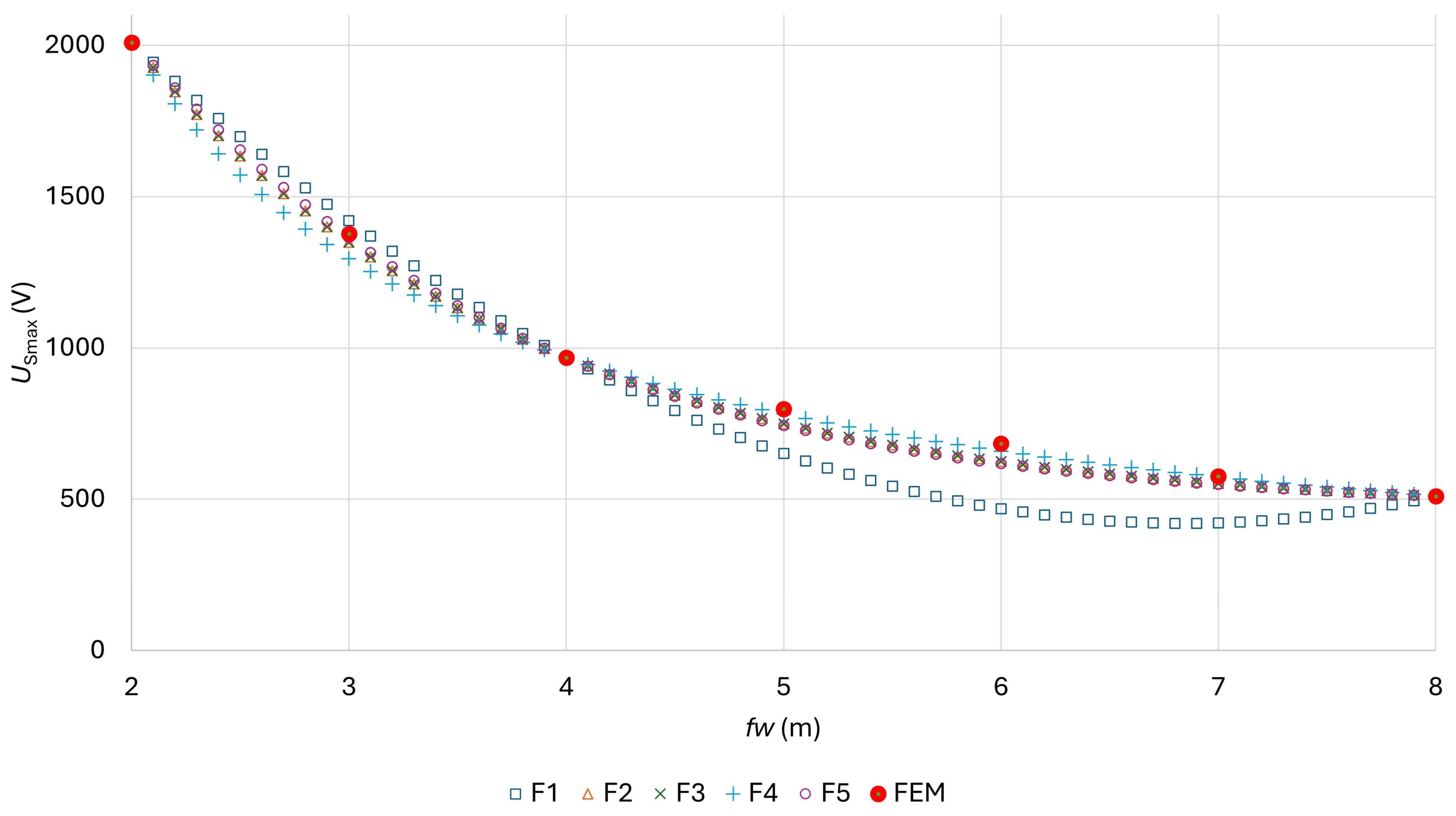
- The F4 function describes the course of Us very well, but there is still some deviation.
5.1.4. Algorithm for Determining the Optimal Foil Width
5.1.5. Determination of the Breaking Strength
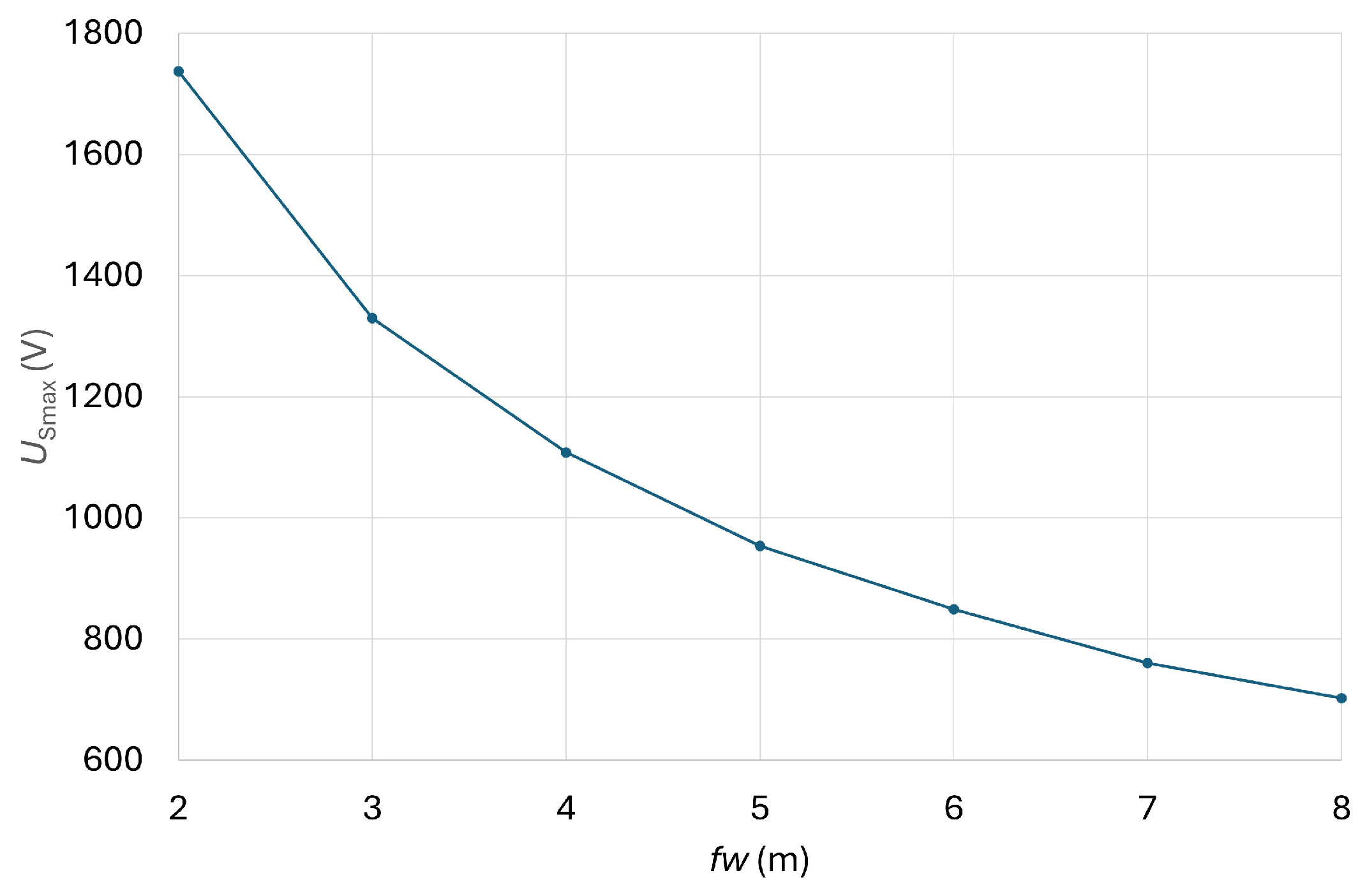
5.2. TP2 Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- SIST EN 50341-1 Standard; Overhead Power Lines for Alternating Voltages Above 1kV—Part 1. Slovenian Institute for Standardization: Ljubljana, Slovenia, 2012.
- Dladla, V.M.N.; Nnachi, A.F.; Tshubwana, R.P. The impact of different fault types on touch voltage, step voltage, and ground potential rise. In Proceedings of the SAUPEC Conference, Durban, South Africa, 25–27 January 2022. [Google Scholar]
- Vycital, V.; Ptacek, M.; Topolanek, D.; Toman, P. On minimization of earthing system touch voltages. Energies 2019, 12, 3838. [Google Scholar] [CrossRef]
- Ellinas, E.D.; Lianos, G.; Kontargyri, V.T.; Christodoulou, C.A.; Gonos, I.F. Performance evaluation of grounding systems of medium-voltage concrete poles: A comprehensive analysis. Appl. Sci. 2024, 14, 3758. [Google Scholar] [CrossRef]
- Datsios, Z.G.; Mikropoulos, P.N. Safety performance evaluation of typical grounding configurations of MV/LV distribution substations. Electr. Power Syst. Res. 2017, 150, 36–44. [Google Scholar] [CrossRef]
- Guizan, R.; Colominas, I.; Paris, J.; Couceiro, I.; Navarrina, F. Numerical analysis and safety design of grounding systems in underground compact substations. Electr. Power Syst. Res. 2022, 203, 107627. [Google Scholar] [CrossRef]
- Zhu, L.; Jiang, H.; Yang, F.; Luo, H.; Li, W.; Han, J. FEM Analysis and Sensor-Based Measurement Scheme of Current Distribution for Grounding Electrode. Appl. Sci. 2020, 10, 8151. [Google Scholar] [CrossRef]
- Zeng, Z.; Udpa, L.; Udpa, S.S. Finite-Element Model for Simulation of Ferrite-Core Eddy-Current Probe. IEEE Trans. Magn. 2012, 46, 905–909. [Google Scholar] [CrossRef]
- Egea, A.; Almandoz, G.; Poza, J.; Ugalde, G.; Escalada, A.J. Axial-Flux-Machine Modeling with the Combination of FEM-2-D an Analytical Tools. IEEE Trans. Ind. Appl. 2012, 48, 1318–1326. [Google Scholar] [CrossRef]
- Fu, W.N.; Ho, S.L.; Zhou, P. Reduction of Computing Time for Steady-State Solutions of Magnetic Field and Circuit Coupled Problems Using Time-Domain Finite-Element Method. IEEE Trans. Magn. 2012, 48, 3363–3366. [Google Scholar] [CrossRef]
- Wang, G.; Wang, S.; Duan, N.; Huangfu, Y.; Zhang, H.; Xu, W.; Qiu, J. Extended Finite-Element Method for Electric Field Analysis of Insulating Plate with Crack. IEEE Trans. Magn. 2015, 51, 7205904. [Google Scholar]
- Trlep, M.; Hamler, A.; Jesenik, M.; Štumberger, B. The FEM-BEM Analysis of Complex Grounding Systems. IEEE Trans. Magn. 2003, 39, 1155–1158. [Google Scholar] [CrossRef]
- Bruckner, F.; Vogler, C.; Feisch, M.; Praetorius, D.; Bergmair, B.; Hubner, T.; Fuger, M.; Suess, D. 3D FEM–BEM-coupling method to solve magnetostatic Maxwell equations. J. Magn. Magn. Mater. 2012, 324, 1862–1866. [Google Scholar] [CrossRef]
- Salas, R.A.; Pleite, J.; Olias, E.; Baarado, A. Theoretical–experimental comparison of a modeling procedure for magnetic components using finite element analysis and a circuit simulator. J. Magn. Magn. Mater. 2008, 320, 1024–1028. [Google Scholar] [CrossRef]
- Kurose, H.; Ohtake, M.; Miyagi, D.; Takahashi, N. 3-D FEM analysis of thermal degradation in writing and reading characteristics of a perpendicular magnetic head. J. Magn. Magn. Mater. 2008, 320, 2917–2920. [Google Scholar] [CrossRef]
- Zona, A.; Ranzi, G. Finite element models for nonlinear analysis of steel–concrete composite beams with partial interaction in combined bending and shear. Finite Elem. Anal. Des. 2011, 47, 98–118. [Google Scholar] [CrossRef]
- Melenk, J.M.; Babuška, J. The partition of unity finite element method: Basic theory and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef]
- Hansbo, A.; Hansbo, P. A finite element method for the simulation of strong and weak discontinuities in solid mechanics. Comput. Methods Appl. Mech. Eng. 2004, 193, 3523–3540. [Google Scholar] [CrossRef]
- Pereira, W.R.; Soares, M.G.; Nato, L.M. Horizontal Multilayer Soil Parameter Estimation Through Differential Evolution. IEEE Trans. Power Deliv. 2016, 31, 622–629. [Google Scholar] [CrossRef]
- Veček, N.; Črepinšek, M.; Mernik, M. On the influence of the number of algorithms, problems, and independent runs in the comparison of evolutionary algorithms. Appl. Soft Comput. 2017, 54, 23–45. [Google Scholar] [CrossRef]
- Veček, N.; Mernik, M.; Črepinšek, M. A chess rating system for evolutionary algorithms: A new method for the comparison and ranking of evolutionary algorithms. Inf. Sci. 2014, 277, 656–679. [Google Scholar] [CrossRef]
- Mallipeddi, R.; Suganthan, P.N.; Pan, Q.K.; Tasgetiren, M.F. Differential evolution algorithm with ensemble of parameters and mutation strategies. Appl. Soft Comput. 2011, 11, 1679–1696. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential Evolution: A Survey of the State-of-the-Art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Saruhan, H. Differential evolution and simulated annealing algorithms for mechanical systems design. Eng. Sci. Technol. Int. J. 2014, 17, 131–136. [Google Scholar] [CrossRef][Green Version]
- Mokan, M.; Sharma, K.; Sharma, H.; Verma, C. Gbest guided differential evolution. In Proceedings of the 9th International Conference on Industrial and Information Systems, Gwalior, India, 15–17 December 2014; pp. 1–6. [Google Scholar]
- Chattopadhyay, S.; Sanyal, S.K. Optimization of Control Parameters of Differential Evolution Technique for the Design of FIR Pulse-shaping Filter in QPSK Modulated System. J. Commun. 2011, 6, 558–570. [Google Scholar] [CrossRef][Green Version]
- He, R.J.; Yang, Z.Y. Differential evolution with adaptive mutation and parameter control using Levy probability distribution. J. Comput. Sci. Technol. 2012, 27, 1035–1055. [Google Scholar] [CrossRef]
- Jesenik, M.; Beković, M.; Hamler, A.; Trlep, M. Analytical modelling of a magnetization curve obtained by the measurements of magnetic materials’ properties using evolutionary algorithms. Appl. Soft Comput. 2017, 52, 387–408. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Sabry, H.Z.; Elaziz, T.A. Real parameter optimization by an effective differential evolution algorithm. Egypt. Inform. J. 2013, 14, 37–53. [Google Scholar] [CrossRef]
- Saad, A.; Engelbrecht, A.P.; Khan, S.A. An Analysis of Differential Evolution Population Size. Appl. Sci. 2024, 14, 9976. [Google Scholar] [CrossRef]
- Wang, X.; Yu, X. Differential Evolution Algorithm with Three Mutation Operators for Global Optimization. Mathematics 2024, 12, 2311. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-Learning-Based Optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Rao, R.V.; Patel, V. An elitist teaching-learning-based optimization algorithm for solving complex constrained optimization problems. Int. J. Ind. Eng. Comput. 2012, 3, 535–560. [Google Scholar] [CrossRef]
- Črepinšek, M.; Liu, S.-H.; Mernik, L. A note on Teaching-learning-based optimization algorithm. Inf. Sci. 2012, 212, 79–93. [Google Scholar] [CrossRef]
- Waghmare, G. Comments on «A note on teachnig-learning-based optimization algorithm». Inf. Sci. 2013, 229, 159–169. [Google Scholar] [CrossRef]
- Črepinšek, M.; Liu, S.-H.; Mernik, L.; Mernik, M. Is a comparison of results meaningful from the inexact replications of computational experiments. Soft Comput. 2016, 20, 223–235. [Google Scholar] [CrossRef]
- Shao, W.; Pi, D.; Shao, Z. A hybrid discrete optimization algorithm based on teaching-probabilistic learning mechanism for no-wait flow shop scheduling. Knowl.-Based Syst. 2016, 107, 219–234. [Google Scholar] [CrossRef]
- Sahu, B.K.; Pati, S.; Mohanty, P.K.; Panda, S. Teaching-learning based optimization algorithm based fuzzy-PID controller for automatic generation control of multi-area power system. Appl. Soft Comput. 2015, 27, 240–249. [Google Scholar] [CrossRef]
- Pickard, J.K.; Carretero, J.A.; Bhavsar, V.C. On the convergence and original bias of the Teaching-Learning-Based-Optimization algorithm. Appl. Soft Comput. 2016, 46, 115–127. [Google Scholar] [CrossRef]
- Lu, S.; Liu, D.; Li, D.; Shao, X. Enhanced Teaching-Learning-Based Optimization Algorithm for the Mobile Robot Path Planning Problem. Appl. Sci. 2023, 13, 2291. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Y.; Yong, L. Teaching-Learning-Based Optimization Algorithm with Stochastic Crossover Self-Learning and Blended Learning Model and Its Application. Mathematics 2024, 12, 1596. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the Performance of Artificial Bee Colony (ABC) Algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A Comparative Study of Artificial Bee Colony Algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Mernik, M.; Liu, S.-H.; Karaboga, D.; Črepinšek, M. On clarifying misconceptions when comparing variants of the Artificial Bee Colony Algorithm by offering a new implementation. Inf. Sci. 2015, 291, 115–127. [Google Scholar] [CrossRef]
- Karaboga, D.; Ozturk, C. A novel clustering approach: Artificial Bee Colony (ABC) algorithm. Appl. Soft Comput. 2011, 11, 652–657. [Google Scholar] [CrossRef]
- Kiran, M.S.; Gündüz, M. The Analysis of Peculiar Control Parameters of Artificial Bee Colony Algorithm on the Numerical Optimization Problems. J. Comput. Commun. 2014, 2, 127–136. [Google Scholar] [CrossRef]
- Gao, K.Z.; Suganthan, P.N.; Pen, Q.K.; Tasgetiren, M.F.; Sadollah, A. Artificial bee colony algorithm for scheduling and rescheduling fuzzy flexible job shop problem with new job insertion. Knowl.-Based Syst. 2016, 109, 1–16. [Google Scholar] [CrossRef]
- Shi, Y.; Pun, C.M.; Hu, H.; Gao, H. An improved artificial bee colony and its application. Knowl.-Based Syst. 2016, 107, 14–31. [Google Scholar] [CrossRef]
- Jitender, A.; Chhabra, K. Harmony search based remodularization for object-oriented software systems. Comput. Lang. Syst. Struct. 2017, 47, 153–169. [Google Scholar]
- Nagy, Z.; Werner-Stark, A.; Dulai, T. An Artificial Bee Colony Algorithm for Static and Dynamic Capacitated Arc Routing Problems. Mathematics 2022, 10, 2205. [Google Scholar] [CrossRef]
- Robles, K.P.V.; Yee, J.-J.; Kee, S.-H. Effect of the Geometrical Constraints to the Wenner Fout-Point Electrical Resistivity Test of Reinforced Concrete Stabs. Sensors 2021, 21, 4622. [Google Scholar] [CrossRef]
- Chik, Z.; Islam, T. Near Surface Soil Characterizations Through Soil Apparent Resistivity: A Case Study. In Proceedings of the 7th International Conference on Intelligent Data Acquisition and Advanced Computing System: Technology and Applications, Berlin, Germany, 12–14 September 2013; pp. 57–60. [Google Scholar]
- Southey, R.D.; Siahrang, M.; Fortin, S.; Dawalibi, F.P. Using Fall-of-Potential Measurements to Improve Deep Soil Resistivity Estimates. IEEE Trans. Ind. Appl. 2015, 51, 5023–5029. [Google Scholar] [CrossRef]
- Yang, H.; Yuan, J.; Zong, W. Determination of Three-Layer Earth Model from Wenner Four-Probe Test Data. IEEE Trans. Magn. 2001, 37, 3684–3687. [Google Scholar] [CrossRef]
- Karnas, G.; Maslowski, G.; Ziemba, R.; Wyderka, S. Influence of Different Multilayer Soil Models on Grounding System Resistance. In Proceedings of the International Conference on Lightning Protection ICLP, Vienna, Austria, 2–7 September 2012; pp. 1–4. [Google Scholar]
- Jesenik, M.; Trbušić, M. The Approach of Using a Horizontally Layered Soil Model for Inhomogeneous Soil, by Taking into Account the Deeper Layers of the Soil, and Determining the Model’s Parameters Using Evolutionary Methods. Appl. Sci. 2025, 15, 1420. [Google Scholar] [CrossRef]
- Ghomeim, S.S.M.; Shoush, K.A. Analytical methods for earth surface potential calculation for grounding grids. Int. J. Eng. Comput. Sci. 2013, 13, 47–53. [Google Scholar]
- Pavel, S.G.; Maier, V.; Ciorca, C.; Beleiu, H.G.; Birou, I. Optimal design of the vertical earthing with electrodes arranged in line. Appl. Sci. 2020, 10, 1177. [Google Scholar] [CrossRef]
- Daadaa, M.; Brettschneider, S.; Volat, C.; Simard, G. Numerical investigation of the use of electrically conductive concrete-encased electrodes as potential replacement for substation grounding systems. Energies 2023, 16, 4410. [Google Scholar] [CrossRef]
- Ribič, J.; Maruša, R. Protection of Buildings in the Vicinity of Transmission Towers Against Potential Rise Above the Ground Electrode-Study Case. IEEE Trans. Power Deliv. 2016, 31, 147–154. [Google Scholar] [CrossRef]
- Liang, X.; Wand, C. Factors Affecting Ground Potential Rise and Fault Currents Along Transmission Lines with Multigrounded Shield Wires. IEEE Trans. Ind. Appl. 2017, 53, 888–900. [Google Scholar] [CrossRef]
- Stanisic, S.; Radakovic, Z. Calculation of Touch Voltage Based on Physical Distribution of Earth Fault Current. IEEE Trans. Power Deliv. 2017, 32, 2246–2254. [Google Scholar] [CrossRef]
- Xiang, Z.X.; Chen, X.; Lv, Q.; Zhang, C.; Ai, J. Optimization Research on Grounding Resistance of Power Transmission Line Tower Foundation. In Proceedings of the 4th International Conference on Intelligent Green Building and Smart Grid, Yichang, China, 6–9 September 2019; pp. 82–86. [Google Scholar]
- IEEE Power and Energy Society. IEEE Guide for Measuring Earth Resistivity, Ground Impedance, and Earth Surface Potentials of Grounding Systems; The Institute of Electrical and Electronics Engineers, Inc.: New York, NY, USA, 2012. [Google Scholar]
- Dawalibi, F.P.; Ma, J.; Southey, R.D. Behaviour of grounding systems in multilayer soils: A parametric analysis. IEEE Trans. Power Deliv. 1994, 9, 334–342. [Google Scholar] [CrossRef]
- Jesenik, M.; Trlep, M. Testing of multi layered soil models based on data obtained from Finite Element Models with known soil structures using metaheuristics for parameters’ determination. Appl. Soft Comput. 2020, 95, 106541. [Google Scholar] [CrossRef]
- Jesenik, M.; Mernik, M.; Trlep, M. Determination of a Hysteresis Model Parameters with the Use of Different Evolutionary Methods for an Innovative Hysteresis Model. Mathematics 2020, 8, 201. [Google Scholar] [CrossRef]
- Barič, T.; Šljivac, D.; Stojkov, M. Validity limits of the expression for measuring soil resistivity by the Wenner method according to IEEE Standard 81-1983. Energija 2007, 56, 730–753. [Google Scholar] [CrossRef]
- Gonos, I.F.; Stathopulos, I.A. Estimation of Multilayer Soil Parameters Using Genetic Algorithms. IEEE Trans. Power Deliv. 2005, 20, 100–106. [Google Scholar] [CrossRef]
- Zhang, B.; Cui, X.; Li, L.; He, J. Parameter Estimation of Horizontal Multilayer Earth by Complex Image Method. IEEE Trans. Power Deliv. 2005, 20, 1394–1401. [Google Scholar] [CrossRef]
- Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms; Joh Wiley and Sons: Hoboken, NJ, USA, 2004. [Google Scholar]






| Variable | Meaning | Variable | Meaning |
|---|---|---|---|
| a, b, c | Function coefficients | NP | Population number |
| b | Depth of the electrodes | OFE’s | Objective function evaluations |
| B | Best OF value | OF | Objective function |
| CR | Crossover probability (DE) | P | Number of parameters |
| CS | Coordinate system | R | Resistance |
| d | Distance between electrodes | ρ | Apparent resistivity |
| F | Step size (DE) | SD | OF standard deviation |
| FE’s | Fitness evaluations | U | Voltage |
| fw | Foil width | u, v, x | Population member |
| h | Thickness of the soil layer | Us | Step voltage |
| I | Current | Ut | Touch voltage |
| ITER | Number of iterations | V | Electric potential |
| J | Bessel function | W | Worst OF value |
| M | Mean OF value | X | Population vector |
| n | Number of measured points | Z | Impedance |
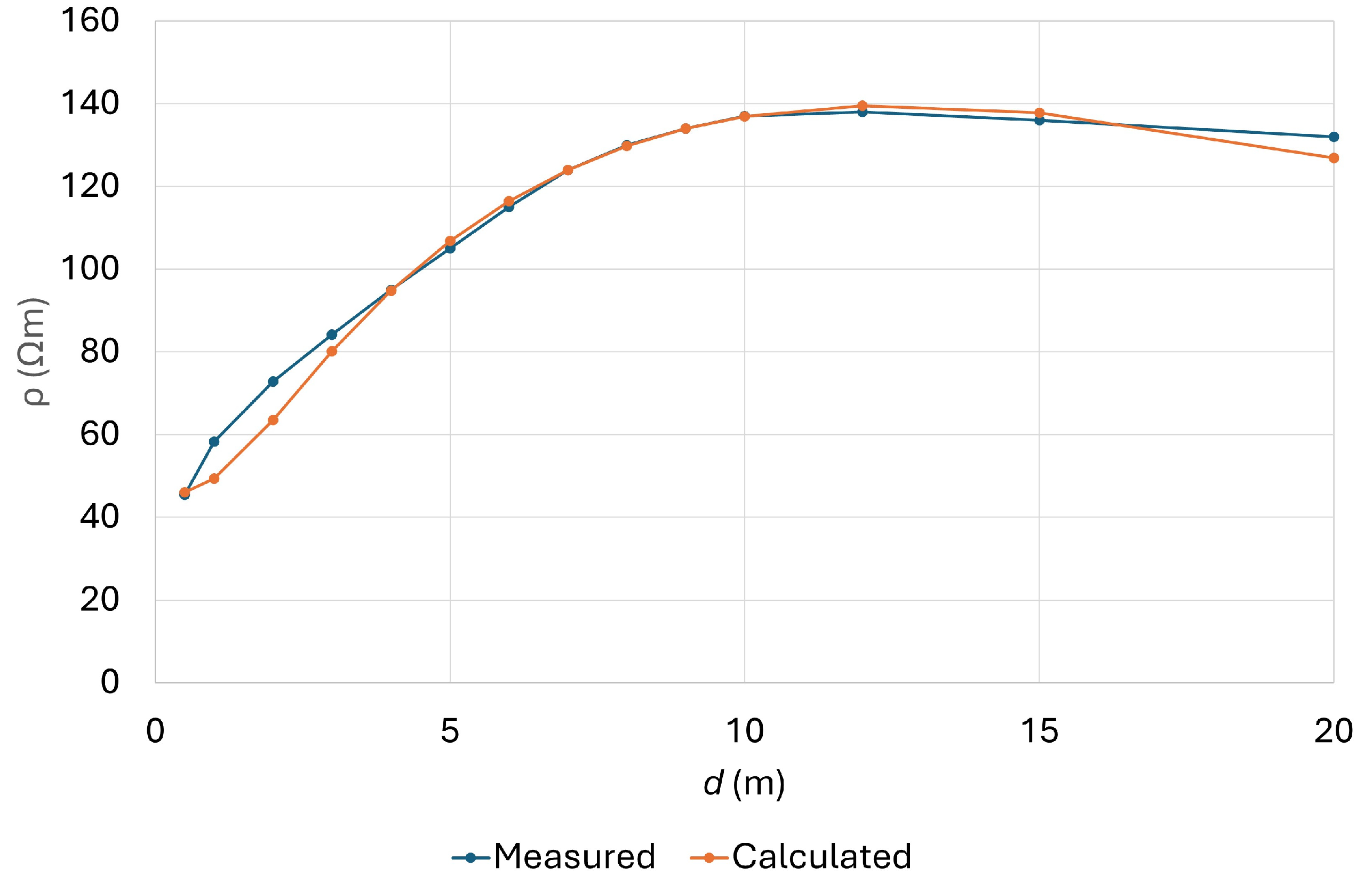
| d (m) | ρ (Ωm) | d (m) | ρ (Ωm) | d (m) | ρ (Ωm) |
|---|---|---|---|---|---|
| 0.5 | 45.5 | 5 | 105 | 10 | 137 |
| 1 | 58.3 | 6 | 115 | 12 | 138 |
| 2 | 72.8 | 7 | 124 | 15 | 136 |
| 3 | 84.2 | 8 | 130 | 20 | 132 |
| 4 | 95 | 9 | 134 |
| Three-Layer Model | Four-Layer Model | |||
|---|---|---|---|---|
| Parameter | Lower Limit | Upper Limit | Lower Limit | Upper Limit |
| Resistance of the first soil layer ρ1 (Ωm) | 45.5 | 45.5 | 45.5 | 45.5 |
| Thickness of the first soil layer h1 (m) | 0.1 | 50 | 0.1 | 33.5 |
| Resistance of the second soil layer ρ2 (Ωm) | 5 | 7000 | 5 | 7000 |
| Thickness of the second soil layer h2 (m) | 0.1 | 50 | 0.1 | 33.3 |
| Resistance of the third soil layer ρ3 (Ωm) | 5 | 7000 | 5 | 7000 |
| Thickness of the third soil layer h3 (m) | - | - | 0.1 | 33.5 |
| Resistance of the fourth soil layer ρ4 (Ωm) | - | - | 5 | 7000 |
| OF and Parameters | ABC | ||
|---|---|---|---|
| Three-Layer | Four-Layer | ||
| OF (%) | B | 3.1398 | 3.1133 |
| W | 3.3201 | 3.8047 | |
| M | 3.2261 | 3.2992 | |
| SD | 4.7245 × 10−2 | 1.5649 × 10−1 | |
| ρ1 (Ωm) | B | 45.5 | 45.5 |
| h1 (m) | B | 1.687 | 1.791 |
| ρ2 (Ωm) | B | 217.1 | 305.6 |
| h2 (m) | B | 11.09 | 3.21 |
| ρ3 (Ωm) | B | 45.8 | 120.8 |
| h3 (m) | B | - | 33.3 |
| ρ4 (Ωm) | B | - | 5.0 |
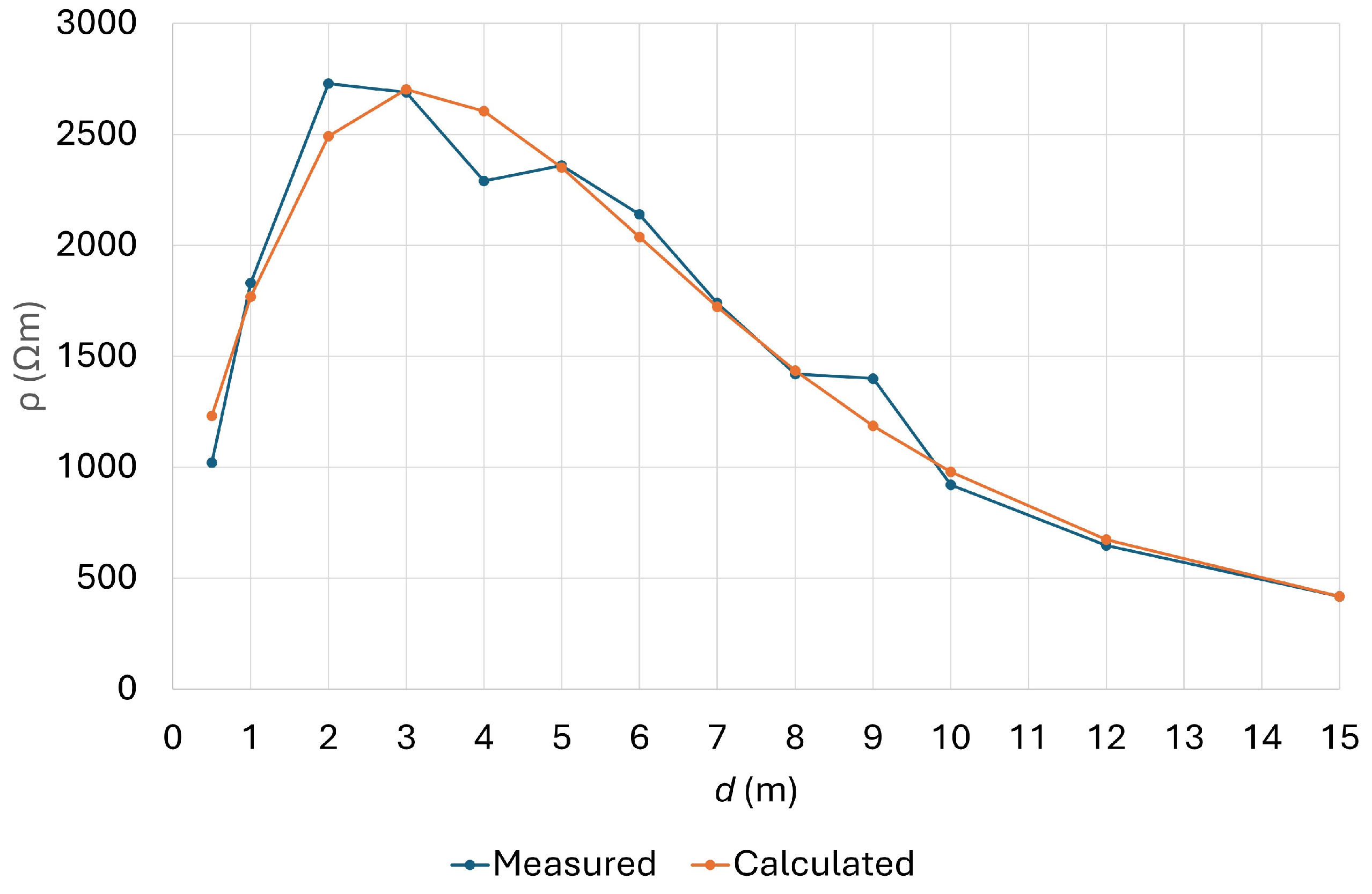
| d (m) | ρ (Ωm) | d (m) | ρ (Ωm) | d (m) | ρ (Ωm) |
|---|---|---|---|---|---|
| 0.5 | 1020 | 5 | 2360 | 10 | 920 |
| 1 | 1830 | 6 | 2140 | 12 | 648 |
| 2 | 2730 | 7 | 1740 | 15 | 418 |
| 3 | 2690 | 8 | 1420 | ||
| 4 | 2290 | 9 | 1400 |
| OF and Parameters | ABC | ||
|---|---|---|---|
| Three-Layer | Four-Layer | ||
| OF (%) | B | 6.2156 | 6.1561 |
| W | 18.0985 | 11.5610 | |
| M | 9.5019 | 7.7921 | |
| SD | 2.6419 | 1.3171 | |
| ρ1 (Ωm) | B | 1010.2 | 1005.3 |
| h1 (m) | B | 0.544 | 0.561 |
| ρ2 (Ωm) | B | 4771.3 | 4960.7 |
| h2 (m) | B | 2.834 | 2.777 |
| ρ3 (Ωm) | B | 179.4 | 143.0 |
| h3 (m) | B | - | 12.009 |
| ρ4 (Ωm) | B | - | 310.8 |
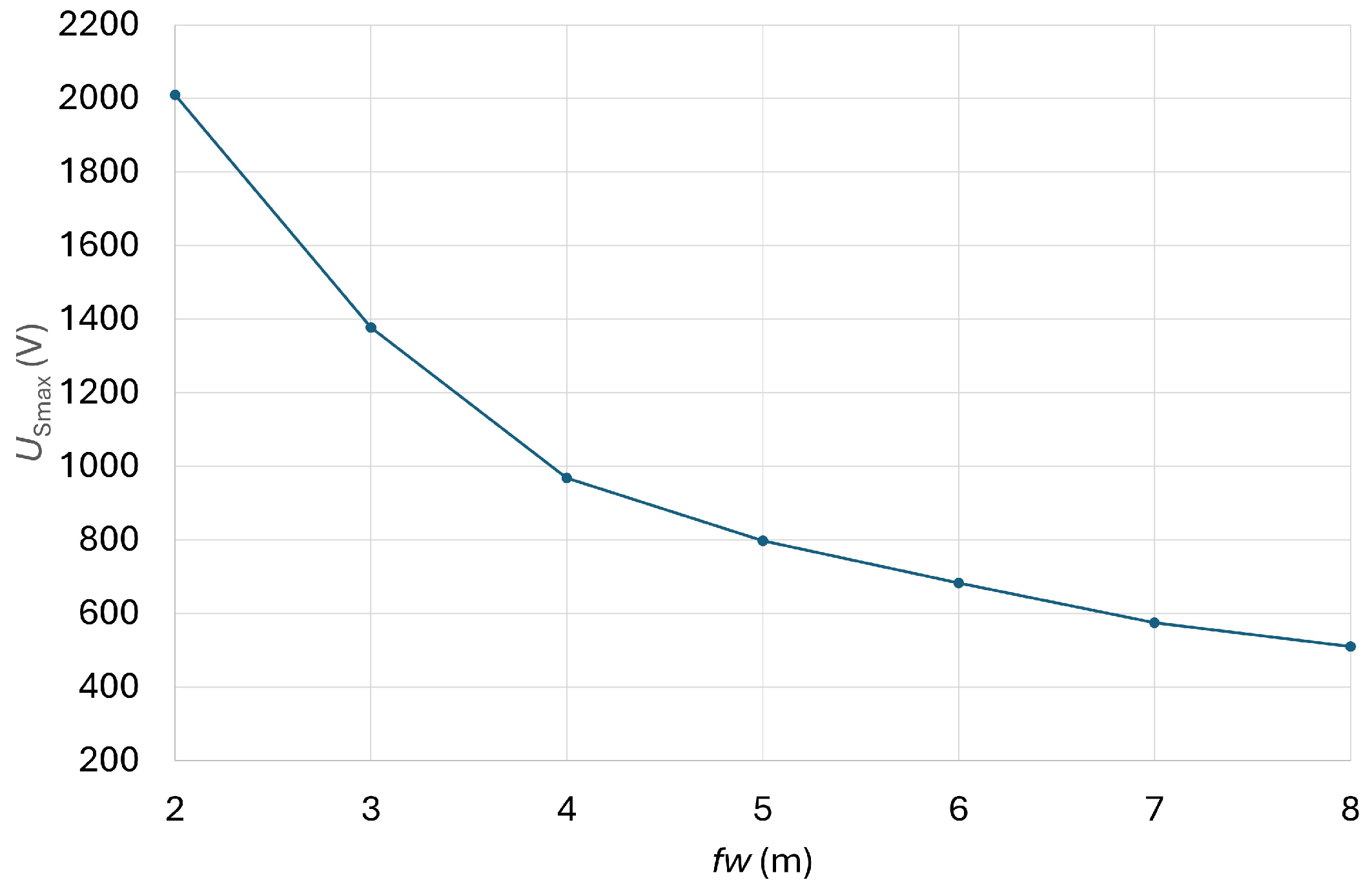
| TP1 | fw (m) | ||||||
|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| USmax (V) | 2009.8 | 1377.2 | 968.4 | 797.7 | 683.6 | 575.6 | 510.7 |
| Method | Number of Parameters (P) | Population Number (NP) | Number of Iterations | Objective Function Evaluations |
|---|---|---|---|---|
| DE/rand/1/exp, DE/rand/2/exp, DE/best/1/bin | P 3 | NP = 10 × P 30 | ITER 30,000 | OFEs = NP × ITER 900,000 |
| TLBO | P 3 | NP = 10 × P 30 | ITER 15,000 | OFEs = NP × 2 × ITER 900,000 |
| ABC | 5 | NP = 10 × P 30 | ITER ≤30,000 | OFEs = NP × ITER + scouts Max. 900,000 |
| OF and Parameters | Method | |||||
|---|---|---|---|---|---|---|
| DE/rand/1/exp | DE/rand/2/exp | DE/best/1/bin | TLBO | ABC | ||
| B | 0 | 0 | 0 | 4.5500 × 10−32 | 5.9706 × 10−15 | |
| OF3 | W | 0 | 0 | 1.2388 × 10−32 | 4.5500 × 10−32 | 3.0295 × 10−13 |
| fw 2, 5, 8 m | M | 0 | 0 | 8.2592 × 10−34 | 4.55 × 10−32 | 3.7803 × 10−14 |
| SD | 0 | 0 | 3.0903 × 10−33 | 2.7369 × 10−47 | 5.9342 × 10−14 | |
| a | B | 4149.47 | 4149.47 | 4149.47 | 4149.47 | 4149.47 |
| b | B | 0.4802 | 0.4802 | 0.4802 | 0.4802 | 0.4802 |
| c | B | 421.66 | 421.66 | 421.66 | 421.66 | 421.66 |
| t (s) | M | 31.7 | 32.1 | 30.8 | 40.5 | 24.4 |
| Function F1 | Used Foil WIDTH | |||
|---|---|---|---|---|
| 2 m, 4 m, 8 m | 2 m, 5 m, 8 m | 2 m, 6 m, 8 m | ||
| OF for three foil widths | 0 | 0 | 0 | |
| A | 3592.9 | 3331.8 | 3163.1 | |
| B | −927.0 | −763.8 | −658.4 | |
| C | 67.71 | 51.39 | 40.85 | |
| OF for all seven foil widths | 2.0497 × 10−1 | 5.7397 × 10−2 | 8.1322 × 10−2 | ∑3.4369 × 10−1 |
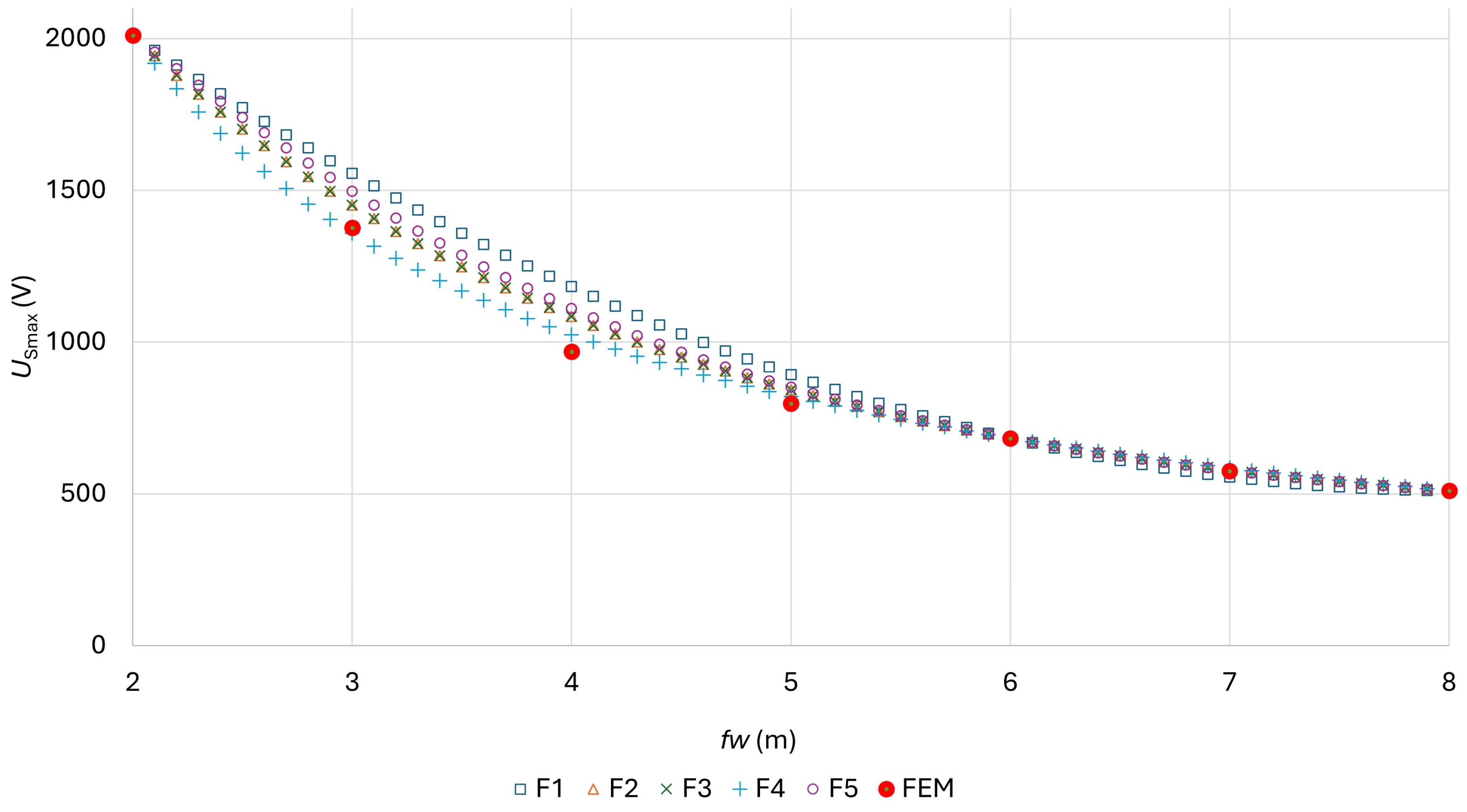
| Function F2 | Used Foil Width | |||
|---|---|---|---|---|
| 2 m, 4 m, 8 m | 2 m, 5 m, 8 m | 2 m, 6 m, 8 m | ||
| OF three foil widths | 1.2799 × 10−32 | 0 | 1.2389 × 10−32 | |
| a | 4707.45 | 4149.47 | 3773.83 | |
| b | −0.55378 | −0.48021 | −0.41956 | |
| c | 454.63 | 421.66 | 379.15 | |
| OF all seven foil widths | 1.3186 × 10−2 | 6.5036 × 10−3 | 2.0229 × 10−2 | ∑3.9919 × 10−2 |
| Function F3 | Used Foil Width | |||
|---|---|---|---|---|
| 2 m, 4 m, 8 m | 2 m, 5 m, 8 m | 2 m, 6 m, 8 m | ||
| OF three foil widths | 1.2799 × 10−32 | 0 | 1.2389 × 10−32 | |
| a | 4707.45 | 4149.47 | 3773.83 | |
| b | 1.7398 | 1.6164 | 1.5213 | |
| c | 454.63 | 421.66 | 379.15 | |
| OF all seven foil widths | 1.3186 × 10−2 | 6.5036 × 10−3 | 2.0229 × 10−2 | ∑ 3.9919 × 10−2 |
| Function F4 | Used Foil Width | |||
|---|---|---|---|---|
| 2 m, 4 m, 8 m | 2 m, 5 m, 8 m | 2 m, 6 m, 8 m | ||
| OF three foil widths | 1.1748 × 10−31 | 2.5723 × 10−30 | 2.9254 × 10−29 | |
| a | 3246.76 | 3656.16 | 4291.50 | |
| b | −0.3101 | −0.1386 | 0.1163 | |
| c | 88.487 | 45.624 | −18.052 | |
| OF all seven foil widths | 5.2605 × 10−3 | 2.6027 × 10−3 | 4.6322 × 10−3 | ∑1.2495 × 10−2 |
| Function F5 | Used Foil Width | |||
|---|---|---|---|---|
| 2 m, 4 m, 8 m | 2 m, 5 m, 8 m | 2 m, 6 m, 8 m | ||
| OF three foil widths | 1.1067 × 10−27 | 2.6596 × 10−28 | 6.4597 × 10−27 | |
| a | 2796.49 | 2530.51 | 2369.74 | |
| b | −0.5997 | −0.5265 | 0.4679 | |
| c | 464.56 | 435.75 | 398.52 | |
| OF all seven foil widths | 1.6360 × 10−2 | 1.0613 × 10−2 | 3.3713 × 10−2 | ∑6.0686 × 10−2 |
| Function F4 | Used Foil Width for Parameter Determination | ||
|---|---|---|---|
| 2 m, 4 m, 8 m | 2 m, 5 m, 8 m | 2 m, 6 m, 8 m | |
| fwoptimal (m) | 5.58 | 5.68 | 5.82 |
| Depth of Burial of Protective Foil (m) | |||
|---|---|---|---|
| 0.3 | 0.5 | 0.7 | |
| USmax (V) | 775.8 | 683.6 | 612 |
| TP2 | fw (m) | ||||||
|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| USmax (V) | 1737.7 | 1329.8 | 1108.4 | 954 | 849.1 | 760.8 | 702.5 |
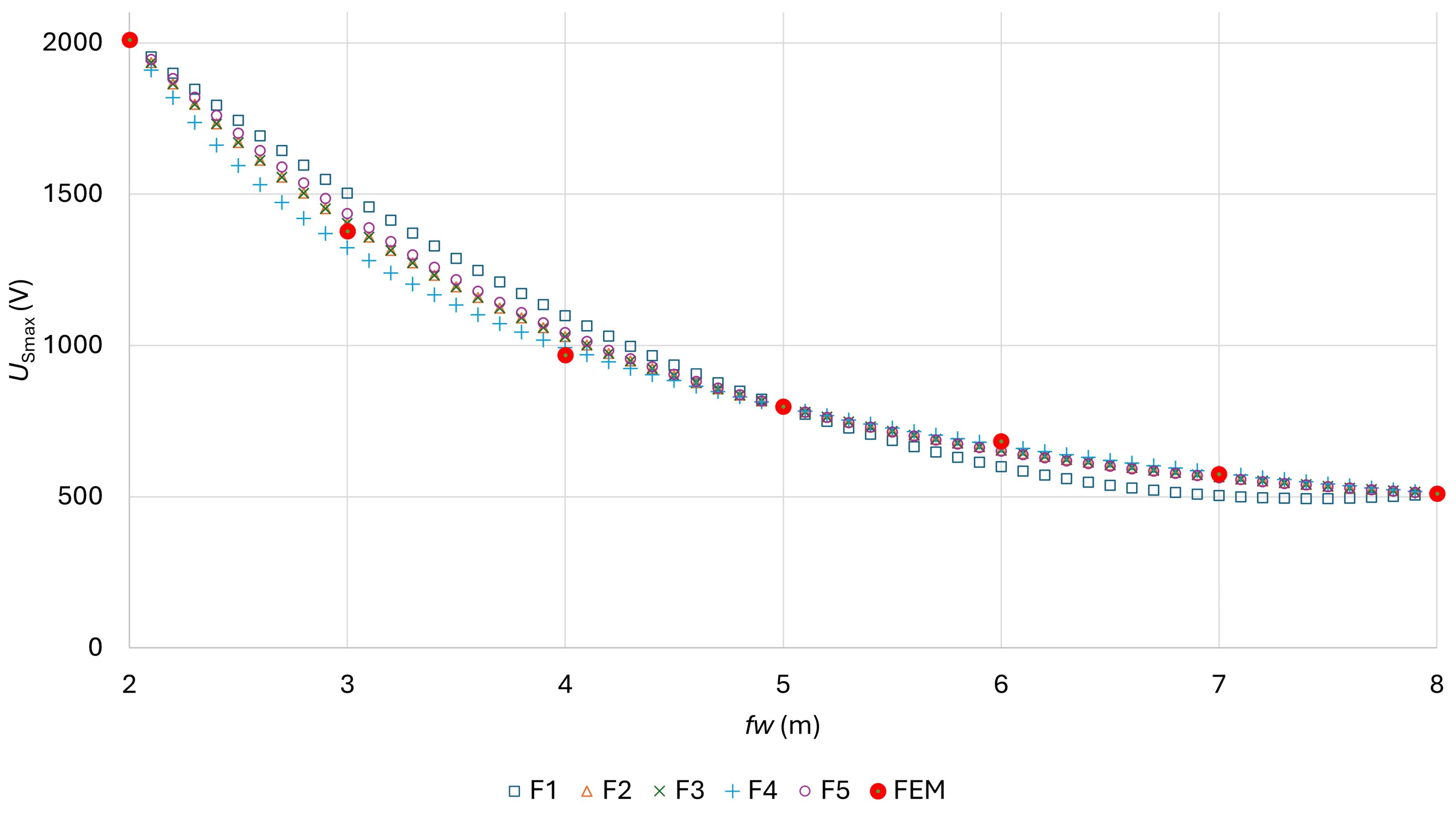
| Function F1 | Used Foil Width | |||
|---|---|---|---|---|
| 2 m, 4 m, 8 m | 2 m, 5 m, 8 m | 2 m, 6 m, 8 m | ||
| OF three foil widths | 0 | 0 | 0 | |
| a | 2651.2 | 2555.8 | 2479.7 | |
| b | −527.8 | −468.2 | −420.6 | |
| c | 35.53 | 29.57 | 24.81 | |
| OF all seven foil widths | 2.2198 × 10−2 | 1.0145 × 10−2 | 1.5177 × 10−2 | ∑4.7520 × 10−2 |
| Function F2 | Used Foil Width | |||
|---|---|---|---|---|
| 2 m, 4 m, 8 m | 2 m, 5 m, 8 m | 2 m, 6 m, 8 m | ||
| OF three foil widths | 0 | 0 | 0 | |
| A | 2546.86 | 2462.06 | 2374.51 | |
| B | 0.4037 | 0.3788 | 0.3496 | |
| C | 601.69 | 583.65 | 557.67 | |
| OF all seven foil widths | 1.4916 × 10−3 | 1.5242 × 10−3 | 3.3845 × 10−3 | ∑6.4003 × 10−3 |
| Function F3 | Used Foil Width | |||
|---|---|---|---|---|
| 2 m, 4 m, 8 m | 2 m, 5 m, 8 m | 2 m, 6 m, 8 m | ||
| OF three foil widths | 0 | 0 | 0 | |
| a | 2546.86 | 2462.06 | 2374.51 | |
| b | 1.4973 | 1.4606 | 1.4185 | |
| c | 601.69 | 583.65 | 557.67 | |
| OF all seven foil widths | 1.4916 × 10−3 | 1.5242 × 10−3 | 3.3845 × 10−3 | ∑6.4003 × 10−3 |
| Function F4 | Used Foil Width | |||
|---|---|---|---|---|
| 2 m, 4 m, 8 m | 2 m, 5 m, 8 m | 2 m, 6 m, 8 m | ||
| OF three foil widths | 9.3215 × 10−31 | 1.4493 × 10−31 | 5.0728 × 10−30 | |
| a | 4364.05 | 4322.29 | 4564.87 | |
| b | 0.8561 | 0.8354 | 0.9547 | |
| c | 209.73 | 213.30 | 192.72 | |
| OF all seven foil widths | 1.2286 × 10−4 | 1.0906 × 10−4 | 2.8286 × 10−4 | ∑5.1478 × 10−4 |
| Function F5 | Used Foil Width | |||
|---|---|---|---|---|
| 2 m, 4 m, 8 m | 2 m, 5 m, 8 m | 2 m, 6 m, 8 m | ||
| OF three foil widths | 0 | 0 | 0 | |
| a | 1653.35 | 1602.19 | 1564.09 | |
| b | 0.4781 | 0.4447 | 0.4119 | |
| c | 630.38 | 611.24 | 586.70 | |
| OF all seven foil widths | 3.5331 × 10−3 | 3.9778 × 10−3 | 8.6763 × 10−3 | ∑1.6200 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jesenik, M.; Kitak, P.; Maruša, R.; Ribič, J. Procedure for the Determination of the Appropriate Protective Foil Size to Reduce Step Voltage Using a FEM Model and Evolutionary Methods. Appl. Sci. 2025, 15, 4611. https://doi.org/10.3390/app15094611
Jesenik M, Kitak P, Maruša R, Ribič J. Procedure for the Determination of the Appropriate Protective Foil Size to Reduce Step Voltage Using a FEM Model and Evolutionary Methods. Applied Sciences. 2025; 15(9):4611. https://doi.org/10.3390/app15094611
Chicago/Turabian StyleJesenik, Marko, Peter Kitak, Robert Maruša, and Janez Ribič. 2025. "Procedure for the Determination of the Appropriate Protective Foil Size to Reduce Step Voltage Using a FEM Model and Evolutionary Methods" Applied Sciences 15, no. 9: 4611. https://doi.org/10.3390/app15094611
APA StyleJesenik, M., Kitak, P., Maruša, R., & Ribič, J. (2025). Procedure for the Determination of the Appropriate Protective Foil Size to Reduce Step Voltage Using a FEM Model and Evolutionary Methods. Applied Sciences, 15(9), 4611. https://doi.org/10.3390/app15094611







