Innovative Grouting Reinforcement Techniques for Shield Tunnels: A Case Study on Surface Settlement Mitigation
Abstract
:1. Introduction
2. Projects and Materials
2.1. Project Overview
2.2. Soil Material
2.3. Soil Reinforcement Measures
3. Research Methods
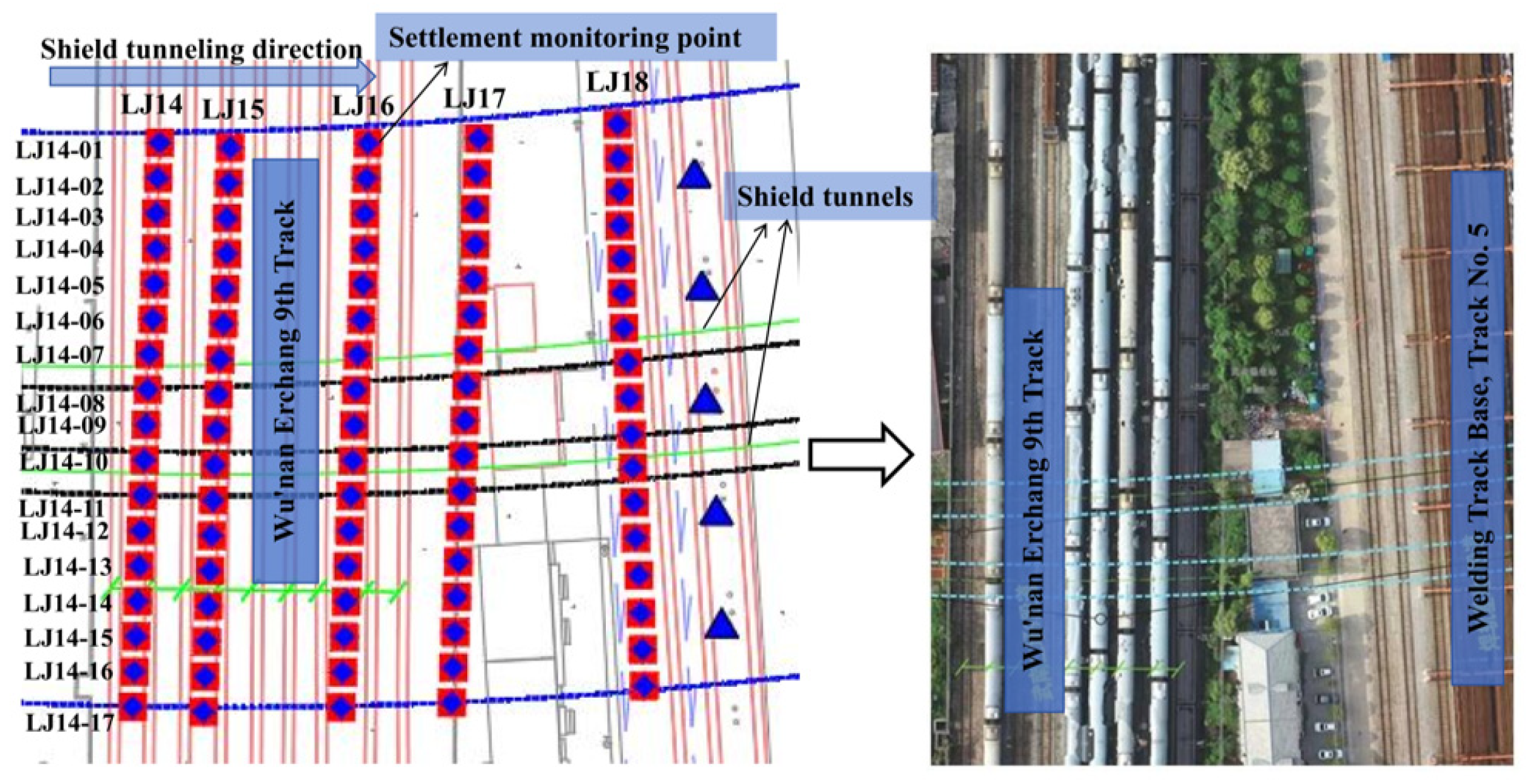
3.1. Field Data Monitoring Methods
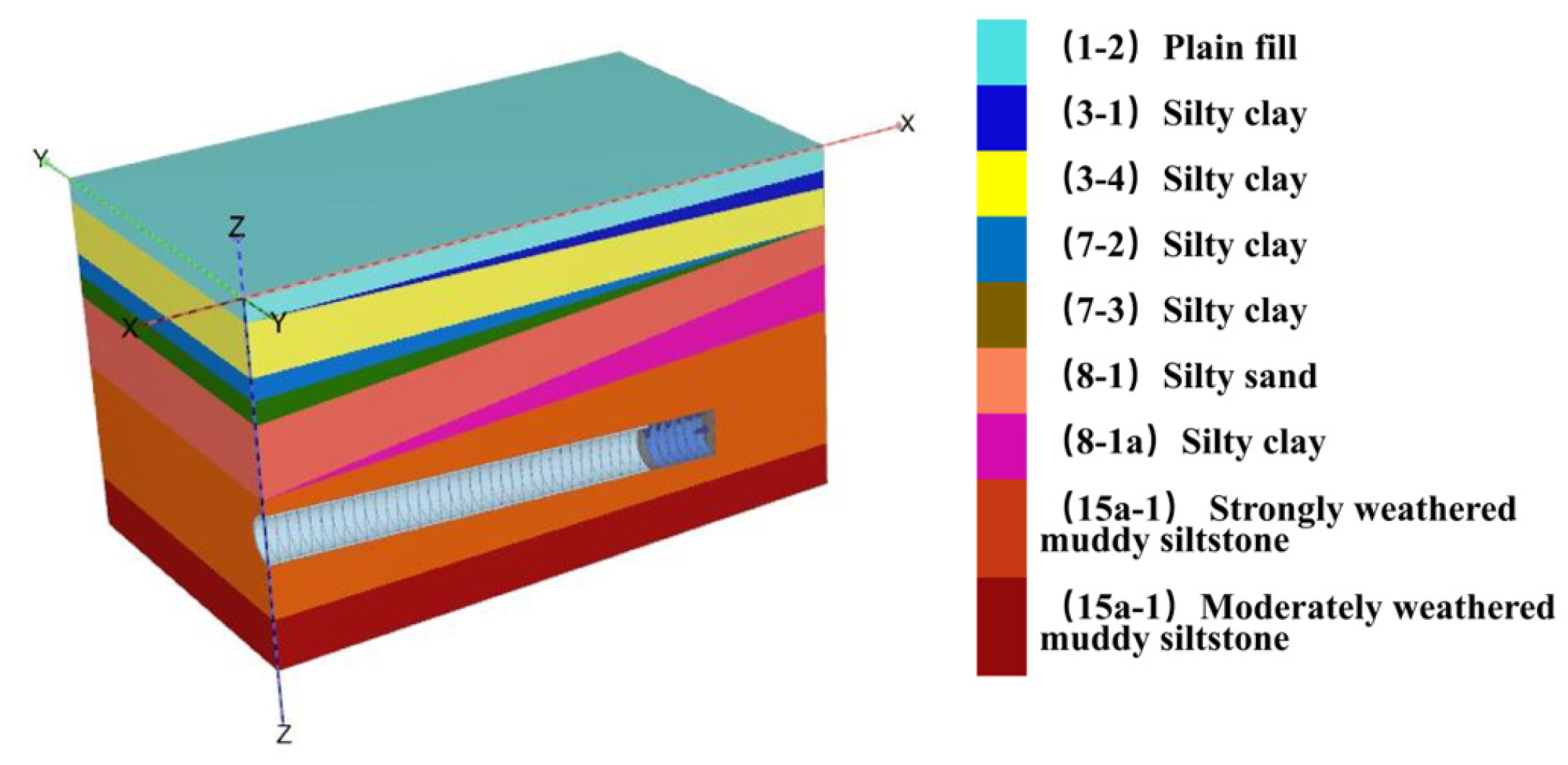
3.2. Numerical Simulation Modeling
3.2.1. Model Assumptions
- (1)
- The shield tunnel lining is idealized as an equivalent homogeneous circular structure, disregarding internal structural details.
- (2)
- The seepage effects of pore water are neglected, focusing solely on the mechanical behavior of the soil.
- (3)
- Geological conditions within the study area are assumed to be homogeneously distributed but stratified according to actual geological data, with the physical and mechanical parameters of each soil layer determined by both field and laboratory tests.
- (4)
- The physical–mechanical properties of grouting materials and soil are treated as constant values, without considering their time-dependent characteristics.
- (5)
- The model boundary is sufficiently distant from the tunnel to minimize boundary effects on the calculation results.
- (6)
- The initial stress field is generated exclusively by the self-weight of the soil, excluding other external forces.
3.2.2. Design of Working Conditions
- (1)
- No reinforcement working condition: no soil reinforcement measures are taken during tunnel excavation.
- (2)
- Flower tube grouting reinforcement condition: A single row of flower tube grouting reinforcement is used within 30 m above and on both sides of the centerline of the tunnel, with a grouting depth of 24 m and a grouting interval of 9 m. The tunnel is reinforced with a single row of flower tube grouting reinforcement.
4. Results of the Study
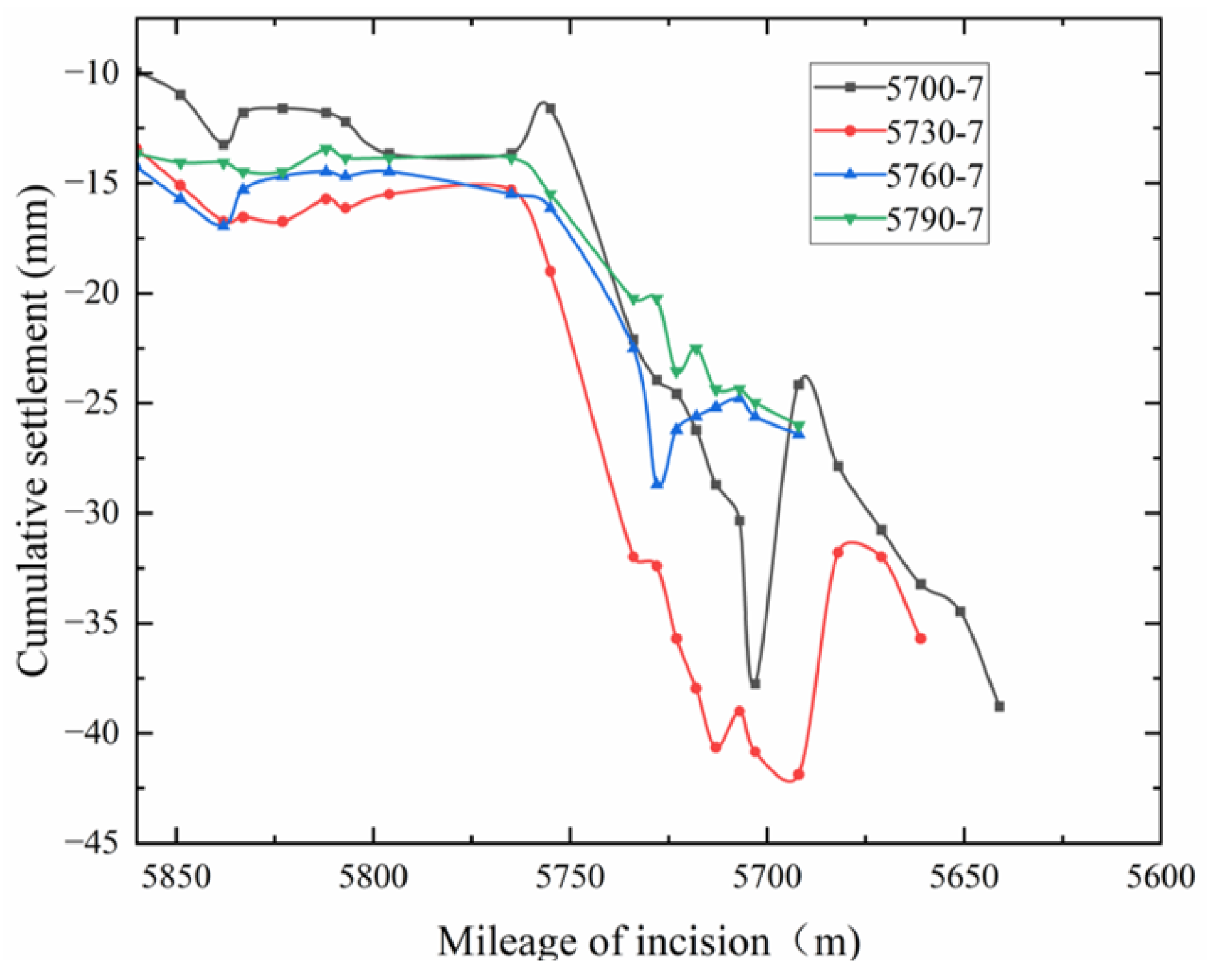
4.1. Unreinforced Surface Settlement Analysis
4.2. Numerical Modeling of Uncemented Surfaces
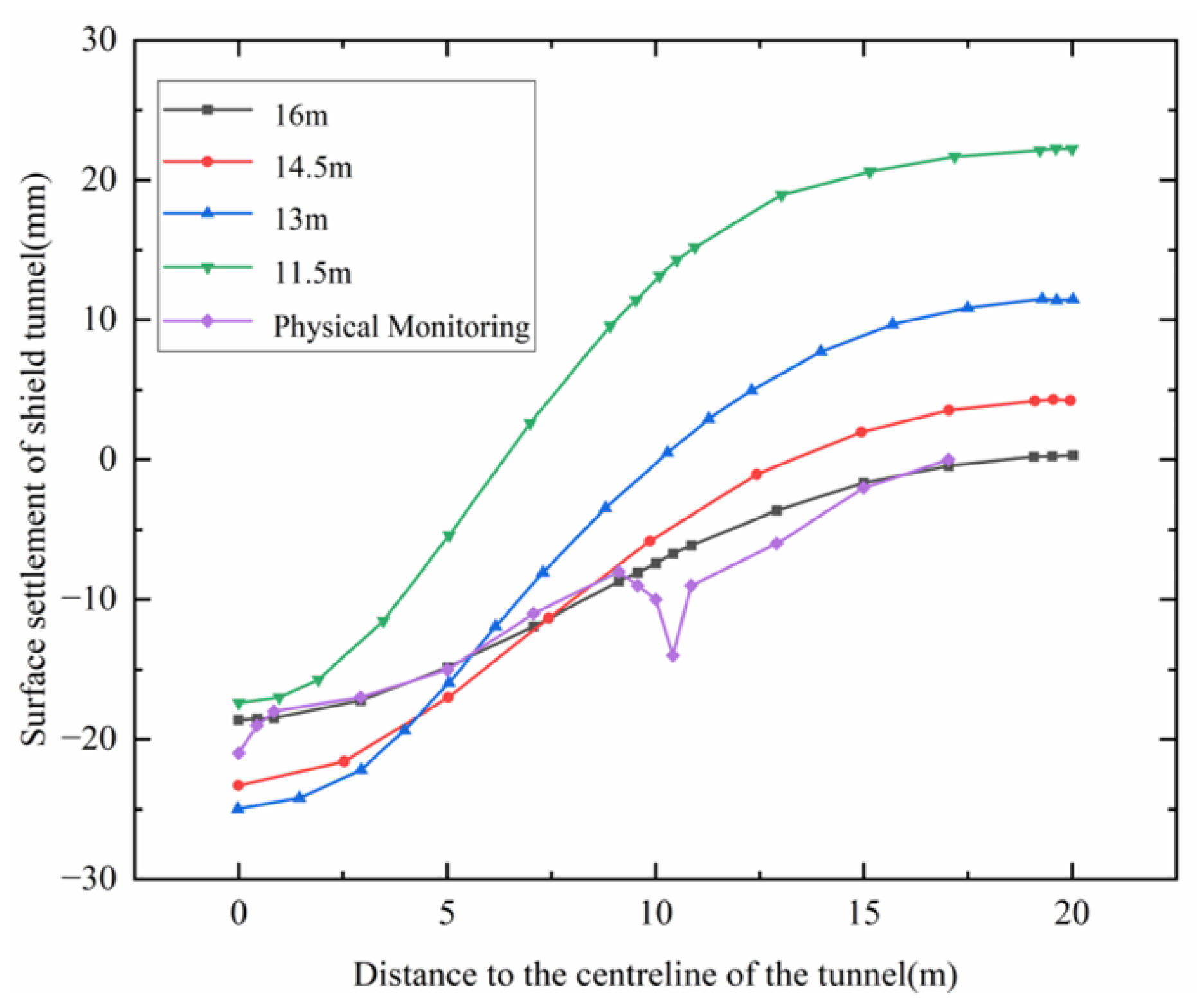
4.2.1. Different Tunnel Depths in Unreinforced Soil
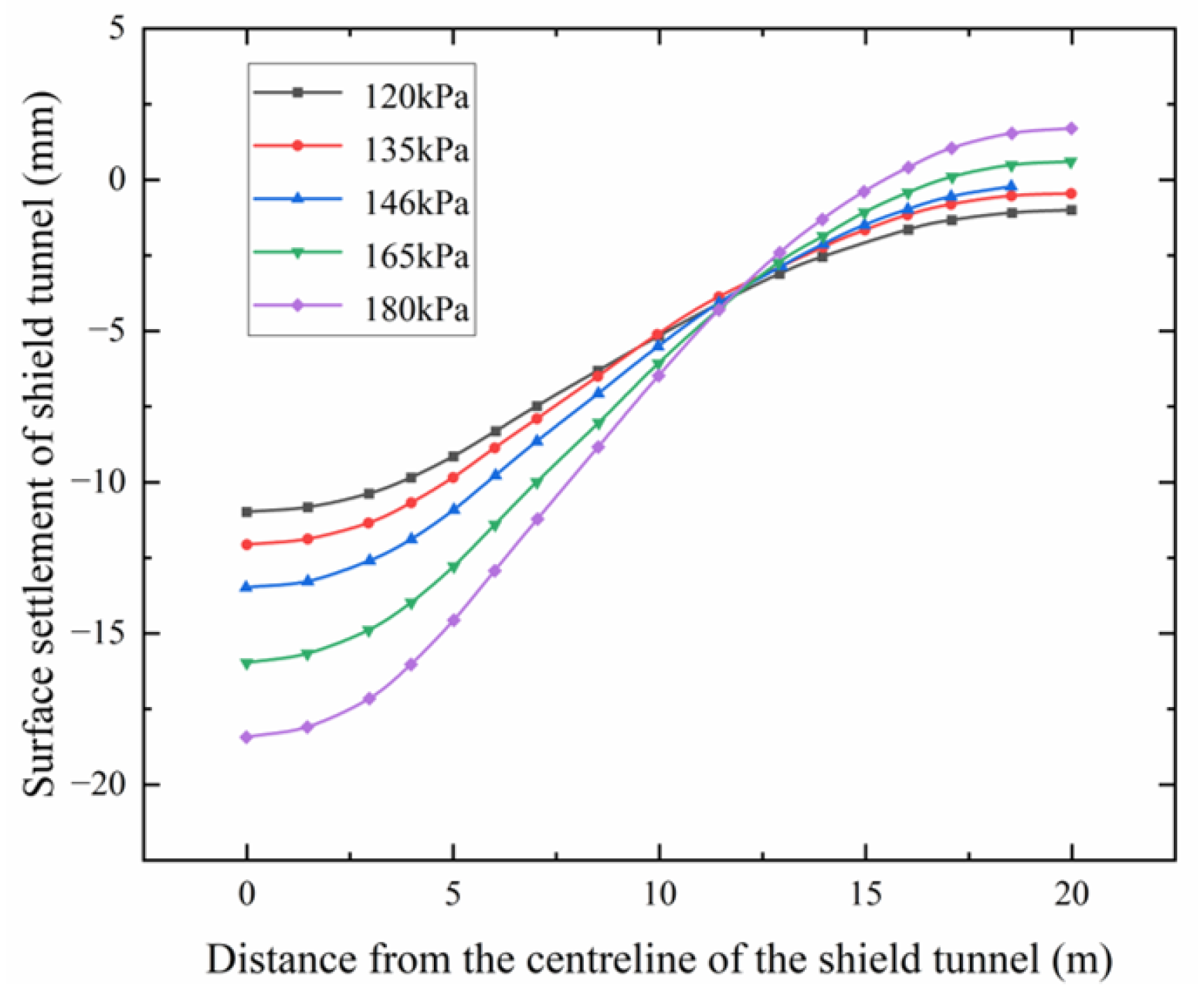
4.2.2. Different Soil Bin Pressures in Unreinforced Soil
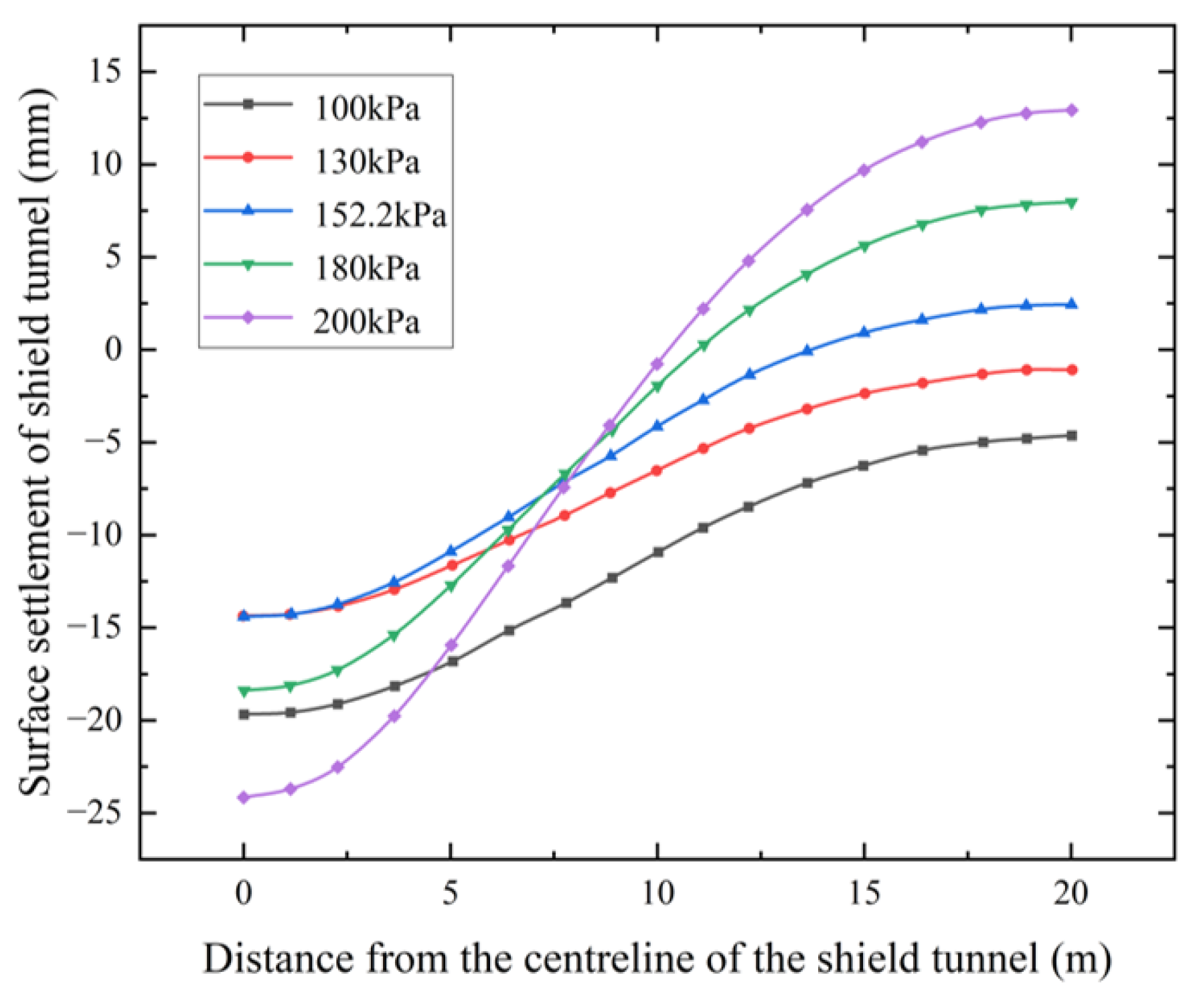
4.2.3. Different Grouting Pressures in Unreinforced Soil
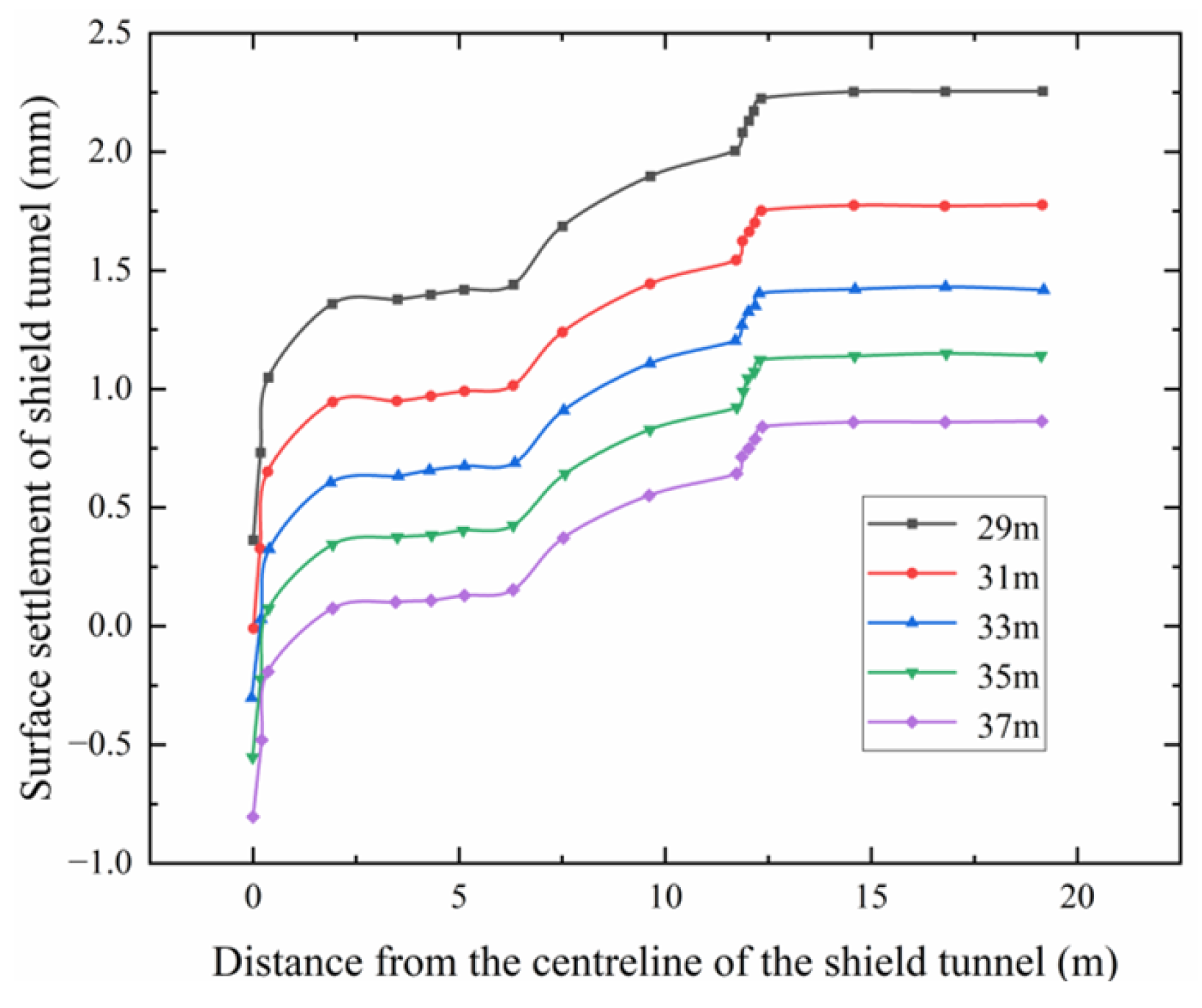
4.3. Analysis of the Amount of Settlement on the Reinforced Surface
4.4. Numerical Simulation Analysis of the Amount of Consolidated Surface Settlement
4.4.1. Different Tunnel Depths in Reinforced Soils
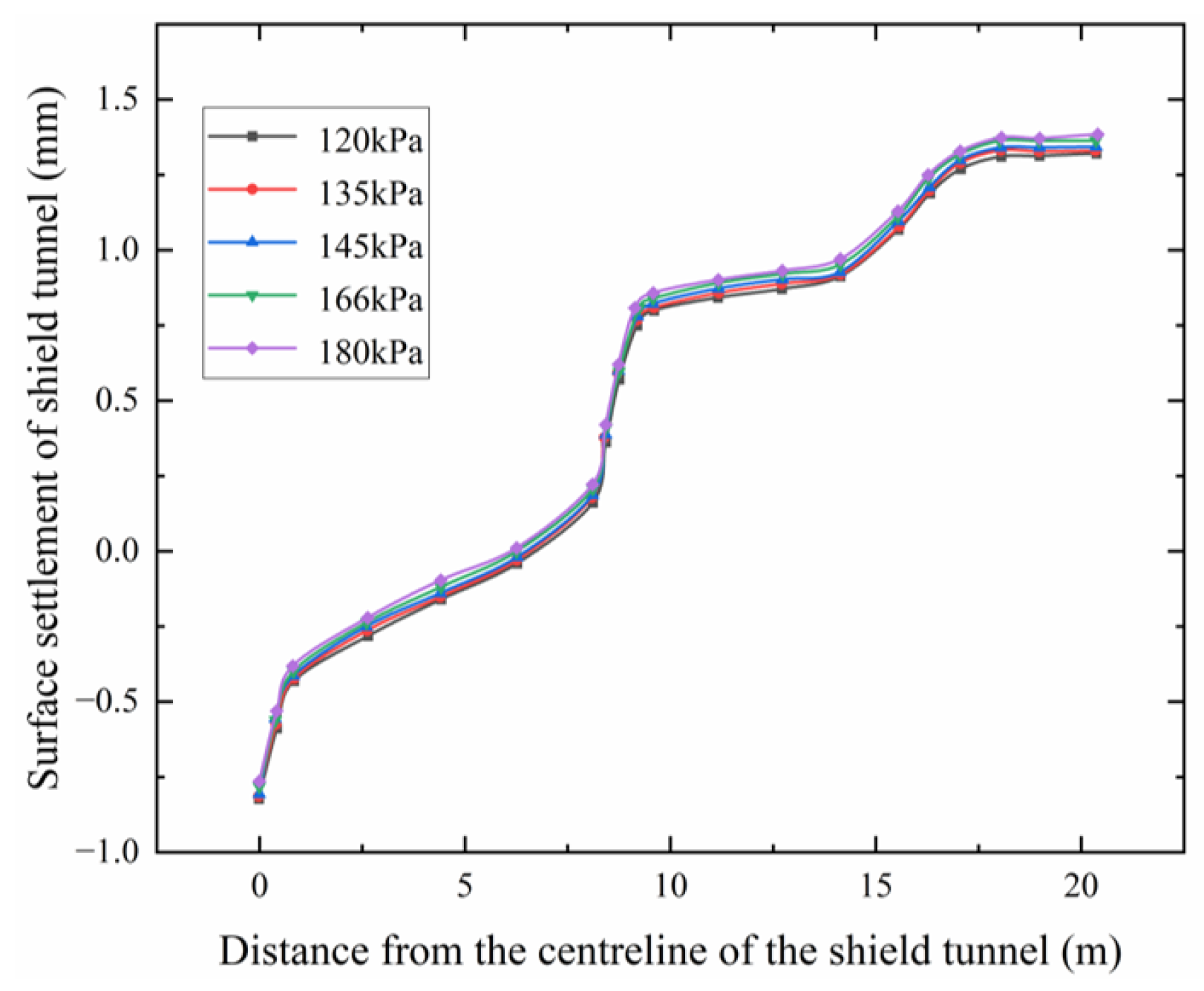
4.4.2. Different Soil Bin Pressures in Reinforced Soils
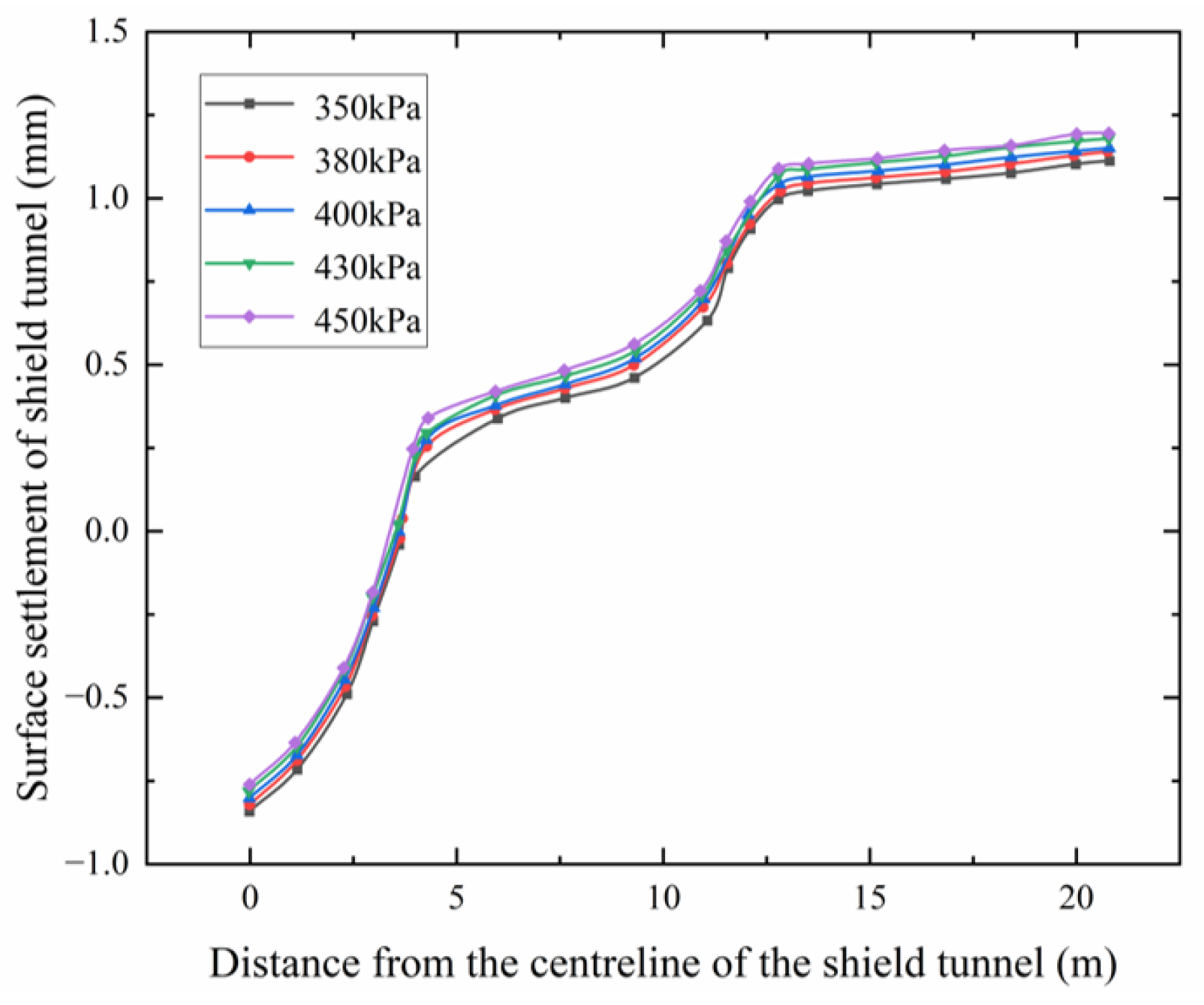
4.4.3. Different Grouting Pressures in Reinforced Soils
5. Analysis of Results
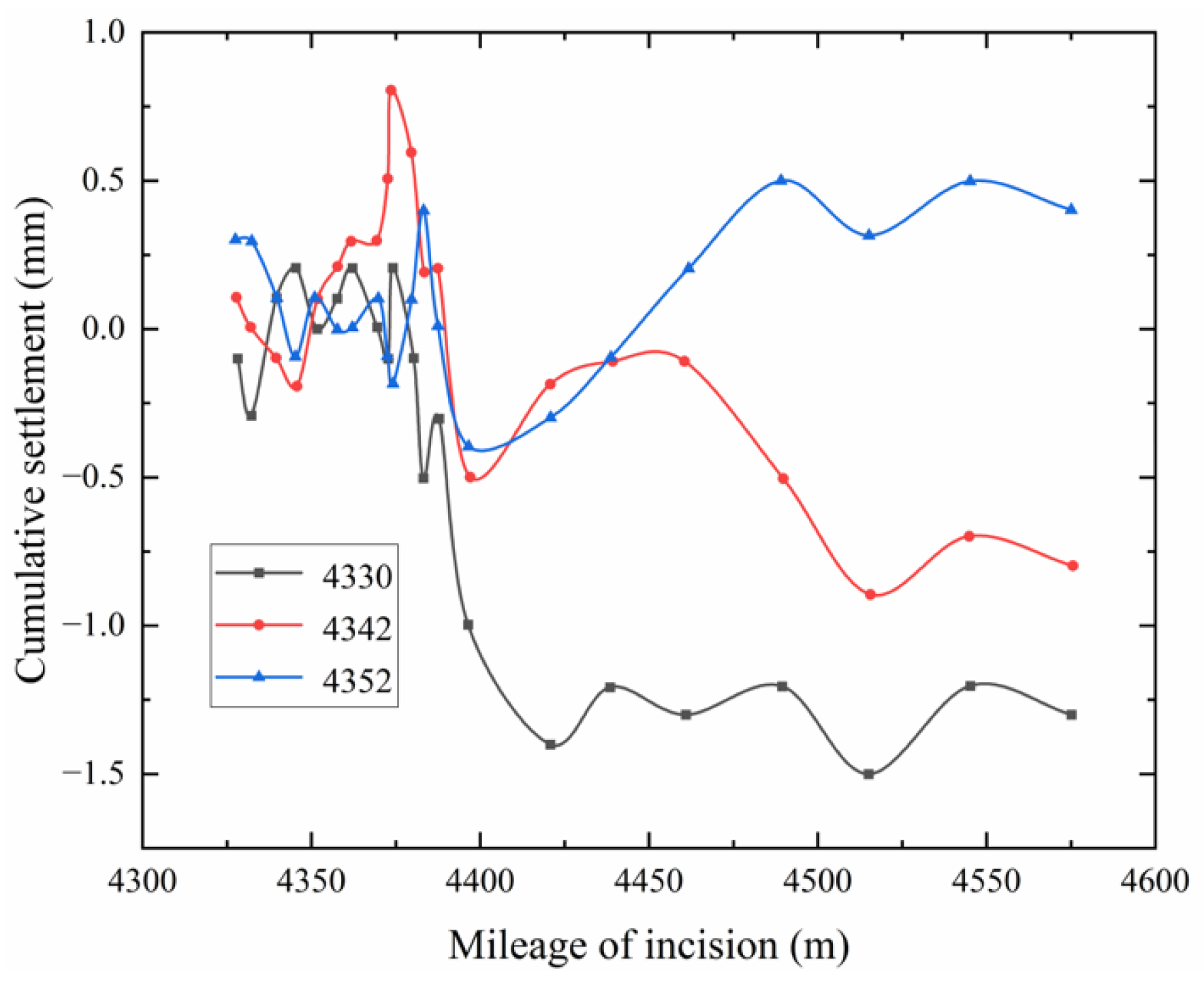
5.1. Comparative Analysis of Field Test Data
5.2. Comparative Analysis of Numerical Simulation Data
- (1)
- As the burial depth of the shield tunnel changes, the surface settlement also varies. Specifically, as the burial depth increases, the soil arch effect at the surface gradually diminishes. Within the burial depth range of 29 m to 37 m, surface settlement is controlled between −1.0 mm and 2.5 mm, indicating a relatively minor change. Moreover, beyond three times the tunnel diameter, surface settlement decays to the stability threshold of ±0.2 mm, with changes in surface settlement gradually stabilizing.
- (2)
- By comparing the effects of silo pressure on surface settlement, it is observed that when silo pressure ranges from 120 kPa to 180 kPa, surface settlement remains between −1.0 mm and 1.5 mm. The variation in surface settlement due to changes in silo pressure is within ±0.2 mm, suggesting that after grouting and strengthening of the surface soil, the impact of silo pressure on surface settlement becomes almost negligible.
- (3)
- When grouting pressure is between 350 kPa and 450 kPa, surface settlement is maintained between −1.0 mm and 1.5 mm. Changes in grouting pressure result in surface settlement variations within ±0.2 mm, indicating that after grouting and reinforcing the surface soil, the influence of grouting pressure on surface settlement is nearly negligible.
- (4)
- After the soil above the shield tunnel is grouted and reinforced, the factors of tunnel depth, grouting pressure, and soil chamber pressure have less influence on the change in surface settlement during shield tunnel excavation, and the effect of early grouting and reinforcement of the soil on the reduction in surface settlement is significant.
5.3. Future Prospects
6. Conclusions
- (1)
- Flower pipe grouting reinforcement technology demonstrates significant efficacy in controlling surface settlement. Research findings indicate that, compared to unreinforced conditions, the implementation of grouting reinforcement reduces average surface settlement by 92%, with maximum settlement controlled within 3 mm. This evidence provides an effective solution for mitigating surface settlement when shield tunnels traverse sensitive areas such as long-distance railroads.
- (2)
- The numerical simulation method demonstrates high reliability in predicting surface settlement caused by shield tunnel construction. The discrepancy between the simulation results and on-site monitoring data is maintained within ±0.5 mm, thereby validating the accuracy of the numerical model and providing a robust technical approach for predicting surface settlement in similar projects.
- (3)
- Under unreinforced conditions, surface settlement exhibits the following trends: tunnel depth is negatively correlated with surface settlement, decreasing by approximately 0.15 mm for every 1 m increase in depth; soil chamber pressure is positively correlated with surface settlement, increasing by approximately 0.08 mm for every 10 kPa increase in pressure; grouting pressure has a critical value of around 400 kPa. Below this critical value, surface settlement decreases as grouting pressure increases; however, once the grouting pressure exceeds this critical value, surface settlement increases with further increases in grouting pressure.
- (4)
- Under flower pipe grouting reinforcement conditions, the influence of tunnel depth, grouting pressure, and soil compartment pressure on surface settlement is markedly diminished, with the degree of impact reduced by approximately 85–95% relative to unreinforced conditions. These results suggest that grouting reinforcement measures can effectively mitigate the effects of construction parameter variations on surface settlement, thereby providing enhanced stability and reliability for shield tunnel construction in sensitive regions.
- (5)
- When the shield tunnel passes through a long-distance railway group, surface grouting reinforcement can effectively reduce the impact caused by shield tunnel excavation, so this engineering method can be usefully and effectively applied to similar projects in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, D.; Zhang, X.; Tang, Y.; Jin, Y.; Cao, K. Study on the Impact of Different Pile Foundation Construction Methods on Neighboring Oil and Gas Pipelines under Very Small Clearances. Appl. Sci. 2024, 14, 3609. [Google Scholar] [CrossRef]
- Liang, R.; Xia, T.; Hong, Y.; Yu, F. Effects of above-crossing tunnelling on the existing shield tunnels. Tunn. Undergr. Space Technol. 2016, 58, 159–176. [Google Scholar]
- Li, X.; Yuan, D. Development of the safety control framework for shield tunneling in close proximity to the operational subway tunnels: Case studies in mainland China. Springerplus 2016, 5, 527. [Google Scholar]
- Liu, B.; Yu, Z.; Han, Y.; Wang, Z.; Zhang, R.; Wang, S. Analytical solution for the response of an existing tunnel induced by above-crossing shield tunneling. Comput. Geotech. 2020, 124, 103624. [Google Scholar]
- Mi, B.; Xiang, Y. Model experiment and calculation analysis of excavation-seepage stability for shallow shield tunneling in sandy ground. Rock Soil Mech. 2020, 41, 4. [Google Scholar]
- Xu, Q.; Zhu, H.; Ma, X.; Ma, Z.; Li, X.; Tang, Z.; Zhuo, K. A case history of shield tunnel crossing through group pile foundation of a road bridge with pile underpinning technologies in Shanghai. Tunn. Undergr. Space Technol. 2015, 45, 20–33. [Google Scholar]
- Zhang, Z.; Huang, M. Geotechnical influence on existing subway tunnels induced by multiline tunneling in Shanghai soft soil. Comput. Geotech. 2014, 56, 121–132. [Google Scholar]
- Fang, Q.; Zhang, D.; Li, Q.; Wong, L.N.Y. Effects of twin tunnels construction beneath existing shield-driven twin tunnels. Tunn. Undergr. Sp. Technol. 2015, 45, 128–137. [Google Scholar]
- Wang, Z.; Zhang, K.; Wei, G.; Li, B.; Li, Q.; Yao, W. Field measurement analysis of the influence of double shield tunnel construction on reinforced bridge. Tunn. Undergr. Space Technol. 2018, 81, 252–264. [Google Scholar]
- Lin, X.; Chen, R.; Wu, H.; Cheng, H. Deformation behaviors of existing tunnels caused by shield tunneling undercrossing with oblique angle. Tunn. Undergr. Space Technol. 2019, 89, 78–90. [Google Scholar]
- Shi, C.; Cao, C.; Lei, M.; Peng, L.; Ai, H. Effects of lateral unloading on the mechanical and deformation performance of shield tunnel segment joints. Tunn. Undergr. Space Technol. 2016, 51, 175–188. [Google Scholar]
- Elwood, D.E.Y.; Martin, C.D. Ground response of closely spaced twin tunnels constructed in heavily overconsolidated soils. Tunn. Undergr. Space Technol. 2016, 51, 226–237. [Google Scholar]
- Fargnoli, V.; Boldini, D.; Amorosi, A. Twin tunnel excavation in coarse grained soils: Observations and numerical back-predictions under free field conditions and in presence of a surface structure. Tunn. Undergr. Space Technol. 2015, 49, 454–469. [Google Scholar]
- Zheng, H.; Li, P.; Ma, G. Stability analysis of the middle soil pillar for asymmetric parallel tunnels by using model testing and numerical simulations. Tunn. Undergr. Space Technol. 2021, 108, 103686. [Google Scholar]
- Yan, B.; Wang, R.; Ding, B.; Dai, F.; Wang, Y. Numerical simulation analysis of tunnel backfill grout based on DEM-FDM coupling and particle inlet. Undergr. Space 2024, 14, 285–299. [Google Scholar]
- Zhang, D.; Huang, Z.; Wang, R.; Yan, J.; Zhang, J. Grouting-based treatment of tunnel settlement: Practice in Shanghai. Tunn. Undergr. Space Technol. 2018, 80, 181–196. [Google Scholar]
- Zhang, X.; Qin, H.; Xu, Y.; Qu, H.; Chen, C. Performance of an operational shield tunnel due to construction of a large cross-sectional straight-walled arch tunnel above-crossing. Alex Eng. J. 2024, 108, 863–877. [Google Scholar]
- Li, Z.; Liu, X.; Wang, J. Elaborate numerical investigation on surcharge-induced mechanical responses and strengthening effects of single-line shield tunnels with typical cross-sections. Tunn. Undergr. Space Technol. 2025, 156, 106237. [Google Scholar]
- Zhang, J.; Yu, J.; Li, C.; Liu, Y.; Tian, L.; He, Y.; Zhang, Q. Deformation and Reinforcement of the Existing Tunnel Affected by New Shield Tunnel Construction with Small Clearance. Buildings 2025, 15, 265. [Google Scholar] [CrossRef]
- Zhu, T.; Huang, F.; Li, S.; Ouyang, T.; Ying, J.; Zhao, H. Optimization of pre-grouting construction and evaluation of grouting effect in a deeply buried silt-filled shield tunnel. Tunn. Undergr. Space Technol. 2024, 152, 105902. [Google Scholar]
- Jin, H.; Yuan, D.; Jin, D.; Wu, J.; Wang, X.; Han, B.; Mao, J. Ground deformation induced by shield tunneling posture in soft soil. Tunn. Undergr. Space Technol. 2023, 139, 105227. [Google Scholar] [CrossRef]
- Liao, S.; Liu, J.; Wang, R.; Li, Z. Shield tunneling and environment protection in Shanghai soft ground. Tunn. Undergr. Space Technol. 2009, 24, 454–465. [Google Scholar]
- Liang, R.; Kang, C.; Xiang, L.; Li, Z.; Lin, C.; Gao, K.; Guo, Y. Responses of in-service shield tunnel to overcrossing tunnelling in soft ground. Environ. Earth Sci. 2021, 80, 183. [Google Scholar] [CrossRef]
- Cao, C.; Shi, C.; Lei, M.; Peng, L.; Bai, R. Deformation Characteristics and Countermeasures of shallow and Large-span Tunnel Under-crossing the Existing Highway in Soft Soil: A Case Study. KSCE J. Civ. Eng. 2018, 22, 3170–3181. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Z.; Yang, Y.; Jiang, Y.; Xu, X.; Hu, Q. Deformation characteristics of existing tunnels induced by above-crossing quasi-rectangular shield tunnel. Transp. Geotech. 2024, 45, 101227. [Google Scholar] [CrossRef]
- Yang, Y.; Liao, S.; Liu, M.; Wu, D.; Pan, W.; Li, H. A new construction method for metro stations in dense urban areas in Shanghai soft ground: Open-cut shafts combined with quasi-rectangular jacking boxes. Tunn. Undergr. Space Technol. 2022, 125, 104530. [Google Scholar] [CrossRef]
- Feng, X.; Wang, P.; Liu, S.; Wei, H.; Miao, Y.; Bu, S. Mechanism and Law Analysis on Ground Settlement Caused by Shield Excavation of Small-Radius Curved Tunnel. Rock Mech. Rock Eng. 2022, 55, 3473–3488. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Liu, K.; Wei, J.; Hu, G.; Pei, S. Application and configuration analysis of electric muck transfer equipment in plateau railway tunnel: A case study in southwest China. Sci. Rep. 2024, 14, 7222. [Google Scholar]
- Yang, J.; Zhang, C.; Fu, J.; Wang, S.; Ou, X.; Xie, Y. Pre-grouting reinforcement of underwater karst area for shield tunneling passing through Xiangjiang River in Changsha, China. Tunn. Undergr. Space Technol. 2020, 100, 103380. [Google Scholar]
- Jin, D.; Yuan, D.; Li, X.; Zheng, H. Analysis of the settlement of an existing tunnel induced by shield tunneling underneath. Tunn. Undergr. Space Technol. 2018, 81, 209–220. [Google Scholar]
- Jallow, A.; Ou, C.; Lim, A. Three-dimensional numerical study of long-term settlement induced in shield tunneling. Tunn. Undergr. Space Technol. 2019, 88, 221–236. [Google Scholar] [CrossRef]
- Li, W.; Wen, H. Research on the Construction Mechanics and Stability Control Technology of Expressway Tunnel Based on Numerical Analysis. Eur. J. Comput. Mech. 2024, 33, 461–482. [Google Scholar] [CrossRef]

| Designation | 1-2 Plain Fill Soil | 3-1 Clay | 3-4 Silty Clay | 7-2 Silty Clay | 7-3 Silty Clay | 8-1 Silty Sand | 8-1a Silty Clay | |
|---|---|---|---|---|---|---|---|---|
| Parameter Name | Unit (of Measure) | |||||||
| Soil heaviness | kN/m3 | 19 | 18.6 | 18 | 18.9 | 19.2 | 21 | 19.4 |
| Modulus of compression | MPa | 4.19 | 5 | 3 | 8.5 | 6.0 | 16 | 6 |
| Poisson’s ratio | 0.34 | 0.33 | 0.36 | 0.34 | 0.35 | 0.3 | 0.33 | |
| Cohesive force | kN/m2 | 12 | 19 | 12 | 16 | 23 | 22 | 25 |
| Friction angle | ° | 8 | 10 | 6 | 9 | 13 | 31 | 15 |
| Materials | Density/(kg/m3) | Modulus of Elasticity/MPa | Poisson’s Ratio | |
|---|---|---|---|---|
| Tube sheet | 2500 | 3.45 × 104 | 0.3 | |
| Grouting materials | pre-hardening | 2000 | 1.20 | 0.3 |
| post-hardening | 2000 | 6.00 | 0.4 | |
| Shield | 7850 | 2 × 105 | 0.3 | |
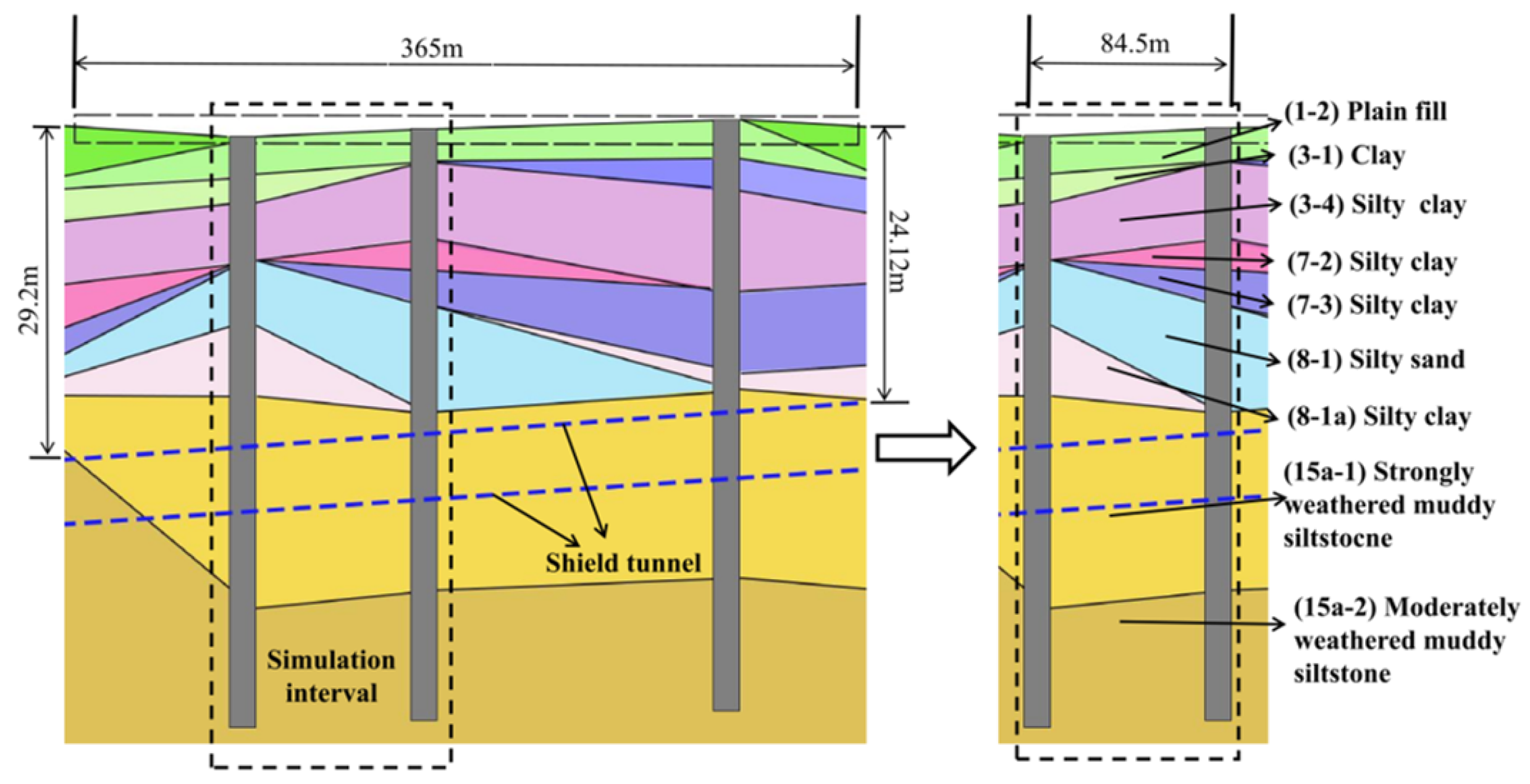
| Layers | Borehole-1 | Borehole-2 | Borehole-3 | Borehole-4 | ||||
|---|---|---|---|---|---|---|---|---|
| Materials | Top (m) | Bottom (m) | Top (m) | Bottom (m) | Top (m) | Bottom (m) | Top (m) | Bottom (m) |
| (1-2) Plain fill | 0.00 | −3.20 | 0.00 | −3.20 | 0.00 | −3.50 | 0.00 | −3.50 |
| (3-1) Silty clay | −3.20 | −3.20 | −3.20 | −3.20 | −3.50 | −6.00 | −3.50 | −6.00 |
| (3-4) Silty clay | −3.20 | −10.40 | −3.20 | −10.40 | −6.00 | −11.30 | −6.00 | −11.30 |
| (7-2) Silty clay | −10.40 | −13.40 | −10.40 | −13.40 | −11.30 | −11.30 | −11.30 | −11.30 |
| (7-3) Silty clay | −13.40 | −16.60 | −13.40 | −16.60 | −11.30 | −11.30 | −11.30 | −11.30 |
| (8-1) Silty sand | −16.60 | −26.50 | −16.60 | −26.50 | −11.30 | −17.00 | −11.30 | −17.00 |
| (8-1a) Silty clay | −26.50 | −26.50 | −26.50 | −26.50 | −17.00 | −23.80 | −17.00 | −23.80 |
| (15a-1) Strongly weathered muddy siltstone | −26.50 | −42.90 | −26.50 | −42.90 | −23.80 | −43.80 | −23.80 | −43.80 |
| (15a-1) Moderately weathered muddy siltstone | −42.90 | −50.00 | −42.90 | −50.00 | −43.80 | −50.00 | −43.80 | −50.00 |
| Programmes | Depth of Burial of Tunnels (m) | Radius of the Tunnel (m) | Grouting Pressure (kPa) | Pressure on Soil Chamber (kPa) |
|---|---|---|---|---|
| Scenario 1 | 11.5 | 3.1 | 152.2 | 146 |
| Scenario 2 | 13 | 3.1 | 152.2 | 146 |
| Scenario 3 | 14.5 | 3.1 | 152.2 | 146 |
| Scenario 4 | 16 | 3.1 | 152.2 | 146 |
| Programmes | Depth of Burial of Tunnels (m) | Radius of the Tunnel (m) | Grouting Pressure (kPa) | Pressure on Soil Chamber (kPa) |
|---|---|---|---|---|
| Scenario 1 | 16 | 3.1 | 152.2 | 120 |
| Scenario 2 | 16 | 3.1 | 152.2 | 135 |
| Scenario 3 | 16 | 3.1 | 152.2 | 146 |
| Scenario 4 | 16 | 3.1 | 152.2 | 165 |
| Scenario 5 | 16 | 3.1 | 152.2 | 180 |
| Programmes | Depth of Burial of Tunnels (m) | Radius of the Tunnel (m) | Grouting Pressure (kPa) | Pressure on Soil Chamber (kPa) |
|---|---|---|---|---|
| Scenario 1 | 16 | 3.1 | 100 | 146 |
| Scenario 2 | 16 | 3.1 | 130 | 146 |
| Scenario 3 | 16 | 3.1 | 152.2 | 146 |
| Scenario 4 | 16 | 3.1 | 180 | 146 |
| Scenario 5 | 16 | 3.1 | 200 | 146 |
| Programmes | Depth of Burial of Tunnels (m) | Radius of the Tunnel (m) | Grouting Pressure (kPa) | Pressure on Soil Chamber (kPa) |
|---|---|---|---|---|
| Scenario 1 | 29 | 3.1 | 400 | 166 |
| Scenario 2 | 31 | 3.1 | 400 | 166 |
| Scenario 3 | 33 | 3.1 | 400 | 166 |
| Scenario 4 | 35 | 3.1 | 400 | 166 |
| Scenario 5 | 37 | 3.1 | 400 | 166 |
| Programmes | Depth of Burial of Tunnels (m) | Radius of the Tunnel (m) | Grouting Pressure (kPa) | Pressure on Soil Chamber (kPa) |
|---|---|---|---|---|
| Scenario 1 | 35 | 3.1 | 400 | 120 |
| Scenario 2 | 35 | 3.1 | 400 | 135 |
| Scenario 3 | 35 | 3.1 | 400 | 145 |
| Scenario 4 | 35 | 3.1 | 400 | 166 |
| Scenario 5 | 35 | 3.1 | 400 | 180 |
| Programmes | Depth of Burial of Tunnels (m) | Radius of the Tunnel (m) | Grouting Pressure (kPa) | Pressure on Soil Chamber (kPa) |
|---|---|---|---|---|
| Scenario 1 | 35 | 3.1 | 350 | 166 |
| Scenario 2 | 35 | 3.1 | 380 | 166 |
| Scenario 3 | 35 | 3.1 | 400 | 166 |
| Scenario 4 | 35 | 3.1 | 430 | 166 |
| Scenario 5 | 35 | 3.1 | 450 | 166 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Q.; Zhang, X.; Shu, H. Innovative Grouting Reinforcement Techniques for Shield Tunnels: A Case Study on Surface Settlement Mitigation. Appl. Sci. 2025, 15, 4623. https://doi.org/10.3390/app15094623
Ma Q, Zhang X, Shu H. Innovative Grouting Reinforcement Techniques for Shield Tunnels: A Case Study on Surface Settlement Mitigation. Applied Sciences. 2025; 15(9):4623. https://doi.org/10.3390/app15094623
Chicago/Turabian StyleMa, Qiang, Xingchi Zhang, and Hang Shu. 2025. "Innovative Grouting Reinforcement Techniques for Shield Tunnels: A Case Study on Surface Settlement Mitigation" Applied Sciences 15, no. 9: 4623. https://doi.org/10.3390/app15094623
APA StyleMa, Q., Zhang, X., & Shu, H. (2025). Innovative Grouting Reinforcement Techniques for Shield Tunnels: A Case Study on Surface Settlement Mitigation. Applied Sciences, 15(9), 4623. https://doi.org/10.3390/app15094623







