Electric Vehicle Routing with Time Windows and Charging Stations from the Perspective of Customer Satisfaction
Abstract
:1. Introduction
- Unlike the cost-focused objective functions in the literature, the objective function of minimizing total tardiness is studied. It takes customer satisfaction into account by considering customer time windows.
- Since the ALNS operators proposed in the literature are not effective for the total tardiness objective function, new operators are proposed to serve this objective function.
2. Related Works
2.1. Studies on Capacitated Electric Vehicle Routing Problem with Time Windows
2.2. Studies on ALNS for CEVRPTW
3. Materials and Methods
3.1. Problem Description
- The demand of each customer is known in advance, and the customer demand cannot be divided (only one vehicle can serve each customer).
- The distances between customers and between the warehouse and the customers are fixed and known in advance.
- Each vehicle has the same capacity and is ready for service in the warehouse.
- Vehicles have a specific battery capacity. The vehicles’ state of charge (SoC) should be considered in route planning.
- In the case of charging needs, a full or partial charging strategy can be applied from the charging strategies.
3.2. Proposed Adaptive Large Neighborhood Search
| Algorithm 1. Proposed hybrid ALNS algorithm |
| Input: , , , , , , , , Initialize , , , , ←, ← , ← repeat if (mod ) then Select route removal operator using Roulette Wheel Selection Select customer insertion operator using Roulette Wheel Selection ← )) else if (mod ) then Select station removal operator using Roulette Wheel Selection Select station insertion operator using Roulette Wheel Selection ← )) else Select customer removal operator using Roulette Wheel Selection Select customer insertion operator using Roulette Wheel Selection ← )) end if end if acceptance rate ← if f() < f() or acceptance rate > random(0,1) then ← if f() < f() then ← end if ← 0 else ← + 1 end if if (mod β) then ← Apply VNS-Based Local Search Procedure end if if (mod ) then Update , , with scores end if until stopping criteria is met; return |
3.2.1. Initial Solution
| Algorithm 2. The proposed heuristic algorithm for initial solution generation |
| Input: Sort all by their in ascending order Calculate the of customers for in do end for for in sorted do if adding the to does not exceed then Append the to else Append the to the new route: end if end for return |
3.2.2. Neighborhood Solutions
3.2.3. Removal Operators
- Tardiness versus Worst-Distance-Customer Removal: The proposed operator evaluates the cost impact of each customer across all routes by considering both their earliest service start time and their distance from the preceding node. The objective is to identify and remove the customer whose presence contributes the most to increased route costs. By eliminating customers with late service start times from the beginning of a route, this approach enhances schedule efficiency and minimizes overall tardiness. The pseudocode is given in Algorithm 3.
| Algorithm 3. Tardiness versus Worst-Distance-Customer Removal |
| Input: the number of customers to be removed from the solution for each in do for each in do if is Customer then ← Find before node ← Append (node, cost) to end if end for end for ← Sort by cost descending ← Remove every in Update and |
- 2.
- Tank-Capacity-Violation-Customer Removal: Unlike other removal strategies, the operator targets inconvenient routes requiring charging stations. It removes the first node and all subsequent nodes from the solution on routes where the vehicle cannot complete its route within the available battery capacity. The goal is to optimize charging efficiency by shortening routes that require charging and eliminating unnecessary charging station visits. This results in more efficient energy use and improves overall route feasibility. The pseudocode is given in Algorithm 4.
| Algorithm 4. Tank-Capacity-Violation-Customer Removal |
| Input: , , for each in routes do if tank capacity violation on the route then ← Find node where SoC is negative if == then ← Get in route Remove else ← Get index Remove end if end if end for Update and |
- 3.
- Time-Window-Violation-Customer Removal: The operator targets infeasible routes where time window constraints are violated. It identifies the first overdue customer and removes both that customer and all subsequent customers from the route. The goal is to improve the feasibility and efficiency of the overall route plan by reconfiguring routes to ensure compliance with time window constraints. Eliminating delayed customer sequences improves compliance with service time requirements and helps minimize overall tardiness. The pseudocode is given in Algorithm 5.
| Algorithm 5. Time-Window-Violation-Customer Removal |
| Input: , , for each in do if time window violation on the then ← Find node where time window violation if == then ← Get in Remove else ← Get index Remove end if end if end for Update and |
- Max-Tardiness-Route Removal: The proposed operator examines each of the routes in the solution and calculates their tardiness. It sums up the total tardiness on a route and keeps the tardiness on the route as costs. It removes the routes with the highest tardiness from the solution. The pseudocode is given in Algorithm 6.
| Algorithm 6. Max-Tardiness-Route Removal |
| Input: W ← Calculate number of routes to be removed from the solution ← [ ] for each in do ← Calculate total tardiness of the Append (, ) to end for ← Sort by cost descending ← Remove every route in Update and |
- 2.
- Infeasible-Route Removal: The proposed operator examines each of the routes in the solution in terms of state of charge status, load capacity, and time window. It removes infeasible routes from the solution. This operator paves the way for the deconstruction of infeasible solutions. The pseudocode is given in Algorithm 7.
| Algorithm 7. Infeasible-Route Removal |
| Input: W ← Calculate number of routes to be removed from the solution ← [ ] for each in do if is not feasible by (tank capacity, payload capacity time window) then Append to end if end for ← Remove every in Update and |
3.2.4. Insertion Operators
- Best-Customer Insertion: The proposed operator examines all routes for each customer in the unserved customer list. For all locations in the routes, the distance to the customer to be added multiplied by the earliest start time to service value is taken as the cost. If the current location is a station or a warehouse, the cost is calculated by taking the nearest customer’s earliest start time to service value. This operator aims to ensure not only distance cost but also time window compatibility in the current route. The pseudocode is given in Algorithm 8.
| Algorithm 8. Best-Customer Insertion |
| Input: ← [ ] ← [ ] for each in do for in do for in do if is Customer then ← Find before node ← Calculate distance from to cost ← if not payload capacity violation then Append to end if end if end for end for if != [ ] then Append every in at position else Append to end if end for while != [ ] do ← [ ] Append every in while payload-capacity violation end while Update and |
- 2.
- Time-Window-Greedy-Customer Insertion: Following the time window constraints, the proposed operator inserts each unserved customer into the first available position in the routes. The insertion decision is made by evaluating the latest start time to service value of customer i and the travel time between customers and . A feasible insertion is determined based on the condition . Thus, instead of only considering the latest start time to service value, the travel time is also considered to obtain a suitable time window. The pseudocode is given in Algorithm 9.
| Algorithm 9. Time-Window-Greedy-Customer Insertion |
| Input: for each in do for in do for in do if is Customer then ← Calculate travel time between and if () then Insert into at position of end if end if end for end for end for Update and |
- 3.
- Time-Window-Feasible-Customer Insertion: The proposed operator differs from the Time-Window-Greedy-Customer Insertion by first reordering the unserved customers based on their latest start time to service value. After sorting, the operator evaluates all feasible insertion positions across the available routes. The insertion process ensures that the updated route remains feasible in terms of both time window constraints and vehicle load capacity. The pseudocode is given in Algorithm 10.
| Algorithm 10: Time-Window-Feasible-Customer Insertion |
| Input: ← [ ] ← Sort by latest start time to service for each in do for in do Find the cost of into every position of route if == [ ] then Append to else Insert to end if end for end for while != [ ] do ← [ ] Append every in while payload capacity violation end while Update and |
3.2.5. Local Search
| Algorithm 11. VNS-based LS |
| Input: , while do Select LS operator using Roulette Wheel Selection ← Local_Search() if f() < f() then ← ← 1 else ← + 1 end if end while return |
4. Experimental Results
4.1. Validation of the Adaptive Large Neighborhood Search
4.2. Trade-Offs Between Cost-Oriented and Customer-Oriented Solutions
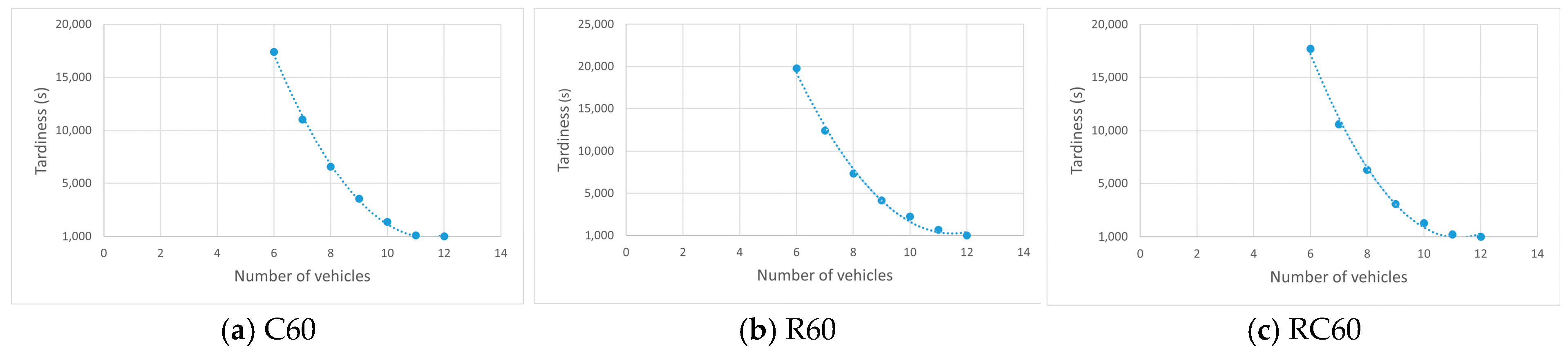
4.3. Evaluation Perspective from Fleet Management
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chandran, M.; Palanisamy, K.; Benson, D.; Sundaram, S. A Review on Electric and Fuel Cell Vehicle Anatomy, Technology Evolution and Policy Drivers towards EVs and FCEVs Market Propagation. Chem. Rec. 2022, 22, e202100235. [Google Scholar] [CrossRef]
- Oliveira, C.M.D.; Albergaria De Mello Bandeira, R.; Vasconcelos Goes, G.; Schmitz Gonçalves, D.N.; D’Agosto, M.D.A. Sustainable Vehicles-Based Alternatives in Last Mile Distribution of Urban Freight Transport: A Systematic Literature Review. Sustainability 2017, 9, 1324. [Google Scholar] [CrossRef]
- Zhao, D.; Li, H.; Hou, J.; Gong, P.; Zhong, Y.; He, W.; Fu, Z. A Review of the Data-Driven Prediction Method of Vehicle Fuel Consumption. Energies 2023, 16, 5258. [Google Scholar] [CrossRef]
- Almaghrebi, A. The Impact of PEV User Charging Behavior in Building Public Charging Infrastructure. Master’s Thesis, University of Nebraska-Lincoln, Lincoln, NE, USA, 2020. [Google Scholar]
- Schiffer, M.; Walther, G. The Electric Location Routing Problem with Time Windows and Partial Recharging. Eur. J. Oper. Res. 2017, 260, 995–1013. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, X.; Zhou, X. Distribution Route Optimization for Electric Vehicles in Urban Cold Chain Logistics for Fresh Products under Time-Varying Traffic Conditions. Math. Probl. Eng. 2020, 2020, 9864935. [Google Scholar] [CrossRef]
- Cokyasar, T.; Subramanyam, A.; Larson, J.; Stinson, M.; Sahin, O. Time-Constrained Capacitated Vehicle Routing Problem in Urban e-Commerce Delivery. Transp. Res. Rec. 2023, 2677, 190–203. [Google Scholar] [CrossRef]
- Florio, A.M.; Absi, N.; Feillet, D. Routing Electric Vehicles on Congested Street Networks. Transp. Sci. 2021, 55, 238–256. [Google Scholar] [CrossRef]
- Erdelic, T.; Carić, T.; Lalla-Ruiz, E. A Survey on the Electric Vehicle Routing Problem: Variants and Solution Approaches. J. Adv. Transp. 2019, 2019, 5075671. [Google Scholar] [CrossRef]
- Bogyrbayeva, A.; Meraliyev, M.; Mustakhov, T.; Dauletbayev, B. Learning to Solve Vehicle Routing Problems: A Survey. arXiv 2022, arXiv:2205.02453. [Google Scholar] [CrossRef]
- Kalaycı, C.B.; Yılmaz, Y. A Review on the Electric Vehicle Routing Problems. Pamukkale Univ. J. Eng. Sci. 2023, 29, 855–869. [Google Scholar] [CrossRef]
- Figliozzi, M.A.; Conrad, R.G. The Recharging Vehicle Routing Problem. In Proceedings of the 2011 Industrial Engineering Research Conference, Reno, NV, USA, 21–25 May 2011. [Google Scholar]
- Schneider, M.; Stenger, A.; Goeke, D. The Electric Vehicle-Routing Problem with Time Windows and Recharging Stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Felipe, Á.; Ortuño, M.T.; Righini, G.; Tirado, G. A Heuristic Approach for the Green Vehicle Routing Problem with Multiple Technologies and Partial Recharges. Transp. Res. E Logist. Transp. Rev. 2014, 71, 111–128. [Google Scholar] [CrossRef]
- Goeke, D.; Schneider, M. Routing a Mixed Fleet of Electric and Conventional Vehicles. Eur. J. Oper. Res. 2015, 245, 81–99. [Google Scholar] [CrossRef]
- Hiermann, G.; Puchinger, J.; Ropke, S.; Hartl, R.F. The Electric Fleet Size and Mix Vehicle Routing Problem with Time Windows and Recharging Stations. Eur. J. Oper. Res. 2016, 252, 995–1018. [Google Scholar] [CrossRef]
- Keskin, M.; Çatay, B. Partial Recharge Strategies for the Electric Vehicle Routing Problem with Time Windows. Transp. Res. Part C Emerg. Technol. 2016, 65, 111–127. [Google Scholar] [CrossRef]
- Barco, J.; Guerra, A.; Muñoz, L.; Quijano, N. Optimal Routing and Scheduling of Charge for Electric Vehicles: A Case Study. Math. Probl. Eng. 2017, 2017, 8509783. [Google Scholar] [CrossRef]
- Montoya, A.; Guéret, C.; Mendoza, J.E.; Villegas, J.G. The Electric Vehicle Routing Problem with Nonlinear Charging Function. Transp. Res. Part B Methodol. 2017, 103, 87–110. [Google Scholar] [CrossRef]
- Keskin, M.; Çatay, B. A Matheuristic Method for the Electric Vehicle Routing Problem with Time Windows and Fast Chargers. Comput. Oper. Res. 2018, 100, 172–188. [Google Scholar] [CrossRef]
- Kancharla, S.R.; Ramadurai, G. An Adaptive Large Neighborhood Search Approach for Electric Vehicle Routing with Load-Dependent Energy Consumption. Transp. Dev. Econ. 2018, 4, 10. [Google Scholar] [CrossRef]
- Kancharla, S.R.; Ramadurai, G. Electric Vehicle Routing Problem with Non-Linear Charging and Load-Dependent Discharging. Expert Syst. Appl. 2020, 160, 113714. [Google Scholar] [CrossRef]
- Futalef, J.P.; Munoz-Carpintero, D.; Rozas, H.; Orchard, M. An Evolutionary Algorithm for the Electric Vehicle Routing Problem with Battery Degradation and Capacitated Charging Stations. Annu. Conf. PHM Soc. 2020, 12, 9. [Google Scholar] [CrossRef]
- Bac, U.; Erdem, M. Optimization of Electric Vehicle Recharge Schedule and Routing Problem with Time Windows and Partial Recharge: A Comparative Study for an Urban Logistics Fleet. Sustain. Cities Soc. 2021, 70, 102883. [Google Scholar] [CrossRef]
- Keskin, M.; Çatay, B.; Laporte, G. A Simulation-Based Heuristic for the Electric Vehicle Routing Problem with Time Windows and Stochastic Waiting Times at Recharging Stations. Comput. Oper. Res. 2021, 125, 105060. [Google Scholar] [CrossRef]
- Zang, Y.; Wang, M.; Qi, M. A Column Generation Tailored to Electric Vehicle Routing Problem with Nonlinear Battery Depreciation. Comput. Oper. Res. 2022, 137, 105527. [Google Scholar] [CrossRef]
- Erdelić, T.; Carić, T. Goods Delivery with Electric Vehicles: Electric Vehicle Routing Optimization with Time Windows and Partial or Full Recharge. Energies 2022, 15, 285. [Google Scholar] [CrossRef]
- Cataldo-Díaz, C.; Linfati, R.; Escobar, J.W. Mathematical Model for the Electric Vehicle Routing Problem Considering the State of Charge of the Batteries. Sustainability 2022, 14, 1645. [Google Scholar] [CrossRef]
- Dönmez, S.; Koç, Ç.; Altıparmak, F. The Mixed Fleet Vehicle Routing Problem with Partial Recharging by Multiple Chargers: Mathematical Model and Adaptive Large Neighborhood Search. Transp. Res. E Logist. Transp. Rev. 2022, 167, 102917. [Google Scholar] [CrossRef]
- Duan, Y.R.; Hu, Y.S.; Wu, P. An Adaptive Large Neighborhood Search Heuristic for the Electric Vehicle Routing Problems with Time Windows and Recharging Strategies. J. Adv. Transp. 2023, 2023, 1–16. [Google Scholar] [CrossRef]
- Yu, V.F.; Anh, P.T.; Chen, Y.W. The Electric Vehicle Routing Problem with Time Windows, Partial Recharges, and Parcel Lockers. Appl. Sci. 2023, 13, 9190. [Google Scholar] [CrossRef]
- Xiao, J.; Du, J.; Cao, Z.; Zhang, X.; Niu, Y. A Diversity-Enhanced Memetic Algorithm for Solving Electric Vehicle Routing Problems with Time Windows and Mixed Backhauls. Appl. Soft Comput. 2023, 134, 110025. [Google Scholar] [CrossRef]
- Wang, D.; Zheng, W.; Zhou, H. Robust Optimization for Electric Vehicle Routing Problem Considering Time Windows Under Energy Consumption Uncertainty. Appl. Sci. 2025, 15, 761. [Google Scholar] [CrossRef]
- Erdoĝan, S.; Miller-Hooks, E. A Green Vehicle Routing Problem. Transp. Res. E Logist. Transp. Rev. 2012, 48, 100–114. [Google Scholar] [CrossRef]
- Toth, P.; Vigo, D. Vehicle Routing: Problems, Methods, and Applications; SIAM: Philadelphia, PA, USA, 2014; ISBN 1611973589. [Google Scholar]
- Laporte, G. Fifty Years of Vehicle Routing. Transp. Sci. 2009, 43, 408–416. [Google Scholar] [CrossRef]
- Cordeau, J.-F.; Laporte, G.; Savelsbergh, M.W.P.; Vigo, D. Vehicle Routing. Handb. Oper. Res. Manag. Sci. 2007, 14, 367–428. [Google Scholar]
- Lin, C.; Choy, K.L.; Ho, G.T.S.; Chung, S.H.; Lam, H.Y. Survey of Green Vehicle Routing Problem: Past and Future Trends. Expert Syst. Appl. 2014, 41, 1118–1138. [Google Scholar] [CrossRef]
- Kim, G. Electric Vehicle Routing Problem with States of Charging Stations. Sustainability 2024, 16, 3439. [Google Scholar] [CrossRef]
- Koç, Ç.; Bektaş, T.; Laporte, G. Decarbonizing Road Freight Transportation: Recent Advances and Future Trends. J. Oper. Res. Soc. 2024, 1–21. [Google Scholar] [CrossRef]
- Guo, S.; Hu, H.; Xue, H. A Two-Echelon Multi-Trip Capacitated Vehicle Routing Problem with Time Windows for Fresh E-Commerce Logistics under Front Warehouse Mode. Systems 2024, 12, 205. [Google Scholar] [CrossRef]
- Ropke, S.; Pisinger, D. An Adaptive Large Neighborhood Search Heuristic for the Pickup and Delivery Problem with Time Windows. Transp. Sci. 2006, 40, 455–472. [Google Scholar] [CrossRef]
- Santini, A.; Ropke, S.; Hvattum, L.M. A Comparison of Acceptance Criteria for the Adaptive Large Neighbourhood Search Metaheuristic. J. Heuristics 2018, 24, 783–815. [Google Scholar] [CrossRef]
- Turkeš, R.; Sörensen, K.; Hvattum, L.M. Meta-Analysis of Metaheuristics: Quantifying the Effect of Adaptiveness in Adaptive Large Neighborhood Search. Eur. J. Oper. Res. 2021, 292, 423–442. [Google Scholar] [CrossRef]
- Windras Mara, S.T.; Norcahyo, R.; Jodiawan, P.; Lusiantoro, L.; Rifai, A.P. A Survey of Adaptive Large Neighborhood Search Algorithms and Applications. Comput. Oper. Res. 2022, 146, 105903. [Google Scholar] [CrossRef]
- Voigt, S. A Review and Ranking of Operators in Adaptive Large Neighborhood Search for Vehicle Routing Problems. Eur. J. Oper. Res. 2024, 322, 357–375. [Google Scholar] [CrossRef]
- Pisinger, D.; Ropke, S. A General Heuristic for Vehicle Routing Problems. Comput. Oper. Res. 2007, 34, 2403–2435. [Google Scholar] [CrossRef]
- Qu, Y.; Bard, J.F. A GRASP with Adaptive Large Neighborhood Search for Pickup and Delivery Problems with Transshipment. Comput. Oper. Res. 2012, 39, 2439–2456. [Google Scholar] [CrossRef]
- Avci, M.G.; Avci, M. An Adaptive Large Neighborhood Search Approach for Multiple Traveling Repairman Problem with Profits. Comput. Oper. Res. 2019, 111, 367–385. [Google Scholar] [CrossRef]
- Erdem, M.; Koç, Ç. Home Health Care and Dialysis Routing with Electric Vehicles and Private and Public Charging Stations. Transp. Lett. 2023, 15, 423–438. [Google Scholar] [CrossRef]
- Erdem, M.; Koç, Ç.; Yücel, E. The Electric Home Health Care Routing and Scheduling Problem with Time Windows and Fast Chargers. Comput. Ind. Eng. 2022, 172, 108580. [Google Scholar] [CrossRef]
- Aslan, O.; Sarıçiçek, İ.; Yazıcı, A. ESOGU-CEVRPTW. Mendeley Data, V1. 2025. Available online: https://data.mendeley.com/datasets/7vjzvxh72d/1 (accessed on 12 April 2025).
- Aslan Yıldız, Ö.; Sarıçiçek, İ.; Yazıcı, A. A Reinforcement Learning-Based Solution for the Capacitated Electric Vehicle Routing Problem from the Last-Mile Delivery Perspective. Appl. Sci. 2025, 15, 1068. [Google Scholar] [CrossRef]
- Electric Vehicle Routing with Charging Stations from The Perspective of Customer Satisfaction. Available online: https://www.youtube.com/watch?v=Jryn4s9A6Os (accessed on 17 February 2025).
- Lu, F.; Du, Z.; Wang, Z.; Wang, L.; Wang, S. Towards enhancing the crowdsourcing door-to-door delivery: An effective model in Beijing. J. Ind. Manag. Optim. 2025, 21, 2371–2395. [Google Scholar] [CrossRef]
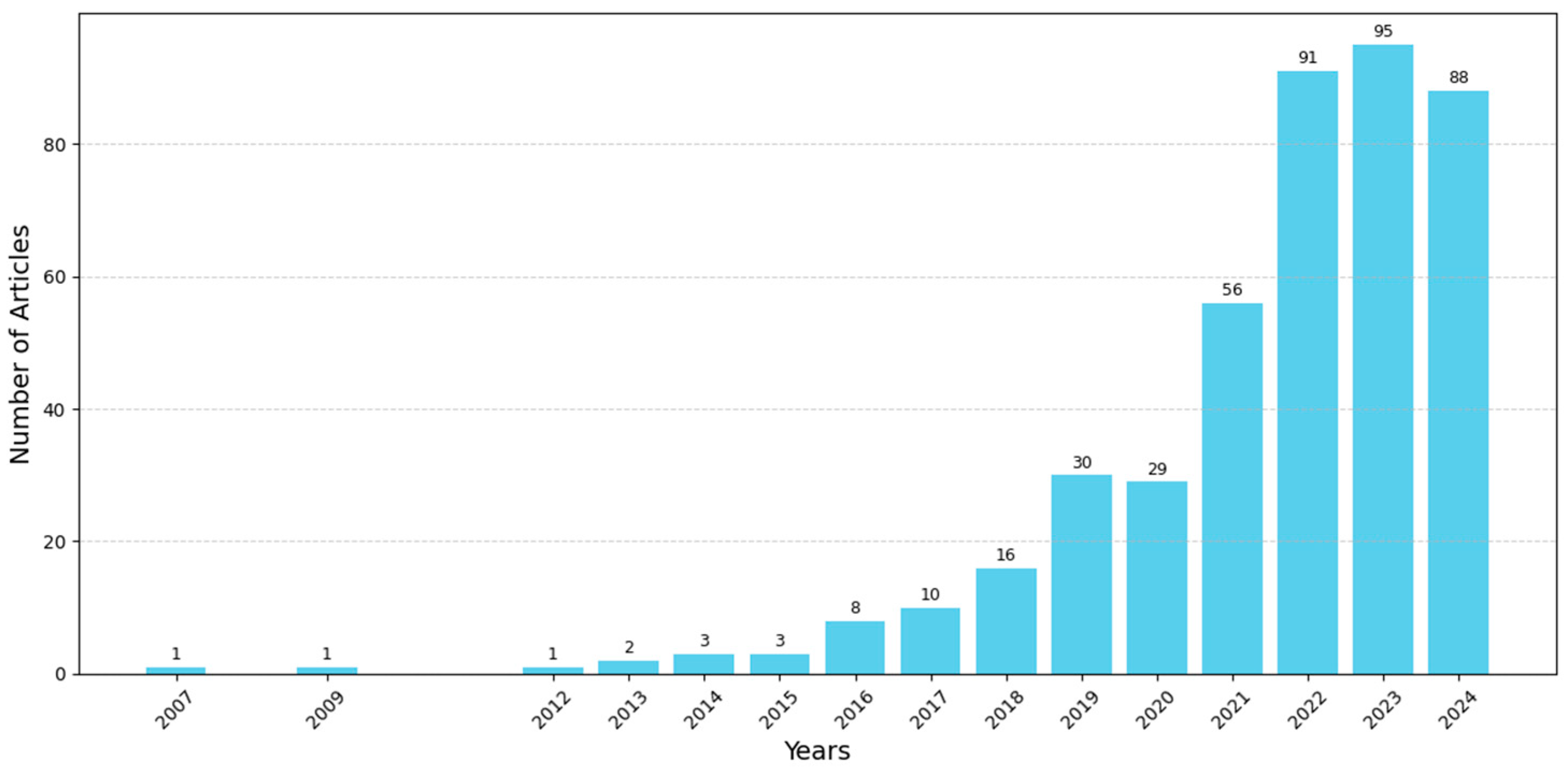




| Study | Minimize Total Distance | Minimize Total Time | Minimize Total Energy | Minimize Total Recharging Cost | Minimize Total Tardiness |
|---|---|---|---|---|---|
| Conrad and Figliozzi, 2011 [12] | ✔ | ✔ | ✔ | ||
| Schneider et al., 2014 [13] | ✔ | ||||
| Felipe et al., 2014 [14] | ✔ | ||||
| Goeke and Schneider, 2015 [15] | ✔ | ✔ | |||
| Hiermann et al., 2016 [16] | ✔ | ||||
| Keskin and Çatay, 2016 [17] | ✔ | ||||
| Barco et al., 2017 [18] | ✔ | ||||
| Montoya et al., 2017 [19] | ✔ | ||||
| Keskin and Çatay, 2018 [20] | ✔ | ✔ | |||
| Kancharla and Ramadurai, 2018 [21] | ✔ | ||||
| Kancharla and Ramadurai, 2020 [22] | ✔ | ||||
| Futelef et al., 2020 [23] | ✔ | ✔ | |||
| Bac and Erdem, 2021 [24] | ✔ | ✔ | ✔ | ||
| Keskin et al., 2021 [25] | ✔ | ||||
| Zang et al., 2022 [26] | ✔ | ✔ | |||
| Erdelic and Caric, 2022 [27] | ✔ | ||||
| Cataldo-Díaz et al., 2022 [28] | ✔ | ||||
| Dönmez et al., 2022 [29] | ✔ | ✔ | |||
| Duan et al., 2023 [30] | ✔ | ✔ | |||
| Yu et al., 2023 [31] | ✔ | ||||
| Xiao et al., 2023 [32] | ✔ | ||||
| Wang et al., 2025 [33] | ✔ | ✔ | |||
| This Study | ✔ | ✔ |
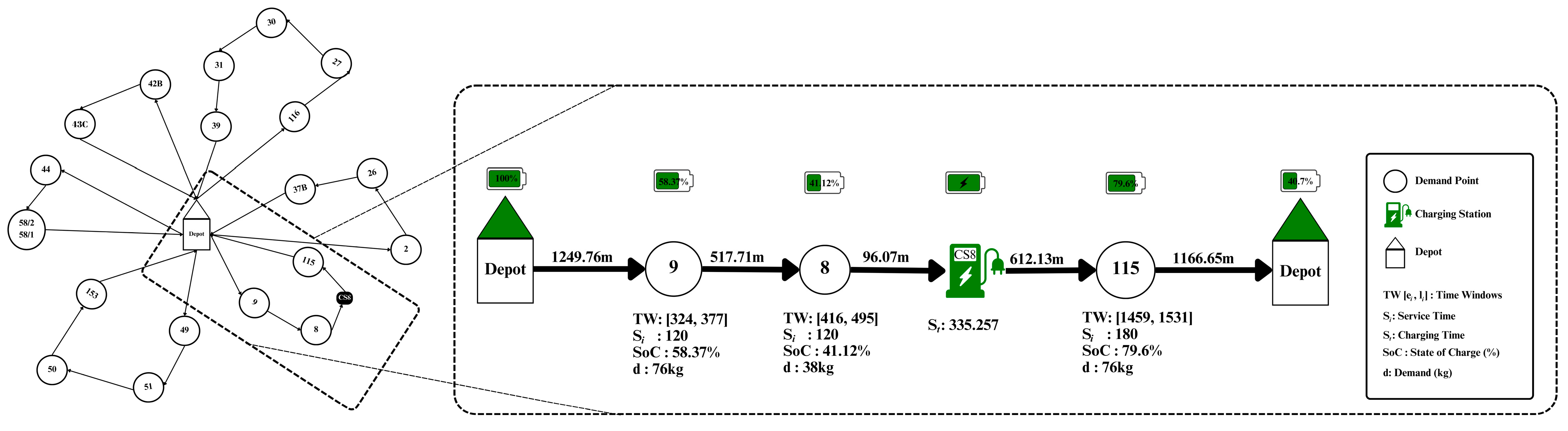
| Solution (S) | Route Detail | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Route 1: | cs5 | → | 75 | → | 42B | → | cs4 | → | 31 | → | 115 | → | 32 | → | cs5 |
| ) | - | 86.60 | - | 102.12 | - | 38.57 | - | 18.18 | - | 88.501 | - | 39.37 | - | 53.973 | - |
| ) | 0 | - | 86.60 | - | 646.12 | - | 807.57 | - | 1337.19 | - | 1580.501 | - | 1799.87 | - | 2033.843 |
| ) | - | - | 120 | - | 120 | - | - | - | 120 | - | 180 | - | 180 | - | - |
| ) | - | - | - | - | - | - | 511.427 | - | - | - | - | - | - | - | - |
| ] | - | - | [424, 487] | - | [649, 729] | - | - | - | [1372, 1448] | - | [1459, 1531] | - | [1322, 1378] | - | - |
| ) | - | - | 0 | - | 0 | - | - | - | 0 | - | 49.50 | - | 421.87 | - | - |
| Total Tardiness | 471.37 | ||||||||||||||
| Customer ID | Location | Earliest Start Time to Service | Latest Start Time to Service | Service Time | Request |
|---|---|---|---|---|---|
| 75 | 39.747233–30.47377 | 424 | 487 | 120 | 38 |
| 42B | 39.752333–30.481199 | 649 | 729 | 120 | 95 |
| 32 | 39.752487–30.488123 | 1322 | 1378 | 180 | 76 |
| 31 | 39.752941–30.483072 | 1372 | 1448 | 120 | 57 |
| 115 | 39.752373–30.490197 | 1459 | 1531 | 180 | 76 |
| Instances | CPLEX | Proposed Hybrid ALNS | Δ% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| # of Route | Total Distance (m) | Total Tardiness (s) | Runtime (s) | # of Route | Total Distance (m) | Total Tardiness (s) | Runtime (s) | ||
| C05 | 2 | 5005.43 | 0 | 0.05 | 2 | 5005.43 | 0 | 0.198 | 0 |
| R05 | 3 | 5726.1 | 0 | 0.12 | 3 | 5726.1 | 0 | 0.201 | 0 |
| RC05 | 4 | 7093.17 | 0 | 0.05 | 4 | 7093.17 | 0 | 0.252 | 0 |
| C10 | 3 | 7530.96 | 0 | 0.23 | 3 | 7530.96 | 0 | 0.265 | 0 |
| R10 | 3 | 6823.93 | 0 | 0.06 | 3 | 6823.93 | 0 | 0.288 | 0 |
| RC10 | 3 | 7349,86 | 0 | 0.19 | 3 | 7349.86 | 0 | 0.272 | 0 |
| C20 | 6 | 12,736.51 | 0 | 0.44 | 6 | 12,736.51 | 0 | 3.123 | 0 |
| R20 | 6 | 14,023.35 | 0 | 4.51 | 6 | 14,023.35 | 0 | 3.035 | 0 |
| RC20 | 6 | 12,447.92 | 0 | 0.36 | 6 | 12,447.92 | 0 | 2.708 | 0 |
| C40 | 11 | 21,145.80 | 0 | 3.41 | 11 | 21,828.27 | 0 | 17.160 | 3.22% |
| R40 | 11 | 26,316.81 | 0 | 75.09 | 11 | 27,193.94 | 0 | 16.397 | 3.33% |
| RC40 | 11 | 23,372.91 | 0 | 19.31 | 10 | 23,931.24 | 0 | 17.838 | 2.38% |
| C60 | 13 | 28,711.04 * | 0 | 10,800 | 12 | 26,769.65 | 0 | 71.939 | −6.76% |
| R60 | 12 | 29,396.37 * | 0 | 10,800 | 12 | 27,550.95 | 0 | 77.537 | −6.27% |
| RC60 | 12 | 30,000.09 * | 0 | 10,800 | 12 | 28,464.34 | 0 | 71.303 | −5.11% |
| Instances | Cost-Oriented Solutions | Customer-Satisfaction-Oriented Solutions | Δ% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| # of Route | Total Distance (m) | Total Tardiness (s) | Runtime (s) | # of Route | Total Distance (m) | Total Tardiness (s) | Runtime (s) | ||
| C05 | 2 | 3956.43 | 3423.137 | 0.177 | 2 | 5005.43 | 0 | 0.198 | 26.51 |
| R05 | 2 | 5064.28 | 2652.562 | 0.180 | 3 | 5726.1 | 0 | 0.201 | 13.06 |
| RC05 | 1 | 4956.02 | 4388.143 | 0.221 | 4 | 7093.17 | 0 | 0.252 | 43.12 |
| C10 | 2 | 5645.72 | 6744.392 | 0.228 | 3 | 7530.96 | 0 | 0.265 | 33.39 |
| R10 | 2 | 4980.35 | 7014.425 | 0.254 | 3 | 6823.93 | 0 | 0.288 | 37.02 |
| RC10 | 2 | 5842.88 | 5013.898 | 0.244 | 3 | 7349.86 | 0 | 0.272 | 25.79 |
| C20 | 4 | 9332.26 | 8005.543 | 2.801 | 6 | 12,736.51 | 0 | 3.123 | 36.48 |
| R20 | 4 | 9975.22 | 11,432.066 | 2.631 | 6 | 14,023.35 | 0 | 3.035 | 40.58 |
| RC20 | 4 | 9401 | 10,434.282 | 2.437 | 6 | 12,447.92 | 0 | 2.708 | 32.41 |
| C40 | 7 | 15,634.88 | 20,972.411 | 12.213 | 11 | 21,828.27 | 0 | 17.160 | 39.61 |
| R40 | 8 | 18,362.61 | 23,123.101 | 11,758 | 11 | 27,193.94 | 0 | 16.397 | 48.09 |
| RC40 | 7 | 16,796.03 | 27,070.676 | 13,054 | 10 | 23,931.24 | 0 | 17.838 | 42.48 |
| C60 | 11 | 25,095.65 | 2342.656 | 28.446 | 12 | 26,075.12 | 0 | 71.939 | 6.67 |
| R60 | 10 | 26,198.41 | 3195.702 | 34.346 | 12 | 27,550.95 | 0 | 77.537 | 5.16 |
| RC60 | 11 | 25,957.16 | 6182.938 | 32.952 | 12 | 28,613.43 | 0 | 71.303 | 9.66 |
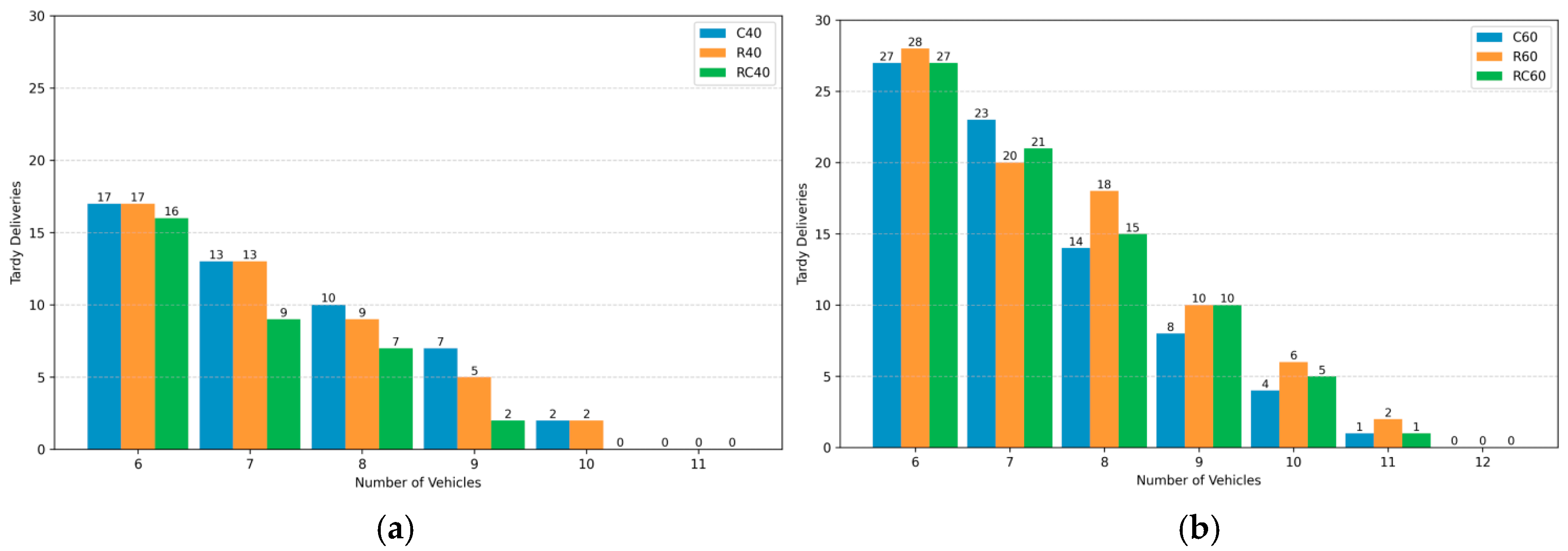
| Test Problems | # of Routes | # of Vehicles | # of Tardy Deliveries | Total Tardiness (s) |
|---|---|---|---|---|
| C40 | 11 | 11 | 0 | 0 |
| C40 | 11 | 10 | 2 | 1095.15 |
| C40 | 11 | 9 | 7 | 2874.56 |
| C40 | 11 | 8 | 10 | 5712.73 |
| C40 | 11 | 7 | 13 | 9236.65 |
| C40 | 11 | 6 | 17 | 14,240.29 |
| R40 | 11 | 11 | 0 | 0 |
| R40 | 11 | 10 | 2 | 804.75 |
| R40 | 11 | 9 | 5 | 3424.78 |
| R40 | 11 | 8 | 9 | 7390.73 |
| R40 | 11 | 7 | 13 | 12,823.69 |
| R40 | 11 | 6 | 17 | 19,573.68 |
| RC40 | 10 | 10 | 0 | 0 |
| RC40 | 10 | 9 | 2 | 1213.66 |
| RC40 | 10 | 8 | 7 | 3883.94 |
| RC40 | 10 | 7 | 9 | 8276.91 |
| RC40 | 10 | 6 | 16 | 13,543.13 |
| Test Problems | # of Routes | # of Vehicles | Tardy Deliveries | Total Tardiness (s) |
|---|---|---|---|---|
| C60 | 12 | 12 | 0 | 0 |
| C60 | 12 | 11 | 1 | 225.94 |
| C60 | 12 | 10 | 4 | 1272.41 |
| C60 | 12 | 9 | 8 | 3080.85 |
| C60 | 12 | 8 | 14 | 6265.13 |
| C60 | 12 | 7 | 23 | 10,587.50 |
| C60 | 12 | 6 | 27 | 17,708.64 |
| R60 | 12 | 12 | 0 | 0 |
| R60 | 12 | 11 | 2 | 673.87 |
| R60 | 12 | 10 | 6 | 2265.83 |
| R60 | 12 | 9 | 10 | 4163.19 |
| R60 | 12 | 8 | 18 | 7337.46 |
| R60 | 12 | 7 | 20 | 12,431.94 |
| R60 | 12 | 6 | 28 | 19,758.54 |
| RC60 | 12 | 12 | 0 | 0 |
| RC60 | 12 | 11 | 1 | 91.79 |
| RC60 | 12 | 10 | 5 | 1352.66 |
| RC60 | 12 | 9 | 10 | 3543.19 |
| RC60 | 12 | 8 | 15 | 6589.23 |
| RC60 | 12 | 7 | 21 | 11,045.43 |
| RC60 | 12 | 6 | 27 | 17,407.87 |
| Regression Statistic | Value |
|---|---|
| Multiple R | 0.980593 |
| R Square | 0.961563 |
| Adjusted R Square | 0.95954 |
| Standard Error | 1.991838 |
| Observations | 21 |
| Coefficients | Standard Error | t Stat | p-Value | |
|---|---|---|---|---|
| Intercept | 54.07143 | 2.003659 | 26.98634 | 1.29 × 10−16 |
| # of Vehicles | −4.7381 | 0.217327 | −21.8017 | 6.6 × 10−15 |
| df | SS | MS | F | Significance F | |
|---|---|---|---|---|---|
| Regression | 1 | 1885.762 | 1885.762 | 475.3121 | 6.6 × 10−15 |
| Residual | 19 | 75.38095 | 3.967419 | ||
| Total | 20 | 1961.143 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ünal, Y.; Sarıçiçek, İ.; Bozkurt Keser, S.; Yazıcı, A. Electric Vehicle Routing with Time Windows and Charging Stations from the Perspective of Customer Satisfaction. Appl. Sci. 2025, 15, 4703. https://doi.org/10.3390/app15094703
Ünal Y, Sarıçiçek İ, Bozkurt Keser S, Yazıcı A. Electric Vehicle Routing with Time Windows and Charging Stations from the Perspective of Customer Satisfaction. Applied Sciences. 2025; 15(9):4703. https://doi.org/10.3390/app15094703
Chicago/Turabian StyleÜnal, Yasin, İnci Sarıçiçek, Sinem Bozkurt Keser, and Ahmet Yazıcı. 2025. "Electric Vehicle Routing with Time Windows and Charging Stations from the Perspective of Customer Satisfaction" Applied Sciences 15, no. 9: 4703. https://doi.org/10.3390/app15094703
APA StyleÜnal, Y., Sarıçiçek, İ., Bozkurt Keser, S., & Yazıcı, A. (2025). Electric Vehicle Routing with Time Windows and Charging Stations from the Perspective of Customer Satisfaction. Applied Sciences, 15(9), 4703. https://doi.org/10.3390/app15094703





