Abstract
Depth completion generates a comprehensive depth map by utilizing sparse depth data inputs, supplemented by guidance provided by an RGB image. Deep neural network models depend on annotated datasets for optimal training. However, when the quantity of training data is limited, the generalization capability of deep neural network (DNN)-based methods diminishes considerably. Moreover, acquiring a large dataset of depth maps is challenging and resource intensive. To address these challenges, we introduce a novel few-shot learning approach for depth completion. Our approach integrates noisy-student training with knowledge distillation (KD) techniques to enhance model performance and generalization. We incorporate both the noisy-student training and KD modules into a basic deep regression network using a non-local spatial propagation network (NLSPN) for depth completion. The noisy-student training framework enhances the model’s performance and generalization capabilities by introducing controlled noise and self-learning mechanisms. Within our few-shot learning framework for depth completion, the KD mechanism transfers advanced capabilities from the teacher model to the student model. Experimental evaluations demonstrate that our approach effectively addresses the challenges associated with depth completion tasks, particularly in scenarios with limited training data and a constrained number of available samples.
1. Introduction
Precise dense depth maps are fundamental to various computer vision applications, including facilitating autonomous navigation [1], augmented reality interactions [2], 3D modeling techniques [3], and supporting real-time localization and mapping systems [4]. Despite advancements in depth-sensing technology, hardware devices often hinder depth sensors from generating dense depth maps for research purposes. To address this limitation, the depth completion technique [5] converts sparse depth inputs into rich, dense depth maps, enabling the derivation of enhanced depth information and corresponding color visuals from limited sparse datasets.
Recent advancements in deep neural networks (DNNs) have substantially enhanced depth completion tasks. The sparse-to-dense method [6] leverages a single deep regression network to handle raw RGB-D data, addressing the challenge of producing dense depth maps from sparsely sampled raw RGB images. Meanwhile, the convolutional spatial propagation network (CSPN) [7] employs an efficient linear propagation model to effectively capture relationships among pixel neighborhoods. This mechanism refines depth outputs obtained from state-of-the-art methods while converting sparse depth samples into dense maps through an integrated propagation mechanism. Building upon this foundation, the non-local spatial propagation network (NLSPN) [8] further advances this approach by introducing a learnable affinity normalization mechanism. This method estimates non-local neighboring pixels and their respective affinities, integrating them with an initial depth map and pixel confidence values to enhance affinity learning and resilience against inconsistencies at depth boundaries. However, most existing DNN-based depth completion techniques rely heavily on extensive supervised data, yet gathering and disposing of large numbers of sparse depth maps are both challenging and expensive [5]. To address this limitation, this study employs a few-shot learning framework to predict the dense depth for the image.
Figure 1d,e illustrate the testing results obtained using the advanced NLSPN [8] architecture. When trained on a randomly selected 10% of the NYUv2 dataset, the model produces outputs that exhibit more noise and blurriness compared to those trained on the full NYUv2 dataset. Therefore, an inadequate dataset jeopardizes the model’s generalization ability. Exploring the impact of a limited training dataset on depth completion is crucial.
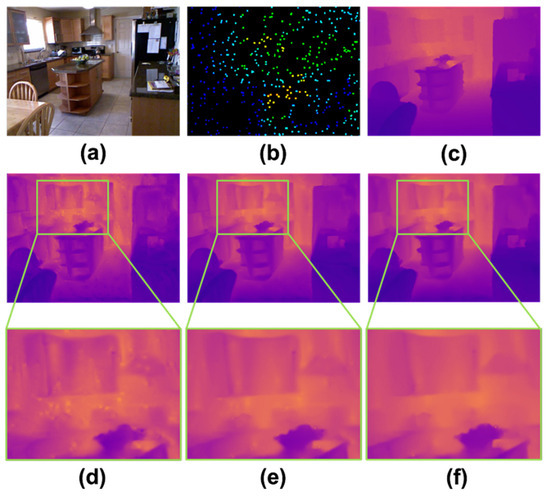
Figure 1.
Results from various depth estimation methods demonstrating the generation of a depth map guided by a reference RGB image and sparse depth inputs. (a) Reference RGB image. (b) Sparse depth dataset. (c) Ground-truth depth map. Depth prediction by NLSPN trained on (d) a 10% subset of the NYUv2 dataset and (e) the full NYUv2 dataset. (f) Depth prediction from the proposed model assessed on a 10% subset of the NYUv2 dataset.
DNN-based depth completion methods typically depend on extensive supervised data samples. However, acquiring and processing large-scale, sparse depth maps are both challenging and costly. Moreover, current real-world datasets lack pixel-accurate ground truth due to depth sensor limitations. Furthermore, semi-dense annotations are often imprecise and affected by occlusions, dynamic objects, and other distortions.
To address data scarcity, several researchers are exploring self-supervised frameworks [9,10] to compensate for limited ground-truth depth information. These methods derive supervisory signals from the dataset itself, eliminating the need for extensive labeled datasets. By leveraging intrinsic data patterns and correlations, self-supervised learning enables depth estimation without requiring manual annotations. This strategy mitigates the difficulty of obtaining extensive labeled depth datasets while enhancing the model’s capacity to deduce depth from partial or corrupted inputs. Knowledge distillation (KD) is crucial in self-supervised learning by boosting performance, stability, and efficiency. KD [11] extracts essential information from a complex teacher model and transfers it to a more compact student model, enhancing efficiency without compromising performance. KD techniques have been extensively studied for image classification tasks; however, their direct application to pixel-level tasks through classification-based KD methods often yields suboptimal results. Imposing the strict alignment of the coarse feature maps between teacher and student models can impose restrictive constraints, neglecting structured relationships among pixels and reducing overall efficiency.
Unlike previous studies that ignore dataset insufficiency, we introduce a few-shot learning framework that integrates self-training with noise and dense-pixel KD. Our approach yields superior performance in both smoothness and detail sharpness while utilizing the same limited dataset (Figure 1f). We train a teacher model on limited labeled data, ensuring a noise-free training process to produce reliable pseudo-labels for the unlabeled data, which retain a high accuracy and remain closely aligned with the true labels. To enhance the student model’s training, we introduce noise augmentation, incorporating both labeled and unlabeled data. We apply Gaussian blur to RGB images and introduce stochastic perturbations to sparse depth data. The training process follows an iterative scheme, where the student model transitions into a teacher role to generate pseudo-labels, while a newly initialized student model is trained to improve performance. To sustain the teacher model’s high performance, dense-pixel KD is employed, leveraging its acquired knowledge as a supervisory signal for the student model’s training [11].
The primary contributions of our study are as follows:
- (1)
- We propose a novel few-shot learning framework for depth completion. This framework utilizes advanced depth completion techniques to produce dense depth maps from datasets that are either incomplete or contain missing data.
- (2)
- We employ noise augmentation and KD techniques, utilizing the deep regression network NLSPN to capture and infer depth-related features from limited datasets. Our approach improves the student model’s resistance to noise, strengthening its overall performance and generalization abilities.
- (3)
- Our experimental results on the NYUv2 dataset show that the proposed method substantially enhances the performance of the student model compared to current techniques. Even when limited to only 10% of the training data, our method improves the accuracy from 97.1% to 99.7%, matching the performance achieved with the complete training set.
2. Related Work
2.1. Depth Completion
As image-guided depth completion techniques become increasingly recognized for their advantages over non-image-guided approaches, significant research efforts have focused on enhancing multimodal data integration. Common methodologies utilize deep learning models that take sparse depth maps alongside RGB images as inputs [6,12] or employ distinct initial convolutional layers for feature extraction [9,13,14]. Another common approach involves two-stage networks that progressively refine predictions from a coarse resolution to a fine resolution [15,16]. However, these approaches often oversimplify the problem, failing to capture the complex spatial relationships that exist between RGB images and their corresponding depth maps.
To improve the precision of data fusion, advanced network architectures have been designed to combine intermediate features extracted from various levels. For instance, the models proposed in [17,18] employed dual-branch encoder architectures that independently process RGB images and raw depth data, linking relevant features before passing them to the decoder. The approach in [19] refined the network design by incorporating multiscale skip connections, improving heterogeneous data sources. While dual-encoder networks primarily emphasize data fusion at the encoding phase, they often overlook the decoding stage. In response, some studies [20,21] introduced dual-encoder–decoder networks to optimize depth completion tasks.
Concurrently, the evolution of SPN-based networks progressed steadily, including CSPN [22], CSPN++ [23], and DySPN [24]. These approaches leverage affinity matrices derived from RGB data to effectively enhance the upsampling of raw sparse depth maps.
2.2. Semi-Supervised Learning
Semi-supervised learning [25,26,27,28,29,30,31] utilizes neural networks trained on datasets that comprise both labeled and unlabeled data. The labeled data provide the necessary information for distinguishing categories, while the unlabeled data offer a structural understanding of the input. Recent progress in semi-supervised learning has markedly improved the efficacy of DNNs while lowering the costs associated with data annotation. Consequently, these techniques are well suited for depth completion tasks, particularly when working with limited datasets.
Current semi-supervised learning approaches [25] enhance image classification by generating and selecting pseudo-labels with high confidence for unlabeled data. The approach in [29] utilizes a teacher–student framework, where the teacher model generates reliable pseudo-labels from unlabeled data to enhance the student model’s performance in object detection. In contrast, the method in [28] introduces a confidence-scoring mechanism based on loss distribution to filter reliable pseudo-labels, thereby enhancing the classification accuracy in low-sample scenarios. The technique in [27] generates and preserves high-confidence pseudo-label samples within the adversarial learning objective domain, addressing domain adaptation issues. Furthermore, the transfer network in [30] is trained using pseudo-labels and employs valuable feature representation knowledge to enhance the training process of semantic segmentation networks.
This study proposes a semi-supervised learning framework utilizing unlabeled depth data and associated pseudo-labels to enhance sparse image datasets.
2.3. Knowledge Distillation
KD [32] transfers valuable insights from a complex teacher model to a more compact and efficient student model. Contemporary KD techniques, predominantly employed in image classification tasks, can be categorized into probability-based, feature-based, and relation-based approaches. The probability-based method [32] relies on the teacher model’s class probabilities as soft labels to train the student model. Feature-based KD [33,34] facilitates knowledge transfer by leveraging intermediate feature maps or their refined versions from the teacher network. Meanwhile, relation-based KD [35] aligns the structural relationships among multiple instances within both the teacher and student networks.
Despite extensive research on KD techniques for image classification, their direct application to dense pixel tasks often yields suboptimal outcomes due to the inflexible alignment of low-resolution feature representations between the teacher and student networks, which can impose constraints that hinder the effective transfer of knowledge. Consequently, these methods may fail to capture the structured relationships among pixels. Unlike image-level recognition, depth completion tasks necessitate dense pixel-wise predictions, making it a more intricate challenge. Therefore, utilizing KD methods to enhance the student model by leveraging the teacher model within our proposed few-shot learning framework for depth completion remains both beneficial and demanding.
2.4. Few-Shot Learning
Few-shot learning seeks to equip models with generalization capabilities from minimal annotated samples, increasingly applied to dense prediction challenges. Conventional methodologies employ meta-learning architectures [36] that acquire cross-task transferable parameter initializations. Prototypical Networks [37] exemplify metric-based techniques, establishing class representations in latent spaces for similarity assessment—particularly beneficial in depth estimation demanding structural coherence.
Recent depth completion studies tackle data limitations via adaptive feature integration. DepthFormer [38] utilizes cross-attention mechanisms to bridge the synthetic-to-real domain knowledge transfer. Such approaches nevertheless face persistent domain adaptation challenges under extreme target data constraints.
Our methodology introduces a foundational divergence through synergistic integration of noisy self-training and pixel-wise knowledge distillation. Unlike prevailing few-shot paradigms concentrating on meta-learning or parametric initialization, we enhance training signals via structured pseudo-label propagation and hierarchical knowledge integration. This innovative framework enables the synergistic utilization of scarce annotated samples and abundant unlabeled instances, circumventing the inefficiency inherent in traditional few-shot methodologies through unified representation learning.
3. The Proposed Method
This study proposes a novel few-shot learning framework based on self-training with noise and pixel-wise knowledge distillation (FSLNKD) for depth completion (Figure 2). This framework is built upon a self-training paradigm that leverages a teacher–student architecture. By incorporating noise samples and pixel-level distillation techniques, our approach effectively enhances the student model’s training process.
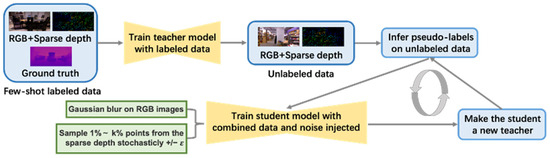
Figure 2.
Configuration of the proposed few-shot learning framework for depth completion with noisy-student training and KD integration.
First, we introduce the teacher–student model, a conventional machine learning method that effectively handles few-shot datasets, particularly in few-shot learning models. The teacher model, characterized by its expressiveness and superior performance, is typically trained on a larger or more complex dataset. It often possesses a greater number of parameters and a deeper structure. The teacher model identifies and transfers the intricate data structures and patterns to the student model. We choose a high-precision depth completion network as our teacher model, which is trained using labeled data—such as the data containing ground-truth annotations. After training, the pre-trained teacher model is utilized to generate pseudo-labels for the unlabeled dataset. The student model, typically less complex with fewer parameters or a shallower architecture, is designed for data-constrained environments. To enhance its performance and generalization capabilities, it leverages knowledge distilled from a more complex teacher model, even with minimal training data. By combining labeled, pseudo-labeled, and noisy samples, the student model is effectively trained.
Second, to enable the student model to derive granular insights from the teacher model, we implement pixel-level distillation to ensure precise knowledge transfer at the pixel scale. This approach proves particularly advantageous in image segmentation and synthesis tasks, where preserving intricate details and spatial consistency is crucial. Within this framework, we adapt KD techniques for depth completion, enabling the student model to generate outputs with fine-grained details comparable to those of the teacher model. This approach allows for the deployment of more compact and computationally efficient student models while maintaining high performance.
Finally, the student model is reconfigured to function as a teacher, enabling an iterative training process, where the teacher model guides the student in re-labeling previously unlabeled data, which are then used to train a new student model. This iterative teacher–student framework improves both the model efficiency and generalization by facilitating effective knowledge transfer. Moreover, it mitigates the challenge of limited data, facilitates model compression, and lays a solid groundwork for future learning tasks.
3.1. Self-Training with Noise for Depth Completion
Algorithm 1 presents the self-training process incorporating noise for depth completion, inspired by the noisy-student approach originally developed to improve ImageNet classification [39].
| Algorithm 1: Self-Training with Noise for Depth Completion | |
| Input: Labeled data, , and unlabeled data, , where rsd denotes the combination of RGB images and sparse depth, and represents the corresponding ground truth. | |
| Output: Student model | |
| 1. For k = 1 to K do | |
| 2. Train the teacher model, , to minimize the loss function that is applied to the annotated dataset: | |
| (1) | |
| 3. Generate pseudo-labels for the unannotated dataset using the trained teacher model: | |
| (2) | |
| 4. Train the student model, , by leveraging both labeled and pseudo-labeled data to minimize the loss function while introducing noise into the student model’s training process: | |
| (3) | |
| 5. k = k + 1; | |
| 6. End for | |
The algorithm introduces an advanced self-training framework in which the teacher model generates high-quality pseudo-labels using clean data. The student model is trained to replicate labels from both annotated and pseudo-labeled datasets, even when exposed to noisy inputs. This approach significantly boosts the student model’s ability to generalize effectively, surpassing the teacher model’s capabilities.
Two types of noise augmentation are introduced to the student: Gaussian blur is applied to RGB images [40] and stochastic perturbation is used for sparse depth [41]. Applying noise augmentation to the two input data types enhances the model’s ability to utilize the limited labeled data more effectively, promoting the extraction of more generalized features. Expanding the training dataset for the student model is crucial. Therefore, random noise is injected into the input variables of the student model during training, ensuring variations in the data at every time step. Incorporating noise into the student model generates new samples in proximity to existing samples, effectively smoothing the structure of the input space. This smoothing effect simplifies the learning process by making the mapping function easier to model. Furthermore, the injected noise mimics potential errors encountered in real-world depth information collection, enhancing the model’s robustness. The two types of noise used in this process are as follows:
(1) Gaussian blur on RGB images: Gaussian blur is a commonly utilized image processing technique that applies a Gaussian function to modify pixel values within the image. This technique reduces sharp edges and fine details, producing a visually softened effect. The Gaussian function, known for its bell-shaped distribution, computes the weight of each pixel based on its distance from the kernel’s center. Pixels closer to the center have a greater influence on the resulting blurred value. Incorporating Gaussian blur into RGB images during self-training introduces controlled noise, which strengthens the model’s capacity to generalize and extract robust features for depth completion. This technique enhances the model’s resilience variations in input data, boosting performance and precision in depth estimation tasks. The 1D Gaussian function is expressed as follows:
In 2D space, the Gaussian function is defined as the product of two independent 1D Gaussian functions, each corresponding to a distinct dimension:
where r denotes the horizontal distance from the origin, d implies the vertical distance from the origin, and signifies the standard deviation of the Gaussian distribution. When extended to two dimensions, Equation (5) creates a surface characterized by concentric circular contours, indicating a Gaussian distribution that radiates symmetrically from the central point.
(2) Stochastic perturbation on sparse depth: To improve the model’s resilience and generalization capability, we introduce stochastic noise perturbation into the sparse depth data. This process involves randomly selecting a subset, with 1–k% of the available depth points, and modifying each chosen point by a small random noise within a range of +/–, where = 0–5 units. By introducing these controlled perturbations, we generate a diverse set of slightly modified depth maps encountered during training, effectively simulating the natural variability and uncertainties in real-world depth measurements. This method fosters greater model resilience and mitigates overfitting by reducing the model’s reliance on specific sparse data patterns, allowing adaptation to a broad spectrum of depth scenarios. This approach substantially improves both the performance and the precision of our framework in depth completion tasks.
Our improvement strategy involves incorporating noise into the student model while retaining a level of complexity equal to or greater than that of the teacher model. This knowledge expansion technique enables the student to outperform the teacher by equipping it with adequate capacity and subjecting it to demanding conditions through controlled noise.
Figure 3 evaluates noise-processing effects through visual comparisons. Figure 3a,b contrast the original RGB image with its Gaussian-blurred counterpart, where edge sharpness and fine details are attenuated to create a smoothed appearance. Subsequent columns analyze prediction outcomes across varying inputs: Figure 3c: baseline results using unmodified data; Figure 3d: predictions with Gaussian-blurred RGB inputs highlighting detail loss impacts; and Figure 3e: outputs combining the original RGB image with stochastically perturbed depth data. Incorporating noise into the student model during training establishes a more rigorous learning environment, promoting the acquisition of robust and generalized features. This regularization technique mitigates overfitting on training data and enhances the model’s adaptability to diverse input scenarios. Furthermore, the student model, possessing a complexity level equal to or greater than that of the teacher model, fully leverages the knowledge transferred from the teacher. By expanding the student model’s capacity, learning becomes more efficient, allowing it to capture and retain more features and patterns. Our approach surpasses the constraints of the teacher model by equipping the student model with both the capability and the challenging conditions necessary for superior learning. This approach promotes the development of a more robust and precise depth completion model and highlights the effectiveness of well-designed student–teacher training frameworks in performance improvements.

Figure 3.
Comparative results of noise-processing techniques. (a) displays the unprocessed RGB image, while (b) shows its Gaussian-blurred counterpart. Prediction outcomes are presented for three scenarios: (c) using the original RGB image with unmodified, sparse depth data, (d) employing the Gaussian-blurred RGB image with the original depth data, and (e) combining the original RGB image with stochastically perturbed depth data.
3.2. Pixel-Wise Knowledge Distillation for Depth Completion
Depth completion, unlike conventional image classification, requires dense predictions at the pixel level. Inspired by Hinton’s KD [11], this approach matches the probability distribution of classes for each pixel between the student and teacher models, as follows:
where and indicate the soft class probabilities at pixel positions (h, w), generated by the student and teacher models, respectively; S denotes the associated similarity matrix; KL refers to the Kullback–Leibler divergence [42]; and T signifies the temperature parameter.
The similarity matrix represents the pixel-to-region similarity matrix, quantifying the extent to which individual pixels correspond to predefined regions or clusters within the image. This similarity or dissimilarity can be determined by various factors, including color similarity (such as using color histograms or color distances, as applied in Euclidean distance), texture-based similarity (using texture features), or an integrated approach combining both elements. Within the depth completion task, similarity measures determine how closely the inpainted region aligns with its surrounding known regions, deducing the missing or damaged parts based on the available surrounding information. For a given input, x, the resulting pixel embeddings are denoted as F. To simplify the notation, let V denote the matrix obtained by concatenating elements along the row dimension. Consequently, S is formulated as follows:
We utilize pixel-wise class probability distillation for the depth completion task, as illustrated in Figure 4.
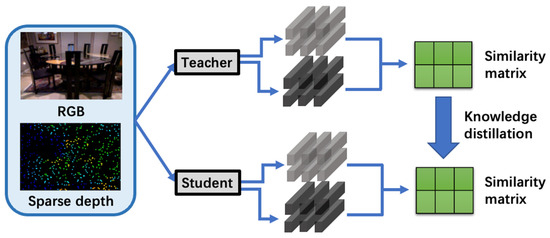
Figure 4.
Application of our proposed dense-pixel KD technique to depth completion.
Our approach enhances depth predictions by utilizing pixel-wise class probability distillation, thereby significantly boosting the accuracy, robustness, and reliability of depth estimates, especially in areas with sparse or uncertain data (Figure 5). This method produces more precise and superior outcomes across diverse applications. Following the preliminary depth estimation or the inpainting of missing depth values, a subsequent pixel-wise class probability distillation process refines these predictions further. By leveraging learned probability distributions, this stage adjusts depth values while incorporating contextual information from adjacent pixels and regions. In depth completion tasks, this technique facilitates more informed decisions when assigning depth values to pixels in inpainted or incomplete areas. By incorporating probability distributions, the approach effectively handles uncertainty and ambiguity in depth estimates. Moreover, it quantifies uncertainty or confidence level for each pixel’s depth prediction—critical for applications demanding reliable depth information. By utilizing intricate pixel depth features, this approach enhances adjustments based on local contextual data and neighboring pixel data. Consequently, the outcome demonstrates improved smoothness and structural consistency. By integrating probability distributions with contextual information for each pixel, the approach refines both the accuracy and dependability of depth predictions. This refined methodology proves highly beneficial for depth completion systems, producing high-quality depth maps for advanced applications across various fields.

Figure 5.
Comparison of prediction results before and after using pixel-wise class probability distillation. (a) Original RGB input. (b) Baseline prediction. (c) Enhanced results following distillation implementation.
3.3. Loss Function
The combined loss function employed for training the student network optimizes performance through a balanced integration of multiple objectives:
where indicates the scaling parameter employed to harmonize the impact of depth and structure distillation losses.
4. Experiments
4.1. Datasets
Our methodology is assessed using the NYUv2 dataset (NYUv2 dataset: https://cs.nyu.edu/~fergus/datasets/nyu_depth_v2.html, accessed on 1 January 2025) [43] and the KITTI Depth Completion (KITTI DC) dataset (KITTI DC dataset: https://www.cvlibs.net/datasets/kitti/eval_depth.php, accessed on 1 January 2025) [44]. The NYUv2 dataset [43] consists of RGB and depth images collected from 464 indoor scenes captured by a Kinect sensor. By the official split, 249 scenes are allocated for training, while the remaining 215 are reserved for testing, with the test set comprising a total of 654 images. From the raw training data, 46,000 images are extracted. To address missing depth values, interpolation is performed using the cross-bilateral filter provided in the official toolkit. All the images are resized to 320 × 240 and center-cropped to 304 × 228. For each image, a random selection of 500 sparse depth samples is made. The model undergoes training for 25 epochs using the loss function, with the learning rate decreasing by a factor of 0.2 every five epochs after the first 10 epochs. The training is conducted with a batch size of 24. To evaluate the model’s few-shot learning capabilities, approximately 20 data points are extracted from each sequence, forming a 20-shot training set comprising around 5000 data points. The model is trained using the reduced dataset, while evaluation is carried out on the designated validation set. The KITTI Depth Completion (KITTI DC) dataset [44] contains over 90,000 synchronized RGB images and sparse LiDAR point clouds captured in outdoor driving scenarios. Following the standard protocol, we excluded the top 100 pixels where LiDAR projections are absent due to sensor mounting positions. All images were center-cropped to 1216 × 240 patches for training consistency. The model was trained for 25 epochs with an initial learning rate that decayed by a factor of 0.4 every 5 epochs after the first 10 epochs, using a batch size of 25.
4.2. Evaluation Metrics
We utilize well established evaluation metrics [6,7,43], where implies the actual depth value at a specific pixel position, , and signifies the predicted depth. The metrics are defined as follows:
Root mean square error (RMSE):
Mean absolute relative error (REL):
Mean absolute error (MAE):
Improved root mean square error (iRMSE):
Improved mean absolute error (iMAE):
Threshold : This metric determines the percentage of that satisfies the condition , where = .
N refers to the total number of pixels.
4.3. Comparison to State-of-the-Art Techniques
We assess our methodology by comparing it against leading, state-of-the-art techniques within the field of guided depth completion.
The sparse-to-dense method [6] processes sparse depth measurements as input, setting unobserved areas to an initial value of zero. By leveraging a guidance image, it systematically generates a dense depth map through an end-to-end process. The sparse-to-dense (SS) method [9] refines the approach in [6] by integrating self-supervision through photometric loss derived from consecutive frames. Meanwhile, CSPN [7] further enhances the SS method [6] by employing a recurrent spatial propagation mechanism to refine depth estimation.
Nconv-CNN [45] integrates a normalized convolutional layer to effectively process sparse inputs while employing a confidence map for unguided depth completion. The output generated by this unguided network is subsequently fused with the RGB image to enhance the performance of guided depth completion. In contrast, DeepLiDAR [12] employs sparse data as its primary input and incorporates surface normal estimation as an intermediary process to generate dense depth maps. This approach relies on ground-truth surface normals for supervised training.
In contrast, -Random is a modified version of deep depth densification () [15] that generates an intermediate dense depth map from sparse data. It employs nearest neighbor interpolation to enhance the initial sparse depth measurements before passing them into a depth completion network. In its initial form, utilizes a uniform grid with over 500 sampled points as sparse measurements, ensuring a well-balanced distribution and higher density. For an equitable assessment, we retrained and reassessed using the same sparse measurement pattern as our approach, referring to this modified version as -Random. In contrast, the NLSPN [8] enhances depth completion by leveraging non-local spatial information to iteratively refine and enhance the depth map.
Table 1 demonstrates that the proposed few-shot learning framework substantially enhances the NLSPN performance [8] across all three evaluation criteria using only one-tenth of the labeled data required for the same task. Table 2 demonstrates our method’s performance on the KITTI benchmark. By leveraging both labeled and pseudo-labeled data through our self-training framework, we achieve competitive results compared to existing supervised approaches while using only 10% of the labeled training samples. The integration of pixel-wise knowledge distillation effectively preserves structural details in challenging outdoor scenarios with dynamic objects and large depth ranges.

Table 1.
Comparison with state-of-the-art methods based on the NYUv2 dataset.

Table 2.
Comparison with state-of-the-art methods based on the KITTI DC test dataset.
The student model significantly outperforms the teacher model by leveraging pseudo-labels strategically. Although the student model emulates the teacher model’s behavior, noise is incorporated into the student model while being excluded from the teacher model. This mechanism enhances the accuracy of the teacher model’s training in pseudo-labels and the generalization of the student models.
Moreover, our proposed dense-pixel-wise KD module retains the advanced capabilities demonstrated in previous iterations. It preserves and progressively enhances the knowledge acquired in earlier stages, strengthening its overall robustness and effectiveness.
Consequently, our few-shot learning framework enhances the performance of the original NLSPN model while substantially reducing the need for labeled data. By strategically incorporating noise and leveraging KD, the student model acquires a more robust understanding, yielding improved generalization. Therefore, the student model surpasses the teacher model, showcasing the effectiveness and scalability of our approach for efficient depth completion.
4.4. Iterative Effect Analysis
We conduct a detailed analysis of the effects of iterative training on the performance of our depth completion frameworks. Our approach conducts the supervised training of the NLSPN model using labeled data, designating this initial model as the “teacher.” Once trained, the teacher model serves as a knowledge source for training a subsequent “student” model, effectively facilitating the transfer of learned insights. Upon reaching an adequate level of training, the student model assumes the role of the teacher for the successive training iterations.
This iterative training process operates cyclically, where each newly trained student model assumes the role of the teacher in subsequent iterations. This continuous cycle of role reversal and training drives a progressive improvement in the model’s capabilities. The performance metrics in Table 3 indicate substantial improvements in each iteration, demonstrating a consistent upward trend. Figure 6 demonstrates that the results improve progressively with each iteration.

Table 3.
Analysis of iterative effects.

Figure 6.
Iterative performance outcomes based on the NYUv2 dataset.
The consistent and progressive performance improvement demonstrates the effectiveness of our iterative training approach. In every cycle, the model’s capacity for depth completion undergoes gradual refinement, ensuring that the knowledge transferred and acquired in each iteration is expanded and optimized. This iterative strategy enhances the precision and overall quality of depth estimation and underscores the robustness and scalability of our training framework, advancing depth completion technology.
4.5. Ablation Study
To evaluate the impact of the proposed self-training with noise and the pixel-wise knowledge distillation module, we conduct a comprehensive ablation study on the NYUv2 dataset. We systematically examine three critical aspects of the methodology.
4.5.1. Contribution of Self-Training with Noise
To evaluate noise-enhanced self-training, three configurations were analyzed:
- Baseline: standard NLSPN model without self-training or noise augmentation.
- Self-training only: teacher–student iterative training framework implemented, excluding noise perturbations.
- Full framework: the integration of self-training with dual noise strategies—RGB Gaussian blur and stochastic perturbation are applied to sparse depth data.
The experimental outcomes are summarized in Table 4. Implementing the self-training framework (Configuration 2) notably elevated model performance over the baseline (Configuration 1), reducing the RMSE from 0.240 to 0.184. Incorporating noise augmentation (Configuration 3) further decreased the RMSE to 0.090, lowered the REL from 0.048 to 0.011, and achieved a of 99.7%. These improvements suggest that simulating real-world input variations through noise strategies strengthens the model robustness and generalizability.

Table 4.
The ablation experiment results for self-training and noise enhancement.
4.5.2. Contribution of Pixel-Wise Knowledge Distillation
To evaluate the pixel-wise knowledge distillation module’s efficacy, we excluded pixel-wise knowledge distillation from the full framework (self-training + noise augmentation) and assessed two variants:
- Full framework: we employed the combined task and KD losses defined in Equation (8).
- KD ablation: we relied solely on the task loss specified in Equation (3), omitting KD components.
Table 5 reveals notable performance deterioration when eliminating KD, with the RMSE rising from 0.090 to 0.163 and the REL increasing from 0.011 to 0.024. This demonstrates pixel-wise KD’s critical role in transferring the teacher model’s structural knowledge for dense pixel prediction, particularly preserving edge precision and spatial coherence through targeted supervision.

Table 5.
The ablation experiment results for pixel-wise knowledge distillation.
4.5.3. Independent Effects of Noise Variants
To isolate individual noise impacts, we performed component-wise ablations:
- RGB Gaussian blur only: Gaussian blur (σ = 1.5) was applied exclusively to RGB inputs with unmodified depth data.
- Depth perturbation only: random displacement (ε = 3) was introduced solely to sparse depth measurements.
- Dual noise: the concurrent implementation of both modalities.
Table 6 demonstrates that individual noise strategies—RGB Gaussian blur or sparse depth perturbation—each enhance performance, while their combined implementation achieves the peak efficacy (RMSE 0.090). This dual-modality approach leverages complementary perturbations across visual and geometric data domains, synergistically improving the robustness against heterogeneous input variations.

Table 6.
Analysis of independent effects of noise types.
4.5.4. Discussion
The ablation studies conducted on the NYUv2 dataset validate three critical observations:
- Self-training: iterative pseudo-label generation mitigates overfitting in limited-data regimes.
- Noise augmentation: simulated input perturbations boost the robustness to real-world data artifacts.
- Pixel-wise knowledge distillation: the teacher–student knowledge transfer preserves structural patterns, proving essential for edge-detail reconstruction in dense prediction tasks.
While these experiments conclusively demonstrate the module efficacy in indoor scenarios, their generalizability across diverse environments remains to be verified. Future work will extend the ablation analysis to outdoor benchmarks like KITTI DC, investigating two critical dimensions:
- Domain-specific adaptation: outdoor environments exhibit fundamentally different noise characteristics—sensor ranges exceed 80 m in KITTI versus 10 m in NYUv2, and the LiDAR sparsity patterns differ from those of Kinect depth sensors. We plan to develop adaptive noise scheduling that dynamically adjusts the perturbation intensity based on depth distribution statistics and scene semantics.
- Cross-domain knowledge transfer: the pixel-wise distillation mechanism currently operates within single domains. We propose cross-domain knowledge bridging where teacher models pretrained on NYUv2 guide student training on KITTI pseudo-labels, potentially reducing annotation dependency. This would require addressing domain gaps through attention-guided feature alignment between indoor structural priors and outdoor geometric regularities.
5. Conclusions
This study developed a few-shot learning framework to address the challenges associated with depth completion, particularly in scenarios where dataset availability is limited. Our method leverages self-training with noise injection to enhance the depth completion algorithm. Incorporating noise significantly enhanced the model’s diversity and generalization capabilities, enabling robust performance across diverse input conditions. Furthermore, including a pixel-wise KD module allowed the model to preserve and reinforce previously learned features, ensuring continuity and stability in its performance. Experiments performed on the NYUv2 dataset underscore the substantial benefits of the proposed framework. The results demonstrate that our approach significantly outperforms the original model, validating the effectiveness of integrating self-training with noise and pixel-wise KD. By addressing the limitations posed by small datasets, this approach enhances the robustness and scalability and ensures accurate depth completion. Therefore, our approach exhibits its practical applicability and establishes a strong foundation for future advancements in depth completion research.
Author Contributions
Formal analysis, S.Z. (Shengjie Zhao); investigation, S.Z. (Shijie Zhang); methodology, S.Z. (Shijie Zhang); writing—original draft preparation, S.Z. (Shijie Zhang); supervision, J.Z. and H.D.; writing—review and editing, J.Z. and H.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the National Key R&D Program of China (Grants 2023YFC3806000 and 2023YFC3806002), the National Natural Science Foundation of China (Grants 61936014 and U23A20382), the Shanghai Municipal Science and Technology Major Project (Grant 2021SHZDZX0100), the Shanghai Science and Technology Innovation Action Plan Project (Grant 22511105300), and the Fundamental Research Funds for the Central Universities.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are presented within the article.
Acknowledgments
We thank LetPub (www.letpub.com.cn, accessed on 24 March 2025) for its linguistic assistance during the preparation of this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CSPN | convolutional spatial propagation network |
| DNN | deep neural network |
| FSLNKD | framework based on self-training with noise and pixel-wise knowledge distillation |
| KD | knowledge distillation |
| NLSPN | non-local spatial propagation network |
| REL | relative error |
| RMSE | root mean squared error |
| SS | sparse-to-dense |
References
- Fu, C.; Mertz, C.; Dolan, J.M. LIDAR and monocular camera fusion: On-road depth completion for autonomous driving. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 273–278. [Google Scholar] [CrossRef]
- Lorenz, M.; Pfeiffer, F.; Klimant, P. Augmented reality for pack optimization using video and depth data. In Proceedings of the 2020 IEEE International Symposium on Mixed and Augmented Reality Adjunct (ISMAR-Adjunct), Recife, Brazil, 9–13 November 2020; pp. 21–23. [Google Scholar] [CrossRef]
- Liu, C.; Kong, D.; Wang, S.; Li, J.; Yin, B. DLGAN: Depth-preserving latent generative adversarial network for 3D reconstruction. IEEE Trans. Multimed. 2021, 23, 2843–2856. [Google Scholar] [CrossRef]
- Luo, R.C.; Hsu, W.L. Robust indoor localization using histogram of oriented depth model feature map for intelligent service robotics. IEEE ASME Trans. Mechatron. 2022, 27, 4033–4044. [Google Scholar] [CrossRef]
- Liu, L.; Liao, Y.; Wang, Y.; Geiger, A.; Liu, Y. Learning steering kernels for guided depth completion. IEEE Trans. Image Process. 2021, 30, 2850–2861. [Google Scholar] [CrossRef] [PubMed]
- Ma, F.; Karaman, S. Sparse-to-dense: Depth prediction from sparse depth samples and a single image. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 4796–4803. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, P.; Yang, R. Depth estimation via affinity learned with convolutional spatial propagation network. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; pp. 108–125. [Google Scholar] [CrossRef]
- Park, J.; Joo, K.; Hu, Z.; Liu, C.-K.; So Kweon, I. Non-local spatial propagation network for depth completion. In Proceedings of the Computer Vision—ECCV 2020, Virtual, 23–28 September 2020; pp. 120–136. [Google Scholar] [CrossRef]
- Ma, F.; Cavalheiro, G.V.; Karaman, S. Self-supervised sparse-to-dense: Self-supervised depth completion from LiDAR and monocular camera. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3288–3295. [Google Scholar] [CrossRef]
- Song, Z.; Lu, J.; Yao, Y.; Zhang, J. Self-supervised depth completion from direct visual-LiDAR odometry in autonomous driving. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11654–11665. [Google Scholar] [CrossRef]
- Liu, Y.; Shu, C.; Wang, J.; Shen, C. Structured knowledge distillation for dense prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 7035–7049. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J.; Cui, Z.; Zhang, Y.; Zhang, X.; Liu, S.; Zeng, B.; Pollefeys, M. DeepLiDAR: Deep surface normal guided depth prediction for outdoor scene from sparse LiDAR data and single color image. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3308–3317. [Google Scholar] [CrossRef]
- Imran, S.; Long, Y.; Liu, X.; Morris, D. Depth coefficients for depth completion. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 12438–12447. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, X.; Shi, J.; Zhang, G.; Bao, H.; Li, H. Depth completion from sparse LiDAR data with depth-normal constraints. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2811–2820. [Google Scholar] [CrossRef]
- Chen, Z.; Badrinarayanan, V.; Drozdov, G.; Rabinovich, A. Estimating depth from RGB and sparse sensing. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Springer: Cham, Switzerland, 2018; pp. 176–192. [Google Scholar] [CrossRef]
- Dimitrievski, M.; Veelaert, P.; Philips, W. Learning morphological operators for depth completion. In Proceedings of the Advanced Concepts for Intelligent Vision Systems (ACIVS 2018), Poitiers, France, 24–27 September 2018; Springer: Cham, Switzerland, 2018; pp. 450–461. [Google Scholar] [CrossRef]
- Jaritz, M.; Charette, R.D.; Wirbel, E.; Perrotton, X.; Nashashibi, F. Sparse and dense data with CNNs: Depth completion and semantic segmentation. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 52–60. [Google Scholar] [CrossRef]
- Shivakumar, S.S.; Nguyen, T.; Miller, I.D.; Chen, S.W.; Kumar, V.; Taylor, C.J. DFuseNet: Deep fusion of RGB and sparse depth information for image guided dense depth completion. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 13–20. [Google Scholar] [CrossRef]
- Li, A.; Yuan, Z.; Ling, Y.; Chi, W.; Zhang, S.; Zhang, C. A multi-scale guided cascade hourglass network for depth completion. In Proceedings of the 2020 IEEE Winter Conference on Applications of Computer Vision (WACV), Snowmass, CO, USA, 1–5 March 2020; pp. 32–40. [Google Scholar] [CrossRef]
- Schuster, R.; Wasenmüller, O.; Unger, C.; Stricker, D. SSGP: Sparse spatial guided propagation for robust and generic interpolation. In Proceedings of the 2021 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2021; pp. 197–206. [Google Scholar] [CrossRef]
- Tang, J.; Tian, F.P.; Feng, W.; Li, J.; Tan, P. Learning guided convolutional network for depth completion. IEEE Trans. Image Process. 2021, 30, 1116–1129. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Wang, P.; Yang, R. Learning depth with convolutional spatial propagation network. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2361–2379. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Wang, P.; Guan, C.; Yang, R. Cspn++: Learning context and resource aware convolutional spatial propagation networks for depth completion. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 10615–10622. [Google Scholar] [CrossRef]
- Lin, Y.; Cheng, T.; Zhong, Q.; Zhou, W.; Yang, H. Dynamic spatial propagation network for depth completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022; pp. 1638–1646. [Google Scholar] [CrossRef]
- Hu, Z.; Yang, Z.; Hu, X.; Nevatia, R. SimPLE: Similar pseudo label exploitation for semi-supervised classification. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 15094–15103. [Google Scholar] [CrossRef]
- Yang, M.; Ling, J.; Chen, J.; Feng, M.; Yang, J. Discriminative semi-supervised learning via deep and dictionary representation for image classification. Pattern Recognit. 2023, 140, 109521. [Google Scholar] [CrossRef]
- Li, J.; Li, G.; Shi, Y.; Yu, Y. Cross-domain adaptive clustering for semi-supervised domain adaptation. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 2505–2514. [Google Scholar] [CrossRef]
- Huang, K.; Geng, J.; Jiang, W.; Deng, X.; Xu, Z. Pseudo-loss confidence metric for semi-supervised few-shot learning. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 8651–8660. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Z.; Hu, H.; Wang, J.; Wang, L.; Wei, F.; Bai, X.; Liu, Z. End-to-end semi-supervised object detection with soft teacher. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 3040–3049. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, J.; Lin, D. Semi-supervised semantic segmentation via gentle teaching assistant. In Proceedings of the Advances in Neural Information Processing Systems 35 (NeurIPS 2022), New Orleans, LA, USA, 28 November–9 December 2022; pp. 2803–2816. [Google Scholar]
- Wang, Y.; Zhang, J.; Kan, M.; Shan, S. Learning pseudo labels for semi-and-weakly supervised semantic segmentation. Pattern Recognit. 2022, 132, 108925. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar] [CrossRef]
- Romero, A.; Ballas, N.; Kahou, S.E.; Chassang, A.; Gatta, C.; Bengio, Y. Fitnets: Hints for thin deep nets. arXiv 2014, arXiv:1412.6550. [Google Scholar] [CrossRef]
- Zagoruyko, S.; Komodakis, N. Paying more attention to attention: Improving the performance of convolutional neural networks via attention transfer. arXiv 2016, arXiv:1612.03928. [Google Scholar] [CrossRef]
- Park, W.; Kim, D.; Lu, Y.; Cho, M. Relational knowledge distillation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3962–3971. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, NSW, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. In Advances in Neural Information Processing Systems 30 (NIPS 2017); NeurIPS: San Diego, CA, USA, 2017; pp. 4080–4090. [Google Scholar]
- Li, Z.; Chen, Z.; Liu, X.; Jiang, J. Depthformer: Exploiting long-range correlation and local information for accurate monocular depth estimation. Mach. Intell. Res. 2023, 20, 837–854. [Google Scholar] [CrossRef]
- Xie, Q.; Luong, M.T.; Hovy, E.; Le, Q.V. Self-training with noisy student improves ImageNet classification. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 10684–10695. [Google Scholar] [CrossRef]
- Zhang, Z.; Klassen, E.; Srivastava, A. Gaussian blurring-invariant comparison of signals and images. IEEE Trans. Image Process. 2013, 22, 3145–3157. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Sun, Y.; Liu, Z.; Sedra, D.; Weinberger, K.Q. Deep networks with stochastic depth. In Proceedings of the Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Cham, Switzerland, 2016; pp. 646–661. [Google Scholar] [CrossRef]
- Yang, X.; Yang, X.; Yang, J.; Ming, Q.; Wang, W.; Tian, Q.; Yan, J. Learning high-precision bounding box for rotated object detection via kullback-leibler divergence. In Proceedings of the Advances in Neural Information Processing Systems 34 (NeurIPS 2021), Virtual, 6–14 December 2021; pp. 18381–18394. [Google Scholar]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor segmentation and support inference from RGBD images. In Proceedings of the Computer Vision—ECCV 2012, Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 746–760. [Google Scholar] [CrossRef]
- Uhrig, J.; Schneider, N.; Schneider, L.; Franke, U.; Brox, T.; Geiger, A. Sparsity invariant CNNs. In Proceedings of the International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 11–20. [Google Scholar] [CrossRef]
- Eldesokey, A.; Felsberg, M.; Khan, F.S. Confidence propagation through CNNs for guided sparse depth regression. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2423–2436. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).






