Dynamic Inversion Method for Concrete Gravity Dam on Soft Rock Foundation
Abstract
:Featured Application
Abstract
1. Introduction
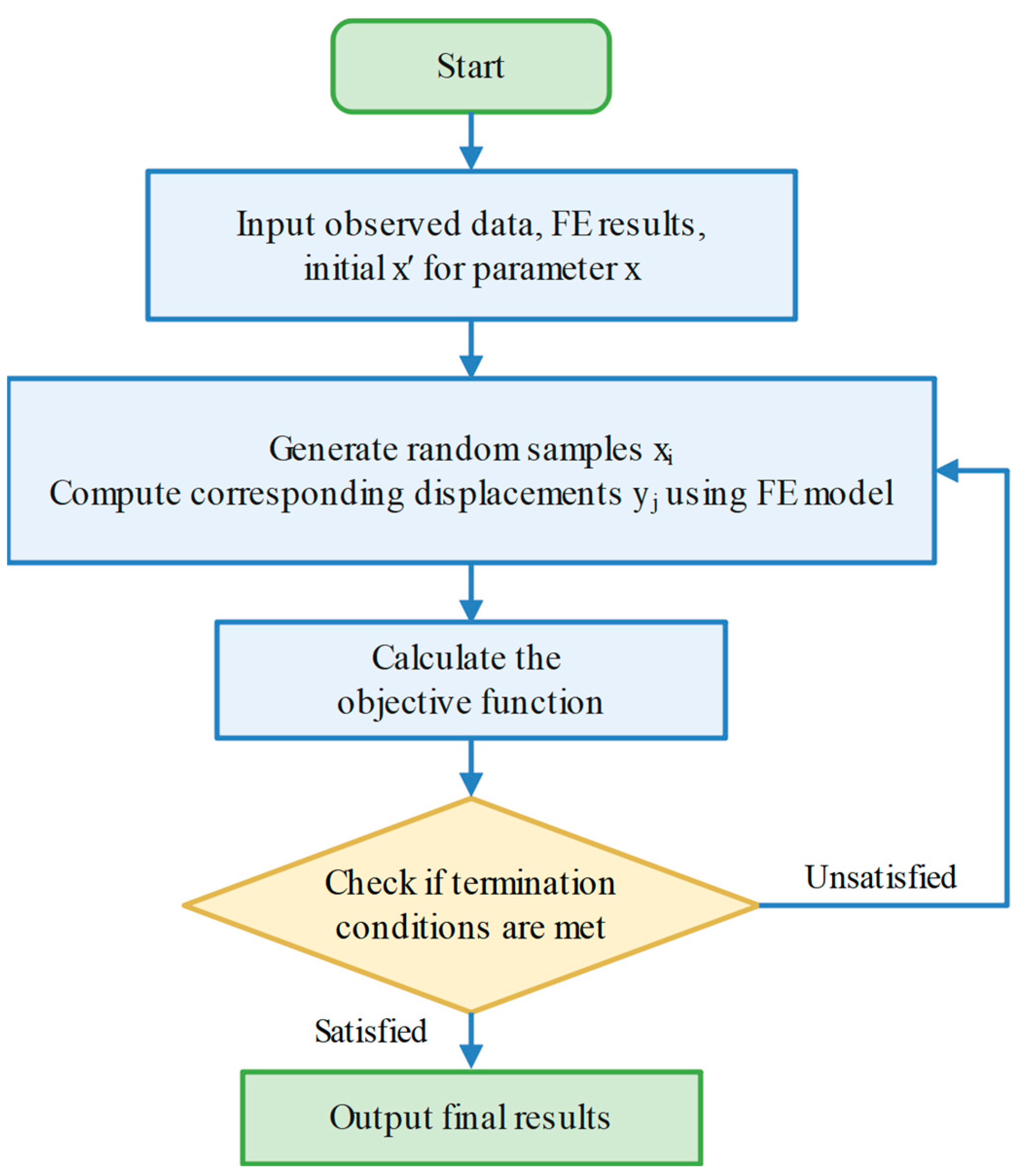
2. Inversion Methods for Mechanical Parameters of Concrete Gravity Dam
3. Improved Particle Swarm Optimization Algorithm
3.1. Particle Swarm Algorithm Fundamentals
3.2. Improvement Strategy
4. Engineering Examples
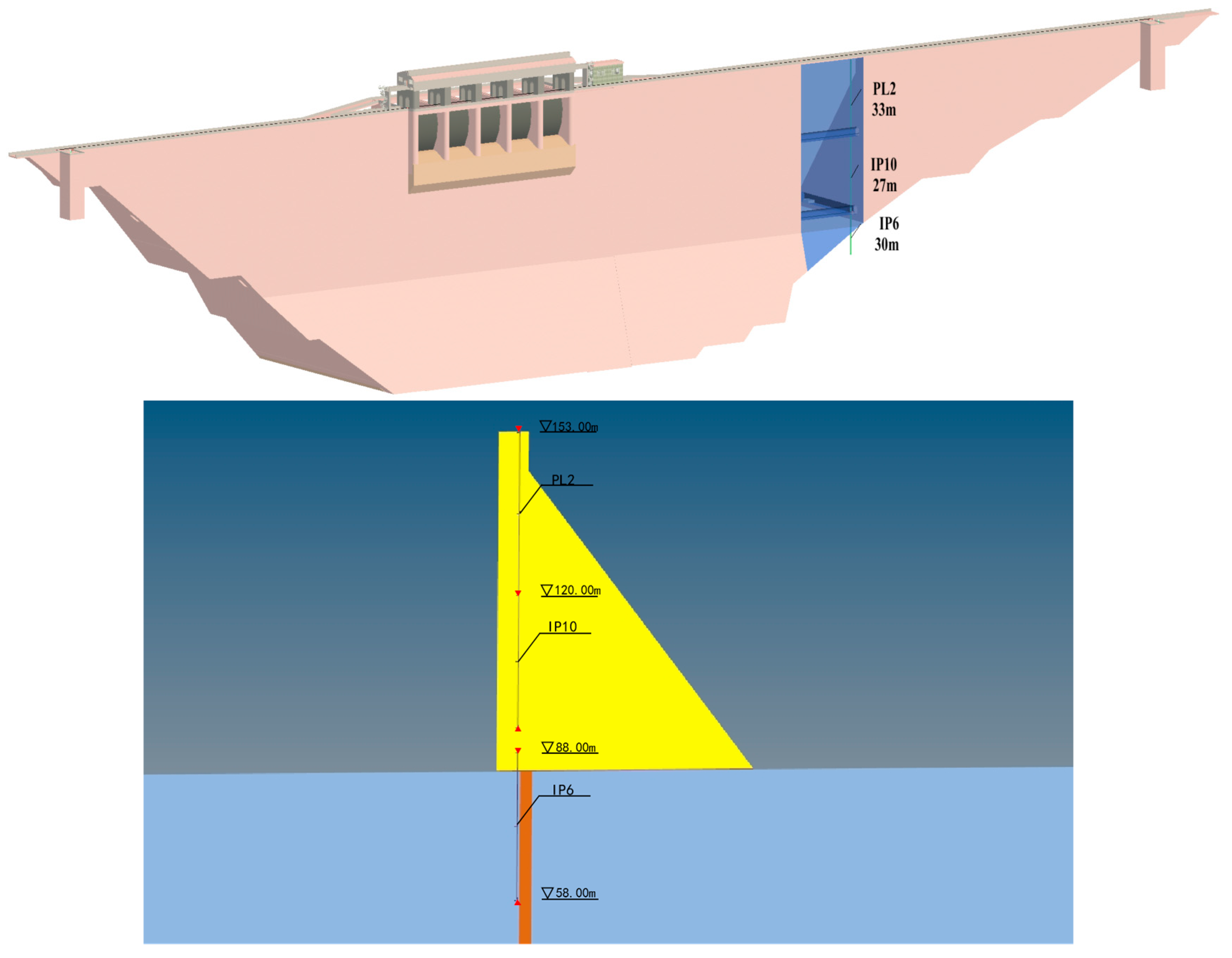
4.1. Overview of the Project
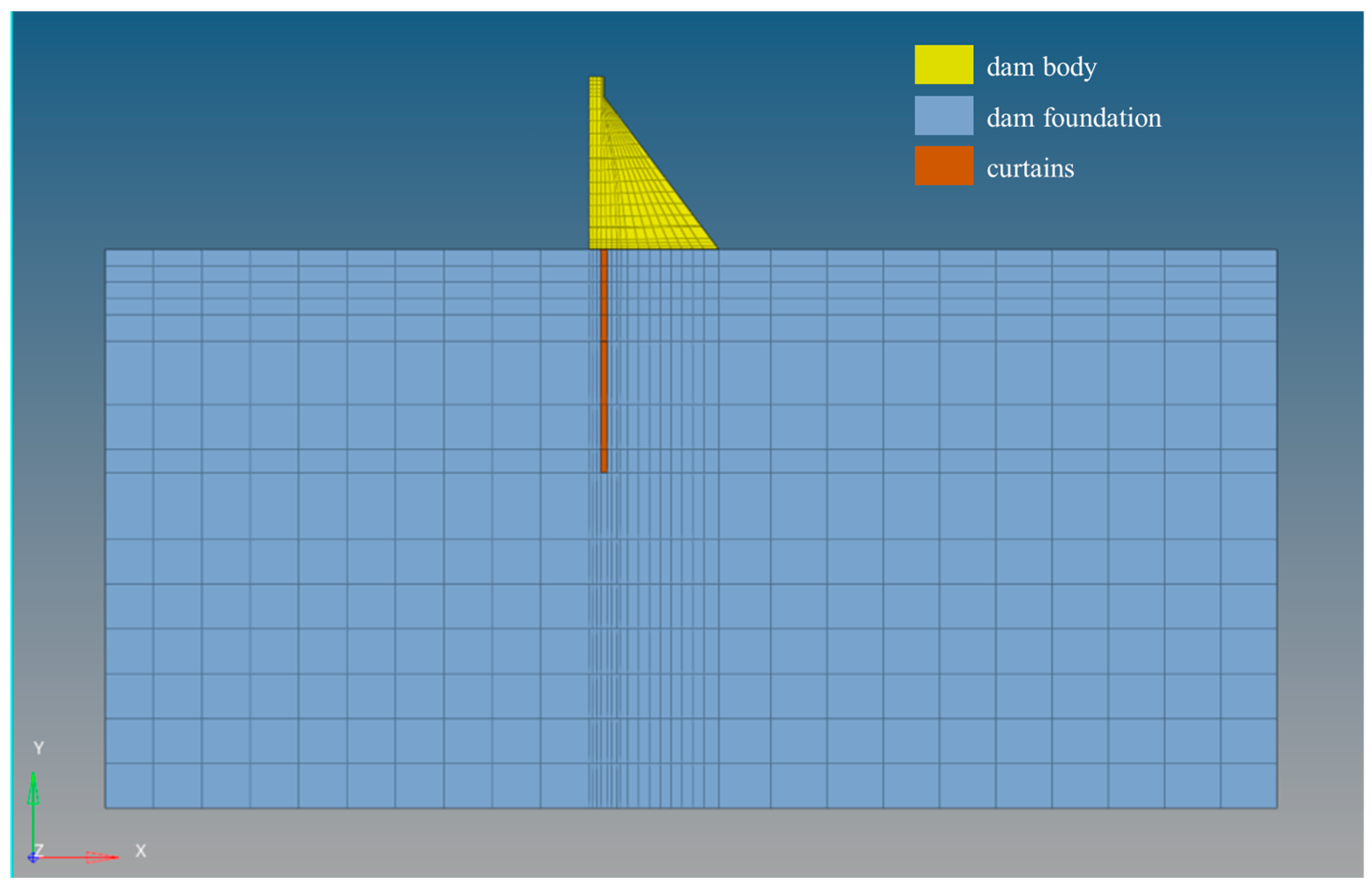
4.2. Finite Element Model and Calculation Parameters
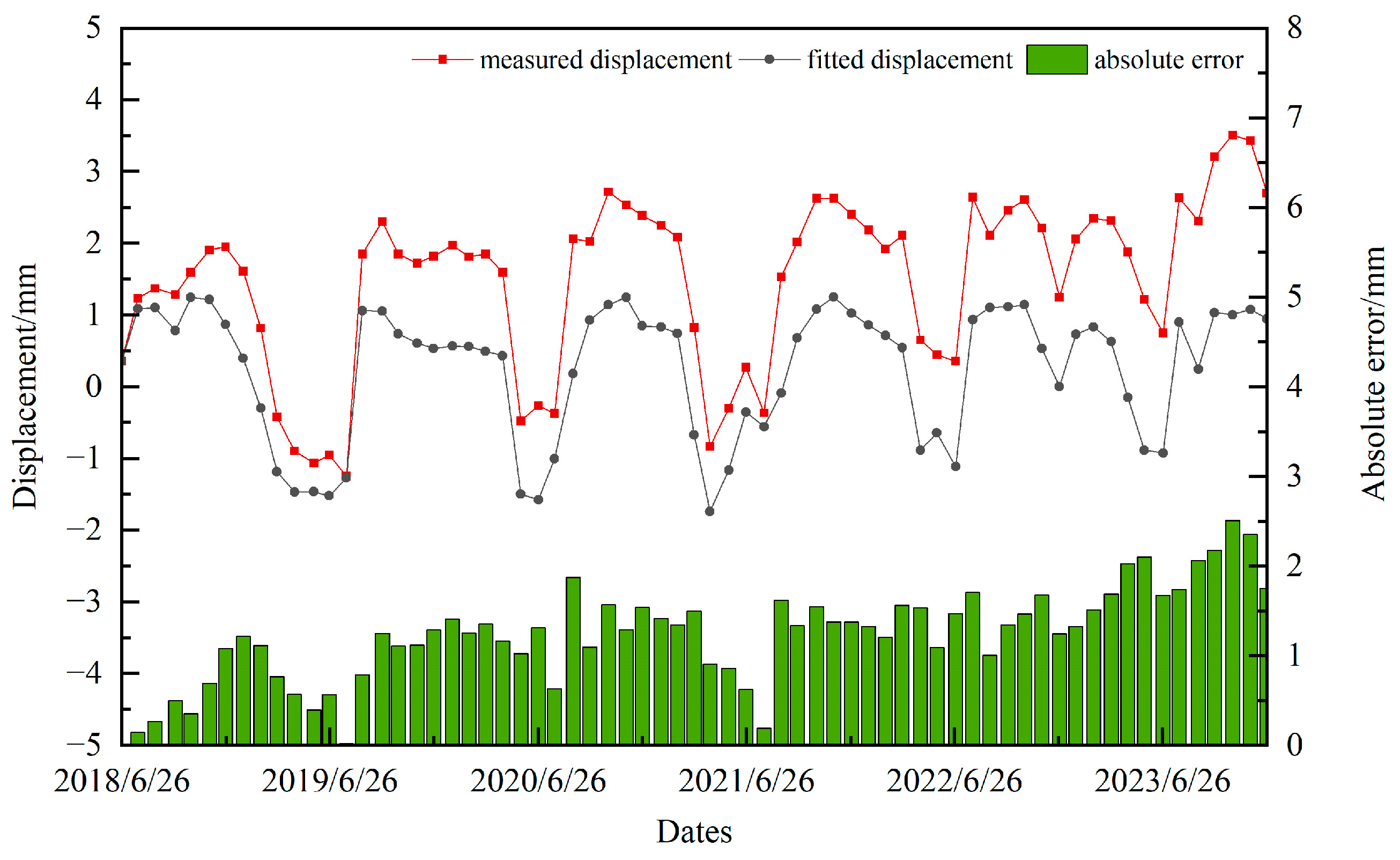
4.3. Comparison and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, S.; Lin, C.; Gu, Y.; Sheng, J.; Hariri-Ardebili, M.A. Dam Deformation Data Preprocessing with Optimized Variational Mode Decomposition and Kernel Density Estimation. Remote Sens. 2025, 17, 718. [Google Scholar] [CrossRef]
- Xiang, Y.; Su, H.; Wu, Z. Inversion of Physico-Mechanical Parameters Based on Dam Safety Monitoring Data. J. Water Resour. 2004, 35, 98–102. [Google Scholar] [CrossRef]
- Lin, C.; Chen, S.; Hariri-Ardebili, M.A.; Li, T. An Explainable Probabilistic Model for Health Monitoring of Concrete Dam via Optimized Sparse Bayesian Learning and Sensitivity Analysis. Struct. Control Health Monit. 2023, 2023, 2979822. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, G.; Wu, Z.; Shen, Z. Optimized Inversion of Time-Varying Parameters of Concrete Dams Based on Deformation Monitoring Data. J. Rock Mech. Eng. 2007, 26, 2941–2945. [Google Scholar]
- Lin, C.; Li, T.; Chen, S.; Yuan, L.; van Gelder, P.; Yorke-Smith, N. Long-term viscoelastic deformation monitoring of a concrete dam: A multi-output surrogate model approach for parameter identification. Eng. Struct. 2022, 266, 114553. [Google Scholar] [CrossRef]
- Lin, C.; Du, X.; Chen, S.; Li, T.; Zhou, X.; van Gelder, P.H.A.J.M. On the multi-parameters identification of concrete dams: A novel stochastic inverse approach. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 3792–3810. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, W.; Wang, K. Simplex Shape Method and Its Application to Inversion analysis of Perimeter Rock Deformation in Guangzhu Power Station. Geotech. Mech. 1991, 12, 57–66. [Google Scholar]
- Wu, X.; Wu, Z.; Gu, C.; Shen, Z.; Shu, Y. Inversion analysis Method of Creep of Crushed Concrete Arch Dam. Dam Obs. Civ. Test. 2000, 24, 22–24, 35. [Google Scholar]
- Niu, J. Inversion analysis of Mechanical Parameters of Crushed Concrete Dam Based on Chaotic Genetic Algorithm. South-to-North Water Divers. Water Sci. Technol. 2012, 10, 140–143. [Google Scholar]
- Wan, Z.; Huang, Y.; Zhu, Z.; Wang, T.; Jing, J.; Xiao, L. Inversion Analysis of Mechanical Parameters During Operation Period of Crushed Concrete Dam in Alpine Area. Water Conserv. Hydropower Technol. 2017, 48, 50–55. [Google Scholar]
- Li, W.; Liu, Q.; Shi, E.; Guo, W. Parameter Inversion and Application of South Water Modeling for Rockfill Based on XGBoost Algorithm. J. Water Resour. Water Transp. Eng. 2023, 111–120. [Google Scholar] [CrossRef]
- Sun, T.; Chen, Y.; Chen, J.; Yang, B.; Tan, C. Stability Modeling of Typical Dam Foundation of Daitengxia Lock and Dam. J. Undergr. Space Eng. 2022, 18, 179–189. [Google Scholar]
- Tang, M.; Duan, B.; Zhang, L.; Chen, J.; Yang, B. Experimental Study on Geomechanical Modeling of Overall Stability of High Gate Dam on Deep and Thick Overburden. Hydropower Gener 2017, 43, 105–109. [Google Scholar]
- Tian, Y.; Chen, W.; Tian, H.; Zhao, M.; Zeng, C. Study on the Design of Buffer Layer Letting Pressure Support Considering the Time-Dependent Weakening of Soft Rock Strength. Geotech 2020, 41 (Suppl. S1), 237–245. [Google Scholar]
- Li, S.; Wei, L.; Niu, J.; Deng, Z.; Wu, B.; Qian, W.; He, F. Time-Dependent Deviation of Bridge Pile Foundations Caused by Adjacent Large-Area Surcharge Loads in Soft Soils and Its Preventive Measures. Front. Struct. Civ. Eng. 2024, 18, 184–201. [Google Scholar] [CrossRef]
- Liu, B.; Li, H.; Wang, G.; Huang, W.; Wu, P.; Li, Y. Dynamic Material Parameter Inversion of High Arch Dam under Discharge Excitation Based on the Modal Parameters and Bayesian Optimised Deep Learning. Adv. Eng. Inform. 2023, 56, 102016. [Google Scholar] [CrossRef]
- Tian, K.; Yang, J.; Cheng, L. Deep Learning Model for the Deformation Prediction of Concrete Dams under Multistep and Multifeature Inputs Based on an Improved Autoformer. Eng. Appl. Artif. Intell. 2024, 137, 109109. [Google Scholar] [CrossRef]
- Yan, S.; Jiayuan, F.; Chuan, L. Prediction Model of Dam Structure Dynamic Deformation Based on Time Attention Mechanism. J. Hydroelectr. Eng. 2022, 41, 72–84. [Google Scholar]
- Liu, C.; Pan, J.; Wang, J. An LSTM-Based Anomaly Detection Model for the Deformation of Concrete Dams. Struct. Health Monit. 2023, 23, 1914–1925. [Google Scholar] [CrossRef]
- Madiniyeti, J.; Chao, Y.; Li, T.; Qi, H.; Wang, F. Concrete Dam Deformation Prediction Model Research Based on SSA–LSTM. Appl. Sci. 2023, 13, 7375. [Google Scholar] [CrossRef]
- Su, H.; Li, J.; Wu, Z. Optimization of inversion analysis of dam and foundation physico-mechanical parameters. J. Water Resour. 2007, S1, 129–134. [Google Scholar]
- Lin, C.; Li, T.; Chen, S.; Lin, C.; Liu, X.; Gao, L.; Sheng, T. Structural identification in long-term deformation characteristic of dam foundation using meta-heuristic optimization techniques. Adv. Eng. Softw. 2020, 148, 102870. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Ocampo, E.; Liu, C.-H.; Kuo, C.-C. Performance Analysis of Partitioned Step Particle Swarm Optimization in Function Evaluation. Appl. Sci. 2021, 11, 2670. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle Swarm Optimization Algorithm: An Overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Rini, D.P.; Shamsuddin, S.M.; Yuhaniz, S.S. Particle Swarm Optimization: Technique, System and Challenges. Int. J. Comput. Appl. 2011, 14, 19–26. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation Conference, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Fernandez-Merodo, J.A.; Castellanza, R.; Mabssout, M.; Pastor, M.; Parma, M. Coupling transport of chemical species and damage of bonded geomaterials. Comput. Geotech. 2007, 34, 200–215. [Google Scholar] [CrossRef]
- Cheng, X. Time-Varying Reliability Analysis Model and Reliability Calculation Method for Rocky Slope Anchoring Project. Ph.D. Thesis, Hunan University, Changsha, China, 2010. [Google Scholar]
- Peng, H.; Liu, D.; Tian, B. Time-Varying Modeling of Safety and Reliability of Concrete Gravity Dams. Hydropower Gener. 2009, 35, 77–79. [Google Scholar]

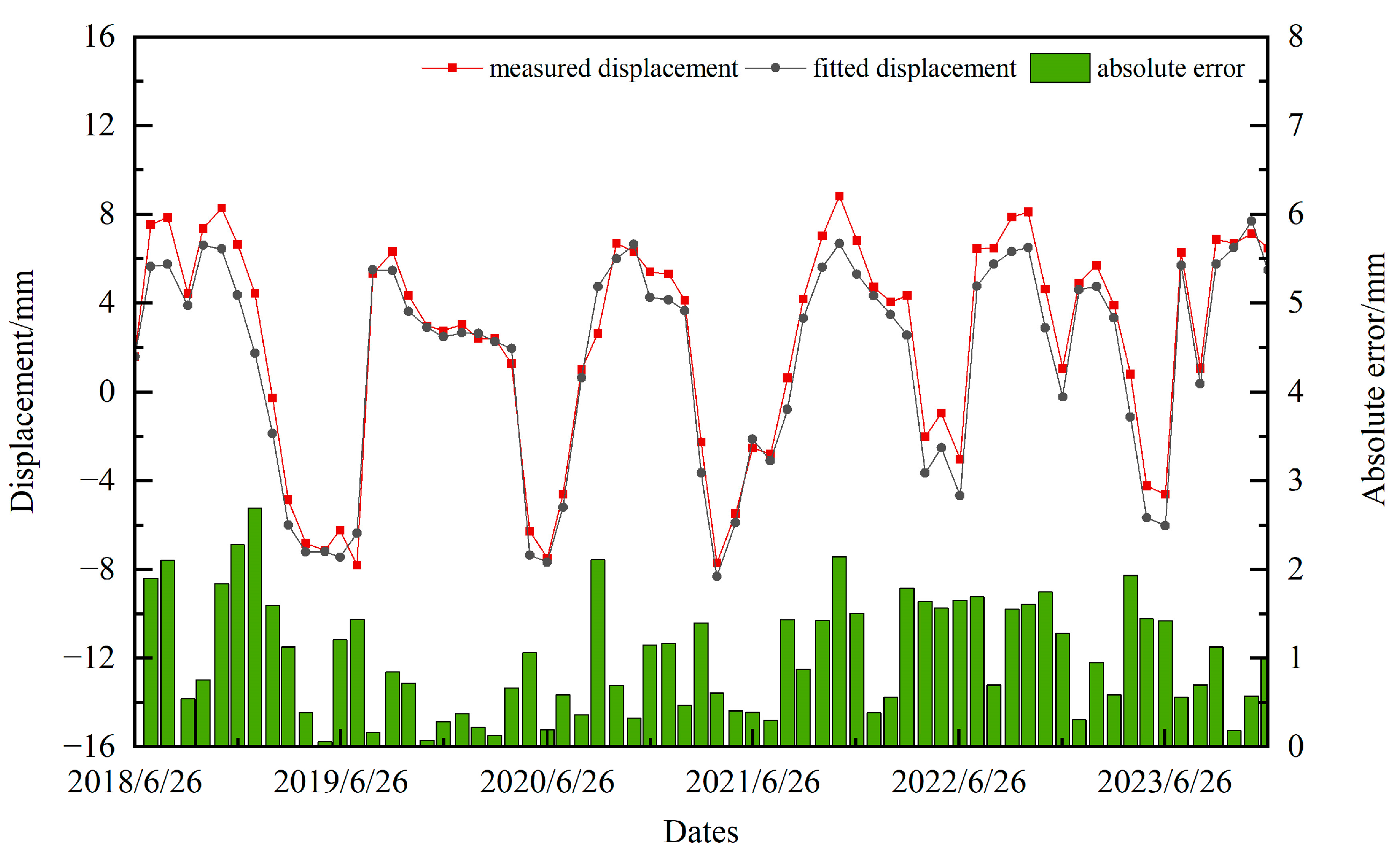

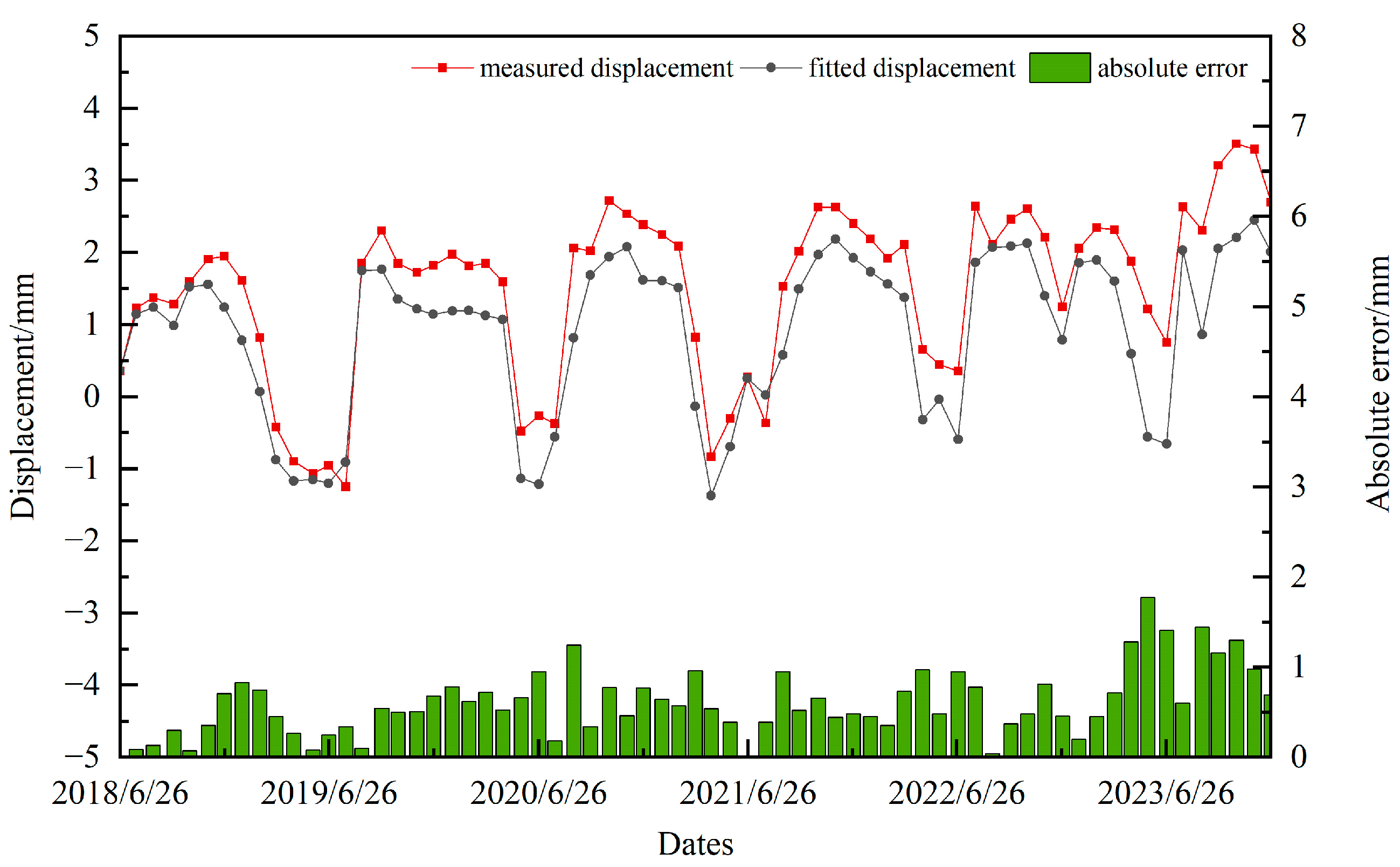
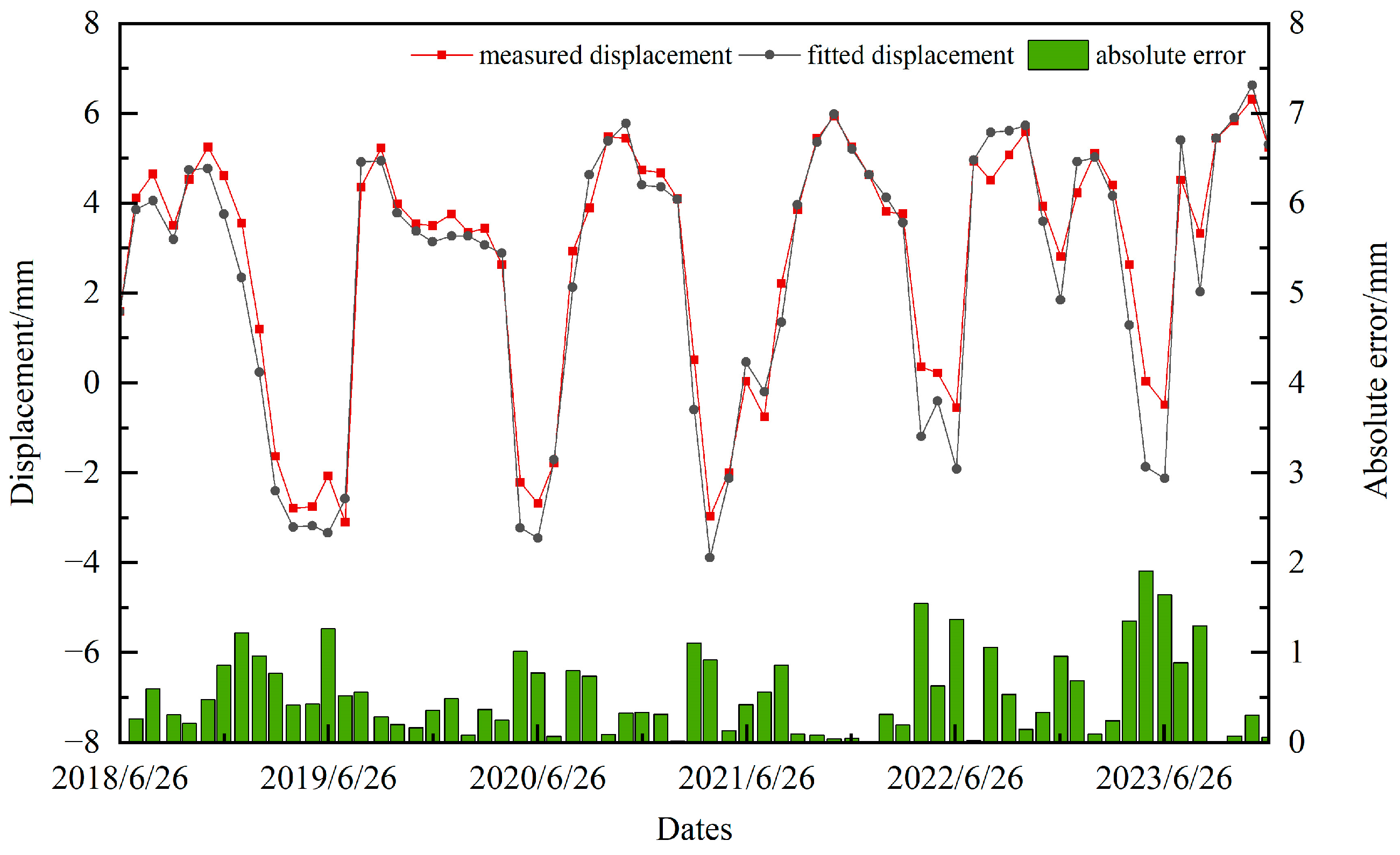
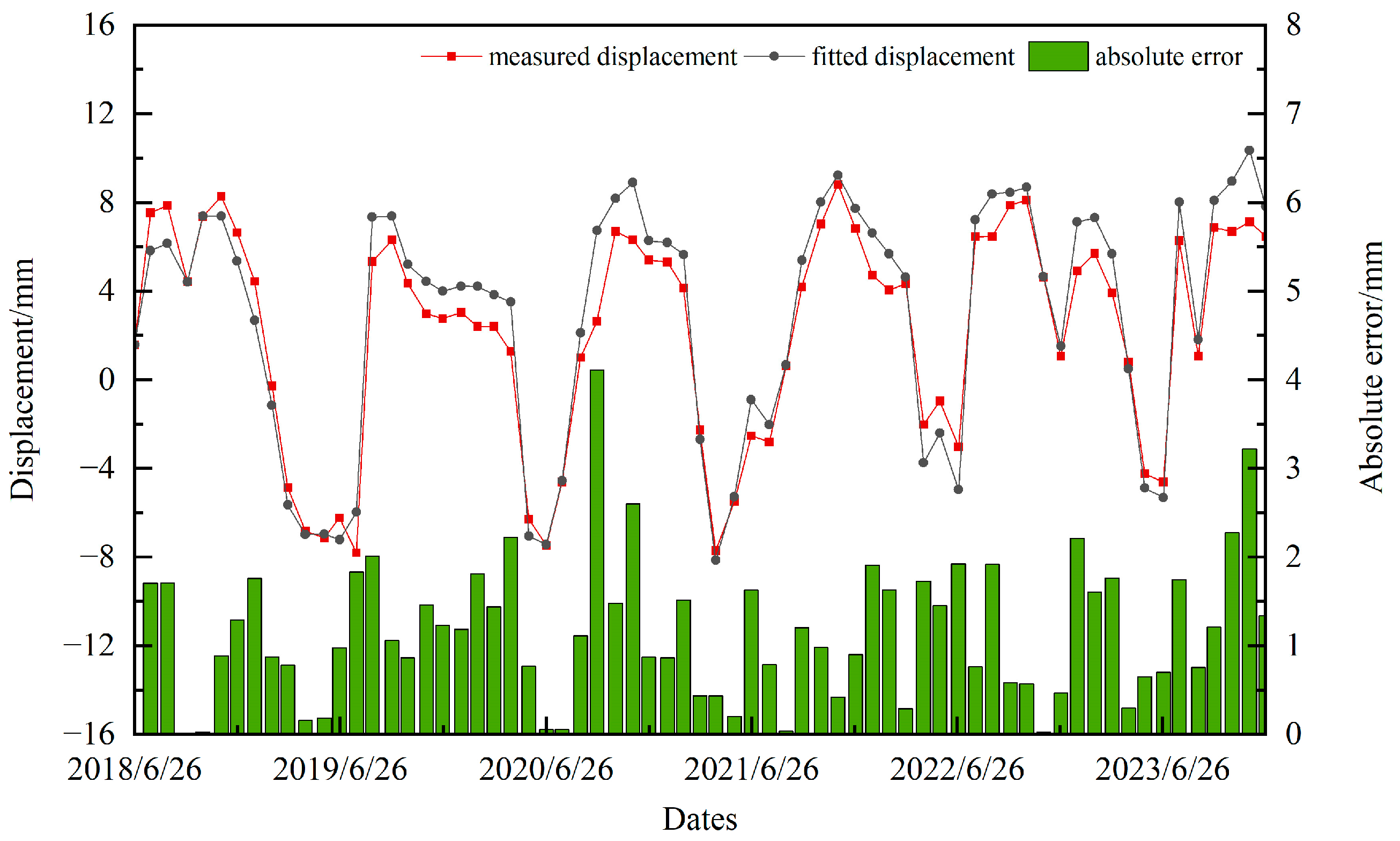
| Evaluation Indicators | IP6 | IP10 | PL2 |
|---|---|---|---|
| RMSE/mm | 1.344 | 0.614 | 1.193 |
| MAE/mm | 1.230 | 0.521 | 1.000 |
| Evaluation Indicators | IP6 | IP10 | PL2 |
|---|---|---|---|
| RMSE/mm | 0.707 | 0.701 | 1.401 |
| MAE/mm | 0.604 | 0.530 | 1.150 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, G.; Lin, C.; Sheng, T.; Xue, W.; Li, T.; Chen, S. Dynamic Inversion Method for Concrete Gravity Dam on Soft Rock Foundation. Appl. Sci. 2025, 15, 4750. https://doi.org/10.3390/app15094750
Yin G, Lin C, Sheng T, Xue W, Li T, Chen S. Dynamic Inversion Method for Concrete Gravity Dam on Soft Rock Foundation. Applied Sciences. 2025; 15(9):4750. https://doi.org/10.3390/app15094750
Chicago/Turabian StyleYin, Guanglin, Chaoning Lin, Taozhen Sheng, Wenbo Xue, Tongchun Li, and Siyu Chen. 2025. "Dynamic Inversion Method for Concrete Gravity Dam on Soft Rock Foundation" Applied Sciences 15, no. 9: 4750. https://doi.org/10.3390/app15094750
APA StyleYin, G., Lin, C., Sheng, T., Xue, W., Li, T., & Chen, S. (2025). Dynamic Inversion Method for Concrete Gravity Dam on Soft Rock Foundation. Applied Sciences, 15(9), 4750. https://doi.org/10.3390/app15094750









