Novel Research on a Finite-Difference Time-Domain Acceleration Algorithm Based on Distributed Cluster Graphic Process Units
Abstract
:1. Introduction
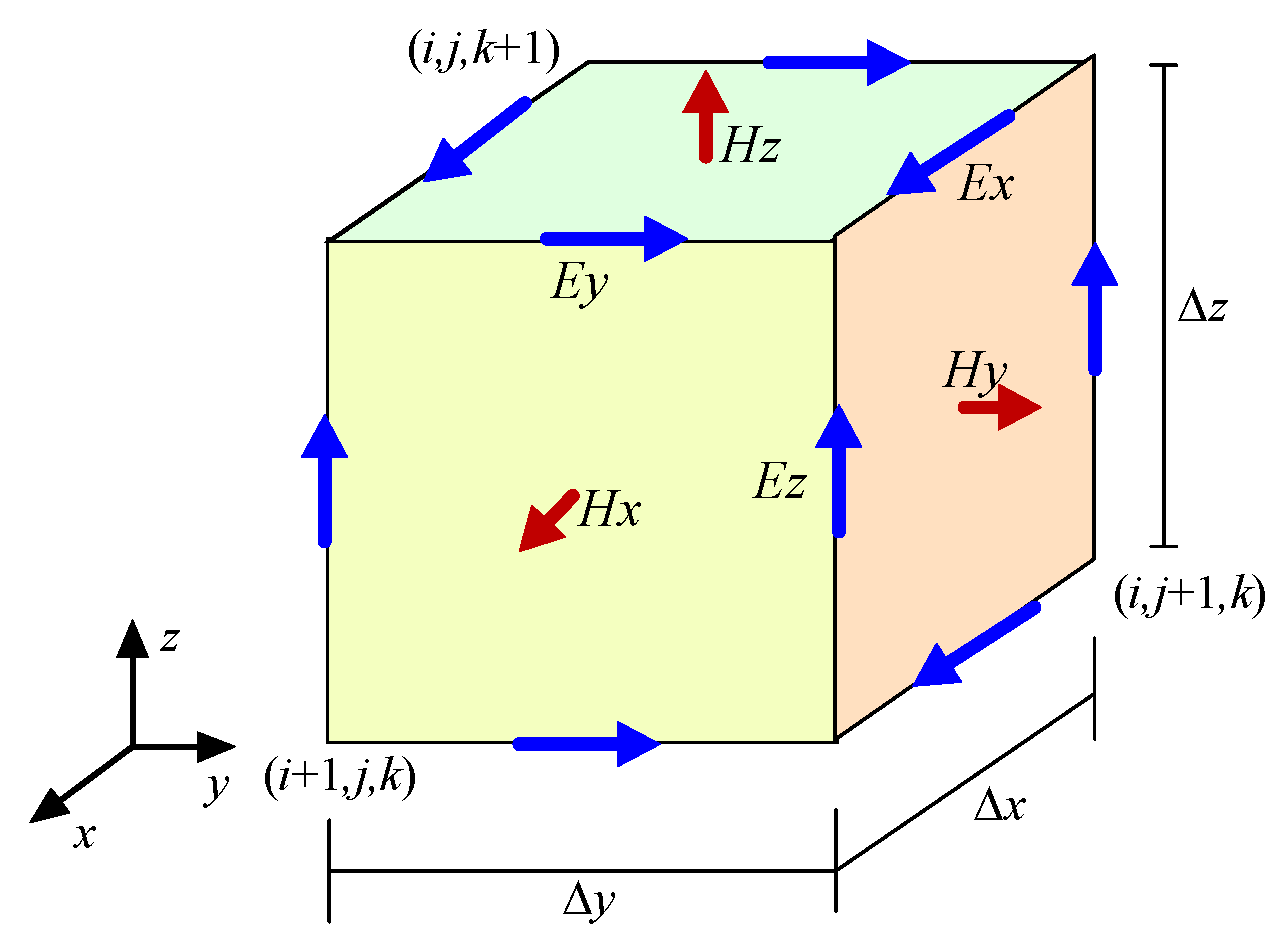
2. The FDTD Algorithm
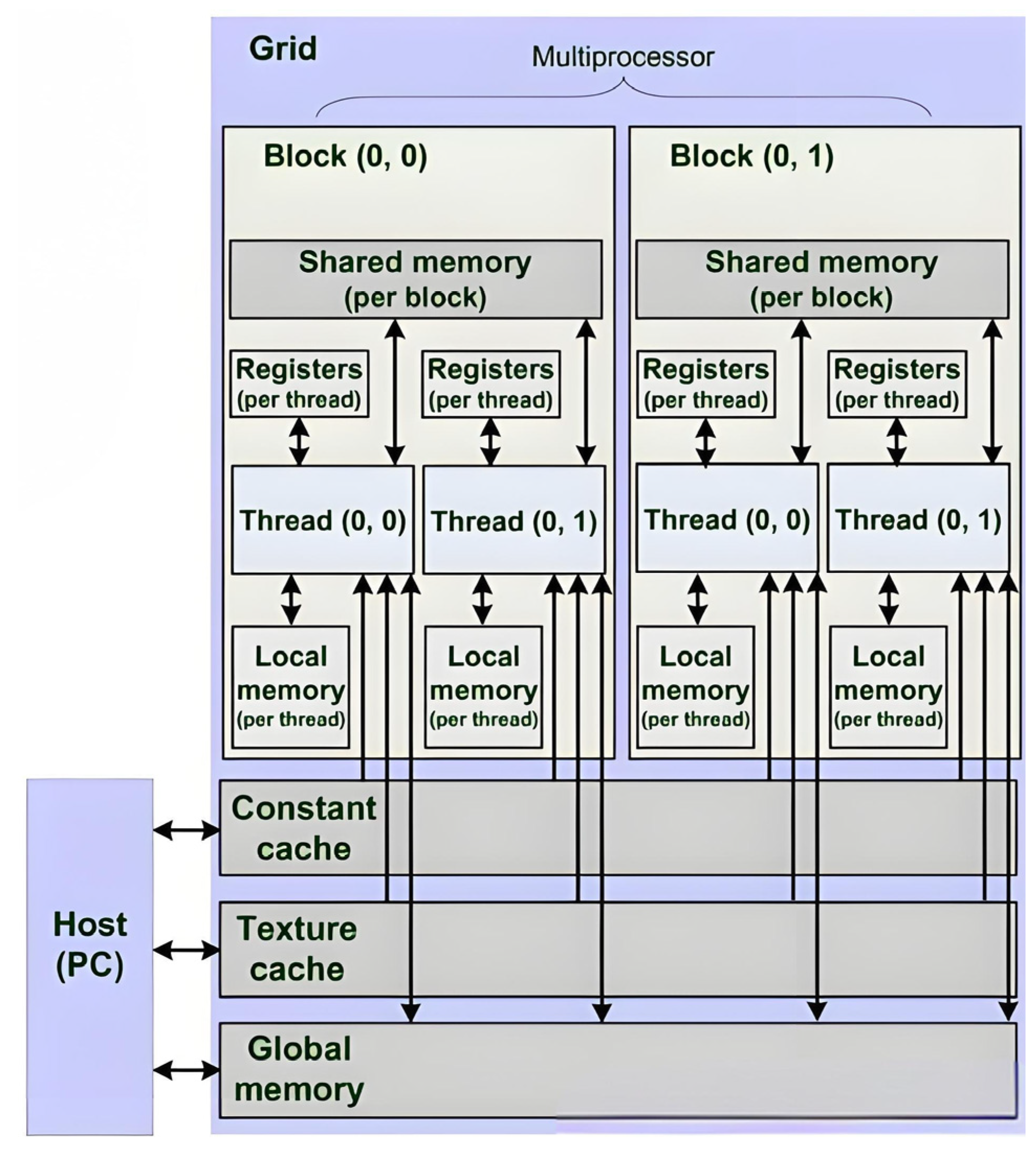
3. Three-Dimensional FDTD Parallel Algorithm on the CUDA Platform
3.1. FDTD Calculation Domain Decomposition Scheme
3.2. Data Transmission Scheme Based on NCCL
3.2.1. GPUs Communicate Indirectly Through the CPU
- (a)
- GPU copies data to CPU: Firstly, the GPU copies the data from its computation results that need to be shared with other GPUs into the CPU memory. This is because, in the traditional multi-GPU communication model, the CPU is responsible for coordinating and forwarding the data, so the data must first be transferred to the CPU’s memory.
- (b)
- The CPU exchanges the data between adjacent processes through MPI (Message Passing Interface) technology: After the data are copied to the CPU memory, the CPU uses MPI technology to exchange the data between adjacent processes. An MPI is a commonly used communication protocol in parallel computing, which can transmit information between multiple processors and ensure that the necessary electromagnetic field data can be shared between different GPUs.
- (c)
- The CPU copies the exchanged data to the GPU memory: After the data exchange is completed, the CPU copies the updated data back to the memory of each GPU so that the GPUs can continue to perform calculations. This step ensures that each GPU has the latest electromagnetic field data so that they can be processed correctly in the following calculations.
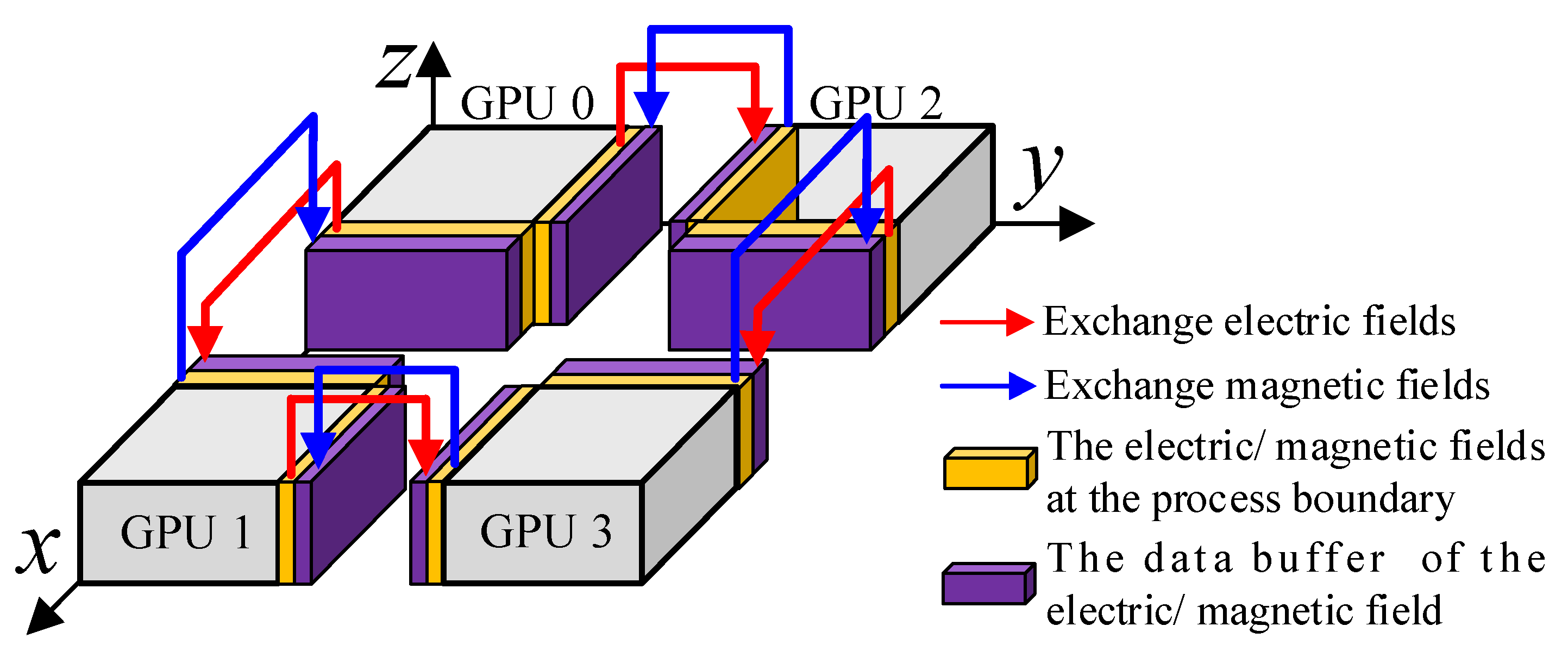
3.2.2. GPUs Communicate Directly Based on NCCL
- (a)
- Send the magnetic field H data of the yellow region to the purple data buffer of the adjacent subdomain;
- (b)
- Electric field E iteration;
- (c)
- Send the electric field data of the yellow region to the purple data buffer of the adjacent subdomain;
- (d)
- Magnetic field iteration.
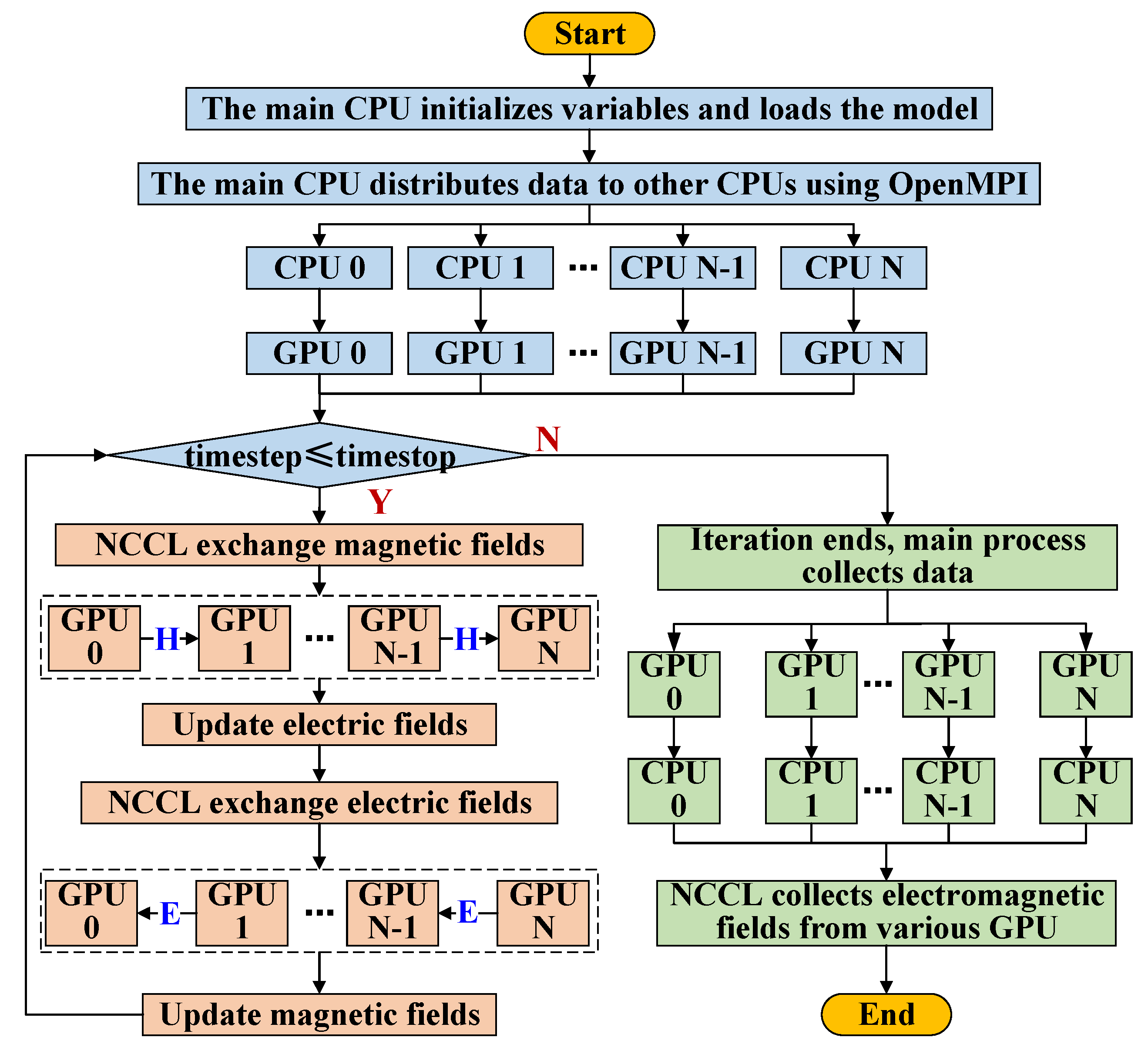
- (a)
- The system starts computing tasks by creating CPU processes that match the number of available GPUs using OpenMPI technology. At this stage, the main process of the CPU plays a crucial role, and is responsible for initializing all the variable information required throughout the entire computation process. This variable information is essential for the subsequent calculations, as it ensures the accuracy and consistency of the calculations.
- (b)
- The CPU main process performs load balancing and partitioning of the computing domain based on the number of processes. This step aims to optimize the allocation of computing resources, ensuring that each CPU process can handle an appropriate amount of data, thereby improving the overall computing efficiency. A segmented computing domain is allocated to each CPU process to prepare for the subsequent computing work. The model data for each CPU process are efficiently copied to the corresponding GPU global memory.
- (c)
- The GPUs fully utilize their powerful computing power by mapping each Yee cell onto a thread and carrying out the computing work in parallel. This calculation mode not only greatly improves the calculation speed, but also ensures the accuracy of the calculation. At each time step, the interaction of electric field data and magnetic field data between the GPUs is achieved through the NCCL technology. The NCCL technology provides an efficient and reliable solution for data communication between GPUs, ensuring the accuracy and consistency of data.
- (d)
- Finally, the collection of the calculation results is the responsibility of OpenMPI. OpenMPI allows for direct access to each GPU storage space, enabling the efficient collection of the computation results.
4. Simulation Results and Analysis
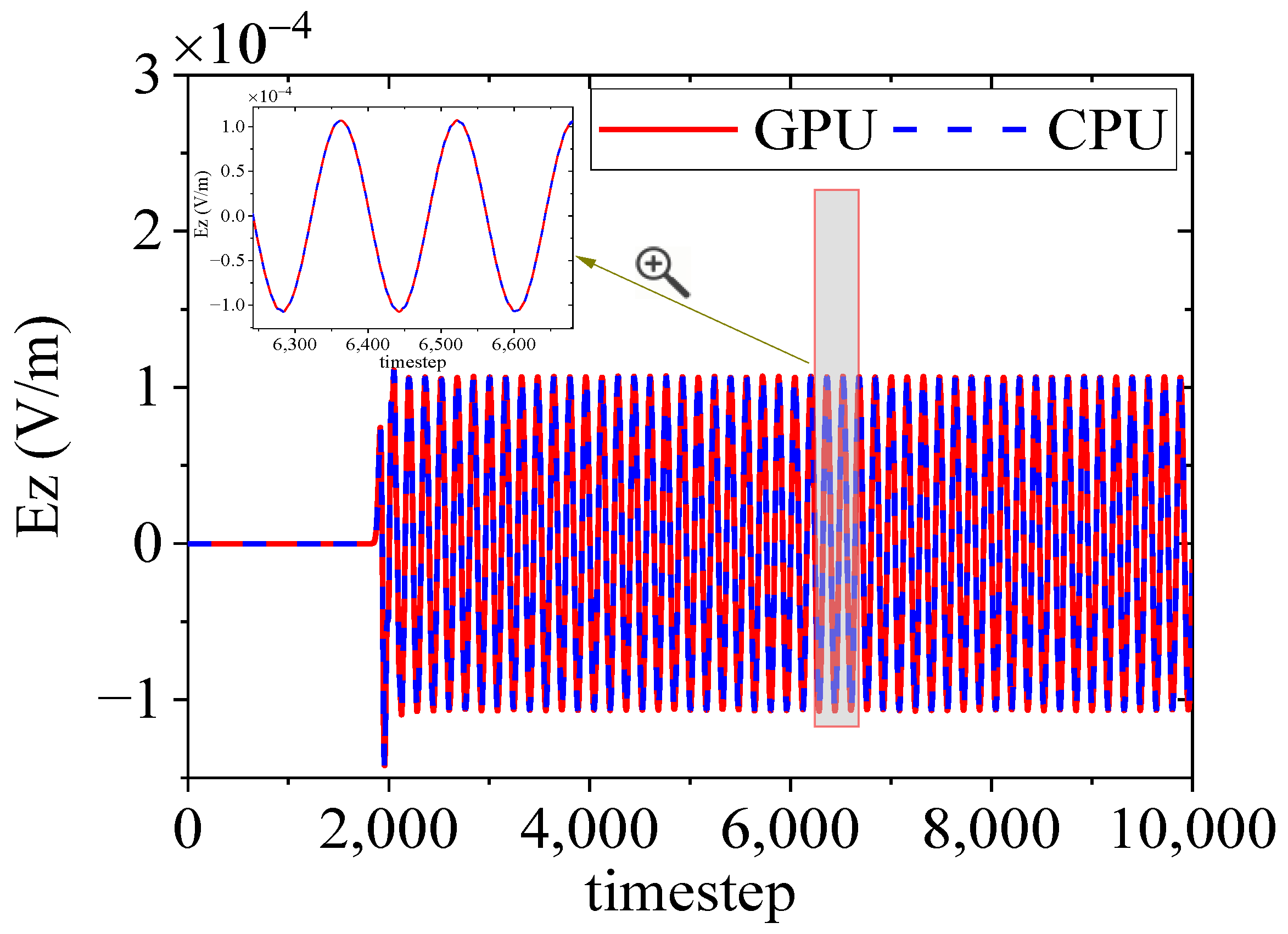
4.1. Free-Space Electric Dipole Radiation
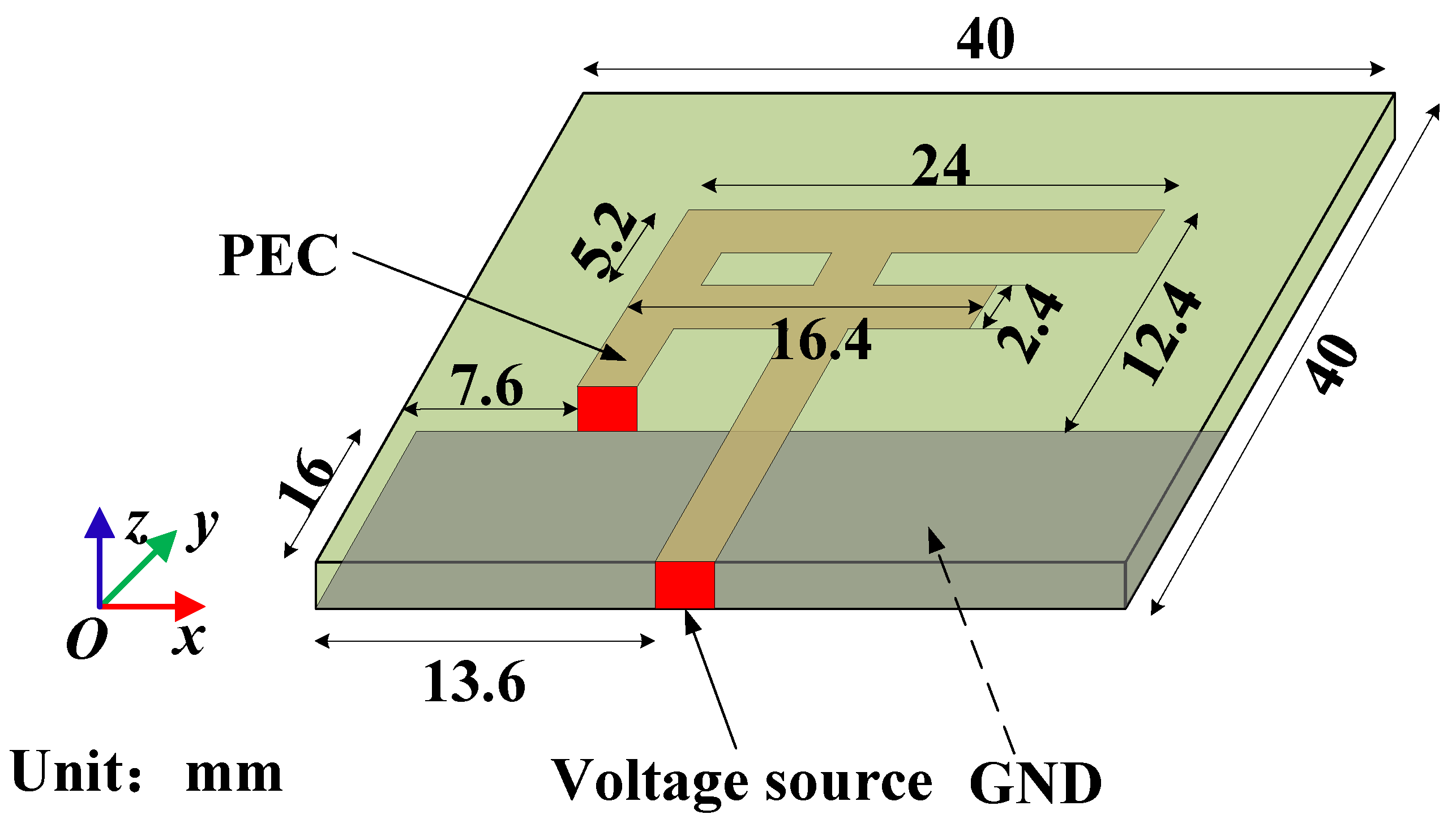
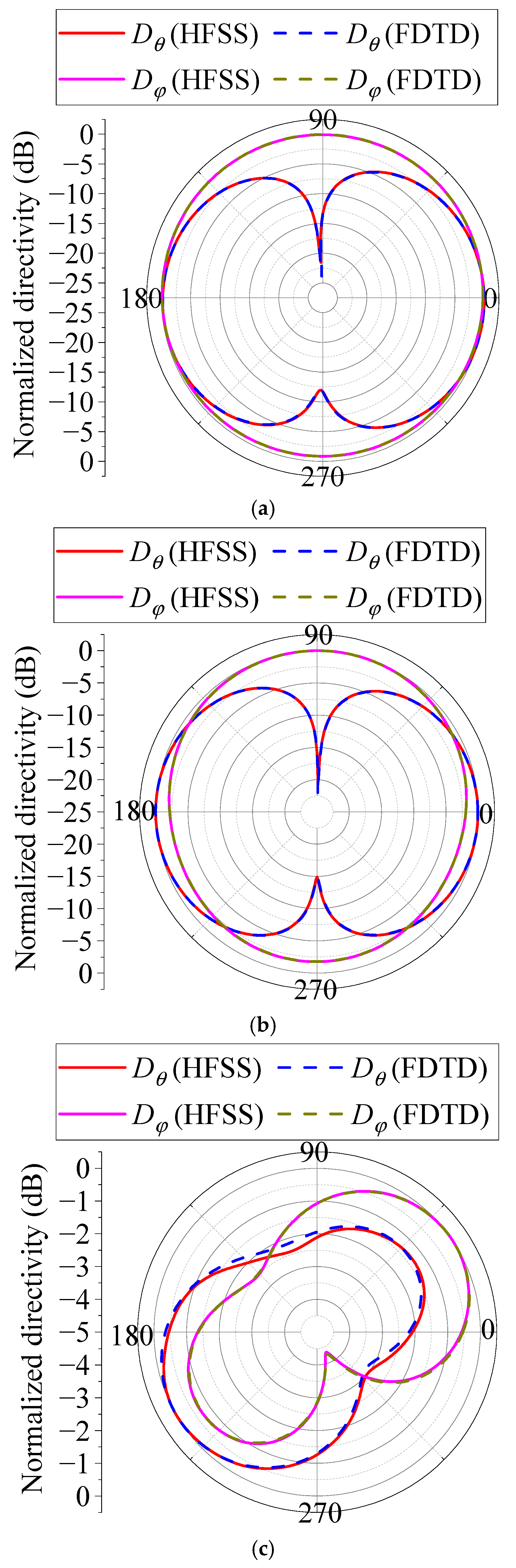
4.2. Antenna Simulation
4.3. The Radio Wave Propagation Problem
5. Conclusions
- (1)
- Compared with an FDTD algorithm on a CPU platform, an FDTD algorithm based on GPUs can significantly improve the computational efficiency.
- (2)
- Compared with traditional CPU forwarding for GPUs communication, GPUs direct communication based on the NCCL technology can improve the computational efficiency.
- (3)
- Due to hardware resource limitations, this paper only performed calculations on four GPUs. As the number of GPUs increases, the efficiency improvement of this new communication mode becomes more significant.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FDTD | Finite-Difference Time Domain |
| GPU | Graphic Process Unit |
| CUDA | Compute Unified Device Architecture |
| NCCL | Collective Communications Library |
| CPU | Central Processing Unit |
References
- Teixeira, F. A summary review on 25 years of progress and future challenges in FDTD and FETD techniques. Appl. Comput. Electrom. 2010, 25, 1–14. [Google Scholar]
- Yang, M.; Liu, K.; Zheng, K.; Wu, Q.; Wei, G. A Hybrid SI-FDTD Method to Analyze Scattering Fields From Underwater Complex Targets. IEEE Trans. Antennas Propag. 2024, 72, 7407–7412. [Google Scholar] [CrossRef]
- Yang, M.; Wu, Q.; Zheng, K.; Zhang, S.; Wei, G. Radiation Field Distribution Above Sea Surface of Underwater Microstrip Antenna Array. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 858–862. [Google Scholar] [CrossRef]
- He, X.; Chen, M.; Wei, B. A Hybrid Algorithm of 3-D Explicit Unconditionally Stable FDTD and Traditional FDTD Methods. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 4653–4657. [Google Scholar] [CrossRef]
- Yee, K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Warren, C.; Giannopoulos, A.; Gray, A.; Giannakis, I.; Patterson, A.; Wetter, L. A CUDA-based GPU engine for gprMax: Open source FDTD electromagnetic simulation software. Comput. Phys. Commun. 2018, 237, 208–218. [Google Scholar] [CrossRef]
- Jia, C.; Guo, L.; Yang, P. EM scattering from a target above a 1-D randomly rough sea surface using GPU-based parallel FDTD. IEEE Antennas Wirel. Propag. Lett. 2014, 14, 217–220. [Google Scholar] [CrossRef]
- Chi, J.; Liu, F.; Weber, E.; Li, Y.; Crozier, S. GPU-accelerated FDTD modeling of radio-frequency field–tissue interactions in high-field MRI. IEEE Trans. Bio-Med. Eng. 2011, 58, 1789–1796. [Google Scholar]
- Gunawardana, M.; Kordi, B. GPU and CPU-based parallel FDTD methods for frequency-dependent transmission line models. IEEE Lett. Electromag. 2022, 4, 66–70. [Google Scholar] [CrossRef]
- Kim, K.; Kim, K.; Park, Q. Performance analysis and optimization of three-dimensional FDTD on GPU using roofline model. Comput. Phys. Commun. 2011, 182, 1201–1207. [Google Scholar] [CrossRef]
- Zygiridis, T.; Kantartzis, N.; Tsiboukis, T. GPU-accelerated efficient implementation of FDTD methods with optimum time-step selection. IEEE Trans. Magn. 2014, 50, 477–480. [Google Scholar] [CrossRef]
- Zhang, B.; Xue, Z.; Ren, W.; Li, W.; Sheng, X. Accelerating FDTD algorithm using GPU computing. In Proceedings of the 2011 IEEE International Conference on Microwave Technology & Computational Electromagnetics, Beijing, China, 22–25 May 2011; IEEE: New York, NY, USA, 2011; pp. 410–413. [Google Scholar]
- Livesey, M.; Stack, J.; Costen, F.; Nanri, T.; Nakashima, N.; Fujino, S. Development of a CUDA implementation of the 3D FDTD method. IEEE Antennas Propag. Mag. 2012, 54, 186–195. [Google Scholar] [CrossRef]
- Feng, J.; Fang, M.; Deng, X.; Li, Z.; Xie, G.; Huang, Z. FDTD Modeling of Nonlocality in Nanoantenna Accelerated by CPU-GPU Heterogeneous Architecture and Subgridding Techniques. IEEE Trans. Antennas Propag. 2024, 72, 1708–1720. [Google Scholar] [CrossRef]
- Cannon, P.; Honary, F. A GPU-accelerated finite-difference time-domain scheme for electromagnetic wave interaction with plasma. IEEE Trans. Antennas Propag. 2015, 63, 3042–3054. [Google Scholar] [CrossRef]
- Liu, S.; Zou, B.; Zhang, L.; Ren, S. A multi-GPU accelerated parallel domain decomposition one-step leapfrog ADI-FDTD. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 816–820. [Google Scholar] [CrossRef]
- Feng, J.; Song, K.; Fang, M.; Chen, W.; Xie, G.; Huang, Z. Heterogeneous CPU-GPU Accelerated Subgridding in the FDTD Modelling of Microwave Breakdown. Electronics 2022, 11, 3725. [Google Scholar] [CrossRef]
- Liu, S.; Zou, B.; Zhang, L.; Ren, S. Heterogeneous CPU+ GPU-accelerated FDTD for scattering problems with dynamic load balancing. IEEE Trans. Antennas Propag. 2020, 68, 6734–6742. [Google Scholar] [CrossRef]
- Baumeister, P.; Hater, T.; Kraus, J.; Wahl, P. A performance model for GPU-accelerated FDTD applications. In Proceedings of the 2015 IEEE 22nd International Conference on High Performance Computing (HiPC), Bengaluru, India, 16–19 December 2015; IEEE: New York, NY, USA, 2016; pp. 185–193. [Google Scholar]
- Chen, Y.; Zhu, P.; Wen, W.; Jiang, J. Accelerating 3D acoustic full waveform inversion using a multi-GPU cluster. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5913815. [Google Scholar]
- Kim, K.; Park, Q. Overlapping computation and communication of three-dimensional FDTD on a GPU cluster. Comput. Phys. Commun. 2012, 183, 2364–2369. [Google Scholar] [CrossRef]
- Foley, D.; Danskin, J. Ultra-Performance Pascal GPU and NVLink Interconnect. IEEE Micro 2017, 37, 7–17. [Google Scholar] [CrossRef]
- Awan, A.; Hamidouche, K.; Venkatesh, A. Efficient large message broadcast using NCCL and CUDA-aware MPI for deep learning. In Proceedings of the 23rd European MPI Users’ Group Meeting, Edinburgh, UK, 25–28 September 2016; ACM: New York, NY, USA, 2016; pp. 15–22. [Google Scholar]
- Boureima, I.; Bhattarai, M.; Eren, M.; Skau, E.; Romero, P.; Eidenbenz, S.; Alexandrov, B. Distributed out-of-memory NMF on CPU/GPU architectures. J. Supercomput. 2024, 80, 3970–3999. [Google Scholar] [CrossRef]
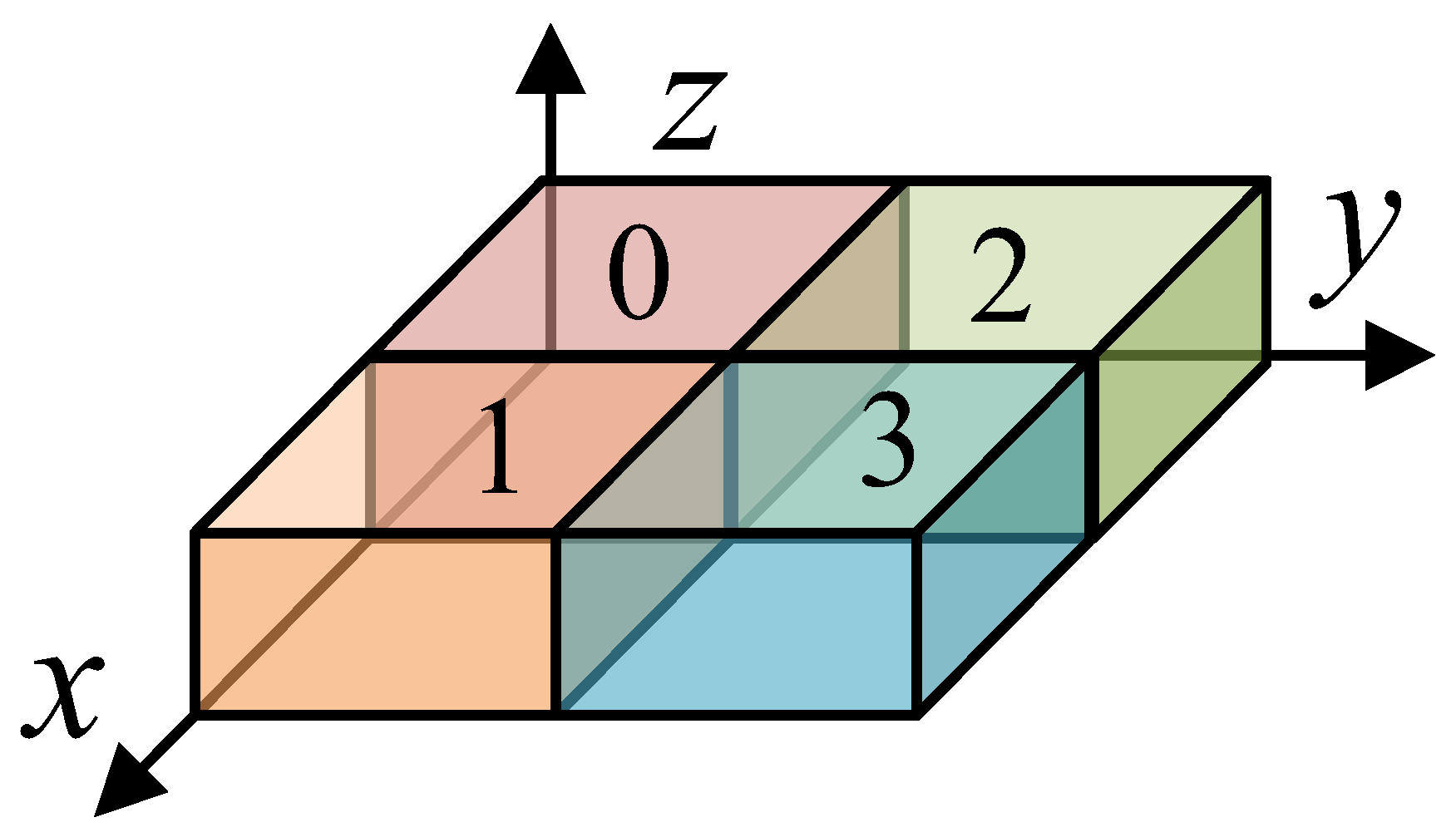


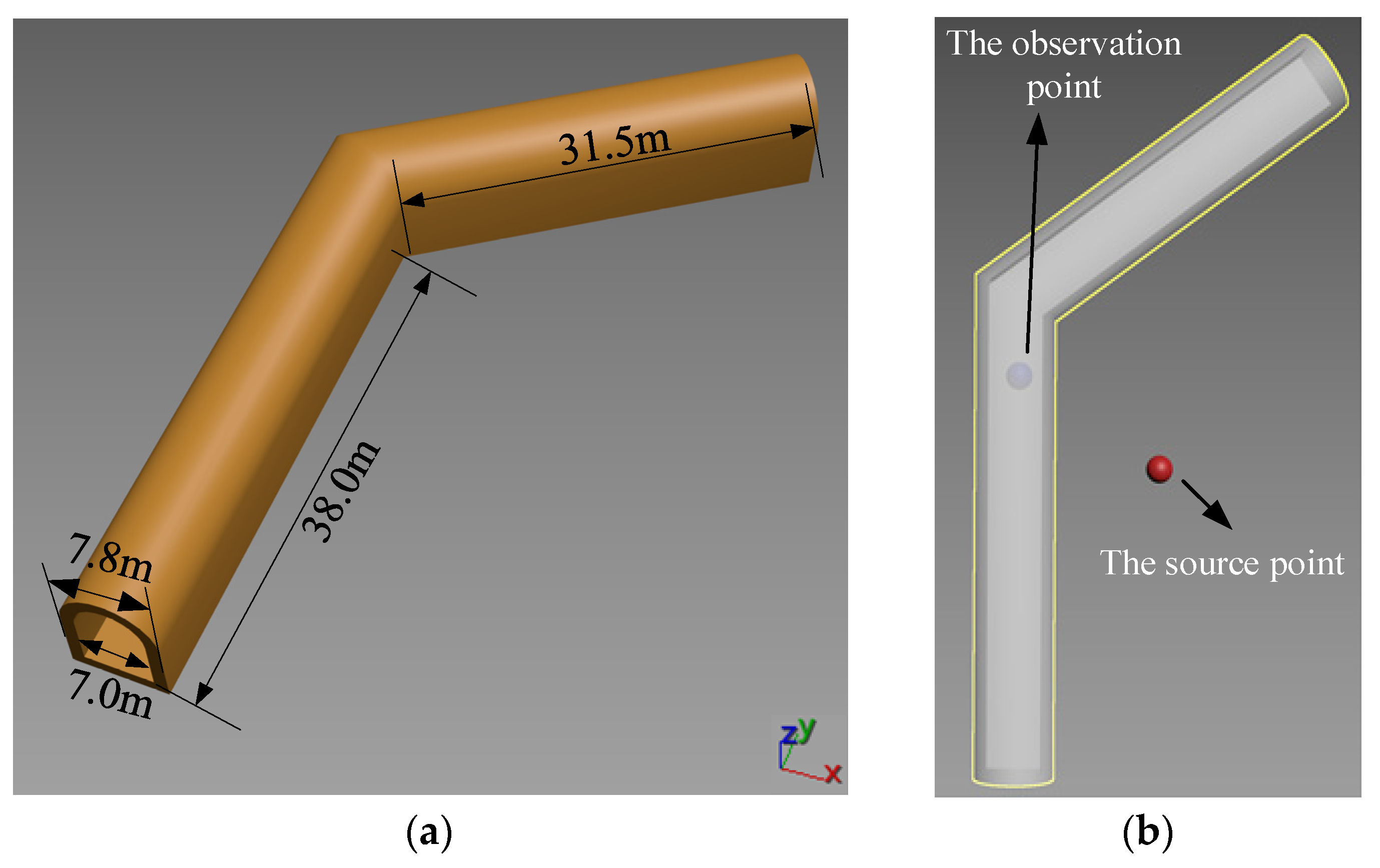
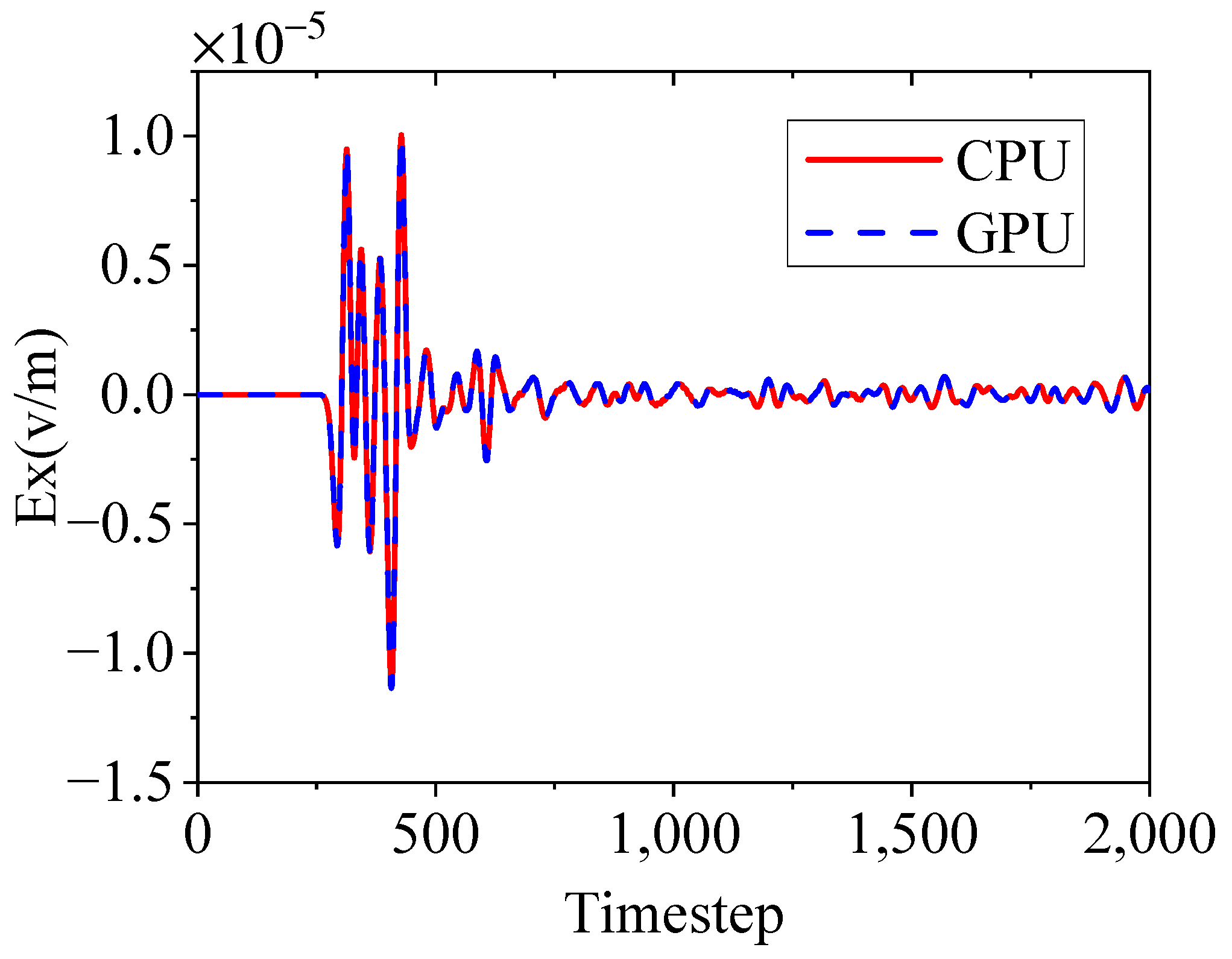
| Hardware | CPU | Single GPU | Dual GPUs at Dual Node | Four GPUs at Dual Node | ||
|---|---|---|---|---|---|---|
| Without NCCL | With NCCL | Without NCCL | With NCCL | |||
| Time (s) | 18,792 | 2380 | 1275 | 1211 | 658 | 604 |
| Speedup | 1 | 7.9 | 14.9 | 15.5 | 28.6 | 31.1 |
| Efficiency | \ | 100.0% | 94.3% | 98.1% | 90.5% | 98.4% |
| Hardware | CPU | Single GPU | Dual GPUs at Dual Node | Four GPUs at Dual Node | ||
|---|---|---|---|---|---|---|
| Without NCCL | With NCCL | Without NCCL | With NCCL | |||
| Time (s) | 20,792 | 1308 | 680 | 658 | 351 | 332 |
| Speedup | 1 | 15.9 | 30.6 | 31.6 | 59.2 | 62.6 |
| Efficiency | \ | 100.0% | 96.2% | 99.4% | 93.1% | 98.4% |
| Hardware | CPU | Single GPU | Dual GPUs at Dual Node | Four GPUs at Dual Node | ||
|---|---|---|---|---|---|---|
| Without NCCL | With NCCL | Without NCCL | With NCCL | |||
| Time (s) | 2540 | 203 | 105 | 102 | 55 | 52 |
| Speedup | 1 | 12.6 | 24.2 | 24.9 | 46.2 | 48.8 |
| Efficiency | \ | 100.0% | 96.0% | 98.8% | 91.7% | 96.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Mu, S.; Han, X.; Wei, B. Novel Research on a Finite-Difference Time-Domain Acceleration Algorithm Based on Distributed Cluster Graphic Process Units. Appl. Sci. 2025, 15, 4834. https://doi.org/10.3390/app15094834
He X, Mu S, Han X, Wei B. Novel Research on a Finite-Difference Time-Domain Acceleration Algorithm Based on Distributed Cluster Graphic Process Units. Applied Sciences. 2025; 15(9):4834. https://doi.org/10.3390/app15094834
Chicago/Turabian StyleHe, Xinbo, Shenggang Mu, Xudong Han, and Bing Wei. 2025. "Novel Research on a Finite-Difference Time-Domain Acceleration Algorithm Based on Distributed Cluster Graphic Process Units" Applied Sciences 15, no. 9: 4834. https://doi.org/10.3390/app15094834
APA StyleHe, X., Mu, S., Han, X., & Wei, B. (2025). Novel Research on a Finite-Difference Time-Domain Acceleration Algorithm Based on Distributed Cluster Graphic Process Units. Applied Sciences, 15(9), 4834. https://doi.org/10.3390/app15094834






