Predicting the Young’s Modulus of Concrete Using a Particle-Based Movable Cellular Automata Method
Abstract
1. Introduction
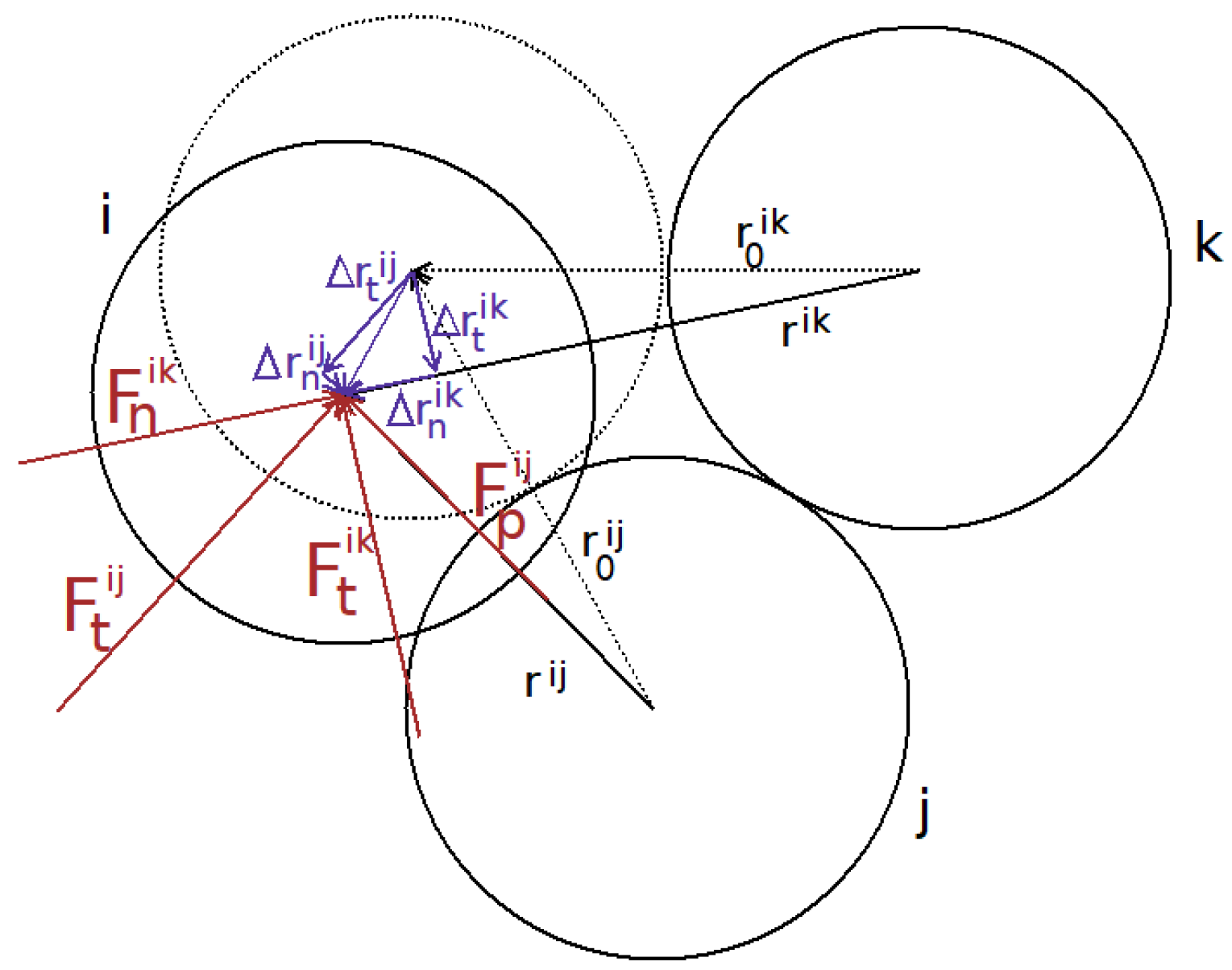
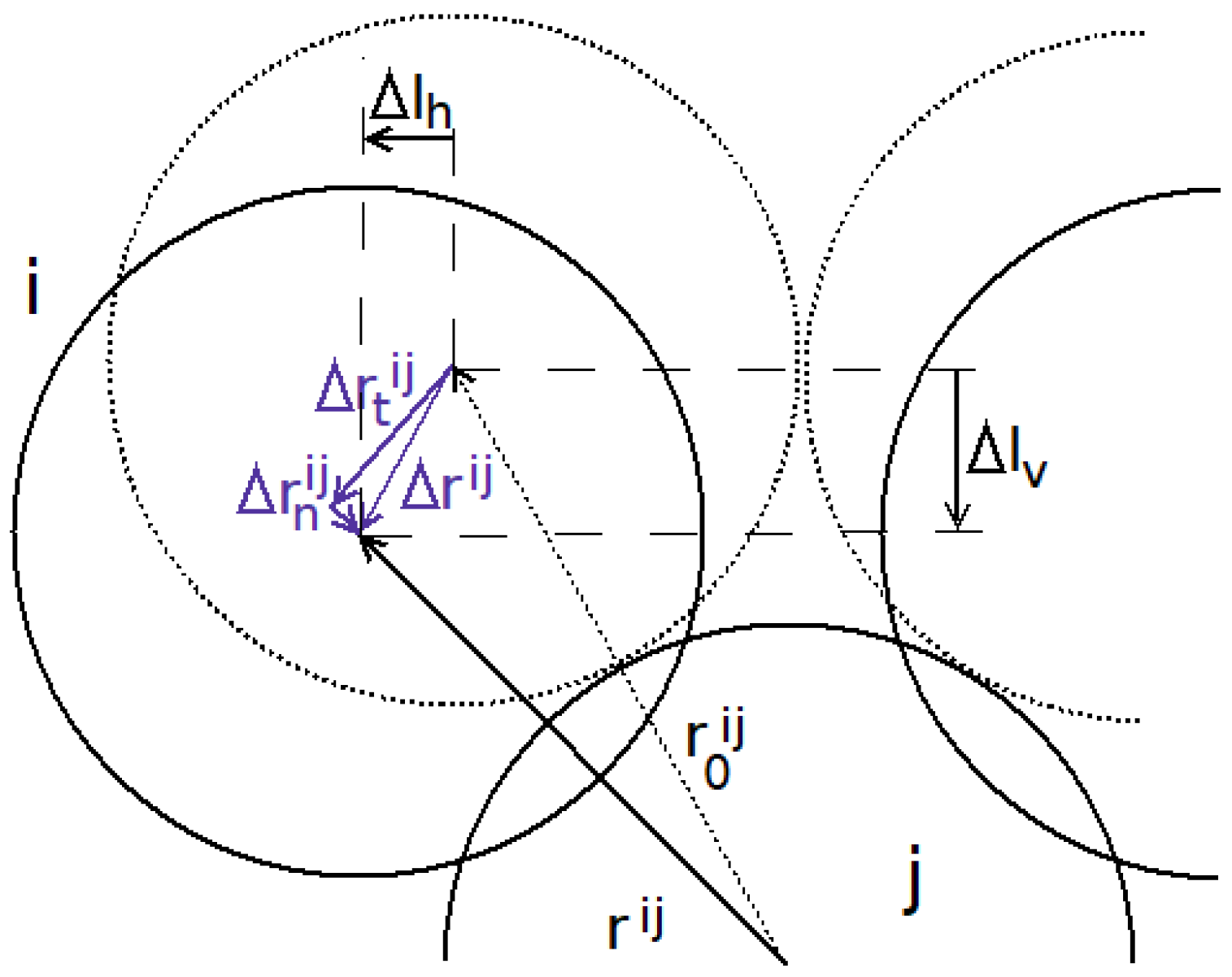
2. The Movable Cellular Automata Method
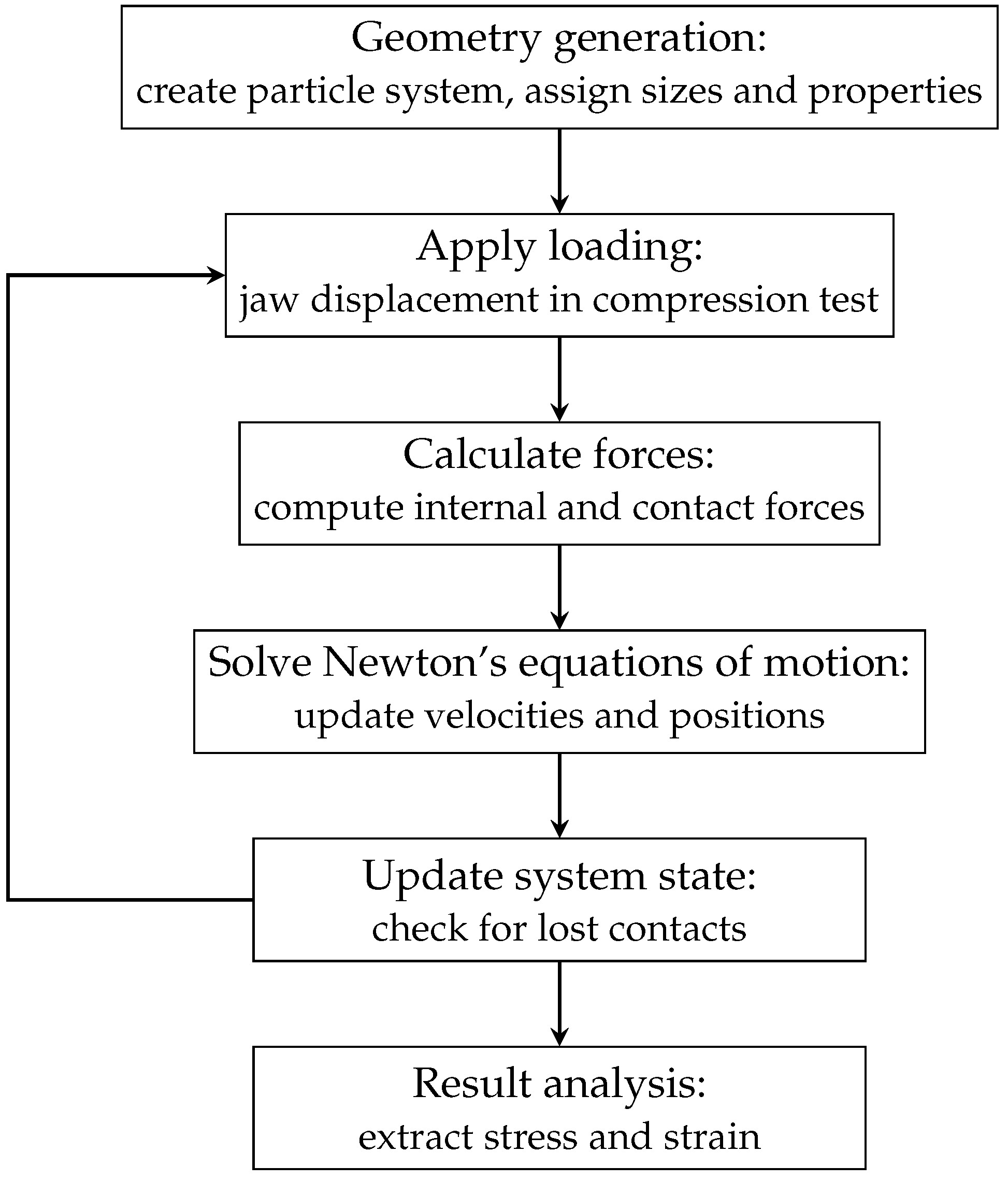
3. Modelling Concrete in Uniaxial Static Compression Test
Parametric Sensitivity Analysis
- Viscous friction of cement paste, with values of 0.01, 0.1, and 1 kg/s.
- Dry friction coefficient of coarse aggregate, with values of 0.1, 0.5, and 0.9.
- Coarse aggregate compressive strength, with values of 120, 180, and 240 MPa.
- Coarse aggregate Poisson’s ratio, with values of 0.2, 0.25, and 0.3.
- Coarse aggregate elastic modulus, with values of 60 GPa, 70 GPa, and 80 GPa.
- Cement content (with values of 30%, 35%, and 40% by volume of the sample) and coarse aggregate content (with values of 20%, 30%, and 40% by volume of the sample), resulting in three different aggregate/cement ratios and six different coarse aggregate/total aggregate ratios.
4. Comparison the MCA Results with Experiments
4.1. Comparison with Mortar
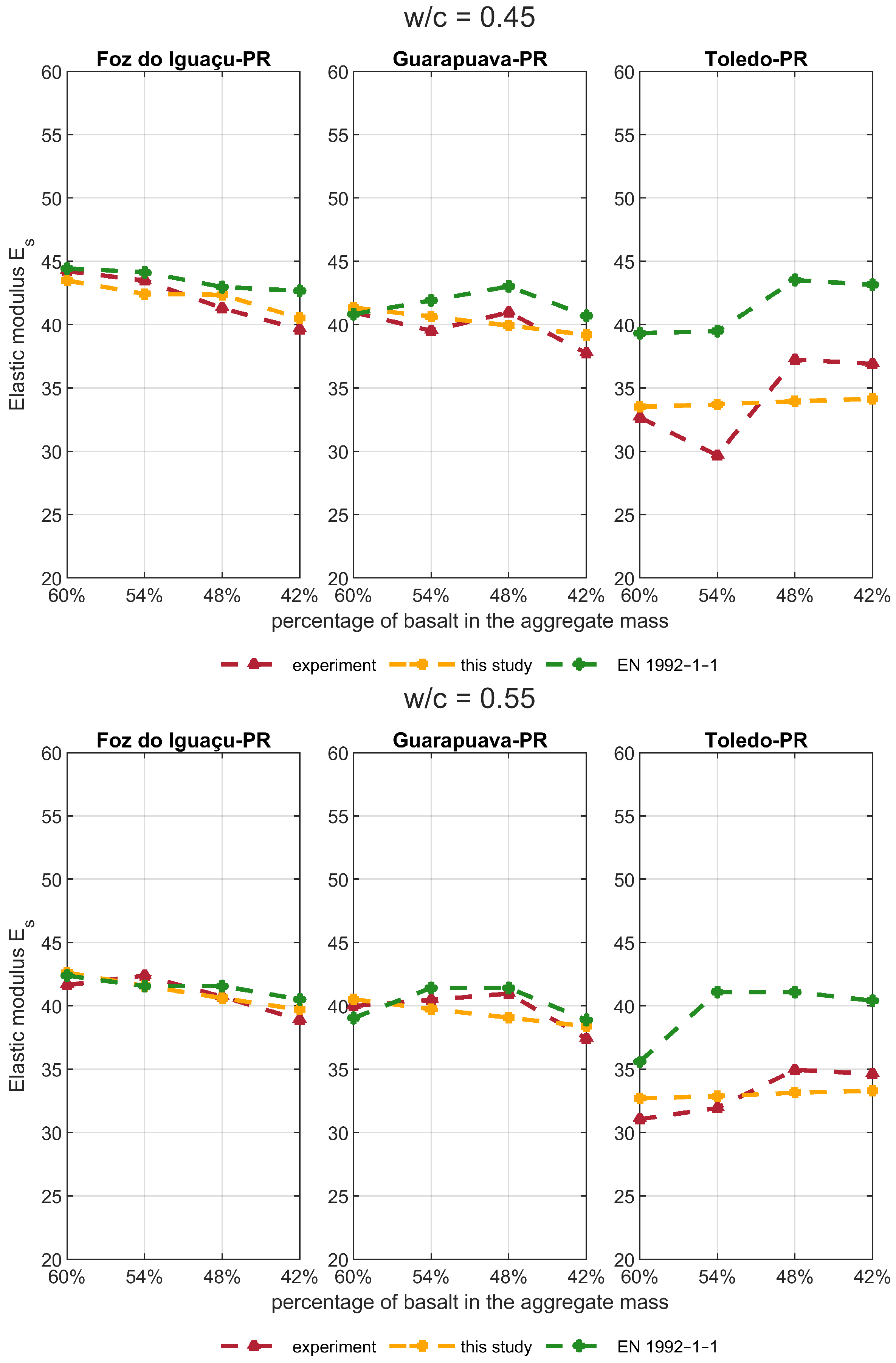
4.2. Comparison with Basaltic Concrete
4.3. Comparison with Lightweight Expanded Clay Aggregate Concrete
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmadi, M.; Kioumarsi, M. Predicting the elastic modulus of normal and high strength concretes using hybrid ANN-PSO. In Materials Today: Proceedings; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Zhang, C.; Liu, P.; Song, T.; He, B.; Li, W.; Peng, Y. Elastic Modulus Prediction of Ultra-High-Performance Concrete with Different Machine Learning Models. Buildings 2024, 14, 3184. [Google Scholar] [CrossRef]
- Baudrit, C.; Dufau, S.; Villain, G.; Sbartaï, Z.M. Artificial Intelligence and Non-Destructive Testing Data to Assess Concrete Sustainability of Civil Engineering Infrastructures. Materials 2025, 18, 826. [Google Scholar] [CrossRef] [PubMed]
- Shemirani, A.B. Prediction of fracture toughness of concrete using the machine learning approach. Theor. Appl. Fract. Mech. 2024, 134, 104749. [Google Scholar] [CrossRef]
- Abed, M.; Mehryaar, E. A Machine Learning Approach to Predict Relative Residual Strengths of Recycled Aggregate Concrete after Exposure to High Temperatures. Sustainability 2024, 16, 1891. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, X.; Yu, Y.; Xie, T.; Yang, G.; Xue, J. Parametric sensitivity analysis and modelling of mechanical properties of normal- and high-strength recycled aggregate concrete using grey theory, multiple nonlinear regression and artificial neural networks. Constr. Build. Mater. 2019, 211, 479–491. [Google Scholar] [CrossRef]
- Han, T.; Siddique, A.; Khayat, K.; Huang, J.; Kumar, A. An ensemble machine learning approach for prediction and optimization of modulus of elasticity of recycled aggregate concrete. Constr. Build. Mater. 2020, 244, 118271. [Google Scholar] [CrossRef]
- Rodsin, K.; Ejaz, A.; Wang, H.; Saingam, P.; Joyklad, P.; Khaliq, W.; Hussain, Q.; Boonmee, C. Machine Learning and Regression Models for Evaluating Ultimate Performance of Cotton Rope-Confined Recycled Aggregate Concrete. Buildings 2025, 15, 64. [Google Scholar] [CrossRef]
- Duan, Z.; Hou, S.; Poon, C.S.; Xiao, J.; Liu, Y. Using Neural Networks to Determine the Significance of Aggregate Characteristics Affecting the Mechanical Properties of Recycled Aggregate Concrete. Appl. Sci. 2018, 8, 2171. [Google Scholar] [CrossRef]
- Li, Z.; Yoon, J.; Zhang, R.; Rajabipour, F.; Srubar, W.V., III; Dabo, I.; Radlińska, A. Machine learning in concrete science: Applications, challenges, and best practices. npj Comput. Mater. 2022, 8, 127. [Google Scholar] [CrossRef]
- Stephen Wolfram. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002. [Google Scholar]
- Encinas, L.H.; White, S.H.; Del Rey, A.M.; Sánchez, G.R. Modelling forest fire spread using hexagonal cellular automata. Appl. Math. Model. 2007, 31, 1213–1227. [Google Scholar] [CrossRef]
- Slimi, R.; El Yacoubi, S.; Dumonteil, E.; Gourbiere, S. A cellular automata model for Chagas disease. Appl. Math. Model. 2009, 33, 1072–1085. [Google Scholar] [CrossRef]
- Sidiropoulos, E.; Tolikas, P. Genetic algorithms and cellular automata in aquifer management. Appl. Math. Model. 2008, 32, 617–640. [Google Scholar] [CrossRef]
- Wu, F. Simulating urban encroachment on rural land with fuzzy-logic-controlled cellular automata in a geographical information system. J. Environ. Manag. 1998, 53, 293–308. [Google Scholar] [CrossRef]
- Betel, H.; Flocchini, P. On the relationship between fuzzy and boolean cellular automata. Theor. Comput. Sci. 2011, 412, 703–713. [Google Scholar] [CrossRef][Green Version]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Camborde, F.; Mariotti, C.; Donzé, F.V. Numerical study of rock and concrete behaviour by discrete element modelling. Comput. Geotech. 2000, 27, 225–247. [Google Scholar] [CrossRef]
- Hentz, S.; Donzé, F.V.; Daudeville, L. Discrete element modelling of concrete submitted to dynamic loading at high strain rates. Comput. Struct. 2004, 82, 2509–2524. [Google Scholar] [CrossRef]
- Suchorzewski, J.; Tejchman, J.; Nitka, M. Discrete element method simulations of fracture in concrete under uniaxial compression based on its real internal structure. Int. J. Damage Mech. 2017, 27, 578–607. [Google Scholar] [CrossRef]
- Zhan, Y.; Gong, J.; Huang, Y.; Shi, C.; Zuo, Z.; Chen, Y. Numerical Study on Concrete Pumping Behavior via Local Flow Simulation with Discrete Element Method. Materials 2019, 12, 1415. [Google Scholar] [CrossRef]
- Arulrajah, A.; Baghban, H.; Narsilio, G.A.; Horpibulsuk, S.; Leong, M. Discrete element analysis of recycled concrete aggregate responses during repeated load triaxial testing. Transp. Geotech. 2020, 23, 100356. [Google Scholar] [CrossRef]
- Rybczynski, S.; Schaan, G.; Dosta, M.; Ritter, M.; Schmidt-Döhl, F. Discrete Element Modeling and Electron Microscopy Investigation of Fatigue-Induced Microstructural Changes in Ultra-High-Performance Concrete. Materials 2021, 14, 6337. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Zhang, L.; Wu, Z.; Liu, A.; Imran, M. Aggregate effect on the mechanical and fracture behaviours of concrete. Int. J. Mech. Sci. 2023, 243, 108067. [Google Scholar] [CrossRef]
- Liu, K.; Chen, Z.; Tao, Q.; Wu, D.; Wu, Q.; Zou, P.; Wang, M.; Li, Y. Dynamic Mechanical Properties and Damage Morphology Analysis of Concrete with Different Aggregates Based on FDM-DEM Coupling. Materials 2024, 17, 5804. [Google Scholar] [CrossRef]
- Nitka, M.; Rucka, M. 3D DEM modelling of acoustic emission in concrete: Insights into elastic waves initiated by microcracks. Ultrasonics 2025, 150, 107799. [Google Scholar] [CrossRef]
- Tan, X.; Hu, Z.; Li, W.; Zhou, S.; Li, T. Micromechanical Numerical Modelling on Compressive Failure of Recycled Concrete using Discrete Element Method (DEM). Materials 2020, 13, 4329. [Google Scholar] [CrossRef] [PubMed]
- Psakhie, S.G.; Horie, Y.; Korostelev, S.Y.; Smolin, A.Y.; Dmitriev, A.I.; Shilko, E.V.; Alekseev, S.V. Method of movable cellular automata as a tool for simulation within the framework of mesomechanics. Russ. Phys. J. 1995, 11, 1157–1168. [Google Scholar] [CrossRef]
- Panin, V.E.; Egorushkin, V.E.; Makarov, P.V. Physical Mesomechanics and Computer Design of Materials. Nauka 1995, 38, 298. [Google Scholar]
- Panin, V.E.; Korotaev, A.D.; Makarov, P.V.; Kuznetsov, V.M. Physical mesomechanics of materials. Russ. Phys. J. 1998, 41, 856–884. [Google Scholar] [CrossRef]
- Psakhie, S.G.; Horie, Y.; Ostermeyer, G.P.; Korostelev, S.Y.; Smolin, A.Y.; Shilko, E.V.; Dmitriev, A.I.; Blatnik, S.; Spegel, M.; Zavsek, S. Movable cellular automata method for simulating materials with mesostructure. Theor. Appl. Fract. Mech. 2001, 37, 311–334. [Google Scholar] [CrossRef]
- Popov, V.L.; Psakhie, S.G.; Dmitriev, A.; Shilko, E. Quasi-fluid nano-layers at the interface between rubbing bodies: Simulations by movable cellular automata. Wear 2003, 254, 901–906. [Google Scholar] [CrossRef]
- Dmitriev, A.I.; Popov, V.L.; Psakhie, S.G. Simulation of surface topography with the method of movable cellular automata. Tribol. Int. 2006, 39, 444–449. [Google Scholar] [CrossRef]
- Österle, W.; Dmitriev, A.I.; Kloß, H. Possible impacts of third body nanostructure on friction performance during dry sliding determined by computer simulation based on the method of movable cellular automata. Tribol. Int. 2012, 48, 128–136. [Google Scholar] [CrossRef]
- Dmitriev, A.I.; Schargott, M.; Popov, V.L. Direct modelling of surface topography development in a micro-contact with the movable cellular automata method. Wear 2010, 268, 877–885. [Google Scholar] [CrossRef]
- Wang, M.; Huang, D.W.; Luo, R.M. Shear failure of tungsten alloy at mesoscale modeled by movable cellular automata. Theor. Appl. Fract. Mech. 2011, 56, 162–168. [Google Scholar] [CrossRef]
- Czopor, J.; Rybaczuk, M. Simulation and experimental investigation of two dimensional cracks propagation in ceramic materials. In Proceedings of Cellular Automata, 6th International Conference on CA for Research and Industry; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Grigoriev, A.; Shilko, E.; Skripnyak, V.; Smolin, A.; Psakhie, S. Multiscale numerical study of fracture and strength characteristics of zirconium alumina concrete with use of the particle-based mca method. Procedia Mater. Sci. 20th Eur. Conf. Fract. 2014, 3, 936–941. [Google Scholar] [CrossRef][Green Version]
- Czopor, J.; Aniszewska, D.; Rybaczuk, M. The influence of defects on strength of ceramics modeled with movable cellular automata. Comput. Mater. Sci. 2012, 51, 151–155. [Google Scholar] [CrossRef]
- Aniszewska, D. Fractal characteristics of defects growth in porous ceramics modeled with the movable cellular automata. Appl. Math. Model. 2015, 39, 2409–2415. [Google Scholar] [CrossRef]
- Aniszewska, D.; Rybaczuk, M. Mechanical properties of silica aerogels modelled by movable cellular automata simulations. Mater. Today Commun. 2021, 27, 102432. [Google Scholar] [CrossRef]
- Neville, A.M. Properties of Concrete, 5th ed.; Pearson: Harlow, UK; New York, NY, USA, 2011. [Google Scholar]
- Monteiro, P.J.M.; Mehta, P.K. Concrete: Microstructure, Properties, and Materials, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Ayanlere, S.A.; Ajamu, S.O.; Odeyemi, S.O.; Ajayi, O.E.; Kareem, M.A. Effects of water-cement ratio on bond strength of concrete. Mater. Today Proc. 2023, 86, 134–139. [Google Scholar] [CrossRef]
- Behnood, A.; Ziari, H. Effects of silica fume addition and water to cement ratio on the properties of high-strength concrete after exposure to high temperatures. Cem. Concr. Compos. 2008, 30, 106–112. [Google Scholar] [CrossRef]
- Sánchez-Mendieta, C.; Galán-Díaz, J.J.; Martinez-Lage, I. Relationships between density, porosity, compressive strength and permeability in porous concretes: Optimization of properties through control of the water-cement ratio and aggregate type. J. Build. Eng. 2024, 97, 110858. [Google Scholar] [CrossRef]
- Yang, J.; Moon, J. Experimental study on tracing the initial water-to-cement ratio of hardened concrete using petrography analysis. Constr. Build. Mater. 2023, 403, 133199. [Google Scholar] [CrossRef]
- Bílek, V.; Soucek, K.; Khestl, F.; Bujdos, D.; Seitl, S. Mechanical and fracture parameters of concretes with different water to cement ratio in two different conditions of curing. Procedia Struct. Integr. 2023, 43, 107–112. [Google Scholar] [CrossRef]
- Abolhasani, A.; Nazarpour, H.; Dehestani, M. The fracture behavior and microstructure of calcium aluminate cement concrete with various water-cement ratios. Theor. Appl. Fract. Mech. 2020, 109, 102690. [Google Scholar] [CrossRef]
- Alexander, K.M.; Ivanusec, I. Long-term effects of cement So3 content on the properties of normal and high-strength concrete. Part I. The effect on strength. Cem. Concr. Res. 1982, 12, 51–60. [Google Scholar] [CrossRef]
- Kakizaki, T.T.M.; Edahiro, H.; Niki, T. Effect of mixing method on mechanical properties and pore structure of ultra high-strength concrete. Aci Symp. Publ. 1992, 132, 997–1016. [Google Scholar]
- Haecker, C.-J.; Garboczi, E.J.; Bullard, J.W.; Bohn, R.B.; Sun, Z.; Shah, S.P.; Voigt, T. Modeling the linear elastic properties of Portland cement paste. Cem. Concr. Res. 2005, 35, 1948–1960. [Google Scholar] [CrossRef]
- ASTM E1875-00e1; Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Sonic Resonance. ASTM: West Conshohocken, PA, USA, 2010.
- Popovics, J.S. A Study of Static and Dynamic Modulus of Elasticity of Concrete; CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- ASTM C215; Standard Test Method for Fundamental Transverse, Longitudinal, and Torsional Resonant Frequencies of Concrete Specimens. ASTM: West Conshohocken, PA, USA, 2020.
- ASTM C597; Standard Test Method for Ultrasonic Pulse Velocity Through Concrete. ASTM: West Conshohocken, PA, USA, 2023.
- Deng, J.L. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Deng, J.L. Introduction to grey theory system. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Taguchi, G. Orthogonal Arrays and Linear Graphs; American Supplier Institute, Inc.: Dearborn, Ml, USA, 1986. [Google Scholar]
- Kacker, R.; Lagergren, E.S.; Filliben, J.J. Taguchi’s Orthogonal Arrays Are Classical Designs of Experiments. J. Res. Natl. Inst. Stand. Technol. 1991, 96, 577. [Google Scholar] [CrossRef]
- Ismail, M.K.A.; Mohamed, Z.; Razali, M. Contact stiffness parameters of soil particles model for discrete element modeling using static packing pressure test. Aip Conf. Proc. 2018, 2020, 020014. [Google Scholar]
- Sitharam, T.G. Discrete element modelling of cyclic behaviour of granular materials. Geotech. Geol. Eng. 2003, 21, 297–329. [Google Scholar] [CrossRef]
- Sadek, M.A.; Chen, Y. Microproperties calibration of discrete element models for soil-tool interaction. In Proceedings of the Conference: American Society of Agricultural and Biological Engineers Annual International Meeting 2014, ASABE, American Society of Agricultural and Biological Engineers, Montreal, QC, Canada, 13–16 July 2014. [Google Scholar]
- Zhou, H.; Chen, Y.; Sadek, M.A. Modelling of soil–seed contact using the Discrete Element Method (DEM). Biosyst. Eng. 2014, 121, 56–66. [Google Scholar] [CrossRef]
- ASTM C469/C469M; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete. ASTM International: West Conshohocken, PA, USA, 2020.
- NBR 5739; Concreto—Ensaio de Compressão dos Corpos-de-Prova Cilíndricos. Associação Brasileira De Normas Técnicas: Rio de Janeiro, Brazil, 2018.
- Guo, Y.B.; Gao, G.F.; Jing, L.; Shim, V.P.W. Dynamic properties of mortar in high-strength concrete. Int. J. Impact Eng. 2022, 165, 104216. [Google Scholar] [CrossRef]
- da Silva, M.L.; Prado, L.P.; Félix, E.F.; de Sousa, A.M.D.; Aquino, D.P. The Influence of Materials on the Mechanical Properties of Ultra-High-Performance Concrete (UHPC): A Literature Review. Materials 2024, 17, 1801. [Google Scholar] [CrossRef]
- Szcześniak, A.; Siwiński, J.; Stolarski, A.; Piekarczuk, A.; Nasiłowska, B. The Influence of the Addition of Microsilica and Fly Ash on the Properties of Ultra-High-Performance Concretes. Materials 2025, 18, 28. [Google Scholar] [CrossRef]
- Smarzewski, P. Mechanical and Microstructural Studies of High Performance Concrete with Condensed Silica Fume. Appl. Sci. 2023, 13, 2510. [Google Scholar] [CrossRef]
- Guo, Y.B.; Gao, G.F.; Jing, L.; Shim, V.P.W. Response of high-strength concrete to dynamic compressive loading. Int. J. Impact Eng. 2017, 108, 114–135. [Google Scholar] [CrossRef]
- Thomaz, W.d.; Miyaji, D.Y.; Possan, E. Comparative study of dynamic and static young’s modulus of concrete containing basaltic aggregates. Case Stud. Constr. Mater. 2021, 15, e00645. [Google Scholar] [CrossRef]
- NBR 8522; Stress-Strain Curve of Concretes with Recycled Concrete Aggregates: Analysis of the NBR 8522 Methodology. IBRACON—Instituto Brasileiro do Concreto: São Paulo, Brazil, 2017.
- Cement—Part 1: Composition, Specifications and Conformity Criteria for Common Cements; European Committee for Standardization (CEN): Brussels, Belgium, 2011.
- Standard Specification for Portland Cement; ASTM International: West Conshohocken, PA, USA, 2012.
- Zisman, W.A. Comparison of the statically and seismologically determined elastic constants of rocks. Proc. Natl. Acad. Sci. USA 1933, 19, 680–686. [Google Scholar] [CrossRef]
- Gueguen, Y.; Palciauskas, V. Introduction to the Physics of Rocks; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- King, M.S. Static and dynamic elastic properties of rocks from the Canadian shield. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 237–241. [Google Scholar] [CrossRef]
- Pereira, M.L.; da Silva, P.F.; Fernandes, I.; Chastre, C. Characterization and correlation of engineering properties of basalts. Bull. Eng. Geol. Environ. 2021, 80, 2889–2910. [Google Scholar] [CrossRef]
- Christaras, B.; Auger, F.; Mosse, E. Determination of the moduli of elasticity of rocks. comparison of the ultrasonic velocity and mechanical resonance frequency methods with direct static methods. Mater. Struct. 1994, 27, 222–228. [Google Scholar] [CrossRef]
- Shen, S.; Gao, Y.; Jia, L. A Comparison of the Relationship between Dynamic and Static Rock Mechanical Parameters. Appl. Sci. 2024, 14, 4487. [Google Scholar] [CrossRef]
- EN1992-1-1; Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2014.
- Uysal, O.; Uslu, İ.; Aktaş, C.B.; Chang, B.; Yaman, İ.Ö. Physical and Mechanical Properties of Lightweight Expanded Clay Aggregate Concrete. Buildings 2024, 14, 1871. [Google Scholar] [CrossRef]


| w/c ratio | 0.3 | 0.31 | 0.34 | 0.4 | 0.43 | 0.45 | 0.5 | 0.55 | 0.6 |
| E [GPa] | 28.23 | 28 | 25.5 | 21.7 | 20.4 | 20 | 17.5 | 16 | 15.24 |
| Mixtures | w/c Ratio | Sand | [67] | This Study | Relative |
|---|---|---|---|---|---|
| V [%] | GPa | GPa | Error | ||
| M60 | 0.43 | 48.61 | 31.86 ± 0.06 | 0.1% | |
| M80 | 0.34 | 46.39 | 34.65 ± 0.06 | 0.7% | |
| M110 | 0.31 | 46.68 | 38.9 * ± 0.6 | 36.43 ** ± 0.04 | 6.3% |
| Mixtures | w/c Ratio | Sand | Granite | [71] | This Study | Relative |
|---|---|---|---|---|---|---|
| V [%] | V [%] | [GPa] | [GPa] | Error | ||
| C60 | 0.43 | 31.60 | 35 | 37.12 ± 0.05 | 0.05% | |
| C80 | 0.34 | 30.15 | 35 | 39.00 ± 0.04 | 5.40% | |
| C110 | 0.31 | 30.34 | 35 | 40.7 * ± 1.1 | 40.18 ** ± 0.04 | 1.28% |
| Basalt from Foz do Iguaçu-PR | |||||
| Mixture | w/c ratio | basalt | basalt | sand | [this study] |
| [% in aggregate mass] | V [%] | V [%] | GPa | ||
| 1 | 0.45 | 60% | 47.44 | 19.20 | 43.48 ± 0.06 |
| 4 | 0.45 | 54% | 42.46 | 24.34 | 42.43 ± 0.08 |
| 7 | 0.45 | 48% | 37.54 | 29.43 | 42.36 ± 0.07 |
| 10 | 0.45 | 42% | 32.67 | 34.47 | 40.50 ± 0.09 |
| 2 | 0.55 | 60% | 47.38 | 22.22 | 42.63 ± 0.09 |
| 5 | 0.55 | 54% | 42.39 | 27.38 | 41.58 ± 0.07 |
| 8 | 0.55 | 48% | 37.46 | 32.48 | 40.62 ± 0.10 |
| 11 | 0.55 | 42% | 32.69 | 37.39 | 39.71 ± 0.07 |
| Basalt from Guarapuava-PR | |||||
| Mixture | w/c ratio | basalt | basalt | sand | [this study] |
| [% in aggregate mass] | V [%] | V [%] | GPa | ||
| 13 | 0.45 | 60% | 48.38 | 18.85 | 41.35 ± 0.07 |
| 16 | 0.45 | 54% | 43.39 | 23.95 | 40.63 ± 0.07 |
| 19 | 0.45 | 48% | 38.43 | 29.01 | 39.94 ± 0.06 |
| 22 | 0.45 | 42% | 33.52 | 34.04 | 39.20 ± 0.08 |
| 14 | 0.55 | 60% | 48.32 | 21.82 | 40.52 ± 0.06 |
| 17 | 0.55 | 54% | 43.32 | 26.94 | 39.76 ± 0.09 |
| 20 | 0.55 | 48% | 38.34 | 32.01 | 39.08 ± 0.06 |
| 23 | 0.55 | 42% | 33.53 | 36.93 | 38.39 ± 0.06 |
| Basalt from Toledo-PR | |||||
| Mixture | w/c ratio | basalt | basalt | sand | [this study] |
| [% in aggregate mass] | V [%] | V [%] | GPa | ||
| 25 | 0.45 | 60% | 48.82 | 18.69 | 33.52 ± 0.07 |
| 28 | 0.45 | 54% | 43.83 | 23.77 | 33.71 ± 0.04 |
| 31 | 0.45 | 48% | 38.86 | 28.82 | 33.96 ± 0.06 |
| 34 | 0.45 | 42% | 33.92 | 33.85 | 34.14 ± 0.07 |
| 26 | 0.55 | 60% | 48.76 | 21.64 | 32.71 ± 0.07 |
| 29 | 0.55 | 54% | 43.75 | 26.73 | 32.88 ± 0.05 |
| 32 | 0.55 | 48% | 38.76 | 31.79 | 33.15 ± 0.06 |
| 35 | 0.55 | 42% | 33.92 | 36.71 | 33.30 ± 0.05 |
| Relationship | Rock Type | Range [GPa] | Ref. | |
|---|---|---|---|---|
| 0.89 | basalt | 10–100 | [79] | |
| 0.82 | igneous-metamorphic | 40–120 | [78] | |
| 0.994 | all types, including basalt | 25–110 | [80] | |
| 0.9653 | igneous rocks | 15–160 | [81] |
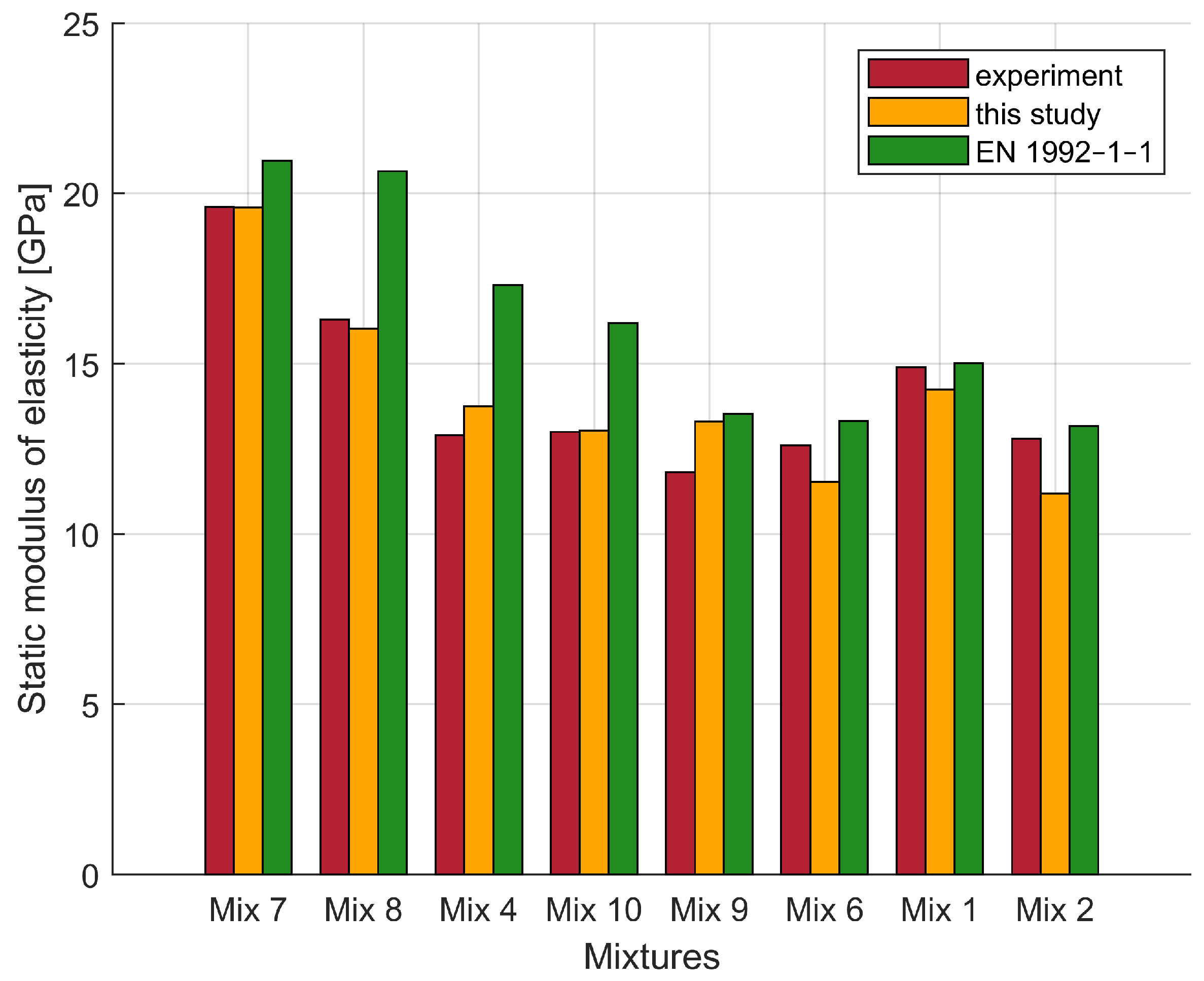
| Mixtures | w/c | Limestone | Coarse LECA | Fine LECA | [83] | [This Study] |
|---|---|---|---|---|---|---|
| Ratio | V [%] | V [%] | V [%] | GPa | GPa | |
| Mix 7 | 0.3 | 30.85 | 27 | - | 19.6 | 19.59 ± 0.07 |
| Mix 8 | 0.3 | 22.52 | 24 | 12 | 16.3 | 16.04 ± 0.06 |
| Mix 4 | 0.4 | 24.518 | 24 | 12 | 12.9 | 13.74 ± 0.05 |
| Mix 10 | 0.4 | 18.111 | 24 | 12 | 13.0 | 13.03 ± 0.04 |
| Mix 9 | 0.5 | 20.963 | 27 | - | 11.8 | 13.30 ± 0.04 |
| Mix 6 | 0.5 | 20.185 | 24 | 12 | 12.6 | 11.53 ± 0.06 |
| Mix 1 | 0.6 | 32.78 | 27 | - | 14.9 | 14.24 ± 0.08 |
| Mix 2 | 0.6 | 24.185 | 24 | 12 | 12.8 | 11.19 ± 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aniszewska, D.; Rybaczuk, M. Predicting the Young’s Modulus of Concrete Using a Particle-Based Movable Cellular Automata Method. Appl. Sci. 2025, 15, 4840. https://doi.org/10.3390/app15094840
Aniszewska D, Rybaczuk M. Predicting the Young’s Modulus of Concrete Using a Particle-Based Movable Cellular Automata Method. Applied Sciences. 2025; 15(9):4840. https://doi.org/10.3390/app15094840
Chicago/Turabian StyleAniszewska, Dorota, and Marek Rybaczuk. 2025. "Predicting the Young’s Modulus of Concrete Using a Particle-Based Movable Cellular Automata Method" Applied Sciences 15, no. 9: 4840. https://doi.org/10.3390/app15094840
APA StyleAniszewska, D., & Rybaczuk, M. (2025). Predicting the Young’s Modulus of Concrete Using a Particle-Based Movable Cellular Automata Method. Applied Sciences, 15(9), 4840. https://doi.org/10.3390/app15094840






