Simulation Analysis of a Three-Degree-of-Freedom Low-Frequency Resonant Mixer
Abstract
:1. Introduction
- This paper explores the dynamic performance characteristics of a three-degree-of-freedom low-frequency resonance mixer, revealing that when operated at the third-order natural frequency, the significant acceleration amplitude and vibration amplitude of the payload assembly contribute to achieving enhanced mixing performance. Concurrently, the smaller acceleration amplitude and vibration amplitude of the excitation assembly ensure stable operation of the drive component attached to it. This provides a reference for future designs of three-degree-of-freedom low-frequency resonance mixers concerning mixing effectiveness and stability.
- From a mechanics perspective, this paper investigates the vibration isolation principle of a three-degree-of-freedom low-frequency resonance mixer when operating at the third-order natural frequency. Factors such as the acceleration amplitude of the three assemblies, the mass of these assemblies, the excitation force, and the phase difference between the assemblies and the excitation force all influence the vibration isolation effect of the mixer. These findings offer valuable insights for enhancing the vibration isolation performance of future three-degree-of-freedom low-frequency resonance mixers.
2. A Three-Degree-of-Freedom Low-Frequency Resonant Mixer
2.1. Principle of Operation
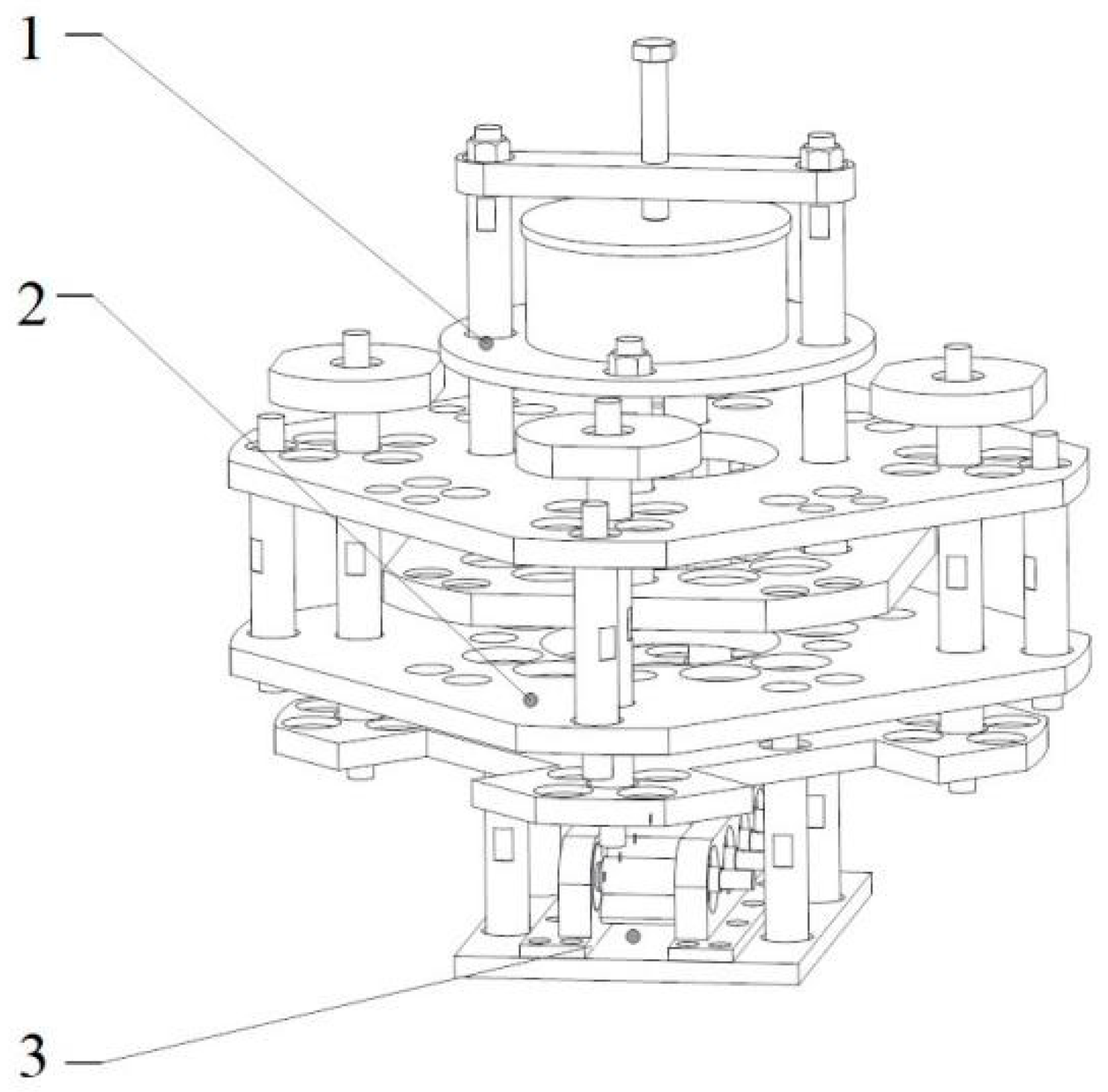
2.2. The Design of a Three-Degree-of-Freedom Low-Frequency Resonant Mixer
3. Dynamic Analysis of the Three-Degree-of-Freedom Low-Frequency Resonant Mixer
3.1. Modal Analysis of the Three-Degree-of-Freedom Low-Frequency Resonant Mixer
3.1.1. Preparatory Work for Modal Analysis of the Three-Degree-of-Freedom Low-Frequency Resonant Mixer
3.1.2. Results of Modal Analysis of the Three-Degree-of-Freedom Low-Frequency Resonant Mixer
3.2. Harmonic Response Analysis of the Three-Degree-of-Freedom Low-Frequency Resonant Mixer
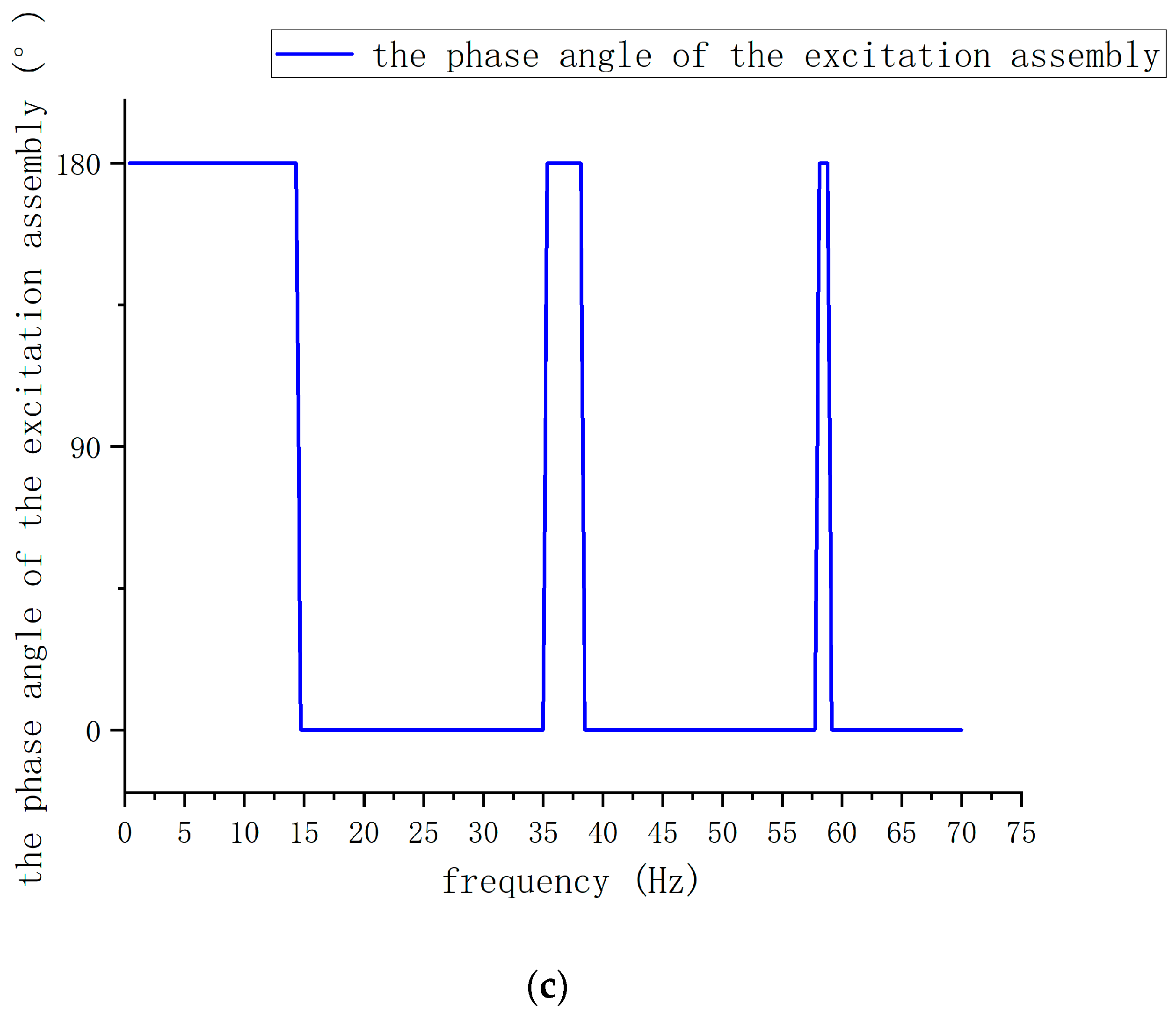
3.2.1. Phase-Frequency Response of the Three-Degree-of-Freedom Low-Frequency Resonant Mixer
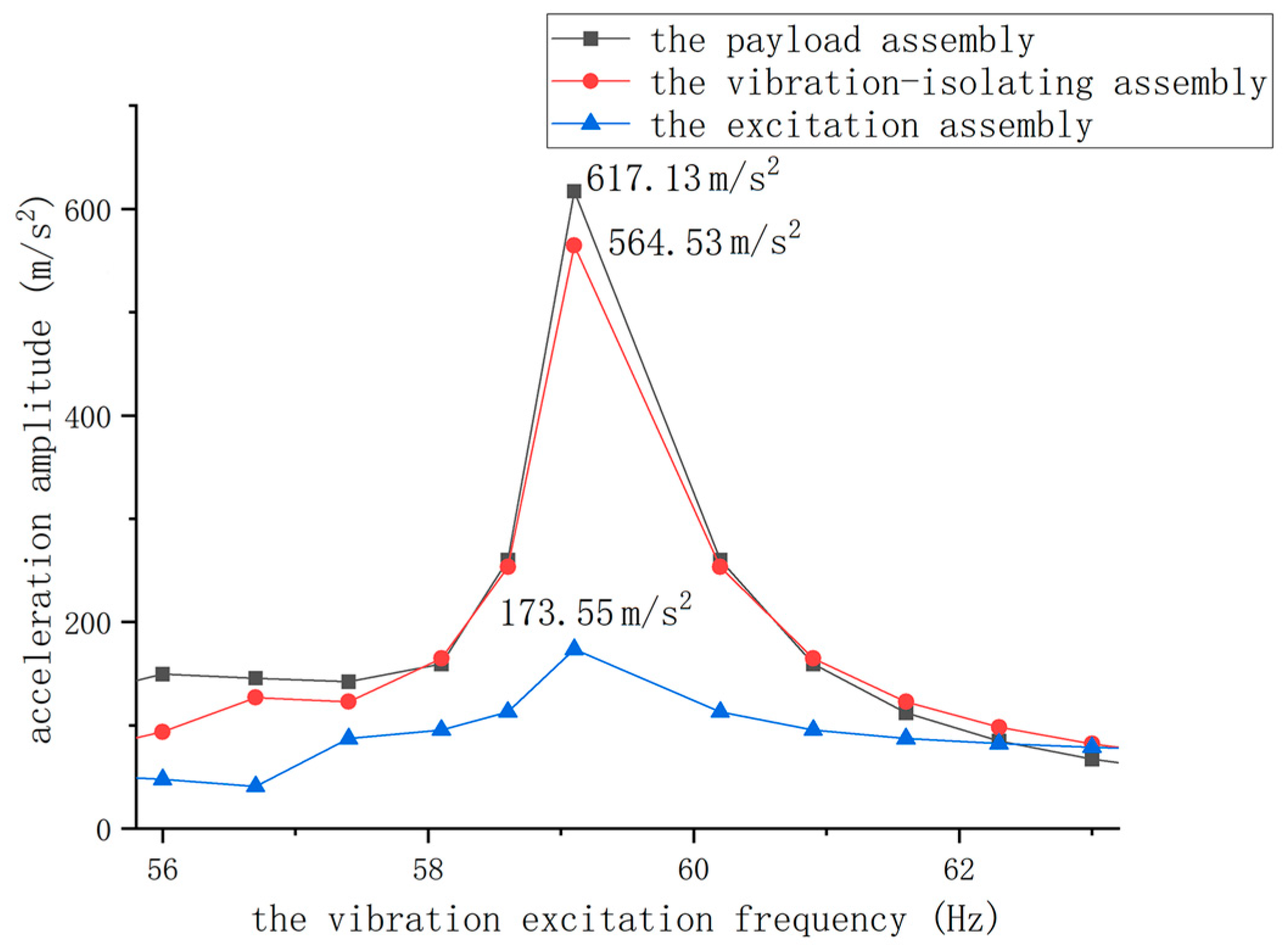
3.2.2. Acceleration Response of the Three-Degree-of-Freedom Low-Frequency Resonant Mixer
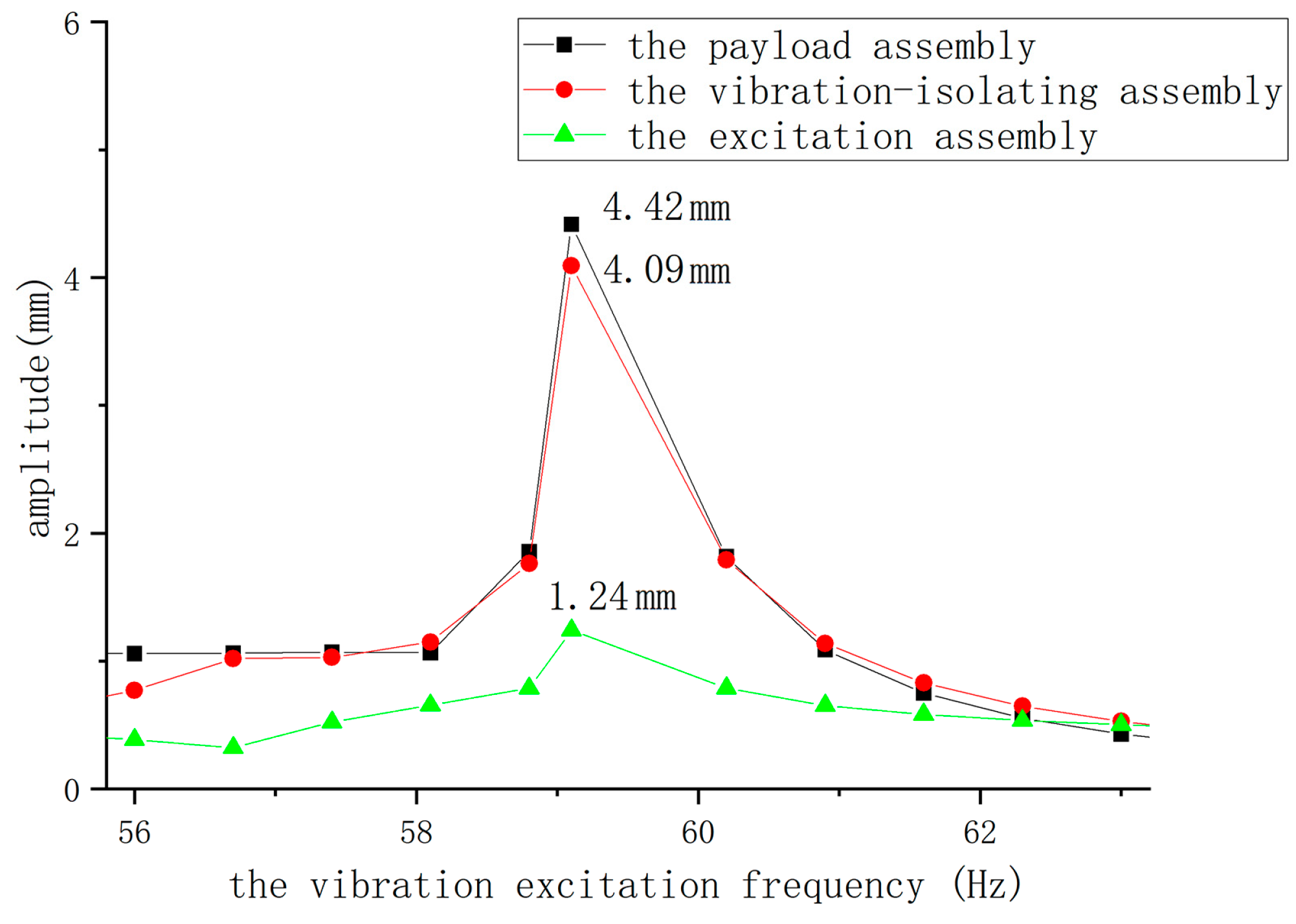
3.2.3. Amplitude-Frequency Response of the Three-Degree-of-Freedom Low-Frequency Resonant Mixer
3.3. GCI Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, Z.M. Study on Energetic Materials Mixing Process and Mechanism by Sympathetic Vibration of High Acceleration and Low Frequency. Ph.D. Thesis, South China University of Technology, Guangzhou, China, 2022; pp. 12+117–119. (In Chinese). [Google Scholar]
- Wang, Y.; Osorio, G.J.; Li, T.; Muzzio, F.J. Controlled shear system and resonant acoustic mixing: Effects on lubrication and flow properties of pharmaceutical blends. Powder Technol. 2017, 322, 332–339. [Google Scholar] [CrossRef]
- Anderson, R.S.; Ende, A.J.D.; Salan, S.J.; Samuels, P. Preparation of an Energetic-Energetic Cocrystal using Resonant Acoustic Mixing. Propellants Explos. Pyrotech. 2014, 39, 637–640. [Google Scholar] [CrossRef]
- Ma, N.; Chen, S.; Jiang, H.; Zhang, Z.; Qin, N. Research Progress and Prospect on Application of Resonance Acoustic Mixing Technology in Energetic Materials Field. Ordnance Ind. Autom. 2017, 36, 20–24. (In Chinese) [Google Scholar] [CrossRef]
- Nagapudi, K.; Umanzor, Y.E.; Masui, C. High-throughput screening and scale-up of cocrystals using resonant acoustic mixing. Int. J. Pharm. 2017, 521, 337–345. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.L.; Liu, H.Y.; Liu, C.R. Experimental Study on the Anti-resonance Characteristic of Fluid-type Floating Raft. J. Vib. Eng. 2013, 26, 641–646. (In Chinese) [Google Scholar] [CrossRef]
- Shin, Y.H.; Kim, K.J.; Chang, P.H.; Han, D.K. Three Degrees of Freedom Active Control of Pneumatic Vibration Isolation Table by Pneumatic and Time Delay Control Technique. J. Vib. Acoust. 2010, 132, 051013. [Google Scholar] [CrossRef]
- Liu, J.T.; Liu, J.; Li, X.H.; Gao, H.B. Analysis and Simulation of Dynamics for a Anti-resonant Vibrating Machine of the Minimum Amplitude. J. Vib. Shock 2009, 28, 109–112. (In Chinese) [Google Scholar] [CrossRef]
- Chen, J.; Yan, B.; Sun, M.Y.; Shi, W.Z.; Lu, Z.W. Study on Effect of Subsystem on Vibration Isolation Performance of Two-stage Vibration Isolation System. J. Vib. Meas. Diagn. 2017, 37, 349–355. (In Chinese) [Google Scholar]
- Chen, J.; Dong, D.W.; Shi, W.Z.; Zhao, M.; Gao, F. Vibration Isolation Design for a Powerpack Two-stage Isolation System with a Subsystem. J. Vib. Shock 2016, 35, 211–218. (In Chinese) [Google Scholar] [CrossRef]
- Wen, B.C.; Li, Y.N.; Zhang, Y.M.; Huang, X.L. Vibration Utilization Engineering; Science Press: Beijing, China, 2005; pp. 34–35. (In Chinese) [Google Scholar]
- Ma, N. New Development of Acoustic Resonance Mixing Technology in China. Chin. J. Explos. Propellants 2023, 46, 757–760. (In Chinese) [Google Scholar]
- Zhan, X.B.; Tang, Y.; Lan, C.Y.; Li, X.W.; Shi, T.L. Analysis on the Dynamic Characteristics and Performances of a Three-mass Resonant Acoustic Mixer. J. Vib. Shock 2020, 39, 204–208. (In Chinese) [Google Scholar] [CrossRef]
- Venturini, S.; Bonisoli, E.; Rosso, C.; Rovarino, D.; Velardocchia, M. Modal Analyses and Meta-Models for Fatigue Assessment of Automotive Steel Wheels. In Model Validation and Uncertainty Quantification, Volume 3; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Zhao, Q.B.; He, B.; Wen, B.C. Effects of Dynamic Parameters on the Performance of a Three-mass Vibrating Machine. J. Vib. Shock 2015, 34, 70–78. (In Chinese) [Google Scholar] [CrossRef]
- Li, J.L.; Ma, J.; Hou, S.C. Analysis of structural vibration modes based on MATLAB. Sci. Technol. Inf. 2024, 22, 216–223. (In Chinese) [Google Scholar] [CrossRef]
- Cui, S.J. Vibratory Synchronization and Coupling Dynamics in a Mechanical System with Multiple Resonant Types. Master’s Thesis, Northeastern University, Shenyang, China, 2018; pp. 9–10. (In Chinese). [Google Scholar]
- Khan, I.; Guo, R.; Farooq, U.; Adhikari, S.; Zhou, H. Parametric Effects on the Mixing Efficiency of Resonant Acoustic Mixing Technology for High Viscosity Mixture; A Numerical Study. SSRN Electron. J. 2023, 11, 266. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, J.B.; Shi, L.C.; Lin, J.B.; Zhang, L.L.; Gao, F.; Li, X.; Tang, Z.P.; Ling, G.L.; Wang, F.; et al. ANSYS Workbench17.0 Finite Element Analysis from Entry to Mastery; Machine Press: Beijing, China, 2017; p. 224. (In Chinese) [Google Scholar]
- Zhang, H.C.; Wang, H.P.; Wang, F.; Liu, X.W.; Jin, D.Y.; Wei, J.H.; Feng, J.H.; Zheng, Z.D.; Gao, J.Y. ANSYS14.0 Theory Analysis and Engineering Application Examples; Machine Press: Beijing, China, 2012; p. 327. (In Chinese) [Google Scholar]
- Dimauro, L.; Venturini, S.; Tota, A.; Galvagno, E.; Velardocchia, M. High-speed tracked vehicle model order reduction for static and dynamic simulations. Def. Technol. 2024, 38, 91–92. [Google Scholar] [CrossRef]
- Wei, L. Finite Element Mode Analysis of Large Vibration Sieve. Coal Process. Compr. Util. 2015, 9, 12–14+8. (In Chinese) [Google Scholar] [CrossRef]
- Sun, C.S.; Li, C.; Deng, Z.K.; Tan, C. Comparison of Instantaneous Phase-frequency Characteristics of Suspended Cables Under External and End Excitation. J. Vib. Shock 2022, 41, 250. (In Chinese) [Google Scholar] [CrossRef]
- Li, Y.Y.; Liu, C.H.; Zhang, Y. Study on the Forced Vibration Characteristics. Chem. Eng. Equip. 2008, 7, 19–20+26. (In Chinese) [Google Scholar] [CrossRef]
- Yang, L.J.; Fang, S.Y. Verification of Grid Independence of Curved Pipe Network Based on FLUENT. J. Beibu Gulf Univ. 2023, 38, 63–69. (In Chinese) [Google Scholar] [CrossRef]




| Spring Rate (N/m) | Data | Quality (kg) | Data |
|---|---|---|---|
| k1 | 1.792 × 106 | m1 | 81 |
| k2 | 1.260 × 106 | m2 | 45 |
| k3 | 1.475 × 106 | m3 | 29 |
| k4 | 8.910 × 105 |
| Modal | Frequency from the Workbench Simulation (Hz) | Frequency from the Matlab Calculations (Hz) | Relative Deviation |
|---|---|---|---|
| 1 | 14.47 | 15.30 | 5.42% |
| 2 | 38.42 | 38.10 | 0.84% |
| 3 | 58.95 | 59.12 | 0.29% |
| Number of Nodes | Third Order Natural Frequency (Hz) | The Amplitude of Vibration of the Payload Assembly (mm) | The Amplitude of the Acceleration of the Payload Assembly (m/s2) |
|---|---|---|---|
| 79,015 | 58.792 | 3.4 | 474.56 |
| 98,036 | 58.947 | 4.42 | 617.13 |
| 193,800 | 58.933 | 3.37 | 610.83 |
| Third Order Natural Frequency (Hz) | The Amplitude of Vibration of the Payload Assembly (mm) | The Amplitude of the Acceleration of the Payload Assembly (m/s2) | |
|---|---|---|---|
| −0.00024 | −0.01144 | −0.01031 | |
| GCI (%) | 0.04 | 2.53 | 2.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Liu, Z.; Chang, B. Simulation Analysis of a Three-Degree-of-Freedom Low-Frequency Resonant Mixer. Appl. Sci. 2025, 15, 4861. https://doi.org/10.3390/app15094861
Liang J, Liu Z, Chang B. Simulation Analysis of a Three-Degree-of-Freedom Low-Frequency Resonant Mixer. Applied Sciences. 2025; 15(9):4861. https://doi.org/10.3390/app15094861
Chicago/Turabian StyleLiang, Jinsheng, Zheng Liu, and Bolun Chang. 2025. "Simulation Analysis of a Three-Degree-of-Freedom Low-Frequency Resonant Mixer" Applied Sciences 15, no. 9: 4861. https://doi.org/10.3390/app15094861
APA StyleLiang, J., Liu, Z., & Chang, B. (2025). Simulation Analysis of a Three-Degree-of-Freedom Low-Frequency Resonant Mixer. Applied Sciences, 15(9), 4861. https://doi.org/10.3390/app15094861






