Modified Local Linear Embedding Algorithm for Rolling Element Bearing Fault Diagnosis

Abstract

Due to the noise accompanied with rolling element bearing fault signal, it can reduce the accuracy of faulty diagnoses. In order to improve the robustness of a faulty diagnosis, this study proposed a fault diagnosis model based on modified local linear embedding (M-LLE) algorithm. Aiming at the characteristics of rolling element bearing fault data, the vibration signal was first analyzed in time domain and frequency domain to construct high dimension eigenvectors. Next, the high-dimensional eigenvectors can be reduced to low-dimensional eigenvectors by M-LLE algorithm. In the M-LLE algorithm, the Mahalanobis distance (MD) metric is adopted to replace Euclidean distance in traditional neighborhood construction and L1-norm is used to standardize weight matrix, which can enhance the anti-noise ability of the Local Linear Embedding (LLE) algorithm. Finally, fault diagnosis results can be obtained when low-dimensional rolling element bearing fault data is classified by K-Nearest Neighbor (KNN) classifier. By simulating the noisy artificial data sets in different degrees, the proposed algorithm can get the perfect local structure of manifolds. The effectiveness of M-LLE algorithm can be proved. In addition, experimental results of real rolling element bearing data which provided by the University of Cincinnati show that the accuracies of all kinds of faults can reach 100%. It can be deemed that the proposed fault diagnosis model can effectively improve the accuracy of fault diagnosis.

1. Introduction

As the critical component of mechanical equipment, once rolling element bearing malfunctions in the process of industrial production, it will bring cascading failures and even cause the system to collapse. So, if the rolling element bearing is broken, it will result in huge economic losses or even a major security accident [1]. Therefore, accurate fault diagnosis of rolling element bearing is an important guarantee for the reliability and effectiveness of mechanical equipment. With the complexity of industrial machinery structure and the diversity of modules, fault signals of rolling element bearing often show non-stationary, non-linear and high-dimensional characteristics [2], and noise is often doped among the collected signals.

In recent years, manifold learning has been applied to mechanical fault diagnosis field because of its good ability in nonlinear dimensionality reduction [3]. The representative methods of manifold learning are listed as following: the Local Linear Embedding (LLE) algorithm proposed by S.T. Roweis [4], Isometric Feature Mapping (ISOMAP) algorithm put forward by Tenenbaum et al. [5], and Local Tangent Space Alignment (LTSA) algorithm advanced by Zhang, Z.Y. et al. [6]. The LLE algorithm is a classical and effective nonlinear dimensionality reduction method, which can learn a high dimensional manifold structure in arbitrary dimension. Furthermore, due to the small computational complexity of LLE algorithm, it is simple and easy to implement. LLE algorithm defines that each sample point and its neighborhood points are located in a local linear manifold surface, so each sample point can be represented by neighborhood points [7]. In fault diagnosis field, LLE algorithm can effectively extract the sensitive features of sample data and filter redundant information, so it can reduce the dimension of original feature space. Liu, X. et al. used LLE to reduce the dimension of observation, the results showed that the precision of fault diagnosis model of rotating machinery platform was effective [8]. Besides, Li, L. et al. proposed a rolling bearing fault diagnosis method based on LLE and least squares support vector machine, and it can effectively identify the nonlinear fault features existing in high dimension space [9]. However, LLE algorithm constructs low dimensional manifold through the weighted method to keep the local geometric relationship of original manifold. Since the local linear definition of LLE algorithm, it causes that LLE algorithm is susceptible to the interference of noise. In the past decade, some algorithms have been proposed to improve the robustness of LLE algorithm. Hong Chang and Dit-Yan Yeung proposed a robust LLE algorithm based on the robust PCA algorithm [10], this method reduced the interference of outliers effectively by adjusting the distribution deviation in the statistical process. Manda Winlaw et al. put forward a robust LLE algorithm based on penalty function, which combined L1 norm with L2 norm in weight function to improve the anti-noise ability [11]. Tao, J.W. and Wang, S.T. adopted L1 norm to construct the weight matrix to improve the ability to resist noise in original LLE algorithm [12]. In order to improve the stability of LLE algorithm under strong noise, Sun, Y. et al. proposed an improved algorithm based on sparse constraint. In the calculation process of this method, the L1 norm is added to penalty constraint, which can make the optimal reconstruction weight matrix become sparser [13]. JAS Rettes et al. constructed reasonable weight by using different neighborhood sizes, thus it can reduce the effect of interference points in dimensionality reduction [14].

The above methods are only adopted a separate improvement to enhance the robustness of LLE algorithm, and only use artificial data sets to simulate. Although these methods can basically recover the low-dimensional manifold in high-dimensional noisy data, the LLE algorithm is not improved comprehensively and the experiments are not validated by real data in the practical application process. The principle of LLE algorithm can be roughly summed up into three steps. Firstly, construct the neighborhood graph of sample data. Then obtain the weight matrix by local linear structure in the neighborhood. Finally, get low-dimensional embedding of sample data by using the weight matrix. Currently, LLE algorithm determines the similarity of neighborhood points by measuring Euclidean distance among sample points [15]. Euclidean distance assumes that all components in the space are irrelevant. However, as for bearing vibration signal, the recent vibration signals are often correlated. It is obvious that if it still uses Euclidean distance in actual application of mechanical fault diagnosis, the true relationship between fault data can be ignored and resulting in unreasonable neighborhood construction. In addition, due to a variety of complex operating conditions factors in actual sampling process, it often contains noise pollution. If we cannot improve the noise reduction capability of LLE algorithm, the mapped structure of low-dimensional data will be distorted and the accuracy of the fault diagnosis will be seriously reduced.

Therefore, aiming at above two problems, we proposed M-LLE algorithm, which improves the ability of LLE algorithm to resist noise. As for the non-stationary, non-linear and high-dimensional characteristics of bearing failure data, MD is used to instead of Euclidean distance in the construction of neighborhood. In the process of weight acquisition, the L1-norm is adopted to standardize the cost function which calculates the weight of M-LLE algorithm. We are taking the distance among sample points and the structural characteristics of manifold into account, so M-LLE algorithm can reduce interference of noise. In order to verify the effectiveness of M-LLE algorithm, we use artificial data sets and the actual bearing fault data to simulate the experiment. The experimental results show that the method proposed in this paper can effectively realize the intrinsic manifold acquisition of noisy high-dimensional data, and the algorithm can significantly improve the diagnostic accuracy in the process of bearing fault diagnosis.

2. LLE Algorithm

LLE algorithm is a local linear algorithm, which is mainly used linear weight coefficient to represent the contribution of each data point in data reconstruction [16]. With condition of remaining the geometric relations in neighborhood being invariant, the data in high-dimensional observation space is mapped to low-dimensional space by linear mapping such as scaling, rotation and translation [17]. In this way, it can preserve the inherent geometry relationship among data points. Suppose that $Y\subset R^d$ is a low-dimensional manifold embedded in the high-dimensional space $R^D$, where $d\ll D$. There are $n$ data points in the high dimension space: $x=\left\{x_i|i=1,\dots ,n ,x_i\in R^D\right\}$. The details of the LLE algorithm are as following:

• For each D-dimensional data point $x_i$, k-nearest neighbor criterion is used to filter the nearest $k$ points $N_i=\left\{x_i^1,x_i^2,x_i^3,\dots ,x_i^k\right\}$. Euclidean distance is adopted to construct the neighborhood graph $G$;
• Each data point can be represented by a weighted linear representation of its surrounding neighborhood points, and minimizing the following objective functions to get the smallest reconstruction error:

  $$\begin{array}{l}min\phi \left(w\right)=min\left({\displaystyle \sum }_{i=1}^n{\left|\right|x_i-{\displaystyle \sum }_{j=1}^k{w}_{ij}{x}_j\left|\right|}^2\right)\\ s.t.\{\begin{array}{c}{w}_{ij}=0, x_{ij}\notin V\\ {\displaystyle \sum }_j{w}_{ij}=1, x_{ij}\in V\end{array}\end{array}$$

  (1)

  where the weight $w_{ij}$ represents the reconstructed contribution of the j-th sample point to the i-th sample point. $V$ represents a neighborhood which is the number of neighborhood points is $k$. If the sample $j$ is the neighborhood of the sample point $i$, $w_{ij}$ is set to 1, otherwise it is set to 0;
• Use $y_i$ to build the d-dimensional embedded space, it is generated by this cost function:

  $$\begin{gathered} \varphi \left(Y\right)=min{{\displaystyle {\sum }_i\left|y_i-{\displaystyle {\sum }_j{w}_{ij}{y}_j}\right|}}^2 \\ s.t. Y{Y}^T=I \end{gathered}$$

  (2)

Based on step 2, the cost function is minimized by the optimal weight $w_{ij}$, and it can obtain the optimized low-dimensional coordinate $y_i$. Where, $Y=\left\{y_i|i=1,\dots ,n ,y_i\in R^d\right\}$, and $I$ is the unit matrix of $d\times d$. To minimize the value of cost function, it takes $Y$ as the eigenvectors which are corresponded to the minimum $d$ nonzero eigenvalues of $M=\left(I-W\right){\left(I-W\right)}^T$.

3. Neighborhood Construction Based on MD

3.1. Introduction of MD

The MD is proposed by the Indian statistician P.C. Mahalanobis, and it represents the covariance distance of data [18]. A major difference from the Euclidean distance is that it takes interrelationships among various features into account, and these features are independent of the measurement scale [19].

In fact, two dimensions in the multidimensional space may be linearly related. Thus, MD utilizes the Joliesky decomposition to eliminate the correlation among different dimensions. Suppose two vectors $X$ and $Y$, where $n$ data points are given: $X=\left\{X_i|i=1,\dots ,n\right\}$, and $n$ data points: $\left\{Y_i|i=1,\dots ,n\right\}$. The variance matrix can be expressed as:

$${\displaystyle \sum }=\frac{1}{n-1}{\displaystyle \sum }_{i=1}^n\left(X_i-\overline{X}\right){\left(Y_i-\overline{Y}\right)}^T$$

(3)

where $\overline{X}$ is the mean of $X$, and $Y$ is the mean of $Y$. The MD between the vector $X$ and $Y$ can be expressed as following:

$$D_M\left(X,Y\right)=\sqrt{{\left(X-Y\right)}^T{{\displaystyle \sum }}^{-1}\left(X-Y\right)}$$

(4)

3.2. Neighborhood Construction Based on MD

In this part, we improve the LLE algorithm in neighborhood construction. In order to solve the problems which bearing failure data has non-stationary, non-linear and high correlation characteristics, M-LLE algorithm uses MD to replace Euclidean distance to construct the neighborhood map.

An improved neighborhood algorithm based on MD is shown as following:

• Initialize the relevant parameters: neighborhood size $k$, and the reduced dimension of the intrinsic dimension $d$. Define a starting point $x_i$, which chooses arbitrarily in high-dimensional space, and the neighborhood of this point is set to $U\left(U=\varnothing \right)$.
• Calculate the covariance matrix ${\displaystyle \sum }$ by (5), so we can determine the relationship between the center point $x_i$ of the neighborhood and the rest of the sample points $x_j \left(j=1, 2, 3,\dots ,n-1\right)$.

  $${\displaystyle \sum }=\frac{1}{n-1}{\displaystyle \sum }_{k=1}^n\left(x_i^k-\overline{ x_i}\right){\left(x_j^k-\overline{ x_j}\right)}^T$$

  (5)
• Using the obtained covariance matrix of sample points and the center point, we can obtain the MD between the center point $x_i$ and the rest of the sample point $x_j\left(j=1, 2, 3,\dots ,n-1\right)$:

  $$D_M\left(x_i, x_j\right)=\sqrt{{\left(x_i- x_j\right)}^T{{\displaystyle \sum }}^{-1}\left(x_i- x_j\right)}$$

  (6)
• Get a descending order of $D_M\left(x_i,x_j\right)$, and select $k$ nearest points as the neighborhood of the center point $x_i$. Set this neighborhood as $U_i$, and update the center point set $U=U{\displaystyle \cup }\{x_i\}$.
• To determine the next center point, we select any one points of $U_i$ as the next center point of $x_i$, and this point does not belong to the center point set $U$.
• When the new center point is determined, the algorithm turns back to step 2 to repeat all above operations.
• Until the number of elements in $U$ is $n$, it means that all the sample points have been completed traversal. Finally, output all sample points $\{x_1, x_2, x_3,\dots , x_n\}$ and their neighborhoods $\{U_1, U_2, U_3,\dots , U_n\}$.

The flow chart of improved neighborhood construction algorithm which based on MD is shown in Figure 1.

When using MD to replace the Euclidean distance in the original LLE algorithm, it is guaranteed that the local linear relationship in the neighborhood is invariant to construct low-dimensional projection. After we adopt the improved neighborhood construction algorithm, the correlation between the data can be eliminated. It will play a very important role in the subsequent realization of obtaining the intrinsic manifold in high-dimensional space.

4. Weight Construction Based on L1-Norm

4.1. The Effect of Noise on Weight Construction

In the process of dimensionality reduction, except selecting reasonable and effective neighborhood, an accurate local linear weight construction is also the key factor affecting the dimensionality reduction effect [20]. The construction of weight matrix is the main basis for getting the mapping from high-dimensional space to low-dimensional space of the manifold structure. If the weight construction is not accurate, it will lead to the deviation of dimensionality reduction and even cause distortions.

Due to complex coupling among the modules on industrial production process, the mechanical fault data can reflect the fault information, but at the same time it often doped with noise. When LLE algorithm is used to reduce the dimension of fault data, noise points can lead to an inaccuracy of weight construction, which will affect the dimensionality reduction and reduce the accuracy of fault diagnosis. There is a detailed analysis of noise effect [21].

Let $x_0$ represents the sample point $x_i$, $\mathrm{U}({\mathrm{x}}_{\mathrm{i}})$ represents the neighborhood of $x_0$. Suppose $x_1, x_2,\dots , x_k\in U( x_0)$, and $x_0={\displaystyle \sum }_{i=1}^k{w}_i{x}_i$, ${\displaystyle \sum }_{i=1}^k{w}_i=1$. We define the data points which contaminated by noise as $\widetilde{x_i}=x_i+{\epsilon }_i \left(i=0,1,2,\dots ,k\right)$, where ${\epsilon }_i \left(i=0,1,2,\dots ,k\right)$ indicates the noise of each neighborhood point. According to LLE algorithm, after noise pollution, there are data points $\widetilde{x_0}={\displaystyle \sum }_{i=1}^k\widetilde{w_i}\widetilde{x_i}$, ${\displaystyle \sum }_{i=1}^k\widetilde{w_i}=1$, and $\widetilde{x_i}\in U\left(\widetilde{x_0}\right)$. $\widetilde{w_i}$ represents the elements in local reconstruction matrix of the contaminated data points.

Then, when the neighborhood points are without noise pollution, its reconstructed weights can be expressed as following:

$$\{\begin{array}{c}{X}_0=\left( x_1, x_2,\dots , x_k\right)\\ W_0={\left( w_1, w_2,\dots , w_k\right)}^T\end{array}$$

(7)

When the polluted neighborhood points and its reconstructed weights can be expressed as following:

$$\{\begin{array}{c}\widetilde{X_0}=\left(\widetilde{x_1},\widetilde{ x_2},\dots ,\widetilde{ x_k}\right)\\ \widetilde{W_0}={\left(\widetilde{w_1},\widetilde{ w_2},\dots ,\widetilde{ w_k}\right)}^T\end{array}$$

(8)

Thus, there are

$$\{\begin{array}{c}{\mathrm{x}}_0=X_0{W}_0\\ \widetilde{x_0}=\widetilde{X_0}\widetilde{W_0}\end{array}$$

(9)

There is a theorem: If it is independent of noise points, different dimensions, and each $\widetilde{W_0}$. The mean value of each noise point is 0, and they have the same variance [21]. The error of reconstructed weight matrix for the data point is $\delta W_0=\widetilde{W_0}-W_0$. The following estimate is made:

$${E\left|\right|\delta W_0\left|\right|}^2\le \frac{k\left(k+1\right){\sigma }^2}{{\lambda }_{min}l}E{||\widetilde{W_0}||}^2$$

(10)

Among them, $\left|\right|·\left|\right|$ is the Euclidean norm, ${\sigma }^2={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{D}}{\sigma }_i^2$, ${\sigma }_i^2=Var\left({\epsilon }_i\right), \left(i=0, 1, 2,\dots ,D\right)$, and ${\epsilon }_i$ represents the k-th component of $\epsilon$, $l=rank\left(X_0\right)$, ${\lambda }_{min}$ is the minimum nonzero eigenvalue of $X_0{}^T{X}_0$. For detailed proof, please refer to document [20].

It can be seen from the above theorem, the main factors affecting the robustness of LLE algorithm are: noise distribution ${\sigma }^2$, neighborhood selection $k$, and the energy of weight matrix $||\widetilde{W_0}||$. Therefore, in order to enhance the ability of LLE algorithm to resist noise, besides the improvement of neighborhood construction, we should also reduce the weight matrix energy. Only by reducing the error of the local linear reconstruction weight matrix, can we overcome the sensitivity of LLE algorithm to noise.

4.2. Weight Construction Based on L1-Norm

Traditional LLE algorithm using L2-norm to calculate weight matrix, so it will enlarge the noise factor and cause the output results being difficult to recover the intrinsic structure. In order to reduce the error in local linear reconstructed weights, and enhance the robustness of LLE algorithm in the noisy environment, when dealing with noisy data, Ke et al. [22] derived that the method based on L1-norm is more robust than based on L2-norm. In addition, when calculating the weight matrix, traditional algorithm only considers distances among neighborhood points, and it does not consider the manifold structure in the neighborhood. Therefore, the calculated weight matrix is not stable in noisy data. Inspired by [23,24,25], L1-norm is introduced to minimize the local error. At the same time, we take distance factor and the structure factor into account, so that the M-LLE algorithm can achieve a better noise immunity.

In traditional LLE algorithm, each sample point can get a weighted linear representation by its neighborhood points, and the residual of local linear reconstruction is as following [23]:

$$\begin{gathered} \xi \left(x\right)={\displaystyle \sum }_{i=1}^n{\left|\right|x_i-{\displaystyle \sum }_{j=1}^k{w}_{ij}{x}_j\left|\right|}^2 \\ s.t. {\sum }_j{w}_{ij}=1 \end{gathered}$$

(11)

In order to minimize the local linear reconstructed residual, we can adopt Lagrange multiplier method to obtain the optimal reconstruction weight $W_i^S$. Since the distance weight matrix $W_i^S$ depicts the distance relationship among the center point and each neighborhood point, it does not take structural factors into consideration. Thus, in the local weight construction, M-LLE algorithm combines the distance relation with the structural relation in neighborhood and redefines the local weight matrix $W_i$:

$$W_i=W_i^S\times W_i^D$$

(12)

$W_i^{S }$ represents the distance matrix calculated by LLE algorithm, and $W_i^D$ represents the structure weight matrix considered the local manifold structure. In the process of calculating the structure weight matrix, L1-norm is used to regulate, and the description is listed as following:

$$W_i^D=exp(-\frac{{\left|\right|x_i-x_j\left|\right|}_1^2}{D_m})$$

(13)

And,

$$D_m=\frac{1}{k}{\displaystyle \sum }_{\mathrm{j}=1}^{\mathrm{k}}\left|\right|x_i-x_j\left|\right|$$

(14)

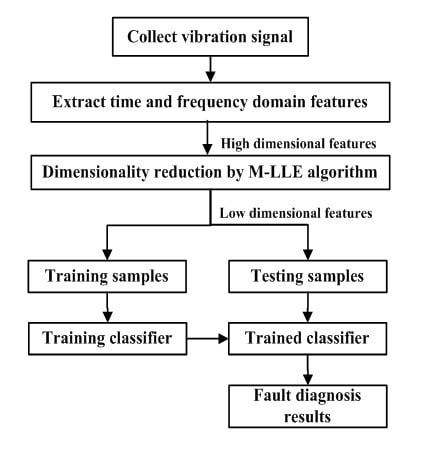
5. Fault Diagnosis Model Based on M-LLE Algorithm

Rolling element bearing is an indispensable component of industrial infrastructure equipment, its health state directly determines the health status of the mechanical system. The timely detection of the mechanical system and taking effective measures for bearing failure are indispensable works in real production process, and also a worthy of the further study of the direction [26]. Because the working condition is complex and the bearing is susceptible to noise interference, it often causes vibration signals show the characteristics of high-dimensional nonlinearity. Obviously, it is difficult to directly carry out effective feature extraction and make fault diagnosis. In this paper, M-LLE algorithm is used to get an effective dimensionality reduction from the obtained fault signals. Therefore, it is convenient to carry out effective and accurate fault diagnosis. Based on above method of neighborhood construction and weight construction, M-LLE algorithm is proposed to improve the robustness and accuracy of the original LLE algorithm. The details of M-LLE algorithm are shown in Algorithm 1.

Algorithm 1 M-LLE Algorithm

Input: Initialize high-dimensional sample points $x_i$, neighborhood size $k$, and intrinsic dimension $d$

Output: Low-dimensional embedded coordinates $\{y_1,y_2,y_3,\dots ,y_n\}$

1: for $i:=1$ to $n$ do

2:  Obtain neighborhood $U_{\mathrm{i}}$ by improved neighborhood construction algorithm

3:  Calculate distance weight matrix $W_i^S$ by Equation (10)

4:  Get structural weight matrix $W_i^D$ by combining Equations (12) and (13) 5:  Acquire local weight matrix $W_i=W_i^S\times W_i^D$ 6:  According to the Equation (3) to get local embedded coordinates $y_i$

7: end

8: return $\{y_1,y_2,y_3,\dots ,y_n\}$

In the process of rolling element bearing fault diagnosis, we obtain the original vibration signals by using the same sampling frequency to carry on the data acquisition. The rolling element bearing is working under a certain load and speed. The collected data is divided into training sample set and testing sample set, and adopting the frequency domain analysis to get signal feature extraction.

However, the characteristics obtained only by signal feature extraction method may tend to characteristic redundancy, or result in partial feature conflict. In order to reduce the inaccuracy of feature extraction, M-LLE algorithm is used to ensure that the dimensionality reduction is under the same geometric relationship premise. This method can effectively extract key characteristics of fault data, and avoid the error caused by artificial selection. Subsequently, fault classifier is trained by training samples which have been reduced to intrinsic dimension, and put low-dimensional testing samples into the trained classifier. Finally, according to the output of classifier, we can determine the working condition and fault type of rolling element bearing. The detailed implementation process of fault diagnosis model based on M-LLE algorithm is shown in Figure 2.

6. Experiments and Analysis

6.1. Artificial Data Set

In this paper, we select three kinds of artificial data sets, which are Swiss-roll, S-curve and Punctured-sphere, in order to verify the effectiveness of the improved LLE algorithm. In Figure 3, the graphs a(1), b(1) and c(1) are the three-dimensional manifolds when the artificial data sets are Swiss-roll, S-curve and Punctured-sphere without noise. In order to verify the effectiveness of manifold learning from the intuitive and quantitative aspects, the evaluation criteria of residual error is introduced in this paper to depict the effect of dimensionality reduction.

$$r=\frac{{{\displaystyle \sum }}_{i=1}^n{\left[D_X\left(i\right)-D_Y\left(i\right)\right]}^2}{n-2}$$

(15)

We measure the embedded quality by using the residual error $r$ between the coordinates $D_X\left(i\right)$ in original higher-dimensional space and the embedded coordinates $D_Y\left(i\right)$ in low-dimensional space [7]. The smaller residual error, the better effectiveness of dimensionality reduction. It is also means the result of dimensionality reduction can preserve the topology of original manifold better. For each kind of artificial data set, the number of sample points is 4000, the manifold is reduced to two dimensions, and the neighborhood size is 25.

For original artificial data sets, they are shown in Figure 3a(1),b(1),c(1). As is shown in Figure 3a(1), the Swiss-roll data set is scroll-like in three-dimensional space, where the color on the manifold is from deep to shallow to represent the data points of the different coordinates in the high dimensional space. As is shown in Figure 3b(1), the S-curve data set is S-shaped in three-dimensional space. The effective expansion of Swiss-roll and S-curve manifolds in two-dimensional space is a rectangular and the sample points of different colors can be separated well. As is shown in Figure 3c(1), the Punctured-sphere data set is a non-closed sphere in a three-dimensional space. When the dimension reduction algorithm is valid, its manifold in two-dimensional space is a circle with separated colors.

For these three kinds of artificial data sets with no noise pollution, Figure 3a(2),b(2),c(2) are shows the embedded results of LLE algorithm. It can be clearly seen that distortion has occurred on embedded manifold, so they are can’t recover the rectangular state of Swiss-roll and S-curve in two dimensions. What’s more, at the edge of Figure 3c(2), some data points are stacked. However, the embedded manifolds which obtained by M-LLE algorithm can get good recoveries of the rectangular in Figure 3a(3),b(3), and the circle in Figure 3c(3). It is clear that data points of different colors can be completely separated and expanded. In addition to the intuitive graphical display, we can also see from the quantitative indicators. The residual errors in Figure 3a(2),b(2) are 0.3292 and 0.2129, but the residual errors of using M-LLE algorithm in Figure 3a(3),b(3) are 0.2612 and 0.1886, which are smaller than using LLE algorithm. It can also be judged by the residual errors in Figure 3c(2),c(3). When we adopt LLE algorithm in Punctured-sphere data set, the residual error of dimensionality reduction is 0.1167. There is no doubt that 0.1167 is higher than 0.1092 in Figure 3 c(3). Therefore, using M-LLE algorithm can effectively preserve the topology of original manifolds, and it is helpful for dimensionality reduction.

The above simulation results have verified the effectiveness of M-LLE algorithm in the noiseless data. Next, in order to prove the robustness of M-LLE algorithm, we introduce the noisy artificial data sets in this study. The settings of the parameters are shown in

Table 1. Parameter settings of the LLE and M-LLE experiments reported in Figure 4.

Parameter	Swiss-Roll	S-Curve	Punctured-Sphere
Dimensionality of data space (D)	3	3	3
Dimensionality of embedding space (d)	2	2	2
The size of nearest neighbor (k)	25	25	25
The number of points	4000	4000	4000
The number of noise points	200	400	600
The percentage of noise	5%	10%	15%

.

As is shown in Figure 4a(1),b(1),c(1), we add 5% noise to Swiss-roll data set, 10% noise to S-curve data set and 15% noise to Punctured-sphere data set. The results of dimensionality reduction by LLE algorithm are shown in Figure 4a(2),b(2),c(2), and Figure 4a(3),b(3),c(3) are the M-LLE embedded results in two dimensions. There is a large distortion in Figure 4a(2), and the residual error is 0.4377, which is larger than the residual error in Figure 4a(3). Besides, by comparing Figure 4b(2) with Figure 4b(3) we can find that M-LLE algorithm is beneficial to restore the manifold structure in the noisy environment, and the residual error is only 0.2085. Figure 4c(2),c(3) are the two-dimensional embedded results in noisy Punctured-sphere data set, which use LLE algorithm and M-LLE algorithm respectively. There are a large number of data points aliasing in the edge of Figure 4c(2), on the contrary, Figure 4c(3) can effectively separate the data points of different colors. What’s more, the residual error in Figure 4c(3) is 0.8856, which is smaller than 0.9761 in Figure 4c(2). It means that M-LLE algorithm can get a better embedded result than LLE algorithm in noisy artificial data sets.

Through the above simulation, we can find that M-LLE algorithm can effectively preserve the intrinsic morphology of manifold in different artificial data sets. In addition, regardless of the degree of noise interference, M-LLE algorithm can get the perfect local structure of manifolds. Therefore, M-LLE algorithm has strong robustness.

6.2. Rolling Element Bearing Fault Data Set

We use the real rolling element bearing fault data provided by the University of Cincinnati [27] to verify effectiveness of proposed method in fault diagnosis application. The mechanical device used in this experiment is shown in Figure 5.

Four Rexnord ZA-2115 double bearings are mounted on the support frame, and the speed is maintained at 2000 r/min. We analyze the health of rolling element bearing by collecting the vibration data of bearing. Among them, vibration signals are obtained by corresponding acceleration sensor, and the frequency of data sampling is 20 kHz.

Figure 6 shows the time domain waveform of different bearing states. The states they depicted are normal state, inner race fault, outer race fault and ball fault. Figure 6a is a diagram of the vibration signal waveform under the normal state, as can be seen from the Figure 6a, it is covered with a lot of noise burr. Figure 6b is the inner fault waveform, affected by bearing surface damage, the vibration signal appeared obvious pulse. Figure 6c is the diagram of outer race fault. Due to the excessive noise, the pulse signal is submerged. Figure 6d is the time domain waveform when the fault occurred to the ball. Because of the rotation of the ball, pulse is periodically distributed, and it is also mixed with noise.

Feature extraction is an important stage of fault diagnosis. It is necessary to extract the corresponding effective features to determine whether the data is normal or faulty. From the time-domain waveforms of different states of rolling element bearing, it can be seen that the amplitude and probability distribution of time-domain signal will change when bearing fails. Besides, frequency components, energy of the different frequency components, and main energy peak position will also change [28]. Therefore, when we collect the vibration signal of rolling element bearing, vibration signal should be extracted from effective features to facilitate the fault identification and diagnosis. In this paper, the following 10 time-domain characteristic parameters and 10 frequency-domain characteristic parameters are adopted to extract useful information of rolling element bearing.

Table 2. Feature extraction in time domain and frequency domain.

Number	Characteristic Equation	Number	Characteristic Equation
1	$c_1={\displaystyle \sum _{n=1}^N}x\left(n\right)/N$	11	$c_{11}={\displaystyle \sum _{k=1}^K}s\left(k\right)/K$
2	$c_2=\sqrt{{\displaystyle \sum _{n=1}^N}{\left(x\left(n\right)-c_1\right)}^2/\left(N-1\right)}$	12	$c_{12}=\frac{{{\displaystyle \sum }}_{k=1}^K{\left(s\left(k\right)-c_{11}\right)}^2}{\left(K-1\right)}$
3	$c_3={\left({\displaystyle \sum _{n=1}^N}\sqrt{\left|x\left(n\right)\right|}/N)\right)}^2$	13	$c_{13}=\frac{{{\displaystyle \sum }}_{k=1}^K{\left(s\left(k\right)-c_{12}\right)}^4}{K{c}_{12}^2}$
4	$c_4=\sqrt{{\displaystyle \sum _{n=1}^N}{\left(x\left(n\right)\right)}^2/N}$	14	$c_{14}=\frac{{{\displaystyle \sum }}_{k=1}^K{f}_{K}s\left(k\right)}{{{\displaystyle \sum }}_{k=1}^{K}s\left(k\right)}$
5	$c_5=max\left|x\left(n\right)\right|$	15	$c_{15}=\sqrt{\frac{{{\displaystyle \sum }}_{k=1}^K{\left(f_k-c_{14}\right)}^{2}s\left(k\right)}{K}}$
6	$c_6={\displaystyle \sum _{n=1}^n}{\left(x\left(n\right)-c_1\right)}^4/\left(N-1\right)c_2{}^4$	16	$c_{16} c_{16}=\sqrt{\frac{{{\displaystyle \sum }}_{k=1}^K{f}_k^{4}s\left(k\right)}{{{\displaystyle \sum }}_{k=1}^K{f}_k^{2}s\left(k\right)}}$
7	$c_7=c_5/c_3$	17	$c_{17}=\frac{{{\displaystyle \sum }}_{k=1}^K{f}_k^{2}s\left(k\right)}{\sqrt{{{\displaystyle \sum }}_{k=1}^{K}s\left(k\right){{\displaystyle \sum }}_{k=1}^K{f}_k^{4}s\left(k\right)}}$
8	$c_8=c_5/c_4$	18	$c_{18}=c_{15}/c_{14}$
9	$c_9=c_4/\left(\frac{1}{N}{\displaystyle \sum _{n=1}^n}\left|x\left(n\right)\right|\right)$	19	$c_{19}=\frac{{{\displaystyle \sum }}_{k=1}^K{\left(f_k-c_{14}\right)}^{4}s\left(k\right)}{K{c}_{15}^2}$
10	$c_{10}=c_5/\left(\frac{1}{N}{\displaystyle \sum _{n=1}^n}\left|x\left(n\right)\right|\right)$	20	$c_{20}=\frac{{{\displaystyle \sum }}_{k=1}^K{\left(f_k-c_{14}\right)}^{1/2}s\left(k\right)}{K{c}_{15}}$

is the information of extracted features.

In Table 2, $x\left(n\right)$ represents the time series of signals, $n=1, 2,\dots ,N$, $N$ is the number of samples, $s\left(k\right)$ represents the spectrum of $x\left(n\right)$, $k=1,2,\dots ,K$, $K$ is the number of lines, $f_k$ is the frequency of the k-th line. The time-domain characteristic parameters $c_1$ and $c_3~c_5$ represent the amplitude and energy of the time-domain signal; $c_2$ and $c_6~c_{10}$ reflect the time series distribution of the time-domain signal. The frequency domain characteristic parameter $c_{11}$ indicates the frequency of vibration energy in the frequency-domain. $c_{12}~c_{13}$, $c_{15}$ and $c_{18}~c_{20}$ represent the dispersion or concentration of the spectrum. $c_{14}$ and $c_{16}~c_{17}$ reflect the changes in the main band position.

The above 20 characteristic parameters can reflect the information of fault data, but they may contain redundant features. The existence of these redundant features can not only increase the complexity of state recognition, but also reduce the accuracy of fault diagnosis. In order to eliminate redundant information in feature selection, it is necessary to further process these features and extract the intrinsic features. It is a benefit to get true state of system and perform corresponding fault diagnosis.

Therefore, we use M-LLE algorithm to reduce the dimension of 20-dimensional fault data, and obtain the intrinsic characteristic information, which is the fundamental basis for judging the fault type. In order to verify the effectiveness of M-LLE algorithm, this paper uses four kinds of state bearing data: normal state, inner race fault, outer race fault and ball fault to make the experiment. Divide each status of rolling element bearing data into 600 groups, and add labels to them. Detailed data are shown in

Table 3. The details of each state of rolling element bearing data.

Operating Condition	Training Samples	Testing Samples	Label
Normal	400	200	1
Outer race	400	200	2
Inner race	400	200	3
Ball	400	200	4

.

We reduce the dimensions of the obtained 20-dimensional data by using LLE algorithm and M-LLE algorithm. Figure 7 shows the different state of the fault data distribution in three-dimensional space. What’s more, the X axis, Y axis and Z axis represent the three features ($K_1$, $K_2$ and $K_3$) respectively, which are obtained by dimensionality reduction. The “*” indicates the normal state data of the rolling bearing, “Δ” indicates the inner ring fault status data of the rolling bearing, “○” indicates the outer ring fault state data of the rolling bearing, and “□” indicates the ball fault state data of the rolling bearing. Figure 7a is the result of reducing dimension by using the traditional LLE algorithm. As is shown in the figure, although four different states of the fault data have clustering effect, there are some data points aliasing among the bearing inner race failure, outer race failure and ball failure. Figure 7b is the result of reducing dimension by using M-LLE algorithm. There is obvious clustering phenomenon in different color bearing state data and there is no aliasing of data comparing with the traditional LLE algorithm. It will lay a solid foundation for the data classification and fault identification in the next step.

According to the fault diagnosis model based on M-LLE algorithm is proposed in the fourth part of this paper, we can obtain final bearing fault diagnosis results by using the KNN classification algorithm. In order to verify the classification effect of M-LLE algorithm and traditional LLE algorithm in rolling element bearing fault diagnosis, we list the comparison results of two methods in

Table 4. The comparison experimental results in fault diagnosis.

State	LLE	Reference [29]	M-LLE
Normal	100%	98.9%	100%
Outer race	82.5%	91.4%	100%
Inner race	98.5%	100%	100 %
Ball	89.5%	87.7%	100 %
Total	92.6%	94.9%	100 %

, and also compare with the reference [29], which adopts the same data set for fault diagnosis. It can be seen from Table 4 that M-LLE algorithm can effectively improve the accuracy of fault diagnosis of rolling element bearings. Although traditional LLE algorithm and the method in reference [29] can achieve 100% in one kind of fault classification, the total accuracy is only 92.6% and 94.9%. When using M-LLE algorithm, the classification accuracy of all kinds of fault can reach 100%.

7. Conclusions

In this paper, we have proposed a robust version of LLE algorithm, named M-LLE algorithm. By using MD and the L1-norm to regulate the weight of the manifold structure, the undesirable effect of the noise on embedded results can be largely reduced. M-LLE algorithm has strong robustness, it can make the local structure of manifold remain intact, and can achieve 100% accuracy in real bearing fault diagnosis. The simulation results on both synthetic and real rolling element bearing data sets show the efficacy of M-LLE algorithm.