Elastic Stability of Perforated Plates Strengthened with FRP under Uniaxial Compression
Abstract
:1. Introduction
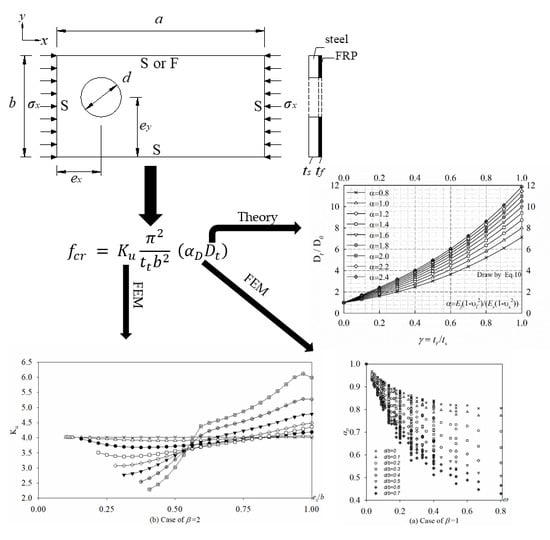
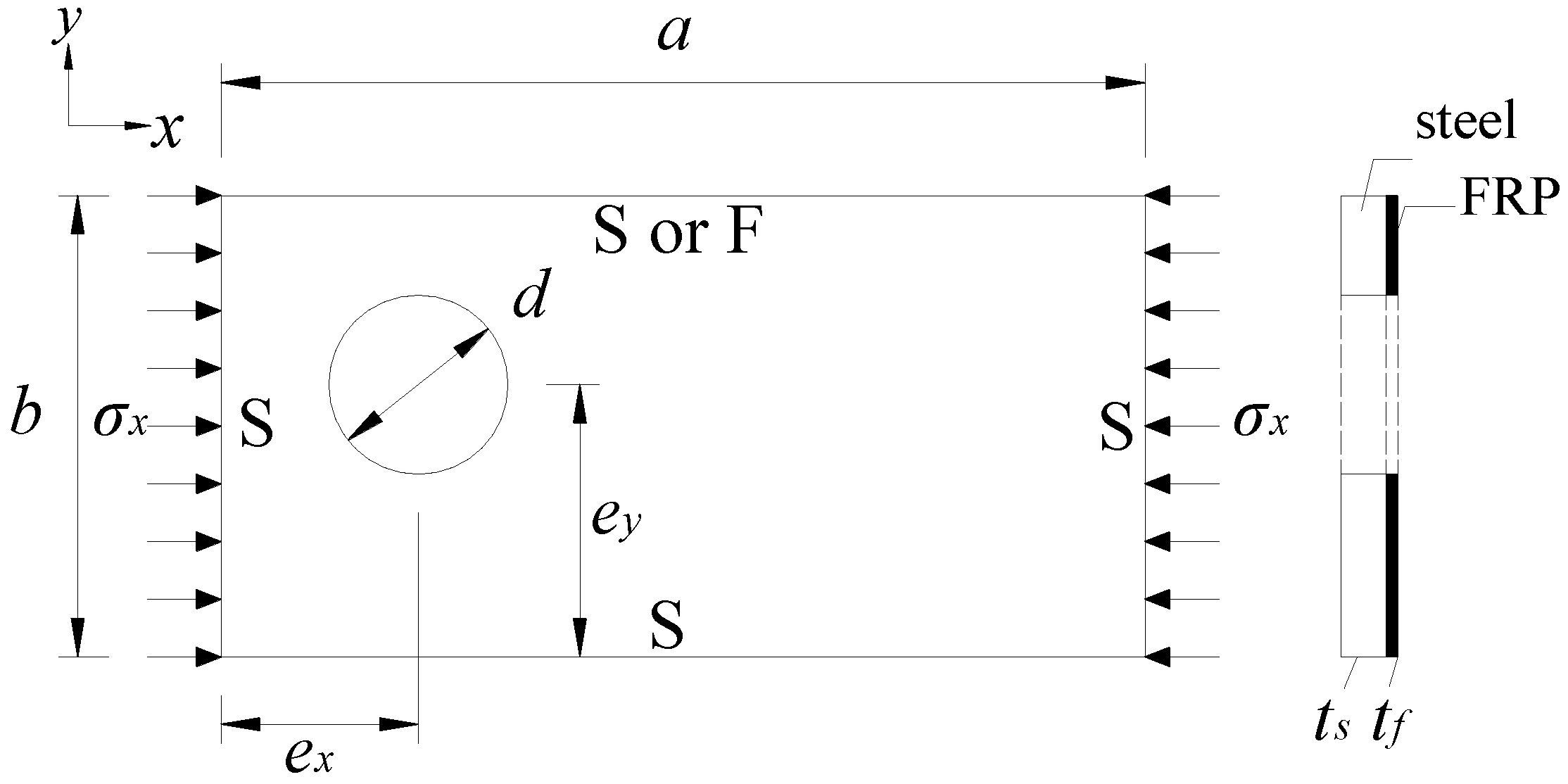
2. Problem Definition
2.1. Basic Information
2.2. Boundary Conditions (BCs) of the Plate
2.3. Load Case
2.4. Parameters Considered in This Study
- The parameters of geometrical and mechanical properties such as tf, ts, Ef, Es appear in the form . In this equation, Ef = 1.6 × 105 MPa, 2.4 × 105 MPa and 4.4 × 105 MPa, Es = 2.0 × 105 MPa, nf varies between 0 and 3 with an increment of 1, tf0 = 0.167 mm, ts = 2 mm, 3 mm and 4 mm.
- The BCs: 4S and 3S1F.
- Plate aspect ratio β: varies between 1 and 4 with increment of 1.
- Hole size d/b: varies between 0 and 0.7 with an increment of 0.1, in some case refines to 0.05.
- Hole position ex/b and ey/b. ex/b varies between 0.05 and 0.5β with an increment of 0.0625. ey/b varies between 0.5 and 0.9 with an increment of 0.025 for BCs of 4S and between 0.05 and 0.95 with an increment of 0.025 for BCs of 3S1F. In all conditions, the distance between hole’s edge and plate’s edge is no less than 0.05b.
3. The Theory of Composite Plate without Holes
3.1. The Transformed Flexural Rigidity Dt
- The method proposed by Pister to calculate the transformed flexural rigidity of the perfectly bonded layered plate is available to calculate the flexural rigidity of the pure steel plate.
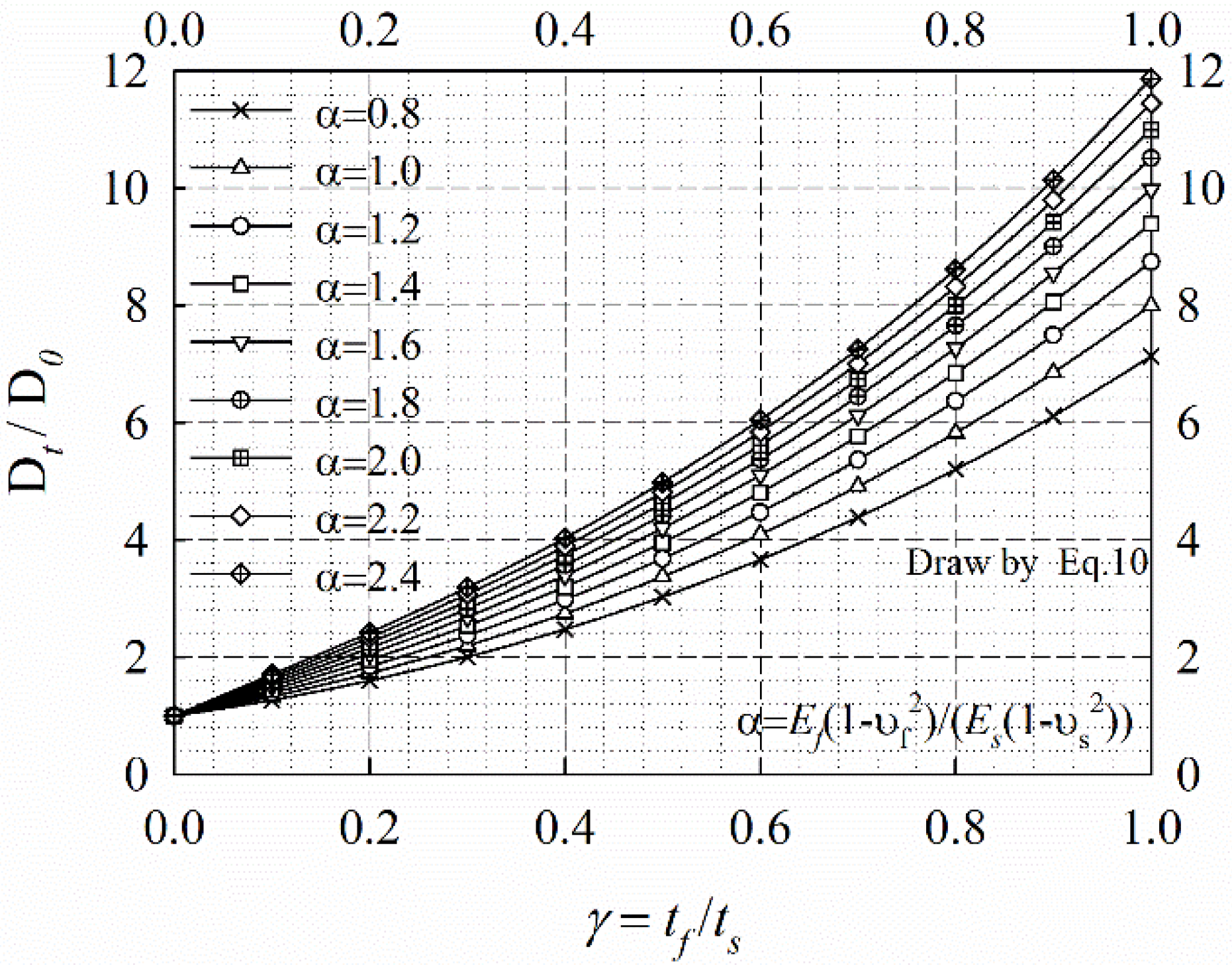
- When γ is in a range of 0 to 0.2 and α is in a range of 0.8 to 2.4, Dt/D0 almost had a linearly related with α and γ. For γ = 0.2, Dt/D0 will increase from 1.48 to 2.44 as α enlarges from 0.8 to 2.4.
- Dt/D0 will have a non-linear increase as γ is enlarged from 0.2 to 0.3.
- When γ is in a range of 0.3 to 1 and α; is in a range of 0.8 to 2.4: for a fixed α, Dt/D0 will had a cubic curvilinear increase as γ is enlarged from 0.3 to 1.0, and for a fixed γ, Dt/D0 will have a linear change as α enlarges from 0.8 to 2.4. When α = 0.8, Dt/D0 will increase from 2.05 to 7.47 as γ enlarges from 0.3 to 1, when α = 2.4, Dt/D0 will increase from 3.22 to 11.73 as γ enlarges from 0.3 to 1.
3.2. The Buckling Coefficient k
3.3. Comparison with the Experimental Results
3.4. The Proposed of Formula Correction
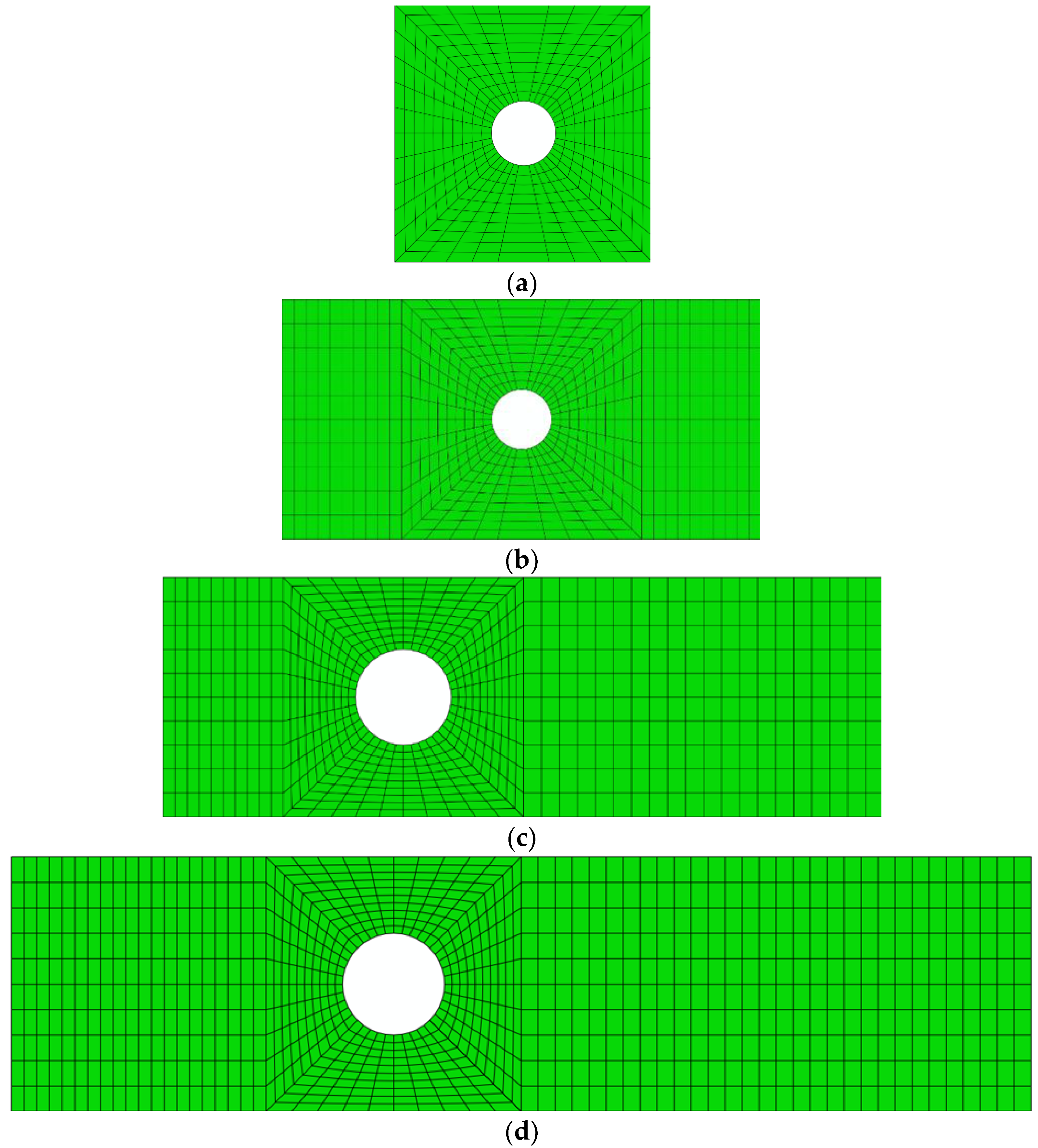
4. Finite Element Model and Verification
4.1. Method of Analysis
4.2. Model Description
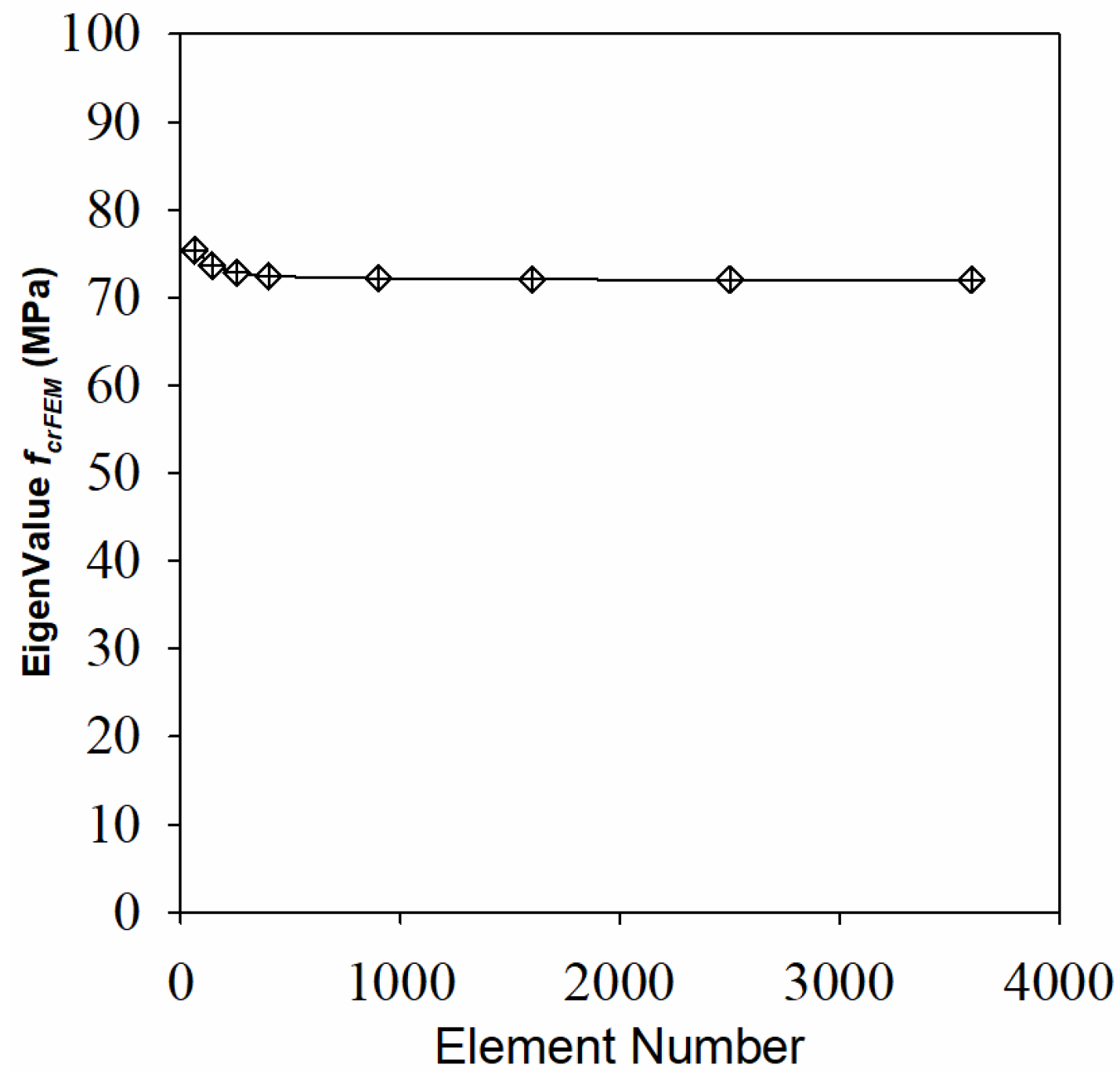
4.3. Model Verification
5. Discussion of the Results
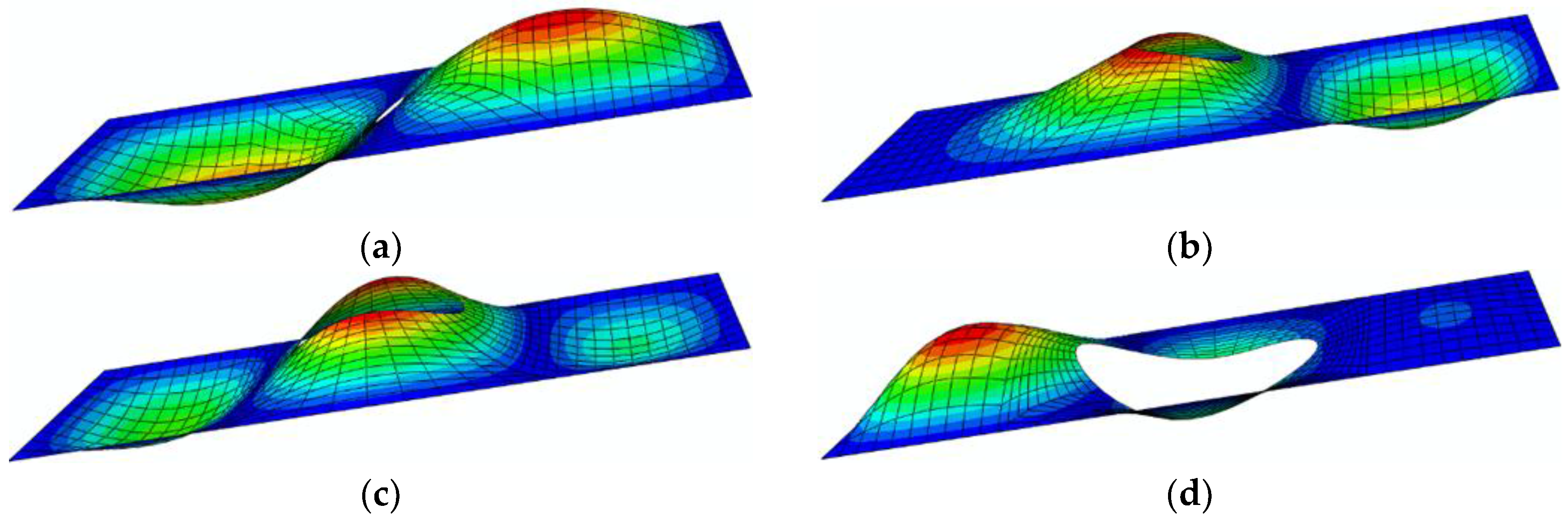
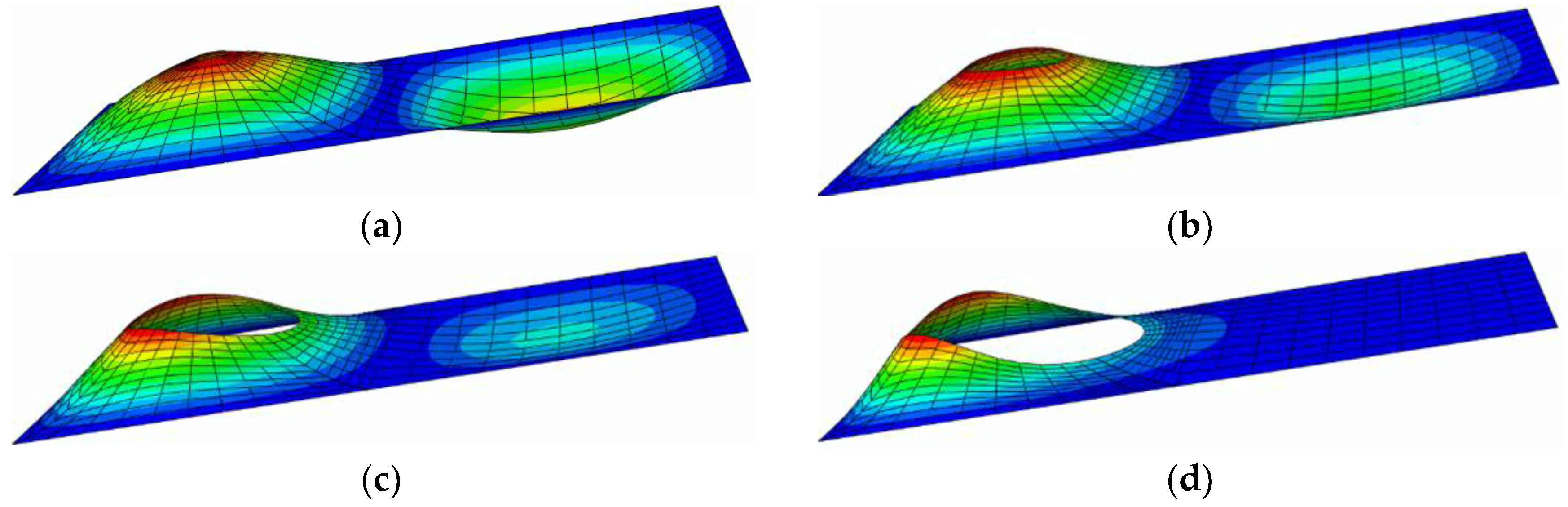
5.1. Buckling Mode Shapes
- From Figure 10a and Figure 11a, it can be seen that when d/b = 0.1, the buckling mode shapes are very close to plates without hole; and as d/b is enlarged, the max deformations of the plate are firstly centered near the hole then gradually transferred between hole and loading edge for 4S (seen from Figure 10b–d and Figure 11b–d).
- From Figure 12, it can be seen that as β increases, the deformations of the existing part have been basically unchanged, and the deformations of the adding part are very small.
- From Figure 13, it can be seen that the mode shapes are essentially unchanged as d/b is enlarged for plates with BCs of 3S1F.
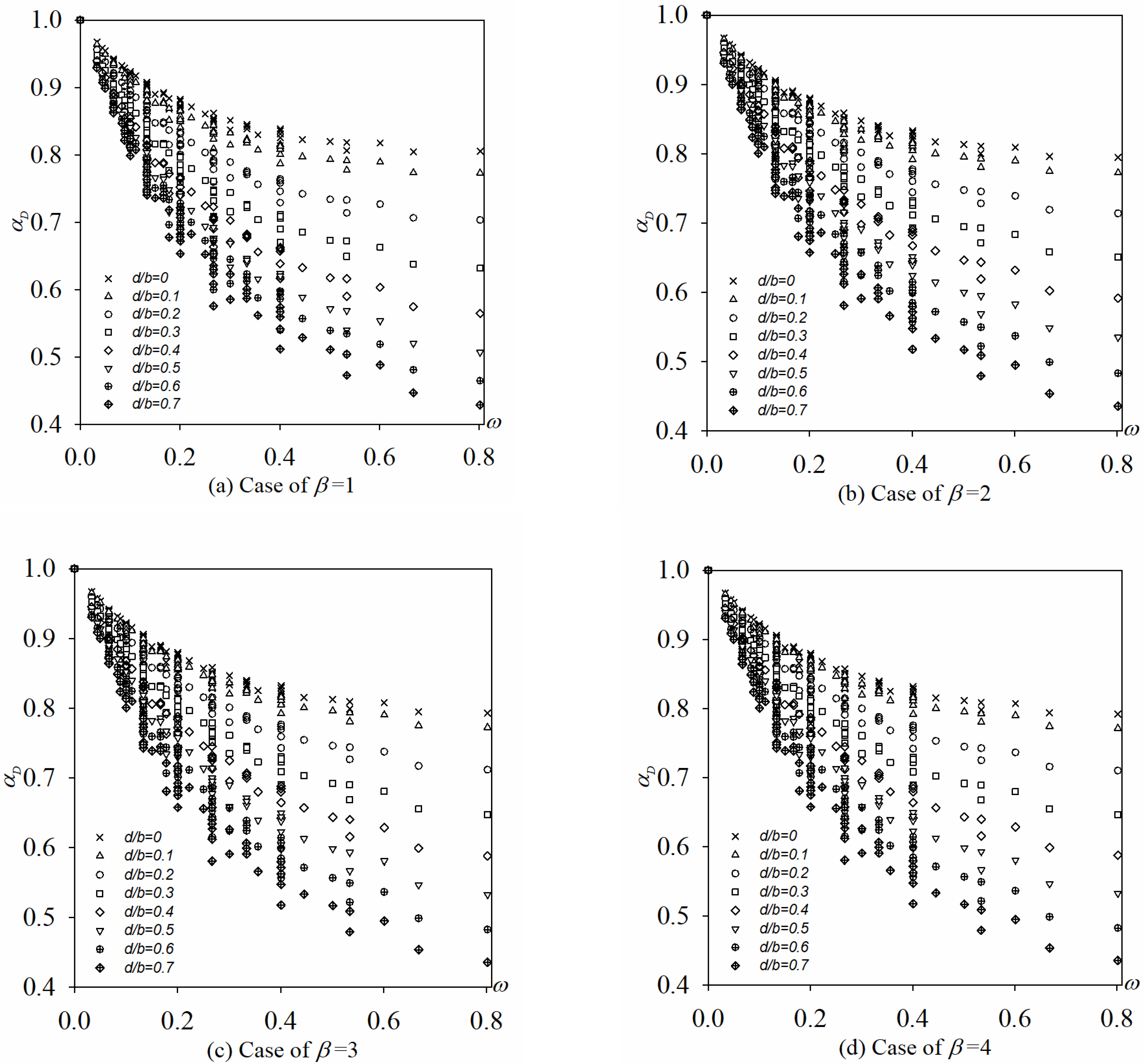
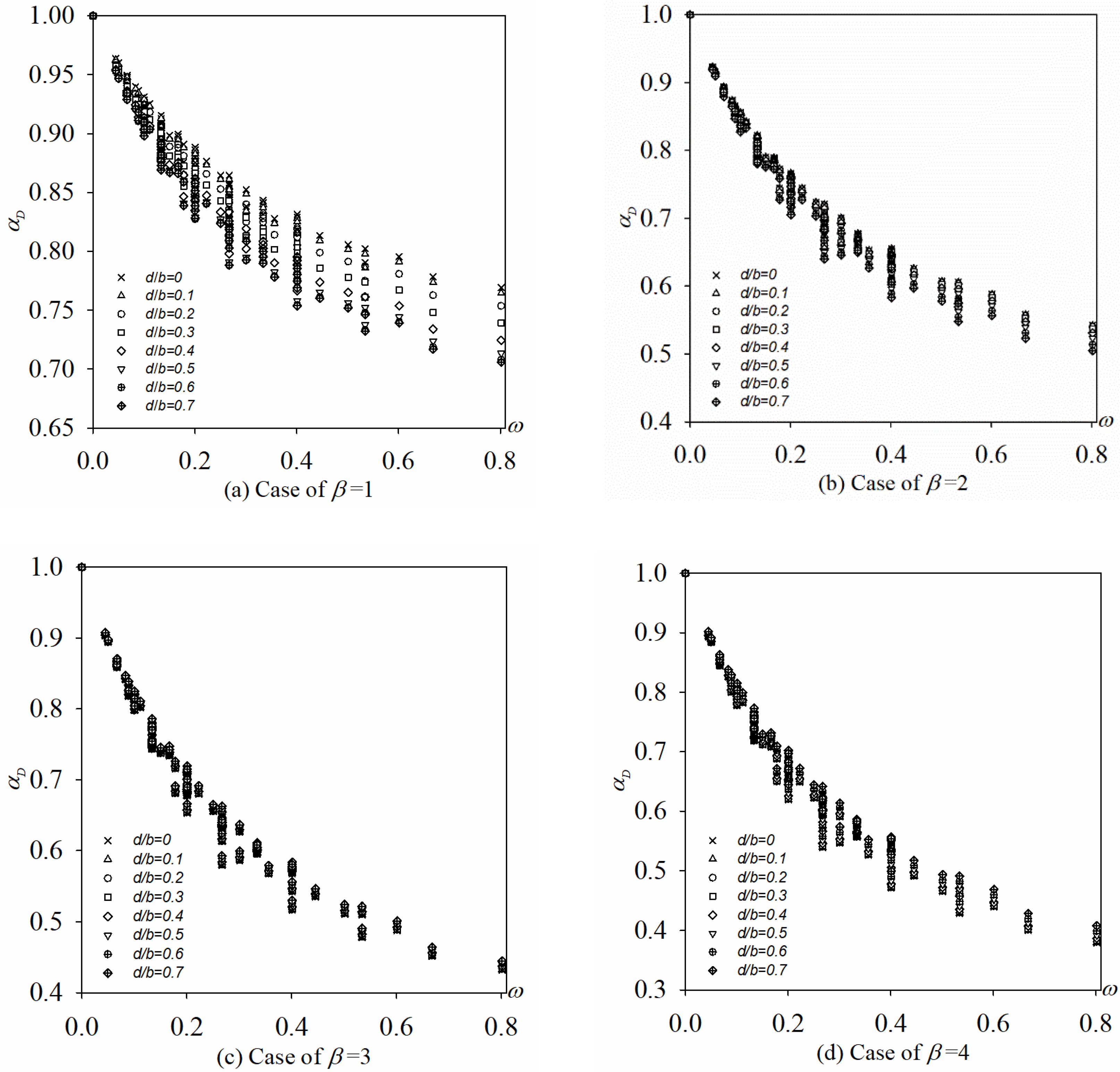
5.2. The Stiffness Modified Factor
5.3. The Buckling Coefficient
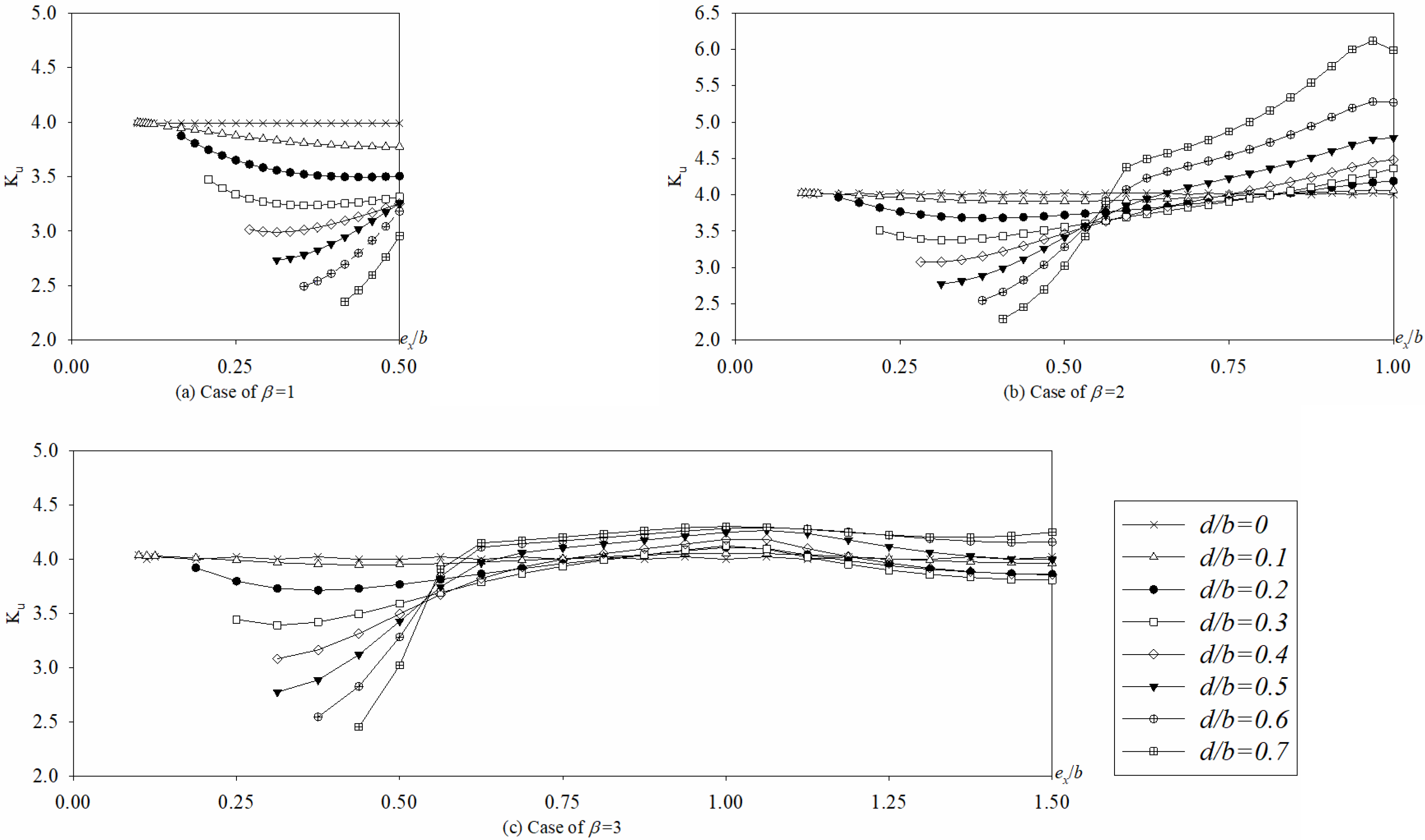
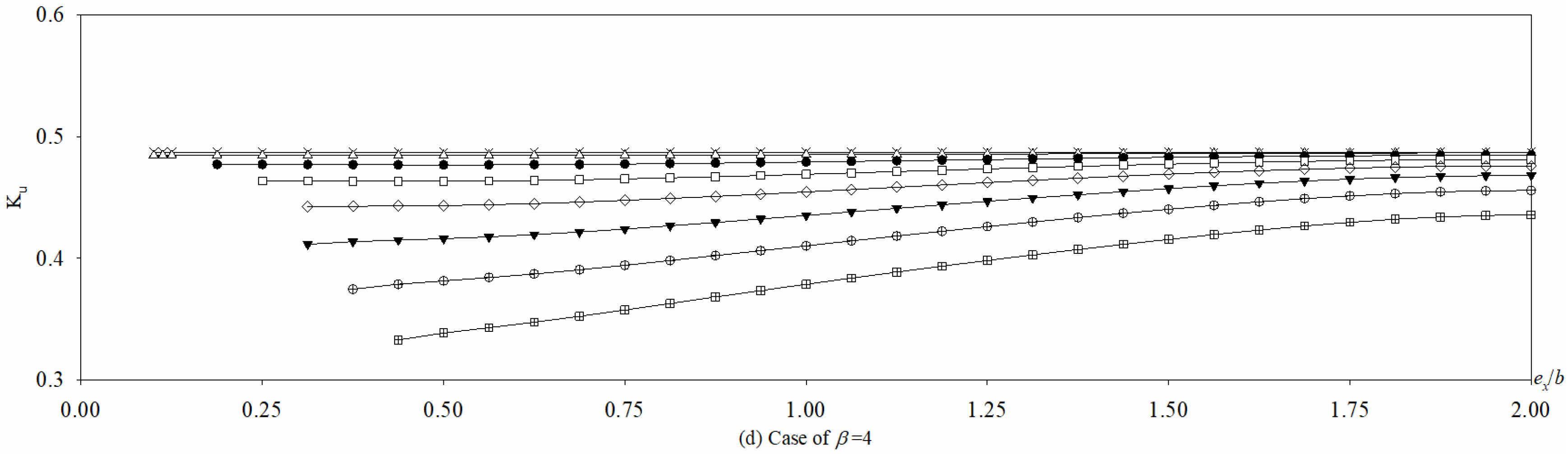
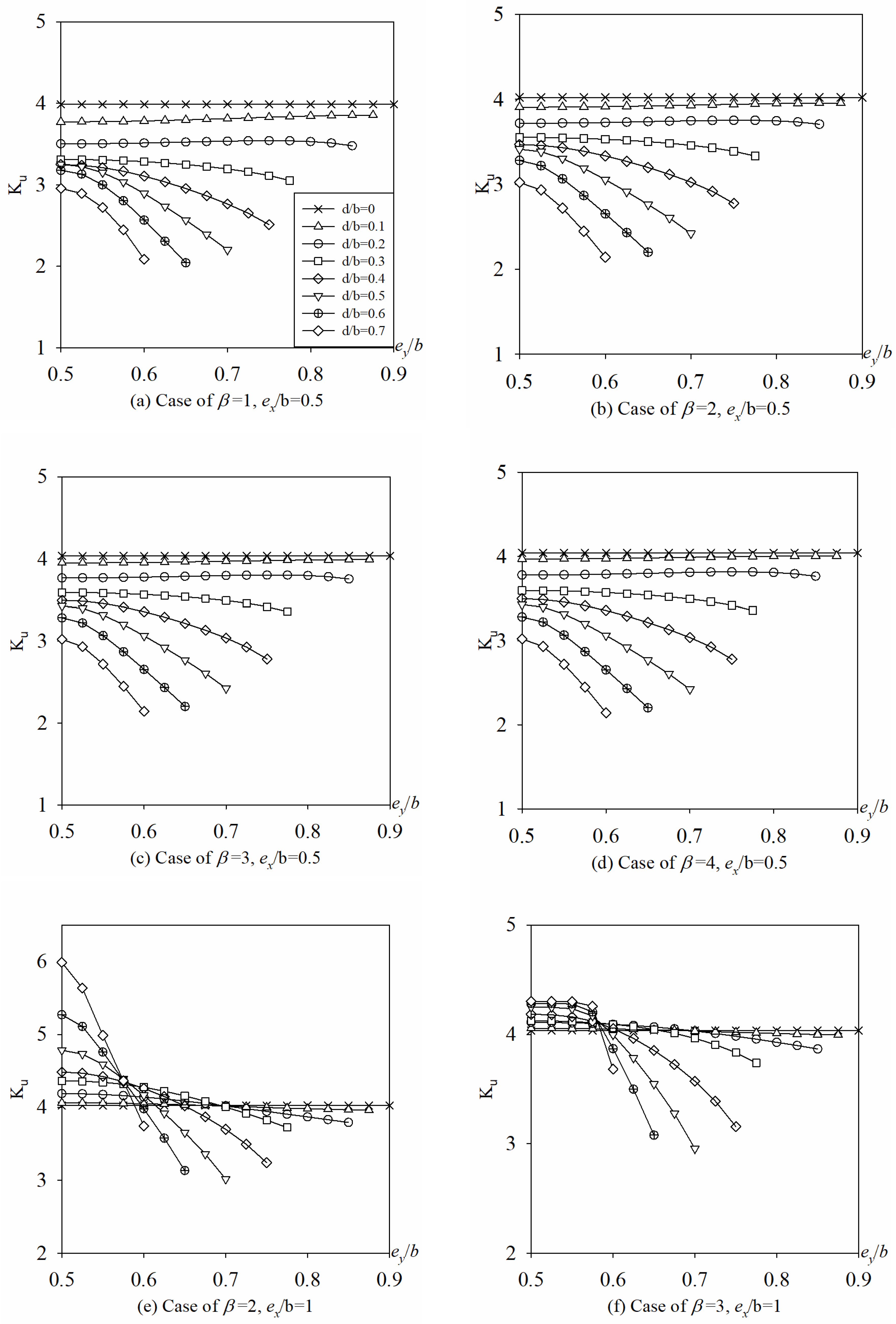
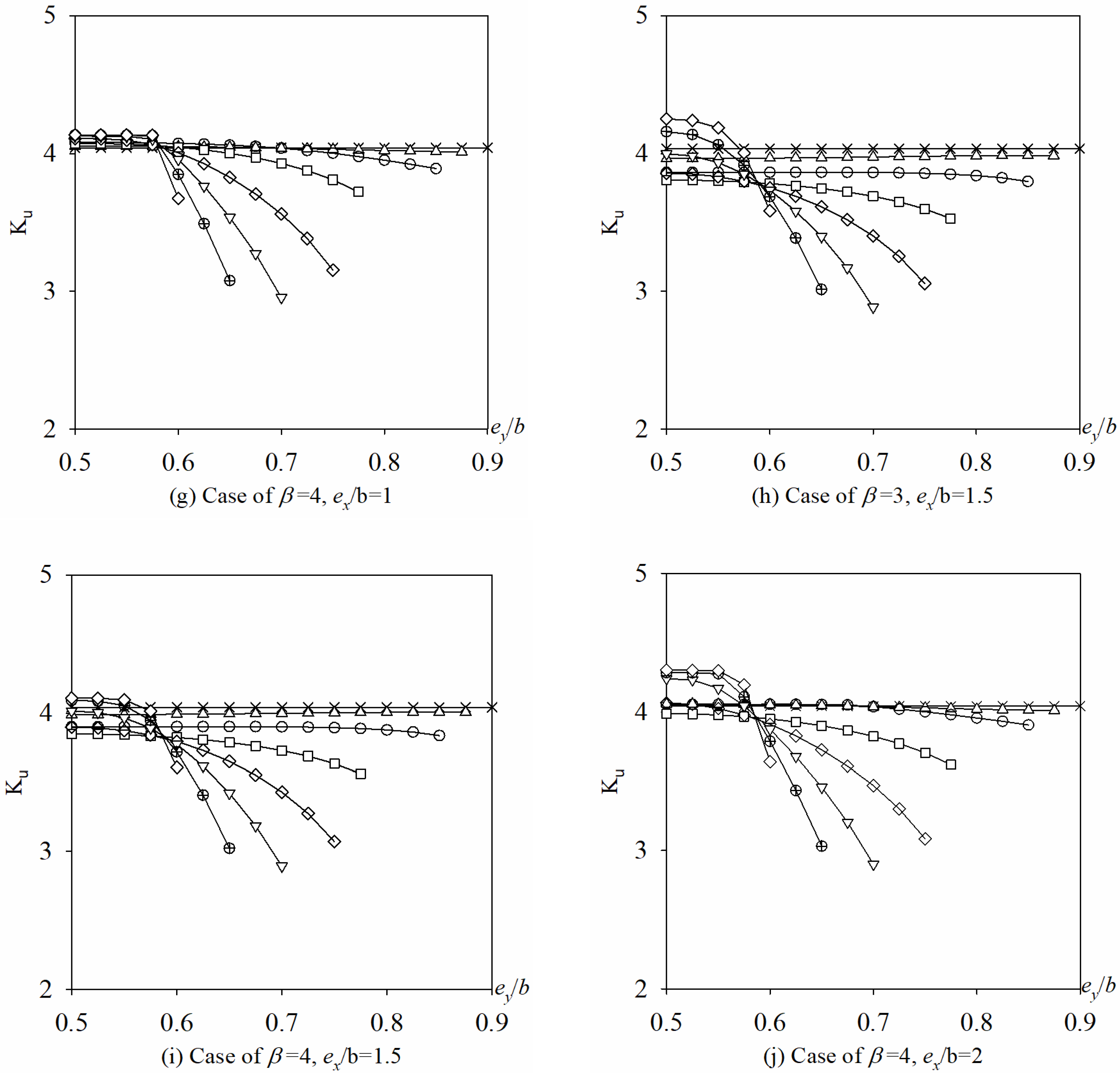
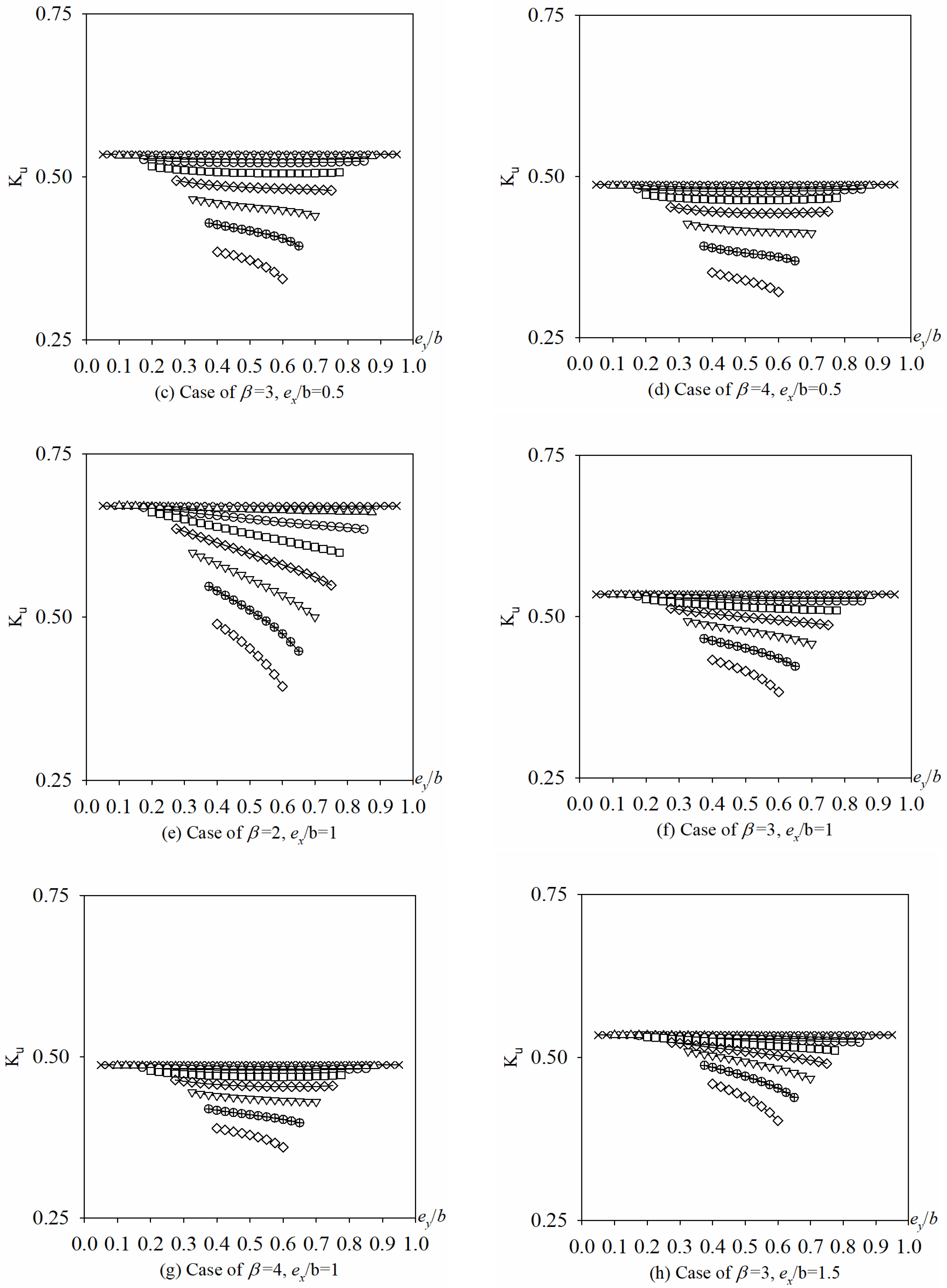
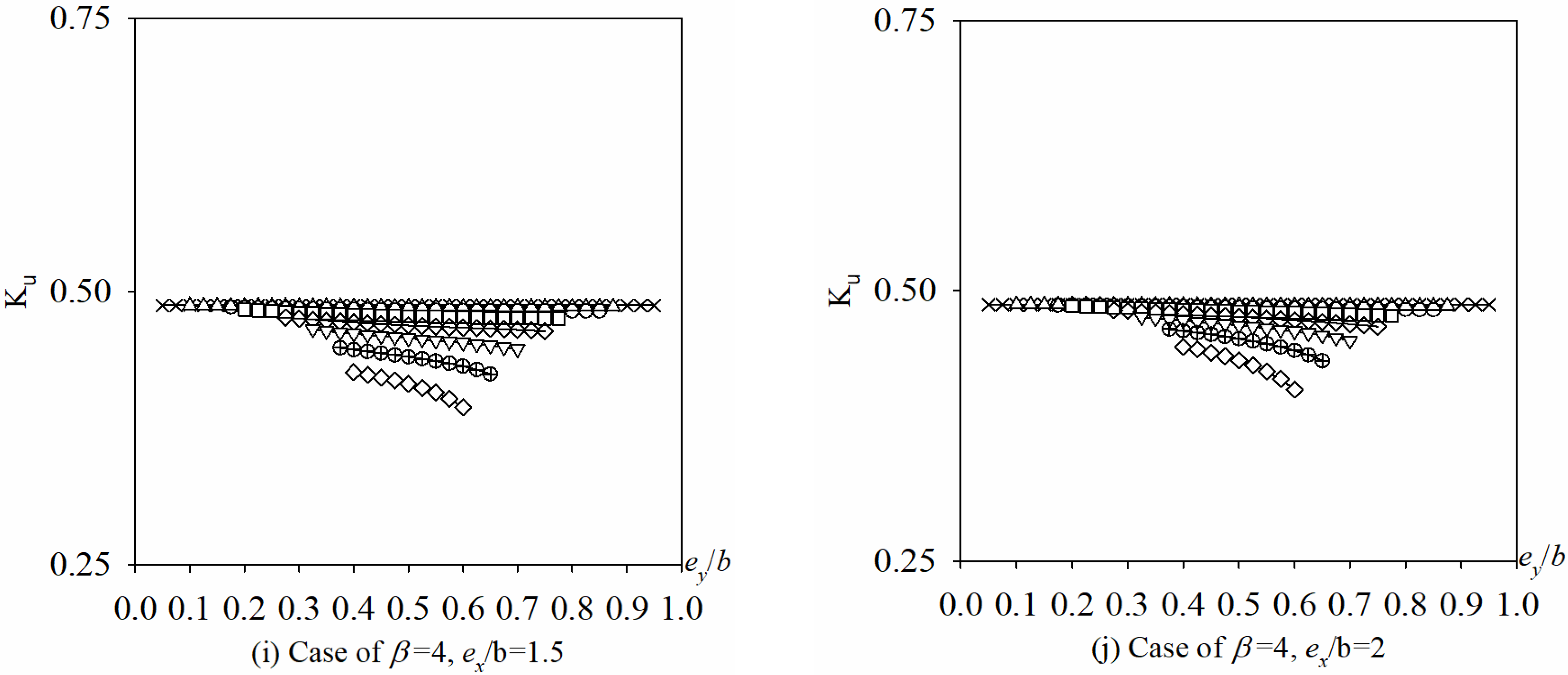
5.3.1. Hole Position Varying Along x-Axis
5.3.2. Hole Position Varying Along y-Axis
5.3.3. Hole Size d/b
6. An Example for the Usage of the Proposed Method
- a = b = 240 mm, d/b = 0.1, ex/b = 0.5, ex/b = 0.5, ts = 2.61 mm, tf0 = 0.167 mm, nf = 1, Es = 2.0 × 105 MPa, Ef = 2.6 × 105 MPa, υs = 0.3, υf = 0.25, fy = 287.8 MPa, BCs: 4S.
- tt = 2.61 + 0.167 = 2.777 (mm), , < 0.2,
- ,
- ω = = 0.0784, from Equation (20)
- = 90.13 (MPa).
- ,
7. Conclusions and Recommendations
- The theory of composite plate proposed by Pister is available to calculate the flexural rigidity of the pure steel plate and the perfectly bonded layered plate, but it should be modified when calculating the flexural rigidity of the perfectly bonded layered plate due to not considered the orthotropic properties of FRP.
- The buckling coefficient k needs to be modified as Ku which considers the change of plate aspect ratio β, hole sizes d/b and the hole position ex (or ey).
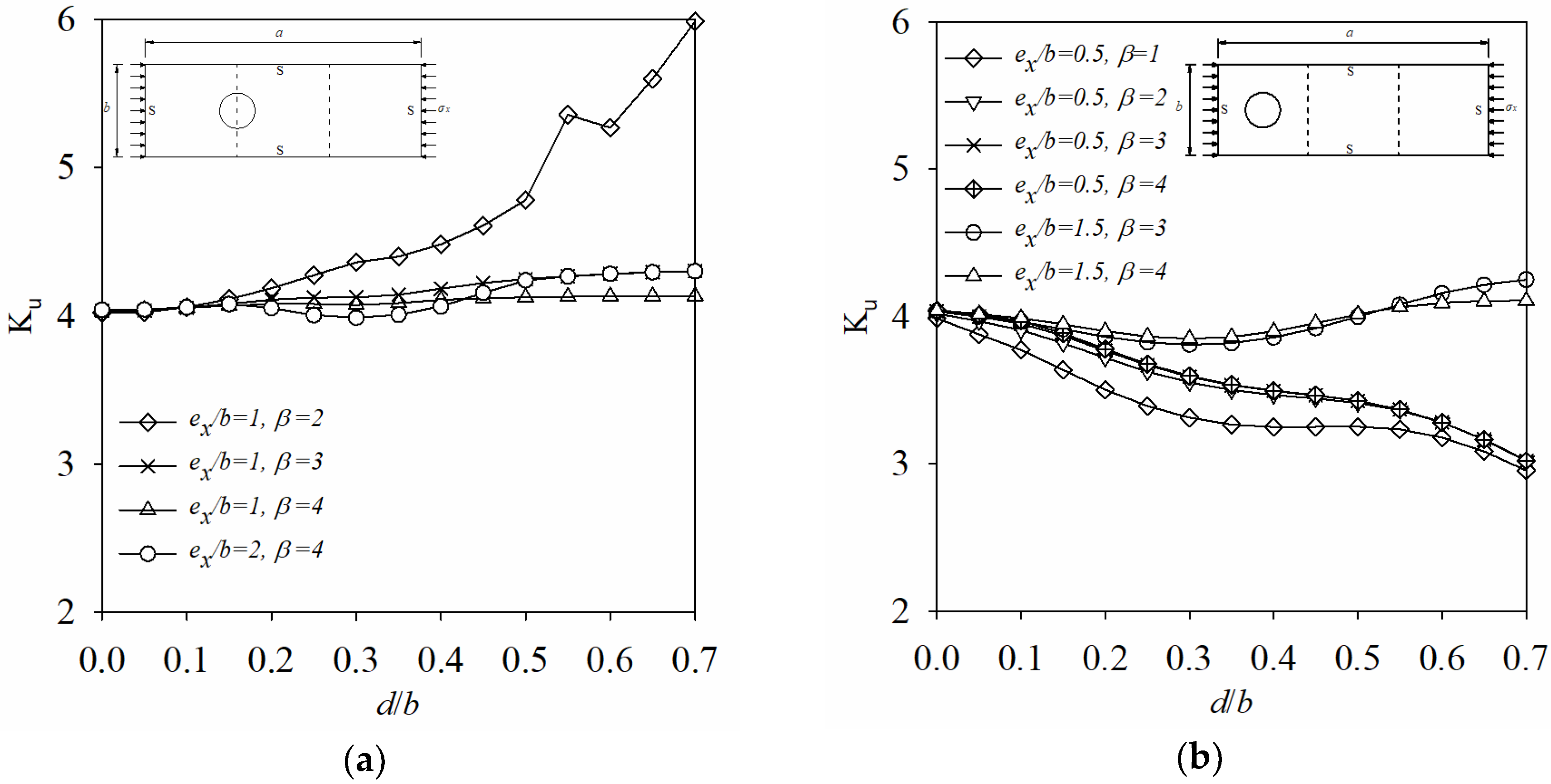
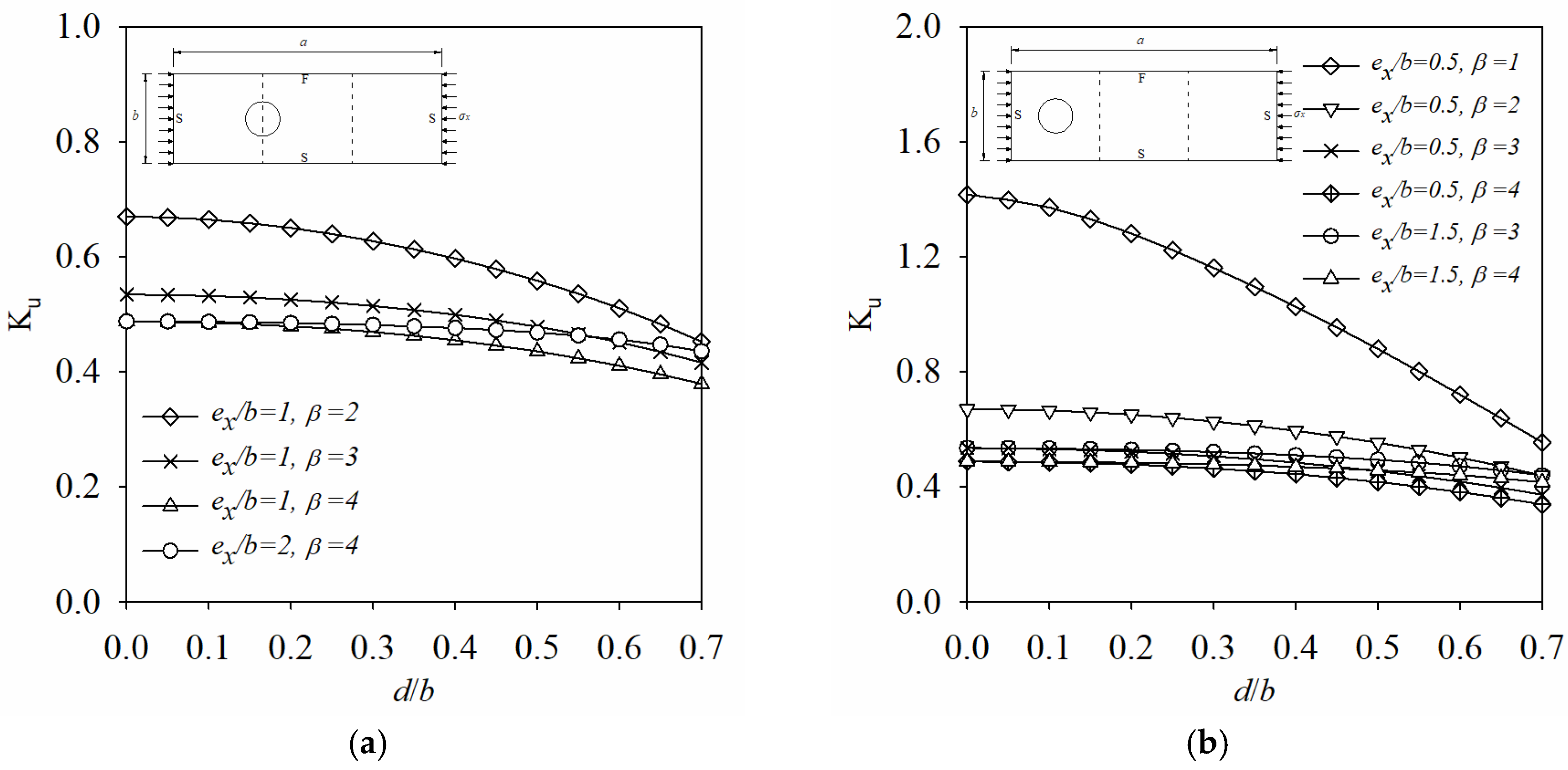
- For BCs of 4S, when ex/b is an integer, the buckling mode shapes change as d/b is enlarged, which cause some discontinuities in Ku vs. d/b curves (Figure 20). And for BCs of 3S1F, the buckling mode shapes is unchanged irrespective of d/b.
- For BCs of 4S, as ex/b is enlarged from 0 to 0.5, Ku decreases but gradual slow for d/b is 0.1, and first increases and then decrease for d/b is 0.2 and 0.3, and drastically increases for d/b is enlarged from 0.4 to 0.7. It means that when d/b is bigger than 0.4 and ex/b is less than 0.5, the buckling coefficient Ku is very unstable, so it should be avoided to place big hole too close to the loading edge in x-axis, especially when d/b is bigger than 0.4.
- For BCs of 3S1F, Ku is very small and stable irrespective of ex/b when β = 1, 2, and β = 3 (or 4) with d/b less than 0.4. When β = 3 or 4 and d/b is bigger than 0.4, Ku increases as the hole moves away from the loading edge towards its center along x-axis. Therefore, it is recommended to place the big hole (d/b ≥ 0.4) close to the middle area of the plate in x-axis, especially when d/b is bigger than 0.4.
- For a small hole size, there is little effect of the hole position ey/b on buckling coefficient Ku regardless of the BCs (4S or 3S1F), and that effect becomes more pronounced as d/b increases. So it is recommended to put the holes near the middle of the plate for 4S and the simple support edge for 3S1F in y-axis.
- As shown in Table 2, the buckling stresses and ultimate loads calculated by the proposed method of this paper combining with the winter equation are very close to the experimental values.
Acknowledgments
Author Contributions
Conflicts of Interest
Glossary/Nomenclature/Abbreviations
| a,b | the lengths in the longitudinal (transverse) directions |
| ts | the thicknesses of the steel plate |
| tf | the total thicknesses of FRP sheet |
| nf | FRP Layers’ number |
| tf0 | single layer of FRP sheet’s thickness |
| d | diameter of the hole |
| ex(y) | the distance along x(y)-axis from the center of the hole to the left(bottom) edge |
| ES,Ef | the elastic modulus of steel and FRP |
| νs,νf | the Poisson ratio of steel and FRP |
| β | Plate aspect ratio, equal to b/a |
| k | the buckling coefficient |
| the flexural rigidity of plate without FRP and strengthened with FRP | |
| fcr | the critical stress of the plate |
| Pcr | the critical load of the plate |
| Pu | the ultimate load of the plate |
| α | reinforcement index of FRP, calculated by Equation (8) |
| γ | reinforcement index of FRP, calculated by Equation (9) |
| ω | reinforcement index of FRP, calculated by Equation (16) |
| Ku | the modified buckling coefficient |
References
- El-Sawy, K.M.; Nazmy, A.S. Effect of aspect ratio on the elastic buckling of uniaxially loaded plates with eccentric holes. Thin Walled Struct. 2001, 39, 983–998. [Google Scholar] [CrossRef]
- Shanmugam, N.E.; Thevendran, V.; Tan, Y.H. Design Formula for Axially Compressed Perforated Plates. Thin Walled Struct. 1999, 34, 1–20. [Google Scholar] [CrossRef]
- Brown, C.J.; Yettram, A.L. The elastic stability of square perforated plates under combinations of bending, shear and direct load. Thin Walled Struct. 1986, 4, 239–246. [Google Scholar] [CrossRef]
- Brown, C.J.; Yettram, A.L.; Burnett, M. Stability of plates with rectangular holes. J. Struct. Eng. 1987, 113, 1111–1116. [Google Scholar] [CrossRef]
- Cheng, B.; Zhao, J. Strengthening of Perforated Plates under Uniaxial Compression: Buckling Analysis. Thin Walled Struct. 2010, 48, 905–914. [Google Scholar] [CrossRef]
- Shaat, A.; Fam, A. Fiber-Element Model for Slender HSS Columns Retrofitted with Bonded High-Modulus Composites. J. Struct. Eng. 2007, 133, 85–95. [Google Scholar] [CrossRef]
- Shaat, A.; Fam, A. Axial loading tests on short and long hollow structural steel columns retrofitted using carbon fibre reinforced polymers. Can. J. Civ. Eng. 2006, 33, 458–470. [Google Scholar] [CrossRef]
- Shaat, A.; Fam, A. Strengthening of short HSS steel columns using FRP sheets. In Proceedings of the 4th International Conference Advanced Composite Materials Bridges Structures, Calgary, AB, Canada, 20–23 July 2004. [Google Scholar]
- Shaat, A.; Fam, A. Control of overall buckling of HSS slender steel columns using CFRP plates. In Proceedings of the First Asia Pacific conference FRP Structures (APFIS2007), Hong Kong, China, 12–14 December 2007; pp. 993–998. [Google Scholar]
- Harries, K.A.; Peck, A.J.; Abraham, E.J. Enhancing stability of structural steel sections using FRP. Thin Walled Struct. 2009, 47, 1092–1101. [Google Scholar] [CrossRef]
- Haedir, J.; Zhao, X.-L. Design of short CFRP-reinforced steel tubular columns. J. Construct. Steel Res. 2011, 67, 497–509. [Google Scholar] [CrossRef]
- Bambach, M.R. Axial Capacity and Crushing of Thin-Walled Metal, Fibre–epoxy and Composite Metal–fibre Tubes. Thin Walled Struct. 2010, 48, 440–452. [Google Scholar] [CrossRef]
- Bambach, M.R.; Elchalakani, M. Plastic Mechanism Analysis of Steel SHS Strengthened with CFRP under Large Axial Deformation. Thin Walled Struct. 2007, 45, 159–170. [Google Scholar] [CrossRef]
- Bambach, M.R.; Jama, H.H.; Elchalakani, M. Axial Capacity and Design of Thin-Walled Steel SHS Strengthened with CFRP. Thin Walled Struct. 2009, 47, 1112–1121. [Google Scholar] [CrossRef]
- Pister, K.S.; Dong, S.B. Elastic bending of layered plates. J. Eng. Mech. Div. 1959, 85, 1–10. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; McGraw-Hill Book Company: New York, NY, USA, 1961. [Google Scholar]
- Gerstle, K.H. Basic Structural Design; McGraw-Hill Book Company: New York, NY, USA, 1967. [Google Scholar]
- Bambach, M. 6-Strengthening of Thin-Walled (Hollow) Steel Sections Using Fibre-Reinforced Polymer (FRP) Composites. In Rehabilitation of Metallic Civil Infrastructure Using Fiber Reinforced Polymer (FRP) Composites, 1st ed.; Karbhari, V.M., Ed.; Woodhead Publishing: Cambridge, UK, 2014; pp. 140–168. ISBN 9780857096654. [Google Scholar]
- Tao, X.; Cao, S. Ultimate capacity of uniaxially compressed perforated steel plates strengthened by using CFRPs. In Civil, Architecture Environmental Engineering; CRC Press/Balkema: Leiden, The Netherlands, 2017; Volume 1, pp. 483–488. [Google Scholar] [CrossRef]
- Narayanan, R.; Chow, F.Y. Ultimate Capacity of Uniaxially Compressed Perforated Plates. Thin Walled Struct. 1984, 2, 241–264. [Google Scholar] [CrossRef]

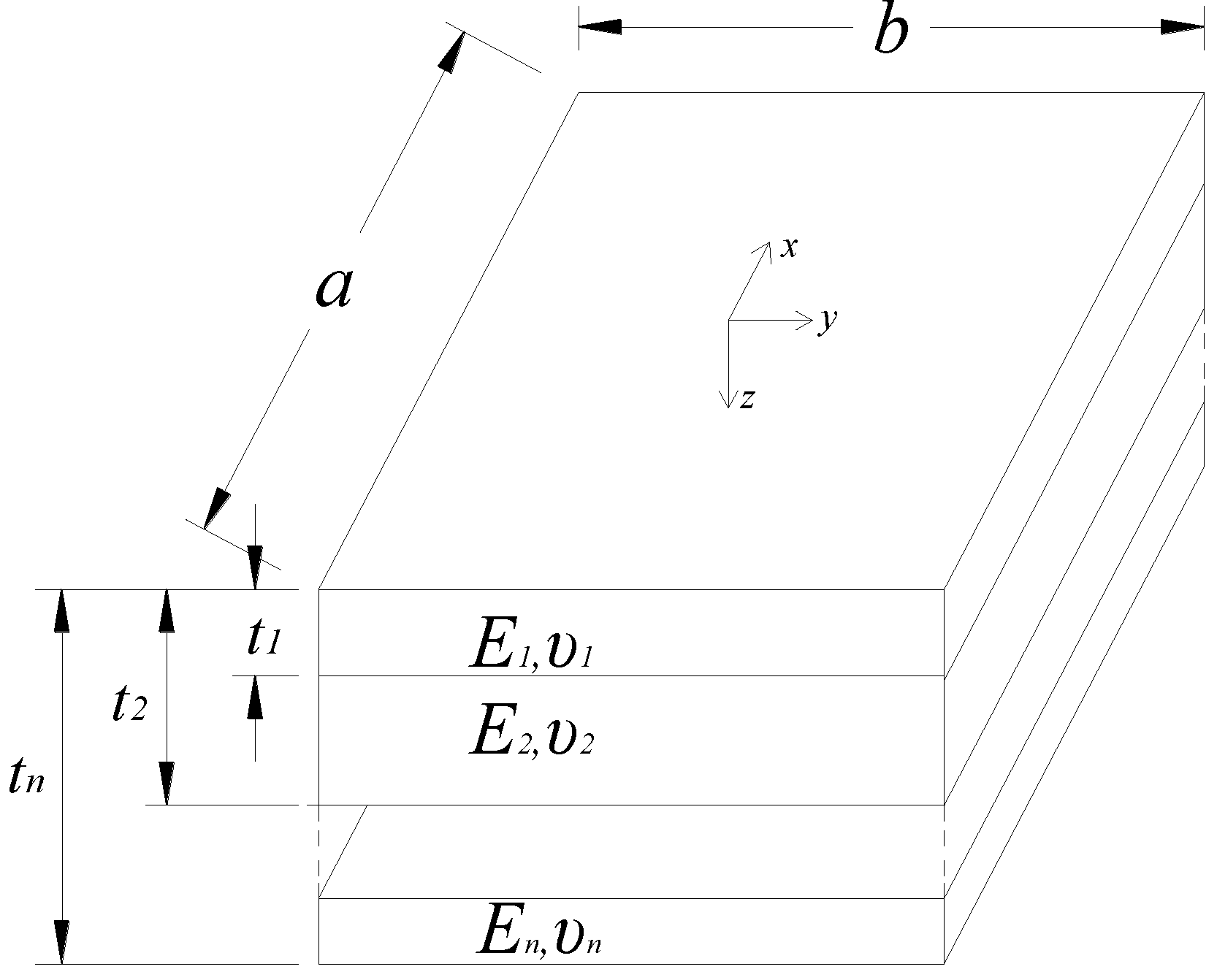







| a (mm) | b (mm) | ts (mm) | tf0 (mm) | Es (MPa) | Ef (MPa) | υs | υf | fy (MPa) | BCs |
|---|---|---|---|---|---|---|---|---|---|
| 240 | 240 | 2.61 | 0.167 | 2.0 × 105 | 2.6 × 105 | 0.3 | 0.25 | 287.9 | 4S |
| NO. | d/b | α | γ(×10-2) | D0 (×105) | DtEq.10 (×105) | DtEq.11 (×105) | PcrExp | fcrExp. | fcrEq.17 | fcrEq.23 | fcrFEM | αD | Ku | fcrCal | PuExp | PuCal |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1.225 | 0 | 3.35 | 3.35 | 3.35 | 55.83 | 89.13 | 88.08 | 88.08 | 87.79 | 1.000 | 4.00 | 88.08 | 94.02 | 87.59 |
| 2 | 0.1 | 1.225 | 0 | 3.35 | 3.35 | 3.35 | 53.78 | 85.85 | 83.08 * | 83.08 * | 83.06 | 1.000 | 3.77 | 83.08 | 90.11 | 85.41 |
| 3 | 0.3 | 1.225 | 0 | 3.35 | 3.35 | 3.35 | 47.89 | 76.45 | 72.95 * | 72.95 * | 72.93 | 1.000 | 3.31 | 72.95 | 79.66 | 80.71 |
| 4 | 0.5 | 1.225 | 0 | 3.35 | 3.35 | 3.35 | 45.12 | 72.03 | 71.62 * | 71.62 * | 71.60 | 1.000 | 3.25 | 71.62 | 74.44 | 80.06 |
| 5 | 0 | 1.225 | 6.4 | 3.35 | 4.18 | 4.14 | 64.88 | 97.34 | 103.24 | 102.25 | 95.66 | 0.946 | 4.00 | 96.76 | 101.86 | 97.03 |
| 6 | 0.1 | 1.225 | 6.4 | 3.35 | 4.18 | 4.14 | 61.90 | 92.87 | 97.39 * | 96.45 * | 89.84 | 0.934 | 3.77 | 90.13 | 96.64 | 94.13 |
| 7 | 0.3 | 1.225 | 6.4 | 3.35 | 4.18 | 4.14 | 58.28 | 87.45 | 85.51 * | 84.68 * | 76.08 | 0.910 | 3.31 | 77.13 | 92.72 | 87.99 |
| 8 | 0.5 | 1.225 | 6.4 | 3.35 | 4.18 | 4.14 | 50.54 | 75.83 | 83.95 * | 83.15 * | 72.44 | 0.887 | 3.25 | 73.77 | 78.35 | 86.30 |
| d/b | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
|---|---|---|---|---|---|---|---|---|
| m | 0.69 | 0.76 | 0.92 | 1.09 | 1.23 | 1.34 | 1.40 | 1.47 |
| n | −0.74 | −0.83 | −1.04 | −1.25 | −1.44 | −1.59 | −1.69 | −1.79 |
| R2 | 0.91 | 0.92 | 0.93 | 0.94 | 0.94 | 0.95 | 0.95 | 0.95 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, X.; Cao, S.; Zhang, L. Elastic Stability of Perforated Plates Strengthened with FRP under Uniaxial Compression. Appl. Sci. 2017, 7, 1188. https://doi.org/10.3390/app7111188
Tao X, Cao S, Zhang L. Elastic Stability of Perforated Plates Strengthened with FRP under Uniaxial Compression. Applied Sciences. 2017; 7(11):1188. https://doi.org/10.3390/app7111188
Chicago/Turabian StyleTao, Xin, Shuangyin Cao, and Long Zhang. 2017. "Elastic Stability of Perforated Plates Strengthened with FRP under Uniaxial Compression" Applied Sciences 7, no. 11: 1188. https://doi.org/10.3390/app7111188
APA StyleTao, X., Cao, S., & Zhang, L. (2017). Elastic Stability of Perforated Plates Strengthened with FRP under Uniaxial Compression. Applied Sciences, 7(11), 1188. https://doi.org/10.3390/app7111188