Virtual Analog Models of the Lockhart and Serge Wavefolders †
Abstract
:1. Introduction
2. The Lockhart Wavefolder
2.1. Circuit Analysis
2.2. Explicit Formulation
2.3. Model Discretization and Evaluation
3. The Serge Middle Wave Multiplier
3.1. Model Equivalence
4. Wavefolding in the Digital Domain
4.1. Evaluating the Lambert-W Function
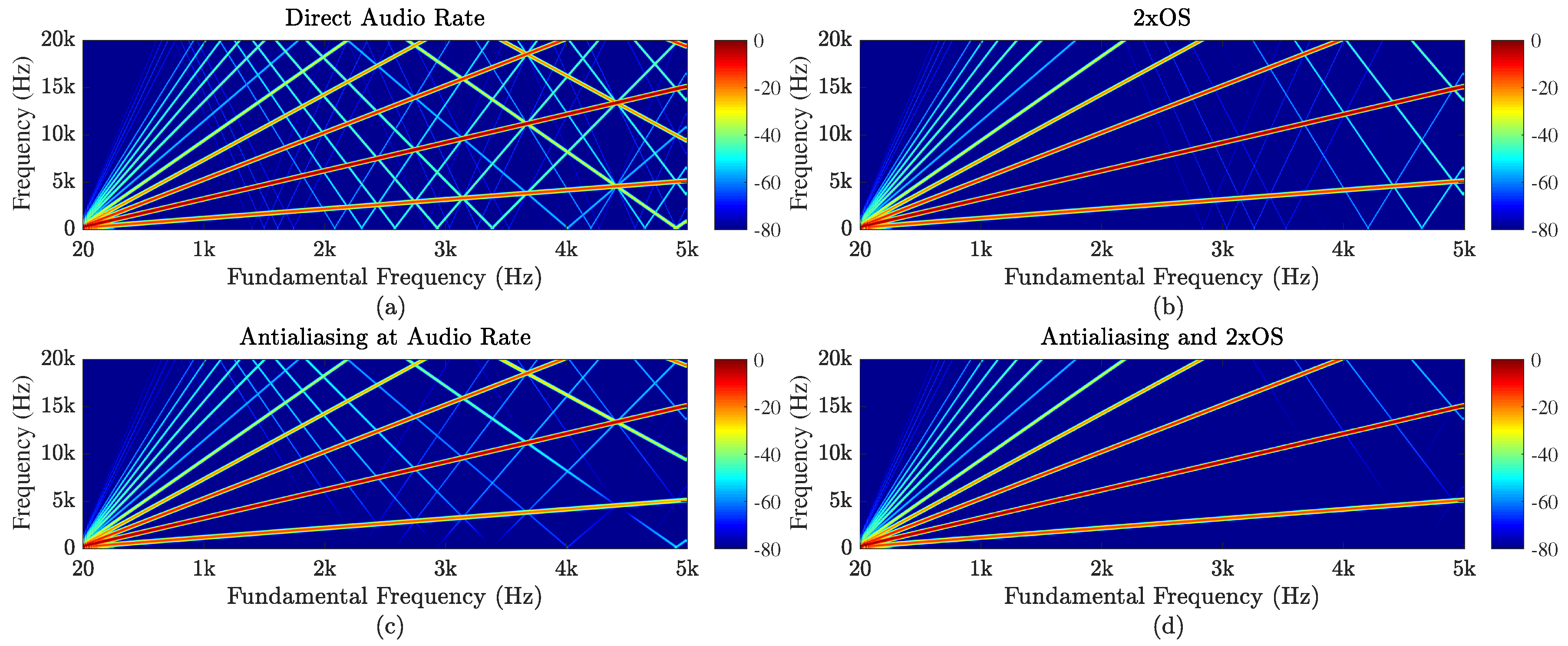
4.2. Aliasing Considerations
5. Results
5.1. Frequency-Domain Behavior
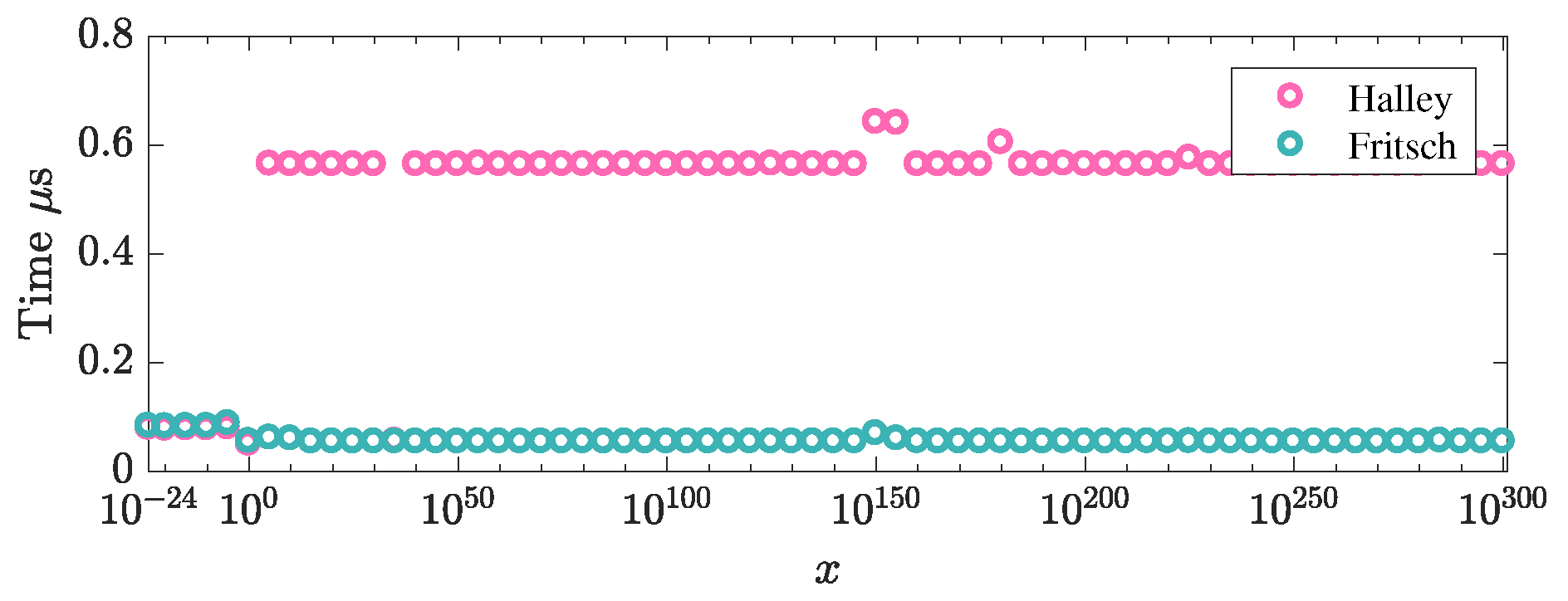
5.2. Computational Costs
6. Practical Synthesis Usage
7. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Le Brun, M. Digital waveshaping synthesis. J. Audio Eng. Soc. 1979, 27, 250–266. [Google Scholar]
- Risset, J.C. An Introductory Catalog of Computer Synthesized Sounds; Bell Laboratories: Murray Hill, NJ, USA, 1969. [Google Scholar]
- Schaefer, R.A. Electronic musical tone production by nonlinear waveshaping. J. Audio Eng. Soc. 1970, 18, 413–417. [Google Scholar]
- Arfib, D. Digital synthesis of complex spectra by means of multiplication of nonlinear distorted sine waves. In Proceedings of the 59th Convention of the Audio Engineering Society, Hamburg, Germany, 28 February–3 March 1978. [Google Scholar]
- Roads, C. A tutorial on non-linear distortion or waveshaping synthesis. Comput. Music J. 1979, 3, 29–34. [Google Scholar] [CrossRef]
- Chowning, J.M. The synthesis of complex audio spectra by means of frequency modulation. J. Audio Eng. Soc. 1973, 21, 526–534. [Google Scholar]
- Ishibashi, M. Electronic Musical Instrument. Patent No. 4,658,691, 21 April 1987. [Google Scholar]
- Kleimola, J. Audio synthesis by bitwise logical modulation. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Espoo, Finland, 1–4 September 2008. [Google Scholar]
- Timoney, J.; Lazzarini, V.; Lysaght, T. A modified FM synthesis approach to bandlimited signal generation. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Espoo, Finland, 1–4 September 2008. [Google Scholar]
- Kleimola, J.; Lazzarini, V.; Timoney, J.; Välimäki, V. Vector phaseshaping synthesis. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Paris, France, 19–23 September 2011. [Google Scholar]
- Pakarinen, J.; Yeh, D.T. A review of digital techniques for modeling vacuum-tube guitar amplifiers. Comput. Music J. 2009, 33, 85–100. [Google Scholar] [CrossRef]
- Hobbs, R.V.; Snoddy, G.T. Tone Modifier for Electrically Amplified Electro-Mechanically Produced Musical Tones. Patent No. 3,213,181, 19 October 1965. [Google Scholar]
- Yeh, D.T.; Abel, J.S.; Smith, J.O., III. Simplified, physically-informed models of distortion and overdrive guitar effects pedals. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Bordeaux, France, 10–15 September 2007. [Google Scholar]
- Werner, K.J.; Nangia, V.; Smith, J.O., III; Abel, J.S. Resolving wave digital filters with multiple/multiport nonlinearities. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Trondheim, Norway, 30 November–3 December 2015. [Google Scholar]
- Buchla Electronic Musical Instruments. The History of Buchla. Available online: https://buchla.com/history/ (accessed on 3 October 2017).
- Parker, J.; D’Angelo, S. A digital model of the Buchla lowpass-gate. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Maynooth, Ireland, 2–5 September 2013. [Google Scholar]
- Esqueda, F.; Pöntynen, H.; Välimäki, V.; Parker, J.D. Virtual analog Buchla 259 wavefolder. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Edinburgh, UK, 5–9 September 2017. [Google Scholar]
- Moog, R.A. A voltage-controlled low-pass high-pass filter for audio signal processing. In Proceedings of the 7th Convention of the Audio Engineering Society, New York, NY, USA, 11–15 October 1965. [Google Scholar]
- Stilson, T.; Smith, J.O., III. Analyzing the Moog VCF with considerations for digital implementation. In Proceedings of the International Computer Music Conference, Hong Kong, China, 19–24 August 1996. [Google Scholar]
- Huovilainen, A. Non-linear digital implementation of the Moog ladder filter. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Naples, Italy, 5–8 October 2004. [Google Scholar]
- Hélie, T. On the use of Volterra series for real-time simulations of weakly nonlinear analog audio devices: application to the Moog ladder filter. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Montreal, QC, Canada, 18–20 September 2006. [Google Scholar]
- D’Angelo, S.; Välimäki, V. Generalized Moog ladder filter: Part II—Explicit nonlinear model through a novel delay-free loop implementation method. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1873–1883. [Google Scholar] [CrossRef]
- Civolani, M.; Fontana, F. A nonlinear digital model of the EMS VCS3 voltage-controlled filter. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Espoo, Finland, 1–4 September 2008. [Google Scholar]
- Fontana, F.; Civolani, M. Modeling of the EMS VCS3 voltage-controlled filter as a nonlinear filter network. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 760–772. [Google Scholar] [CrossRef]
- Huovilainen, A. Design of a Scalable Polyphony-MIDI Synthesizer for a Low Cost DSP. Master’s Thesis, Aalto University, Espoo, Finland, 2010. [Google Scholar]
- Rest, M.; Parker, J.; Werner, K.J. WDF modeling of a Korg MS-50 based non-linear diode bridge VCF. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Edinburgh, UK, 5–7 September 2017. [Google Scholar]
- Yeh, D.T.; Abel, J.S.; Smith, J.O., III. Simulation of the diode limiter in guitar distortion circuits by numerical solution of ordinary differential equations. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Bordeaux, France, 10–15 September 2007. [Google Scholar]
- De Paiva, R.C.D.; Pakarinen, J.; Välimäki, V.; Tikander, M. Real-time audio transformer emulation for virtual tube amplifiers. EURASIP J. Adv. Signal Process. 2011, 2011, 1–15. [Google Scholar]
- Dunkel, W.R.; Rest, M.; Werner, K.J.; Olsen, M.J.; Smith, J.O., III. The Fender Bassman 5F6-A family of preamplifier circuits—A wave digital filter case study. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Brno, Czech Republic, 5–9 September 2016. [Google Scholar]
- Huovilainen, A. Enhanced digital models for analog modulation effects. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Madrid, Spain, 20–22 September 2005. [Google Scholar]
- Holters, M.; Zölzer, U. Physical modelling of a wah-wah effect pedal as a case study for application of the nodal DK method to circuits with variable parts. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Paris, France, 19–23 September 2011. [Google Scholar]
- Eichas, F.; Fink, M.; Holters, M.; Zölzer, U. Physical modeling of the MXR Phase 90 guitar effect pedal. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Erlangen, Germany, 1–5 September 2014. [Google Scholar]
- Parker, J. A simple digital model of the diode-based ring modulator. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Paris, France, 19–23 September 2011. [Google Scholar]
- Werner, K.J.; Abel, J.S.; Smith, J.O. A physically-informed, circuit-bendable, digital model of the Roland TR-808 bass drum circuit. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Erlangen, Germany, 1–5 September 2014. [Google Scholar]
- Werner, K.J.; Abel, J.S.; Smith, J.O. The TR-808 cymbal: A physically-informed, circuit-bendable, digital model. In Proceedings of the International Computer Music Conference (ICMC)/Sound and Music Computing Conference (SMC), Athens, Greece, 14–20 September 2014. [Google Scholar]
- De Paiva, R.C.D.; Pakarinen, J.; Välimäki, V. Reduced-complexity modeling of high-order nonlinear audio systems using swept-sine and principal component analysis. In Proceedings of the 45th Audio Engineering Society Conference: Applications of Time-Frequency Processing in Audio, Helsinki, Finland, 1–4 March 2012. [Google Scholar]
- Eichas, F.; Zölzer, U. Black-box modeling of distortion circuits with block-oriented models. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Brno, Czech Republic, 5–9 September 2016. [Google Scholar]
- Eichas, F.; Möller, S.; Zölzer, U. Block-oriented gray box modeling of guitar amplifiers. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Edinburgh, UK, 5–9 September 2017. [Google Scholar]
- Stilson, T.; Smith, J.O., III. Alias-free digital synthesis of classic analog waveforms. In Proceedings of the International Computer Music Conference, Hong Kong, China, 19–24 August 1996. [Google Scholar]
- Brandt, E. Hard sync without aliasing. In Proceedings of the International Computer Music Conference, Havana, Cuba, 17–23 September 2001. [Google Scholar]
- Välimäki, V.; Pekonen, J.; Nam, J. Perceptually informed synthesis of bandlimited classical waveforms using integrated polynomial interpolation. J. Acoust. Soc. Am. 2012, 131, 974–986. [Google Scholar] [CrossRef] [PubMed]
- Välimäki, V. Discrete-time synthesis of the sawtooth waveform with reduced aliasing. IEEE Signal Process. Lett. 2005, 12, 214–217. [Google Scholar]
- Välimäki, V.; Nam, J.; Smith, J.O., III; Abel, J.S. Alias-suppressed oscillators based on differentiated polynomial waveforms. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 786–798. [Google Scholar]
- Kleimola, J.; Välimäki, V. Reducing aliasing from synthetic audio signals using polynomial transition regions. IEEE Signal Process. Lett. 2012, 19, 67–70. [Google Scholar] [CrossRef]
- Franck, A.; Välimäki, V. Higher-order integrated wavetable synthesis. In Proceedings of the International Conference on Digital Audio Effects (DAFx), York, UK, 17–21 September 2012. [Google Scholar]
- Esqueda, F.; Bilbao, S.; Välimäki, V. Aliasing reduction in clipped signals. IEEE Trans. Signal Process. 2016, 60, 5255–5267. [Google Scholar] [CrossRef]
- Esqueda, F.; Välimäki, V.; Bilbao, S. Rounding corners with BLAMP. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Brno, Czech Republic, 5–9 September 2016. [Google Scholar]
- Parker, J.; Zavalishin, V.; Le Bivic, E. Reducing the aliasing of nonlinear waveshaping using continuous-time convolution. In Proceedings of the International Conference on Digital Audio Effects (DAFx), Brno, Czech Republic, 5–9 September 2016. [Google Scholar]
- Bilbao, S.; Esqueda, F.; Parker, J.D.; Välimäki, V. Antiderivative antialiasing for memoryless nonlinearities. IEEE Signal Process. Lett. 2017, 24, 1049–1053. [Google Scholar] [CrossRef]
- Esqueda, F.; Pöntynen, H.; Parker, J.D.; Bilbao, S. Virtual analog model of the Lockhart wavefolder. In Proceedings of the 14th Sound and Music Computing Conference (SMC), Espoo, Finland, 5–8 July 2017. [Google Scholar]
- Lockhart, R., Jr. Non-selective frequency tripler uses transistor saturation characteristics. Electron. Des. 1973, 17. [Google Scholar]
- Hutchins, B.A. Frequency multiplication and division methods. Electronotes 1976, 70, 3–17. [Google Scholar]
- Stone, K. Simple wave folder for music synthesizers. Available online: https://www.cgs.synth.net/modules/cgs52_folder.html (accessed on 19 September 2017).
- Stone, K.; CGS, Melbourne, Australia. Private communication, 2017.
- Usson, Y. Yusynth Metalizer. Available online: http://yusynth.net/modular/en/metalizer/ (accessed on 18 September 2017).
- Banwell, T.; Jayakumar, A. Exact analytical solution for current flow through diode with series resistance. Electron. Lett. 2000, 36, 291–292. [Google Scholar] [CrossRef]
- De Paiva, R.C.D.; D’Angelo, S.; Pakarinen, J.; Välimäki, V. Emulation of operational amplifiers and diodes in audio distortion circuits. IEEE Trans. Circuits Syst. II Exp. Briefs 2012, 59, 688–692. [Google Scholar] [CrossRef]
- Werner, K.J.; Nangia, V.; Bernardini, A.; Smith, J.O., III; Sarti, A. An improved and generalized diode clipper model for wave digital filters. In Proceedings of the 139th Convention of the Audio Engineering Society, New York, NY, USA, 29 October–1 November 2015. [Google Scholar]
- Bernardini, A.; Werner, K.J.; Sarti, A.; Smith, J.O., III. Modeling nonlinear wave digital elements using the Lambert function. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1231–1242. [Google Scholar] [CrossRef]
- Veberič, D. Lambert W function for applications in physics. Comput. Phys. Commun. 2012, 183, 2622–2628. [Google Scholar] [CrossRef]
- Linear Technology. LTspice. Available online: http://www.linear.com (accessed on 2 October 2017).
- Serge Modular Music Systems, San Francisco, CA, USA. New Products from Serge Modular: Series 79 Synthesizer Systems. 1980. Available online: http://www.serge.synth.net/documents/catalog/SergeModular-Series79%20.pdf (accessed on 21 September 2017).
- Stone, K. Serge Wave Multipliers for music synthesizers. Available online: https://www.cgs.synth.net/modules/cgs113_vcm.html (accessed on 21 September 2017).
- Fukushima, T. Precise and fast computation of Lambert W-functions without transcendental function evaluations. J. Comput. Appl. Math. 2013, 244, 77–89. [Google Scholar] [CrossRef]
- Lehtonen, H.M.; Pekonen, J.; Välimäki, V. Audibility of aliasing distortion in sawtooth signals and its implications for oscillator algorithm design. J. Acoust. Soc. Am. 2012, 132, 2721–2733. [Google Scholar] [CrossRef] [PubMed]



















| Component | Value (k) | Component | Value (V) |
|---|---|---|---|
| R | 15 | 15 | |
| 1–50 | −15 |
| Name | Value | Name | Value | Name | Value |
|---|---|---|---|---|---|
| R | 15 k | A | 25.864 mV | ||
| 1–50 k | 1 | – | – |
| Component | Value (k) | Component | Description |
|---|---|---|---|
| 33 | Diodes | 1N4148 or similar | |
| 100 | Op-Amp | TL072 or similar | |
| 100 | – | – |
| Name | Value | Name | Value |
|---|---|---|---|
| 2.52 nA | 33 k | ||
| 1.752 | 25.864 mV |
| Amplitude (V) | Audio Rate | Audio Rate | OSx2 | OSx4 | OSx8 | OSx2 |
|---|---|---|---|---|---|---|
| (ms) | w/Antialiasing (ms) | (ms) | (ms) | (ms) | w/ Antialiasing (ms) | |
| 1 | 11.5 | 12.5 | 23.4 | 46.6 | 92.9 | 25.4 |
| 5 | 11.6 | 12.6 | 23.3 | 46.8 | 92.7 | 25.3 |
| 10 | 11.5 | 12.6 | 23.7 | 46.7 | 92.9 | 25.5 |
| 15 | 11.5 | 12.7 | 23.5 | 46.5 | 92.9 | 25.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esqueda, F.; Pöntynen, H.; Parker, J.D.; Bilbao, S. Virtual Analog Models of the Lockhart and Serge Wavefolders. Appl. Sci. 2017, 7, 1328. https://doi.org/10.3390/app7121328
Esqueda F, Pöntynen H, Parker JD, Bilbao S. Virtual Analog Models of the Lockhart and Serge Wavefolders. Applied Sciences. 2017; 7(12):1328. https://doi.org/10.3390/app7121328
Chicago/Turabian StyleEsqueda, Fabián, Henri Pöntynen, Julian D. Parker, and Stefan Bilbao. 2017. "Virtual Analog Models of the Lockhart and Serge Wavefolders" Applied Sciences 7, no. 12: 1328. https://doi.org/10.3390/app7121328
APA StyleEsqueda, F., Pöntynen, H., Parker, J. D., & Bilbao, S. (2017). Virtual Analog Models of the Lockhart and Serge Wavefolders. Applied Sciences, 7(12), 1328. https://doi.org/10.3390/app7121328





