An Experimental Study on Hysteresis Characteristics of a Pneumatic Braking System for a Multi-Axle Heavy Vehicle in Emergency Braking Situations

Featured Application

The obtained data and model from the research can be useful for the design of a pneumatic braking system and the development of advanced brake control strategy with respect to multi-axle heavy vehicles in the future.

Abstract

This study aims to investigate the hysteresis characteristics of a pneumatic braking system for multi-axle heavy vehicles (MHVs). Hysteresis affects emergency braking performance severely. The fact that MHVs have a large size and complex structure leads to more nonlinear coupling property of the pneumatic braking system compared to normal two-axle vehicles. Thus, theoretical analysis and simulation are not enough when studying hysteresis. In this article, the hysteresis of a pneumatic brake system for an eight-axle vehicle in an emergency braking situation is studied based on a novel test bench. A servo drive device is applied to simulate the driver’s braking intensions normally expressed by opening or moving speed of the brake pedal. With a reasonable arrangement of sensors and the NI LabVIEW platform, both the delay time of eight loops and the response time of each subassembly in a single loop are detected in real time. The outcomes of the experiment show that the delay time of each loop gets longer with the increase of pedal opening, and a quadratic relationship exists between them. Based on this, the pressure transient in the system is fitted to a first-order plus time delay model. Besides, the response time of treadle valve and controlling pipeline accounts for more than 80% of the loop’s total delay time, indicating that these two subassemblies are the main contributors to the hysteresis effect.

1. Introduction

Multi-axle heavy vehicles (MHVs) are usually used as land transport platforms for large-scale equipment. Compared with ordinary vehicles, MHVs have large inertia and a long wheelbase, and they usually work in complicated and changeable driving conditions. Hence, good braking performance is an important guarantee for fast maneuvering and safe driving. At present, the pneumatic braking system (PBS) is widely employed in MHVs with the advantages of large braking force, good reliability and easy maintenance [1].

Due to compressibility of gas, PBS will inevitably perform a hysteresis effect, which may easily lead to serious traffic accident in an emergency braking condition [2]. For example, when a vehicle runs at a normal speed of 20 m/s (approximately 70 km/h), if the braking time is delayed 0.5 s, the braking distance will increase by nearly 10 m. This delay could lead to heavy longitudinal loads along the vehicle instantaneously [3]. The consequences will be more serious for the MHV owing to its large inertia.

Currently, electronic brake systems (EBSs), electronic brake force distribution (EBD) and other advanced control technologies have been successfully applied to the majority of passenger cars, while the applications on MHV are still relatively narrow and immature [4]. In this case, scholars have undertaken a large amount of related research recently, and various technologies have been proposed and successfully implemented for better pneumatic braking performance of MHVs, including sliding mode controllers [5,6,7], nonlinear model predictive controllers [8], indirect adaptive robust controllers (IARC) [9], and novel braking actuators [10]. Nevertheless, the braking performance of MHV is still much poorer than that of the passenger car [7]. The reason may be the following. Most of these studies have paid much attention only to the optimization and improvement of braking control strategies [11]. Actually, the response time of valves as well as the long pipeline length tremendously limit the performance of the pneumatic brake system, making it harder to control [9,12]. Therefore, the properties of PBS itself is the basis for studying braking control strategies.

Hysteresis is an inherent property of the PBS, which with no doubt has a significant impact on braking performance. Research on hysteresis characteristics can be divided into the system level and component level. Most literature has focused on the latter, such as treadle valves [13], brake pipelines [14], relay valves [15], proportional valves [16], and other subassemblies. However, subassemblies in a loop are connected to each other and affect each other; analysis of individual subassembly seems to be insufficient. In terms of the system level, Selvaraj [17] and He [18] established simulation models of the PBS on two-axle vehicles using AMEsim (Advanced Modeling Environment for performing Simulation of engineering systems) and MWorks, respectively. Pugi and his team [3,19] have conducted in-depth research on the pneumatic braking plant of a railway vehicle and established a complete parametric simulation library using Matlab-Simulink, which makes customizable design possible. As for MHVs, existing literature concerned with the hysteresis effect is rare, and the few accessible studies mainly concentrate on road tests [20]. However, road tests imply high risk, have high costs, and involve a limited range of working conditions. In addition, sensors are not easily placed or replaced on subassemblies after the vehicle is completely assembled. Hence, a test bench for studying hysteresis characteristics of PBS for MHV is necessary.

A PBS on an MHV is usually composed of a service brake circuit, a parking brake circuit and an auxiliary braking circuit. When a driver encounters an emergency braking condition, pushing the brake pedal is probably the most common behavior. Therefore, the opening and moving speed of the pedal directly reflect the driver’s braking intentions, and they have the most direct influence on the hysteresis effect of the PBS since the brake pedal is the power source of the service brake circuit [21,22]. Hence, this paper pays more attention to the service brake circuit.

In this paper, a novel test bench of PBS for an 8-axle vehicle is described in detail. The influence of opening and moving speed of the brake pedal, as well as the response time of subassemblies on hysteresis effect in service braking circuit is analyzed. This research may provide a reference for further experimental study of hysteresis effect of the PBS, and the obtained data and laws may be useful for system design or the development of advanced control strategy on MHVs in the future.

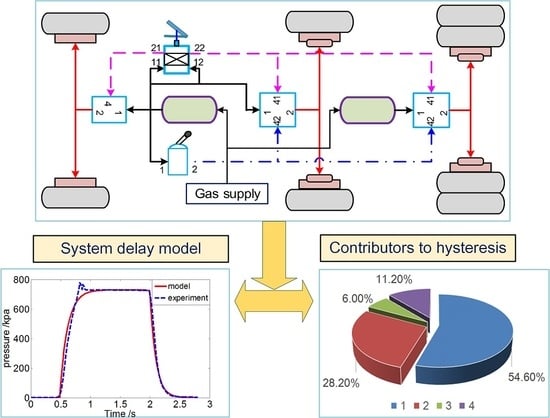
2. System Principle

A PBS in an MHV is briefly shown in Figure 1. The system is composed of service brake circuit and parking brake circuit. Usually, double circuits are employed in the service brake circuit, just for avoiding the braking failure in case one of the two circuits has stochastic fault. Each circuit in the system mainly consists of gas reservoirs, control valves, brake chambers and brakes. The gas source of the whole vehicle is provided by an air compressor and stored in a main reservoir with large capacity as well as several normal ones with relatively small capacity. Control valves mainly comprise a hand brake valve and a treadle valve located in the cab, several relay valves, and delay relay valves arranged in the rear axle of the chassis. Drum brakes, which can offer more powerful braking force compared to disc brakes, are widely used in MHVs [23].

The structure of the service brake circuit of a PBS on MHV can be simplified as shown in Figure 2. This circuit is made up of three parts: the gas supply part, pneumatic transmission part and mechanical actuator part. In this paper, we focus on the pneumatic transmission part because hysteresis is mainly caused by the long-distance pressure transmission in this part [24]. A complete working procedure of the service brake can be divided into the brake process, brake keeping process and brake release process. Taking the S-cam drum brake as an example, the working procedure can be described as follows. When encountering an emergency braking situation, the driver steps on the brake pedal quickly and the treadle valve is opened soon; this behavior meters out the compressed gas from the supply ports (port 11 and 12) of the treadle valve to its delivery ports (port 21 and 22). Then, the compressed gas travels to port 4 of the relay value through controlling pipeline, making the relay value open. Next, high-pressure gas moves into the brake chamber through braking pipeline and presses the diaphragm, pushing the plunger out. The ejected plunger then drives the brake arm, rotating the S-cam and expanding the brake shoes. As a result, the pads produce a friction torque, compelling the rotating hub to stop quickly. When the brake pedal is released by the driver, the gas is rapidly exhausted from the brake chamber, resulting in the opposite rotating direction of the S-cam. Subsequently, the contact between the pad and the hub is broken and the brake is finally released.

3. Test System Design

3.1. General Setup

Referring to a real-world 8-axle vehicle, the test bench of PBS for an eight-axle vehicle is designed as shown in Figure 3. The test bench is composed of two parts, the operation desk and control desk.

(1)

The operation desk consists of gas supply devices, servo drive device, valves, pipelines, and load simulators; the test bench is shown in Figure 4. The gas supply device consists of several reservoirs and a pressure-regulating valve used for setting the working pressure of the system, as displayed in Figure 4b. A low-friction and high-precision linear servo drive device is used to drive the treadle valve, so as to accurately simulate the driver’s intensions expressed by pedal opening and moving speed. It is composed of a servo motor and screw transmission, as shown in Figure 5. Sixteen load simulators (manual control) made up of disc springs are applied to simulate different load torques of 16 wheels. The force sensor arranged between the brake chamber and load simulator is used for detecting the brake force. In order to avoid function failure or error accumulation of subassemblies, these used key pneumatic components are calibrated beforehand on a specific test bench, as shown in Figure 4c.

(2)

The control desk is composed of hardware and software. The hardware includes an Advantech 610H industrial personal computer (IPC) (Advantech, Taipei, China), a Panasonic programmable logic controller (PLC) ( Panasonic, Osaka, Japan), NI PCI-6229 data acquisition (DAQ) cards (National Instruments, Austin, TX, USA) and fast-response sensors. Communication between the PLC and the host computer is implemented through the object linking and embedding for process control (OPC) protocol using the transmission control protocol (TCP)/internet protocol (IP) interface. The test software is developed on the NI LabVIEW platform (version 14.0, National Instruments, Austin, TX, USA, 2014). The software has rich functions such as convenient data acquisition, processing, preservation and real-time display.

3.2. Arrangement of Sensors

The layout of gas transmission path of PBS on the test bench is shown in Figure 6. There are double service brake circuits, the front circuit including four loops (dark red) and the rear circuit including the other four loops (magenta); each loop corresponds to an axle. The parking brake circuit (blue) is also described in the figure. Due to the symmetrical arrangement of two brake chambers on one bridge, sensors are placed only in one side of the bridge.

Hysteresis characteristics of PBS on an MHV are mainly displayed in two aspects. On one hand, the delay time of each loop is different because of different gas transmission path. On the other hand, the delay time of a certain loop is the accumulation of response time of each subassembly. Both the times need to be detected on this test bench. In order to measure the delay time of each loop in service brake circuit, pressure sensors marked $f_A,f_B,f_C,f_D$ and $r_E,r_F,r_G,r_H$, are respectively placed on the entrance of brake chamber in the front four loops and rear four loops, as shown in Figure 6. To detect response time of each subassembly, pressure sensors marked $f_i,r_i(i=1,2,3,4)$ are respectively laid on the C-loop in the front circuit and E-loop in the rear circuit (Note: $f_4,r_4$ are the same as $f_C,r_E$. A displacement sensor marked TD (Treadle displacement sensor) is used for measuring pedal propulsion displacement, as shown in Figure 7.

3.3. Key Parameters of the Test Bench

Control valves in this experiment include the relay valve, treadle valve, hand brake valve and delay relay valve; they are all produced by Westinghouse Air Brake Company (WABCO) and have been offered by a vehicle research insitute. Brake chambers of the QF series are produced by the Sanjiang Mechanical Company (Yibin, China). In order to obtain meaningful experimental results, these key subassemblies are the same as the real ones equiped on a certain eight-axle heavy vehicle. Gas supply pressure of the circuit is set at 800 kpa by the regulate valve shown in Figure 4b, which is the rated working pressure according to the National Standard GB12676-1999. Considering the size on a real-world eight-axle vehicle, the length of controlling pipeline is chosen as 4 m for the front circuit and 10 m for the rear one on the test bench. Meawhile, the lengths of braking pipeline in loop A, D, E and H are chosen as 1 m ,and in loop B, C, F and G as 2 m. Other key parameters are shown in

Table 1. Key parameters of test bench. (FS: full scale).

Name	Type	Range	Precision
Servo driver	TJE075-S100	0–40 mm	0.5% FS (measurement) 1% FS (control)
Pressure sensor	MEAS	0–1.6 Mpa	0.3% FS
Force sensor	PST2T	0–20000 N	0.5% FS
Displacement sensor	DA35	0–35 mm	0.5% FS
pipeline	Φ10PA	0–2 Mpa	-
Control valves	WABCO	-

.

3.4. Testing Conditions

In order to study the influence of opening and moving speed of the brake pedal on hysteresis characteristics in service circuit, different propulsion displacements and action time of the servo drive device were set in different testing conditions. As for the brake process and brake release process in a certain condition, the two parameters were set the same except for the opposite moving direction of the servo motor. The detailed testing groups are shown in

Table 2. Testing conditions.

Group	Propulsion Displacement (l/mm) (Brake and Brake Release)	Action Time (t/s) (Brake and Brake Release)
1	6	0.20
2	8	0.27
3	10	0.33
4	12	0.40
5	14	0.46
6	14	2.50

. Firstly, in the first to the fifth groups, the propulsion speeds ($v_T=l/t$) were approximately equal while the displacements were different, just for studying the relationship between hysteresis and opening. Secondly, in the fifth to the sixth group the propulsion displacements were the same while speeds were different, just for studying the relationship between hysteresis and moving speed. Given the fact that the rated stroke of pushrod in the tested treadle valve is 15 mm, maximum propulsion displacement of the servo drive device was set to 14 mm for protecting the valve. Each experiment group was repeated five times for less random error, and their mean values were used for subsequent calculations.

4. Results and Discussion

According to GB12676-1999(Road vehicle-braking systems-structure, performance and test methods. China) and GB7258-2012(Safety specifications for power-driven vehicles operating on roads. China), for a PBS, the delay time of a certain loop can be defined as follows,

$$\{\begin{array}{l}{\Delta }_{del\_up}=t_{{\gamma }_p\_up}-t_{start\_up}\\ {\Delta }_{del\_down}=t_{{\gamma }_p\_down}-t_{start\_down}\end{array},$$

(1)

where ${\Delta }_{del\_up}$ and ${\Delta }_{del\_down}$ are respectively the delay time in brake process and brake release process. $t_{start\_up}$ is the time when the brake pedal starts to move to begin the brake process, while $t_{start\_down}$ is the time when the brake pedal starts to move to begin the brake release process. Both of these are measured by a TD sensor. $t_{{\gamma }_p\_up}$ and $t_{{\gamma }_p\_up}$ are the times when the pressure in the brake chamber reach 75% and 15% of the steady value, and their corresponding pressures are marked as ${\gamma }_{p\_up}$ and ${\gamma }_{p\_down}$, respectively. For a clear description, the working procedure of a PBS is displayed in Figure 8.

4.1. Hysteresis Effect of 8 Axle

The experimental results obtained under the testing condition of group 1 are shown in Figure 9, including the original data curve and the calculated delay time of eight axles based on Formula (1). The standard deviation is used to weigh the random error. Moreover, the delay times of eight axles under the testing conditions of all the testing groups are calculated as shown in

Table 3. Delay time of eight loops under the testing condition of all the groups.

Testing Groups
Loop		1		2		3		4		5		6
		Up	Dw	Up	Dw	Up	Dw	Up	Dw	Up	Dw	Up	Dw
Delay Time/Δdel	A	0.38	0.48	0.42	0.62	0.48	0.72	0.58	0.88	0.67	1.02	2.49	2.66
	B	0.31	0.45	0.34	0.51	0.42	0.73	0.50	0.84	0.62	0.93	2.41	2.63
	C	0.37	0.47	0.36	0.55	0.45	0.72	0.52	0.83	0.61	0.95	2.42	2.67
	D	0.39	0.53	0.42	0.65	0.49	0.78	0.61	0.86	0.66	1.04	2.47	2.71
	E	0.47	0.55	0.52	0.67	0.55	0.81	0.68	0.92	0.72	1.10	2.56	2.73
	F	0.41	0.54	0.45	0.62	0.52	0.75	0.65	0.89	0.70	1.04	2.50	2.68
	G	0.42	0.53	0.46	0.63	0.53	0.76	0.67	0.91	0.72	1.06	2.52	2.69
	H	0.48	0.59	0.55	0.69	0.57	0.83	0.69	0.97	0.78	1.12	2.57	2.75

Note: In this table, ${\Delta }_{del\_up}$ is denoted as “up”, ${\Delta }_{del\_down}$ is denoted as “dw”.

. From this table, we know that the delay time of each loop is different from each other in both the brake process and brake release process. The asynchronous response of the multi-axle vehicle leads to different braking torques on different axes at the same braking moment, which may seriously affect the braking stability. The hysteresis effect in brake release process is relatively more obvious. This effect may lead to an unexpected once-more brake action due to a slow gas exhaust of the loop, which will result in difficult restarting of the vehicle. Therefore, when developing the hysteresis compensation control strategy for multi-axle vehicle, different delay times of every loop both in the brake process and brake release process should be taken into consideration.

4.1.1. Relationship between Pedal Opening and Delay Time

The swing angle of the pedal arm or the linear displacement of the brake’s master cylinder is usually used for evaluating the pedal opening [25]; the latter is adopted in this paper because of the easily measured moving displacement of the servo drive device. Thus, the pedal opening can be denoted as:

$$0\le \psi =\frac{l}{l_{max}}\le 100\%,$$

(2)

where $l$ is the measured displacement and $l_{max}$ is the rated moving displacement, here $l_{max}=15\mathrm{m}\mathrm{m}$, and $\psi$ is the pedal opening. When analyzing the experimental results from group 1 to group 5 in Table 3, we know that the delay time of each loop was not the same due to different pedal opening though the pedal’s moving speeds being approximately equal. For the full eight loops, the delay time of the rear four loops (E, F, G and H) are higher than the front four loops (A, B, C and D). For a certain loop, the higher the pedal opening, the longer the delay time. In order to explore the quantitative relationships between them, polynomial fitting is carried out for both the brake process and the brake release process using least squares method.

$${\{\begin{array}{l}{\Delta }_{del\_up}=K_{1\_up}{\psi }^2+K_{2\_up}\psi +W_{up}\\ {\Delta }_{del\_down}=K_{1\_down}{\psi }^2+K_{2\_down}\psi +W\end{array}}_{down},$$

(3)

where $K_{1\_up}$, $K_{2\_up}$, $K_{1\_down}$, $K_{2\_down}$ are coefficient matrixes and $W_{up},W_{down}$ are constant matrixes. The fitting results are shown in Figure 10, and the corresponding fitting parameters are shown in

Table 4. Fitting parameters.

Loop	K1		K2		W		R2
	Up	Down	Up	Down	Up	Down	Up	Down
A	0.597	0.290	−0.238	0.621	0.378	0.192	0.997	0.996
B	0.759	0.158	−0.423	0.746	0.356	0.109	0.998	0.985
C	0.754	0.117	−0.520	0.778	0.447	0.130	0.980	0.993
D	0.393	0.321	0.026	0.497	0.308	0.287	0.975	0.990
E	0.353	0.407	0.026	0.473	0.401	0.299	0.958	0.997
F	0.355	0.653	0.115	0.087	0.299	0.394	0.975	0.999
G	0.397	0.533	0.081	0.298	0.316	0.324	0.971	0.999
H	0.601	0.450	−0.243	0.409	0.488	0.352	0.977	0.998

.

The fitting coefficient of determination $R^2$ can be calculated as follows,

$$R^2=1-\frac{{{\displaystyle \sum }}_{a=1}^n{(y_a-y_a^{\prime })}^2}{{{\displaystyle \sum }}_{a=1}^n{(y_a-\overline{y})}^2},$$

(4)

where $y_a$ is the original data, $y_a^{\prime }$ is the obtained fitting data, $\overline{y}$ is the average value of the original data, and $n$ is the number of original data. Each calculated R² is close to 1, indicating that the fitting is very good.

4.1.2. First-Order Plus Time Delay Model

There is an obvious hysteresis of the PBS according to the above analysis. In this paper, a simplified model of the system is proposed to benefit the further development of brake controller. Considering the inherent hysteresis characteristics obtained in Section 4.1.1 and [26,27], the system can be approximately fitted to a first-order plus time delay model. This model relates the opening of the treadle valve and the pressure transient in the brake chamber. The governing equation of the model can be described like this,

$$T\frac{dP(t)}{dt}+P(t)=Ku(t-\tau ),$$

(5)

where T is the time constant of the system, K is the gain, and $\tau$ is the delay time. $P(t)$ and $u(t)$ are the output and input of the system. Here, they refer to the pressure transients in the brake chamber and the opening of the brake pedal, respectively. Taking the Laplace transform of the Equation (5), we obtain the transfer function of the system.

$$G(s)=\frac{K{e}^{-\tau s}}{(Ts+1)},$$

(6)

Figure 11 shows a schematic description of the first-order plus time delay model of the PBS. Past research on the PBS has shown that the moving displacement of treadle valve plunger has a linear relationship with the desired braking pressure. Therefore, according to Formula (2) we assume that the relationship between pedal opening and the desired braking pressure can be expressed in Formula (7). As for the parameter $\tau$, it can be defined as Formula (8).

$$P_d=a\psi +b,$$

(7)

$$\{\begin{array}{l}{\tau }_{up}={\Delta }_{del\_up}-{\tilde{T}}_{up}\\ {\tau }_{down}={\Delta }_{del\_down}-{\tilde{T}}_{down}\end{array},$$

(8)

where $a$, $b$ are constants, related to the type of the used treadle valve and brake pedal. ${\tau }_{up}$, ${\tau }_{down}$ are the pure time delay of the system in brake process and brake release process, respectively. ${\tilde{T}}_{up}$, ${\tilde{T}}_{down}$ are the time constants related to $T$. Where ${\tilde{T}}_{up}$ is the time spent when the pressure in the chamber varies from 0 to 75% of the steady value in brake process, ${\tilde{T}}_{down}$ is the time spent when the pressure in the chamber varies from the steady value to 15% in the brake release process.

With the method of system identification, the simulation model of the system can be established. In view of the deviation of hysteresis characteristics of each loop, eight loops correspond to eight different models, as shown in Figure 12, and their relevant parameters are listed in (9). We find that the models approximately coincide with the experimental results.

$$\{\begin{array}{l}T=[\begin{array}{cccc}\begin{array}{cccc}0.124& 0.118& 0.075& 0.170\end{array}& 0.114& 0.171& \begin{array}{cc}0.169& 0.184\end{array}\end{array}]\\ {\tilde{T}}_{up}=[\begin{array}{cccc}\begin{array}{ccc}\begin{array}{cc}0.170& 0.160\end{array}& 0.100& 0.240\end{array}& 0.150& 0.240& \begin{array}{cc}0.230& 0.250\end{array}\end{array}]\\ {\tilde{T}}_{down}=[\begin{array}{cccc}\begin{array}{ccc}\begin{array}{cc}0.210& 0.200\end{array}& 0.130& 0.300\end{array}& 0.200& 0.310& \begin{array}{cc}0.300& 0.330\end{array}\end{array}]\end{array},$$

(9)

Figure 13 shows the variation of the brake chamber pressure in the loop A when the brake pedal opening is set at 67% and 93%, respectively. It can be observed that the simulation results agree reasonably well with the experimental data in both the brake process and brake release process, which validate the accuracy of the model. Models of other loops are validated as well.

4.1.3. Relationship between Moving Speed and Delay Time

When concentrating on the results of group 5 and group 6 in Table 3, we know that when the pedal openings are the same, the faster the pedal is driven, the shorter the delay time is, and this law exists in both the brake process and brake release process. According to literature [28], the moving speed of brake pedal is easily influenced by driver’s driving habits, so it is not advisable to be used as the parameter for recognizing driver’s braking intention directly. Therefore, this paper does not pay much attention to the relationship between moving speed and delay time.

4.2. Response Time of Subassemblies in a Single Axle

Subassemblies in a single loop consist of treadle valve, control pipeline, relay valve, brake pipeline and brake chamber. Delay time of a loop is the accumulation of the response time of each subassembly. Sensors used for measuring the response time are arranged as shown in Figure 7. $t_{{}_{res\_(f,r)j}}^{(up,down)}$ ($j=1,2,3,4$) represents the response time of each subassembly in the front (C) or rear (E) loop in brake process or brake release process. Specifically, $t_{{}_{res\_(f,r)1}}^{(up,down)}$, $t_{{}_{res\_(f,r)2}}^{(up,down)}$, $t_{{}_{res\_(f,r)3}}^{(up,down)}$, $t_{{}_{res\_(f,r)4}}^{(up,down)}$ represents the response time of treadle valve, controlling pipeline, relay valve and braking pipeline, respectively. Hence, the delay time of the two loops can be described as,

$$\{\begin{array}{c}\Delta t_{{}_{del\_f}}^{(up,down)}={\displaystyle {\displaystyle \sum }_{j=1}^n}{t}_{{}_{res\_fj}}^{(up,down)}\\ \Delta t_{{}_{del\_r}}^{(up,down)}={\displaystyle {\displaystyle \sum }_{j=1}^n}{t}_{{}_{res\_rj}}^{(up,down)}\end{array},$$

(10)

where $\Delta t_{{}_{del\_f}}^{(up,down)}$, $\Delta t_{{}_{del\_r}}^{(up,down)}$ are the delay time of the front loop C and rear loop E, respectively. The original measured data of the two loops under the testing condition of group 1 are shown in Figure 14.

Subsequently, a method for calculating the response time of each subassembly in a single loop is given as follows.

$$\{\begin{array}{l}\Delta t_{{}_{del\_fi}}^{(up,down)}=t_{{}_{{\gamma }_p\_fi}}^{(up,down)}-t_{start\_(up,down)}\\ t_{{}_{res\_fj}}^{(up,down)}=\Delta t_{{}_{del\_fi}}^{(up,down)}-\Delta t_{{}_{del\_f(i-1)}}^{(up,down)}\end{array},$$

(11)

$$\{\begin{array}{l}\Delta t_{{}_{del\_ri}}^{(up,down)}=t_{{}_{{\gamma }_p\_ri}}^{(up,down)}-t_{start\_(up,down)}\\ t_{{}_{res\_rj}}^{(up,down)}=\Delta t_{{}_{del\_ri}}^{(up,down)}-\Delta t_{{}_{del\_r(i-1)}}^{(up,down)}\end{array},$$

(12)

where $\Delta t_{{}_{del\_fi}}^{(up,down)}$ and $\Delta t_{{}_{del\_ri}}^{(up,down)}$ are the delay time of each subassembly in the front and rear loop, respectively, and they are calculated in the same way as ${\Delta }_{del\_(up,down)}$ mentioned in Section 4.1. $t_{{}_{{\gamma }_p\_fi}}^{(up)}$, $t_{{}_{{\gamma }_p\_ri}}^{(up)}$ are the times when the pressure in a subassembly increase to 75% of its steady value in the brake process, and $t_{{}_{{\gamma }_p\_fi}}^{(down)}$, $t_{{}_{{\gamma }_p\_ri}}^{(down)}$ are the times when the pressure in a subassembly decreases to 15% of its steady value in the brake release process. These times are measured by sensors $f_i$ and $r_i$. Finally, the response times of each subassembly in two loops are acquired, as shown in Figure 15 and Figure 16.

Finally, the proportion of response time of each subassembly can be calculated using the following formula and the corresponding results are shown in Figure 17.

$${\phi }_{{}^{res\_(f,r)j}}^{(up,down)}=\frac{t_{{}_{res\_(f,r)j}}^{(up,down)}}{\Delta t_{{}_{del\_(f,r)}}^{(up,down)}},$$

(13)

From Figure 17, it can be observed that the response time of the treadle valve and the controlling pipeline are much longer than that of the controlling pipeline and braking pipeline. The sum response time accounts for more than 80% of the total delay time of both the two loops in the brake process, as well as more than 85% in the brake release process. The results indicate that treadle valve and controlling pipeline are the main contributors to the hysteresis effect of the service circuit.

5. Conclusions

In this paper, a pneumatic braking system for an eight-axle vehicle is introduced. In order to accurately study the hysteresis effect of the system in emergency braking situation, a test bench is built. Not only the delay time of each loop corresponding to each axle but also the response time of each subassembly in a single loop is detected in real time. Moreover, the driver’s different braking intensions expressed by opening and moving speed of brake pedal are accurately simulated by a servo drive device.

The acquired data are processed to search for relationships between the pedal’s opening as well as moving speed and hysteresis times of eight loops in service brake circuit. The results show that under the same braking conditions, delay times of the front four loops are shorter than those of the rear four loops, and the delay times of a certain loop in the brake release process are longer than those in the brake process Under the different braking conditions, when the braking speeds are similar, the larger the pedal opening, the longer the delay time, and a quadratic curve relationship exists between the two. Given this fact, the pressure transients of each loop in the system can be fitted to a corresponding first-order plus time delay model. When the pedal openings are the same, the faster the braking speed, the shorter the delay time. In addition, response time of each subassembly in a loop is also obtained. The sum response time of treadle valve and controlling piping accounts for more than 80% of total delay time of a loop in both the brake process and brake release process, which indicates that these two subassemblies are the main contributors to the hysteresis effect of the loop.

For further study of the pneumatic braking system for MHV, the structure of the treadle valve needs to be optimized to shorten its response time, and more reasonable layout of the system should be studied for reducing the gas transmission distance. Additionally, the development of an advanced brake control strategy for the PBS in MHVs based on the established first-order plus time delay models will be a research challenge.