An Efficient Retrieval Technique for Trademarks Based on the Fuzzy Inference System

Abstract

The existing trademark image retrieval (TIR) approaches mostly use complex image features, the integration of multi features, a tree structure, etc. to enable highly accurate retrieval. However, there is the heavy computational burden for complex image features and maximum similarity subtree isomorphism (MSSI) measurement. This paper aims to provide an efficient solution for TIR in real-time applications, especially in measuring the similarity between multi-object trademark images. In particular, we propose a novel algorithm for tree similarity measurement based on the fuzzy inference system (FIS) to improve retrieval efficiency. Furthermore, the integration of global and local geometric descriptors is used to enable accurate retrieval. The global descriptor is computed by employing the Hu moments, while the local descriptors are generated by using a tree structure based on the five geometric features: convexity, eccentricity, compactness, circle variance, and elliptic variance. During the retrieval process, the similarity coefficient between the query and the database image is obtained from the similarity of the global and local descriptors. The proposed technique is evaluated using 1800 trademark images, including 12 different classes and 416 trademark images. Additionally, the three common indices, the precision/recall rate, the Bull’s eye score, and the average normalized modified retrieval rank (ANMRR) are used as the performance indices. The experimental results show that the proposed technique is superior to the other two competitive approaches. It shows 19.43% and 26.78% precision/recall improvement, 19.56% and 30.58% improvement in the average Bull’s eye score, and 0.167 and 0.236 improvement in the ANMRR score, respectively, for the 416 query images. It can be concluded from the experimental analysis that the proposed technique not only provides reliable retrieval results but also improves the retrieval efficiency by 151 times in the retrieval process.

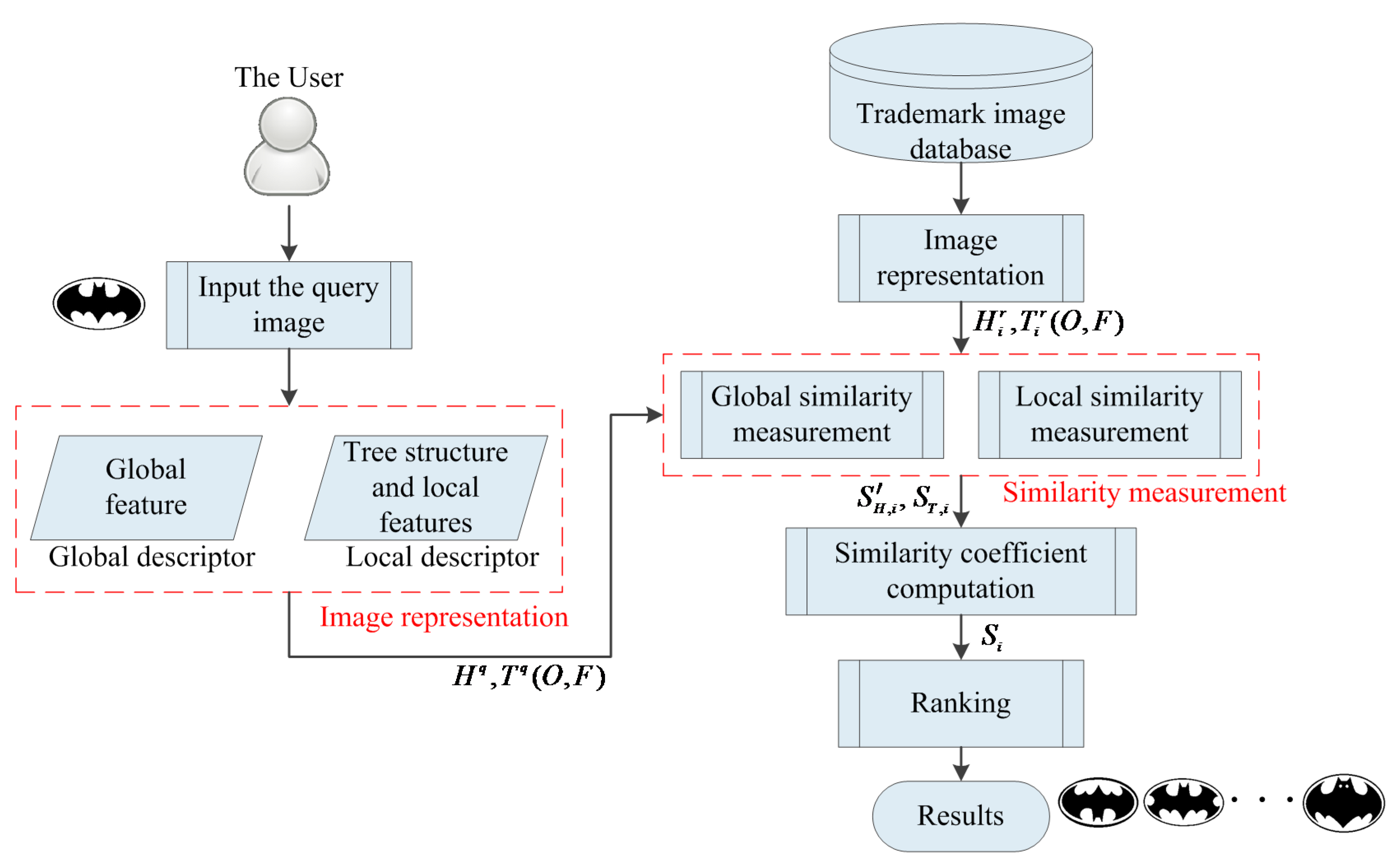
1. Introduction

Nowadays, content-based image retrieval (CBIR) [1,2,3] is the most common approach for image retrieval, aiming to retrieve similar or relevant images using the visual contents of or the keywords in the query image. Several popular CBIR systems such as query by image content (QBIC), Virage, Photobook, VisualSeek, WebSeek, and Google’s similar images search engine, etc. have been developed, and the specific merits of each of the systems have been covered in detail [4]. A practical application of CBIR is trademark image retrieval (TIR). According to a survey [5], worldwide trademark applications have been linearly increased over the past 25 years. A trademark identifies the brand owner of a particular product or service; it also represents the entire business and valuation of the enterprise. Therefore, enforcing the rights of ownership of registered trademarks is a commercial necessity. However, the process of registering a new trademark is important and may be undertaken more than a year before an application is accepted. Therefore, an aim of trademark image retrieval systems is to limit the number of trademarks in order to reduce the time of manual verification. Furthermore, a trademark retrieval system, to be practical, has to be able to work in real time with a good precision/recall curve (a minimum number of irrelevant trademarks are shown to the officer) to ensure its usefulness.

The success of a TIR system is dependent upon the method of feature extraction and feature similarity measure. Searches for similar trademarks include a visual and percipient assessment. Visual similarity in the trademark retrieval problem is usually considered through the similarity of content features such as shape, color, or texture [3]. In [6], psychology studies indicate that humans are more prone to identify and distinguish objects based on their shape rather than color and texture. In addition, in [7], the authors conclude that humans can easily discriminate shapes by their contours, and the contour of a shape has importance, not its interior content. Therefore, the technique of this paper is focused on the shape of trademarks. Broadly, shape defines the contour as well as the whole area of an image, and it can provide a greater robustness property for finding the relevant image in the database. The shape feature can be further categorized into two groups: region and geometric based [8,9,10].

In the region-based feature, the image moment was widely used in the TIR system, which represents the mass distribution of objects in space. Low-order moments cannot describe the shape accurately; hence, high-order moments are desirable but are more prone to noise. There are different region-based descriptors like Hu’s moment (HM), generic Fourier descriptor (GFD), Legendre moments (LMs), Zernike moments (ZMs) [11,12,13], etc. ZMs have certain desirable properties like rotation invariance and robustness to noise and also have better retrieval performance than the other region-based descriptors [8]. On the other hand, several approaches based on geometric-based features are proposed for TIR, including Fourier description, curvature scaled space [14], edge directions histograms [15], Triangle-Area Representation (TAR) [16], the local patterns of an image [17], etc. A comparative retrieval study between a region and a geometric-based feature found that the matching of the geometric-based feature was significantly more effective than the matching of the region-based feature [18]. There is consensus that the use of multiple region-based features or the integration of region and geometric-based features work better than any single ones, while integrating various shape descriptors is generally necessary.

Although an effective approach has been employed for feature representation, an inappropriate choice of feature similarity measure leads to poor retrieval results in a TIR system. To achieve both the advantage of the region and geometric-based features, a two-component solution (TCS) has been proposed with region and geometric-based features [15,19,20]. Wei et al. [20] present two-component feature matching, which employs the Euclidean distance with a threshold and penalty value. It is important to decide the appropriate threshold and penalty value in the TCS. To avoid this problem, Anuar et al. [15] proposed a TIR technique employing two shape descriptors, the ZMs and edge gradient co-occurrence matrix (EGCM), with the TCS. In the first stage of TCS, the authors utilized the superior properties of the ZMs to retrieve similar trademarks in a database, which are fed into the next stage. In the second stage, a weighting strategy was employed to combine the similarity coefficients of the ZMs and EGCM for the candidate trademarks in the first stage. However, relying on a single feature is not a good way to effectively find the relevant image, despite the advantages of ZMs. Therefore, a number of studies have proposed structures to bridge the global and local properties of an image. Alajlan et al. [21] propose a curvature tree (CT) with a TAR feature to describe the topology of the trademark (foreground) and the holes (background), and they report better accuracy with this than by employing single region-based descriptors in a medical image database. For further retrieving a complex trademark with multiple objects, Liu et al. [22] presented the fusion of geometric features, including a blurred shape model, a Voronoi diagram for the density of an object and the spatial location of an object, based on a tree representation model (TRM) for retrieving similar trademarks. This TRM is similar to the CT, but it outperforms TIR. Although the CT and TRM have good retrieval results for complex multi-object images, both of these image representations have two drawbacks in terms of similarity measurement. The first drawback of the tree similarity algorithm is that it has a heavy computational burden in finding the maximum similarity subtree isomorphism (MSSI) with a recursive procedure. In additional, another drawback is a selection problem of the weighting values between multiple features in a tree node. A similar selection problem also existed in the TCS, the threshold value of a feature similarity.

There are many techniques that aim to avoid these selection problems such as Machine Learning techniques [19,23,24] and Relevance Feedback techniques [25]. The property of the image retrieval requires that the computer retrieves images that are similar to human perception and does not depend on rigid distance metrics to measure feature similarity. Tursun et al. [24] used a learning-based feature using Convolutional Neural Networks (CNN), which is the first study using CNN for trademark retrieval. It relies on finding an end-to-end mapping directly from the raw input to the required output, whereby the best representation for the problem at hand is obtained from the data directly. In the literature [2,26,27,28,29,30], fuzzy theory is employed to deal with the vagueness and ambiguity of human judgment in terms of image similarity. It provides flexible and fuzzy mapping from low-level features to high-level human concepts. Ionescu et al. [26] proposed a novel fuzzy similarity measure based on the generalization of the Hamming distance (FHD) for estimating the color histograms of two images. Chiu et al. [27] proposed an unsupervised fuzzy clustering algorithm to automatically classify database images into perceptually meaningful clusters. El Adel et al. [29] presented a fuzzy decision support system (FDSS) with three input features, three normalized distance vectors of shape, texture, and color, respectively, to measure the degrees of similarity between a query image and all reference images.

This study is motivated by developing an efficient TIR technique in real time application, which can rapidly extract visually similar trademarks from a large database. To improve computational efficiency and retrieval accuracy during the retrieval process, the simple and robust integration of global and local descriptors is employed to describe multiple objects in an image. In addition, the local descriptor utilizes a tree representation to organize multiple objects, and the five local geometric features of each object are assigned to the tree node. However, the heavy computational burden of isomorphism between two trees is an important issue. Therefore, we proposed a novel algorithm of tree similarity measure based on the fuzzy inference system (FIS). In this algorithm, the weighting of subtrees with an optimal assignment method significantly enhances the computational performance. Finally, we use a weighting strategy to integrate the similarity of global and local descriptors for the similarity coefficient between the query image and the database image. The remainder of this paper is organized as follows. Section 2 outlines an overview of the proposed TIR technique. Section 3 describes the processes of image representation: tree structure and feature extraction. Section 4 presents the similarity measurement. Section 5 contains the experimental setup and discusses the experimental result of the proposed technique. Finally, the conclusions of this study are given in Section 6.

2. Architecture of the Proposed Technique

This paper proposes an efficient retrieval technique to extract visually similar trademarks from a database. It aims to provide all possible trademarks in the database to the user, which resemble the shape of the queried trademark. For building a technique with high efficiency and accuracy, we use the integration of global and local descriptors for trademark retrieval. The entire architecture of the proposed technique is shown in Figure 1. This paper does not create any data for retrieving images from a large database; all of the images in the database are directly fed into the retrieval process to search similar images for the input query image. In the beginning of the retrieval process, the query image is inputted by the user, and then the multiple objects in the image are further represented as global and local descriptors by the image representation in order to obtain high efficiency retrieval performance. A tree structure based on the five local geometric features is employed in the local descriptors in order to completely describe the multiple objects. During the retrieval process, the tree structure is also used to organize multiple objects and the five local geometric features for the database image; the local geometric features are further assigned to the tree node for measuring the local similarity between the query and database image. Finally, the similarity coefficient between the query image and the database image is measured from the similarity of the global and local descriptors. Here, the local similarity is obtained from our newly proposed tree similarity measurement based on the fuzzy inference system (FIS). When all of the database images are retrieved, all of the similarity coefficients of the database image will be stored in the memory. The retrieved results are further arranged by their corresponding similarity coefficients. The details of the proposed technique are described in Section 3 and Section 4, respectively.

3. Image Representation

In recent years, trademark image designing has become more and more complicated. Thus clearly describing complicated images for retrieval is an important issue. To represent images compactly, a tree structure is employed to organize the multiple objects in an image, the global and local geometric features are directly extracted from several geometric descriptors, and the local features are further assigned to the tree node. A tree structure is a common method of representing the hierarchical nature of a structure. It simulates a set of linked nodes with a hierarchical tree structure with a root value and the subtrees of the children with a parent node. Figure 2 shows three processes in image representation: tree structure and global and local feature extractions.

3.1. Tree Representation

In this section, the connected component detection is first applied to detect the objects in an image. By using the authors’ previous work [31], this work can rapidly detect objects, and the holes are also regarded as an object for representation. Following object detection, all of the objects are described in a tree structure. In the tree structure, the primary object is first detected and defined as the root node of the tree structure. Next, the object that locates in the primary object is defined as the child of the root. If the child is a non-terminal node, it will be treated as a parent in the next tree level. This process will be repeated and is complete when all of the children are terminal nodes. This tree structure representation is similar to a curvature tree in the literature [21]. The difference is that the feature of a tree node is different. An example illustrating how to build a the tree structure is shown in Figure 3. The primary object, the white background object, is denoted as $O_{0,1}$, and it is set as the root of the tree structure. Further, the object that locates the primary object will be set as the child of the root. It is therefore stored in the next tree level, $j=1$, and denoted as $O_{1,1}$. Since the object $O_{1,1}$ is a non-terminal node, it can be seen in Figure 3 and three objects locate $O_{1,1}$. Those objects are defined as children of $O_{1,1}$ and are denoted as $O_{2,1}$, $O_{2,2}$, and $O_{2,3}$ in the next tree level, $j=2$. In level 3, it is the same as in the previous step, and the three objects are located in their parent node $O_{2,1}$ and are denoted as $O_{3,1}$, $O_{3,2}$, and $O_{3,3}$. The process is performed while $O_{2,2}$ and $O_{2,3}$ are terminal nodes here. After the hierarchical tree structure is built, which is presented as $T(O,F)$, the geometric features $F_f^{j,i}$ are extracted and assigned to the corresponding node $O_{j,i}$ in the tree structure. Consequently, the global and local feature extractions are introduced in the next subsection.

3.2. Feature Extraction

One of the key elements in a successful retrieval system is image feature description. The simple and robustness feature descriptors are employed in this paper to obtain high performance. The global geometric feature descriptor, Hu moments [32], and the five local geometric features [8] are used to describe the global image properties and the local properties of an image, respectively. An illustration of the five local geometric features is shown in Figure 4.

The global geometric feature, a Hu moment with a $p+q$ order, is defined as:

$$m_{pq}={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{x}^p{y}^{q}f(x,y)}}$$

(1)

where $f(x,y)$ is the image intensity at pixel (x, y) and $M\times N$ is the image size.

Then, the central moments are defined as:

$${\mu }_{pq}={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{\left(x-\overline{x}\right)}^p·{\left(y-\overline{y}\right)}^q·f(x,y)}}$$

(2)

where $\overline{x}=m_{10}/m_{00}$ and $\overline{y}=m_{01}/m_{00}$.

Invariant ${\eta }_{pq}$, with respect to both translation and scale, can be constructed from central moments by dividing through a properly scaled zero-th central moment ${\mu }_{00}$, which is shown as:

$${\eta }_{pq}={\mu }_{pq}/\left({\mu }_{00}{}^{\rho }\right)$$

(3)

where $\rho =1+\left(p+q\right)/2$.

Finally, the seven invariants with respect to translation, scale, and rotation are computed from the scale invariants up to order three. The formulas are described as follows:

$$\begin{array}{ll}{I}_1=& {\eta }_{20}+{\eta }_{02}\\ I_2=& {\left({\eta }_{20}-{\eta }_{02}\right)}^2+4·{\eta }_{11}^2\\ I_3=& {\left({\eta }_{30}-3·{\eta }_{12}\right)}^2+{\left(3·{\eta }_{21}-{\eta }_{03}\right)}^2\\ I_4=& {\left({\eta }_{30}+{\eta }_{12}\right)}^2+{\left({\eta }_{21}+{\eta }_{03}\right)}^2\\ I_5=& \left({\eta }_{30}-3·{\eta }_{12}\right)·\left({\eta }_{30}+{\eta }_{12}\right)·\left[{\left({\eta }_{30}+{\eta }_{12}\right)}^2-3·{\left({\eta }_{21}+{\eta }_{03}\right)}^2\right]+\\ & \left(3·{\eta }_{21}-{\eta }_{03}\right)·\left({\eta }_{21}+{\eta }_{03}\right)·\left[3·{\left({\eta }_{30}+{\eta }_{12}\right)}^2-{\left({\eta }_{21}+{\eta }_{03}\right)}^2\right]\\ I_6=& \left({\eta }_{20}-{\eta }_{02}\right)·\left[{\left({\eta }_{30}+{\eta }_{12}\right)}^2-{\left({\eta }_{21}+{\eta }_{03}\right)}^2\right]+4·{\eta }_{11}·\left({\eta }_{30}+{\eta }_{12}\right)·\left({\eta }_{21}+{\eta }_{03}\right)\\ I_7=& \left(3·{\eta }_{21}-{\eta }_{03}\right)·\left({\eta }_{30}+{\eta }_{12}\right)·\left[{\left({\eta }_{30}+{\eta }_{12}\right)}^2-3·{\left({\eta }_{21}+{\eta }_{03}\right)}^2\right]-\\ & \left({\eta }_{30}-3·{\eta }_{12}\right)·\left({\eta }_{21}+{\eta }_{03}\right)·\left[3·{\left({\eta }_{30}+{\eta }_{12}\right)}^2-{\left({\eta }_{21}+{\eta }_{03}\right)}^2\right]\end{array}$$

(4)

The seven invariant Hu moments, $H=\left\{I_1,I_2,\dots ,I_7\right\}$, are treated as the global features.

On the other hand, the local geometric descriptors are described in the following. The convexity calculates the ratio of perimeters of the convex hull $P_{convexhull}$ and the original contour $P$, which is defined as:

$$F_1=\frac{P_{convexhull}}{P}$$

(5)

The principal axes of an object can be uniquely defined as the two segments of lines crossing each other orthogonally in the centroid of the object and represent the directions with zero cross-correlation, which is called the eccentricity. The covariance matrix $C$ of a contour is considered before calculating the eccentricity, which is defined as:

$$C=\frac{1}{N}{\displaystyle \sum _{i=0}^{N-1}\left(\begin{array}{c}{x}_i-g_x\\ y_i-g_y\end{array}\right)}{\left(\begin{array}{c}{x}_i-g_x\\ y_i-g_y\end{array}\right)}^T=\left(\begin{array}{cc}{c}_{xx}& c_{xy}\\ c_{xy}& c_{yy}\end{array}\right)$$

(6)

where $\left(x_i,y_i\right)$ is the contour point of an object and $\left(g_x,g_y\right)$ is the center of gravity; moreover, $N$ is the number of contour points. The lengths of the two principal axes equal the eigenvalues ${\lambda }_1$ and ${\lambda }_2$ of the covariance matrix $C$, respectively. So the eigenvalues ${\lambda }_1$ and ${\lambda }_2$ can be calculated by:

$$\{\begin{array}{c}{\lambda }_1=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left[c_{xx}+c_{yy}+\sqrt{{\left(c_{xx}+c_{yy}\right)}^2-4\left(c_{xx}\times c_{yy}\right)-c_{xy}^2}\right]\\ {\lambda }_2=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left[c_{xx}+c_{yy}-\sqrt{{\left(c_{xx}+c_{yy}\right)}^2-4\left(c_{xx}\times c_{yy}\right)-c_{xy}^2}\right]\end{array}$$

(7)

Then, the eccentricity can be calculated:

$$F_2=\frac{{\lambda }_2}{{\lambda }_1}$$

(8)

Compactness is often defined as the ratio of squared perimeter and the area of an object $A_O$:

$$F_3=\frac{P^2}{A_O}$$

(9)

The circle variance is the proportional mean-squared error with respect to a solid circle:

$$F_4=\frac{{\sigma }_O}{{\mu }_O}$$

(10)

where ${\mu }_O$ and ${\sigma }_O$ are the mean and standard deviation of the radial distance from the centroid $\left(g_x,g_y\right)$ of the shape to the contour points $\left(x_i,y_i\right)$, respectively. They are the following formulae, respectively:

$${\mu }_O=\frac{1}{N}{\displaystyle \sum _{i=0}^{N-1}{d}_i}\mathrm{and}{\sigma }_O=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=0}^{N-1}{(d_i-{\mu }_O)}^2}}$$

(11)

and where $d_i=\sqrt{{(x_i-g_x)}^2+{(y_i-g_y)}^2}$.

Elliptic variance is the mapping error of a shape to fit an ellipse that has an equal covariance matrix in the shape $C_{elliptic}=C$ (cf. Equation (4)). It is practically effective to apply the inverse approach, yielding:

$$d_i^{\prime }=\sqrt{{\left(\begin{array}{c}{x}_i-g_x\\ y_i-g_y\end{array}\right)}^T·C_{ellipse}^{-1}·\left(\begin{array}{c}{x}_i-g_x\\ y_i-g_y\end{array}\right)}$$

(12)

$${\mu }_O^{\prime }=\frac{1}{N}{\displaystyle \sum _{i=0}^{N-1}{d}_i^{\prime }}\mathrm{and}{\sigma }_O^{\prime }=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=0}^{N-1}{(d_i^{\prime }-{\mu }_O^{\prime })}^2}}$$

(13)

Then, the elliptic variance is calculated by:

$$F_5=\frac{{\sigma }_O^{\prime }}{{\mu }_O^{\prime }}$$

(14)

After the image representation process, the proposed similarity measure algorithm based on the global and local descriptors is introduced in the next section.

4. Similarity Measurement

This section will show how to use the geometric features to measure the similarity between the query image and the database image based in terms of the global and local descriptors. There are two parts of the similarity measurement in our proposed technique: global and local. To achieve accurate and robust retrieval results, we combine the global and local similarities with a weighting strategy as a final output similarity coefficient. For measuring the partial similarity coefficient in the local part, we further proposed a core algorithm based on separated weighting subtrees and the fuzzy inference system (FIS), which is described in Section 4.2.

4.1. Global Similarity Measurement

The global dissimilarity is directly measured from $H$ using a Euclidean distance metric and is defined by Equation (15):

$$S_H(H^q,H^r)=\sqrt{({\displaystyle \sum _{i=1}^7{(H_i^q-H_i^r)}^2})}$$

(15)

where $H_i^q$ and $H_i^r$ are the i-th invariant Hu moments of the query and retrieved image, respectively. However, the proposed similarity measurement is based on feature similarity not dissimilarity. Therefore, the global similarity is obtained from Equation (16) within a range (0, 1) [32]. If the query image and the retrieved image are the same, the global similarity coefficient $S_H^{\prime }$ will be 1. The formula is defined as:

$$S_H^{\prime }(H^q,H^r)=\left(\frac{S_H-{\overline{S}}_H}{3{\sigma }_{S_H}}+1\right)/2$$

(16)

where ${\overline{S}}_H$ and ${\sigma }_{S_H}$ are the mean and standard deviation of $S_H$, respectively.

4.2. Local Similarity Measurement

In the local similarity measurement, the core algorithm is constructed from a concept of tree similarity measure based on the tree structure with a weighting strategy in order to provide an efficient retrieval process. It is called the weighting subtree. The local similarity coefficient $S_T$ is the sum of the similarities of the separated weighting subtrees. This algorithm does not need to find the maximum similarity subtree isomorphism (MSSI) between the two tree structures with the recursive process; it therefore is an efficient algorithm with the details being described in Section 4.2.2. The core function of the local similarity algorithm based on the tree nodes in the separated weighting subtrees is first introduced in the following subsection.

4.2.1. Node Similarity Measurement

The FIS is used to estimate the node similarity between the tree nodes with corresponding local features in the separated weighting subtrees. It is the core method of the local similarity measurement. The FIS aims to instruct the weight assignment among the five geometric features of a node. The process of the FIS is called the ‘fuzzification-fuzzy inference engine-defuzzification’ routine. The key step, the fuzzy inference engine, is executed by a logical rule consisting of some IF-THEN rules established using fuzzy logic.

• Fuzzification:
  The first step is to transform the input crisp values such as either ‘0’ or ‘1’ into grades of membership for the linguistic terms of fuzzy sets. The membership function is used to associate a grade with each linguistic term. Selecting a proper membership function is an application dependent problem. Some of most commonly used prototype membership functions are cone, exponential, and triangular functions. Two factors are considered when selecting the membership function for our system: the retrieval accuracy and the computational burden for evaluating a membership function. We chose the triangular function as the membership function since it has good expressiveness and high computational efficiency in the literature [30,33], as shown in Figure 5. The input and output linguistic terms of this paper are $\tilde{A}$ = {‘not similar’, ‘similar’} and $\tilde{B}$ = {‘not similar’, ‘similar’, ‘very similar’}, respectively. To satisfy the requirement of the membership function in the FIS, the input crisp values must be transformed into similarity values, $x_f$. The designed formula based on the Manhattan distance is defined as:

  $$x_f=1-\frac{D_f}{\max (F_f^q,F_f^r)}$$

  (17)

  where$f=1,\dots ,5$, $D_f=\left|F_f^q-F_f^r\right|$, and $F_f^q$ and $F_f^r$ are the f-th local geometric features of the query and retrieved image, respectively.
  Using Equation (17), the five features of a node described in Section 3, namely, (1) convexity, (2) eccentricity, (3) compactness, (4) circle variance, and (5) elliptic variance are transformed to the similarity crisp values, $x_f$. The similarity crisp values are further converted into grades of membership ${\tilde{x}}_f$ for the linguistic terms of fuzzy sets.
• Fuzzy inference engine:
  The fuzzy inference engine employs fuzzy IF-THEN rules to express input-output relationships and models the qualitative inputs and reasoning process for creating the output. The law to design or build a set of fuzzy rules is based on a human being’s knowledge or experience, which depends on each different actual application. The IF part is mainly used to capture knowledge using the elastic conditions, and the THEN part can be utilized to give the conclusion in linguistic variable form. This IF-THEN rule is widely used by the fuzzy inference system to compute the degree to which the input data matches the condition of a rule. In this paper, there are five input variables and two linguistic terms, so we have $2^5=32$ possible rules. One of the fuzzy IF-THEN rules is represented by:

  $$R^L:IF{\tilde{x}}_{1}is{\tilde{A}}_1^L,\dots ,and{\tilde{x}}_{5}is{\tilde{A}}_5^L,THEN\tilde{y}is{\tilde{B}}^L$$

  (18)

  where $L\in \left\{1,2,\dots ,N_L\right\}$ and $N_L$ is the number of fuzzy rules. In addition, ${\tilde{A}}_f^L$ and ${\tilde{B}}^L$ are denoted as the linguistic terms for the grade of membership, ${\tilde{x}}_f$ and $\tilde{y}$, in the L-th rule, respectively. Here we demonstrate the three fuzzy IF-THEN rules in our rule base as the following:

  $$\begin{array}{ll}{R}^1:& IF{\tilde{x}}_{1}issimilar,and{\tilde{x}}_{2}issimilar,and{\tilde{x}}_{3}issimilar,\\ & and{\tilde{x}}_{4}issimilar,and{\tilde{x}}_{5}issimilar,THEN\tilde{y}isverysimilar\\ ⋮& \\ R^7:& IF{\tilde{x}}_{1}isnotsimilar,and{\tilde{x}}_{2}isnotsimilar,and{\tilde{x}}_{3}issimilar,\\ & and{\tilde{x}}_{4}issimilar,and{\tilde{x}}_{5}issimilar,THEN\tilde{y}issimilar\\ ⋮& \\ R^{17}:& IF{\tilde{x}}_{1}isnotsimilar,and{\tilde{x}}_{2}isnotsimilar,and{\tilde{x}}_{3}isnotsimilar,\\ & and{\tilde{x}}_{4}issimilar,and{\tilde{x}}_{5}issimilar,THEN\tilde{y}isnotsimilar\end{array}$$

  (19)
  The output results are then aggregated using the Mamdani-type inference [33], a MAX-MIN compositional operator. There are two steps in the MAX-MIN compositional operator. In the first step, we use the minimum inference engine to integrate the fuzzy sets in the rule $R^L$, such that:

  $${\tilde{B}}^L(y)={\tilde{A}}_1^L(x)\wedge \dots \wedge {\tilde{A}}_5^L(x),L\in \left\{1,2,\dots ,N_L\right\}$$

  (20)

  where ${\tilde{A}}_f^L(·)$ calculates the membership value of its operand. Then, the second step integrates the overall fuzzy set ${\tilde{B}}^L(y)$ by standard union:

  $$\tilde{B}(y)={\displaystyle \underset{L=1}{\overset{N_L}{{\displaystyle \cup }}}{\tilde{B}}^L}={\tilde{B}}^1(y)\oplus {\tilde{B}}^2(y)\oplus \dots \oplus {\tilde{B}}^{N_L}(y)$$

  (21)
• Defuzzification:
  After the reasoning results, the fuzzy output is still a linguistic variable, and this linguistic variable needs to be converted into a crisp variable via the defuzzification process. Two commonly used methods of defuzzification are the center of area (COA) method and middle of maximum method (MOM). In this paper, the COA was used based on its better results; the formula of the COA is expressed as:

  $$\_nodefunc(O_{j,i}^q,O_{j,i}^r)=y^{*}=\frac{{\displaystyle \sum _{i=0}^{N_{ql}}\tilde{B}\left(y_i\right)y_i}}{{\displaystyle \sum _{i=0}^{N_{ql}}\tilde{B}\left(y_i\right)}}$$

  (22)

  where $O_{j,i}^q$ and $O_{j,i}^r$ are the tree nodes of the query image and the retrieved image, respectively, $N_{ql}$ is the number of quantization levels of the output, and $y_i$ is the amount of output at the quantization level $i$. Following the defuzzification process, the center of gravity $y^{*}$ of the fuzzy set $\tilde{B}(y)$ can be obtained. By using the FIS, the similarity between two nodes, $O_{j,i}^q$ and $O_{j,i}^r$, can be estimated by the core function, $\_nodefunc()$, based on their five feature distances.

As mentioned above, the node similarity of the weighting subtree in local similarity measurement is presented. In the following, the details of the novel tree similarity measure based on separated weighting subtrees are presented to evaluate the partial similarity of local parts.

4.2.2. Weighting Subtree Similarity Measurement

The weighting subtree constitutes a subtree structure and the corresponding weighting coefficients. The tree represents a set of linked nodes in a hierarchical tree structure with a root and subtrees of children with a parent node. Any one of the nodes at each level has exactly one parent node, except the root, whereas a node can have any number of children. The structure of the weighting subtree is declared with only two levels, and if a node has any children, the node and its children will be separated as a subtree. Accordingly, the tree may be separated into several subtrees. On the other hand, the five local features (Section 3.2) are assigned to the corresponding node. For achieving high discrimination, the weighting coefficients are assigned to different tree levels. This provides the distinguishing features for the different tree levels. In this study, the designed weighting of the weighting subtree parent level will be set as $w_{parent}^{st}=0.5$, and the weighting of the child level is designed as $w_{child}^{st}=0.5/n$; $n$ represents the amount of children, st represents the index of the subtrees, and the sum of the weighting coefficients equals 1. Since the root node represents the background of the retrieved image, it does not calculate the local feature. Therefore, the weighting value will be set to 0 and the weighting of the child level is designed as $w_{child}^{st}=1.0/n$. An example shows how to separate the subtrees and design the weighting of the separated subtree; it is shown in Figure 6. In this case, two weighting subtrees, Figure 6b,c, can be separated from the example tree. The weighting of each subtree level in each subtree can be calculated as 0.5, 0.1667, 0.5, and 0.25, respectively.

After the concept of the weighting strategy is given, the two sets of weighting subtrees in the two different trees, ${\mathrm{ST}}^q$ and ${\mathrm{ST}}^r$, are extracted, and the similarity between the two trees, $T^q$ and $T^r$, can be further estimated.

During the similarity estimation between $T^q$ and $T^r$, the cross-matching strategy is used to obtain the maximum similarity between the two weighting subtree sets. Further, in the similarity estimation of the two weighting subtrees, we estimate the similarity from the subtrees at the same level. This means that the similarities of the two weighting subtrees are individually estimated by their parent level and child level. The part of similarity in the child level is calculated from the child nodes, and therefore the number of child nodes may cause an unmatched problem in the two different weighting subtrees. An example with a different count of child nodes is given in Figure 7. It shows that the two subtrees in the sets of ${\mathrm{ST}}^q$ and ${\mathrm{ST}}^r$, respectively, have a different number of child nodes ($n\ne m$) in Figure 7a,b. $n$ and $m$ represent the amount of the children of subtrees $s{t}^q$ and $s{t}^r$, respectively.

For estimating the similarity in the child level with the unmatched problem, the Hungarian algorithm is employed to solve this problem. The Hungarian algorithm [21] is an optimal method to solve the assignment problem with minimum cost in polynomial time, and it works on a dissimilarity matrix. The elements of the matrix $\Phi$ in the similarity version are similarity coefficients estimated from the pair nodes in the child level. Since the computation of the Hungarian algorithm is based on the dissimilarity matrix, each element of the matrix in the similarity version is subtracted from an upper bound value to obtain the dissimilarity version of the matrix. The upper bound value is chosen as the maximum value of the matrix $\Phi$ in the similarity version.

After the two sets of weighting subtrees, ${\mathrm{ST}}^q$ and ${\mathrm{ST}}^r$, are obtained from the two trees, further the local similarity coefficient between two trees, $T^q$ and $T^r$, can be estimated. The processes of the local similarity measurement are introduced below. First, we estimate the similarity of pairs of subtrees, $s_{ij}^{st}$, in the two sets , which is defined as:

$$s_{ij}^{st}=w_{parent}^{st}·\_nodefunc(O_{1,1}^q,O_{1,1}^r)+\varphi$$

(23)

where $i\in \left\{1,2,\dots ,s{t}^q\right\}$, $j\in \left\{1,2,\dots ,s{t}^r\right\}$, $s{t}^q$ and $s{t}^r$ are the total number of subtrees in ${\mathrm{ST}}^q$ and ${\mathrm{ST}}^r$. $\_nodefunc()$ is the core function, which estimates the similarity for a pair of nodes, and $\varphi$ is the sum of the similarity of the child nodes, which is defined as:

$$\varphi =w_{child}^{st}·\left(\max \left(\Phi \right)·\min (n,m)-Hungarian(\max (\Phi )\ast ones(n,m)-\Phi )\right)$$

(24)

where $Hungarian()$ represents the Hungarian algorithm, and $\Phi$ presents the similarity matrix. The elements of the similarity matrix $\Phi$ are represented as follows:

$${\mathrm{\Phi }}_{ij}=\_nodefunc(O_{2,i}^q,O_{2,j}^r)$$

(25)

where $i\in \left\{1,2,\dots ,n\right\}$, $j\in \left\{1,2,\dots ,m\right\}$, and n and m are the total number of child nodes in $T_{sq}^q$ and $T_{sr}^r$, respectively.

In the same way the Hungarian algorithm for solving the unmatched problem in the child level is utilized to estimate the maximum similarity between the two trees, $T^q$ and $T^r$. Therefore, the overall similarity between the two subtree sets is estimated by the Hungarian algorithm, which is given by:

$$S_T(T^q,T^r)=\max \left(S^{st}\right)·\min (s{t}^q,s{t}^r)-Hungarian(\max (S^{st})\times ones(s{t}^q,s{t}^r)-S^{st})$$

(26)

where $S^{st}$ presents the similarity matrix. The elements of the similarity matrix $S^{st}$ are obtained from Equation (22). Finally, the local similarity coefficient $S_T$ between the two trees can be estimated by using Equations (22)–(25).

After the global and local similarity measurements are presented in Section 4.1 and Section 4.2, the final similarity coefficient is computed by:

$$S=w_H·S_H^{\prime }+w_T·S_T$$

(27)

where $w_H+w_T=1$, $w_H$ and $w_T$ are the weights of the global and local similarity coefficients, respectively.

5. Experimental Results and Discussion

This section describes a series of experimental results showing the performance between the proposed technique and other two competitive approaches, Zernike moments with edge gradient co-occurrence matrix (ZMEG) [15] and Zernike moments with local directional pattern (ZMLDP) [12]. In the trademark retrieval system, efficiency and accuracy are common indices for evaluation. Accuracy can be defined in terms of precision and recall rates. The precision rate can be defined as the percent of retrieved images similar to the query image among the total number of retrieved images. The recall rate is defined as the percent of retrieved images similar to the query image among the total number of images similar to the query in the database. Furthermore, the Bull’s eye score (BES) and the average normalized modified retrieval rank (ANMRR) are used to evaluate the retrieval performance. All experiments were performed on a personal computer with an Intel Core i5 3.2 GHZ CPU and 8 GB of memory using Microsoft Visual Studio 2010 (Microsoft, Redmond, WA, USA).

5.1. Experiment Setup

To achieve objective evaluation, an large trademark database is collected from three different image databases, including MPEG-7, [20,22]. The aim is to observe the performance of the proposed technique in terms of its retrieval accuracy and efficiency through the large trademark database. The well-known MPEG-7 CE-2 region-based database consists of about three thousand binary trademarks. For the sake of simplicity, MPEG-7 is an abbreviation of the MPEG-7 CE-2 region-based database in this paper. Although MPEG-7 provides a set of trademarks, the images are not exclusively designed for performance evaluation of a TIR system. Further, classifying all the images of MPEG-7 is also extremely difficult work. Therefore, we use the existing seven group images from [20,22], where five group images are from MPEG-7. These seven group images will be the query images for observing the retrieval performance of the proposed technique. As suggested above, the large trademark database of this paper contains about 1800 trademark images, including 12 different classes and 416 query images, as shown in Figure 8.

As mentioned above, the performance indices, except efficiency, including (1) precision and recall (P-R) rates, (2) BES, and (3) ANMRR are described in the following. The precision and recall rates are presented as:

$$\begin{array}{c}precision=n_{sl}/n_{rt}\\ recall=n_{sl}/n_{rq}\end{array}$$

(28)

where $n_{sl}$ is the total number of relevant retrieved images, $n_{rt}$ is the total number of retrieved images, and $n_{rq}$ is the total number of relevant images in the entire database.

The bull’s eyes score is measured based on the top $2·n_{rq}$ retrieved images and defined as:

$$BES=\frac{n_{sl}}{n_{rq}}$$

(29)

where $n_{sl}$ is the total number of relevant images in the top $2·n_{rq}$ retrieved images.

The last performance index, ANMRR, is a normalized ranking method. This index is defined as:

$$ANMRR=\frac{1}{n_{rq}}{\displaystyle \sum _{i=1}^{n_{rq}}NMRR(i)}$$

(30)

$$NMRR(q)=\frac{MRR(q)}{2·n_{rq}+0.5-0.5·n_{rq}}$$

(31)

where the NMRR score ranges from 0 to 1, where 0 indicates perfect retrieval. The modified retrieval rank (MRR) is calculated from the average ranking rate (AVR) and is defined as:

$$MRR(q)=AVR(q)-0.5-\frac{n_{rq}}{2}$$

(32)

$$AVR(q)={\displaystyle \sum _{k=1}^{n_{rq}}\frac{Rank(k)}{n_{rq}}}$$

(33)

where $Rank(k)$ is the rank of the relevant index in the retrieved images.

After the indices are defined, the performances of the proposed technique and the other two competitive approaches are evaluated by those indices in the following experiments. In order to clearly certify our technique as better than the two competitive approaches, the experiential set up of the two competitive approaches is introduced below. In the first approach, ZMEG, there are two important factors to control the retrieved performance, which are the weighting values of the global feature, Zernike moments (ZM), and of the local feature, namely, the edge gradient co-occurrence matrix (EGCM), similarities, and similarity metric. In the following experiments, we set the weighting values to 0.3 and 0.7, respectively. Additionally, the similarity metric is using Manhattan distance for the global and local features. Regarding the second approach, ZMLDP, we analyze a variety of local features combined with the global features in the feature extraction. Therefore, we choose the best feature combination, ZM and local directional pattern (LDP), as the index of the literature. For the similarity metric, the global and local feature metrics use the Euclidean distance (L₂ norm) and the Chi-square distance, respectively.

5.2. Analysis for Parameters Setting

As mentioned in Section 4.2.2, the two critical weights of global and local in the final similarity measurement are very important and will impact the performance directly. Therefore, we first use the test database to select the critical weights. Here, the range of test weighting values, $w_H$ and $w_T$, are from 0 to 1, increasing and decreasing by steps of 0.1, respectively. The performance indices, BES and ANMRR, are used to evaluate the performance using the test weighting values. The results are shown in Figure 9, where the best results are shown when $w_H$ = 0.7 and $w_T$ = 0.3; the BES and ANMRR are 71.65% and 0.328, respectively. Based on this test, the two critical values are set to 0.7 and 0.3 for the following experiments.

5.3. Analysis for the Effect of Fuzzy Inference System

This paper proposed an efficient similarity measure algorithm for tree structures based on FIS. The FIS is the core method in the local similarity measurement. It aims to instruct the weight assignment among the five geometric features for each node. In this experiment, we demonstrate the effect of FIS using precision-recall rates. We further use three different weighting sets to manually assign the similarities of five geometric features between two tree nodes and compare these with the performance of the FIS, as shown in Figure 10. The first weighting set for five geometric features, ‘convexity’, ‘eccentricity’, ‘compactness’, ‘circle variance’, and ‘elliptic variance’, is {0.2, 0.2, 0.2, 0.2 and 0.2}; the second set is {0.25, 0.25, 0.15, 0.175, 0.175}; and the third set is {0.22, 0.22, 0.18, 0.19, 0.19}. The ratios of the five similarities are decided by the importance of the features; on the other hand, this depends on the human’s experience. The result shows that the use of FIS is superior to the manual weighting strategy and adaptively constructs the weighting assignment among the five geometric features.

5.4. Performance of the Precision-Recall Rates

To assess the retrieval performance of the proposed technique, all of the database images are represented as the query image. Figure 11 shows the obtained average precision rate with respect to the different scales of recall rate. The results show that the proposed technique has surpassed the overall performance of the other competitive methods, producing an improvement of 19.43% and 26.78% compared to the ZMEG and ZMLDP precision/recall performance, respectively. It is also interesting to observe that the precision/recall performance of the proposed technique without the global descriptor, Hu moments, is better than that of ZMEG after the 30% recall rate. This indicates that, although the local descriptor with the proposed tree similarity algorithm has not been able to provide effective retrieval performance for multi-object images, it is still useful and worth combining with the global property feature. To clearly show the performance of each class, we further use the BES and retrieval ranking to compare the performance between our technique and the other two approaches in the next experiment.

5.5. Performance of Bull’s Eye Score and the Retrieval Ranking

In this experiment, all of the classes are used to evaluate performance using the Bull’s eye score and the ANMRR value. Figure 12 and

Table 1. Averages of the Bull’s eye and average normalized modified retrieval rank (ANMRR) scores.

Methods	Bull’s Eye Score	ANMRR
Proposed technique	72.26%	0.324
ZMEG [15]	52.7%	0.491
ZMLDP [12]	41.68%	0.56

show the Bull’s eye score and the ANMRR value of the proposed technique and the two competitive approaches, ZMEG and ZMLDP. The results show that the average BES of the proposed technique exceeds ZMEG and ZMLDP by 19.56% and 30.58, respectively. In terms of ranking capability, our technique also provides better performance, where the ANMRR score improves by 0.167 and 0.236, respectively. As seen in the experiment results, the proposed technique is better than the two competitive approaches.

However, the value of a TIR system is to search the trademark images that are highly isomorphic, invariantly rotated, and scaled to the query image. Therefore, we illustrate the comparison of the performance of the ranking capability of our technique with that of the competitive approaches. Here, the ranking capability is computed by the precision, and we set that $n_{rt}$ as half of the number of classes in Equation (28). The largest precision represents the best retrieved result. Figure 13 shows the retrieval results of the query image in class 1 by using the proposed technique and the two competitive approaches, but the ranks of results do not include the query image. Here, we search the 43 images, half the class 1, in the database for the query image. The red Arabic numeral is presented as the non-relevant image. The results show that, comparatively, the proposed technique provides the better ranking performance for this image since its precision is 95.34%. It is observed that the first 40 retrieved images are correctly retrieved, and there are only two incorrect images in the first 43 retrieved images, half of the number of the first class. Additionally, the precision of ZMEG is 58.14%, as there are 18 non-related images in the first 43 retrieved images, and the precision of ZMLDP is 55.81%, as there are 19 non-related images in the first 43 retrieved images. In the above experiments, the results show that the proposed technique can effectively and accurately find the relevant images in a database.

5.6. Performance of Efficiency

The computationally most expensive parts of our technique are the local descriptor in image representation and the local similarity measurement. In the local descriptor, the tree structure is first used to organize k objects in an image; therefore, the order of the tree structure grows linearly with the number of objects and holes in the image. Next, the local features of each tree node are obtained by the five geometric features: convexity, eccentricity, compactness, circle variance, and elliptic variance. The computation of these five features is based on the N points of the boundary. In [8], the time complexity of these five features is $O(N)$. Accordingly, the total time complexity of extracting the local descriptor is $O(k·5·N)$ in the worst case, i.e., $O(k·N)$.

The local similarity measurement is mainly based on the weighting subtree and FIS. Therefore, the computational complexity of the local similarity algorithm is dependent on the number of subtrees, the number of children of a subtree node, and the operation time of FIS, $\_nodefunc()$. For obtaining the maximum similarity between two subtree sets of $s{t}^q$ and $s{t}^r$ subtrees, the bipartite matching method using the Hungarian algorithm is used to assign the $s{t}^q·s{t}^r$ similarities. The Hungarian algorithm has a polynomial-time complexity of $O(n_1·n_2{}^2)$ [21]. In addition, bipartite matching is also used in the similarity measurement of the child level between two subtrees. Here, we assume that the number of child nodes per subtree is the same; hence, the $s{t}^q$ and $s{t}^r$ subtrees have n and m child nodes, respectively. Let n and m be the maximum number of child nodes. Therefore, the local similarity measurement has a complexity of $O(s{t}^q·(s{t}^r{)}^2+s{t}^q·s{t}^r·(n{m}^2))$ without the computational complexity of the node similarity. In this paper, Mamdani-type inference is used in our FIS. This inference has $O(x_f·N_L)$ time complexity, with $x_f$ and $N_L$ being the number of input dimensions and the number of fuzzy rules [34], resepctively. Finally, the total time complexity of the worst case is $O(s{t}^q·(s{t}^r{)}^2+s{t}^q·s{t}^r·(n{m}^2))+n·m·x_f·N_L$.

This experiment also provides an analysis of the efficiency performance of the retrieval system. Twelve classes (416 trademark images) are used to assess the computational burden. The efficiency index is the average execution time for the twelve classes.

Table 2. Comparison of computation times in the retrieval process (Unit: ms).

Approach	Image Representation	Similarity Measurement	Full Retrieval Time
Proposed technique	1.65	0.04	1.69
ZMEG [15]	254.87	0.001	254.871
ZMLDP [12]	325.04	0.021	325.061

shows the computational burden for the proposed technique, ZMEG, and ZMLDP. As can be seen in terms of image representation, the computation of the global and local descriptors in the proposed technique is highly efficient. In particular, the proposed novel similarity measure based on the weighted subtree and the corresponding fuzzy sets is more efficient than that of ZMLDP. The computational advantage range compared to that of ZMEG and ZMLDP is between 151 and 193 times greater. Clearly, the results of the proposed technique are superior to the results of the other approaches. Based on the convincing experimental results, the proposed technique not only provides high accuracy but also retrieves the query image in 2 ms.

5.7. Discussion

There are some limitations of the proposed technique. These above-mentioned experiments raised the idea that the proposed technique has surpassed the overall performance of the other competitive approaches; however, it does not perform well in the cases of classes 2, 4, 5, 8, 9, and 12, especially for classes 2 and 5. Therefore, we can nevertheless confirm that the proposed technique is slightly sensitive to the structural changes of tree and non-rigid body deformation. The two example images from classes 2 and 5 are shown with the degree of variant in Figure 14. The first three columns of Figure 14 show the images of the structural changes of the tree, and the other three columns show the images of the non-rigid body deformation. In the cases of test classes 2 and 5, the BESs of our system are less than those of ZMEG at 8% and the ANMRR scores are also slightly less than those of the ZMEG at 0.07. This indicates that the proposed technique is not sufficiently capable of handling to the structural changes of the tree or significantly deformed images. Nevertheless, an aim of the TIR system is to help the user to find visually similar images from the database such as the types of invariance of rotation, scaling, and translation, as well as rigid body deformation. We further observe the retrieval results of our system for the query image from class 5, as shown in Figure 15. The result shows that, although only 13 of the top 32 images in the retrieved result are relevant images, the shape of the bat is similar in the first 11 relevant images. As a consequence, we speculated that the proposed technique appears to be consistent with the aim of TIR system.

6. Conclusions

This study proposes an efficient retrieval technique to extract visually similar trademarks from a database of trademark images, especially in terms of the similarity measurement. A novel algorithm for a tree similarity measure based on the weighting subtree and FIS is introduced to measure the similarity between two tree structures. The major two components of the tree similarity algorithm are (1) the use of the weighting subtree with the optimal assignment method to improve the computational performance and (2) the proposition of using FIS in order to instruct the weight assignment among the five geometric features of a tree node. In addition, the integration of global and local geometric descriptors also has the value of a TIR system, which is invariant under rigid transformations and scaling and is also insensitive to small boundary deformations. The experimental results show that the proposed technique is not only superior to the overall retrieval performance of the two competitive approaches but also has over 151 times the computational advantage.