Room Response Equalization—A Review

Abstract

Room response equalization aims at improving the sound reproduction in rooms by applying advanced digital signal processing techniques to design an equalizer on the basis of one or more measurements of the room response. This topic has been intensively studied in the last 40 years, resulting in a number of effective techniques facing different aspects of the problem. This review paper aims at giving an overview of the existing methods following their historical evolution, and discussing pros and cons of each approach with relation to the room characteristics, as well as instrumental and perceptual measures. The review is concluded by a discussion on emerging topics and new trends.

1. Introduction

When sound is reproduced by one or more loudspeakers, the perception of the desired auditory illusion is modified by the listening environment. To some extent this may be seen as positive, since spaciousness and depth is added, but the environment and the sound reproduction system can also introduce undesired artifacts. Excessive reflections or resonances within the listening environment may result in an undesired alteration of the auditory illusion. A non-ideal reproduction system may even add some artifacts (e.g., frequency band extension, nonlinearities) to the original sound.

Room response equalization (RRE) has been studied in theory and applied in practice for improving the quality of sound reproduction contrasting the detrimental effects of the room environment and reproduction system. In an RRE system, the room transfer function (RTF) characterizing the path from the sound reproduction system to the listener is equalized with a suitably designed equalizer that can be realized in several manners. The basic idea is to measure the room impulse response (RIR) using a microphone, and then obtain the equalizer through its inversion. However, several issues influence this method, and thus a wide variety of techniques have been developed over the last 40 years. The reader should be aware that many different names have been used in the literature for RRE, such as “room equalization”, “room correction”, “room compensation”, “room inversion”, “room dereverberation”, “dereverberation”, “reverberation reduction”, and others. In this review, the collective term RRE is used to denote any technique that aims to design an equalizer from measurements of the RTF.

Borrowing the words of [1], there is a “multidimensionality of alternatives for room inverse filter design”. In particular, the inversion of the RIR can be performed considering a non-parametric approach such as least-mean-squares or direct inversion of the frequency response [1,2], a parametric approach such as autoregressive-moving average (ARMA) modeling [1,3], or temporal decay control at low frequency [1,4]. However, as reported in [1], this is not the only classification possible: RRE can also be classified into minimum- or mixed-phase. The former aims only at the equalization of RTF magnitude, while the latter also acts on the excess-phase RTF component.

In this review paper, a general classification is presented aiming at a broader view on the state-of-the-art in RRE. Figure 1 provides a conceptual scheme of this classification, clustering the various techniques that will be presented in the following. As shown in Figure 1, the RRE approaches are divided into single-point (single-input/single-output—SISO, multiple-input/single-output—MISO) and multi-point (single-input/multiple-output—SIMO, multiple-input/multiple-output—MIMO) room equalizers. A single position room equalizer estimates the equalization filter on the basis of the measurement in a single location of the RTF [5]. It is effective only in a limited zone around the measured point (of the size of a fraction of the acoustic wavelength). In reality, the RTF varies significantly with respect to the position in the room [6,7] and time [2], as the room can be considered a “weakly non-stationary” system [8]. To enlarge the equalized zone and to contrast the room response variations, multi-point equalizers have been proposed [9]. A multi-point room equalizer uses multiple measurements of the RTF at different locations in order to design the equalizer. These approaches can be used for fixed and adaptive equalization. The former is based on RTFs measured at fixed positions at a certain time. The latter is capable of tracking and adapting to changes in the room response due to its time varying nature resulting for instance from temperature changes or movement of people or other obstacles. Different pre-processing techniques are applied to contrast audible distortions caused by fixed equalization in scenarios where RTFs vary. Different equalizer design techniques can also be adopted (classified in the following as minimum-phase or mixed-phase). More recently [10], equalization in spatio-temporally transformed domains for the adaptive equalization of massive multichannel sound reproduction systems has been investigated, and is presently a topic of active research.

This paper aims to provide an up-to-date review on RRE, discussing the pros and the cons of each technique, following the historical evolution. It is worth underlining that the RRE problem is analyzed from the viewpoint of impulse response analysis. All approaches that are not directly based on RIR analysis (e.g., parametric or graphic equalizers) are not discussed. The reader is referred to [11] for a comprehensive review on this topic. Another research field related to RRE which is not addressed in this paper is sound spatialization. The reader is referred to [12] for a recent review.

This review article is organized as follows: Section 2 describes the characteristics of room impulse responses and its perception by the human auditory system. Section 3 introduces the basic concept of RRE, explaining the main challenges in inverting room responses. Section 4 describes the approaches used for equalizer design following their historical evolution. Section 5 discusses pre-processing techniques used to cope for RIR variations by exploiting human perception. Section 6 covers the evolution from single-point to multi-point equalization using multiple microphones placed within the room. Section 7 reports adaptive approaches for RRE in the framework of single-point and multi-point equalization. Section 8 introduces innovative approaches following a wave-theoretical view on the problem. Section 9 describes instrumental and perceptual measures used for state-of-the-art evaluation of RRE approaches. Section 10 reports emerging methods and new trends in the field. Finally, Section 11 concludes this review.

2. The Room Response and Its Perception

The characteristics of the room response in the time and frequency domain are related to the acoustic properties of the environment that influence human perception. Due to this aspect, it is sensible to shape the impulse response analysis in order to handle important issues that should be considered in the RRE procedure to reach a sound listening improvement. This includes knowledge on human perception and psychoacoustics to be exploited explicitly in the equalization procedure.

An impulse response, obtained from a sound source in a specific position of a real environment, can be divided into three parts [13]: (i) direct sound; (ii) early reflections, and (iii) late reflections, as reported in Figure 2a. The transition from early reflections to late reflections is given by the mixing time, estimating the time elapsed from early to late reflections. It can be estimated in several manners [14,15]. Direct sound and early reflections are fundamental for the localization of the sound source and perception of its timbre [16,17,18], while the late reverberation provides cues on the spaciousness of the room [19]. Studies on the perception of reflections and their influence on the timbre can be found in [19,20,21,22,23,24,25]. The spectral content of direct and reflected sound is different. Walls, drapes, and upholstery typically absorb the high frequencies of reflections. The effect is boosted by multiple reflections, with the late reverberation typically having a much lower energy in the high frequencies.

At low frequencies, the wavelength is comparable to typical room dimensions: standing waves may appear in a room for steady-state signals, resulting in well defined position-dependent maxima and minima of the magnitude response. At these frequencies, the room response has a smooth behavior characterized by well separated resonances and notches, as illustrated in Figure 2b. The resonances and notches are determined by interference patterns caused by the direct sound and reflections, with notches appearing when the path-length difference is an odd number of half wavelengths. The notches become increasingly dense with increasing frequency. For frequencies greater than the Schroeder frequency [13], the frequency response becomes extremely irregular. Spectral peaks are more audible than notches [20], but wide-bandwidth notches are also audible [26]. At high frequencies, the peaks and notches strongly depend on the position in the room and on factors like the room humidity and temperature [27,28,29] or obstacle movements [30,31,32,33,34]. It must be pointed out that these large variations in the response have little influence on the subjective impression of the listener [18]. It has been suggested [19,22,24] that the ear is more sensitive to signal onsets (i.e., to the full spectrum of the initial part of the RIR) and that it largely ignores the high-frequency components of the late reverb [35]. This aspect should be considered in the equalizer design.

The perception of high frequencies is particularly affected by the frequency resolution of the human auditory system. The resolution of the ear is nonlinear and nonuniform with frequency, with an almost logarithmic dependency on frequency [36]. This aspect has led to the introduction of psychoacoustic frequency scales in the equalizer development with the aim of modifying the spectral content according to human perception. The mel scale [37], the Bark (critical band rate) scale [38], and the ERB (equivalent rectangular bandwidth) scale [39] are examples of psychoacoustic frequency scales that usually build on a filterbank model of hearing. The mel scale is a perceptual scale of pitches judged by listeners to be equal in distance from one another. The Bark scale is based on the critical bands (i.e., the bandwidth of the auditory filters modeling hearing and frequency masking at different frequencies). The ERB is also related to the Bark scale and to auditory filters, since the ERB filters pass the same amount of energy as the auditory filters they correspond to. It can be concluded that the logarithmic frequency scale of human hearing largely explains the low sensitivity to peaks and notches at high frequencies, and this aspect should be considered in the equalizer design.

The temporal integration and masking properties of the human auditory system also affect the perception of reflections. The ear perceives sounds by integrating them with a window of around 60 ms duration, having an equivalent rectangular duration of 5 ms [40]. The window is asymmetrical, with a slower rise and faster decay. The ear is insensitive to temporal events shorter than about 2 ms [41]. Masking indicates a condition where sounds which presented isolated would be audible are hidden by the presence of a higher level sound (the masker). We can have both simultaneous and non-simultaneous masking. Simultaneous masking depends on the frequency of the masker and the masked signal. It has its maximum effect when the two differ by less than a critical bandwidth. It diminishes quickly when the frequency of the masker is greater than the masked signal, while it diminishes more slowly when the frequency of masker is lower than the masked signal [42,43]. Non-simultaneous masking refers to situations where the masker and masked sound are separated in time. It is divided into backward masking, with the masked sound preceding the masker, and forward masking, with the masked sound following the masker. Backward masking is quite limited in time [43]: its effect disappears after 15–20 ms [44,45], with the most significant portion fading out after 5 ms [46]. Forward masking has a longer extension of 100–200 ms. Its behavior is similar to simultaneous masking, and it depends on the frequency relationship between masker and masked sound. According to [39], its effect starts as simultaneous masking and then fades out over time with a straight line in a graph representing the masking reduction in dB versus time [43]. An average forward masking curve has been introduced in [43,47]. For the first 10 ms, the curve has a constant value equal to −9 dB, which is the maximum level of masking in [19], and then it decays over time. This phenomenon can be exploited in the equalization procedure as discussed in the next sections.

The audibility of room reflections also depends on the direction of arrival of the direct sound and reflections with respect to the listener [48], on the loudness of the direct sound (reflections can be more easily perceived with louder direct sound), on the kind of signal [19], and on the spectral content of direct sound and reflections (masking has a stronger effect if the spectral content of direct sound and reflections coincides) [48].

In the following sections, different RRE techniques are discussed highlighting the problems following from the physical properties of the room response and how the characteristics of the human auditory system can be included.

3. Invertibility of the Room Response

The first research paper on RRE can be attributed to Neely and Allen in 1979 [5]. In their seminal paper, they studied the invertibility of the RTF and implications. Considering the RTF of a synthetic room, they showed that if the reflectivity of the wall is low (below 36%) the RTF is minimum-phase and thus invertible. On the contrary, with larger wall reflection coefficients, as those of typical rooms (in the range 70%–90%), the RIR is non-minimum-phase. However, it is still possible to equalize the minimum-phase part of the room response (i.e., the amplitude response and the minimum-phase part of the phase response) by factoring the RTF $H\left(z\right)$ into a product of a minimum-phase term $H_{\mathrm{m}}\left(z\right)$ and a stable all-pass filter $A\left(z\right)$,

$$H\left(z\right)=H_{\mathrm{m}}\left(z\right)·A\left(z\right).$$

(1)

The equalization filter is simply computed by taking the inverse z-transform of the reciprocal of the spectrum of $H_{\mathrm{m}}\left(z\right)$. By listening to the result of the minimum-phase equalization, Neely and Allen reported that “The room effect had been removed, but a tone, much like a bell chime, sounded in the background” [5].

The original approach of [5] is in reality affected by several problems, many discovered by researchers only in later studies. Following the chronological order in which these problems were addressed:

• When the room response is non-minimum-phase, an exact inverse cannot be implemented with a single sound source, since the inverse is either unstable or acausal.
• The exact equalization of the room response—or of its minimum-phase part—requires very long filters.
• The equalizer is affected by any imperfection in the measurement of the room response [6,34].
• The room response strongly depends on the location of the loudspeaker and the microphone used for the measurement [6,31,32,33,34,48,49].
• Exact equalization is possible only in one location, and the extent of the equalized zone is just a fraction of the acoustic wavelength [6]. At high frequencies, the equalized zone can be smaller than the inter-aural distance of the ears (around 18 cm).
• The notches of the room response—which are affected by the noise floor—are highly boosted by the equalizer with the generation of an often audible tone-like noise (the bell chime experienced by Neely and Allen) [50,51,52].
• The room response is actually slowly time-varying, affected by humidity and temperature [28,29] and by movement of people or other obstacles in the enclosure.
• The human ear is sensitive to the excess-phase of the RTF [53].
• The equalizer should preserve the natural roll-off of loudspeakers at low and high frequencies [54,55]. Amplifying these frequencies could cause an unnatural boost of the loudspeaker response, causing nonlinear effects, energy dissipation, and possible damages.

In what follows, we will discuss the different solutions that have been devised in order to contrast the above-mentioned problems. In particular, we will review the techniques used to design the equalizer, considering both minimum-phase and mixed-phase equalization strategies, and pre-processing techniques used to contrast the effects of the variations of the room response with position and time. As much as possible, we will try to follow the chronological order in which the techniques were proposed to illustrate the evolution of RRE.

4. Equalizer Design Techniques

In the techniques we discuss, the room response equalizer is designed on the basis of measurements of the RIR or RTF in one or more locations within the desired listening area. As we will see in Section 5, the room response is pre-processed in most cases in order to contrast some of the detrimental effects discussed in Section 3. In any case, a prototype room response is usually obtained and used for the equalizer design.

Most of the equalizer design techniques can be classified into the following five classes:

• Homomorphic filtering;
• Linear predictive coding (LPC) analysis;
• Least-squares (or other) optimization techniques;
• Frequency domain deconvolution;
• Multiple-input/multiple-output inverse theorem (MINT) solutions.

The first two techniques are generally used for minimum-phase equalization, the latter three for mixed-phase equalization.

4.1. Homomorphic Filtering

Homomorphic filtering was already proposed for minimum phase equalization in the seminal paper of Neely and Allen [5], but many other authors introduced modified versions of the homomorphic technique [56,57,58]. In homomorphic filtering, the minimum phase part of the room response is extracted from the causal part of the complex cepstrum. A stable infinite impulse response (IIR) equalizer is then obtained by direct inversion of the minimum-phase part. Since the excess-phase part of the RTF was found to carry most of the reverberant energy [59], in [6,56] the homomorphic technique was also used for mixed-phase equalization. In particular, the minimum-phase equalizer was complemented with an excess-phase equalizer, designed with a least-squares technique. Another possibility for implementing an excess-phase equalizer is to use a matched filter—i.e., a filter having an impulse response that is the time-reversal of the impulse response of the excess-phase system [57]. However, mixed-phase equalization based on homomorphic technique was found to be oversensitive to errors in the initial homomorphic decomposition of the room response [56,60]. Improvements to the homomorphic technique were reported in [57] and [58]. In [57], an iterative homomorphic technique is proposed by iteratively flattening the RTF magnitude response. The technique overcomes potential numerical problems and “provides more insight into subjective aspects of magnitude and phase equalization in the reduction of acoustic reverberation” [57]. In [58], some of the low-frequency dominant poles of the filter transfer function are replaced by new ones with smaller magnitude before computing the inverse filter. The technique allows the extent of oscillations associated with these poles to be reduced. The main disadvantage of the homomorphic technique is the large length of the all-zero (finite impulse response) model of the room response and the high sensitivity of the model to “changes in source/receiver placement” [61]. From this point of view, the LPC analysis provides more robust results [61].

4.2. LPC Analysis

In LPC analysis, the room response is modeled with a minimum-phase all-pole filter and the equalizer is a finite impulse response (FIR) filter. The all-pole model can be obtained by different techniques, including the efficient Levison–Durbin algorithm [62]. LPC analysis has been one of the most successful approaches for minimum-phase equalization, and has been successfully used by many researchers [61,63,64,65,66,67,68,69,70,71,72,73,74,75]. An all-pole filter can adequately model the spectral peaks of the room response, while it provides a less accurate model of the notches. We should remember that in the human auditory system the spectral peaks are more audible than the notches [20]. Moreover, the room response varies significantly with respect to the position in correspondence to notches [49]. An all-pole equalizer can compensate the most audible parts of the room response (the spectral peaks), without boosting the notches, which is another desirable property of the equalizer.

The main limitation of LPC analysis is the fact that it can be used only for minimum-phase equalization, and it must be complemented with other techniques to equalize the excess-phase.

4.3. Least-Squares Optimization Methods

Mixed-phase equalization requires the approximation of the inverse of a non-minimum phase response, which is acausal. In order to approximate an acausal impulse response, it was proposed in [76] to add a delay in the response of the equalizer and to design the equalizer by minimizing a least-squares error criterion. The approach proposed in [76] was thereafter followed and improved upon by many researchers, for both single-position and multiple-position equalization [77] (see Section 6). Mixed-phase equalization requires the introduction of a delay in the equalizer. This delay should be kept as low as possible (on the order of a few milliseconds according to the backward masking characteristics of the ear [46]), since it can give rise to annoying artifacts in the form of pre-ringing or pre-echo effects. At the same time, the delay should be sufficiently long to obtain reasonable mixed-phase equalization. The least-squares optimization has been the key ingredient of many adaptive solutions, starting from the seminal paper of [77], as detailed in Section 7. Other least-squares optimization criteria considering further constraints have also been proposed; e.g., deconvolution with regularization [51], room response reshaping [78], Kautz filters [55], and short filters [79].

The main limitations of the least-squares methods are the high sensitivity to the peaks and notches of the room response, the non-uniform distribution of errors in the spectrum, and the possibility of pre-ringing or pre-echo artifacts caused by the equalizer delay.

4.4. Frequency Domain Deconvolution

Another technique used for the equalizer design is based on frequency domain deconvolution. As initially proposed in [80], the equalizer can be directly designed in the discrete Fourier transform (DFT) domain by considering the reciprocal of the room response. In [80], the technique is applied to the DFT of a windowed impulse response in order to correct only the early reflections of the room response that affect the perception of timbre and to obtain a short equalizer response. In general, this technique can be applied both for minimum-phase and mixed-phase equalization (adding an appropriate delay), but the room response must be properly pre-processed. In particular, the depth of the notches of the room response should be suitably limited to avoid excessive gains and long impulse responses of the equalizer, which could result in tonal artifacts [52]. In [50], the equalizer is designed by dividing the complex spectrum of a target response with the complex spectrum of the measured room response. To avoid the problem of notches, a positive bias is added to the measured room response. This technique is known as “deconvolution with regularization”, with the bias called “regularization parameter”. The concept was formalized by Kirkeby and colleagues in [51,81] by considering a least-squares optimization criterion with a “penalty effort”. It is also known as the “Kirkeby algorithm”. In [52], the technique was applied to RRE. The regularization parameter controls the longest time constant of the inverse filters [81] in practice. In order to ensure that the time constant is neither too long nor too short, the regularization parameter must be set appropriately [51]. In [82], the authors show how the poles of the deconvolution solution are influenced by the regularization parameter. In particular, for each zero close to the unit circle, a triplet of two poles and one zero is generated, with one of the poles outside the unit circle. This pole is responsible for an acausal response, and thus modeling delay should be introduced. In [43], an analysis of RRE based on the Kirkeby algorithm on the basis of psychoacoustic criteria is provided. In the considered conditions, it was shown that the “errors in the dereverberation process manifested themselves as extremely audible and annoying resonances. These arose from the presence of deep spectral notches in the transfer functions of loudspeaker–room combinations, which created tonal artifacts that occurred long before and after the direct-arrival sounds. Furthermore, an extreme sensitivity to changes in position was found, which prevented the optimization of dereverberation over practically sized listening areas. The quality of the dereverberation was found to degrade even further for larger acoustic spaces.” Despite these limitations, deconvolution with regularization approaches has been successfully applied in combination with other techniques used to avoid perceivable distortions. For example, it has been combined with frequency warping [83,84], or used in wave field synthesis [85].

4.5. Multiple-Input/Multiple-Output Inverse Theorem Methods

A method for the exact inversion of the RIR—even when it is non-minimum phase—was proposed in [86,87]. The method is based on a principle called the multiple-input/multiple-output inverse theorem (MINT). With this method, the inverse is constructed from multiple FIR filters, by adding “some extra acoustic signal-transmission channels produced by multiple loudspeakers or microphones.” In practice, the MINT states that it is possible to obtain an exact inversion of the room response if the number of loudspeakers is larger than the number of microphones (i.e., measurement points). Thus, the approach is intrinsically multi-channel. Let us consider the case of a system with two loudspeakers and one microphone. Let us indicate with $G_1\left(z\right)$ and $G_2\left(z\right)$ the transfer functions from the loudspeakers to the microphones, and with $H_1\left(z\right)$ and $H_2\left(z\right)$ the transfer functions of the equalizers associated to each loudspeaker. Then, for exact inversion of the room response, $H_1\left(z\right)$ and $H_2\left(z\right)$ must satisfy the following condition:

$$H_1\left(z\right)G_1\left(z\right)+H_2\left(z\right)G_2\left(z\right)=1.$$

(2)

As shown in [87], the solution of Equation (2) exists if $G_1\left(z\right)$ and $G_2\left(z\right)$ are relatively prime (i.e., do not have common zeros), and when the solution exists the orders of $H_1\left(z\right)$ and $H_2\left(z\right)$ are lower than $G_2\left(z\right)$ and $G_1\left(z\right)$, respectively. The approach is very powerful because it allows the acausality problem of the equalizer to be overcome. However, the MINT approach also exhibits strong limitations. In [88], the MINT is analyzed under a numerical perspective, studying the condition number of the time domain matrix that is inverted. It is shown that the condition number of the time domain matrix is related to the singular values of the transfer matrix evaluated over frequency. The condition number decreases and the numerical performance is enhanced as the number of loudspeakers is increased. However, the condition number increases “at the rate of approximately 1 bit” (i.e., of approximately 6 dB) for each microphone added [88]. Moreover, an analysis of the MINT technique is also presented in [89], discussing the conditions which must be fulfilled for an exact inverse filter matrix to exist. Additionally, [89] demonstrates that the number of loudspeakers must exceed the number of microphones in a manner consistent with the findings of [87]. Moreover, an explicit formula is derived specifying the number of required inverse filter coefficients for the existence of an exact inverse. The paper also investigates the spatial extent of the zones of equalization produced by inverse filtering. It is shown that the equalized zone scales in size in accordance with the acoustic wavelength at the highest frequency of interest.

The low extent of the equalized zone and the numerical sensitivity to errors in the measured responses appear to be the main limitations of the MINT. An improvement of the method has been proposed in [90], where more control points are considered without increasing the number of inverse filters. Another improvement is discussed in [91], where an iterative method is applied to the MINT considering an optimally-stopped weighted conjugate gradient. To improve the computational efficiency of the MINT, an oversampled subband approach with decimation has been presented in [92].

4.6. Alternative Classification of Equalizers

As explained earlier, equalizers may be classified in several ways, and the above design techniques have already been classified into minimum-phase or mixed-phase. Another interesting classification of the equalizer design methods was provided in [55]. According to [55], the equalizer design methods can be classified into “indirect” and “direct” methods. As shown in Figure 3, indirect methods estimate a model of the room response—possibly processed—to obtain the equalizer by model inversion. Direct methods instead minimize the error between the equalized room response and a target response. From this point of view, homomorphic filtering, LPC analysis, and frequency domain deconvolution constitute indirect methods, while least-squares optimization constitutes a direct method. Multiple-input/multiple-output inverse theorem techniques can be classified as both direct and indirect methods, since they compute the equalizer considering the inversion of a matrix of room responses. However, according to Equation (2) they can also be estimated by minimizing the error with respect to an ideal response.

5. Pre-Processing Techniques

The main techniques that have been developed to overcome the limitations of RRE dictated by the characteristics of the room response, also taking advantage of the psychoacoustic properties of the ear, are discussed in the following. These approaches are capable of modifying the measured RIR and should be applied before the actual equalization procedure. They are suitable for both single-point and multi-point equalization.

The major problems of RRE that were addressed in the early approaches were the very long impulse responses of the equalizer, the limited region of space in which the RRE is effective, and the slow time variations of the room response. The very long impulse response of an exact equalizer is due to the spectral characteristics of the room response, as shown in Figure 2b, with many peaks and notches that increase their density towards high frequencies. The notches correspond to zeros close to the unit circle in the RTF. Thus, the inverse filter has poles close to the unit circle that determine the long impulse response. The notches at high frequencies are extremely variable with position and time, determining the small extent in space and time in which the equalizer is effective. Movements of listening position of 10 cm can cause variations of up to 20 dB in the room response [93], and a pre-processing technique is required to contrast these variations.

5.1. Short Filters

One of the first expedients to improve RRE resorted in using short equalization filters. By considering a coarse model of the room response which tries to capture and correct only the general trend of the room response, avoiding modeling the sharp peaks and notches, it is possible to reduce the temporal length of the equalizer impulse response. This solution is also beneficial for enlarging the extent of the equalized zone and to cope with the room response variations in time [2]. One of the most effective techniques for designing short equalization filters is that based on LPC analysis [61], which obtains a good modeling of the peaks of the room response, with a coarser modeling of notches.

5.2. Non-Uniform Frequency Resolution

To improve the accuracy and effectiveness of equalization, the equalizer should take advantage of the characteristics of the room response and the human ear. At low frequencies, the room frequency response is more regular and the peaks and notches are mostly insensitive to the position in the room. The resolution of the ear is nonuniform and nonlinear, with a logarithmic dependence on frequency. At high frequencies, the ear is rather insensitive to notches of the room response and to high-frequency reverberation. Accordingly, the equalizer should provide fine resolution at low frequencies and a coarser resolution at higher frequencies. Many techniques have been developed following this strategy:

• Complex smoothing,
• Frequency warping,
• Kautz filters and parallel IIR filters with fixed poles,
• Multirate approaches.

5.2.1. Complex Smoothing

Fractional octave-band smoothing of the power spectrum has been widely applied in audio processing. Its use can be traced back to analog equalizers (as for example the one-third-octave-band filterbank analyzers), and was later extended to digital spectrum analyzers. In [35,94], the authors extend the technique by introducing a methodology for smoothing the complex transfer function of the measured room response with fractional octave profiles. The technique can be implemented in the time or frequency domains. It is perceptually compliant since the spectral smoothing follows the frequency resolution of the ear, with a fine resolution at low frequencies and a lower resolution at high frequencies. As a result, in the time domain the application of complex smoothing can retain the initial high-frequency content of the early components (i.e., the transient behavior of the direct sound and of the first reflections) and then can progressively introduce a low-pass filtering of the later components (i.e., of room reverberation) [95]. This is also desirable from another psychoacoustic point of view. In dispersive room environments, the ear is very sensitive to the signal onsets (i.e., to the full frequency range of the first part of the RIR), while it is less sensitive to the high-frequency components of late reflections [19,22,24,35]. When the complex smoothed impulse responses are used for the design of an RRE, they allow the avoidance of compensating sharp notches at high frequencies in order to obtain a reduced length of the equalizer, and they provide a more robust equalization with lower sensitivity to possible changes in the listener position and to other variations in the room response [2,35]. Figure 4 shows the complex smoothing effect on an RTF for different resolutions. By introducing an appropriate delay in the equalizer, complex smoothing allows the mixed-phase equalization of a room response. As an alternative to complex smoothing, frequency-dependent signal windowing [96] or a separate smoothing of the magnitude and phase of the transfer function [97] have been proposed.

5.2.2. Frequency Warping

Another technique that provides a nonuniform frequency resolution is “frequency warping” [98]. The original idea of frequency warping is presented in [99], where a nonuniform Fourier transform is introduced. The technique consists of replacing the unit delay $z^{-1}$ of digital filters with a first-order all-pass filter,

$$D_1\left(z\right)=\frac{z^{-1}-\lambda }{1-\lambda z^{-1}},$$

(3)

thus obtaining a bilinear mapping of the unit circle on itself. The warping effect can be adjusted to approximate the spectral representation of the ear [100]. In [101], analytic expressions that approximate the Bark and ERB scale are provided. They allow for a very good approximation of the Bark scale and less accurate approximation of the ERB scale, due to the higher frequency resolution required, particularly at low frequencies. The effect of the frequency warping can be easily reversed by again replacing the unit delay $z^{-1}$ with the all-pass filter

$${\tilde{D}}_1\left(z\right)=\frac{z^{-1}+\lambda }{1+\lambda z^{-1}}.$$

(4)

Figure 5 shows an example of the effect of frequency warping on an RTF for different values of $\lambda$. The reader should note the expansion of the low frequency range and the compression of the high frequencies obtained with positive values of the warping parameter $\lambda$.

Warped FIR and IIR filters can be obtained by replacing the tapped delay line with a chain of first-order all-pass filters, but while the implementation of warped FIR filters is immediate [66], warped IIR filters require appropriate structures to avoid delay-free loops [102]. Warped FIR filters are strictly related to the Laguerre filters [103], the only difference being the fact that in a Laguerre filter there is an additional prefilter placed before the all-pass chain [66]. A logarithmic frequency scale can also be approximated, but in this case the all-pass chain has to be replaced with a filterbank formed by all-pass filters.

Frequency warping has been exploited in many audio applications, from LPC analysis [100], audio equalization [104,105], loudspeaker equalization [106,107,108], and physical modeling of guitar bodies [109], to head-related transfer function (HRTF) filtering [66,109]. The reader is referred to [66] for a review of frequency warping techniques and their applications. In the context of RRE, frequency warping has been used by many researchers in minimum-phase equalization to improve the equalizer performance by expanding the resolution at low frequencies and compressing it at high frequencies. A psychoacoustically-motivated frequency scale—in most cases the Bark scale—is used. For example, in the approach of [70,71], a prototype room response is first frequency warped to an approximate Bark scale. Then, an all-pole model of the room response is obtained in the warped domain using LPC analysis. Eventually, a minimum-phase equalizer is derived in the time domain by de-warping the inverse of the all-pole model with (4). The main disadvantage of this approach is represented by the high computational cost of the frequency warping operation. In [73,75], frequency warping was efficiently implemented by nonlinearly sampling a high-resolution fast Fourier transform (FFT) of the prototype room response.

5.2.3. Kautz Filters and Parallel IIR Filters with Fixed Poles

Kautz filters are rational orthonormal filter structures. They are orthonormal since they have orthonormal impulse responses. Continuous-time rational transfer functions with orthonormal impulse responses were studied by Kautz in [110]. Discrete-time orthonormal transfer functions were later studied by Broome in [111], who named them “discrete Kautz functions”. Kautz filters can be considered as a generalization of warped FIR filters and Laugerre filters, where the chain of all-pass filters with equal poles is replaced by a chain of all-pass filters with individual poles, possibly complex [54]. Figure 6 shows the results of Kautz modelling a measured RTF.

By properly choosing the poles, it is possible to realize an arbitrary allocation of the frequency resolution of the designed filter. An approximation of the log-frequency scale resolution with Kautz filters can be found in [55]. The poles can be chosen a priori on the basis of the desired resolution, but they can also be tuned to the specific application by matching the pole frequency with the resonances of the system to be modeled [54]. In practice, fine tuning of the poles is necessary when designing low-order models for highly resonant systems [54]. Once the poles are chosen, system identification using Kautz filters can benefit from the orthogonality of the impulse responses. The reader is referred to [54] for a discussion about pole fitting and identification methods.

Kautz filters have been used for RRE, exploiting the nonuniform frequency resolution of these filters. They have been applied both for minimum-phase and mixed-phase equalization, using both fixed poles or tuned poles [54,55]. When a fixed pole approach is used, the Kautz filters can also be designed and implemented in the form of a filterbank of second-order sections [112,113,114], with advantages for the computational complexity. In [114,115], the theoretical equivalence of parallel filters and Kautz filters is shown, and formulas to convert the parameters of the two structures into each other are given. Figure 7 reports a parallel filter design example following the methodology of [114].

5.2.4. Multirate Approaches

Another possibility for achieving a nonuniform frequency resolution is given by multirate approaches. In these approaches the spectrum is divided into different bands, that are down-sampled and separately processed with filters of different length. In most of the proposed approaches, one of the filters covers the low frequencies [50,72,116,117,118,119,120] which is used for modal equalization and low resonances control (see Section 6.5) or for bass management. Generally, the low-frequency filters must compensate very long reverberation times, and thus the filters benefit from the high down-sampling at low frequencies. The filters used for mid and high frequencies generally use a lower resolution compared to the low frequencies, with strong computational savings.

For example, in [119] the authors propose a dual band equalization procedure. The low frequency channel is restricted approximately to the Schroeder frequency through down-sampling. An FFT-based technique with regularization is used to design a minimum-phase equalizer with homomorphic filtering. The upper band is also equalized with a minimum-phase equalizer designed with LPC analysis and warping techniques. In [120], the same authors have instead divided the spectrum into three bands: the low-, mid-, and high-frequency bands. The low band is again restricted approximately to the Schroeder frequency—specifically 150 Hz—through down-sampling, but the equalizer is now designed with the LPC technique. In the mid-frequency band from 150 Hz to 900 Hz, the equalizer is designed with a warped LPC technique to focus attention to the lower part of the band. Above 900 Hz, the high-frequency spectrum is smoothed to reduce sensitivity to position, and then the equalizer is found by inverting the smoothed spectrum, imposing a slightly decreasing target function. The authors have also combined this basic equalizer with an excess phase equalizer in the low-frequency band, and a pre-processing based on a deconvolution technique in the first 10 ms after the direct sound.

In [72], the authors have combined the multi-point fuzzy c-means clustering technique of [121] (see Section 6.2) with a dual-band multirate approach, separating the low-frequency band below 80 Hz from the high-frequency band beyond 80 Hz. The low-frequency band is decimated by a factor of 256 to work with small length room responses, prior to applying the fuzzy c-means clustering technique for designing the equalizer.

5.3. Room Impulse Response Reshaping

Another possibility for taking into account the psychoacoustic characteristics of the ear is that of reshaping the impulse response in such a way that the alteration of the room becomes inaudible. In RIR shortening, the attenuation of the original RIR is accelerated so that the reverberation effect is weakened. Different techniques have been proposed in the literature [78,122,123,124,125,126,127,128,129,130]. In what follows, we review the most relevant methods. Most of these methods are not RRE methods in a strict sense, but they could be easily combined with RRE techniques.

The first attempts of RIR reshaping [122,123] tried to adapt the concepts of channel shortening developed in the telecommunication area [131,132,133,134], applying least-squares optimization algorithms. By properly designing a reshaping filter, it is possible to maximize the energy of the equalized RIR in a desired time window, minimizing at the same time the tails of the room response in an undesired window. In this way, for example, it is possible to directly maximize the D50 measure for intelligibility of speech, which is the ratio of the energy within 50 ms after the first peak of an RIR versus the energy of the complete response. The least-squares optimization of the reshaping filter segregating the desired time window from the undesired window provided unsatisfactory results [122] in the form of audible late echoes or spectral distortions. These problems are caused by the strong separation imposed considering non-overlapping desired and undesired windows, and by the least-squares optimization that leads to a non-uniform error distribution. Thus, already in [122] the authors modified the channel shortening paradigm with the aim of shaping the desired impulse response to a shorter reverberation time, considering a gradual transition between the desired and undesired windows.

The approach was improved in [78,124,126,127]. These approaches exploit the psychoacoustic properties of the human auditory system, and in particular the forward-masking effect. They aim to obtain an equalized response that decays sufficiently quickly to avoid audible echoes, such that the reverberation time is masked by the direct sound according to the forward-masking effect of the human auditory system. The desired and undesired windows are here specified according to the average forward masking curve of [47] and [43]. Moreover, to avoid the problems due to least-squares optimization, infinity-norm and p-norm optimization (with large values of p) are proposed. The approach is also applied to multi-channel problems in [125,130].

No spectral requirement is imposed by any of the above-mentioned RIR reshaping approaches. In most cases, these approaches usually yield a flat overall frequency response, but with very long impulse responses they may lead to spectral distortions [128]. To contrast this problem, in [128] the objective function is modified to incorporate a p-norm-based regularization term in the frequency domain, thus imposing the joint optimization in time and frequency domains. In [135], the regularization term is replaced by an integrated spectral flatness measure, which allows the integration of the concept of auditory scales into the equalizer design. Thus, the approaches of [128,135] combine RIR reshaping with RRE.

6. From Single-Point to Multi-Point Equalization

Another classification of RRE is relative to the number of microphones or control points used. Classical approaches are based on the use of one RIR captured near the listener position (see Section 4), implying a specific sweet spot where the equalization is effective [136]. The objective of multi-point equalizers is to enlarge the equalized zone [137], also improving the robustness of the equalizer towards measurement errors and variations of the room response, implicitly exploiting the variation between the multiple measurements. In what follows, a review of multi-point equalization methods is given, taking into account that most of the techniques discussed in the previous sections have also been applied to multi-point RRE.

6.1. Average and Weighted Average Methods

One of the earliest multi-point approaches was proposed by Elliot and Nelson. In [77], the authors presented a method for designing an equalization filter for sound reproduction systems by adjusting the filter coefficients so as to minimize the sum of squared errors between the equalized responses at multiple points in the room and a delayed version of the original signal. The paper considers both fixed and adaptive equalizers based on filtered-x algorithms. The approach is effective and has also been applied in many other improved techniques [9,31,33,118]. The main limitation is given by the fact that the implicit averaging in the sum of squared errors cannot exploit the similarities in the room responses, nor can favorite equalization at certain positions. In the context of car audio equalization [118], the technique was improved by considering multi-point equalization with a weighted average of the errors. The solution provided improvements in the response at the selected location, “without significant degradations at other points” [118].

6.2. Clustering Methods

We can exploit the similarities between different spatially distributed room responses by clustering them according to a chosen distance measure. In [138], the “extremely large set” of possible RTFs within an enclosure was grouped together and equalized by a smaller number of equalizers. The RTFs were modeled with all-pole filters using LPC analysis, and thus minimum-phase equalizers were designed. Then, vector quantization was performed to optimally classify the all-pole filters. The classification can be used as a spatial equalization library, achieving reduction in reverberation over a wide range of positions within the enclosure, depending on the actual position of the listener. The main limitation of this method is the necessity to extract and memorize a large set of room responses and equalizers and to track the position of the listener.

A fuzzy c-means clustering method is applied in [30,70,71,72,121,139,140]. In the approach of [121,139], “representative prototypical room responses” are derived from several measured room responses that share similar characteristics using the fuzzy c-means unsupervised learning method. The prototypical responses are then combined to form “a general point response” based on the fuzzy standard additive model of Kosko [141,142]. The method employs a weighting according to “the level of activation” of a prototype, depending upon the degrees of assignment of the room responses to the cluster containing the prototype. The equalizer is then computed from the inverse of the general point response using LPC analysis, “obtaining a significant improvement in equalization performance over the spatial averaging methods” with the suppression of the peaks in the room magnitude spectra [139]. The method was further improved in [70,71,140] by applying the fuzzy c-means clustering to warped impulse responses, thus taking advantage of the perceptual properties of the ear. The approach was also combined with multirate filtering in [72] to allow effective filtering of the low frequency response at low sampling rates with computational savings.

The approach of [70,139] was later improved by applying frequency warping and fuzzy c-means clustering to the magnitude room responses [73,75], with a strong improvement in terms of computational complexity. A weighted fuzzy c-means clustering was also proposed in [143], where the RIR samples were weighted in a different manner to account for the different effect they have on RRE.

6.3. Prototype Approach

The fuzzy c-means clustering approach of [70,139] is also a first example of a “multi-point prototype approach”. These methods use measurements of the room response in different locations to extract a prototype response which is representative of the perceptual acoustic situation that has to be corrected. A single equalizer is then designed with indirect or direct methods [55], on the basis of this prototype response.

Different approaches for the determination of the prototype response were studied in [144]. In particular, the fuzzy c-means method was compared with the mean average, the median, the min-max, and the root-mean-square average, and applied to fractional octave complex-smoothed spectra. The equalizer was then derived by inversion or the Kirkeby algorithm [81], or LPC analysis, with minimum-phase equalization. In the considered conditions, the mean average gave the best results, with the other methods also providing similar performance. The prototype extraction approach based on mean average was also combined with the method of [73] and applied to room-response equalization [75,145]. Subjective listening tests confirmed the good results obtained with the approach [75]. The approach was further extended in [146,147] by also considering a group-delay equalization. In [146], after the determination of the minimum-phase equalizer, the smoothed phase responses measured at different positions are corrected with the phase response of the equalizer and are used to determine the group delay responses. A prototype group delay is computed by averaging the group delay at the different positions, and after spectral smoothing is used to extract an all-pass FIR group-delay equalizer. In [147], the prototype phase response used to determine the phase equalizer is extracted only from the early reflections, which represent the contribution of the direct sound, discarding the late reflections that represent the reverberation of the environment. The mixing time between early and late reflections is calculated using the approach presented in [147,148] based on Gaussianity estimators. The prototype function is truncated using the mixing time, and an FIR phase equalizer is obtained with the matched filter technique; i.e., time-reversing the all-pass impulse response. With this approach, pre-ringing artifacts are avoided, since only the early reflections are considered in the equalizer. In fact, taking into consideration only the first reflections, only the main characteristics of the room are considered and those parts of the impulse response which contain zeros that vary with the position and according to [149] produce the pre-ringing artifacts are avoided.

A prototype approach is also followed in [93,150,151,152,153]. According to the authors, “part of the impact of a listening room is natural to the human ear and should not be removed by a room correction system” [93]. In particular, sound reproduction in a room normally causes an increased sound pressure level at the lower frequencies, because of the lower absorption typically found at these frequencies. Since this effect is natural to the human ear, as it provides the sense of being in a room, room equalization systems should not be allowed to remove the smooth increase in level at low frequencies, also referred to as the “room gain”. The room gain describes how the room efficiency increases at low frequencies compared to high frequencies [152]. Moreover, the prototype response should preserve the basic characteristics of the loudspeaker; i.e., the equalizer should not try “to make all loudspeakers sound alike”. Thus, the developed system estimates the main characteristics of the loudspeaker: lower cut-off frequency and slope, sensitivity, directivity index, and upper cut-off for the treble driver. The equalizer is designed by acquiring information both of local properties at the listening position and on the acoustic power in the three-dimensional sound field. The RRE is based on measuring the sound pressure at the listening position and in at least three other randomly selected positions. The measurement in the listening position holds information on the perceived sound field, while the other room measurements hold information on the energy in the three-dimensional sound field. The information is then used to calculate lower and upper gain limits for the designed equalizer. The prototype response is automatically calculated based on the measurements. At low frequencies, the prototype response is designed to provide the same room gain of a listening room conforming to the IEC 268–13 standard [154], approximating a smooth room gain with a second-order shelving function, which adds 6 dB level smoothly below 120 Hz [152]. The equalizer is minimum phase and designed on basis of the homomorphic technique [151].

6.4. Common Acoustical Poles Compensation

At low frequencies strong resonances can appear in the room response. These resonances are often independent of the position and are associated with long slowly-decaying modes. Different techniques have been proposed to compensate the low-frequency response. Many of these techniques exploit multi-point measurements to determine the spectral properties of the resonances.

A model for a RTF using common acoustical poles corresponding to the resonances of a room is proposed in [63]. The common acoustical poles are estimated as the common pole values of many low-frequency RTFs estimated for different source and receiver positions. The poles are computed from an LPC model of the room response, estimated by two possible methods: (i) using a least-squares method, assuming all measured RTFs have the same LPC coefficients and (ii) averaging the LPC coefficients estimated from each measured RTF. The estimated poles correspond to the major resonance frequencies of the room. Then, using the estimated common poles, the method of [63] models the RTF with different moving average coefficients. The model is called by the authors the common acoustical pole and zero model, since it is a zero-pole model formed by the common acoustical poles and the zeros provided by the moving average coefficients. The approach was later expanded in [64,65]. In [64], a multi-point equalization filter using the common acoustical poles is proposed. The common acoustical poles are again estimated as common LPC coefficients from multiple measurement of the RTFs. The equalization is then achieved with an FIR filter having the inverse characteristics of the common acoustical pole function. As for the other all-pole models, the equalization filter is a minimum-phase equalizer that cannot compensate for the notches of the frequency response. Nevertheless, the filter can suppress the common peaks due to resonances in the multiple positions, and has low sensitivity to changes in the receiver position. In [65] a pre-conditioning stage is added to the common acoustical poles equalizer. The pre-conditioning stage suppresses low-Q resonances in the entire spectrum, while a second stage based on the common acoustical poles suppresses or minimizes the low-frequency resonances. In [155], an empirical technique to select an appropriate order for the common acoustical pole model is proposed. The technique selects the first order for which a further growth does not lead to an improvement in the modeling accuracy for at least one of the measured RIRs. The model order depends on the chosen maximum frequency of the modeled poles. The iterative algorithm of [156] is also based on the common-acoustical-pole and zero model. It designs biquadratic filters suitable for multi-point RRE.

The common acoustical poles compensation could also benefit from the filterbank technique based on second-order sections of [112,113,114,115], exploiting in particular the logarithmic frequency resolution and the ability to customize the pole positions.

6.5. Modal Equalization

Modal equalization has also been proposed at low frequencies [4,157]. Modal equalization aims to control excessively long decays in listening rooms caused by low-frequency modes, minimizing the audibility of these resonances. Modal equalization balances the rate of sound decay of the low-frequency modes to correspond to the reverberation time at mid and high frequencies. This is not an RRE technique by itself, but it can be used with conventional magnitude equalization to optimize the reproduced sound quality. In [157], two methods for implementing active modal equalization are proposed. The first approach considers a single loudspeaker and filters the sound such that the mode decay rates are controlled (e.g., using a filter with couples of zeros placed in correspondence to the poles responsible for the resonances). The second approach implements modal equalization by one or more secondary loudspeakers. A correction filter is considered for each secondary loudspeaker in order to produce a compensatory sound. The first approach was studied in depth, and different techniques for identifying the modes, estimating their parameters, and designing the equalizer are presented. Estimation of the modal decay parameters is based on the nonlinear optimization of the model for exponential decay plus stationary noise floor presented in [158].

6.6. Plane Wave Approach

Another possibility for equalizing the sound in the low-frequency region is that offered by the plane wave approach. In rectangular rooms with a symmetric arrangement of loudspeakers in two opposite walls, it has been shown in theory [159] and experiments [160] that equalization within the entire room can be achieved at low frequencies. The approach generates a plane wave that propagates from one wall to the opposite one, where it is absorbed by the loudspeakers. In the experiments of [160], the signals fed to the loudspeakers are determined with the RRE approach of [89]. The error sensors are positioned in two planes perpendicular to the direction of propagation of the simulated plane wave. The desired signal in the planes is a Dirac delta function with a delay corresponding to the time it takes the sound to travel the distance between the planes. A plane wave approach has also been studied by the authors of [161,162,163,164,165]. First, in [161], the authors developed an application based on finite-difference time domain approximation for studying low frequencies in audio reproduction. In particular, a rectangular room has been simulated by using a discrete model in time and space. Then, in [162] the application was used to study different configurations of loudspeakers in the room to reduce the effect of the acoustic modes. It is shown that by increasing the number of loudspeakers, the variation of the room response across positions is improved at the expense of an increment in the magnitude deviation at every position. The application has also been used to assess the effect of different equalization techniques, such as multi-point equalization and equalization of the acoustic radiation power of the loudspeaker. Eventually, a solution for equalizing the low-frequency sound field using multiple loudspeakers—named controlled acoustic bass system (CABS)—was proposed and studied in [163,164,165]. This solution creates a traveling plane wave in one side of the room and cancels it at the opposite wall using extra loudspeakers, with delayed and anti-phase response to remove back-wall reflections. Using the application of [161] and real measurements in rectangular rooms, the authors have shown that the CABS solution can produce a uniform acoustic field in the low-frequency range. In [166], the approach of [159,163] is further extended to rooms of arbitrary shape with multiple loudspeakers “situated in more normal locations” considering a 5.0 loudspeaker set-up. Additionally, [167] has addressed the problem of a non-rectangular room and of an asymmetric loudspeaker set-up. In [167] a multiple-input/multiple-output (MIMO) equalization technique that prescribes only the magnitude of the room response in the control points is proposed. The approach allows a smaller magnitude deviation to be obtained compared to the previous plane-wave approaches.

To improve equalization with plane waves, a control approach called effort variation regularization was proposed in [168]. In this approach, the conventional cost function of RRE of [169]—based on the minimization of the least-squares error in multiple control points—is modified by adding a regularization term proportional to the squared deviations between source strengths. The approach can be applied both in the frequency and time domain. Simulation results show that the technique can lead to smaller global reproduction errors and better equalization performance at listening positions away from the control points, than the Tikhonov regularization or the approach based on feeding the same signal to all loudspeakers placed on the same wall.

6.7. Other Low-Frequency RRE Approaches

At very low frequencies, instead of a plane wave, it is much more efficient to use a pressure-field chamber approach [170]. This approach is obtained by sending the same signal to all loudspeakers. This generates a standing wave pattern inside the room, which is homogeneous at wavelengths considerably larger than the room. For this reason, in [170] a hybrid-field playback approach is proposed which combines the efficiency of the pressure-field playback at the very low frequencies with the homogeneous sound-field obtained with the plane wave approach at higher frequencies.

In [79], the problem of multiple-loudspeaker low-frequency RRE for a wide listening area, with the equalized loudspeaker supported by the remaining ones, is addressed as a multipoint error minimization problem between the desired response and the synthesized magnitude response. The cost function is minimized, imposing physical and psychoacoustical criteria. In particular, to obtain short equalization filters, a temporal masking constraint is imposed on the equalization filters. To avoid perceivable echoes, a combination of delay and gain relative to the main loudspeaker is considered, with the auxiliary loudspeaker signals that should fall below the echo threshold [171]. To avoid modifications in the spatial perception, the delay of the auxiliary loudspeaker signals is enforced to be at least of 1 ms in order to exploit the precedence effect. To avoid boosting the notches, a maximum-gain is imposed on the equalizers. The room equalization filters are computed considering a convex optimization framework that takes all these constraints into account .

6.8. Quasi-Anechoic Approach

An approach that is complementary to the low-frequency techniques introduced in the previous sub-section is the quasi-anechoic approach of [172]. At mid- and high- frequencies, the timbre perception and localization is dominated by the direct sound. Thus, in [172], a quasi-anechoic loudspeaker response is obtained as a gated version (up to the first reflection) of the RIR and is used to design the equalizer in two steps. First, a mixed phase equalizer is derived from the quasi-anechoic RIR, computing the inverse filter with a least-squares approach. The quasi-anechoic loudspeaker response has a short length and the delay introduced by the equalizer is too short to produce pre-ringing artifacts. Then, a minimum-phase equalizer is used to correct the remaining part of the room response (i.e., the magnitude spectrum modifications caused by reverberation).

In [173], the quasi-anechoic approach is combined with the prototype approach described in Section 6.3. In particular, a novel prototype function is derived from the combination of quasi-anechoic impulse responses with the impulse responses recorded in the real environment to be equalized. The approach is used to equalize the direct sound only in the mid–high-frequency range, while applying full equalization in the modal frequency range. The approach is motivated again by the fact that at mid and high frequencies the timbre perception and localization is dominated by the direct sound. Thus, the measurable but mostly inaudible magnitude deviations due to reflections should not be equalized [174]. In [173], several experiments were conducted in order to validate the proposed approach, reporting objective measurements and subjective listening tests in comparison with approaches of the state-of-the-art. In this context, Figure 8 report the results of the equalization procedure. In particular, Figure 8a shows four impulse responses acquired in a real room—the prototype function and the equalizer obtained with the multi-point approach of [173] and the single-point equalizer derived as an inverse filter of the smoothed frequency response of IR1. Figure 8b shows the effect of the equalization procedure on the IRs applying the multi-point approach, while Figure 8c shows the effect of the single-point equalizer. It is evident that the performance of the single-point equalizer is very good only for IR1, while the multi-point equalizer exhibits flatter frequency responses compared to those obtained with the single-point approach.

7. Adaptive Single-Point and Multi-Point Equalization

The room is generally a time-varying environment (a “weakly non-stationary” system as defined in [2]) that changes as a function of several parameters, such as the position of physical objects in the room, the opening of doors, as well as the movement of people and other obstacles in the enclosure [6,175]. Additionally, temperature variations can lead to large variations in the RIR, as reported by [176]. Furthermore, variations of the source and receiver positions, and of loudspeaker and microphone characteristics may occur as reported in [6]. Thus, adaptive solutions suitable to track and correct slow variations in the room response should be adopted. Different adaptive RRE techniques have been proposed in the literature. The approaches are here classified considering the number of input and output channels as SISO/SIMO, and MISO/MIMO, where input refers to the number of loudspeakers and output to the number of microphones, since these classes share similar problems in the identification procedure.

7.1. SISO/SIMO Approaches

These techniques can be classified into time domain and frequency domain approaches.

7.1.1. Time Domain Approaches

A first adaptive equalizer was proposed in [77], considering the variability of the environment from different points of view. The approach was based on a single-point technique, adaptively minimizing in the time domain the mean-squared error between the equalized response and a delayed single-channel version of the original signal using a filtered-x algorithm. The equalization was effective for the considered position, but a degradation in other points of the enclosure was introduced, as also described in Section 6. Therefore, a multi-point approach was also presented by the same authors in [77], where the equalizer was designed by adaptively minimizing the sum of squared errors between the equalized responses in several positions and a delayed version of the input signal. Unfortunately, the approach is very sensitive to peaks and notches in the room response and to room response variations at different positions. As a consequence, pre-echo problems can easily be experienced.

7.1.2. Frequency Domain Approaches

Working in the frequency domain, a single-point RRE technique was proposed in [177]. Here, the loudspeaker and microphone signals are split into subbands (a 20-band filterbank) and the equalization is achieved by adaptively updating the filter weights in these subbands. The approach is interesting because it combines simplicity, robustness towards peaks and notches of the room response, and the ability to track room response variations. It was improved in [178] by introducing a frequency-dependent step size. In this way, it is possible to optimize the adaptive equalization in each subband, improving the overall convergence speed. In [179], a further improvement of the previous methods [177,178] has also been presented to cope with the online identification of the impulse response. In particular, the room response estimation is obtained by means of inserting artificial test signals in such a way that they remain inaudible to listeners by exploiting frequency masking. The signal is then analyzed in the frequency domain to identify the test signal and to determine the RIR. In [180] the approach of [177,178] was elaborated and improved by developing a multi-point solution. After identification in frequency bands, a fractional octave smoothing is applied to the impulse responses, and a prototype filter is computed from the mean of the room magnitude responses. The obtained results have shown that the performance of this rather simple structure can be improved by considering a multi-point solution, which results in an increased width of the equalized zone. In [84], the approach of [180] was further elaborated considering frequency warping in the low-frequency region to improve perception. Specifically, the room responses at different positions in the zone to be equalized are estimated in the warped domain and the common trend of these responses is extracted as a prototype function. This allows the equalizer resolution to be increased at frequencies where the human auditory system is more sensitive. Adaptive versions of the filterbank techniques of [112,113,114,115] could also be used for the same purpose.

7.2. MISO/MIMO Approaches

The adaptive RRE techniques proposed in [84,178,180] (and many other papers) consider the equalization of a single sound source (i.e., of a single audio reproduction channel), due to the problem of estimating several impulse responses at the same time. If two or more channels are employed, the covariance matrix of a multichannel adaptive algorithm becomes ill-conditioned due to the correlations between the channels for typical reproduction techniques. The ill-conditioning generally causes convergence problems. This was shown, for instance, for stereophonic acoustic echo cancellation [181]. To cope with the non-uniqueness problem, a method to reduce the inter-channel coherence is usually exploited. In this context, many of the techniques used to reduce the channel cross-correlations often introduce significant distortions, which are unacceptable in high-quality sound reproduction systems [181,182]. Therefore, a suitable technique which is capable of decorrelating the loudspeaker signals and of preserving the audio quality must be considered. The approach in [183] introduces a multichannel solution which also considers the non-uniqueness problem. The room responses are estimated with good accuracy by reducing the inter-channel coherence using a technique that produces only a mild degradation of the sound quality. Specifically, the low-frequency region is decorrelated by exploiting the missing-fundamental phenomenon, while the high frequencies are decorrelated with a second-order time-varying all-pass filter combined with a multiple notch filter [184]. The equalizer is designed in the warped frequency domain to improve the equalization in the low-frequency region and, at the same time, to reduce the computational cost of the design. In [185], the adaptive multichannel and multi-position RRE system briefly introduced in [183] is fully detailed and extended, providing a real-time implementation in commercial Hi-Fi products.

To improve the convergence speed and the robustness of the adaptive identification algorithm in the presence of low signal-to-noise ratio, the use of a biased adaptive algorithm has recently been proposed in [186] for a MIMO system. In detail, the algorithm is based on the improved proportionate normalized least-mean squares algorithm (IPNLMS) within the conventional filtered-x scheme (IPNLMS-FX), previously introduced for active noise control (ANC) [187], and here extended towards multichannel equalization. However this method requires an a priori estimation of the impulse responses, which is not available in many practical applications. With the same purpose of improving convergence and robustness, a combination of block-based adaptive filters (also employing biased algorithms) was proposed in [188].

It is worth underlining that if a binaural system is considered, a natural decorrelation among stereo channels is obtained. A stereo representation of an adaptive RRE system can be achieved without channel decorrelation, as reported in [169,189]. An improvement of this technique is presented in [190], where a subband structure is proposed to reduce the computational complexity of the procedure.

8. Fixed and Adaptive Wave Domain Equalization

The equalization approaches reviewed so far considered the reproduced sound field at one or more points in space. These points should ideally coincide with a potential listener position or restricted listening area. A broader view of equalization can be gained by taking the entire reproduced sound field within the desired—potentially large—listening area into account. This can be achieved by taking the spatio-temporal character of the sound field instead of the sound pressure at a limited number of points into consideration. In order to lay the grounds, the background of equalization following such a field-centered view is reviewed in the next subsection. This is followed by a review of representative approaches in the subsequent subsections.

8.1. Physical Background

The Helmholtz integral equation (HIE) [191] provides the solution of the inhomogeneous wave equation with respect to homogeneous boundary conditions. This covers—among others—the sound field reproduced by a distribution of loudspeakers in a room. The HIE states that the sound pressure within a source and scatterer free volume V is uniquely determined by the sound pressure and its directional gradient at the boundary $\partial V$ of the volume. This finding can be exploited for the analysis of sound fields as well as for their synthesis. For the analysis of sound fields, it is sufficient to capture the sound pressure and its gradient at the border of the volume of interest. The same holds for the synthesis of sound fields where placing loudspeakers around a listening area allows full control of the sound field within that area. However, in terms of technical complexity, it is generally not desirable to capture both the sound pressure and its directional gradient using two different types of microphones placed at the boundary of the listening area. The same also holds for the synthesis using loudspeakers. Here one would have to employ monopole and dipole loudspeakers. Microphones and loudspeakers with the properties of a monopole are desirable over their dipole counterparts. It has been shown [192] that the HIE can be reduced to a monopole-only variant under some practically feasible limitations. This lays the theoretical ground of RRE within an extended listening area. In summary, the sound field within the listening area can be analyzed and controlled by a continuous distribution of microphones and loudspeakers located on the boundary of the listening area. However, the solution of the underlying continuous problem requires the solution of integral equations derived from the HIE [193]. Operator theory provides a solution to this problem by expanding Green’s function into orthogonal basis functions. A closer look onto this will be taken in the subsequent section on wave domain adaptive filtering.

For a practical implementation of the principles outlined above, only a finite number of microphones and loudspeakers can be used. Hence, the continuous distribution of microphones and loudspeakers must be sampled spatially. The geometry and sampling is illustrated in Figure 9.

The wave-theoretical view on RRE introduced above requires a sufficiently dense sampling of the loudspeaker and microphone contour. For typical systems, this calls for a high number of loudspeakers and microphones even when the upper frequency limit is quite low. Spatial sampling has been investigated intensively for different geometries and techniques [194,195,196]. The full three-dimensional coverage of the listening areas boundary by loudspeakers and microphone is often not feasible in practice. The limitations of considering only a planar listening area leveled with the listener’s ears which is surround by loudspeakers are discussed in [197].

8.2. Wave-Domain Adaptive Filtering

An adaptive solution to the computation of RRE filters is desirable since the acoustic transfer paths may change, for instance due to people entering the room or due to temperature changes. As an example, the consequences of varying the room temperature on RRE using static filters are illustrated in [198]. A wide variety of adaptation algorithms have been developed in the past. Since RRE is an inverse problem, the class of filtered-x algorithms is well suited. The filters may be computed adaptively with the multichannel filtered-x recursive least-squares algorithm (X-RLS) [199]. However, in the context of multichannel RRE, an adaptive solution has three fundamental issues: (1) ill-conditioning; (2) non-uniqueness; and (3) numerical complexity. The first problem is related to the spatio-temporal correlation of typical loudspeaker signals, the second to the underlying optimization problem, and the third to the size of typical MIMO systems following the wave-theoretical view. A solution to the third problem—which also augments the other two issues—has been proposed by wave domain adaptive filtering (WDAF) [10,200]. Here the underlying MIMO system is decoupled by a set of spatio-temporal transforms, as illustrated in Figure 10.

The transforms ${\mathcal{T}}_1$ through ${\mathcal{T}}_3$ are motivated by the physical background of the room equalization problem and its solution using orthogonal expansions, as outlined in the previous section. In terms of the underlying multichannel problem, this can be achieved by diagonalization of the MIMO systems using a generalized singular value decomposition (GSVD). This approach is known as eigenspace adaptive filtering (EAF) [193]. As a consequence, the adaptation problem is reduced to the adaptation of the main diagonal elements of the MIMO room equalization filter $\underline{\tilde{\mathbf{C}}}$ in the transformed domain. In this way, the computational complexity is lowered significantly and the non-uniqueness problem is improved. However, EAF requires that the transfer paths from the loudspeakers to the microphones are known, which contradicts the idea of an adaptive computation of the equalization filters. Using analytic transformations which are based upon the free-field solutions of the wave equation, an approximate diagonalization of the MIMO system has been achieved [10,200].

The original approach focused on adapting only the diagonal paths in the transformed domain. In [201], this was extended towards a flexible adaptation framework also considering off-diagonal paths. The full adaptation of all paths in the transformed domain is investigated in [202]. Invertible transformations for WDAF have been introduced in [203], while a subband approach to WDAF has been published in [204]. Furthermore, strategies for the use of irregularly-spaced loudspeaker arrays have been proposed in [205].

8.3. Transform Domain Approaches

WDAF utilizes a set of transformations that transform the multichannel adaptive equalization problem into a transformed domain. This basic idea of applying a spatial transformation has also been applied to non-adaptive room equalization aiming at a large listening area. In [206], the sound field has been decomposed into circular/cylindrical basis functions for a concentric setup of loudspeaker and microphone array. This is essentially a two-dimensional problem. The equalization filters have been computed by least-squares optimization in the transformed domain. Room equalization has also been considered in the context of multizone synthesis by formulating the three-dimensional problem in the spherical harmonics domain (e.g., [207]).

A rather different approach is discussed in [208]. Here the original HIE is interpreted such that the sound field exterior to a spherical loudspeaker array is attenuated by the usage of variable directivity loudspeakers. The attenuation of the exterior sound field leads to less reflections traveling back into the listening area. Although such loudspeakers have not yet been realized, the simulation results look promising. The equalization problem is considered in the spherical harmonics domain, where the filters are computed by least-squares optimization.

8.4. Room Geometry-Aware Methods

The knowledge of the room geometry can be used to compute the resulting sound field in the room, for instance by the mirror image method. The control capabilities of a sound field synthesis system can then be used to cancel out the assumed contributions from the room. Methods which explicitly exploit knowledge on the room geometry can be seen as a specialization of the methods discussed so far, since they are based on a wave-theoretic view of the problem. A method for the equalization of early reflections for wave field synthesis (WFS) has been published in [209]. Here the mirror image sources are canceled out by anti-phase virtual point sources placed at the pre-computed positions of the image sources. A similar approach is presented in [210] for higher-order Ambisonics. An approach to room equalization for a linear loudspeaker array producing beams for a virtual surround system is discussed in [211]. The equalization of room reflections is achieved by accounting for the reflection of the beams in the room. The equalization filters are computed by solving the underlying least-squares problem in closed-form. In [212], a method is presented which is based on numerically simulating the impulse responses between the loudspeakers and control points. Only the early reflections are considered. The simulated impulse responses are fed into a MIMO solver for derivation of the equalization filters.

8.5. MIMO and SIMO Approaches

As an alternative to the wave-theoretic approach discussed so far, the acoustic paths between the loudspeakers and microphones can be interpreted as independent linear time-invariant systems. All resulting transfer functions can be combined together into a multiple-input/multiple-output (MIMO) system. MIMO room equalization approaches differ, amongst others, with respect to the loudspeaker and microphone positions (control points), and the particular technique used to compute the equalization filters. The difference between the wave-theoretic and the MIMO approaches discussed in the sequel is that the computation of equalization filters is not performed in a spatially transformed domain. Although the placement of the loudspeakers and microphones on the border of the listening area is motivated by the HIE, MIMO approaches may depart from this placement. As stated above, a sufficient number of loudspeakers and microphones must be used in order to synthesize and capture the entire sound field up to a given frequency. If the sampling is not dense enough, equalization may only be achieved at or in close vicinity to the microphone positions.

A non-adaptive MIMO approach which directly emerges from the discretization of the HIE is presented in [213]. The MIMO system is inverted in order to compute equalization filters for global equalization. As an alternative, a local solution is also discussed. A similar approach is followed in [85] for wave field synthesis. Channel shortening has also been investigated in the context of MIMO equalization [214,215] based on a least-squares solution.

The computation of equalization filters generally constitutes an inverse problem. Various algorithms have been proposed that improve the numerical and computational efficiency, as well as the numerical conditioning—for instance, a fast iterative MIMO inversion algorithm working in the DFT-domain [216], or a DFT-domain approximation of the MIMO filtered-x algorithm [217]. In [216], a steepest-descent and approximative Gauss–Newton iterative algorithm for the design of a MIMO equalizer is presented. In [218], a method for coping with the low conditioning of the transfer function matrix at some frequencies is proposed. The problem is amended by studying the structure of the MIMO transfer function matrix and replacing its inverse matrix by a pseudo-inverse that allows a range of acceptable solutions. Polynomial-based MIMO formulations of the room equalization problem are discussed in [219,220] with extensions towards explicitly controlling the number of active loudspeakers used for equalization [221].

There are also a number of specialized equalization approaches for specific scenarios. For instance, the equalization of multichannel stereophonic systems under the constraint that stereophonic pairs of loudspeakers should have similar transfer functions is discussed in [222,223,224]. The approach is split into two stages: (i) equalization of a single path also utilizing the other loudspeakers and (ii) similarity optimization between two channels that are used for stereophonic imaging. The room equalization in cars has been considered in various studies. A non-adaptive MIMO equalization approach utilizing IIR or FIR filters is presented in [225]. The optimization is performed in terms of the overall magnitude response to avoid coloration/tonal issues. A combined room equalization and cross-talk canceling approach for cars is discussed in [226].

Besides the MIMO approaches reviewed so far, single loudspeaker room equalization approaches have also been investigated which utilize multiple microphones. This constitutes a single-input/multiple-output (SIMO) problem. A non-adaptive polynomial multivariate control approach combined with a constrained mean squared error design and zero clustering is discussed in [149]. A statistic inferential method which considers the statistical variation between the different microphone positions for improved robustness and an enlarged listening area is presented in [227].

9. Evaluation Methods for RRE

One important aspect is the evaluation of RRE results, considering instrumental measures or subjective listening tests. The former aims at measures which are in relation with the goal of the procedure—for example, quantifying the similarity between the target function and the equalization result. However, an important role should be assigned to perceptual evaluation, since the final judgment is always performed by the human listener in the specific environment. In this section, we first analyze instrumental parameters used as a primary analysis stage of the obtained results. Then, a review of the most common listening test procedures is reported.

9.1. Instrumental Measures

In the following section, the most common instrumental measures for RRE evaluation are reviewed. Throughout the section, $h\left(n\right)$ denotes the RIR in the discrete time domain, while $H\left(e^{j\omega }\right)$ denotes its discrete-time Fourier transform with $\omega$ being the normalized angular frequency.

9.1.1. Spectral Deviation Measures

The spectral deviation was first used for the evaluation of the RRE procedure in [76], and was then adopted in many other papers [92,228]. The spectral deviation, $S_{\mathrm{D}}$, of a frequency response $E\left(e^{j\omega }\right)$ can be expressed as

$$S_{\mathrm{D}}=\sqrt{\frac{1}{Q_{\mathrm{h}}-Q_{\mathrm{l}}+1}\sum _{i=Q_{\mathrm{l}}}^{Q_{\mathrm{h}}}{\left(10{log}_{10}\left|E\left(e^{j\frac{2\mathsf{\Pi }}{N}i}\right)\right|-D\right)}^2},$$

(5)

where

$$D=\frac{1}{Q_{\mathrm{h}}-Q_{\mathrm{l}}+1}\sum _{i=Q_{\mathrm{l}}}^{Q_{\mathrm{h}}}\left(10{log}_{10}\left|E\left(e^{j\frac{2\mathsf{\Pi }}{N}i}\right)\right|\right),$$

(6)

where $Q_{\mathrm{l}}$ and $Q_{\mathrm{h}}$ are the lowest and highest frequency indexes, respectively, of the equalized band.

Usually, the experimental results provide an initial spectral deviation $S_{\mathrm{D},\mathrm{in}}$, calculated with $E\left(e^{j\omega }\right)=H\left(e^{j\omega }\right)$, and a final spectral deviation $S_{\mathrm{D},\mathrm{fin}}$, computed after equalization by considering $E\left(e^{j\omega }\right)=H\left(e^{j\omega }\right)·H_{\mathrm{inv}}\left(e^{j\omega }\right)$, where $H_{\mathrm{inv}}\left(e^{j\omega }\right)$ represents the designed equalizer. Figure 11 shows the curves used for the $S_{\mathrm{D}}$ calculation. A Mean Spectral Deviation Measure (MSDM) that represents the mean value of the final spectral deviation measures over the entire set of measured RIRs has also been considered [74,146].

In analogy to the mean spectral deviation measure, which gives a measure of the deviation of the magnitude frequency response from a flat one [228], a mean group delay deviation measure was introduced in [147,229] to quantify the average variation in terms of group delay:

$$G{D}_{\mathrm{D}}=\frac{1}{M}\sum _{l=1}^M\sqrt{\frac{1}{Q_{\mathrm{h}}-Q_{\mathrm{l}}+1}\sum _{i=Q_{\mathrm{l}}}^{Q_{\mathrm{h}}}{\left({GD}_l\left(i\right)-K_l\right)}^2},$$

(7)

where

$$K_l=\frac{1}{Q_{\mathrm{h}}-Q_{\mathrm{l}}+1}\sum _{i=Q_{\mathrm{l}}}^{Q_{\mathrm{h}}}{GD}_l\left(i\right),$$

(8)

$Q_{\mathrm{l}}$ and $Q_{\mathrm{h}}$ are the lowest and the highest frequency indexes, respectively, of the equalized band, and ${GD}_l\left(i\right)$ is the group delay of the M RIRs for the i-th frequency index.

The objective of mixed-phase equalization is to achieve a linear phase, and therefore the group delay should be as flat as possible: using this parameter it is possible to quantify the distance of the obtained group delay from a constant delay.

9.1.2. Sammon Map

The Sammon map was introduced for the evaluation of RRE in [230]. It is a non-linear projection method that maps multidimensional data onto fewer dimensions (e.g., two or three). The main property of the Sammon map is that it retains the geometrical distances between signals in a multidimensional space in two or three dimensions. Given the M magnitude responses $|H_k\left(e^{j\omega }\right)|$, $k=1,\dots ,M$, of the measured RIRs, the Sammon map algorithm iteratively minimizes—by a gradient descent scheme—the cumulative sum of the differences between the Euclidean distances in the high and low dimensional space. The following objective function is minimized:

$$\begin{array}{cc}\hfill J_{\mathrm{Sammon}}& =\frac{1}{{\displaystyle \sum _{l=1}^M\sum _{m=l+1}^M{d}_{lm}}}\sum _{l=1}^M\sum _{m=l+1}^M\frac{{\left(d_{lm}-d_{lm}^{\prime }\right)}^2}{d_{lm}},\hfill \end{array}$$

(9)

with

$$\begin{array}{cc}\hfill d_{lm}& =\sum _{w=1}^W{\left(|H_l(e^{j\frac{2\mathsf{\Pi }}{N}w})|-|H_m(e^{j\frac{2\mathsf{\Pi }}{N}w})|\right)}^2,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill d_{lm}^{\prime }& =\sum _{i=1}^L{\left|r_l\left(i\right)-r_m\left(i\right)\right|}^2,\hfill \end{array}$$

(11)

where W is the number of equally-spaced frequencies and L is the dimension of the Sammon map space.

In the Sammon map, the point associated with $H_k\left(e^{j\omega }\right)$ is represented as $\left(r_k\left(1\right),\dots ,r_k\left(L\right)\right)$. Considering a two-dimensional mapping $(L=2)$, upon convergence, the points $\left(r_k\left(1\right),r_k\left(2\right)\right)$ with $k=1,\dots ,M$ are configured on a two-dimensional plane such that the relative distances between the different $H_k\left(e^{j\omega }\right)$ are visually discernible. After equalization, the resulting performance can be determined from the size and shape of the region defined by the equalized frequency responses on the map. A circular shape around zeros indicates uniform equalization at all locations [230]. Figure 12 shows the results obtained using the Sammon map: it can be observed that for IRs without equalization (Figure 12a), the points are located far from the center of the map, while for IRs with equalization (Figure 12b), the points are uniformly distributed around the center of the map.

9.1.3. Energy Decay Reliefs

The effect of equalization can be evaluated considering the energy decay relief (EDR), which is a time-frequency generalization of the energy decay curve (EDC) used to calculate the reverberation time $T60$. Since room modes are characterized by peaks in the frequency response and extended ringing in the time domain, the EDR measure can help to understand the effect of the equalization procedure. The EDR is defined as the time-frequency representation of the RIR energy decay [231,232], and working in the continuous-time domain, it is calculated as follows:

$$ED{R}_h\left(t,f\right)={\int }_t^{+\infty }{\rho }_h\left(\tau ,f\right)d\tau ,$$

(12)

where ${\rho }_h\left(\tau ,f\right)$ is the energetic time-frequency representation of the RIR using a short-time Fourier transform (STFT) procedure applied with a rectangular analysis window.

Figure 13 shows the EDR calculated before and after the equalization procedure. Considering the temporal behavior, the plots show a reduction in decay times, while in the frequency domain, a reduction of the frequency peaks can be observed. Generally, after the equalization procedure a more uniform behavior is obtained, with a reduction of peaks and notches.

9.1.4. Acoustic Parameters

The quality of an audio signal can be evaluated considering some objective quality measures based on the RIR [233]. Acoustic parameters obtained using objective measures were first used for the assessment of RRE in [6]. The following acoustic parameters have been used in many papers about RRE:

• the definition index, which is defined as the percentage ratio of the energy of the first 50 ms or 80 ms after the main peak to the remaining energy of the RIR (D50 or D80) [13,234];
• the clarity index, which is defined as the logarithmic ratio of the energy of the first 50 ms or 80 ms after the main peak to the remaining energy of the RIR (C50 or C80) [13,235];
• the early decay time, which is defined as the time in which the first 10 dB fall of a decay process occurs, multiplied by a factor of 6 (EDT) [13,236];
• the direct-to-reverberation-ratio (DRR), also known as direct-to-reverberant-energy-ratio [233,237,238] is defined as the logarithmic ratio between the main peak and the remaining RIR;
• the central time (CT) [13,239] is the center of gravity of the energy of the RIR.

9.2. Perceptual Evaluation

To assess the audio quality, listening tests have to be performed following an appropriate procedure. Many proposals for the perceptual evaluation of an audio system can be found in the literature [240,241]. However, focusing on RRE and referring to the state-of-the-art, the perceptual assessment of RRE systems should adhere to the following standards:

• ITU-R BS.1116-1 [242]: “Methods for subjective assessment of small impairments in audio systems including multichannel sound systems”,
• ITU-R BS.1534-1 [243]: “Method for the subjective assessment of intermediate quality level of coding systems”,
• ITU-R BS.1284-1 [244]: “General methods for the subjective assessment of sound quality”.

All these recommendations provide a description of the test methodology, test procedure, and statistical methods to elaborate the acquired data. However due to the broadness of this topic, the discussion will be focused only on the most relevant procedures that have been applied to RRE.

The ITU-R BS.1284-1 recommendation provides a guide to the general assessment of perceived audio quality, and has been applied in [75,145] for the assessment of RRE. It is worth noting that ITU-R BS.1284-1 is based on ITU-R BS.1116-1. According to the guidelines of [244], expert listeners should be preferred to “give a better and a quicker indication of the likely results in the long term.” The subjective listening test is conceived as a comparison test, and the listeners should be instructed to provide a score using a seven-grade scale with a recommended resolution of 1 decimal place, as reported in [244]. The test is based on paired comparisons with references, and the score is given after listening to a repetition (four times consecutively) of the predetermined programme sequence. In the case of the assessment of an equalization procedure, the following sequence is considered in [75,145]:

• reference sequence without equalization;
• same sequence, equalized with one of the selected equalization techniques;
• reference sequence without equalization (repeated);
• same sequence, equalized with one of the selected equalization techniques (repeated).

As recommended in [244], the stimuli should never exceeded 20 s in length, thus lengths were limited between 15 to 20 s. Moreover, care was taken in order to guarantee that the tested musical items did not appear to be interrupted. For each reference signal, the presentation order of the different equalization methods was randomized and the listener did not know which equalization methodology was under test. Following the recommendation, before the listening test, a training set was subministrated to the listeners. As reported in [145], in order to familiarize with the test procedure, the test materials and the test environment, the subjects had the possibility to listen to each audio item in all conditions under evaluation. While the ITU-R BS.1284-1 recommendation suggests several attributes for characterizing the perceived sound quality, in [75,145] three attributes have been considered; i.e., “transparency” (all details of the performance can be clearly perceived), “timbre” (accurate portrayal of the different sound), “main impression” (the integrity of the total sound image and the interaction between other parameters). In order to test the room response equalizer using different spectral content, different music genres were considered as reference signals. Finally, the obtained results were processed to derive the mean values and the confidence intervals. A significance level of 0.05 was considered for computing the confidence intervals.

10. Emerging Topics and New Trends

In this section, emerging topics and new trends related to RRE are analyzed. In particular, the necessity of improving the performance of the equalization algorithms combined with the increasing interest in new technologies have led to innovative applications and interesting developments.

10.1. Personal Sound Zones

In the last years, there is an increasing interest in the possibility of reproducing different content in adjacent spatially restricted zones for multiple listeners by reducing the interference between the zones. These approaches are known as personal sound zones [245], multi-zone synthesis, or multi-zone sound control. A recent review on this topic can be found in [246], and more details in the numerous published papers on the subject [247,248,249,250,251,252,253,254,255,256,257,258,259,260,261,262,263,264,265,266,267,268,269,270,271,272,273,274]. At the current state, the achievable suppression between the zones is limited by various acoustical and practical restrictions, resulting in a limited applicability to real-world scenarios. In [262], an overview is presented on the major challenges that have to be dealt with for multi-zone sound control in a reverberant environment. Interference mitigation and room compensation robust to changes and uncertainties in the acoustic environment remain as challenging problems. An approach to room equalization for sound pressure control over a region of space combined with a wave domain sound field representation is presented in [262]. The approach is reported to be robust at low frequencies, but ineffective at high frequencies where the reverberant sound field is diffuse, calling for a very high number of loudspeakers.

10.2. Portable Devices

In recent years the use of portable devices has increased enormously, reaching a very high level of expansion. However, due to the loudspeakers’ characteristics and their interactions with the room environment, many of these devices are capable of satisfying just the basic audio requirements. This situation can be partially improved taking into consideration the acoustics of these devices and applying advanced audio techniques. In [275], a multi-point equalization procedure is introduced to improve the non-ideal response of a portable system such as the mobile phone. Objective measurements and subjective listening test results have confirmed the positive effect of the algorithms on personal portable devices. In [276], a static and an adaptive algorithm for frequency response linearization applied to mobile computers is reported. Subjective listening tests have underlined an improvement in the listener’s perception, confirming the validity of such approaches.

10.3. Nonlinear Equalization

Sound reproduction systems can exhibit an undesirable behavior not only due to the room acoustics, but also due to loudspeaker and amplifier systems that can produce linear and nonlinear distortions. In order to remove the nonlinear effects, in [277,278,279] equalizers that involve Volterra filters to model the amplifier-loudspeaker-enclosure are used before driving the output signal through the loudspeakers. In this way it is possible to equalize not only the linear behavior of the system, but also its nonlinear behavior considering adaptive procedures.

10.4. Room Equalization with Moving Microphone

One of the main issues of multi-point equalization is the measurement of the RIRs, which requires a long time to achieve a certain spatial resolution inside the listening area. A solution to this problem can be found by using time-variant system identification techniques [280,281]. Here RIRs are measured by applying a dynamic method based on the use of one moving microphone instead of estimating the RIRs independently. This procedure allows to obtain a dense grid of RIRs from one spatially continuous measurement that can be used in multi-point equalization to estimate the prototype function and equalization filters.

11. Conclusions

In this paper, following the historical path, a complete overview of the state-of-the-art has been presented. In order to underline the evolution and the potentiality of RRE, different classifications have been considered for the approaches. A first classification can be done considering the number of impulse responses used for the estimation of the equalization filter (i.e., single-point or multi-point equalizers). The former is effective only on a reduced zone around the measurement point, while the latter is capable of enlarging the equalized zone and contrasting the room response variations. The second classification can be performed considering an instantaneous or continuous measurement of the impulse responses (i.e., fixed or adaptive approaches). The former consists of a-priori measurement of the impulse responses, while the latter is based on a continuous update of the impulse responses and thus of the equalizer to cope with the temporal variations of the environment. Within this general classification, we must consider pre-processing techniques that are used to contrast the audible distortions caused by equalization errors due to the RIRs variations, minimum-phase and mixed-phase, direct and indirect approaches for different equalizer design techniques, and wave domain filters for the equalization of massive multichannel sound reproduction systems. Following this classification, different approaches have been described.

Table 1. Comparison of the state-of-the-art approaches considering the aforementioned classification criteria. MINT: multiple-input/multiple-output inverse theorem; SISO: single-input/single-output; SIMO: single-input/multiple-output; MIMO: multiple-input/multiple-output.

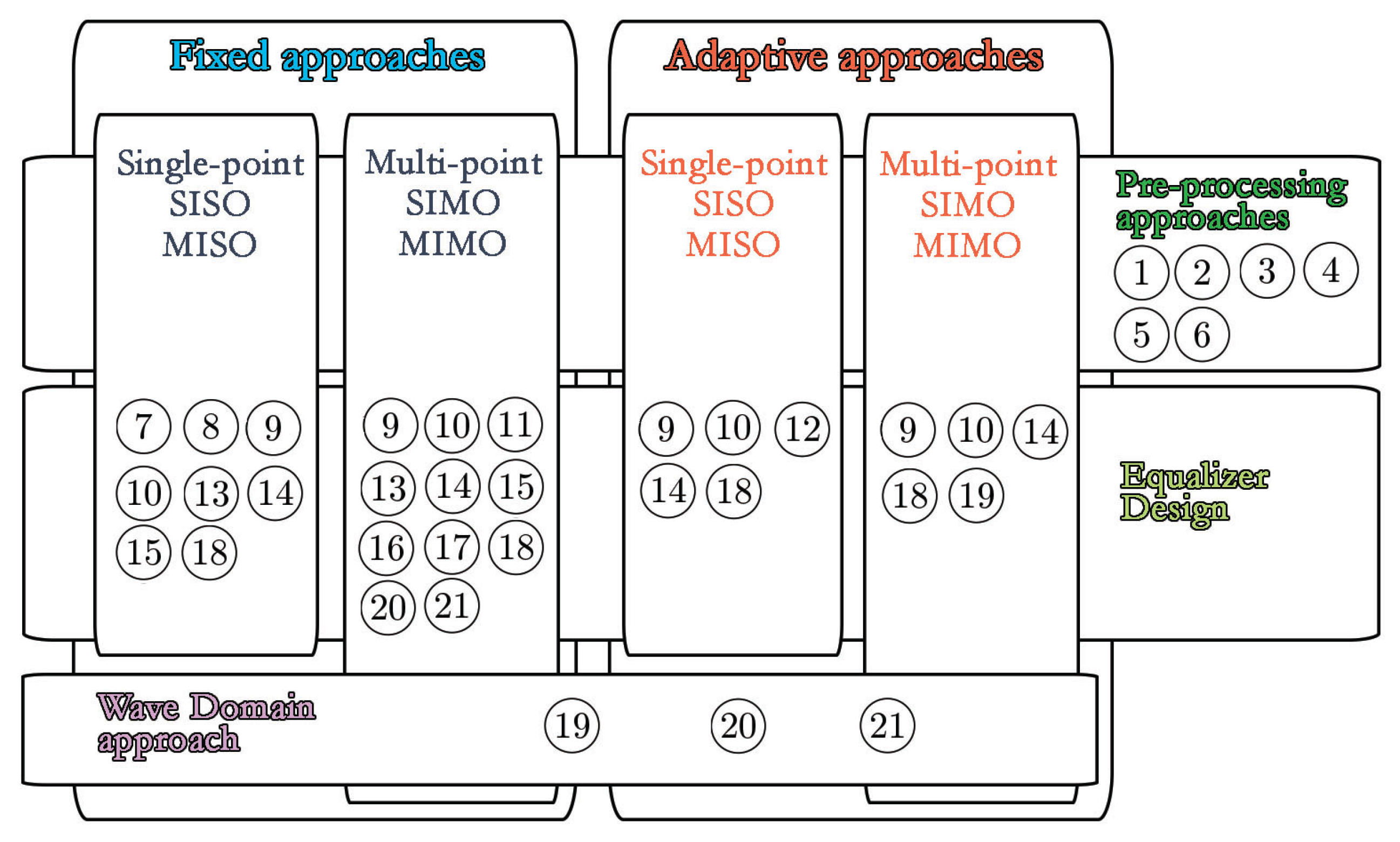
	Pre-Processing	Minimum Phase	Mixed Phase	Fixed	Adaptive	Single-point	Multi-point	Direct	Indirect	Wave Domain	Section
Short filters [61]	√	√	√					√	√		5.1
Complex smoothing [35,94]	√	√	√					√	√		5.2.1
Frequency warping [98]	√	√	√					√	√		5.2.2
Kautz filters [110]	√	√	√					√	√		5.2.3
Multirate approaches [50,72,116,117,118,119,120]	√	√	√					√	√		5.2.4
Room impulse response reshaping [78,122,123,124,125,126,127,128,129,130]	√		√						√		5.3
Homomorphic filtering [5,56,57,58]		√	√	√		√			√		4.1
Linear predictive coding analysis [61,63,64,65,66,67,68,69,70,71,72,73,74,75]		√		√		√			√		4.2
Least-squares optimization techniques [76]			√	√	√	√	√	√			4.3
Frequency domain deconvolution [51,80,81]		√	√	√		√			√		4.4
MINT solutions [86,87]			√	√			√	√	√		4.5
Average and weighted average methods [77]			√		√	√		√			6.1
Clustering methods [30,70,71,72,121,138,139,140]			√	√		√	√		√		6.2
Prototype approach [73,144,146,147]		√	√	√	√	√	√		√		6.3
Common acoustical poles compensation [63,64,65]		√		√			√		√		6.4
Modal equalization [4,157]			√	√			√		√		6.5
Plane wave approach [159,160,161,162,163,164,165]			√	√			√				6.6
Quasi-anechoic approach [172,173]				√	√	√	√	√			6.8
SISO/SIMO in time domain [77,169,189]		√	√		√	√	√	√	√		7.1.1
SISO/SIMO in frequency domain [177,178,179,180]		√	√		√	√	√	√	√		7.1.2
MIMO approaches [183,185,186]		√	√		√		√	√	√		7.2
Wave domain adaptive filtering [10,200,201]			√		√		√	√		√	8
Transform domain approaches [206,208]			√	√			√	√		√	8
Room geometry aware methods [209,210,211,212]				√			√			√	8

summarizes the state-of-the-art methods as function of classification criteria, i.e., pre-processing techniques, minimum phase and mixed phase technique, fixed and adaptive approaches, single-point and multi-point approaches, direct and indirect methods according to the definition of Section 4.6, and wave domain methods. It is evident that several methods can cover more than one aspect, extending the potential and the effectiveness of the methodology. In this context, the instrumental measurement and perceptual evaluation of the equalization results become crucial: some examples of the main approaches from the state-of-the-art in this field have been reported. Finally, a general discussion on emerging methodologies and new trends for RRE has been presented. It is evident that the increasing availability of personal devices will lead to an increased use of RRE techniques to enhance their performance.