Ablation of Copper Metal Films by Femtosecond Laser Multipulse Irradiation
Abstract
:1. Introduction
2. Theoretical Background
2.1. Two Temperature Model
2.2. Dynamic Thermal Properties
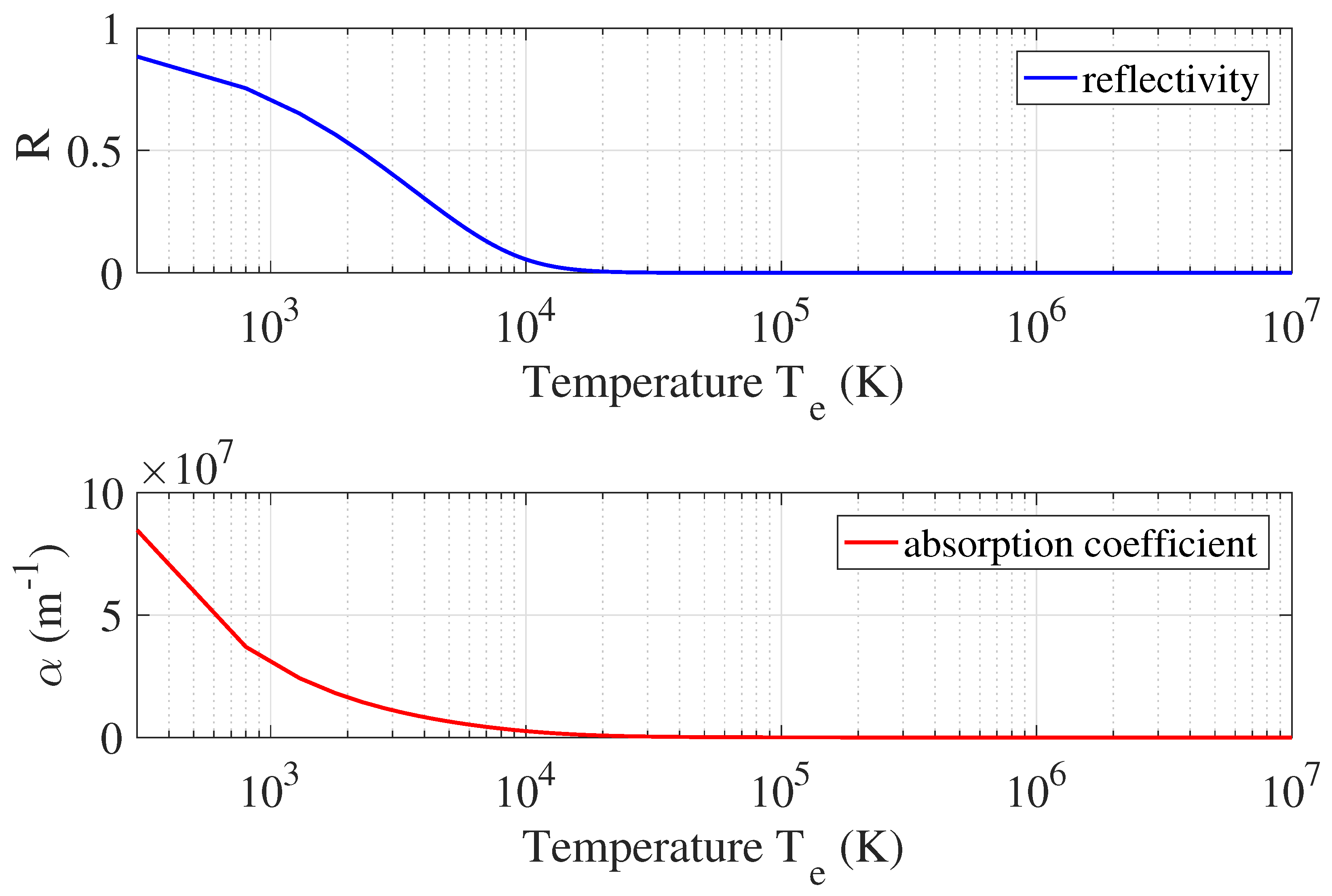
2.3. Dynamic Optical Properties
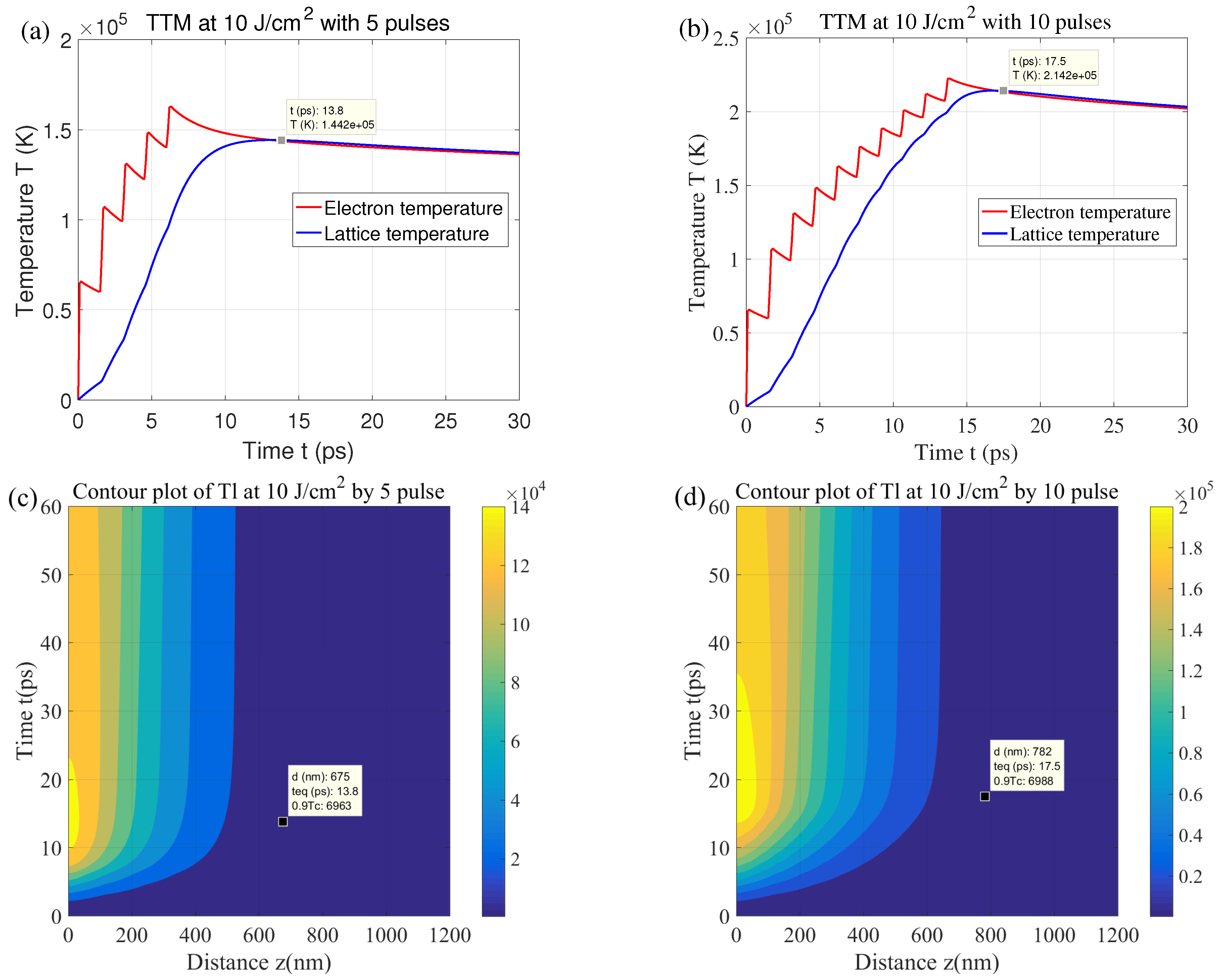
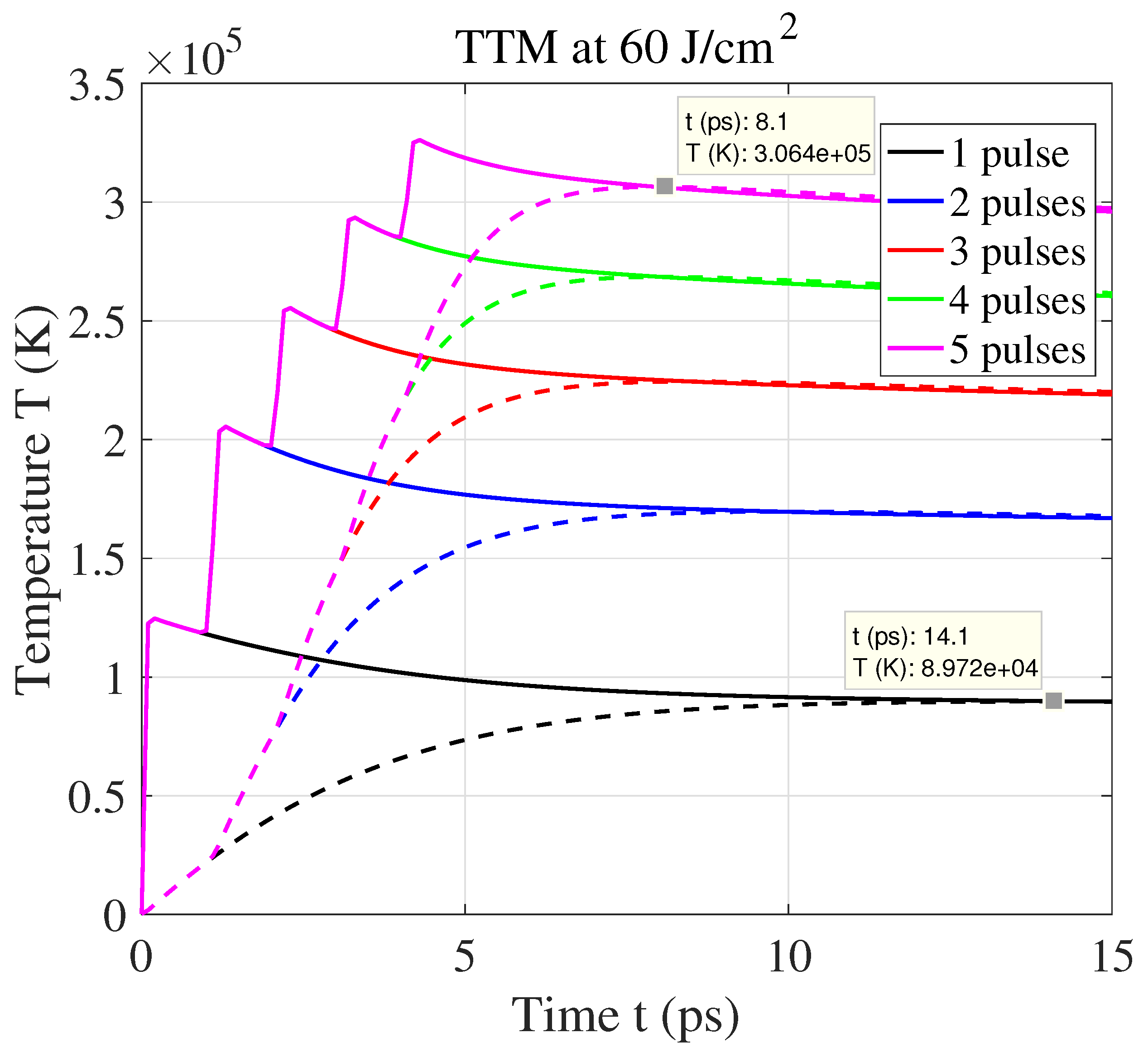
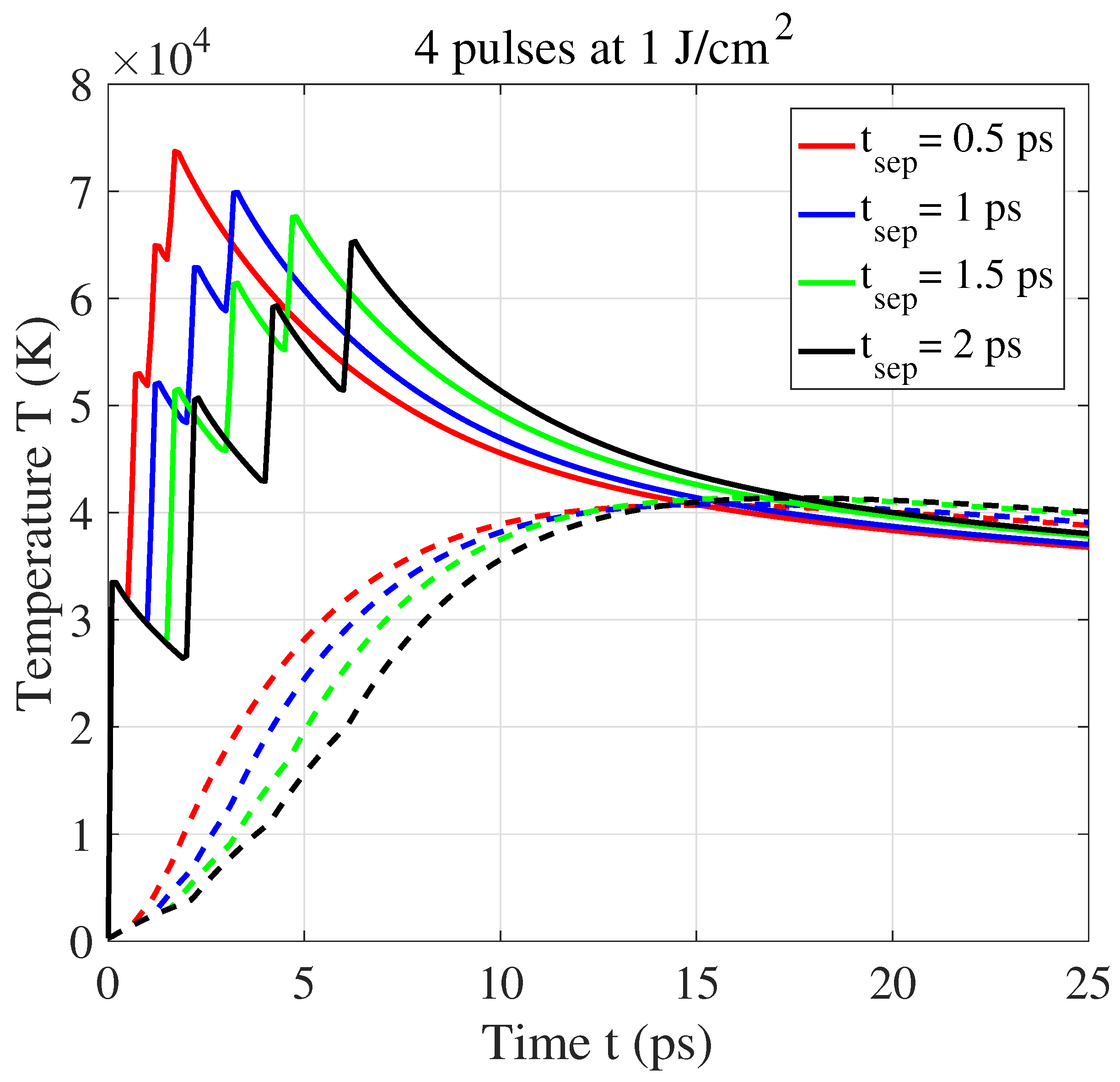
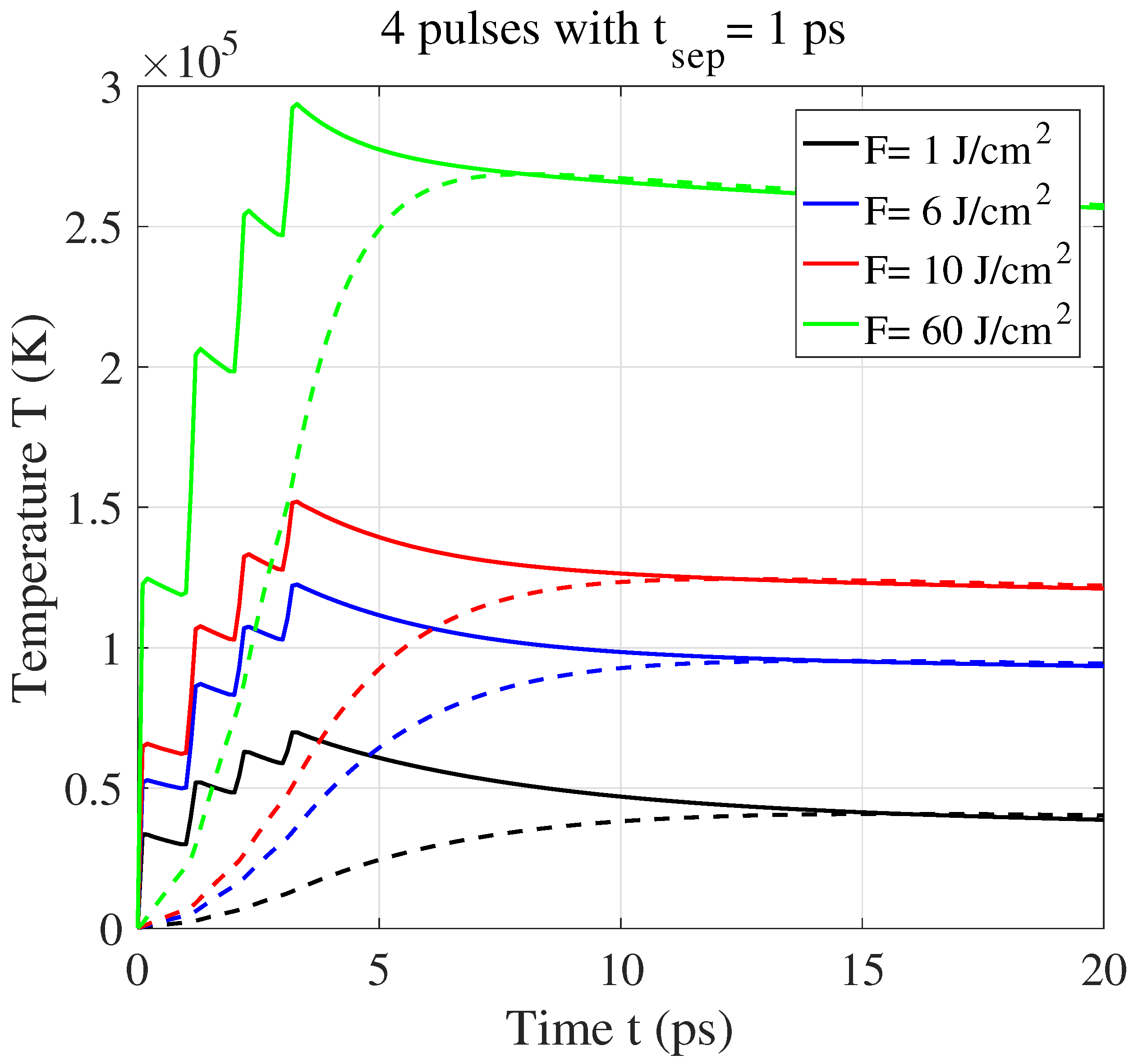
3. Results and Discussion
4. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| TTM | Two Temperature Model |
| CE | Coulomb Explosion |
| FTAE | Fast Thermal Accumulation Effect |
| MD | Molecular Dynamics |
References
- Chichkov, B.N.; Momma, C.; Nolte, S.; Von Alvensleben, F.; Tünnermann, A. Femtosecond, picosecond and nanosecond laser ablation of solids. Appl. Phys. A 1996, 63, 109–115. [Google Scholar] [CrossRef]
- Momma, C.; Nolte, S.; Chichkov, B.N.; Alvensleben, F.V.; Tünnermann, A. Precise laser ablation with ultrashort pulses. Appl. Surf. Sci. 1997, 109, 15–19. [Google Scholar] [CrossRef]
- Nolte, S.; Momma, C.; Jacobs, H.; Tünnermann, A.; Chichkov, B.N.; Wellegehausen, B.; Welling, H. Ablation of metals by ultrashort laser pulses. JOSA B 1997, 14, 2716–2722. [Google Scholar] [CrossRef]
- Leitz, K.H.; Redlingshöfer, B.; Reg, Y.; Otto, A.; Schmidt, M. Metal ablation with short and ultrashort laser pulses. Phys. Procedia 2011, 12, 230–238. [Google Scholar] [CrossRef]
- Tatra, S.; Vázquez, R.G.; Stiglbrunner, C.; Otto, A. Numerical simulation of laser ablation with short and ultra-short pulses for metals and semiconductors. Phys. Procedia 2016, 83, 1339–1346. [Google Scholar] [CrossRef]
- Mannion, P.T.; Magee, J.; Coyne, E.; O’connor, G.M.; Glynn, T.J. The effect of damage accumulation behaviour on ablation thresholds and damage morphology in ultrafast laser micro-machining of common metals in air. Appl. Surf. Sci. 2004, 233, 275–287. [Google Scholar] [CrossRef]
- Gamaly, E.G.; Rode, A.V.; Luther-Davies, B.; Tikhonchuk, V.T. Ablation of solids by femtosecond lasers: Ablation mechanism and ablation thresholds for metals and dielectrics. Phys. Plasmas 2002, 9, 949–957. [Google Scholar] [CrossRef] [Green Version]
- Stoian, R.; Rosenfeld, A.; Ashkenasi, D.; Hertel, I.V.; Bulgakova, N.M.; Campbell, E.E.B. Surface charging and impulsive ion ejection during ultrashort pulsed laser ablation. Phys. Rev. Lett. 2002, 88, 097603. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Tsai, H.L. Modeling of ultrashort laser pulse-train processing of metal thin films. Int. J. Heat Mass Transf. 2007, 50, 3461–3470. [Google Scholar] [CrossRef]
- Cheng, C.; Xu, X. Mechanisms of decomposition of metal during femtosecond laser ablation. Phys. Rev. B 2005, 72, 165415. [Google Scholar] [CrossRef]
- Cheng, C.W.; Wang, S.Y.; Chang, K.P.; Chen, J.K. Femtosecond laser ablation of copper at high laser fluence: Modeling and experimental comparison. Appl. Surf. Sci. 2016, 361, 41–48. [Google Scholar] [CrossRef]
- Byskov-Nielsen, J.; Savolainen, J.M.; Christensen, M.S.; Balling, P. Ultra-short pulse laser ablation of copper, silver and tungsten: Experimental data and two-temperature model simulations. Appl. Phys. A 2011, 103, 447–453. [Google Scholar] [CrossRef]
- Rethfeld, B.; Sokolowski-Tinten, K.; Von Der Linde, D.; Anisimov, S.I. Timescales in the response of materials to femtosecond laser excitation. Appl. Phys. A 2004, 79, 767–769. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.; Zhu, X. Theoretical studies of ultrafast ablation of metal targets dominated by phase explosion. Appl. Phys. A 2007, 89, 571–578. [Google Scholar] [CrossRef]
- Ren, Y.; Cheng, C.W.; Chen, J.K.; Zhang, Y.; Tzou, D.Y. Thermal ablation of metal films by femtosecond laser bursts. Int. J. Therm. Sci. 2013, 70, 32–40. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, Y.; Chen, J.K. Ultrafast solid–liquid–vapor phase change in a thin gold film irradiated by multiple femtosecond laser pulses. Int. J. Heat Mass Transf. 2009, 52, 3091–3100. [Google Scholar] [CrossRef]
- Eaton, S.M.; Zhang, H.; Herman, P.R.; Yoshino, F.; Shah, L.; Bovatsek, J.; Arai, A.Y. Heat accumulation effects in femtosecond laser-written waveguides with variable repetition rate. Opt. Express 2005, 13, 4708–4716. [Google Scholar] [CrossRef] [PubMed]
- Ancona, A.; Döring, S.; Jauregui, C.; Röser, F.; Limpert, J.; Nolte, S.; Tünnermann, A. Femtosecond and picosecond laser drilling of metals at high repetition rates and average powers. Opt. Lett. 2009, 34, 3304–3306. [Google Scholar] [CrossRef] [PubMed]
- Kerse, C.; Kalaycıoğlu, H.; Elahi, P.; Çetin, B.; Kesim, D.K.; Akçaalan, Ö.; Yavaş, S.; Aşık, M.D.; Öktem, B.; Hoogland, H.; et al. Ablation-cooled material removal with ultrafast bursts of pulses. Nature 2016, 537, 84–88. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Povarnitsyn, M.E.; Levashov, P.R.; Knyazev, D.V. Simulation of ultrafast bursts of subpicosecond pulses: In pursuit of efficiency. Appl. Phys. Lett. 2018, 112, 051603. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, I.H.; Xu, X. Heat transfer in femtosecond laser processing of metal. Numer. Heat Transf. Part A Appl. 2003, 44, 219–232. [Google Scholar] [CrossRef]
- Nowak, D.; Lee, M.J. Optical and Thermal Effective Masses of Copper. Phys. Rev. B 1972, 5, 2851. [Google Scholar] [CrossRef]
- Kittel, C.; McEuen, P.; McEuen, P. Introduction to Solid State Physics; Wiley: New York, NY, USA, 1996; Volume 8, pp. 323–324. [Google Scholar]
- Anisimov, S.I.; Rethfeld, B. Theory of ultrashort laser pulse interaction with a metal. In Nonresonant Laser-Matter Interaction (NLMI-9); International Society for Optics and Photonics: Bellingham, WA, USA, 1997; Volume 3093, pp. 192–204. [Google Scholar]
- Chen, J.K.; Latham, W.P.; Beraun, J.E. The role of electron-phonon coupling in ultrafast laser heating. J. Laser Appl. 2005, 17, 63–68. [Google Scholar] [CrossRef]
- Nash, D.J.; Sambles, J.R. Surface plasmon-polariton study of the optical dielectric function of copper. J. Mod. Opt. 1995, 42, 1639–1647. [Google Scholar] [CrossRef]
- Ren, Y.; Chen, J.K.; Zhang, Y. Optical properties and thermal response of copper films induced by ultrashort-pulsed lasers. J. Appl. Phys. 2011, 110, 113102. [Google Scholar] [CrossRef]
- Adachi, S. The Handbook on Optical Constants of Metals: In Tables and Figures; World Scientific: Singapore, 2012. [Google Scholar]
- Cheng, C.W.; Chen, J.K. Drilling of Copper Using a Dual-Pulse Femtosecond Laser. Technologies 2016, 4, 7. [Google Scholar] [CrossRef]
- Kotsedi, L.; Kaviyarasu, K.; Fuku, X.G.; Eaton, S.M.; Amara, E.H.; Bireche, F.; Ramponi, R.; Maaza, M. Two temperature approach to femtosecond laser oxidation of molybdenum and morphological study. Appl. Surf. Sci. 2017, 421, 213–219. [Google Scholar] [CrossRef] [Green Version]
- Sundaram, S.K.; Mazur, E. Inducing and probing non-thermal transitions in semiconductors using femtosecond laser pulses. Nat. Mater. 2002, 1, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Abdelmalek, A.; Bedrane, Z.; Amara, E.H. Thermal and non-thermal explosion in metals ablation by femtosecond laser pulse: Classical approach of the Two Temperature Model. J. Phys. Conf. Ser. 2018, 987, 012012. [Google Scholar] [CrossRef]

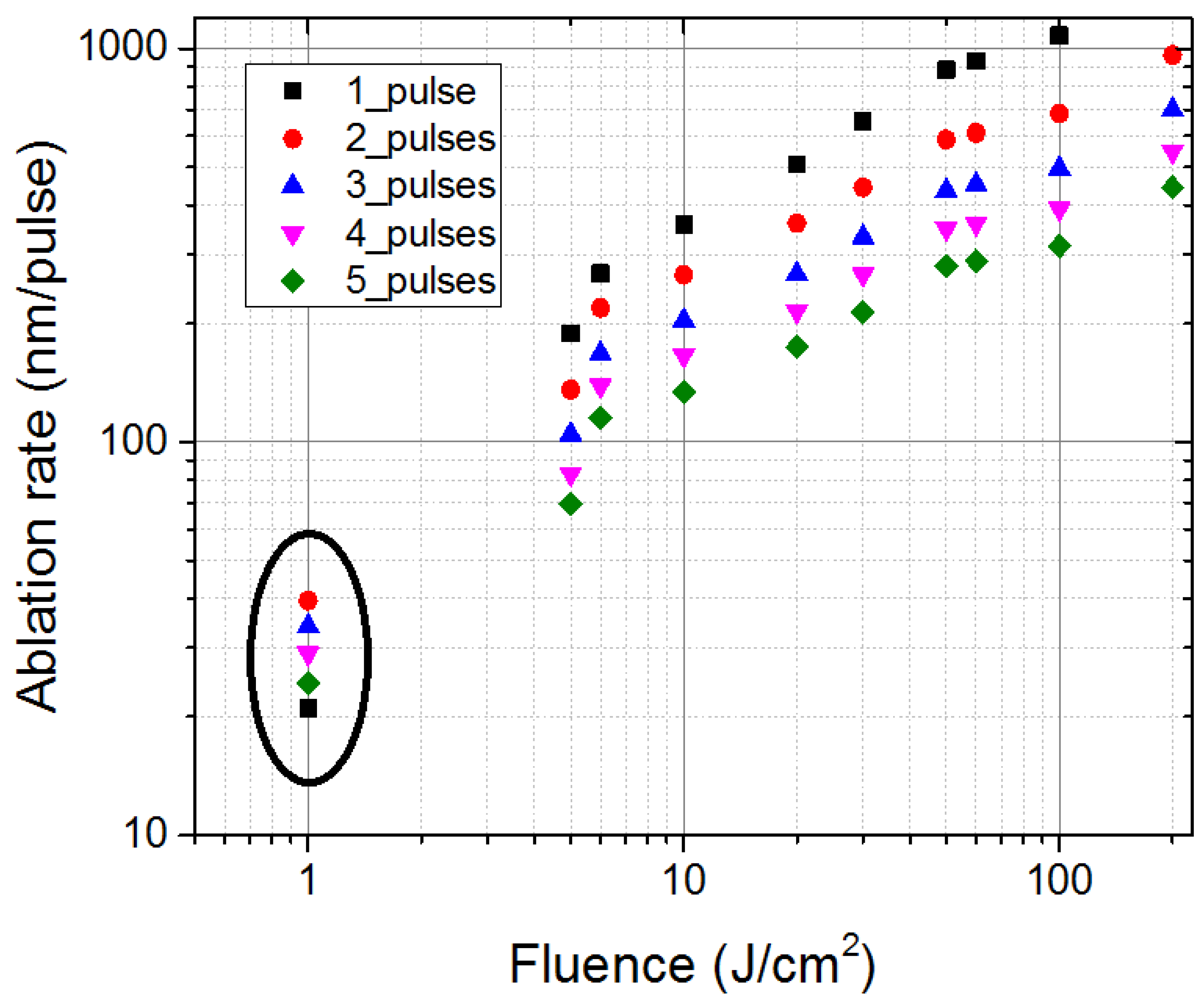
| Fluence () | N = 1 | N = 2 | N = 3 | N = 4 | N = 5 |
|---|---|---|---|---|---|
| Ablation Depth (nm) | |||||
| 1 | 21 | 78 | 102 | 116 | 122 |
| 5 | 189 | 272 | 314 | 332 | 348 |
| 6 | 268 | 438 | 503 | 556 | 575 |
| 10 | 357 | 532 | 611 | 664 | 671 |
| 20 | 509 | 720 | 802 | 861 | 871 |
| 30 | 653 | 888 | 997 | 1067 | 1070 |
| 50 | 883 | 1175 | 1307 | 1394 | 1398 |
| 60 | 931 | 1222 | 1357 | 1439 | 1447 |
| 100 | 1080 | 1367 | 1485 | 1566 | 1575 |
| 200 | 1547 | 1927 | 2096 | 2192 | 2216 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelmalek, A.; Bedrane, Z.; Amara, E.-H.; Sotillo, B.; Bharadwaj, V.; Ramponi, R.; Eaton, S.M. Ablation of Copper Metal Films by Femtosecond Laser Multipulse Irradiation. Appl. Sci. 2018, 8, 1826. https://doi.org/10.3390/app8101826
Abdelmalek A, Bedrane Z, Amara E-H, Sotillo B, Bharadwaj V, Ramponi R, Eaton SM. Ablation of Copper Metal Films by Femtosecond Laser Multipulse Irradiation. Applied Sciences. 2018; 8(10):1826. https://doi.org/10.3390/app8101826
Chicago/Turabian StyleAbdelmalek, Ahmed, Zeyneb Bedrane, El-Hachemi Amara, Belén Sotillo, Vibhav Bharadwaj, Roberta Ramponi, and Shane M. Eaton. 2018. "Ablation of Copper Metal Films by Femtosecond Laser Multipulse Irradiation" Applied Sciences 8, no. 10: 1826. https://doi.org/10.3390/app8101826
APA StyleAbdelmalek, A., Bedrane, Z., Amara, E. -H., Sotillo, B., Bharadwaj, V., Ramponi, R., & Eaton, S. M. (2018). Ablation of Copper Metal Films by Femtosecond Laser Multipulse Irradiation. Applied Sciences, 8(10), 1826. https://doi.org/10.3390/app8101826






