3.1. Failure Mode and Analysis
Figure 9a–d show the failure modes of the four columns. No debonding was observed at the interface between the concrete and SMRC. For each column, the crack pattern of the SMRC surface is plotted. Multiple distributed cracks were observed in the four columns. When the column failed, crushed concrete was observed in the compression zone.
In S-0, the first crack appeared when the load was increased to 73 kN. The distance between the crack and the actuator was 110 cm, as shown in
Figure 9a. With the increase of the load, the crack was widened and propagated; more cracks appeared in the column at the tensile side. After the column failed, 13 major cracks were observed. The average spacing of the major cracks was 115 mm. The maximum crack width was 4.2 mm.
In S-1, the first crack in the SMRC appeared, when the load was increased to 143 kN. The distance between the crack and the actuator was 110 cm, as shown in
Figure 9b. The second crack in the SMRC appeared near the mid-span, when the load was increased to 162 kN, and the strain gauges that were attached on the SMRC failed because of the cracks. No crack was observed in the normal concrete until the load was increased to 220 kN. The crack was at the cross section that was about 45 cm away from the actuator. At the same time, five cracks were observed in the SMRC. The five cracks were, respectively, 110 cm, 72 cm, 45 cm, 33 cm, and 85 cm away from the actuator. After the column failed, 12 major cracks were observed in the SMRC; the average spacing between the major cracks was 125 mm; the maximum crack width was 7.1 mm. A limited number of microcracks were observed in the vicinity of the major cracks. The steel mesh in the SMRC was ruptured.
In S-2, the first crack in the SMRC appeared, when the load was increased to 155 kN. The distance between the crack and the actuator was 105 cm, as shown in
Figure 9c. The first crack in the normal concrete was observed when the load was increased to 250 kN. The crack was at the cross section that was about 27 cm away from the actuator. At the same time, six cracks were observed in the SMRC. The six cracks were respectively 105 cm, 120 cm, 98 cm, 86 cm, 65 cm, and 27 cm away from the actuator. As the load was further increased, a number of densely distributed microcracks appeared. After the column failed, the maximum crack width was 2.4 mm. A limited number of wires of the steel meshes were ruptured.
In S-3, the first crack in the SMRC appeared, when the load was increased to 158 kN. The distance between the crack and the actuator was 115 cm, as shown in
Figure 9d. The first crack in the normal concrete was observed when the load was increased to 285 kN. The crack was at the cross section that was about 48 cm away from the actuator. At the same time, five cracks were observed in the SMRC. The five cracks were, respectively, 115 cm, 66 cm, 95 cm, 51 cm, and 105 cm away from the actuator. Similar to S-2, as the load was further increased, a number of densely distributed microcracks appeared. After the column failed, the maximum crack width was 1.8 mm. No wire of the steel meshes was ruptured.
Further analysis is conducted to understand the crack patterns.
Figure 10a illustrates a segment of a column for analyzing stresses in the steel bar, steel mesh and concrete. The stress in the steel bar is denoted by σ
s, which reaches the maximum value at the crack section. Between two adjacent cracks, σ
s decreases because a part of tensile force is resisted by the concrete due to force transfer between steel bar and concrete. The stress reduction is denoted by Δσ
s. Similarly, the stress in steel wire is denoted by σ
w; and, the stress reduction is denoted by Δσ
w. The shear stress between steel bar and concrete is denoted by τ
s; the shear stress between steel bar and concrete is denoted by τ
w. Both τ
s and τ
w are zero at the crack section and the center between two adjacent cracks.
Equations (1) and (2) can be obtained according to the force equilibrium of the segmental model [
36].
where
and
are the total areas of cross section of steel bar and steel wire, respectively;
and
are the areas of concrete and resin concrete in effective tensile zone, respectively;
and
are the tensile strengths of concrete and resin concrete, respectively;
is the minimum spacing of cracks; and,
is the average bond stress between SMRC and concrete.
As shown in
Figure 10b,c, the Equations (3) and (4) can be obtained according to the force equilibrium of the isolated bodies of steel bar and steel wire, respectively.
where
and
are the total perimeters of steel bar and steel wire, respectively;
and
are the mean values of bonding stress between steel bar and concrete, and between steel wire and resin concrete, respectively.
Based on Equations (1) to (4), the average spacing of the cracks (
) can be expressed in Equation (5).
Equation (5) shows that the average spacing of cracks decreases with the total perimeter of steel wires. The average crack width can be solved using the different strains in the steel wire and the resin concrete between two adjacent cracks. Yuan et al. [
36] investigated the relationship between the crack width and the spacing between adjacent cracks that are based on the flexural structures reinforcement test. The crack width decreases with the decreasing of spacing between adjacent cracks.
3.3. Load-Deflection Curves
Figure 13 shows the relationship between the load and the mid-span deflection. When compared with S-0 that was not strengthened, the other three columns (S-1 to S-3) that were strengthened while using SMRC had higher load capacities and peak deflections. In each curve, the peak load represents the load capacity, and the mid-span deflection of the load capacity represents the peak deflection. As the number of steel mesh increases from one to three, the load capacity is increased from 492 kN to 539 kN, while the peak deflection is reduced from 11.8 mm to 10.1 mm. The main reason why the peak deflection decreases with the increasing of layer number of steel mesh is that the whole stiffness of the specimen increases with more steel meshes.
There are three phases for the load-deflection curve [
37]. The first phase is the linear elastic phase. In this phase, the load that is applied on the column is small and there are no cracks on the SMRC or RC column. The second phase is the crack propagation phase. With the increase of the load, the resin concrete begins to crack. The cracks occur in different position of resin concrete, and the spacing between these cracks is large. Besides, some cracks on the RC column can be observed. The third phase is steel bar yielding phase. When the load applied on the column approaches the load capacity, the steel bars yield. Many cracks occur on the resin concrete in a short period with small spacing. Obvious flexural deformation for column can be observed. Also, the stress of steel mesh increases rapidly because of the yielding of steel bar.
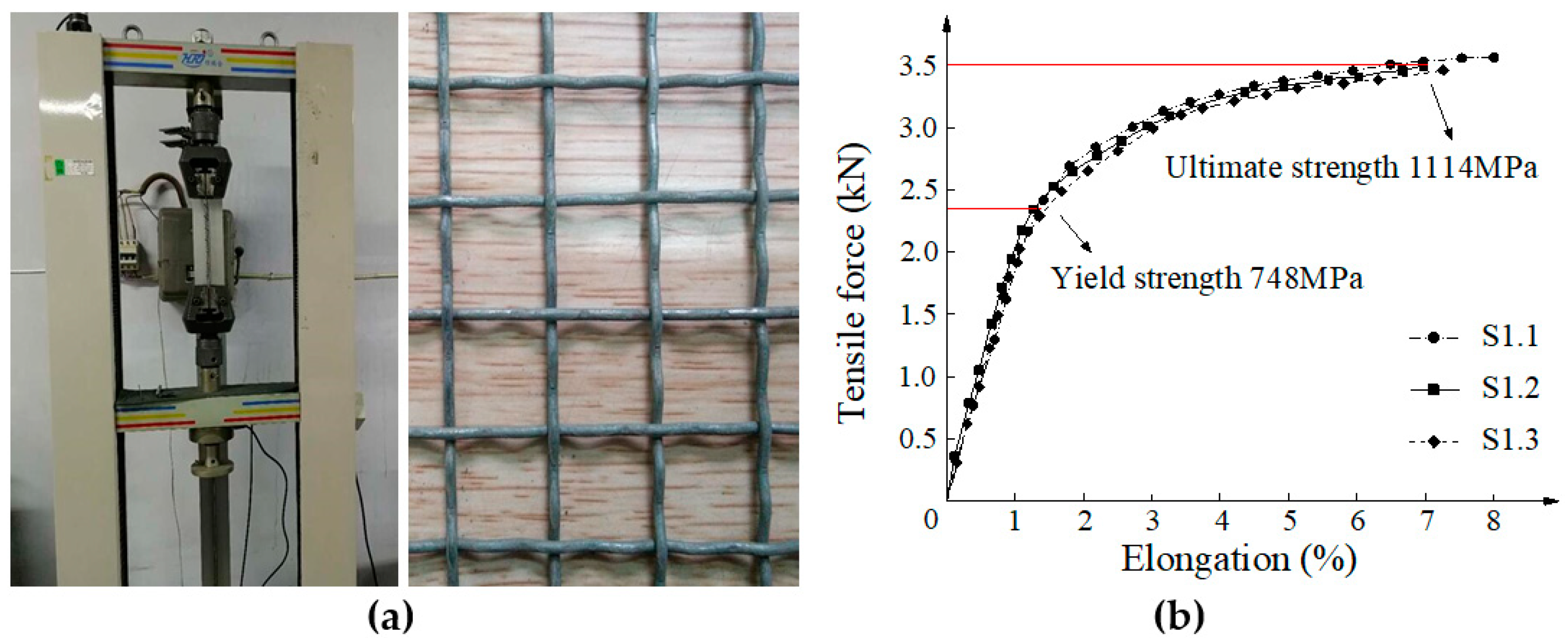
Table 2 summarizes the compressive test results of the four columns. When compared with S-0, the use of one steel mesh in the SMRC increases the cracking load by 96%, the load capacity by 23%, and the peak deflection by 22%. The result indicates that the use of SMRC can delay the presence of crack, enhance the load capacity, and improve the deformability. Increasing the steel mesh layer number from one to three increases the cracking load by 10% and the load capacity by 10%, and it decreases the peak deflection by 14%, and the maximum crack width by 75%. The result indicates that the increase of steel mesh layer can delay the presence of crack, enhance the load capacity and reduce the maximum crack width, but it may compromise the deformability. The main reason why the reinforcement material can improve the deformability of the RC column is the high-performance of resin concrete. As can be seen in
Figure 3b, the ultimate tensile strain of resin concrete is much larger than the normal concrete.