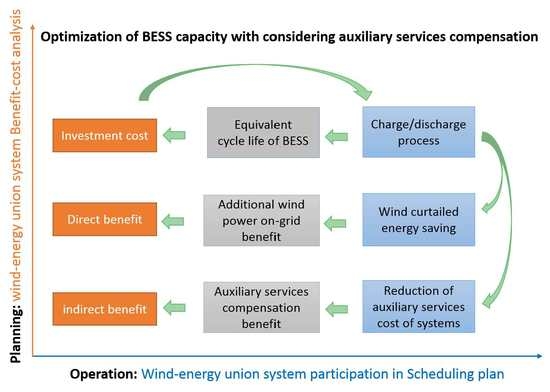
Optimization of Battery Energy Storage System Capacity for Wind Farm with Considering Auxiliary Services Compensation
Abstract
:1. Introduction
2. Problem Formulation
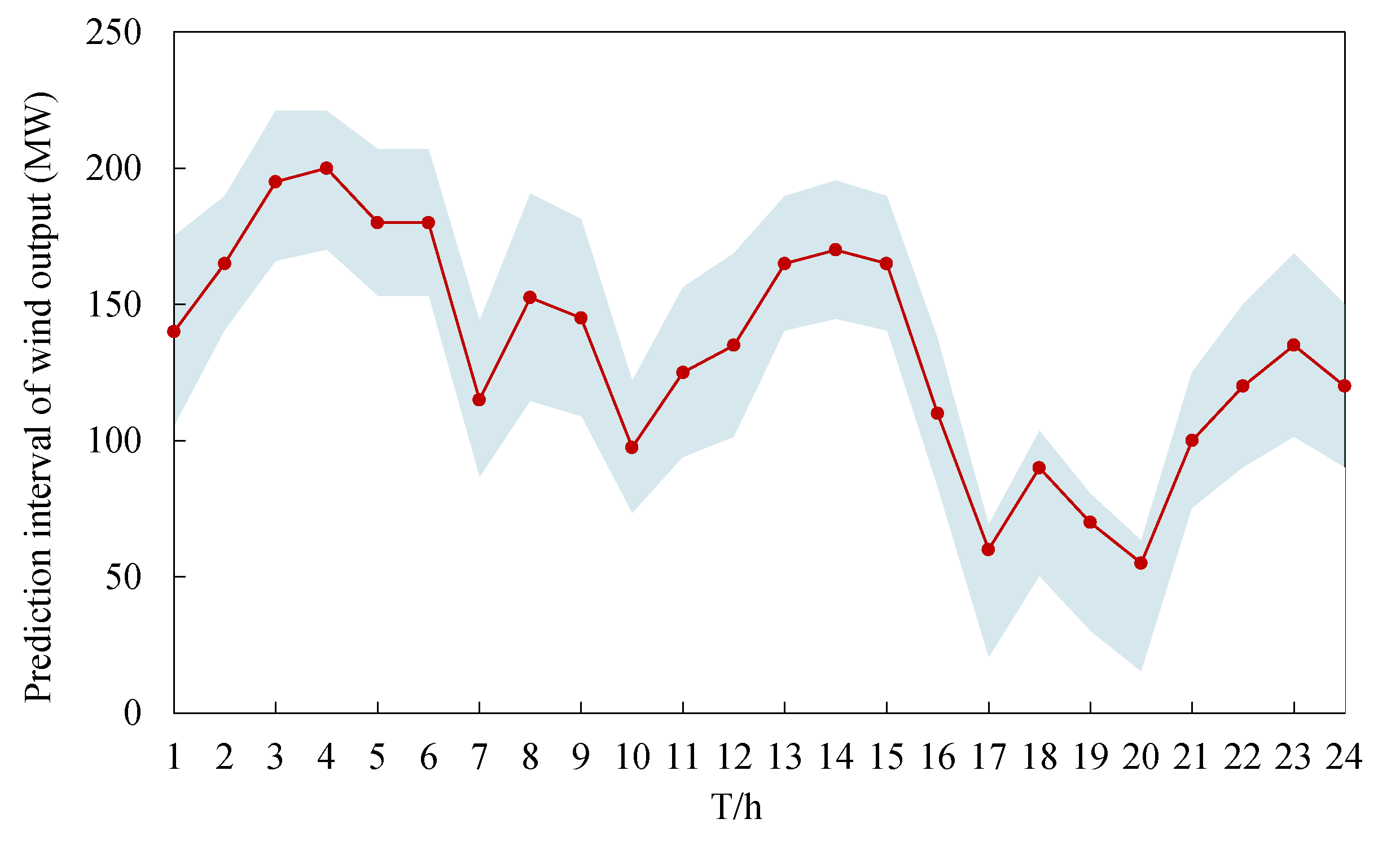
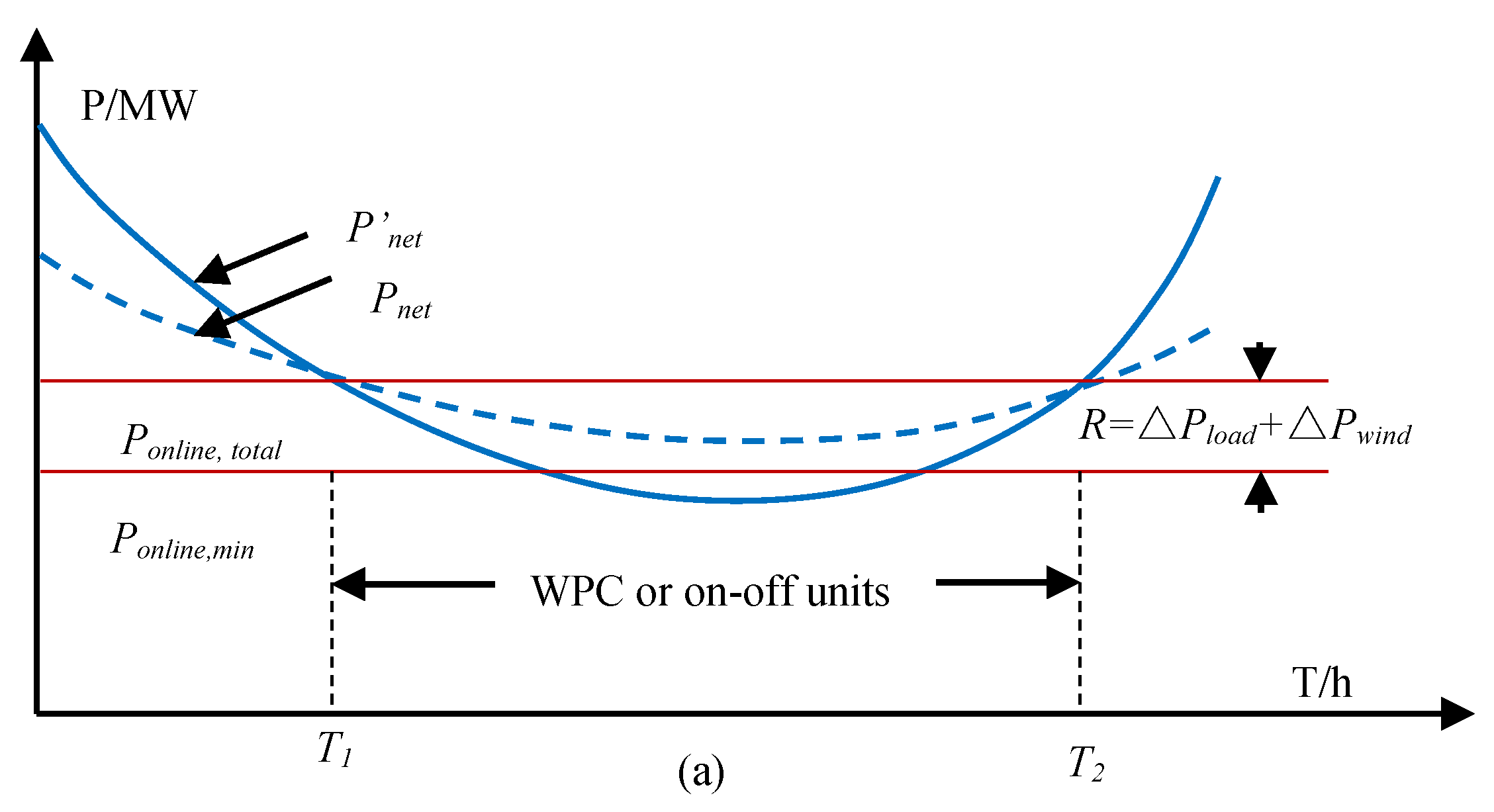
2.1. Wind Output Characteristics
2.1.1. Variability
2.1.2. Uncertainty
2.2. Auxiliary Services Eased by BESS
2.2.1. BESS Participation in the Scheduling Plan
2.2.2. Quantification the Ancillary Services Cost
2.3. Mathematical Description of BESS
2.3.1. Equivalent Loss of Cycle Life
2.3.2. Constraints of BESS Accounting to the Scheduling
3. Optimal Model
3.1. Objective Function
3.2. Constraints
3.3. System Performance Indices
4. Case Study
4.1. Basic Data
4.2. Operation Results Without BESS
- Case 1: The optimal scheduling results of systems without wind power integration is calculated.
- Case 2: With allowing wind power curtailment, the scheduling results with wind power integration is considered.
4.3. Operation Results with BESS
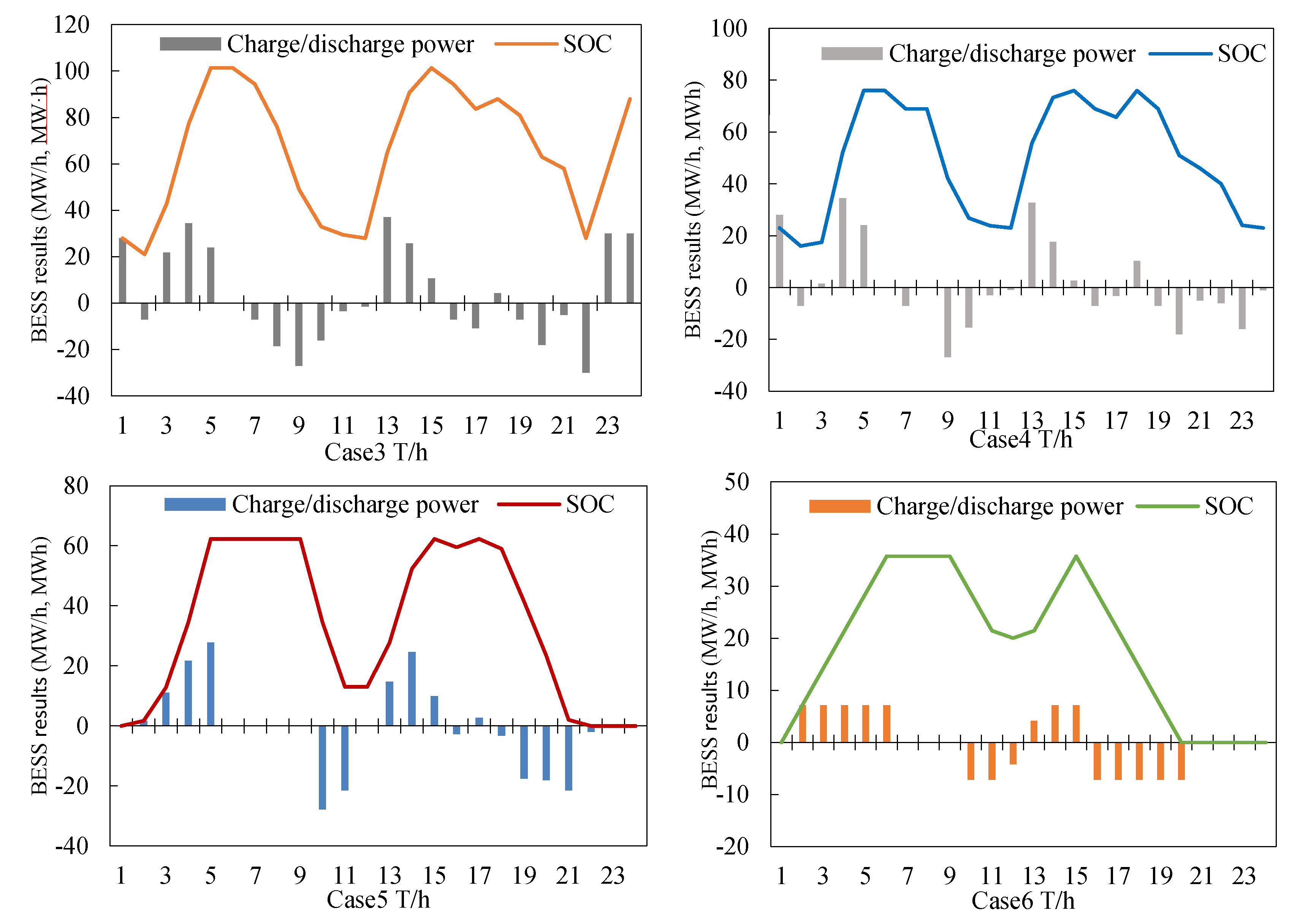
- Case 3: both the auxiliary service compensation and BESS reserve wind forecast error are considered, that is, the proposed model;
- Case 4: without auxiliary service compensation and with BESS reserve wind uncertainty;
- Case 5: with auxiliary service compensation, and without BESS reserve wind uncertainty; and,
- Case 6: neither auxiliary service compensation nor BESS reserve wind uncertainty is considered.
4.4. Sensitivity Analysis
4.4.1. On-grid Price of Wind Power
4.4.2. Investment Cost and Cycle Life of BESS
4.4.3. Reserve Level of BESS
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Pnet,t | net load of systems with wind power integration in hour t |
| Pload,t | forecast value of load demand in hour t |
| Pwind,t | forecast output of wind farm in hour t |
| up/down ramp demand of the net load in hour t | |
| maximum/minimum output of unit i | |
| ui,t | on-off state of unit i in hour t |
| Pgi,t | output of unit i in hour t |
| △Pload,t | spinning reserve demand of the load demand in hour t |
| upper and down limitation of wind prediction interval | |
| Ng | number of conventional units |
| Ponline,max/Ponline,min | upper/lower limitation of the online units |
| Ponline,total | total output of the online conventional units |
| P’net | net load of systems with wind farm configuration BESS |
| R | total spinning reserve capacity required by the system |
| Pcap | rated power of BESS |
| Scap | rate capacity of BESS |
| Cserve | difference auxiliary service cost of systems with and without BESS |
| Cfixed | fixed cost item of auxiliary service |
| Cvary | variable cost item of auxiliary service |
| CAI | daily investment cost per capacity of conventional units |
| rated power of the conventional unit i | |
| output of unit i with configuration BESS in hour t | |
| MBESS/M | number of units participating the auxiliary service with/without BESS |
| unit coal cost of conventional units with/without BESS | |
| T | one scheduling period |
| D | charge/discharge depth of BESS |
| Lcyc,D | cycle life of BESS under the charge/discharge depth of D |
| Lcyc,N | cycle life of BESS with fully charge/discharge |
| NB | charge/discharge number of BESS though the life cycle |
| Tlife | equivalent operation years of BESS |
| Ps,t | output of BESS in hour t |
| Punion,t | output of wind energy union system in hour t |
| Ssoc,t | state of charge (SOC) of BESS in hour t |
| △t | scheduled interval |
| charge/discharge status of BESS at time t | |
| charge/discharge effectiveness of BESS | |
| Cost | total investment cost of BESS |
| Save | directly benefit from saving wind curtailed energy |
| Cc(p,n) | capital recovery factor with annual interest rate p |
| CE | unit capacity cost of BESS |
| COM | unit operation and maintenance cost of BESS |
| amortized power cost per year | |
| amortized capacity cost per year | |
| r | kW·h/kW cost ratio of BESS |
| on-grid price of wind power | |
| Pwloss,t/PBwloss,t | curtailed wind energy with and without BESS in hour t |
| auxiliary service cost caused by wind power with/without BESS | |
| Ri | ramping ability of unit i |
| maximum/minimum online time of unit i | |
| CGen | operating cost function of conventional units |
| f(Pgi,t) | quadratic fuel cost function with coefficients ai, bi, ci |
| Si | on-off cost of unit i |
| q | curtailed rate of wind power |
| Ncyc | equivalent cycle numbers of BESS though a scheduling period |
| reserve level provided by BESS for the uncertainty of wind power |
References
- Yang, Z.G.; Zhang, J.L.; Kintner-Meyer, M.C.W.; Liu, X.C.; Choi, D.; Lemmon, J.P.; Liu, J. Electrochemical energy storage for green grid. Chem. Rev. 2011, 111, 3577–3613. [Google Scholar] [CrossRef] [PubMed]
- Dunn, B.; Kamath, H.; Tarascon, J.M. Electrical energy storage for the grid: A battery of choices. Science 2011, 334, 928–934. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J.; Zhao, J.H.; Yang, H.M.; Wang, D.X.; Dong, Z.Y. Planning of solar photovoltaics, battery energy storage system and gas micro turbine for coupled micro energy grids. Appl. Energy 2018, 219, 361–369. [Google Scholar] [CrossRef]
- Kou, P.; Gao, F.; Guan, X.H. Stochastic predictive control of battery energy storage for wind farm dispatching: Using probabilistic wind power forecasts. Rene. Energy 2015, 80, 286–300. [Google Scholar] [CrossRef]
- Wen, S.L.; Lan, H.; Fu, Q.; Yu, D.; Yu, D.C.; Zhang, L.J. Economic allocation for energy storage system considering wind power distribution. IEEE Trans. Power Syst. 2015, 30, 644–652. [Google Scholar] [CrossRef]
- Ghofrani, M.; Arabali, A.; Etezadi-Amoli, M.; Fadali, M.S. Energy storage application for performance enhancement of wind integration. IEEE Trans. Power Syst. 2013, 28, 4803–4811. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H.; Aichhorn, A.; Zheng, J.P.; Greenleaf, M. Sizing strategy of distributed battery storage system with high penetration of photovoltaic for voltage regulation and peak load shaving. IEEE Trans. Smart Grid. 2014, 5, 982–991. [Google Scholar] [CrossRef]
- Dong, J.J.; Gao, F.; Guan, X.H.; Zhai, Q.Z.; Wu, J. Storage-reserve sizing with qualified reliability for connected high renewable penetration micro-grid. IEEE Trans. Sustain. Energy 2016, 7, 732–743. [Google Scholar] [CrossRef]
- Qin, M.W.; Chan, K.W.; Chuang, C.Y.; Luo, X.; Wu, T. Optimal planning and operation of energy storage systems in radial networks for wind power integration with reserve support. IEEE Gener. Transm. Distrib. 2016, 10, 2019–2025. [Google Scholar] [CrossRef]
- Kargarian, A.; Hug, G. Optimal sizing of energy storage systems: A combination of hourly and intra-hour time perspectives. IEEE Gener. Transm. Distrib. 2016, 10, 594–600. [Google Scholar] [CrossRef]
- Luo, F.; Meng, K.; Dong, Z.Y.; Zheng, Y.; Chen, Y.Y.; Wong, K.P. Coordinated operational planning for wind farm with battery energy storage system. IEEE Trans. Sustain. Energy 2015, 6, 253–262. [Google Scholar] [CrossRef]
- Akhavan-Hejazi, H.; Mohsenian-Rad, H. Optimal operation of independent storage systems in energy and reserve markets with high wind penetration. IEEE Trans. Smart Grid. 2014, 5, 1088–1097. [Google Scholar] [CrossRef]
- Halamay, D.A.; Brekken, T.K.; Simmons, A.; McArthur, S. Reserve requirement impacts of large-scale integration of wind, solar, and ocean wave power generation. IEEE Trans. Sustain. Energy 2011, 2, 321–328. [Google Scholar] [CrossRef]
- Ding, H.J.; Hu, Z.H.; Song, Y.H. Rolling optimization of wind farm and energy storage system in electricity markets. IEEE Trans. Power Syst. 2015, 30, 2676–2684. [Google Scholar] [CrossRef]
- Jiang, X.; Chen, H.K.; Xiang, T.Y. Assessing the effect of wind power peaking characteristics on the maximum penetration level of wind power. IET Gener. Trans. Distrib. 2015, 9, 2466–2473. [Google Scholar] [CrossRef]
- Zhang, N.; Kang, C.Q.; Xia, Q.; Liang, J. Modeling conditional forecast error for wind power in generation scheduling. IEEE Trans. Power Syst. 2014, 29, 1316–1324. [Google Scholar] [CrossRef]
- Wu, D.L.; Wang, Y.; Guo, C.X.; Liu, Y.; Gao, Z.X. An economic dispatching model considering wind power forecast error in electricity market environment. Autom. Electr. Power Syst. 2012, 36, 23–28. [Google Scholar]
- Su, C.C.; Hsu, Y.Y. Fuzzy dynamic programming: Application to unit commitment. IEEE Trans. Power Syst. 1991, 6, 1231–1237. [Google Scholar] [CrossRef]
- Ela, E.; Kirby, B.; Navid, N. Effective ancillary services market designs on high wind power penetration systems. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting (PESGM), San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Østergaard, P.A. Ancillary services and the integration of substantial quantities of wind power. Appl. Energy 2006, 83, 451–463. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Gao, F.; Yang, K.; Hui, D.; Li, D. Cycle-life energy analysis of LiFePO4 batteries for energy storage. Proc. CSEE 2013, 33, 41–45. [Google Scholar]
- Zhou, C.K.; Qin, K.J.; Allan, M.; Zhou, W.J. Modeling of the cost of EV battery wear due to V2G application in power systems. IEEE Trans. Energy Conver. 2011, 26, 1041–1049. [Google Scholar] [CrossRef]
- Chen, W.Z.; Li, Q.B.; Shi, L.; Luo, Y.; Zhan, D.D.; Shi, N.; Liu, K. Energy storage sizing for dispatch ability of wind farm. In Proceedings of the 2012 11th International Conference on Environment and Electrical Engineering, Venice, Italy, 18–25 May 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Wang, X.Y.; Vilathgamuwa, D.M.; Choi, S.S. Determination of battery storage capacity in energy buffer for wind farm. IEEE Trans. Energy Convers. 2008, 23, 868–878. [Google Scholar] [CrossRef]
- Tek, K.A.; Brekken, A.Y.; Jouanne, A.V.; Yen, Z.Z.; Hapke, H.M.; Halamay, D.A. Optimal energy storage sizing and control for wind power applications. IEEE Trans. Sustain. Energy 2011, 2, 69–77. [Google Scholar]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No.04CH37508), New Orleans, LA, USA, 2–4 September 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 3, pp. 284–289. [Google Scholar]



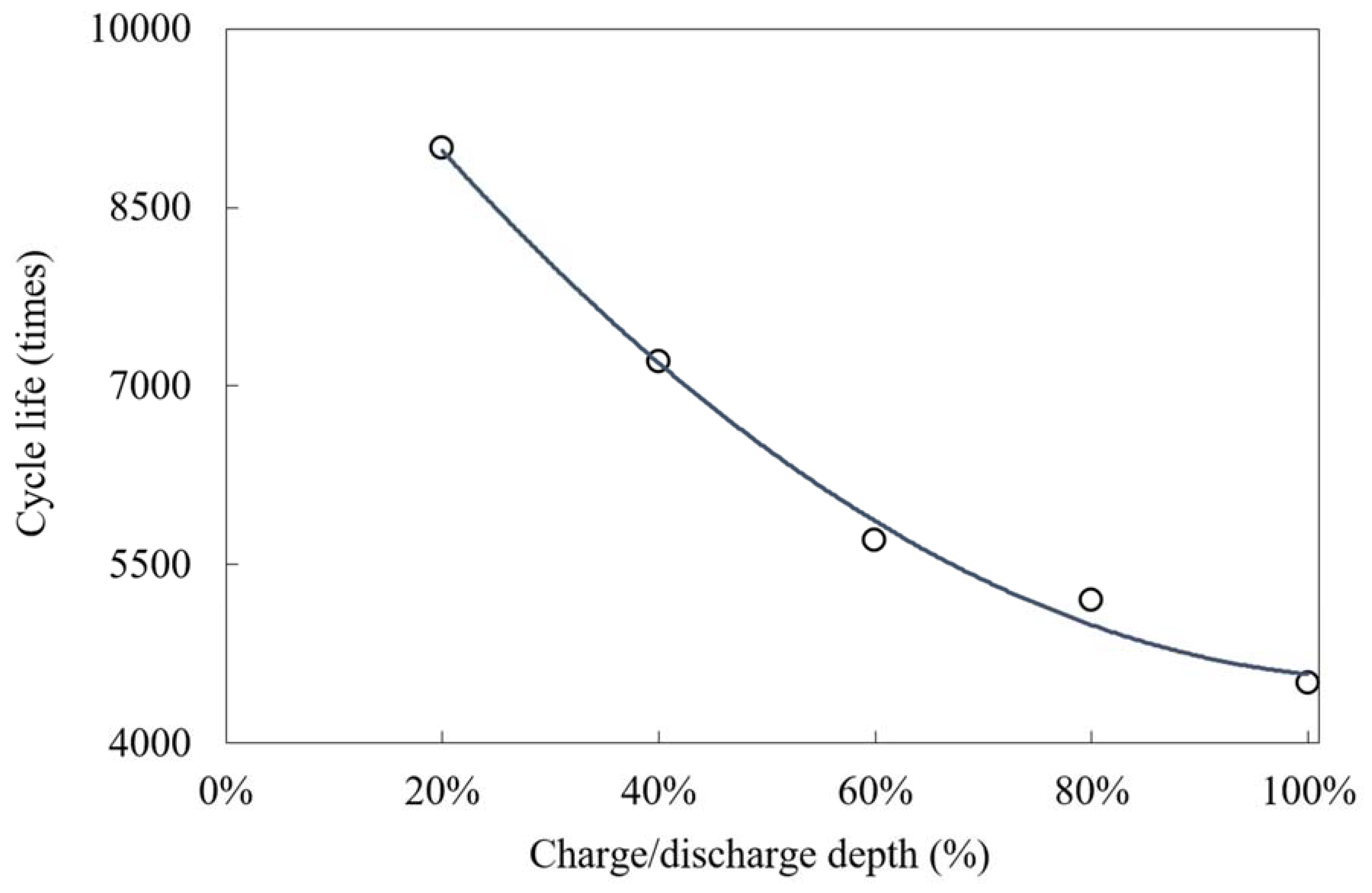



| Discharge Depth (%) | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
|---|---|---|---|---|---|
| Cycle (time) | 9000 | 7200 | 5700 | 5200 | 4500 |
| Units | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Pmax (MW) | 455 | 455 | 130 | 130 | 162 | 80 | 85 | 55 | 55 | 55 |
| Pmin (MW) | 150 | 150 | 20 | 20 | 25 | 20 | 25 | 10 | 10 | 10 |
| c ($/h) | 1000 | 970 | 700 | 680 | 450 | 370 | 480 | 660 | 665 | 670 |
| b ($/MW·h2) | 16.19 | 17.26 | 16.60 | 16.50 | 19.70 | 22.26 | 26.74 | 25.92 | 27.27 | 27.29 |
| a (10−3 $/MW·h2) | 0. 48 | 0.31 | 2.0 | 2.1 | 3.98 | 7.12 | 7.9 | 4.13 | 2.22 | 1.73 |
| Ri (MW/h) | 130 | 130 | 60 | 60 | 90 | 40 | 40 | 20 | 20 | 20 |
| Si ($) | 4500 | 5000 | 550 | 560 | 900 | 170 | 260 | 30 | 30 | 30 |
| Initial status (h) | 8 | −8 | −5 | −5 | −5 | −3 | −3 | −1 | −1 | −1 |
| Case | cg ($/MW·h) | q (%) | |
|---|---|---|---|
| 1 | 21.201 | - | 382 |
| 2 | 21.579 | 6.09% | 437 |
| Case | cg ($/MW·h) | f ($) | q (%) | Pcap (MW) | Scap (MW·h) | Ncyc (time) |
|---|---|---|---|---|---|---|
| Case 3 | 21.238 | 2990 | 0.0% | 58 | 122.4 | 1.73 |
| Case 4 | 21.305 | −1540 | 0.64% | 55 | 88.9 | 1.71 |
| Case 5 | 21.290 | 1790 | 3.61% | 27.75 | 60.25 | 1.85 |
| Case 6 | 21.544 | 1050 | 4.32% | 7.15 | 35.75 | 1.56 |
| On-Grid Price ($/kW·h) | f ($) | Pcap (MW·h) | Scap (MW·h) |
|---|---|---|---|
| 0.084 | 2990 | 58 | 122.4 |
| 0.080 | 2321 | 54 | 102.4 |
| 0.076 | 1845 | 35.25 | 63.25 |
| 0.072 | 740 | 27.75 | 60.25 |
| 0.068 | 322 | 7.15 | 14.25 |
| 0.064 | 0 | 0 | 0 |
| cg ($/MW·h) | f ($) | q (%) | Pcap (MW·h) | Scap (MW·h) | |
|---|---|---|---|---|---|
| 100% | 21.238 | 2990 | 0.0% | 58 | 122.4 |
| 80% | 21.324 | 3160 | 1.10% | 44.8 | 95.2 |
| 60% | 21.323 | 3930 | 1.84% | 34.8 | 79.6 |
| 40% | 21.312 | 3560 | 2.54% | 31.2 | 70.35 |
| 20% | 21.307 | 2910 | 3.23% | 29.5 | 61.25 |
| 0% | 21.290 | 1790 | 3.61% | 27.75 | 60.25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Nan, G.; Liu, H.; Guo, Z.; Zeng, Q.; Jin, Y. Optimization of Battery Energy Storage System Capacity for Wind Farm with Considering Auxiliary Services Compensation. Appl. Sci. 2018, 8, 1957. https://doi.org/10.3390/app8101957
Jiang X, Nan G, Liu H, Guo Z, Zeng Q, Jin Y. Optimization of Battery Energy Storage System Capacity for Wind Farm with Considering Auxiliary Services Compensation. Applied Sciences. 2018; 8(10):1957. https://doi.org/10.3390/app8101957
Chicago/Turabian StyleJiang, Xin, Guoliang Nan, Hao Liu, Zhimin Guo, Qingshan Zeng, and Yang Jin. 2018. "Optimization of Battery Energy Storage System Capacity for Wind Farm with Considering Auxiliary Services Compensation" Applied Sciences 8, no. 10: 1957. https://doi.org/10.3390/app8101957
APA StyleJiang, X., Nan, G., Liu, H., Guo, Z., Zeng, Q., & Jin, Y. (2018). Optimization of Battery Energy Storage System Capacity for Wind Farm with Considering Auxiliary Services Compensation. Applied Sciences, 8(10), 1957. https://doi.org/10.3390/app8101957