Ant Colony Optimization and Genetic Algorithm for Fuzzy Stochastic Production-Distribution Planning
Abstract
1. Introduction
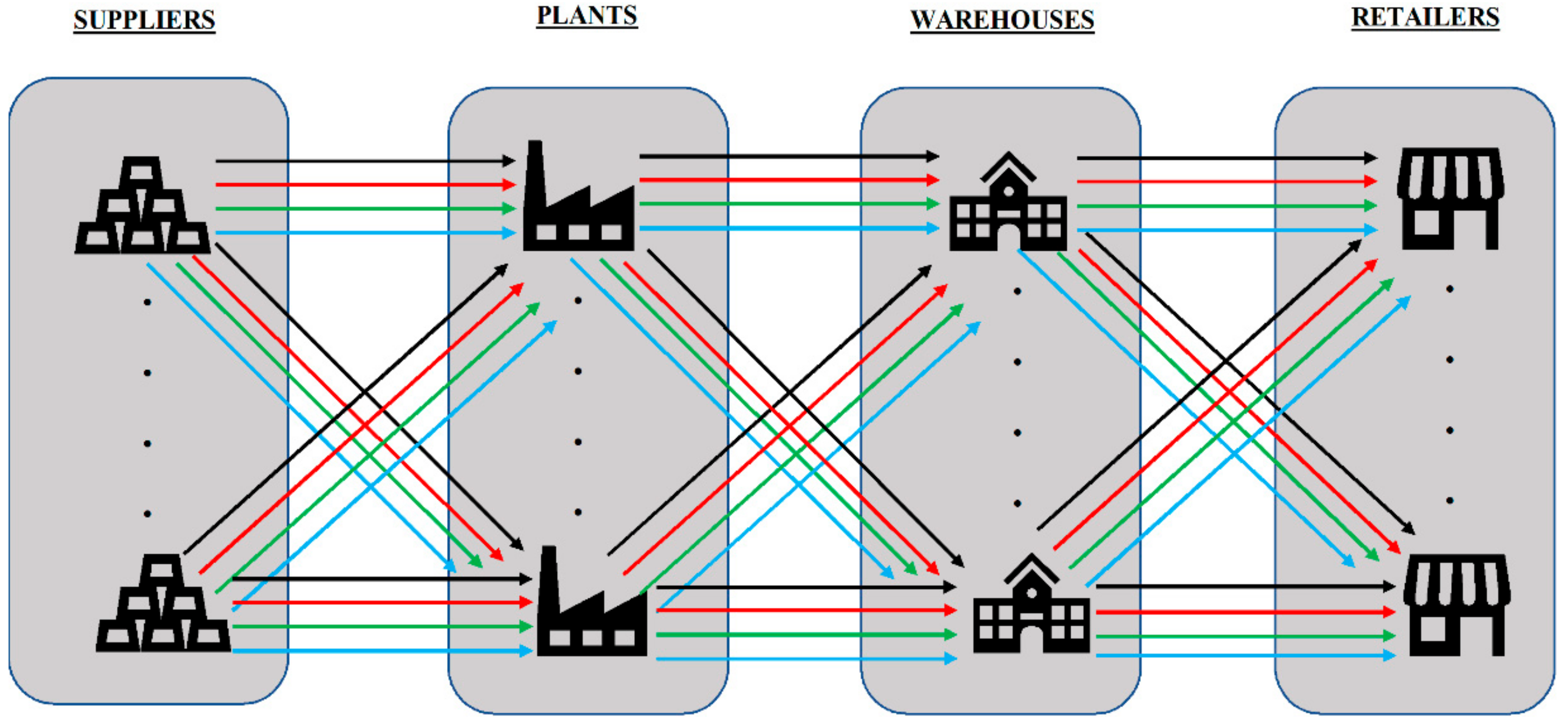
2. Problem Formulation
3. The Proposed Solution Algorithms
3.1. Ant Colony Optimization (ACO)
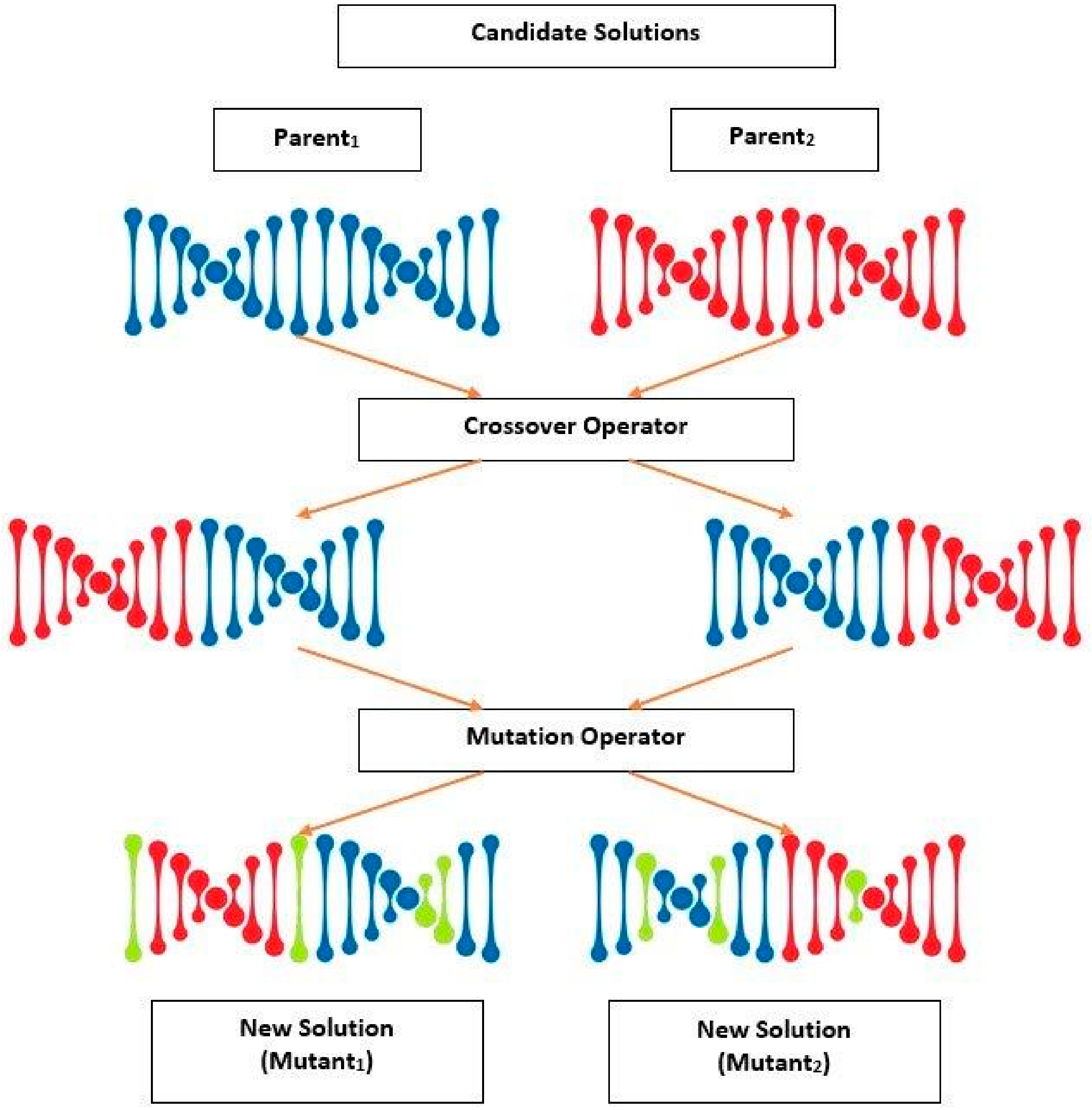
3.2. Genetic Algorithm (GA)
3.2.1. Selection Operator
3.2.2. Crossover Operator
3.2.3. Mutation Operator
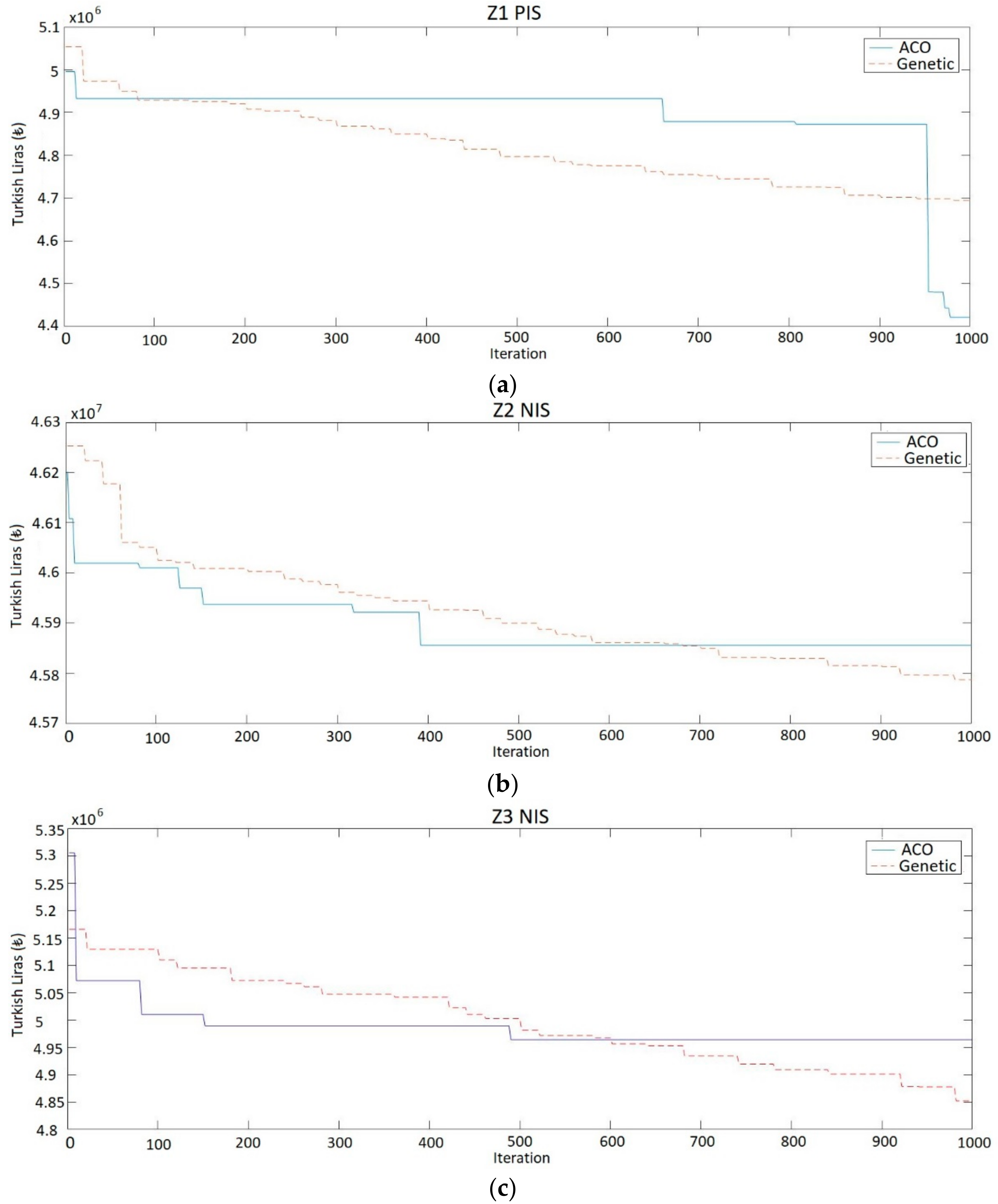
4. Computational Experiments
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Indices | |
| i | Raw materials |
| j | Products |
| s | Suppliers |
| p | Plant |
| w | Warehouses |
| r | Retailers |
| k | Transportation path |
| c | Customers |
| t | Time period |
| Parameters | |
| raw material i price in s at t | |
| on hand quantity of i in s at t | |
| transportation capacity of k between s and p at t | |
| fixed cost of using k between s and p at t | |
| variable cost of transporting i from s to p by using k at t | |
| required transporting capacity of i | |
| required i quantity for producing j | |
| required storing capacity for i | |
| raw material storage capacity of p | |
| holding cost of i in p at t | |
| manufacturing time of j in p at t | |
| manufacturing cost of j in p at t (regular time) | |
| regular capacity (time) in p at t | |
| manufacturing cost of j in p at t (overtime) | |
| overtime capacity (time) in p at t | |
| products storage capacity in p | |
| holding cost of j in p at t | |
| required storing capacity for j | |
| transportation capacity of k from p to w at t | |
| fixed cost of using k from p to w at t | |
| variable cost of transporting j from p to w by using k at t | |
| required transporting capacity of j | |
| transportation capacity of k from w to r at t | |
| fixed cost of using k from w to r at t | |
| variable cost of transporting j from w to r by using k at t | |
| holding cost of j in w at t | |
| products storage capacity in w | |
| holding cost of j in r at t | |
| storage capacity in r | |
| backorder cost of j in r at t | |
| demand of c for j from r at t | |
| price of j at period t | |
| Decision Variables | |
| transported quantity of i from s to p by using k at t | |
| stored quantity of i in p at the end of t | |
| quantity of j produced at regular time in p at t | |
| quantity of j produced at over time in part | |
| transported quantity of j from p to w by using k at t | |
| stored quantity of j in p at the end of t | |
| stored quantity of j in w at the end of t | |
| transported quantity of j from w to r by using k at t | |
| stored quantity of j in r at the end of t | |
| backorder quantity of j in r for c at the end of t | |
| sold quantity of j from r to c at t | |
Appendix A
| Parameter | Domain |
|---|---|
| FTCSspkt | U~[1000; 3500] |
| RRCi | U~[0.85; 1.53] |
| RRMij | [0, 1, 2, 3] |
| IRCi | U~[0.55; 1.20] |
| TSCp | U~[900; 2500] |
| UPTjpt | U~[5; 8.70] |
| PICp | [1000, 2200, 2800] |
| RHCj | [2, 2.3, 2.9] |
| FTCPpwkt | U~[670; 1700] |
| RTCj | [2.5, 2, 3] |
| FTCWwrkt | U~[900; 2300] |
| WICw | U~[16000; 24000] |
| RICr | U~[3500; 4100] |
| Domain | |||
|---|---|---|---|
| Parameter | Pessimistic | Possibilistic | Optimistic |
| RUPist | U~[27; 30] | U~[30; 50] | U~[50; 55] |
| RCist | U~[144,000; 168,000] | U~[180,000; 210,000] | U~[216,000; 273,000] |
| VTCSispkt | U~[3; 6] | U~[7; 10] | U~[11; 14] |
| SRCipt | U~[0.72; 0.98] | U~[1; 1.25] | U~[1.3; 1.54] |
| RPCjpt | U~[10.8; 11.9] | U~[12; 17] | U~[17.1; 19.8] |
| ARCpt | U~[62,560; 66,240] | U~[68,000; 72,000] | U~[7,3440; 77,760] |
| OPCjpt | U~[0.8; 0.98] | U~[1; 2] | U~[2; 2.4] |
| AOCpt | U~[20,240; 23,000] | U~[23,000; 30,000] | U~[30,000; 33,600] |
| PHCjpt | U~[4.5; 5] | U~[5; 7] | U~[7; 8.8] |
| VTCPjpwkt | U~[1.7; 2] | U~[2; 8] | U~[8; 9.2] |
| VTCWjwrkt | U~[0.85; 1] | U~[1; 3] | U~[3; 3.45] |
| WHCjwt | U~[5.95; 7] | U~[7; 10] | U~[10; 11.5] |
| HCRjrt | U~[6.3; 7] | U~[7; 10] | U~[10; 11] |
| BCRjrt | U~[1.8; 2] | U~[2; 5] | U~[5; 5.5] |
| POPjt | U~[800; 960] | U~[1000; 1200] | U~[1200; 1440] |
| Domain | ||||
|---|---|---|---|---|
| Parameter | Pessimistic | Possibilistic | Optimistic | Description |
| TCSPspkt | U~[182,400; 211,200]; | U~[228,000; 264,000] | U~[273,600; 316,800] | High (Pra) |
| U~[152,000; 168,000] | U~[190,000; 220,000] | U~[228,000; 264,000] | Medium (Prb) | |
| U~[106,400; 123,200] | U~[133,000; 15,4000] | U~[159,600; 184,800] | Low (Prc) | |
| TCPWpwkt | U~[33,120; 36,800] | U~[36,800; 43,700] | U~[43,700; 48,070] | High (Pra) |
| U~[28,800; 32,000] | U~[32,000; 38,000] | U~[38,000; 41,800] | Medium (Prb) | |
| U~[23,040; 25,600] | U~[25,600; 30,400] | U~[30,400; 33,440] | Low (Prc) | |
| TCWRwrkt | U~[38,400; 46,080] | U~[48,000; 57,600] | U~[57,600; 69,120] | High (Pra) |
| U~[32,000; 40,000] | U~[40,000; 48,000] | U~[48,000; 57,600] | Medium (Prb) | |
| U~[25,600; 30,720] | U~[32,000; 38,400] | U~[38,400; 46,080] | Low (Prc) | |
| Domain | ||||
|---|---|---|---|---|
| Parameter | Pessimistic | Possibilistic | Optimistic | Description |
| Mean Parameter of CDPjrt | U~[10,400; 12,480] | U~[13,000; 15,600] | U~[15,600; 18,720] | High (Prhigh) |
| U~[8000; 9600] | U~[10,000; 12,000] | U~[12,000; 14,400] | Medium (Prmedium) | |
| U~[6000; 7200] | U~[7500; 9000] | U~[9000; 10,800] | Low ((Prlow) | |
| Parameter | Domain | Description | ||
| Standard Deviation of CDPjrt | U~[1800; 2500] | High (Prhigh) | ||
| U~[2528; 3300] | Medium (Prmedium) | |||
| U~[1000; 1800] | Low ((Prlow) | |||
| Start Initialize transportation routes (UKPZ0, UKSZ0, UKWZ0), Iteration limit N, cooling rate β, j = 0, neighborhood parameter a, maximum neighborhood limit K, starting temperature T0 and maximum temperature Tend Evaluate objective function with current transportation routes. Compute F(UKPZ0, UKSZ0, UKWZ0) and set Fbest = F(UKPZ0, UKSZ0, UKWZ0) while(T > Tend) while(j < N) set neighbor routes i = 1 while(i ≤ K) a = random [1, −1] ) ) accept the new solution vector and j = j + 1 end ELSE accept or reject with acceptance probability Generate a uniform random number p’ with a range [0,1] IF p’ < p accept the new solution and j = j + 1 end ELSE reject the new solution end end i = i + 1 end end Tnext = β x T end Stop Procedure |
References
- Sakalli, U.S. Optimization of Production-Distribution Problem in Supply Chain Management under Stochastic and Fuzzy Uncertainties. Math. Probl. Eng. 2017, 2017, 4389064. [Google Scholar] [CrossRef]
- Amirtaheri, O.; Zandieh, M.; Dorri, B.; Motameni, A.R. A bi-level programming approach for production-distribution supply chain problem. Comput. Ind. Eng. 2017, 110, 527–537. [Google Scholar] [CrossRef]
- Akbari, A.A.; Karimi, B. A new robust optimization approach for integrated multi-echelon, multi-product, multi-period supply chain network design under process uncertainty. Int. J. Adv. Manuf. Technol. 2015, 79, 229–244. [Google Scholar] [CrossRef]
- Yu, V.F.; Normasari, N.M.E.; Luong, H.T. Integrated location-production-distribution planning in a multiproducts supply chain network design model. Math. Probl. Eng. 2015, 2015, 473172. [Google Scholar] [CrossRef]
- Mousazadeh, M.; Torabi, S.A.; Zahiri, B. A robust possibilistic programming approach for pharmaceutical supply chain network design. Comput. Chem. Eng. 2015, 82, 115–128. [Google Scholar] [CrossRef]
- Niknamfar, A.H.; Niaki, S.T.A.; Pasandideh, S.H.R. Robust optimization approach for an aggregate production–distribution planning in a three-level supply chain. Int. J. Adv. Manuf. Technol. 2015, 76, 623–634. [Google Scholar] [CrossRef]
- Su, W.; Huang, S.X.; Fan, Y.S.; Mak, K.L. Integrated partner selection and production–distribution planning for manufacturing chains. Comput. Ind. Eng. 2015, 84, 32–42. [Google Scholar] [CrossRef]
- Nishi, T.; Konishi, M.; Ago, M. A distributed decision making system for integrated optimization of production scheduling and distribution for aluminum production line. Comput. Chem. Eng. 2007, 31, 1205–1221. [Google Scholar] [CrossRef]
- Haq, A.N.; Vrat, P.; Kanda, A. An integrated production–inventory–distribution model for manufacture of urea: A case. Int. J. Prod. Econ. 1991, 25, 39–49. [Google Scholar] [CrossRef]
- Yilmaz, P.; Çatay, B. Strategic level three-stage production distribution planning with capacity expansion. Comput. Ind. Eng. 2006, 51, 609–620. [Google Scholar] [CrossRef]
- Boudia, M.; Louly, M.A.O.; Prins, C. A reactive GRASP and path relinking for a combined production–distribution problem. Comput. Oper. Res. 2007, 34, 3402–3419. [Google Scholar] [CrossRef]
- Hamedi, M.; Farahani, R.Z.; Husseini, M.M.; Esmaeilian, G.R. A distribution planning model for natural gas supply chain: A case study. Energy Policy 2009, 37, 799–812. [Google Scholar] [CrossRef]
- Lee, Y.H.; Kim, S.H. Production–distribution planning in supply chain considering capacity constraints. Comput. Ind. Eng. 2002, 43, 169–190. [Google Scholar] [CrossRef]
- Safaei, A.S.; Husseini, S.M.; Farahani, R.Z.; Jolai, F.; Ghodsypour, S.H. Integrated multi-site production–distribution planning in supply chain by hybrid modelling. Int. J. Prod. Res. 2010, 48, 4043–4069. [Google Scholar] [CrossRef]
- Mohamed, Z.M. An integrated production–distribution model for a multinational company operating under varying exchange rates. Int. J. Prod. Econ. 1999, 58, 81–92. [Google Scholar] [CrossRef]
- Tang, J.; Yung, K.-L.; Ip, A.W.H. Heuristics-based integrated decisions for logistics network systems. J. Manuf. Syst. 2004, 23, 1–13. [Google Scholar] [CrossRef]
- Dhaenens-Flipo, C.; Finke, G. An integrated model for an industrial production–distribution problem. IIE Trans. 2001, 33, 705–715. [Google Scholar] [CrossRef]
- Aliev, R.A.; Fazlollahi, B.; Guirimov, B.G.; Aliev, R.R. Fuzzy-genetic approach to aggregate production–distribution planning in supply chain management. Inf. Sci. 2007, 177, 4241–4255. [Google Scholar] [CrossRef]
- Gunnarsson, H.; Rönnqvist, M.; Carlsson, D. Integrated production and distribution planning for Södra cell AB. J. Math. Model. Algorithms 2007, 6, 25–45. [Google Scholar] [CrossRef]
- Ferrio, J.; Wassick, J. Chemical supply chain network optimization. Comput. Chem. Eng. 2008, 32, 2481–2504. [Google Scholar] [CrossRef]
- Bashiri, M.; Badri, H.; Talebi, J. A new approach to tactical and strategic planning in production–distribution networks. Appl. Math. Model. 2012, 36, 1703–1717. [Google Scholar] [CrossRef]
- Raa, B.; Dullaert, W.; Aghezzaf, E. A matheuristic for aggregate production–distribution planning with mould sharing. Int. J. Prod. Econ. 2013, 145, 29–37. [Google Scholar] [CrossRef]
- Kanyalkar, A.P.; Adil, G.K. Aggregate and detailed production planning integrating procurement and distribution plans in a multi-site environment. Int. J. Prod. Res. 2007, 45, 5329–5353. [Google Scholar] [CrossRef]
- Kanyalkar, A.P.; Adil, G.K. An integrated aggregate and detailed planning in a multi-site production environment using linear programming. Int. J. Prod. Res. 2005, 43, 4431–4454. [Google Scholar] [CrossRef]
- Nasiri, G.R.; Zolfaghari, R.; Davoudpour, H. An integrated supply chain production–distribution planning with stochastic demands. Comput. Ind. Eng. 2014, 77, 35–45. [Google Scholar] [CrossRef]
- Coronado, J.L. An Optimization Model for Strategic Supply Chain Design under Stochastic Capacity Disruptions; Texas A&M University: College Station, TX, USA, 2007. [Google Scholar]
- Demirli, K.; Yimer, A.D. Production-distribution with fuzzy costs. In Proceedings of the NAFIPS 2006—2006 Annual Meeting of the North American Fuzzy Information Processing Society, Montreal, QC, Canada, 3–6 June 2006; pp. 702–707. [Google Scholar]
- Gholamian, N.; Mahdavi, I.; Tavakkoli-Moghaddam, R.; Mahdavi-Amiri, N. Comprehensive fuzzy multi-objective multi-product multi-site aggregate production planning decisions in a supply chain under uncertainty. Appl. Soft Comput. 2015, 37, 585–607. [Google Scholar] [CrossRef]
- Nazim, M.; Hashim, M.; Nadeem, A.H.; Yao, L.; Ahmad, J. Multi objective production–distribution decision making model under fuzzy random environment. In Proceedings of the Eighth International Conference on Management Science and Engineering Management, Lisbon, Portugal, 25–27 July 2014; pp. 591–601. [Google Scholar]
- Xu, J.; Wei, P. Production-distribution planning of construction supply chain management under fuzzy random environment for large-scale construction projects. J. Ind. Manag. Optim. 2013, 9, 31–56. [Google Scholar] [CrossRef]
- Chen, M.; Wang, W. A linear programming model for integrated steel production and distribution planning. Int. J. Oper. Prod. Manag. 1997, 17, 592–610. [Google Scholar] [CrossRef]
- Cohen, M.A.; Lee, H.L. Strategic analysis of integrated production-distribution systems: Models and methods. Oper. Res. 1988, 36, 216–228. [Google Scholar] [CrossRef]
- Bilgen, B. Application of fuzzy mathematical programming approach to the production allocation and distribution supply chain network problem. Expert Syst. Appl. 2010, 37, 4488–4495. [Google Scholar] [CrossRef]
- Selim, H.; Araz, C.; Ozkarahan, I. Collaborative production–distribution planning in supply chain: A fuzzy goal programming approach. Transp. Res. Part E Logist. Transp. Rev. 2008, 44, 396–419. [Google Scholar] [CrossRef]
- Pyke, D.F.; Cohen, M.A. Performance characteristics of stochastic integrated production-distribution systems. Eur. J. Oper. Res. 1993, 68, 23–48. [Google Scholar] [CrossRef]
- Al-e-Hashem, S.M.J.M.; Baboli, A.; Sadjadi, S.J.; Aryanezhad, M.B. A multiobjective stochastic production-distribution planning problem in an uncertain environment considering risk and workers productivity. Math. Probl. Eng. 2011, 2011, 406398. [Google Scholar]
- Fahimnia, B.; Farahani, R.Z.; Marian, R.; Luong, L. A review and critique on integrated production–distribution planning models and techniques. J. Manuf. Syst. 2013, 32, 1–19. [Google Scholar] [CrossRef]
- Masulli, F.; Mitra, S. Natural computing methods in bioinformatics: A survey. Inf. Fusion 2009, 10, 211–216. [Google Scholar] [CrossRef]
- Mitra, S.; Datta, S.; Perkins, T.; Michailidis, G. Introduction to Machine Learning and Bioinformatics; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Zhang, X.; Feng, T.; Niu, Q.; Deng, X. A Novel Swarm Optimisation Algorithm Based on a Mixed-Distribution Model. Appl. Sci. 2018, 8, 632. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, J. Optimization of China crude oil transportation network with genetic ant colony algorithm. Information 2015, 6, 467–480. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Li, V.C.; Chiang, C.-J. An ant colony optimization heuristic for an integrated production and distribution scheduling problem. Eng. Optim. 2014, 46, 503–520. [Google Scholar] [CrossRef]
- Cheng, B.-Y.; Leung, J.Y.-T.; Li, K. Integrated scheduling of production and distribution to minimize total cost using an improved ant colony optimization method. Comput. Ind. Eng. 2015, 83, 217–225. [Google Scholar] [CrossRef]
- Calvete, H.I.; Galé, C.; Oliveros, M.-J. Bilevel model for production–distribution planning solved by using ant colony optimization. Comput. Oper. Res. 2011, 38, 320–327. [Google Scholar] [CrossRef]
- Fahimnia, B.; Luong, L.; Marian, R. Genetic algorithm optimisation of an integrated aggregate production–distribution plan in supply chains. Int. J. Prod. Res. 2012, 50, 81–96. [Google Scholar] [CrossRef]
- Khalifehzadeh, S.; Seifbarghy, M.; Naderi, B. Solving a fuzzy multi objective model of a production–distribution system using meta-heuristic based approaches. J. Intell. Manuf. 2017, 28, 95–109. [Google Scholar] [CrossRef]
- Armentano, V.A.; Shiguemoto, A.L.; Løkketangen, A. Tabu search with path relinking for an integrated production–distribution problem. Comput. Oper. Res. 2011, 38, 1199–1209. [Google Scholar] [CrossRef]
- Chan, F.T.S.; Chung, S.H.; Wadhwa, S. A hybrid genetic algorithm for production and distribution. Omega 2005, 33, 345–355. [Google Scholar] [CrossRef]
- Gen, M.; Syarif, A. Hybrid genetic algorithm for multi-time period production/distribution planning. Comput. Ind. Eng. 2005, 48, 799–809. [Google Scholar] [CrossRef]
- Altiparmak, F.; Gen, M.; Lin, L.; Karaoglan, I. A steady-state genetic algorithm for multi-product supply chain network design. Comput. Ind. Eng. 2009, 56, 521–537. [Google Scholar] [CrossRef]
- Taha, H.A. Operations Research: An Introduction (for VTU); Pearson Education: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Zimmermann, H.-J. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1978, 1, 45–55. [Google Scholar] [CrossRef]
- Lai, Y.-J.; Hwang, C.-L. Fuzzy mathematical programming. In Fuzzy Mathematical Programming; Springer: Berlin/Heidelberg, Germany, 1992; pp. 74–186. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.-B.; Mao, C.-P. A modified ant colony system for solving the travelling salesman problem with time windows. Math. Comput. Model. 2007, 46, 1225–1235. [Google Scholar] [CrossRef]
- Yu, B.; Yang, Z.-Z.; Yao, B. An improved ant colony optimization for vehicle routing problem. Eur. J. Oper. Res. 2009, 196, 171–176. [Google Scholar] [CrossRef]
- T’kindt, V.; Monmarché, N.; Tercinet, F.; Laügt, D. An ant colony optimization algorithm to solve a 2-machine bicriteria flowshop scheduling problem. Eur. J. Oper. Res. 2002, 142, 250–257. [Google Scholar] [CrossRef]
- Pandey, H.M.; Chaudhary, A.; Mehrotra, D. A comparative review of approaches to prevent premature convergence in GA. Appl. Soft Comput. 2014, 24, 1047–1077. [Google Scholar] [CrossRef]
- Chowdhury, B.; Garai, G. A review on multiple sequence alignment from the perspective of genetic algorithm. Genomics 2017, 109, 419–431. [Google Scholar] [CrossRef] [PubMed]
- Florentino, H.O.; Cantane, D.R.; Santos, F.L.P.; Bannwart, B.F. Multiobjective genetic algorithm applied to dengue control. Math. Biosci. 2014, 258, 77–84. [Google Scholar] [CrossRef] [PubMed]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligenc; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Goldberg, D.E. Optimization & Machine Learning. In Genetic Algorithm Search; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Tao, G.; Michalewicz, Z. Inver-over operator for the TSP. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Amsterdam, The Netherlands, 27–30 September 1998; pp. 803–812. [Google Scholar]
- Du, K.L.; Swamy, M.N.S. Particle Swarm Optimization. In Search and Optimization by Metaheuristics; Birkhäuser: Cham, Switzerland, 2016. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]



| Cost Maximization Problem (Z1NIS, Z2PIS, Z3PIS) |
| Define iteration limit, objective tolerance, pheromone update constant (iter_lim, tol, ph) |
| Define transportation path using same initializing values (iter_lim/2) weight matrix for each set (UKSW, UKPW, UKWW) |
| Create random initializing transportation path route randomly using weight matrix |
| Evaluate GAMS using existed route, calculate fitness and save |
| İnitialize ant population (antpop) |
| for j = 2: iter_lim |
| Create fabric-supplier binary relation matrix (UKS) |
| for i = 1: antpop |
| Create random route according to weight matrix (UKSW) |
| end |
| Create fabric-supplier binary relation matrix (UKP) |
| for i = 1: antpop |
| Create random route according to weight matrix (UKPW) |
| end |
| Create fabric-supplier binary relation matrix (UKW) |
| for i = 1: antpop |
| Create random route according to weight matrix (UKWW) |
| end |
| Evaluate existing route (transportation path) in GAMS (zj) |
| Calculate pheromone values (ph) for each route |
| if zj > zbest/tol |
| ph = zj/zbest |
| else |
| ph = zbest/zi |
| Update transportation path weight matrix for active node (UKSW, UKPW, UKWW) |
| end |
| Begin; |
| Define iteration limit, mutation constant, cross-over position, |
| Generate initial Transportation Relation Population tppop |
| Generate UKS |
| For i = 1 to (s ∗ p) |
| For j = 1 to (t ∗ k) |
| tp(i,j) = rand[0 1] |
| End |
| End |
| Generate UKP |
| For i = (s ∗ p + 1) to (s ∗ p + p ∗ w) |
| For j = 1 to (t ∗ k) |
| tp(i,j) = rand[0 1] |
| End |
| End |
| Generate UKP |
| For i = (s ∗ p + p ∗ w + 1) to ((s ∗ p + p ∗ w + w ∗ r) |
| For j = 1 to (t ∗ k) |
| tp(i,j) = rand[0 1] |
| End |
| End |
| Evaluate each individual solution using GAMS and save fitness values |
| For i = 1 to Iteration Limit |
| Select parental individuals by Roulette Wheel Selection operator |
| Generate new candidate offspring solutions by Crossover operator |
| Improve candidate solutions using Mutation Operator |
| Evaluate each offspring solution using GAMS and save new fitness values |
| End |
| Return Best Solution |
| End |
| Problem | s | p | w | r | t | k |
|---|---|---|---|---|---|---|
| 1 | 5 | 1 | 5 | 5 | 3 | 3 |
| 2 | 5 | 1 | 5 | 10 | 3 | 3 |
| 3 | 5 | 1 | 10 | 10 | 3 | 3 |
| 4 | 5 | 2 | 10 | 10 | 3 | 3 |
| 5 | 10 | 2 | 10 | 10 | 3 | 3 |
| Problem 1 | Problem 2 | Problem 3 | Problem 4 | Problem 5 | ||||
|---|---|---|---|---|---|---|---|---|
| Z1 | PIS | Optimal | 1,108,835 | 1,404,026 | 1,659,658 | 1,776,098 | 1,972,490 | |
| ACO | Best | 1,108,835 | 1,404,026 | 1,721,895 | 1,864,015 | 2,094,193 | ||
| Gap (%) | 0 | 0 | 0.0375 | 0.0495 | 0.0617 | |||
| GA | Best | 1,108,835 | 1,404,026 | 1,712,435 | 1,851,760 | 2,087,683 | ||
| Gap (%) | 0 | 0 | 0.0318 | 0.0426 | 0.0584 | |||
| SA | Best | 1,108,835 | 1,404,026 | 1,736,500 | 1,879,467 | 2,126,739 | ||
| Gap (%) | 0 | 0 | 0.0463 | 0.0582 | 0.0782 | |||
| NIS | Optimal | 2,709,941 | 3,017,161 | 3,286,451 | 3,480,057 | 3,837,795 | ||
| ACO | Best | 2,709,941 | 3,017,161 | 3,134,946 | 3,293,178 | 3,556,101 | ||
| Gap (%) | 0 | 0 | 0.0461 | 0.0537 | 0.0734 | |||
| GA | Best | 2,709,941 | 3,017,161 | 3,175,369 | 3,315,798 | 3,625,949 | ||
| Gap (%) | 0 | 0 | 0.0338 | 0.0472 | 0.0552 | |||
| SA | Best | 1108835 | 1,404,026 | 3,481,338 | 3,709,045 | 4,177,056 | ||
| Gap (%) | 0 | 0 | 0.0593 | 0.0658 | 0.0884 | |||
| Z2 | PIS | Optimal | 15,658,380 | 16,184,285 | 16,301,772 | 16,831,979 | 1,7763,954 | |
| ACO | Best | 15,658,380 | 16,184,285 | 15,468,751 | 15,845,625 | 16,632,390 | ||
| Gap (%) | 0 | 0 | 0.0511 | 0.0586 | 0.0637 | |||
| GA | Best | 15,658,380 | 16,184,285 | 15,511,136 | 15,862,457 | 16,678,576 | ||
| Gap (%) | 0 | 0 | 0.0485 | 0.0576 | 0.0611 | |||
| SA | Best | 1108835 | 1,404,026 | 17,260,316 | 17,885,661 | 18,979,008 | ||
| Gap (%) | 0 | 0 | 0.0588 | 0.0626 | 0.0684 | |||
| NIS | Optimal | 11,063,345 | 11,864,926 | 12,303,159 | 12,627,619 | 12,966,067 | ||
| ACO | Best | 11,063,345 | 11,864,926 | 12,754,685 | 13,199,650 | 13,642,896 | ||
| Gap (%) | 0 | 0 | 0.0367 | 0.0453 | 0.0522 | |||
| GA | Best | 11063345 | 11,864,926 | 12,744,842 | 13,168,081 | 13,609,184 | ||
| Gap (%) | 0 | 0 | 0.0359 | 0.0428 | 0.0496 | |||
| SA | Best | 1108835 | 1,404,026 | 12,912,165 | 13,312,036 | 13,767,370 | ||
| Gap (%) | 0 | 0 | 0.0495 | 0.0542 | 0.0618 | |||
| Z3 | PIS | Optimal | 2,365,633 | 2,760,450 | 2,980,651 | 3,277,653 | 3,413,026 | |
| ACO | Best | 2,365,633 | 11,864,926 | 2,893,020 | 3,125,898 | 3,240,668 | ||
| Gap (%) | 0 | 0 | 0.0294 | 0.0463 | 0.0505 | |||
| GA | Best | 2,365,633 | 11864926 | 2,888,251 | 3,148,513 | 3,262,853 | ||
| Gap (%) | 0 | 0 | 0.031 | 0.0394 | 0.044 | |||
| SA | Best | 1108835 | 1,404,026 | 3,098,983 | 3,462,185 | 3,612,347 | ||
| Gap (%) | 0 | 0 | 0.0397 | 0.0563 | 0.0584 | |||
| NIS | Optimal | 1,083,653 | 1,377,620 | 1,648,027 | 1,740,722 | 1,915,385 | ||
| ACO | Best | 1,083,653 | 1,377,620 | 1,722,188 | 1,834,025 | 2,034,713 | ||
| Gap (%) | 0 | 0 | 0.045 | 0.0536 | 0.0623 | |||
| GA | Best | 1,083,653 | 1,377,620 | 1,713,618 | 1,815,747 | 2,019,199 | ||
| Gap (%) | 0 | 0 | 0.0398 | 0.0431 | 0.0542 | |||
| SA | Best | 1,108,835 | 1,404,026 | 1,733,395 | 1,844,469 | 2,046,397 | ||
| Gap (%) | 0 | 0 | 0.0518 | 0.0596 | 0.0684 | |||
| Z4 | Optimal | 0.685 | 0.693 | 0.618 | 0.635 | 0.709 | ||
| ACO | Best | 0.685 | 0.693 | 0.581909 | 0.594932 | 0.65859 | ||
| Gap (%) | 0 | 0 | 0.0584 | 0.0631 | 0.0711 | |||
| GA | Best | 0.685 | 0.693 | 0.582156 | 0.596138 | 0.660504 | ||
| Gap(%) | 0 | 0 | 0.058 | 0.0612 | 0.0684 | |||
| SA | Best | 1,108,835 | 1,404,026 | 0.658912 | 0.682181 | 0.763735 | ||
| Gap (%) | 0 | 0 | 0.0662 | 0.0743 | 0.0772 | |||
| Total Sold Quantity of Product at Periods | Backorder Quantity of Product at Periods | Inventory Level of Product at Periods in Retailers | Inventory Level of Product at Periods in Warehouses | Total Production Quantity in Each Plant at Periods | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GA | ACO | GA | ACO | GA | ACO | GA | ACO | GA | ACO | GA | ACO | GA | ACO | |
| p1 | p1 | p2 | p2 | p3 | p3 | |||||||||
| j1.t1 | 6699.43 | 6619.75 | 574.61 | 654.30 | 0.00 | 0.00 | 0.00 | 0.00 | 1834.28 | 0.00 | 2004.95 | 3345.89 | 2860.20 | 3273.86 |
| j1.t2 | 6364.37 | 6619.75 | 909.67 | 654.30 | 0.00 | 0.00 | 0.00 | 0.00 | 2748.15 | 895.47 | 1840.83 | 3345.89 | 1775.39 | 2378.39 |
| j1.t3 | 6553.76 | 6619.75 | 720.28 | 654.30 | 0.00 | 0.00 | 0.00 | 0.00 | 2568.38 | 2400.90 | 1957.15 | 978.87 | 2028.22 | 3239.98 |
| j2.t1 | 5822.66 | 6008.03 | 834.75 | 649.37 | 0.00 | 0.00 | 0.00 | 0.00 | 2411.49 | 2793.11 | 2106.34 | 1794.34 | 1304.83 | 1420.59 |
| j2.t2 | 5822.66 | 6024.95 | 834.75 | 632.46 | 0.00 | 0.00 | 0.00 | 0.00 | 1680.00 | 2808.02 | 2921.17 | 1509.36 | 1221.49 | 1707.57 |
| j2.t3 | 5822.66 | 6012.11 | 834.75 | 645.29 | 0.00 | 0.00 | 0.00 | 0.00 | 1680.00 | 1257.98 | 2780.30 | 3024.45 | 1362.36 | 1729.68 |
| j3.t1 | 6664.43 | 6064.51 | 0.00 | 599.92 | 0.00 | 0.00 | 0.00 | 0.00 | 3108.48 | 4699.02 | 1694.07 | 0.00 | 1861.88 | 1365.49 |
| j3.t2 | 6664.43 | 6064.51 | 0.00 | 599.92 | 0.00 | 0.00 | 0.00 | 0.00 | 3182.22 | 3600.60 | 0.00 | 483.02 | 3482.21 | 1980.89 |
| j3.t3 | 6664.43 | 6064.51 | 0.00 | 599.92 | 0.00 | 0.00 | 0.00 | 0.00 | 3397.94 | 4274.15 | 313.08 | 878.78 | 2953.41 | 911.59 |
| Total Purchased Raw Material Quantities by Plants at Periods | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GA | ACO | GA | ACO | GA | ACO | GA | ACO | GA | ACO | GA | ACO | |
| i1 | i1 | i2 | i2 | i3 | i3 | i4 | i4 | i5 | i5 | i6 | i6 | |
| p1,t1 | 6080 | 2793 | 7234 | 8379 | 1834 | 0 | 13,571 | 16,890 | 3669 | 0 | 17,817 | 19,683 |
| p1,t2 | 7176 | 4599 | 5040 | 8424 | 2748 | 895 | 13,975 | 14,505 | 5496 | 1791 | 18,403 | 18,209 |
| p1,t3 | 6817 | 6060 | 5040 | 3774 | 2568 | 2401 | 14,442 | 16,481 | 5137 | 4802 | 18,691 | 20,140 |
| p2,t1 | 6116 | 8486 | 6319 | 5383 | 2005 | 3346 | 9193 | 5140 | 4010 | 6692 | 13,305 | 10,280 |
| p2,t2 | 6603 | 8201 | 8764 | 4528 | 1841 | 3346 | 4762 | 6304 | 3682 | 6692 | 9524 | 11,160 |
| p2,t3 | 6695 | 4982 | 8341 | 9073 | 1957 | 979 | 5677 | 6640 | 3914 | 1958 | 10,414 | 10,643 |
| p3,t1 | 7025 | 7968 | 3914 | 4262 | 2860 | 3274 | 9751 | 8791 | 5720 | 6548 | 13,916 | 13,485 |
| p3,t2 | 4772 | 6464 | 3664 | 5123 | 1775 | 2378 | 13,444 | 10,029 | 3551 | 4757 | 16,440 | 14,115 |
| p3,t3 | 5419 | 8210 | 4087 | 5189 | 2028 | 3240 | 12,251 | 7704 | 4056 | 6480 | 15,641 | 12,674 |
| i7 | i7 | i8 | i8 | i9 | i9 | i10 | i10 | i11 | i11 | i12 | i12 | |
| p1,t1 | 3669 | 1791 | 11,737 | 16,890 | 8492 | 5586 | 10,903 | 8379 | 7234 | 8379 | 8628 | 12,191 |
| p1,t2 | 5496 | 4802 | 11,227 | 13,610 | 8856 | 7407 | 10,536 | 10,215 | 5040 | 8424 | 8044 | 10,009 |
| p1,t3 | 5137 | 6692 | 11,874 | 14,080 | 8497 | 7318 | 10,177 | 8576 | 5040 | 3774 | 8476 | 9806 |
| p2,t1 | 4010 | 6692 | 7189 | 1794 | 8223 | 10,280 | 10,329 | 12,075 | 6319 | 5383 | 5494 | 1794 |
| p2,t2 | 3682 | 1958 | 2921 | 2958 | 9524 | 9710 | 12,445 | 11,220 | 8764 | 4528 | 2921 | 2475 |
| p2,t3 | 3914 | 6548 | 3720 | 5661 | 9475 | 8007 | 12,255 | 11,031 | 8341 | 9073 | 3406 | 4782 |
| p3,t1 | 5720 | 4757 | 6890 | 5517 | 8330 | 9389 | 9635 | 10,809 | 3914 | 4262 | 5029 | 4152 |
| p3,t2 | 3551 | 6480 | 11,668 | 7650 | 5994 | 8172 | 7215 | 9879 | 3664 | 5123 | 8186 | 5669 |
| p3,t3 | 4056 | 0 | 10,223 | 4464 | 6781 | 9939 | 8144 | 11,669 | 4087 | 5189 | 7269 | 3553 |
| Cooperated Suppliers | |
|---|---|
| GA | s2, s5, s7, s8, s13, s17, s18, s27, s28, s29, s31, s34, s37 |
| ACO | s2, s5, s6, s7, s8, s9, s10, s11, s12, s13, s14, s17, s18, s19, s20, s21, s23, s25, s27, s28, s29, s31 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
SAKALLI, U.S.; ATABAS, I. Ant Colony Optimization and Genetic Algorithm for Fuzzy Stochastic Production-Distribution Planning. Appl. Sci. 2018, 8, 2042. https://doi.org/10.3390/app8112042
SAKALLI US, ATABAS I. Ant Colony Optimization and Genetic Algorithm for Fuzzy Stochastic Production-Distribution Planning. Applied Sciences. 2018; 8(11):2042. https://doi.org/10.3390/app8112042
Chicago/Turabian StyleSAKALLI, Umit Sami, and Irfan ATABAS. 2018. "Ant Colony Optimization and Genetic Algorithm for Fuzzy Stochastic Production-Distribution Planning" Applied Sciences 8, no. 11: 2042. https://doi.org/10.3390/app8112042
APA StyleSAKALLI, U. S., & ATABAS, I. (2018). Ant Colony Optimization and Genetic Algorithm for Fuzzy Stochastic Production-Distribution Planning. Applied Sciences, 8(11), 2042. https://doi.org/10.3390/app8112042





