Abstract
For a mobile robot, navigation skills that are safe, efficient, and socially compliant in crowded, dynamic environments are essential. This is a particularly challenging problem as it requires the robot to accurately predict pedestrians’ movements, analyse developing traffic situations, and plan its own path or trajectory accordingly. Previous approaches still exhibit low accuracy for pedestrian trajectory prediction, and they are prone to generate infeasible trajectories under complex crowded conditions. In this paper, we develop an improved socially conscious model to learn and predict a pedestrian’s future trajectory. To generate more efficient and safer trajectories in a changing crowed space, an online path planning algorithm considering pedestrians’ predicted movements and the feasibility of the candidate trajectories is proposed. Then, multiple traffic states are defined to guide the robot finding the optimal navigation strategies under changing traffic situations in a crowded area. We have demonstrated the performance of our approach outperforms state-of-the-art approaches with public datasets, in low-density and simulated medium-density crowded scenarios.
1. Introduction
Robots are expected to coexist with humans and perform a variety of tasks. Navigation skills are essential for autonomous mobile robots. However, robot navigation in crowded, dynamic environments in a safe, efficient, and socially compliant manner is a challenging problem [1]. To achieve this, robots need to not only accurately predict motions of pedestrians, but also analyze the developing traffic situations [2], and plan their own paths or trajectories accordingly. The purpose of this is to improve pedestrian movement prediction, include prediction based on a social model to robot trajectory planning, and propose a novel navigation strategy for robots in a dynamic environment.
The techniques for prediction of the pedestrians’ trajectory prediction have attracted much attention from academia. One method relies on closed-form solutions for Bayesian filtering, such as Kalman filters (KF) [3], including the interacting multiple model-Kalman filter (IMM-KF) [3], which uses KF extensions to multiple linear dynamical models, and unscented KF [4], which uses KF extensions to nonlinear dynamical models. Recently, Donghan et al. [5] developed a parallel interacting multiple model-unscented Kalman filter (PIMM-UKF) approach to estimate human motion states, and then predicted the position and velocity of humans for a finite horizon. Schulz et al. [6] combined pedestrian intention recognition with path prediction, through an interacting multiple model filter in combination with a latent-dynamic conditional random field model. However, most of these research works are limited by independent models that fail to capture the complex interactions between the humans in the crowd. An alternative and recent method utilizes learning techniques to model the joint distribution of future trajectories of interacting agents based on a spatially local interaction model. Trautman et al. [7] proposed an interactive Gaussian process approach, whose kernels were used to model human dynamics, to capture cooperative collision avoidance between humans and a robot. Alahi et al. [8] proposed long-short term memory (LSTM) networks with “social” pooling layers, which learned general human movements and predicted their future trajectories. Recently, we proposed a socially conscious model considering the added features that affect the pedestrian’s future trajectory, such as the walking direction of other pedestrians [9]. However, these approaches do not carefully distinguish the effects of a pedestrian’s own history trajectory, and that of others, to the pedestrian’s future trajectory, and this may hinder the improvement of model accuracy.
Developing efficient online path planning algorithms to generate robots’ safe and smooth trajectory is a basic problem in robot navigation. Safe trajectory generation is a very active field in mobile robotics and there are many recent contributions. Ravankar [10] and David [11] reviewed the state-of-the-art in smooth trajectory generation with comparisons in terms of kinematic feasibility and safe path generation recently. Additionally, the approaches that are available with robot operating system (ROS) integration are worth mentioning. One approach called the dynamic window approach (DWA) is adopted extensively for mobile robot navigation [12]. Recently, Rösmann et al. [13,14] presented an online trajectory planning and optimization algorithm called the timed-elastic-band (TEB) approach, which had been generalized to an efficient time-optimal model predictive control approach for dynamic systems. Furthermore, to overcome the shortcomings of traditional local planners that are unable to transit across obstacles, they proposed a state-of-the-art planner that switched to the current globally optimal trajectory among the candidate trajectories of distinctive topologies maintained and optimized in parallel in the case of dynamic environments [15]. However, the planner has not been integrated with the prediction model of human trajectory, which results in an unintelligent manner in which robots respond to human motion. When the pedestrian movement speed is relatively high, or the space among pedestrians is relatively small, the generated trajectory of topology in front of the pedestrian may not be feasible.
Online decision making for robots in crowded and dynamic environments is also a fundamental challenge. The approaches fall into two major groups. (1) The first one models the decision making and planning as a partially observable Markov decision process (POMDP) [16]. Bai et al. [17] applied a state-of-the-art approximate online POMDP planning algorithm to autonomous driving in a complex, dynamic environment. Until now, there have been few reports on navigation in a medium-density crowd, the reason may be that the computational cost is still high. (2) The second approach uses a cooperative collision avoidance model between humans and the robot to conduct cooperative planning for robots, such as works [7,18]. However, the modeling process is not a trivial work, and an alternative simple and practical navigation strategy is required.
This paper aims to predict the movement of pedestrians, and then solve the navigation problem of robots crossing low-density and medium-density crowds. First, an improved socially conscious model is used to learn and predict the pedestrian’s future trajectory, in which the effect of other pedestrians’ moving direction is considered, and the effect of a pedestrian’s own history trajectory on the pedestrian’s future trajectory is enhanced. Second, local trajectory for obstacle avoidance optimization based on the predicted pedestrian trajectory and chasing cost judgment is performed to generate safer and more efficient trajectories. Third, we have designed the five following travel modes for robot navigation in different traffic states: Free mode, high-speed-follow mode, travelable mode, low-speed-follow mode, and probing mode. In the two following modes, the followability and reachability tests are conducted and evaluated and the optimal following target is selected; in the probing mode, a short trajectory ending at the boundary of the safe space of the nearest pedestrian ahead is planned to deal with the congested traffic state, which happens often in medium-density crowds. Finally, the improved socially conscious model is tested with public datasets, and our proposed navigation approach is validated in simulated low-density and medium-density crowded scenarios. The results show that our proposed human trajectory prediction model and robot navigation approach outperform the state-of-art methods, and a robot can navigate safely and smoothly in a crowded unstructured environment with our proposed navigation method.
In summary, we make the following contributions:
- We present an improved socially conscious model in which a pooled layer between the current pedestrian trajectory sequence input and the pedestrian position estimation layer is added, which models pedestrian trajectories more accurately;
- we present a novel online path planning algorithm that integrates TEB with pedestrians’ predicted movement and feasibility detection, and is capable of generating efficient and safe trajectories in changing crowed space;
- we present multiple modes of travel to guide the robot to find the optimal navigation strategy under changing traffic situations in a crowed area; and
- we demonstrate the proposed algorithms with an experiment in eight scenarios.
The paper is structured as follows: We first present the related work in Section 1. In Section 2, we propose human trajectory predictions with an improved socially conscious model, and the online trajectory planning method for robots based on multiple modes of travel is described. In Section 3, our proposed approach is validated in several low-density crowded scenarios and a medium-density scenario with simulation, and the performance is compared with the state-of-art methods. The discussion and conclusion are summarized in Section 4.
2. Methods
2.1. Human Trajectory Prediction with an Improved Socially Conscious Model
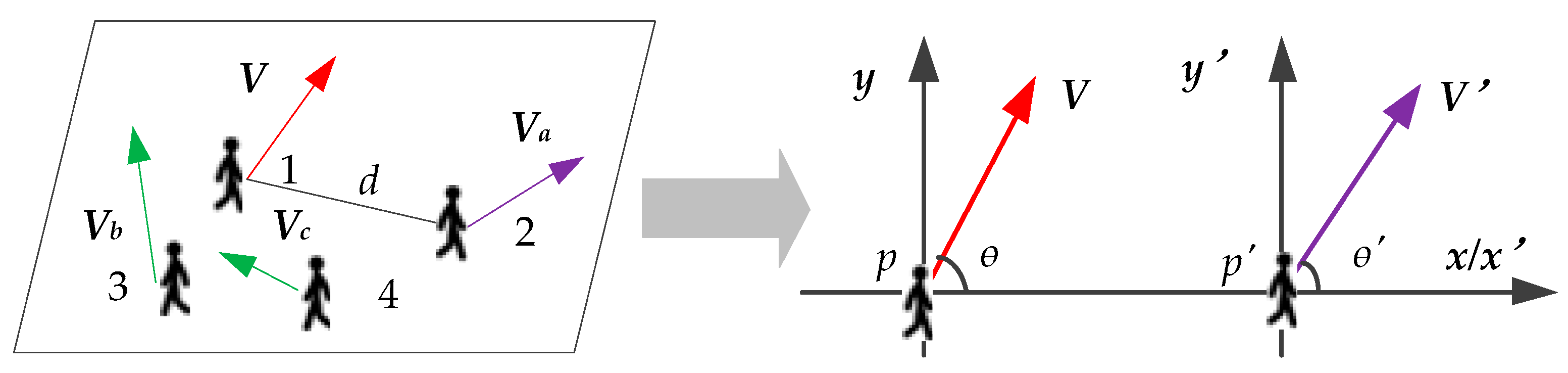
In the socially conscious model [9], two main factors are considered that affect the pedestrians’ walk in the crowd, i.e., relative distance and moving direction based on the basic social-LSTM [8]. The distribution of pedestrians in a certain frame of the video is shown in Figure 1. The socially conscious model is applied to show how the current direction and distance of relative movements between pedestrians will affect the target pedestrian’s movement.
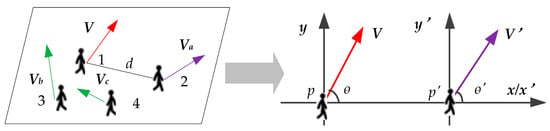
Figure 1.
Distribution of pedestrians at a certain moment. The arrows represent the walking direction of pedestrians, the red color represents the target pedestrian, i.e., pedestrian 1, other colors represent other individuals in the crowd, V represents the walking speed, and d represents the distance between pedestrian 1 and pedestrian 2. The right picture shows the relative motion coordinate system of p′ to p.
In the current frame, a target pedestrian, p (red), is first selected, and then another pedestrian, p′ (other colors), is selected. Taking the current positions of the two persons as the origins and taking the displacement of p′ relative to p as the x-axis, two coordinate systems are established to determine the relative motion tendency of p′. The coordinate systems divide the plane into eight quadrants, as shown in the right half of Figure 1. Let I, II, III, and IV represent the first, second, third, and fourth quadrants of the coordinate system of p. Algorithm 1 gives a method to determine whether the relative motion direction of p′ will affect p, where fij[p,p′] is a function to indicate whether an influence exists between p and p′. If yes, it is set to “1”; otherwise, it is set to “0”. After completing the judgment of all other pedestrians in the figure, another pedestrian is selected as the target pedestrian. This process is repeated until the relationships of all pairs of pedestrians are judged.
| Algorithm 1. Jugement of the effect the relative motion direction of p′ on p |
| 1: if θ∈I and θ < θ’ < 180° then fij[p,p′] = 1 2: elseif θ∈II and θ < θ’ < 180° then fij[p,p′] = 1 3: elseif θ∈III and 180° < θ’ < θ then fij[p,p′] = 1 4: elseif θ∈IV and 180° < θ’ < θ then 1ij[p,p′] = 1 5: else 1ij[p,p′] = 0 |
Let d represent the distance between p and p′, and the influence of the trajectory between p and p′ is inversely proportional to d. The influence among pedestrians in a crowd manifests as a combination of attraction and exclusion. Therefore, we take 1/d as the relative distance influence term in the model. As a result, the socially conscious pooling layer, , is defined as follows:
where φ(·) is an embedding function andWs is the embedding weight. A pooling layer, , is created to take the current pedestrian’s historical coordinate sequence as the input according to Equation (2); then, and are concatenated and the result is transferred into LSTM cells according to Equation (3).
The hidden states, , are used as the input of the fully connected layer, Wn, to predict the distribution of human trajectory, which is a bivariate Gaussian distribution with a three-dimensional vector, including the parameters, .
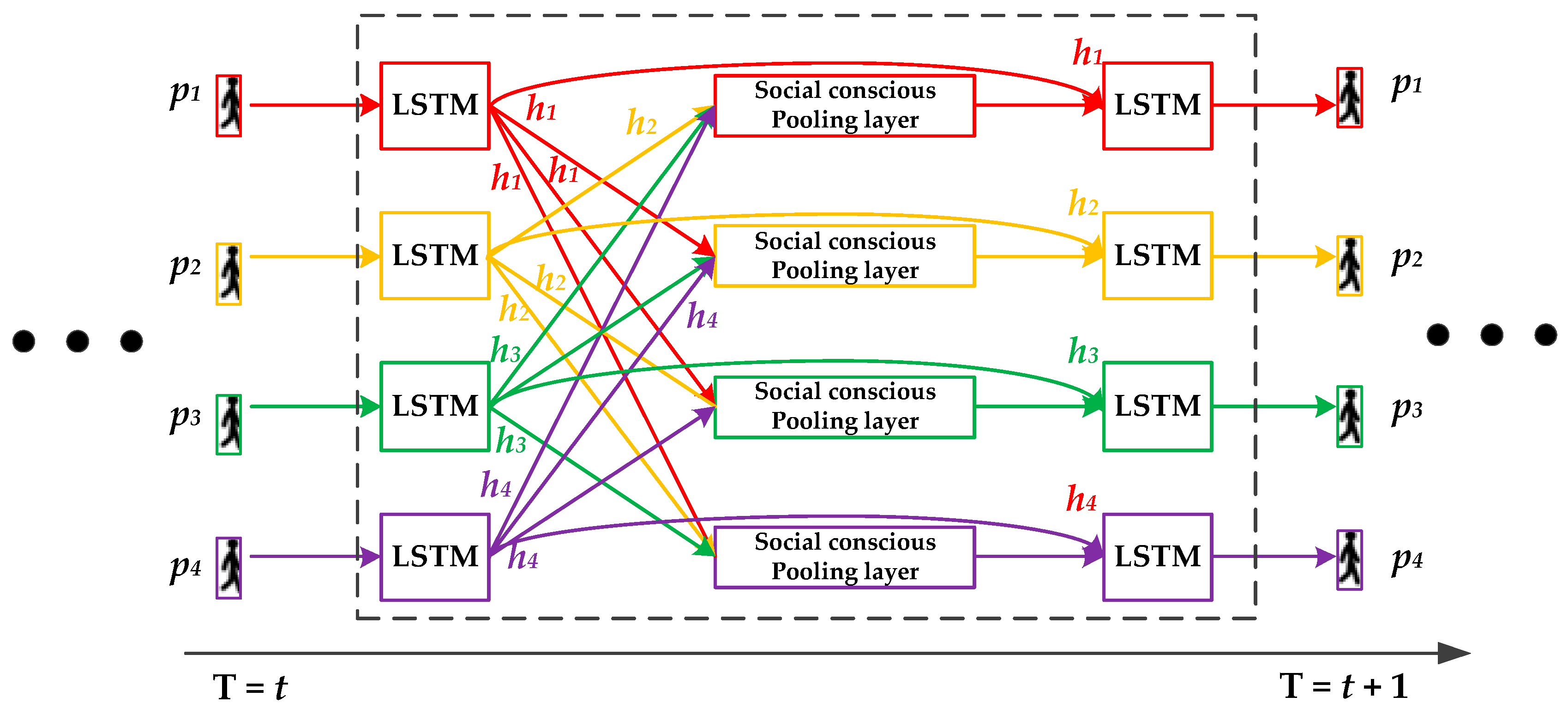
The main structure of the socially conscious model for the four pedestrians is shown in Figure 2. The middle dashed box represents the neural network structure, where each LSTM unit processes a pedestrian’s trajectory and connects to others through a socially conscious pooling layer.
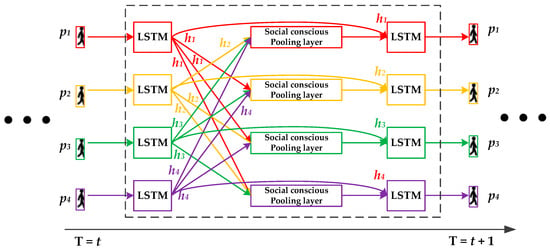
Figure 2.
Overview of the socially conscious model.
To improve the prediction accuracy of the model, during the training process, we add a pooling layer, , to the socially conscious model between the current pedestrian trajectory sequence input and position estimation, which is a two-dimensional Gaussian distribution, resulting in an improved socially conscious model.
The adjusted loss function, Li, is shown in Equation (6), where a is the adjustment parameter (here, it is set to 0.3). After the model is trained, a complete pedestrian trajectory prediction model is obtained. Taking the observed historical trajectory at time step, t = 1, 2, …, Tobs as input, the estimated position can be obtained by sampling from the bivariate Gaussian distribution as follows:
N(·) randomly outputs a two-dimensional normal distribution random number according to the input parameters.
2.2. Trajectory Detection and Optimization Based on Predicted Pedestrians’ Positions
There are two tasks for trajectory detection. The first task is to search for admissible candidate trajectories, each of which forms an initial pose to a final pose for a robot while maintaining following three kinds of conditions, as follows: Separation from pedestrians or other obstacles, kinematic constraints, and dynamic constraints. The second task is to find a trajectory with minimal time among the admissible candidate trajectories. As described in [15], the presence of pedestrians introduces multiple homologous trajectories corresponding to admissible candidate trajectories of distinctive topologies. Additionally, we assume that the optimized trajectory with a global minimum is a subset of homologous trajectories with local minima. The global path planner in this paper uses the move_base function package from ROS [19], and the local path planner in this paper is that we improve the TEB planner.
2.2.1. Local Trajectory for Obstacle Avoidance Optimization Based on Predicted Pedestrian Trajectory
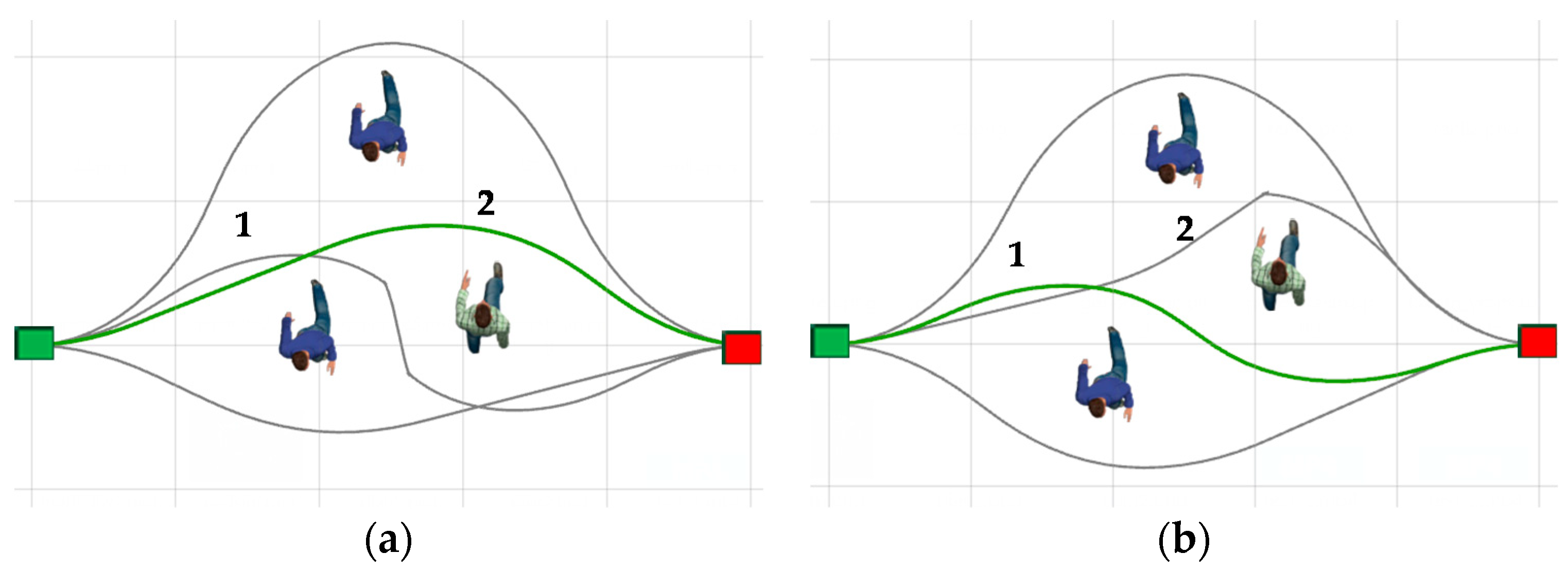
The movements of pedestrians cause the optimal local trajectory of the relevant topology to change, which manifests an increase or decrease in cost and the failure or formation of a feasible trajectory, as shown in Figure 3. The robot searches for the feasible trajectory online and optimizes it. When it detects that there is no feasible trajectory in the current topology or that the optimal trajectory is not optimal, it switches to the optimal trajectory in another topological space.
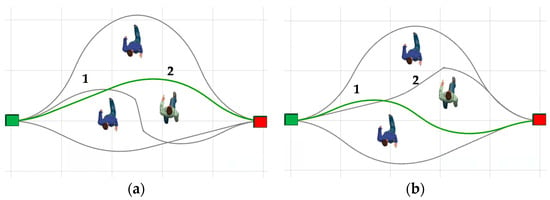
Figure 3.
The movements of pedestrians cause the optimal local trajectories of the relevant topology to change: (a) The optimal local trajectories before the movements; (b) the optimal local trajectories after the movements, boxes in green and red are the robot’s initial position and goal position, respectively; the trajectories in green and grey are globally optimal trajectories and candidate local trajectories, respectively.
There is a problem with the above method. When a pedestrian is at position pt at time t, to make the robot continue to move with pedestrian avoidance, there are four steps that must conducted, as follows: Pedestrian detection, position extraction, trajectory planning, and control law generation. When the move command is transmitted to the robot at time, t + , the pedestrian actually reaches a new position, ; therefore, the optimal trajectory corresponding to has changed, and the trajectory being executed is not optimal or is even unfeasible. In low-density and medium-density crowds, as the number of pedestrians increases, the gap between the trajectory generated by this delayed response mode may become worse.
To reduce the adverse effect of a delayed response and improve the navigation efficiency of the robot, we incorporate the predicted position of pedestrians at the future time, t + t′, the costs of all the feasible trajectories, t + t’, are predicted, and the optimized trajectory with the lowest global cost is selected. In this paper, t’ takes two values, i.e., 0.5 s and 0.2 s, with an assumed pedestrian velocity of 1.5 m/s, the predicted displacements are 0.75 m and 0.3 m separately. With the 0.75 m predicting displacement, the robot has a large enough distance to the pedestrian in his/her walking direction and leads to remarkable variations in the cost of local optimal trajectories at both the front and back sides of the pedestrian, which will benefit global optimal trajectory planning, and the large distance to the pedestrian also ensures the safety of the planned trajectory. Additionally, considering the possible predicting error caused by a sudden change in the pedestrian’s movement, such as the pedestrian slowing down or changing his/her direction, with the 0.3 m predicting displacement, the safety of the planned trajectory can still be ensured.
2.2.2. Trajectory Chasing Cost Judgment
Pedestrian movements are complex and there may be other pedestrians nearby. The trajectories of distinctive topologies crossing pedestrians who walk with different velocities and spaces to each other change with the movements. Since the robot cannot run too fast in a crowd for safety reasons, if crossing a highly moving crowd, the robot may spend a great amount of energy chasing pedestrians while becoming farther away from the goal position. In order to avoid this situation of continuous energy consumption, we propose a new concept named chasing cost and take it into account in the optimal trajectory selection.
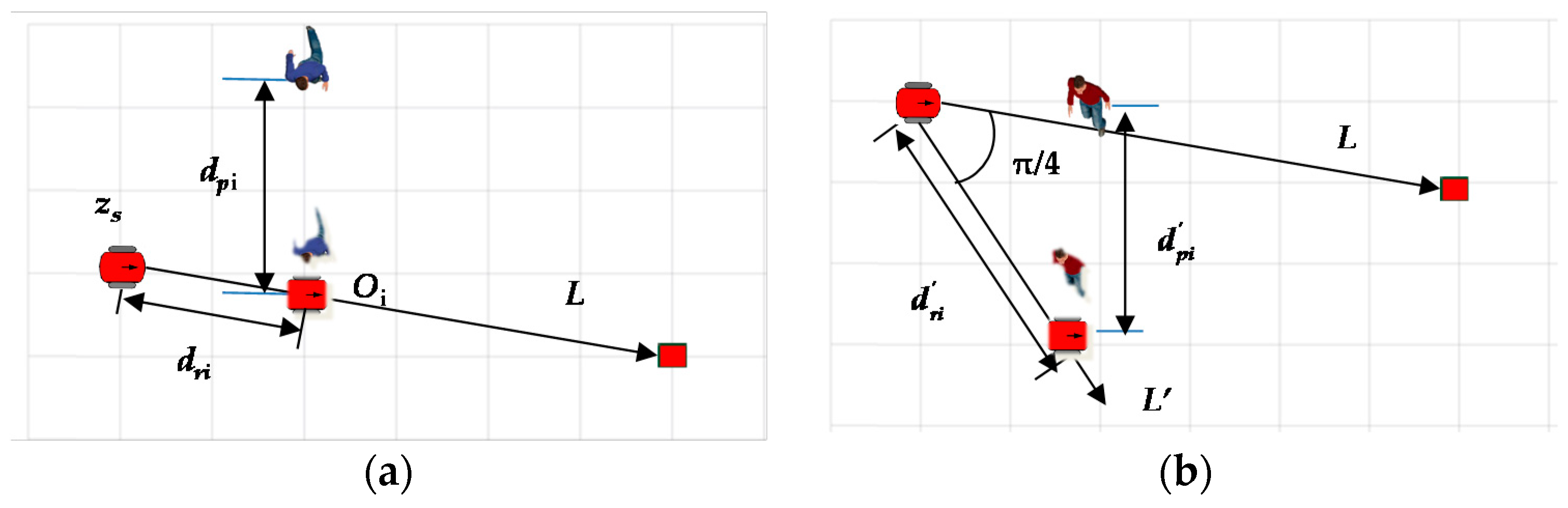
For convenience of description, we represent the topology in front of pi as Gf(pi), and the topology behind pi as Gb(pi), and let the robot detect a sector area with a radius of 3 m and a circumferential angle of 90° in front of the robot during navigation. Figure 4 shows the calculation of the trajectory chasing cost in Gf(pi) with different velocities. L is the straight line connecting the current position of the robot, zs, with the goal point. The following judgment criteria are proposed to evaluate the chasing cost of trajectories in Gf(pi) and Gb(pi):
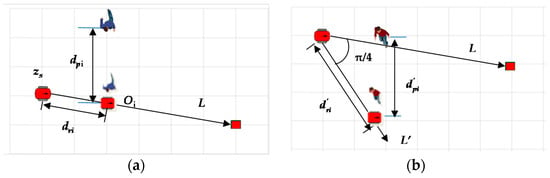
Figure 4.
Calculation of the trajectory chasing cost in Gf(pi) for pi in different velocity ranges: (a) (1.2 m/s, 3 m/s); (b) [0.5 m/s, 1.2 m/s].
Assume the robot runs with a maximal velocity of 2 m/s, and, when navigating in crowds, its averaged velocity is in the interval [0.5 m/s, 1.2 m/s].
- If the pedestrian’s walking speed, 1.2 m/s, the robot will have difficulty to catch up with pi. It is judged as follows (as shown in Figure 4a): The predicted trajectory of pi is extended by 0.7m (safe separation) and intersects with L at point Oi, and the distance between Oi and zs is dri. The robot is assumed to follow L at a speed of 1.2 m/s. If the robot arrives at Oi before pi (as in Equation (8)), the trajectory of Gf(pi) can be chosen.
- If [0.5 m/s, 1.2 m/s], the robot is able to catch up with pi and the judgement method is as follows (as shown in Figure 4b): The robot is assumed to catch up at a speed of 1.2 m/s along with L′ at the angle of π/4 from L, which is along its detection area edge and is the worst case for chasing; similar to the previous method, if the robot catches up successfully (as in Equation (9)), the trajectory of Gf(pi) can be chosen.
- If vpi < 0.5 m/s, the robot will be sure to catch up with pi and any trajectory of Gf(pi) can be chosen.
If the above conditions are not met, it is confirmed that the chasing cost of the trajectory of Gf(pi) is too high, and the trajectory of Gf(pi) is unfeasible, then go to the step of judging the trajectory chasing cost of Gb(pi):
- If there is a pedestrian, pj, walking towards L behind pi in the robot’s detection area, and the trajectory of Gb(pi) is also of Gf(pj), then the trajectory chasing cost of Gf(pj) is judged according to the above method. If it is successful, the trajectory of Gb(pi) can be chosen; if not, it is confirmed that the trajectory chasing cost of Gf(pj) is too high, and the trajectory of Gf(pj) is unfeasible, then go to the step of judging the trajectory chasing cost of Gb(pj).
- If there is no such pedestrian behind pi, the trajectory of Gb(pi) can be chosen.
2.2.3. The Overall Steps of the Trajectory Planning
In the global path planning, the predicted pedestrians’ occupied zones at t + 0.2 s and t + 0.5 s should not be penetrated in the detection area of the traffic state (DATS). The global planner is assumed to have properly arranged and ordered intermediate goals for the online trajectory planner. The steps of local trajectory planning are as follows:
- Sample a specified number of waypoints, ζi, that do not intersect with any predicted pedestrians’ occupied zones at t + 0.2 s and t + 0.5 s and obstacle regions by the probabilistic roadmaps (PRM) approach for faster computation [20].
- Construct an exploration graph, G = {V, E}, in which V is the set of vertices that include the robot’s current position, zs; goal point, zg; and waypoints, ζi. E is the set of forward-directed edges that connect waypoint seeds with the orientation close to the direction from zs to zg, and do not intersect with any predicted occupied zones and obstacle regions [15].
- Based on the resulting graph, G, extract each simple path from zs to zg by utilizing a depth-first search.
- Identify the relevant topologies implicated by the predicted pedestrians’ occupied zones and obstacle regions and calculate the H-signature for each resulting path (H-signature for trajectories of the same topology are equal). Only one initial trajectory is reserved for each topology and other trajectories are filtered out.
- Optimize these initial trajectories in parallel by the TEB approach [14], and sort them based on costs from low to high.
- Exclude the trajectories that penetrate groups detected by a modified Density-based spatial clustering of applications with noise (DBSCAN) method [21].
- Judge the chasing costs of trajectories according to the method described in Section 2.2.2. If there is a feasible trajectory, the DATS is in the travelable state, and the first feasible trajectory found is the global optimal trajectory. If there is no feasible trajectory found, that current traffic state is no longer considered to be in the travelable state, and check if there is a low-speed-follow target and safe space ahead.
2.3. Navigation Based on Multiple Travel Modes and Predicted Pedestrians’ Positions
Due to changes in the distribution of pedestrians, the traffic situations in the area where they are located will change. To generate a safe and efficient traffic trajectory, the robot needs to formulate a corresponding traffic strategy according to the traffic state in the detection area. The detection area of the traffic state (DATS) is set to be a sector area with radius 5 m and circumferential angle 90° in front of the robot. The predicted position of pedestrians in this area based on the improved socially conscious model will be considered when planning the trajectory.
The traffic states are divided into the five following categories according to the crowd density from low to high: Completely smooth, smooth, walkable, slow-moving, and congested. To guide the robot to find the optimal navigation strategy, five travel modes are defined, as follows: Free mode, high-speed-follow mode, travelable mode, low-speed-follow mode, and probing mode, as shown in Table 1. The priority of the five traffic states in DATS is sorted from high to low. If a state with a higher priority is detected, the robot preferentially enters the corresponding travel mode. In Section 2.3.1, we present the follow target detection and follow mode switching method for smooth and slow-moving states; in Section 2.3.2, the trajectory planning strategies for completely smooth and congested states are described. The trajectory detection and optimization for a travelable state is elaborated in in Section 2.2.

Table 1.
Travel modes for different traffic states.
2.3.1. Follow Target Detection and Follow Mode Switching Method for Smooth and Slow-Moving States
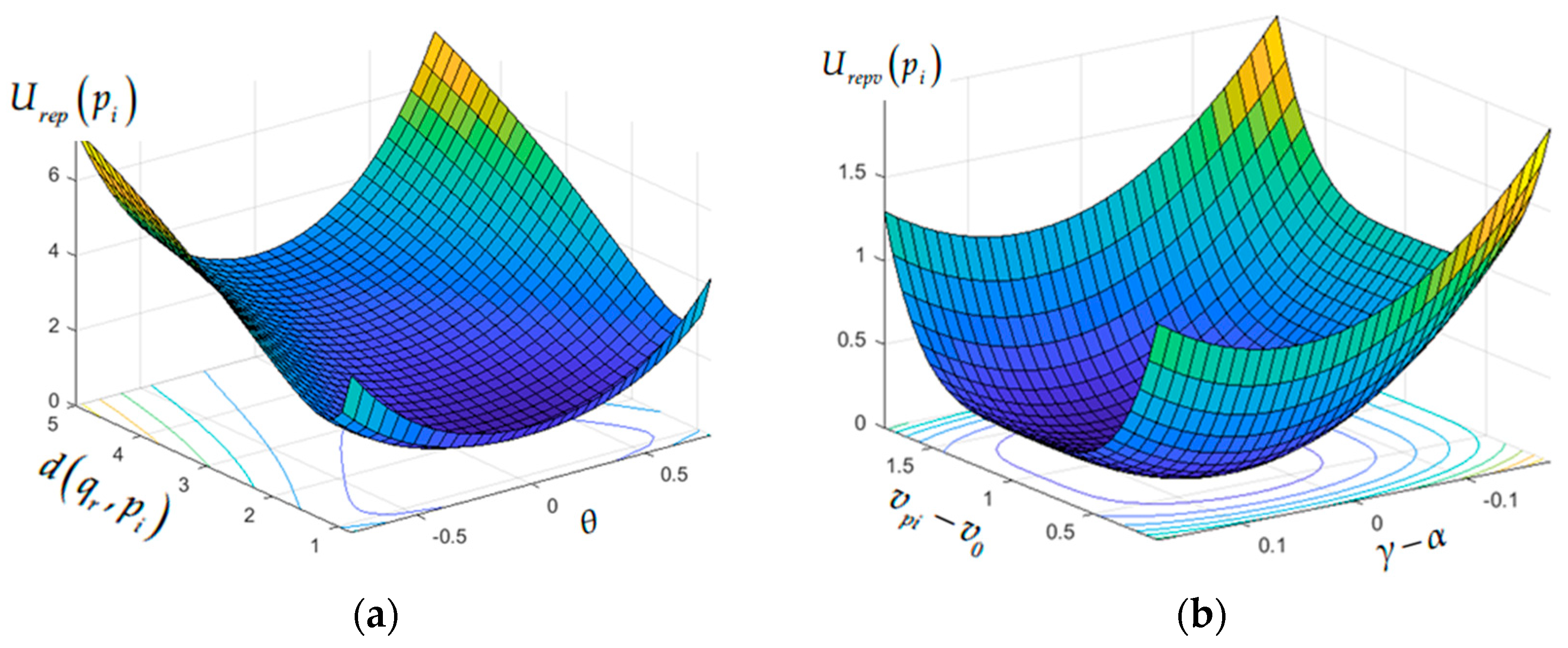
The ideal follow-up target should have the following characteristics: The speed direction should be pointing to the robot’s goal position; the speed magnitude should be similar to the robot’s normal moving speed; the position should be within a safe and comfortable distance and reasonable angle to the robot. Given the current position of the robot, qr, inspired by the artificial potential field [22], we define a function (Equation (12)) to evaluate the followability of a pedestrian, pi. The function includes two penalty terms: The deviation from the ideal position penalty term, Urep(p), (10) and the deviation from the ideal speed penalty term (11). In Equation (10), the function, d(qr,pi), represents the distance between the robot and the pedestrian, pi; d0 represents the ideal distance; θ represents the angle between the vector of pi to qr and the vector of qr to the goal position; and N(·) is a normalization function. The variation of function, Urep(pi), with d(qr,pi) and θ is shown in Figure 5a. When the distance of a pedestrian in DATS is too small (less than 0.8 m in this paper), the function is given a large penalty value of 1000. In Equation (11), v0 represents the ideal walking speed of the pedestrian, α represents the direction angle of the vector of pi to the goal point (ideal speed direction), and γ represents the speed direction of the pedestrian. The variation of the function, Urepv(pi), with the walking speed deviation from the ideal walking speed, vpi − v0, and the direction deviation from the desired angle, γ-α, is shown in Figure 5b. When the pedestrian’s speed is too small (<0.1 m/s in this paper) or the direction deviates from the ideal direction by more than π/18, a large penalty value of 1000 will be assigned to the function. Compared with the position, the speed of the pedestrian has a greater influence on followability performance. Therefore, the minimum value of the speed penalty function is 0, and the minimum value of the position penalty function is designed to be 1.
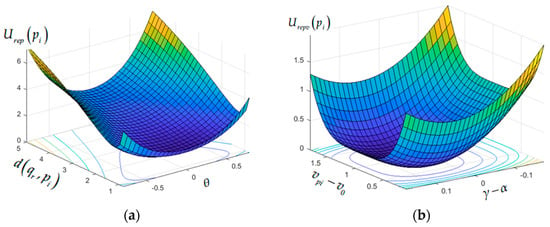
Figure 5.
(a) The variation of function, Urep(pi), with d(qr,pi) and θ; (b) the variation of the function, Urepv(pi), with the walking speed deviation from the ideal walking speed, vpi-v0, and the direction deviation from the desired angle, γ-α.
If the value of Utotal(pi) is within 2, the pedestrian, pi, will be treated as a candidate high-speed-follow target; if it is in the interval (2, 12), pi will be treated as a low-speed-follow target. If it is greater than 12, pi cannot be regarded as a candidate following target. Then, for all candidate follow-up targets, according to the Utotal(pi) order from low to high, the reachability detection is performed as follows: Select the following point (the point at 1.2 m behind the pedestrian in this paper); judge whether a feasible trajectory from the robot’s current position to the following point exists via the method in Section 2.2; if yes, it is reachable, stop detecting and set the current detected pedestrian to be a followable target, then move to the following point along the selected trajectory; if no, it is unreachable, determine whether the next candidate target is reachable.
In the process of following the pedestrian, pi, the speed in the next 0.5 s is predicted, and the variation of Utotal(pi) based on the pedestrian’s future 0.5 s is monitored. When Utotal(pi) increases from a value less than 2 to a value greater than 2, or increasing from a value in the interval (2, 12) to a value greater than 12, the travelling mode changes, and the current following target is discarded and the next candidate following target will be detected.
2.3.2. Trajectory Planning Strategy for Completely Smooth and Congested States
If there are no people in DATS, then the traffic state is completely smooth, and the robot enters the free mode. The corresponding trajectory planning strategy is the same as the approach in Section 3.2, without considering the influence of walking pedestrians.
If there is no feasible trajectory and no target can be followed, then DATS is in the congested state, and the robot enters the probing mode, repeating the following process: (1) Find the nearest pedestrian, pi, who does not satisfy the conditional expressions, (10) or (11). (2) Set the point along L that is 0.7 m away from pi as the temporary goal point of the robot and attempt to plan a new feasible trajectory. If there is no feasible trajectory, the robot will wait until a feasible trajectory is found. In the probing mode, the robot continuously checks whether the conditions of other states are satisfied according to the priority. If yes, it immediately jumps out of the current state and enters the corresponding state.
3. Results and Analysis
3.1. Human Trajectory Prediction
The improved socially conscious model is an LSTM network. An embedding layer, whose dimension is 64, for the spatial coordinates, is used as the input to the LSTM. The dimension of hidden states for all the LSTM models is 128. The embedded layer uses ReLU (rectified Linear Units) for non-linearization. 80% of the data is used for training and the remaining 20% for verification. 50 epochs were trained totally. During the model training, the learning rate is set to 0.001, dropout is set to 0.8, and the RMS-prop in [23] is used as the optimizer. The proposed socially conscious model is implemented on a single GTX1080 GPU. The model reads the newly input data and generates the predicted data obeying the trained two-dimensional normal distribution through the sampling function in Numpy. In order to improve the stability of the prediction data, multiple generation operations are performed, and the average value is calculated as the final prediction result.
Similar to Social-LSTM [8], eight time steps (3.2 s) are observed and 12 time steps (next 4.8 s) are predicted. In this paper, we compare our proposed improved socially conscious model with the state-of-the-art Social-LSTM in [8] with the datasets, ETH [24] and UCY [25]. A total of five sub-datasets are included in this paper, and the leave-one-out method is adopted. Prediction performance is evaluated with two different metrics [24]: Average displacement error (ADE) and final displacement error (FDE). Table 2 shows the prediction error reduction percentage, which shows that our proposed improved socially conscious model has a smaller average displacement error and final displacement error, and proves the effectiveness of our proposed model.

Table 2.
Prediction error reduction percentage.
Compared with the social-LSTM [8], the improved socially conscious model has a higher prediction accuracy in all datasets. One reason is that the social-LSTM considers the influence of pedestrians in a small area around the target pedestrian, and does not take into account the relative directions of pedestrians. However, our proposed model considers more pedestrians in larger areas and filters out the pedestrians with negligible influences as judged by their relative directions. Additionally, the introduction of the pooling layer between the current pedestrian trajectory sequence input and position estimation output, which enhances the effect of a pedestrian’s own history trajectory, can significantly reduce the prediction error of the model.
3.2. Trajectory Planning
We have conducted comprehensive evaluations of the proposed navigation method and compared it with the state-of-the-art methods in the literature. A robot with a differential drive is used in the simulation experiments. The simulator is a virtual machine running with Intel Core E5-2620 12 × 2.1 GHz and 32 GB RAM. The evaluation function of the robot trajectory performance is defined as follows:
If the goal position is not reached, is set to “−100”. For a successful path, ρ, the path cost is the sum of the four parts in Equation (12). is a function that penalizes the pedestrian, ’s, collision with the robot during the robot’s march process. The value of is set to −100 when one collision happens, otherwise, it remains at 0. is a function, which punishes the robot’s penetration to a pedestrian’s safety area, but without collision. The value of is set to −10 when one penetration occurs, otherwise, it remains at 0. is a smooth penalty function, it is set to −5 when one return occurs, otherwise, it remains at 0. is a reward function, which is linear with the average velocity of the trajectory, and the maximum velocity (2 m/s) corresponds to the value 100, the minimum velocity (0.1 m/s) corresponds to the value 0. λ is a weight coefficient (here, ).
3.2.1. Validation Experiment with Simulated a Low-Density Crowd
To comprehensively evaluate our proposed method, a comparative experiment of three scenarios has been designed. The first scenario is to validate the improvement of predicting the pedestrian position with the improved socially conscious model when dealing with two pedestrians walking towards each other. The second scenario is to validate the necessity of trajectory planning with pedestrian position prediction when dealing with a low-density crowd. The third scenario is to validate the necessity of the trajectory planning approach with chasing cost judgment. The simulations are performed in Stage [23] based on ROS. We use a dynamics model for Pioneer 3-DX and a constant velocity model for pedestrian motions. These simulated pedestrians do not react to robot movements. The simulated robot Pioneer 3-DX are equipped with a simulated laser sensor, hokuyo UTM-30LX, which is supported by ROS. In the simulated environment in this paper, the coordinates of the pedestrians are input to the robot system as a known volume.
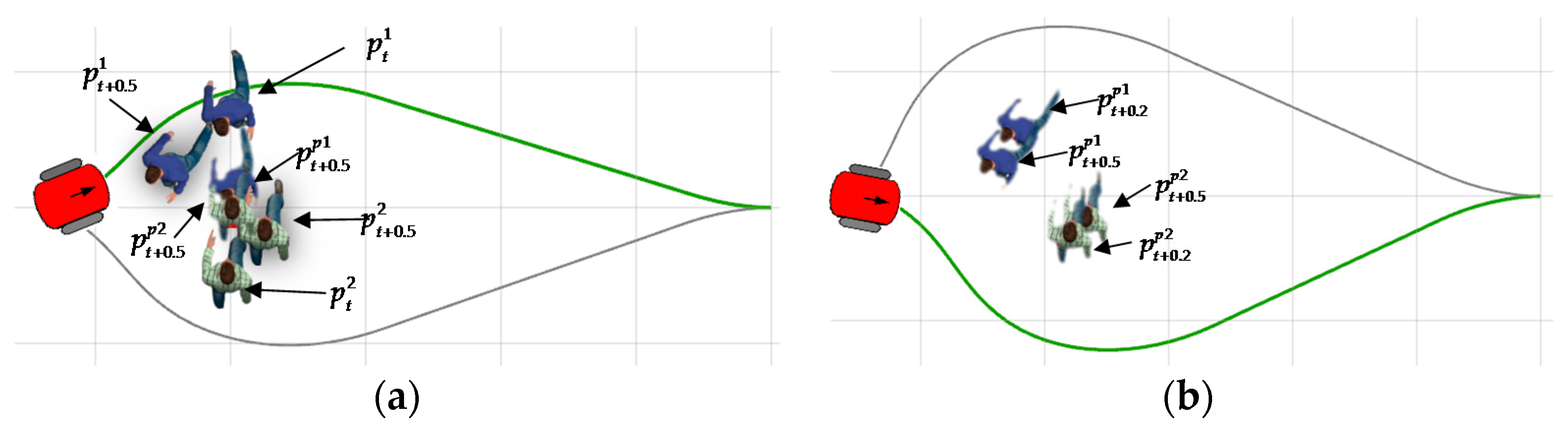
In the first scenario, the initial positions of pedestrians, p1 and p2, are and , respectively, and the ground-truth positions after 0.5 s are and . The pedestrian’s movements are simulated by playing back the recorded data. The robot’s task is to predict the position of pedestrians based on different prediction methods, and then generate obstacle avoidance trajectories. The positions of p1 and p2 after 0.5 s predicted by the constant-speed model are and , respectively, and two pedestrians will collide; the optimal obstacle avoidance trajectory generated by the constant-speed model leads to a small distance of 0.2 m away from the pedestrian’s actual position, , which penetrates in the pedestrian’s safety zone, as shown in Figure 6a. The positions of p1 and p2 predicted by the improved socially conscious model after 0.2 s and 0.5 s are , , , and , respectively, as shown in Figure 6b. The optimal obstacle avoidance trajectory generated by our proposed method leads to a minimum distance of 0.7 m away from the pedestrian’s actual position, , which shows the improvement of safety.
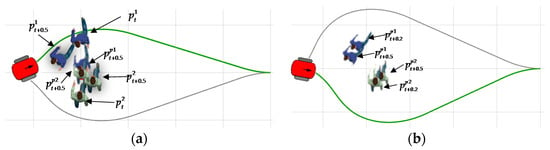
Figure 6.
Obstacle avoidance trajectories generated based on different pedestrian position predicting models: (a) the constant-speed model; (b) the improved socially conscious model.
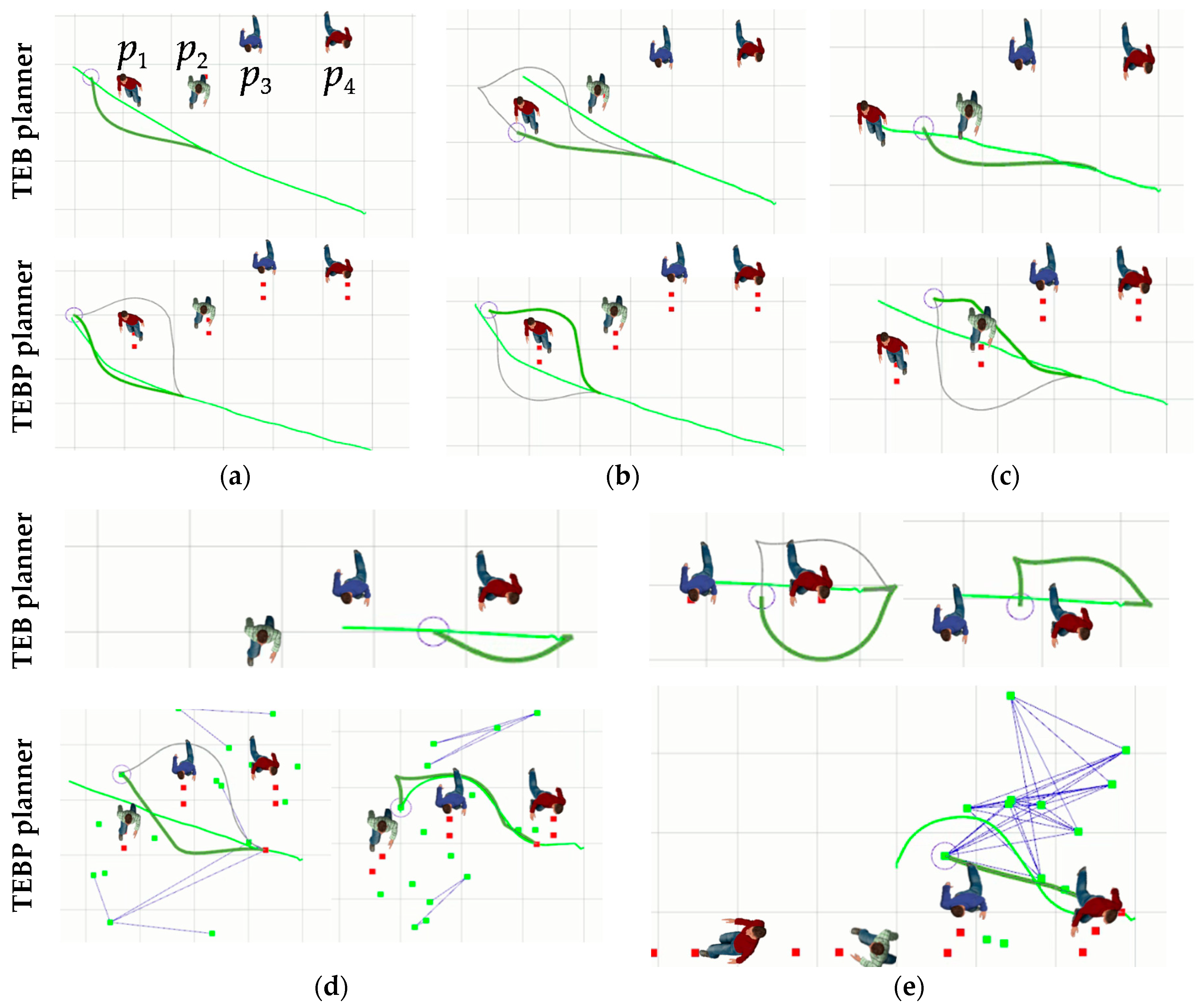
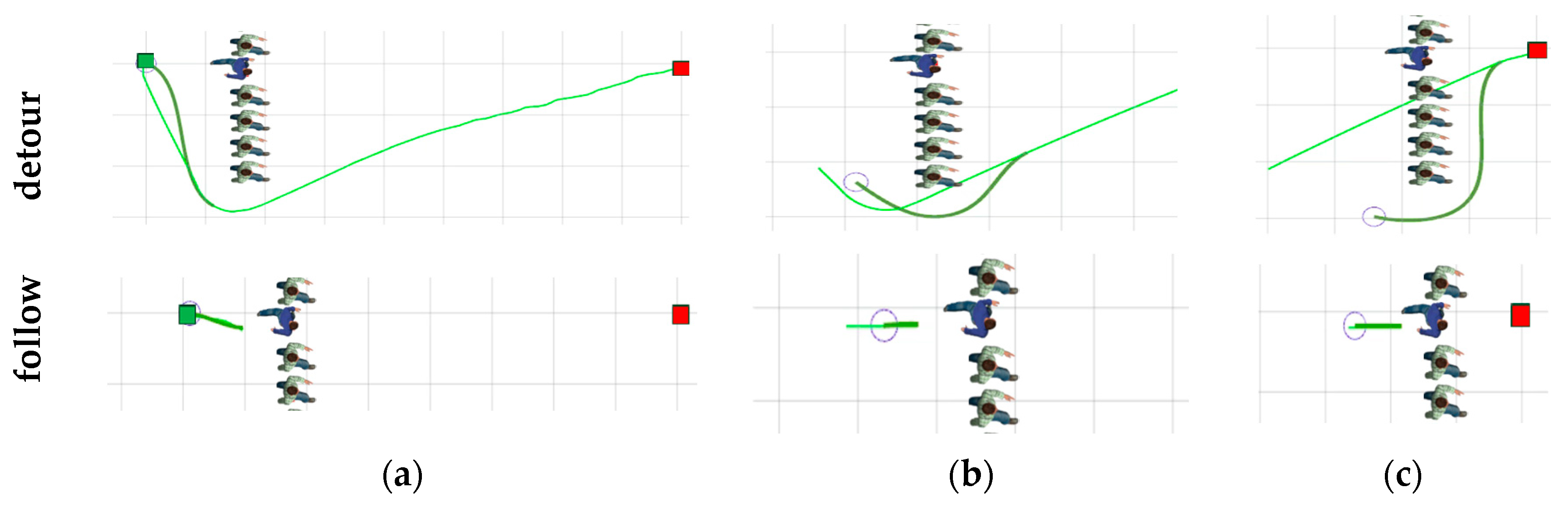
In the second scenario, there are four pedestrians numbered p1 to p4. The original TEB approach and our proposed TEB approach with pedestrian trajectory prediction (TEBP) are compared in the local trajectory planner. Figure 7 shows the robot’s trajectory planning process of avoiding four pedestrians, which is as follows: (1) The TEB and TEBP planner begin to select the trajectory of Gf(p1); however, the robot with the TEB planner hit p1, while the TEBP planner smoothly switched to the trajectory of Gb(p1), as shown in Figure 7b. (2) The TEB planner selects the trajectory of Gf(p2), while the TEBP planner smoothly switches from the trajectory of Gf(p2) to Gb(p2), as shown in Figure 7c. (3) The TEB planner selects the trajectory of Gf(p3), while the TEBP planner first selects the trajectory of Gf(p3), and after running for a distance, it switches to Gb(p3), and this results in a return in this switching process, as shown in Figure 7d. (4) The TEB planner first selects the trajectory of Gf(p4), and after driving for a distance, it switched to Gb(p4), and this switching process results in a return; while the TEBP planner realizes smooth switching of this process, as shown in Figure 7e. The green dots in Figure 7 are the sampling points to generate new trajectories, and the points are continuously sampled in parallel during the navigation. The average velocity of the robot with the TEB planner is 1.12 m/s, while that with the TEBP planner is 1.21 m/s. In this scenario, the TEB planner generates trajectories with an evaluation function value of −54, and the TEBP planner generates trajectories with an evaluation function value of 50.5. This shows that our proposed TEB approach with pedestrian trajectory prediction (TEBP) performs better.
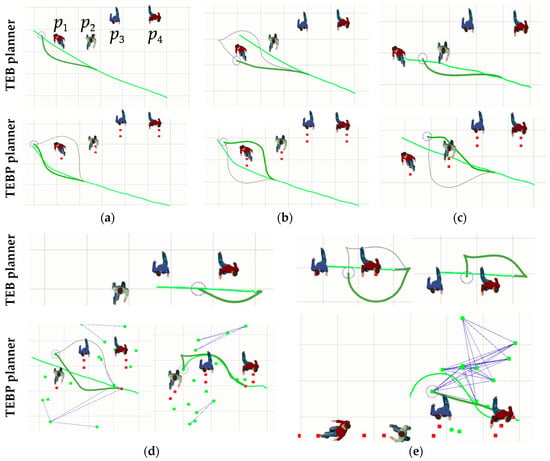
Figure 7.
The trajectory planning process of avoiding four pedestrians with timed-elastic-band (TEB) and TEB with pedestrian trajectory prediction (TEBP) planners: (a) Initial state; (b) avoiding p1; (c) avoiding p2; (d) avoiding p3; and (e) avoiding p4. The red dots represent the predicted pedestrians’ positions, and the green dots are sampling points to generate new trajectories. The circle in grey is the robot.
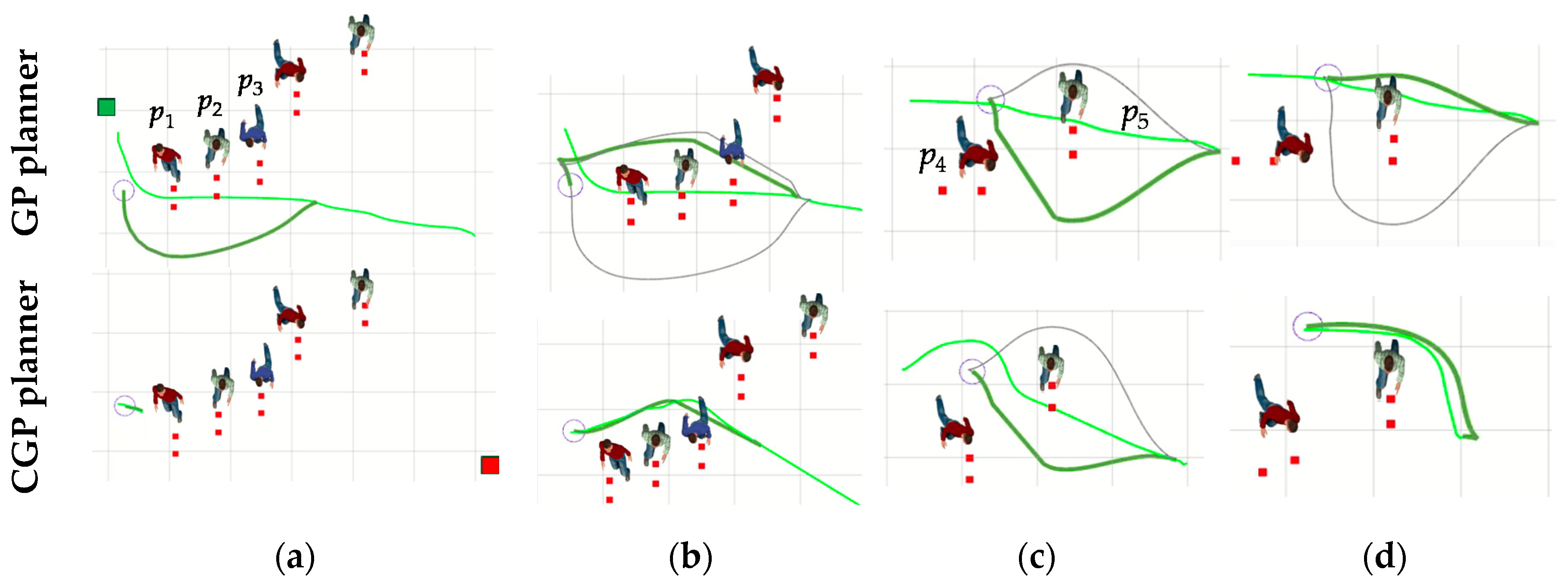
In the third scenario, there are five pedestrians, which are numbered p1 to p5 from left to right. Their velocities are 1.5 m/s, 1.4 m/s, 1.4 m/s, 1.2 m/s, and 1.2 m/s, respectively. The planner consisting of a global path planner and a TEBP local planner is denoted as the “GP” planner, and the GP planner with chasing cost judgment is denoted as the “CGP” planner. The robot with CGP planner detects the feasibility of the trajectories according to the method in Section 3.2.2. When there is no feasible trajectory, the robot will enter the probing mode. Figure 8 shows the trajectory planning process with the GP and CGP planners for the robot to avoid the five pedestrians, which is as follows: The GP planner starts with selecting the trajectory of Gf(p1), as shown in Figure 8a, after the robot travels for a distance, the GP planner switches to the trajectory, Gb(p1), which results in a return, as shown in Figure 8b; while the CGP planner judges that trajectory of Gf(p1) is unfeasible, and there is no feasible trajectory of Gb(p1) found, then the robot enters the probing mode, and sets the point 0.7 m away from p1 along L as the temporary goal point of the robot, as shown in Figure 8a. When the feasible global trajectory of Gb(p1) and Gb(p2) is found, the robot enters the travelable mode, as shown in Figure 8b. In Figure 8c, the GP planner selects the trajectory of Gf(p5). After running for a distance, it switches to the trajectory of Gb(p5), and the global path remains unchanged, as shown in Figure 8d. However, when the CGP planner judges that the trajectory of Gf(p5) is unfeasible, it switches to the trajectory of Gb(p5), as shown in Figure 8c,d.
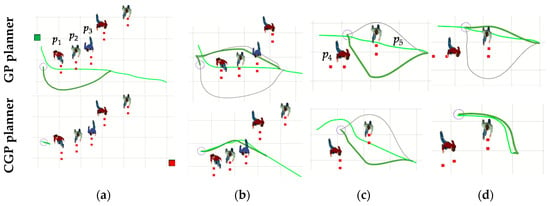
Figure 8.
The trajectory planning process of avoiding five pedestrians with GP and CGP planners: (a,b) Avoiding p1, p2, and p3; (c,d) avoiding p5.The average velocity of the robot with the GP planner is 1.25 m/s, and the evaluation function value of the trajectory is 62.5; while the average velocity with the CGP planner is 1.39 m/s, and the evaluation function value of the trajectory is 69.5. This shows the necessity and effectiveness of trajectory planning with chasing cost judgment, which is proposed in our approach.
3.2.2. Validation Experiments with a Real Low-Density Crowd
In this section, validation experiments on an actual robot system (e.g., [26]), a PatrolBot that is equipped with a Microsoft Kinect Sensor V2 and a laser (Sick LMS 200), are conducted to show the benefit of integration of human trajectory prediction. The Kinect V2 is used to recognize the pedestrians via the skeletal tracking algorithm [19].
In the first scenario, the PatrolBot is commanded to navigate to the goal position and it encounters a pedestrian with a walking direction perpendicular to its path. The original TEB planner and our proposed CGP planner are utilized to generate the trajectory, respectively. Figure 9 shows the robot’s navigation process of avoiding one pedestrian, p. When using the TEB planner, the robot selects the trajectory of Gf(p) at first, as shown in Figure 9a. Then it switches to the trajectory of Gb(p) after a sharp return, as shown in Figure 9c,d. By contrast, when using the CGP planner, the switching process is smoother, as shown in Figure 9c,d. The average velocity of the robot with the TEB planner is 0.45 m/s, while that with the CGP planner is 0.67 m/s. In this scenario, the TEB planner generates trajectories with an evaluation function value of 17.5, and the CGP planner generates trajectories with an evaluation function value of 33.5.

Figure 9.
The robot’s navigation process of avoiding one pedestrian with TEB and CGP planners: (a) the robot selects the trajectory of Gf(p); (b,c,d) a sharp return happens with TEB planner, however, no sharp return happens with CGP planner.
In the second scenario, the PatrolBot encounters two pedestrians with walking directions perpendicular to its path. The original TEB planner and our proposed CGP planner are utilized to generate the trajectory, respectively. Figure 10 shows the robot’s navigation process of avoiding two pedestrians, p1 and p2. When using the TEB planner, the robot selects the trajectory of Gf(p1) and Gf(p2) at first because it believes that the gap between the two pedestrians is enough to pass through, as shown in Figure 10a. Then, it switches to the trajectory of Gb(p1) after a sharp return, as shown in Figure 10c,d. By contrast, when using the CGP planner, there is no return in the switching process, as shown in Figure 10c,d. The average velocity of the robot with the TEB planner is 0.31 m/s, while that with the CGP planner is 0.53 m/s. In this scenario, the TEB planner generates trajectories with an evaluation function value of 10.5, and the CGP planner generates trajectories with an evaluation function value of 26.5.

Figure 10.
The robot’s navigation process of avoiding two pedestrians with TEB and CGP planners: (a,b) the robot selects the trajectory of Gf(p1) and Gf(p2); (c,d) a sharp return happens with TEB planner, however, no sharp return happens with CGP planner.
The results show the improvement of efficiency when integrating the TEB approach with human trajectory prediction.
3.3. Navigation Based on Multiple Travel Modes and Predicted Pedestrians’ Positions
3.3.1. Comparation of Navigation with Multiple Travel Modes and with the Travelable Mode Only
In this scenario, two cases are compared, as follows: A simulated robot with and without the follow mode. In the case without the follow mode, the robot selects a trajectory that bypasses the front pedestrian (as shown in Figure 11a). Since the velocity of the robot is close to that of the pedestrians, the robot gradually approaches the goal position along the detour, and cannot reach the goal position until the crowd passes the goal position (as shown in Figure 11c). In the case with the follow mode, the robot applies our proposed method to select the pedestrian wearing the blue costume to follow (as shown in Figure 11a), and keeps following him until reaching the goal position (as shown in Figure 11c). In the first case, the average velocity of the robot is 1.02 m/s and the evaluation function value is 50.1. In the second case, the average velocity of the robot is 1.2 m/s and the evaluation function value is 60. This proves the necessity and effectiveness of the following mode, which is included in our approach.
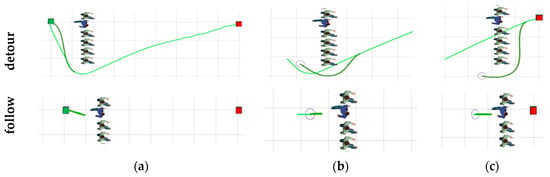
Figure 11.
Performance comparison between planners with and without the follow mode. The green curves and lime curves represent the local trajectories and global path, respectively. (a,b,c) The trajectories generated in three positions with and without the follow mode.
In the second scenario, two cases are compared: The Patrobot navigation with multiple travel modes and with the travelable mode only. The PatrolBot is commanded to navigate to the goal position and it encounters two pedestrians with walking directions similar to its path. Figure 12 shows the robot’s navigation process. When navigating with multiple travel modes, the robot cannot find a safe travelable trajectory at first. Then, it selects one pedestrian as the target to be followed after the followability evaluation, and switches to the low-speed-follow mode. Finally, it reaches to the goal position. By contrast, when navigating with the travel mode only, the robot continuously searches for the safe travelable trajectory. If there is no safe travelable trajectory, it will explore other trajectories randomly to detour the pedestrians, as shown in Figure 12c. The PatrolBot collides with the wall and adjusts its trajectory again in the exploration process, as shown in Figure 12d–f. Finally, it reaches the goal position when the pedestrians disappear, Figure 12h. The average velocity of the robot with multiple travel modes is 0.45 m/s and the evaluation function value is 22.5. While the average velocity of the robot with the travelable mode is only 0.31 m/s and the evaluation function value is −84.5. This proves the necessity and effectiveness of the proposed multiple travel mode.

Figure 12.
The robot’s navigation process with multiple travel modes and with the travelable mode only: (a,b) the robot explores trajectories randomly to detour the pedestrians ; (c,d) the robot collides with the wall; (e,f,g) the robot adjusts its trajectory again in the exploration process; (h) the robot reaches the goal position.
3.3.2. Validation Experiment in a Complex Medium-Density Crowd Environment
To further test the performance of our proposed navigation strategy and trajectory planning algorithm in a complex medium-density crowd, we used the ROS packages for a 2D pedestrian simulator based on the social force model of Helbing et al. [27] developed in the social situation-aware perception and action for cognitive robots (SPENCER) project [28]. The custom mobile robot is equipped with a front-facing stereo camera system, four RGB-D sensors, and a pair of 2D laser scanners [28]. In this scenario, the coordinates of the simulated pedestrians are known and sent to the robot system in real time, and the simulated robot uses the laser sensors only. A portion of the observed pedestrian trajectories are collected as the dataset to train the improved socially conscious model, and the performance of our proposed navigation approach is tested with the complex medium-density crowd environment. The ADE reduction percentage and FDE reduction percentage of our proposed improved socially conscious model is 6.2% and 7.9%, respectively, in this scenario.
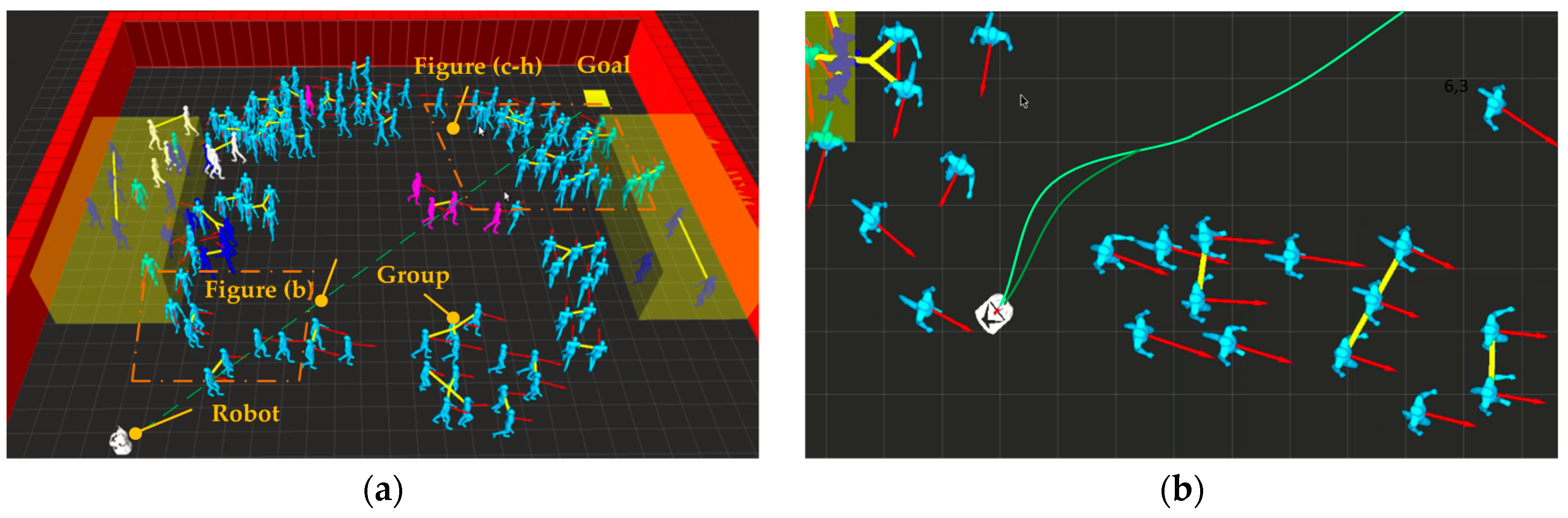
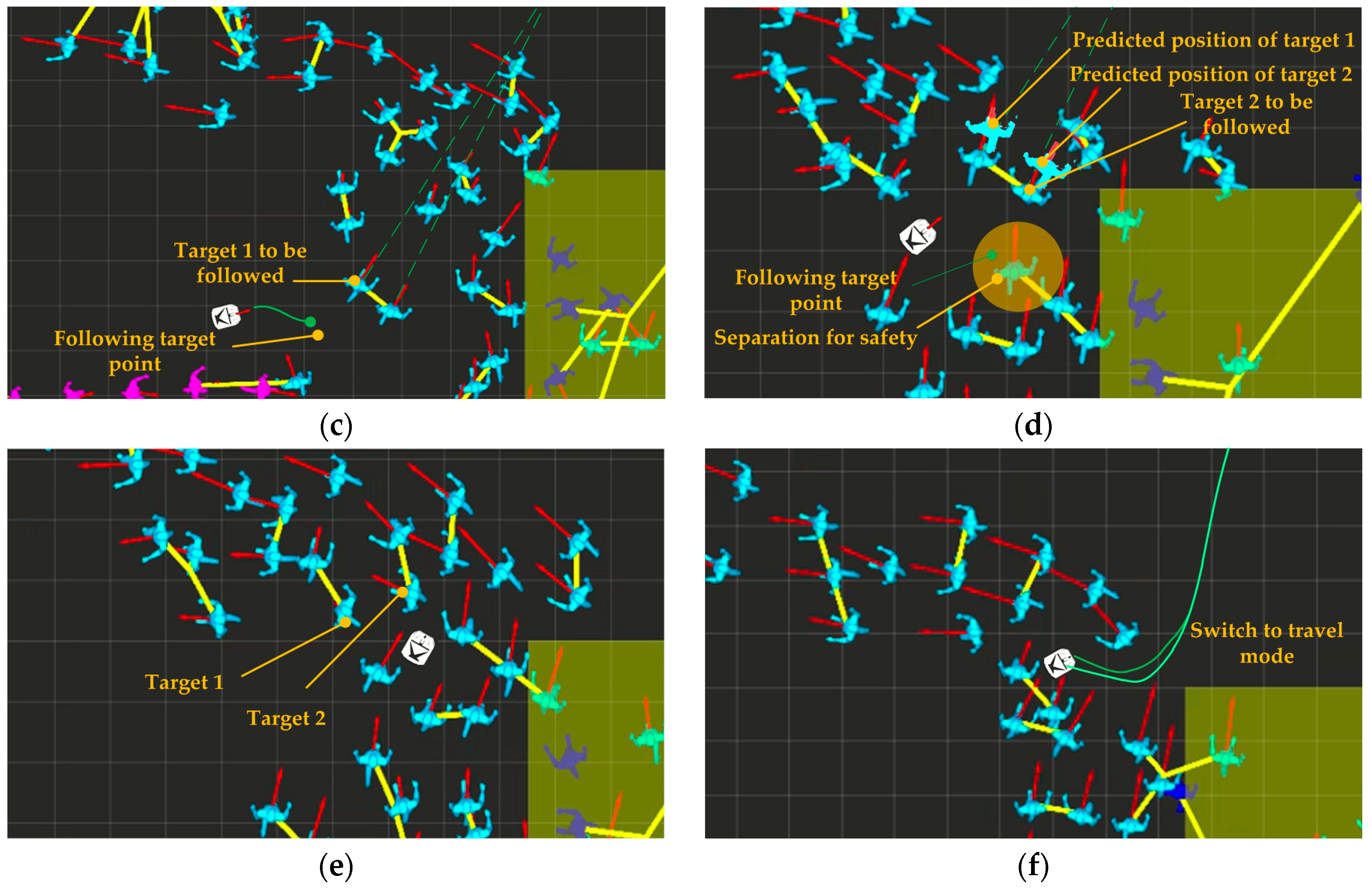
Figure 13a is an overall view of this scenario, and the regions in the two dotted line frames indicate the regions of Figure 13b,c–h, respectively. In the figure, the pedestrians connected by the yellow line represent identified groups, and the task of the robot is to reach the goal position from its current position. In Figure 10b, the robot detects that DATS is in a travelable state. The robot generates a trajectory with our proposed CGP planner, and passes through the crowds for the first time without collision. In Figure 10c, the robot finds that the followability evaluation function of target 1 is within 2, and it is also reachable judged with the method in Section 2.2. Therefore, it is confirmed that DATS is in smooth state, and target 1 is selected as the target to be followed and the robot switches to the high-speed-follow mode. In Figure 13d, during following the target 1, the robot predicts that the moving direction of target 1 is on the verge of deviating from the ideal moving direction, and the value of the followability evaluation function would increase to 420; at the same time, the followability evaluation function of the candidate low-speed-follow target 2 would be in the interval [2,12], but the ideal following target point is within the safe area of another pedestrian and, therefore, target 2 cannot be used as a followable target. Subsequently, the CGP planner does not find a feasible travel trajectory, and the robot determines that DATS is in the congested state and switches to the probing mode. In Figure 13e, the robot constantly monitors the traffic state of DATS while waiting. In Figure 13f, the robot finds a feasible trajectory and switches to the travelable mode, and finally passes through the crowd and reaches the final goal position. During the navigation, the robot has no collision with pedestrians. The average velocity is 0.3 m/s due to the long waiting time, and it crosses seven pedestrians’ safe zones in total. The evaluation function value is −55. When the robot navigates without the probing mode, the average velocity is 0.15 m/s, and it crosses eight pedestrians’ safe zones totally. The evaluation function value is −72.5. This proves the necessity and effectiveness of the probing mode, which is included in our approach.
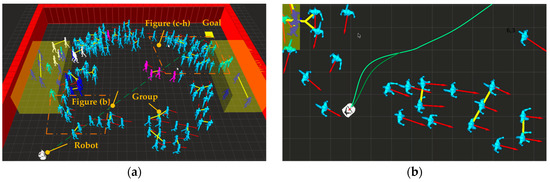
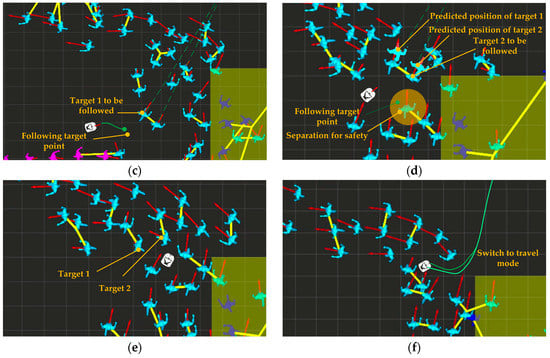
Figure 13.
Experiment in a complex crowd simulation environment: (a) Overview of the scenario; (b) the robot passes through the crowd for the first time; (c) the robot chooses to follow the target 1; (d) the robot is detecting the accessibility of the candidate following target 2; (e) the robot is in the probing mode; (f) the robot switches to the travelable mode.
4. Discussion and Conclusions
This paper proposes an improved socially conscious model for human trajectory prediction and a novel approach for robot navigation under changing traffic situations in a crowded area. We analyse and discuss our proposed methods as follows, and reveal the advantages and limitations.
First, the added pooling layers in the improved socially conscious model can significantly reduce the prediction error of the model compared with Social-LSTM. This finding suggests that the relative distance and walking direction of pedestrians around the target pedestrian are both important; furthermore, the influence of the target pedestrian’s own historical trajectory is larger than that of others around him/her. However, if the distribution of the training data is inconsistent with the current pedestrian’s walking pattern, the predicting error still exists and cannot be ignored. One way to improve the model predicting accuracy may be to explicitly consider the pedestrian’s destination, intention, and environmental static obstacles as reported in [29], and another way may be to automatically classify the personality and characterize each pedestrian’s behavior based on a weighted combination of different personality traits [30].
Second, the trajectories generated by the TEB trajectory planning method with predicted pedestrian trajectory are safer, more efficient, and more socially compatible. The reason is that the introduction of the pedestrian’s predicted position makes the trajectory cost of the pedestrian’s frontal topology increase, and the trajectory cost of the pedestrian’s backside decrease; the increase of the cost difference benefits the optimal trajectory searching. Furthermore, the optimal trajectory generation in advance and the increased distance between the robot and pedestrians at their front sides improves the navigation safety and efficiency. The proposed pedestrian’s positions’ prediction after 0.2 s as the occupation area handles the prediction error very well. These results prove that the proposed trajectory planning method achieves our original intention.
Third, the generated trajectory’s comprehensive performance with chasing cost judgment is improved. The reason is that the global trajectory of the robot is constrained so that it does not deviate too far from the shortest distance; on the other hand, discarding trajectories whose chasing costs are too high is beneficial to reduce the energy consumption of the robot, which is similar to an actual human’s trajectory selection strategy.
However, there are some limitations of this method, as follows: (1) In terms of the smoothness of the trajectories, the inescapable switching between different topological trajectories is sometimes not smooth and the curve has C0 continuity only [10], especially when the robot is close to pedestrians. However, the trajectory with C2 continuity, which preserves acceleration, is expected, so additional works that focus on smoothing the switching trajectories are needed. (2) In terms of computational time, the added human trajectory prediction and chasing cost judgment cost some time. Although the calculation of pedestrians’ new predicted trajectories is in parallel with planning based on the old predicted trajectories, the cost time cannot be ignored. The global trajectory searching takes some time and the efficiency needs to be improved. The improvement of the efficiency of the trajectory planning and the safety of the generated trajectory contradict each other, and they should be balanced. (3) The issue of real-time detection is not the research focus. However, when the proposed approach is applied in the real world, this issue becomes indispensable. When the density of the crowds is low, the skeleton tracking is effective. However, when the density is high, the problem occlusion of pedestrians should be considered. Therefore, one of the future works is to combine the prediction system with real-time detection of pedestrians via multiple vision sensors. (4) In terms of kinematic feasibility of the robots, we have used Pioneer 3-DX and Patrolbot, which are differential drive robots. However, other robots, like Summit XL or others with car-like models, might not execute these sharp turns particularly at relatively high speeds. The TEB planner provides local plans that are feasible for Ackermann drives and the planner supports car-like robots. The kinematic feasibility of the robots to execute the generated trajectories needs to be further modified and validated on car-like robot models. (5) The rapidly-exploring random tree (RRT) [31] algorithm is also a famous trajectory planning method. To compare with RRT and combine the RRT method with pedestrian trajectory prediction is one of the future works.
Fourth, robots with multiple travel modes can navigate safely in a medium-density crowded unstructured environment. We used the following mode and probing mode to deal with the “freezing robot problem” (FRP) [18], which is simple and feasible compared with existing solutions, such as [7,17,18], avoiding complex robot-human interaction modeling and learning. However, the navigation efficiency is still relatively low in the case of medium or high density of population, and the validation is conducted in a simulated environment only, ignoring the cooperative navigation behavior between pedestrians and robots in the real world, which is the direction of our future research. More results for testing the real mobile bot (e.g., [32]) in more dense area experiments in real world are required in the future.
In conclusion, the proposed navigation approach based on human trajectory prediction and multiple travel modes proves to be a novel and feasible solution in crowded, unstructured, and dynamic environments that is safe, efficient, and socially compliant.
Author Contributions
J.Z. and proposed Y.H. the idea of the paper; Z.C. and C.S. conceived and designed the experiments. C.S. and Z.C. performed the experiments. Z.C., B.Z. and Y.Y. analyzed the data and wrote the paper. All authors have read and approved the final manuscript.
Funding
This work is financially supported by Shenzhen Key Laboratory Project (Grant No. ZDSYS201707271637577), in part by Shenzhen Peacock Plan (Grant No. KQTD2016113010571019), Shenzhen Fundamental Research Funds (Grant Nos. JCYJ20160608153218487 and JCYJ20160429190300857) and National Natural Science Foundation of China (Grant No. U1713221).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vemula, A.; Muelling, K.; Oh, J. Social attention: Modeling attention in human crowds. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1–7. [Google Scholar]
- Keller, C.G.; Gavrila, D.M. Will the pedestrian cross? A study on pedestrian path prediction. IEEE Trans. Intell. Transp. Syst. 2014, 15, 494–506. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Tao, J.; Klette, R. Tracking of 2d or 3d irregular movement by a family of unscented kalman filters. J. Inf. Commun. Converg. Eng. 2012, 10, 307–314. [Google Scholar] [CrossRef]
- Lee, D.; Liu, C.; Liao, Y.-W.; Hedrick, J.K. Parallel interacting multiple model-based human motion prediction for motion planning of companion robots. IEEE Trans. Autom. Sci. Eng. 2017, 14, 52–61. [Google Scholar] [CrossRef]
- Schulz, A.T.; Stiefelhagen, R. A controlled interactive multiple model filter for combined pedestrian intention recognition and path prediction. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Las Palmas, Spain, 15–18 September 2015; pp. 173–178. [Google Scholar]
- Trautman, P.; Ma, J.; Murray, R.M.; Krause, A. Robot navigation in dense human crowds: Statistical models and experimental studies of human–robot cooperation. Int. J. Robot. Res. 2015, 34, 335–356. [Google Scholar] [CrossRef]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Li, F.-F.; Savarese, S. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 961–971. [Google Scholar]
- Song, C.; Chen, Z.; Zhao, B.; Qi, X.; Hu, Y.; Liu, S.; Zhang, J. Human trajectory prediction for automatic guided vehicle with recurrent neural network. J. Eng. 2018. [CrossRef]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Hoshino, Y.; Peng, C.-C. Path smoothing techniques in robot navigation: State-of-the-art, current and future challenges. Sensors 2018, 18, 3170. [Google Scholar] [CrossRef] [PubMed]
- González, D.; Pérez, J.; Milanés, V.; Nashashibi, F. A review of motion planning techniques for automated vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1135–1145. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef]
- Rösmann, C.; Feiten, W.; Wösch, T.; Hoffmann, F.; Bertram, T. Trajectory modification considering dynamic constraints of autonomous robots. In Proceedings of the ROBOTIK 2012—7th German Conference on Robotics, Munich, Germany, 21–22 May 2012; pp. 1–6. [Google Scholar]
- Rösmann, C.; Hoffmann, F.; Bertram, T. Kinodynamic trajectory optimization and control for car-like robots. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 5681–5686. [Google Scholar]
- Rösmann, C.; Hoffmann, F.; Bertram, T. Integrated online trajectory planning and optimization in distinctive topologies. Robot. Autonom. Syst. 2017, 88, 142–153. [Google Scholar] [CrossRef]
- Ye, N.; Somani, A.; Hsu, D.; Lee, W.S. Despot: Online pomdp planning with regularization. J. Artif. Intell. Res. 2017, 58, 231–266. [Google Scholar] [CrossRef]
- Bai, H.; Cai, S.; Ye, N.; Hsu, D.; Lee, W.S. Intention-aware online pomdp planning for autonomous driving in a crowd. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 454–460. [Google Scholar]
- Vemula, A.; Muelling, K.; Oh, J. Modeling cooperative navigation in dense human crowds. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1685–1692. [Google Scholar]
- Goebel, R.P. Ros by Example; Lulu. com: Morrisville, NC, USA, 2015. [Google Scholar]
- Jaillet, L.; Simeon, T. Path deformation roadmaps: Compact graphs with useful cycles for motion planning. Int. J. Robot. Res. 2008, 11–12, 1175–1188. [Google Scholar] [CrossRef]
- Rösmann, C.; Oeljeklaus, M.; Hoffmann, F.; Bertram, T. Online trajectory prediction and planning for social robot navigation. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 1255–1260. [Google Scholar]
- Lee, M.C.; Park, M.G. Artificial potential field based path planning for mobile robots using a virtual obstacle concept. In Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Kobe, Japan, 20–24 July 2003; pp. 735–740. [Google Scholar]
- Dauphin, Y.; de Vries, H.; Bengio, Y. Equilibrated adaptive learning rates for non-convex optimization. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 1504–1512. [Google Scholar]
- Pellegrini, S.; Ess, A.; Schindler, K.; Van Gool, L.J. You’ll never walk alone: Modeling social behavior for multi-target tracking. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 261–268. [Google Scholar]
- Lerner, A.; Chrysanthou, Y.; Lischinski, D. Crowds by example. In Computer Graphics Forum; Wiley Online Library: Hoboken, New Jersey, USA, 2007; pp. 655–664. [Google Scholar]
- Patil, M.; Abukhalil, T.; Patel, S.; Sobh, T. Ub robot swarm—Design, implementation, and power management. In Proceedings of the 2016 12th IEEE International Conference on Control and Automation (ICCA), Kathmandu, Nepal, 1–3 June 2016; pp. 577–582. [Google Scholar]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. E 1995, 51, 4282. [Google Scholar] [CrossRef]
- Linder, T.; Arras, K.O. People detection, tracking and visualization using ros on a mobile service robot. In Robot Operating System (ROS); Springer: Berlin, Germany, 2016; pp. 187–213. [Google Scholar]
- Zhong, J.; Cai, W.; Luo, L.; Zhao, M. Learning behavior patterns from video for agent-based crowd modeling and simulation. Autonom. Agents Multi-Agent Syst. 2016, 30, 990–1019. [Google Scholar] [CrossRef]
- Bera, A.; Randhavane, T.; Prinja, R.; Manocha, D. Sociosense: Robot navigation amongst pedestrians with social and psychological constraints. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 7018–7025. [Google Scholar]
- LaValle, S.M.; Kuffner, J.J., Jr. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Patil, M.; Abukhalil, T.; Patel, S.; Sobh, T. Ub swarm: Hardware implementation of heterogeneous swarm robot with fault detection and power management. Int. J. Comput. 2016, 15, 162–176. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).