Three-Dimensional Nanofluid Flow with Heat and Mass Transfer Analysis over a Linear Stretching Surface with Convective Boundary Conditions
Abstract
1. Introduction
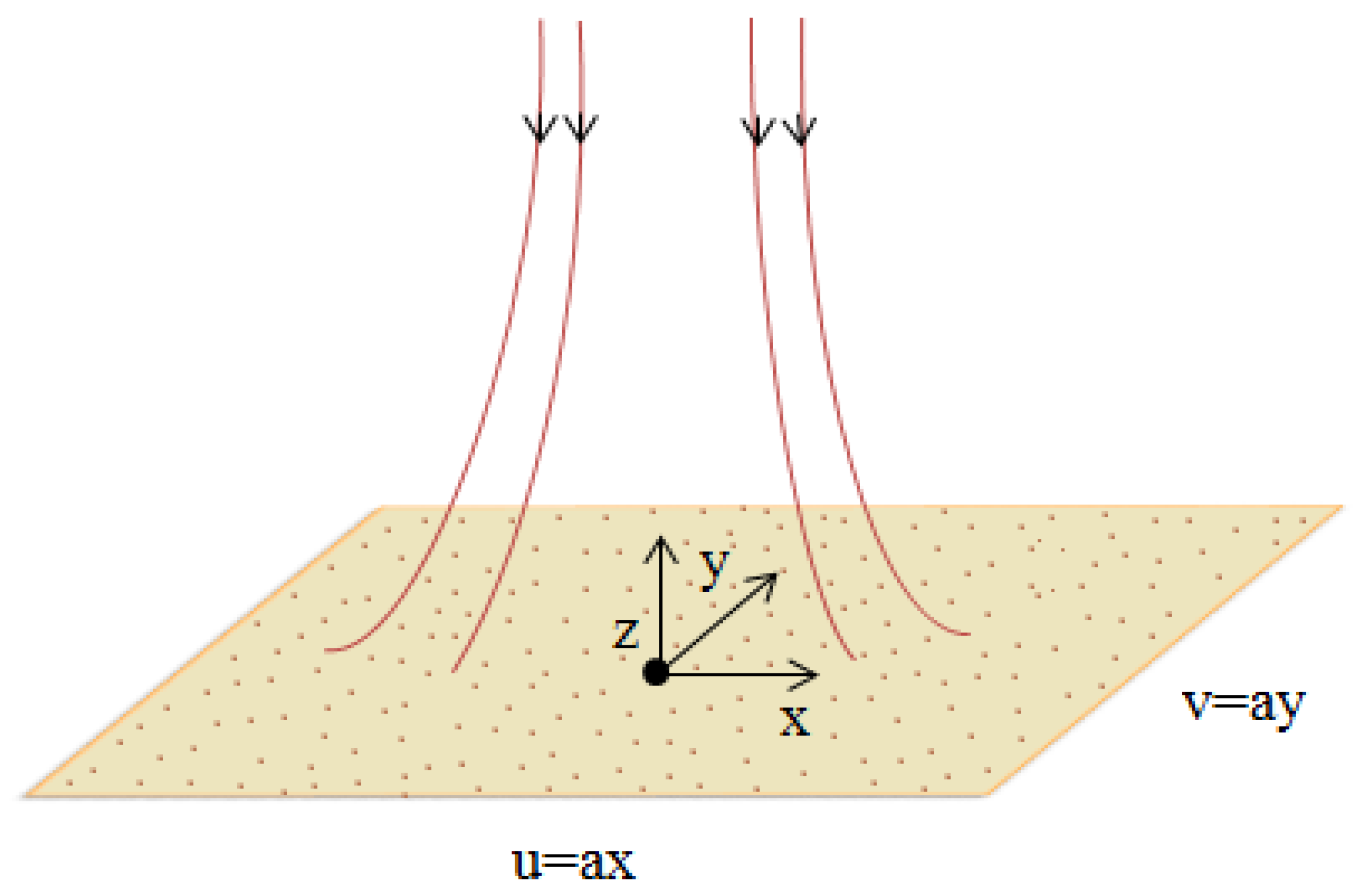
2. Problem Formulation
3. Solution by Homotopy Analysis Method
4. Discussion
5. Conclusions
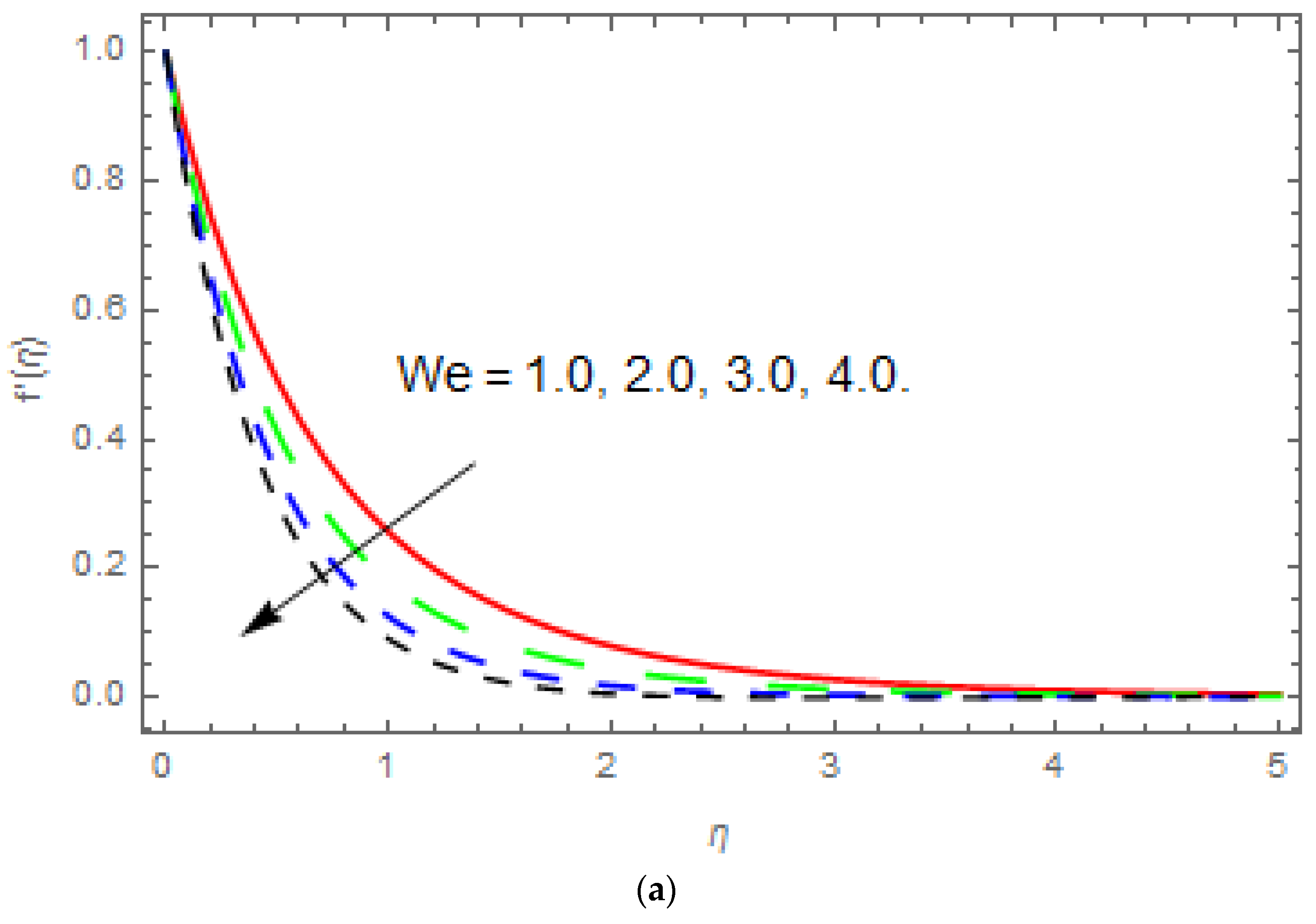
- The velocity function improves with enhancement of the stretching parameter, while reduces with an increase in and .
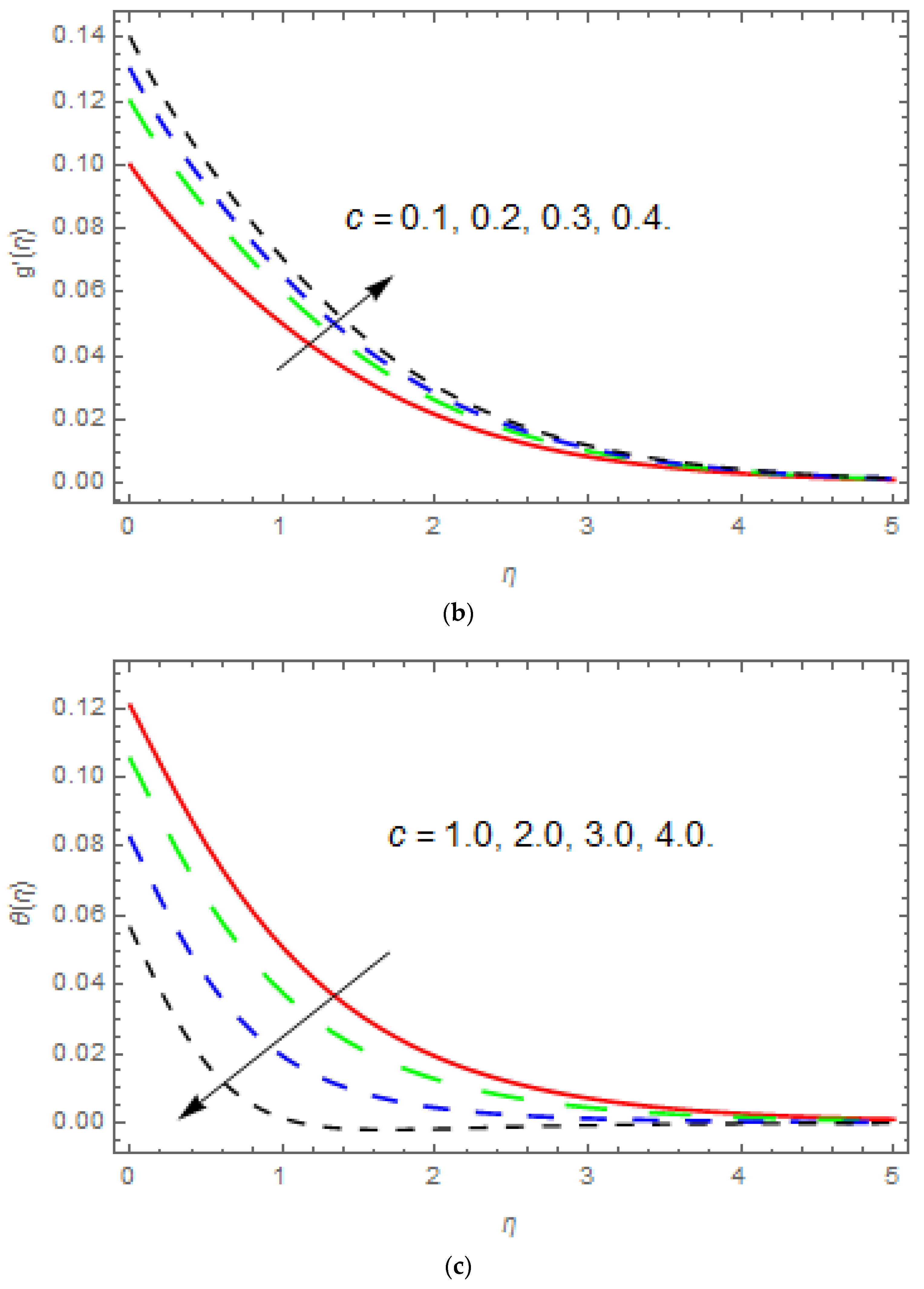
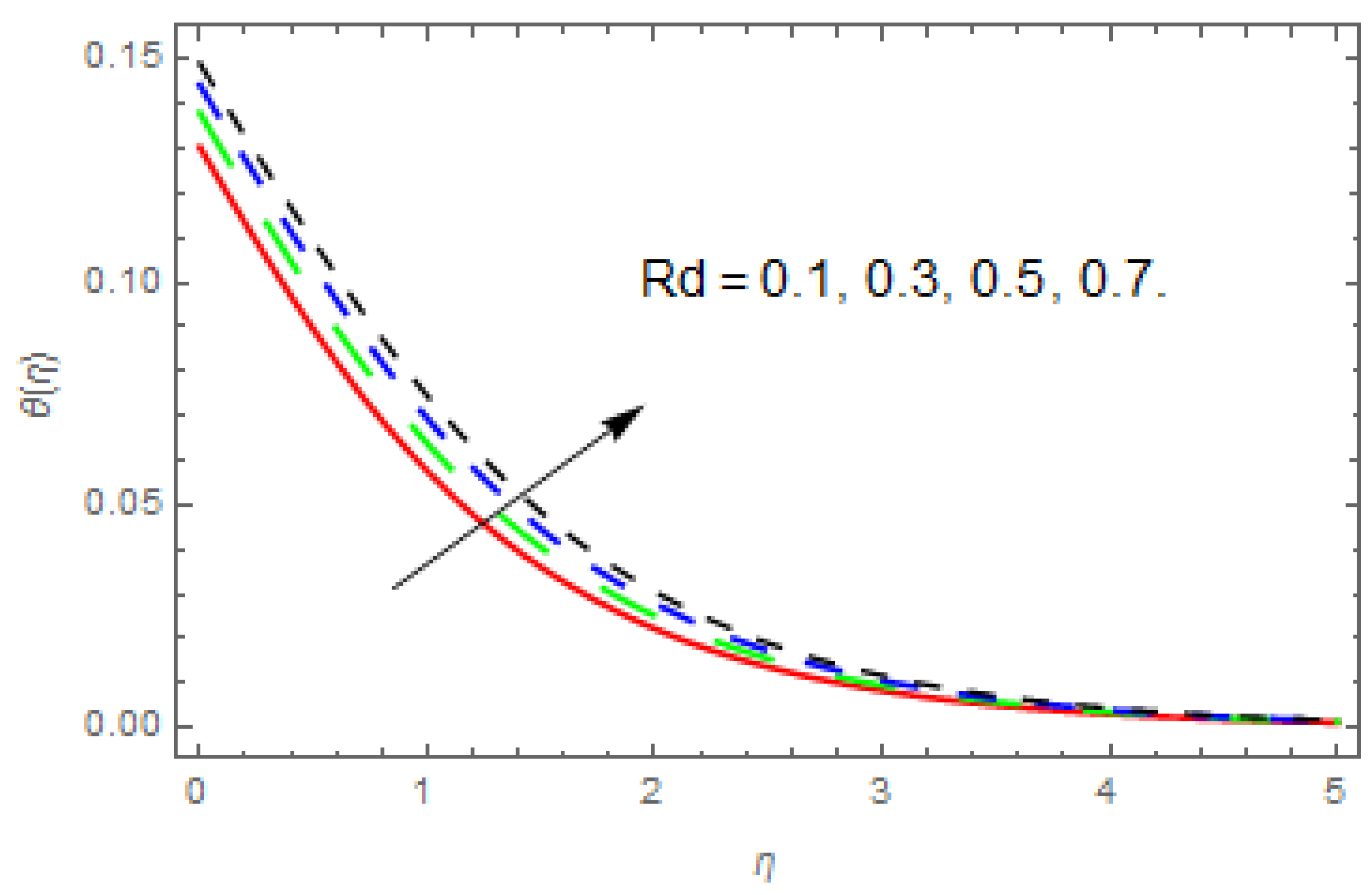
- The temperature function improves with an increase in , , and , while reduces with an increase in and .
- The concentration function enhances with an increase in and , while reduces with an increase in and .
- It is observed that increasing and reduces the surface drag forces and , while increasing augmented the surface drag forces and .
- . It is concluded from Table 2, that the higher values of and enhance the heat transfer rate, while the augmented values of and decline the heat transfer rate.
Author Contributions
Funding
Conflicts of Interest
References
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. Am. Inst. Chem. Eng. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Int. J. Appl. Mech. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Williamson, R.V. The flow of pseudoplastic materials. Int. J. Ind. Eng. Chem. 1929, 21, 1108–1111. [Google Scholar] [CrossRef]
- Ariel, P.D. The three-dimensional flow past a stretching sheet and the homotopy perturbation method. Int. J. Appl. Math. 2007, 54, 920–925. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Lee, C. MHD flow of a Casson fluid over an exponentially shrinking sheet. Sci. Iran. 2012, 19, 1550–1553. [Google Scholar] [CrossRef]
- Nadeem, S.; Akram, S. Peristaltic flow of a Williamson fluid in an asymmetric channel. Int. J. Nonlinear Sci. Numer. Simul. 2010, 15, 1705–1712. [Google Scholar] [CrossRef]
- Pop, I.; Na, T.Y. Unsteady flow past a stretching sheet. Int. J. Acta Mech. 1996, 4, 413–422. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary layer behavior on continuous solid surfaces and boundary layer on a continuous flat surface. J. Am. Inst. Chem. Eng. 1961, 7, 221–225. [Google Scholar] [CrossRef]
- Tsou, F.K.; Sparrow, E.M.; Goldstein, R.J. Flow and heat transfer in the boundary layer on a continuous moving surface. Int. J. Heat Mass Transf. 1967, 10, 219–235. [Google Scholar] [CrossRef]
- Malik, M.Y.; Bilal, S.; Salahuddin, T.; Khalil, U.R. Three-Dimensional Williamson Fluid Flow over a Linear Stretching Surface. Math. Sci. Lett. 2017, 6, 53–61. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Ericksod, L.E.; Fan, L.T.; Fox, V.G.; McCormack, P.D.; Crane, L. Phvsical fluid dynamics. Ind. Eng. Chem. 1966, 6, 19. [Google Scholar]
- Abdei-Aziz, M. Effect on the flow and heat transfer over an unsteady stretching sheet. Int. Commun. Heat Mass Transf. 2009, 36, 521–524. [Google Scholar] [CrossRef]
- Mukhopadyay, S. Effect of thermal radiation on unsteady mixed convection flow and heat treansfer over a porous stretching surface in porous medium. Int. J. Heat Mass Transf. 2009, 52, 3261–3265. [Google Scholar] [CrossRef]
- Shateyi, S.; Motsa, S.S. Thermal radiation effects on heat and mass transfer over an unsteady stretching surface. Math. Probl. Eng. 2009, 13, 965603. [Google Scholar] [CrossRef]
- Abdei-Aziz, M. Thermal-diffusion and diffusion-thermo effects on combined heat and mass transfer by hydromagnetic three-dimensional free convection over a permeable stretching surface with radiation. Phys. Lett. 2007, 372, 263–272. [Google Scholar] [CrossRef]
- Cortell, R. Effects of viscous dissipation and radiation on thermal boundary layer over a non-linearly stretching sheet. Phys. Lett. A 2008, 372, 631–636. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Heat transfer over a stretching surface with variable heat flux in viscous fluid. Phys. Lett. A 2008, 372, 559–561. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Islam, S.; Idress, M.; Khan, W.; Islam, S.; Gul, T. Impact of Thermal Radiation and Heat Source/Sink on Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface. Math. Comput. Appl. 2018, 23, 20. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Islam, S.; Idress, M.; Khan, W. Magnetohydrodynamic CNTs Casson Nanofl uid and Radiative heat transfer in a Rotating Channels. J. Phys. Res. Appl. 2018, 1, 017–032. [Google Scholar] [CrossRef]
- Kashif, A.A.; Irfan, A.A.; Sikandar, M.A.; Ilyas, K. On the thermal analysis of magnetohydrodynamic Jeffery fluid via modern non integer order derivative. J. King Saud Univ. Sci. 2018. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical investigation of nanofluid free convection under the influence of electric field in a porous enclosure. J. Mol. Liq. 2018, 249, 1212–1221. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Fe3O4-Ethylene glycol nanofluid forced convection inside a porous enclosure in existence of Coulomb force. Mol. Liq. 2018, 249, 429–437. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Magnetic field influence on nanofluid thermal radiation in a cavity with tilted elliptic inner cylinder. J. Mol. Liq. 2017, 229, 137–147. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Magnetohydrodynamic nanofluid forced convection in a porous lid driven cubic cavity using Lattice Boltzmann method. J. Mol. Liq. 2017, 231, 555–565. [Google Scholar] [CrossRef]
- Nadeem, S.; Ul Haq, R.; Noreen, S.A.; Khan, Z.H. MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alex. Eng. J. 2013, 52, 577–582. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Ayaz, H.; Khan, S. Radiative Heat and Mass Transfer Analysis of Micropolar Nanofluid Flow of Casson Fluid between Two Rotating Parallel Plates with Effects of Hall Current. ASME J. Heat Transf. 2018. [Google Scholar] [CrossRef]
- Shah, Z.; Bonyah, E.; Islam, S.; Khan, W.; Ishaq, M. Radiative MHD thin film flow of Williamson fluid over an unsteady permeable stretching. Heliyon 2018, 4, e00825. [Google Scholar] [CrossRef] [PubMed]
- Shah, Z.; Dawar, A.; Islam, S.; Khan, I.; Ching, D.L.C. Darcy-Forchheimer Flow of Radiative Carbon Nanotubes with Microstructure and Inertial Characteristics in the Rotating Frame. Case Stud. Therm. Eng. 2018. [Google Scholar] [CrossRef]
- Khan, A.; Shah, Z.; Islam, S.; Khan, S.; Khan, W.; Khan, Z.A. Darcy–Forchheimer flow of micropolar nanofluid between two plates in the rotating frame with non-uniform heat generation/absorption. Adv. Mech. Eng. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Jawad, M.; Shah, Z.; Islam, S.; Islam, S.; Bonyah, E.; Khan, Z.A. Darcy-Forchheimer flow of MHD nanofluid thin film flow with Joule dissipation and Navier’s partial slip. J. Phys. Commun. 2018. [Google Scholar] [CrossRef]
- Khan, N.; Zuhra, S.; Shah, Z.; Bonyah, E.; Khan, W.; Islam, S. Slip flow of Eyring-Powell nanoliquid film containing graphene nanoparticles. AIP Adv. 2018, 8, 115302. [Google Scholar] [CrossRef]
- Bhatti, M.A.; Tehseen, R.; Mohammad, A.; Mohamed, Y.Z. Entropy generation on MHD Eyring-Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef]
- Darbari, B.; Rashidi, S.; Abolfazli Esfahani, J. Sensitivity analysis of entropy generation in nanofluid flow inside a channel by response surface methodology. Entropy 2016, 18, 52. [Google Scholar] [CrossRef]
- Hassan, M.; Marin, M.; Abdullah, A.; Ellahi, R. Convection heat transfer flow of nanofluid in a porous medium over wavy surface. Phys. Lett. A 2018, 382, 2749–2753. [Google Scholar] [CrossRef]
- Ahmed, Z.; Nouman, I.; Tehseen, A.; Rahmat, E. The sustainable characteristic of Bio-bi-phase flow of peristaltic transport of MHD Jeffery fluid in human body. Sustainability 2018, 10, 2671. [Google Scholar]
- Ghofrane, S.; Sébastien, P. Further investigation on laminar forced convection of nanofluid flows in a uniformly heated pipe using direct numerical simulations. Appl. Sci. 2016, 6, 332. [Google Scholar]
- Hussain, F.; Ellahi, R.; Zeeshan, A. Mathematical models of electro magnetohydrodynamic Multiphase Flows Synthesis with Nanosized Hafnium Particles. Appl. Sci. 2018, 8, 275. [Google Scholar] [CrossRef]
- Pieters, G.J.M.; Duijn, C.J.V. Transient growth in linearly stable gravity-driven flow in porous media. Eur. J. Mech. 2006, 25, 83–94. [Google Scholar] [CrossRef]
- Machrafi, H.; Rednikov, A.; Colinet, P.; Dauby, P.C. Bénard instabilities in a binary-liquid layer evaporating into an inert gas: Stability of quasi-stationary and time-dependent reference profiles. Eur. Phys. J. Spec. Top. 2011, 192, 71–81. [Google Scholar] [CrossRef]
- Ozen, O.; Narayanan, R. The physics of evaporative and convective instabilities in bilayer systems. Linear Theory Phys. Fluids 2004, 16, 4644. [Google Scholar] [CrossRef]
- Lapwood, E.R. Convection of a fluid in a porous medium. Math. Proc. Camb. Philos. Soc. 1948, 44, 508–521. [Google Scholar] [CrossRef]
- Sulochana, C.; Ashwinkumar, G.P.; Sandeep, N. Similarity solution of 3D Casson nanofluid flow over a stretching sheet with convective boundary conditions. J. Niger. Math. Soc. 2016, 35, 128–141. [Google Scholar] [CrossRef]
- Taza, G.; Abdul, S.K.; Saeed, I.; Aisha, M.A.; Ilyas, K.; Ali, S.A.; Abdullah, K.A. Muradullah. Heat transfer investigation of the unsteady thin film flow of Williamson fluid past an inclined and oscillating moving plate. Appl. Sci. 2017, 7, 369. [Google Scholar]
- Jang, S.P.; Choi, S.U.S. Role of Brownian motion in the enhanced thermal conductivity of nanofluids. Appl. Phys. Lett. 2004, 84, 4316. [Google Scholar] [CrossRef]
- Machrafi, H.; Lebon, G. The role of several heat transfer mechanisms on the enhancement of thermal conductivity in nanofluids. Contin. Mech. Thermodyn. 2016, 28, 1461–1475. [Google Scholar] [CrossRef]
- Anoop, K.B.; Kabelac, S.; Sundararajan, T.; Das, S.K. Rheological and flow characteristics of nanofluids: Influence of electroviscous effects and particle agglomeration. J. Appl. Phys. 2009, 106, 034909. [Google Scholar] [CrossRef]
- Azizian, R.; Doroodchi, D.; Moghtaderi, B. Effect of Nanoconvection Caused by Brownian Motion on the Enhancement of Thermal Conductivity in Nanofluids. Ind. Eng. Chem. Res. 2012, 51, 1782–1789. [Google Scholar] [CrossRef]
- Hammed, K.; Haneef, M.; Shah, Z.; Islam, I.; Khan, W.; Asif, S.M. The Combined Magneto hydrodynamic and electric field effect on an unsteady Maxwell nanofluid Flow over a Stretching Surface under the Influence of Variable Heat and Thermal Radiation. Appl. Sci. 2018, 8, 160. [Google Scholar] [CrossRef]
- Muhammad, S.; Ali, G.; Shah, Z.; Islam, S.; Hussain, A. The Rotating Flow of Magneto Hydrodynamic Carbon Nanotubes over a Stretching Sheet with the Impact of Non-Linear Thermal Radiation and Heat Generation/Absorption. Appl. Sci. 2018, 8, 482. [Google Scholar] [CrossRef]












| Previous Results [43] | Previous Results [43] | |||||
|---|---|---|---|---|---|---|
| 1.0 | 0.1 | 0.5 | −1.489532 | −1.23942 | −0.695215 | −2.04702 |
| 1.1 | −1.564022 | −1.25192 | −1.564022 | −2.23996 | ||
| 1.2 | −1.682498 | −1.26417 | −2.647314 | −2.38904 | ||
| 0.2 | −1.731420 | −1.06979 | −1.892121 | −1.22441 | ||
| 0.3 | −1.544321 | −0.83279 | −1.744322 | −0.42052 | ||
| 0.4 | −1.324151 | −0.38181 | −1.212141 | 0.35420 | ||
| 0.6 | −1.829575 | −1.28570 | −1.829575 | −1.82788 | ||
| 0.7 | −2.083805 | −1.32900 | −2.083805 | −1.60457 | ||
| 0.8 | −2.310564 | −1.36945 | −2.310564 | −1.38981 |
| Previous Results [43] | ||||||
|---|---|---|---|---|---|---|
| 1.0 | 0.4 | 0.3 | 0.01 | 0.01 | 0.261896 | 0.119212 |
| 1.1 | 0.318272 | 0.120401 | ||||
| 1.2 | 0.379145 | 0.121608 | ||||
| 0.5 | - | 0.127300 | ||||
| 0.6 | - | 0.134579 | ||||
| 0.7 | 0.140705 | |||||
| 0.4 | - | 0.155214 | ||||
| 0.5 | - | 0.192457 | ||||
| 0.6 | - | 0.241744 | ||||
| 0.02 | 0.293770 | 0.155120 | ||||
| 0.06 | 0.274299 | 0.154747 | ||||
| 0.08 | 0.255629 | 0.154467 | ||||
| 0.03 | 0.285647 | 0.155044 | ||||
| 0.05 | 0.253739 | 0.154874 | ||||
| 0.07 | 0.222739 | 0.154704 |
| Le | Previous Results [43] | ||||
|---|---|---|---|---|---|
| 1.0 | 0.1 | 0.01 | 0.01 | 0.223924 | 0.291024 |
| 1.1 | 0.255507 | 0.293757 | |||
| 1.2 | 0.289266 | 0.296524 | |||
| 0.2 | - | 0.291022 | |||
| 0.3 | - | 0.291021 | |||
| 0.4 | - | 0.291019 | |||
| 0.02 | 0.213208 | 0.200865 | |||
| 0.03 | 0.144515 | 0.290705 | |||
| 0.04 | 0.089302 | 0.290545 | |||
| 0.02 | 0.272275 | 0.290847 | |||
| 0.03 | 0.286051 | 0.290671 | |||
| 0.04 | 0.290593 | 0.290494 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, A.S.; Nie, Y.; Shah, Z.; Dawar, A.; Khan, W.; Islam, S. Three-Dimensional Nanofluid Flow with Heat and Mass Transfer Analysis over a Linear Stretching Surface with Convective Boundary Conditions. Appl. Sci. 2018, 8, 2244. https://doi.org/10.3390/app8112244
Khan AS, Nie Y, Shah Z, Dawar A, Khan W, Islam S. Three-Dimensional Nanofluid Flow with Heat and Mass Transfer Analysis over a Linear Stretching Surface with Convective Boundary Conditions. Applied Sciences. 2018; 8(11):2244. https://doi.org/10.3390/app8112244
Chicago/Turabian StyleKhan, Abdul Samad, Yufeng Nie, Zahir Shah, Abdullah Dawar, Waris Khan, and Saeed Islam. 2018. "Three-Dimensional Nanofluid Flow with Heat and Mass Transfer Analysis over a Linear Stretching Surface with Convective Boundary Conditions" Applied Sciences 8, no. 11: 2244. https://doi.org/10.3390/app8112244
APA StyleKhan, A. S., Nie, Y., Shah, Z., Dawar, A., Khan, W., & Islam, S. (2018). Three-Dimensional Nanofluid Flow with Heat and Mass Transfer Analysis over a Linear Stretching Surface with Convective Boundary Conditions. Applied Sciences, 8(11), 2244. https://doi.org/10.3390/app8112244






