Four-Probe Bridges for In-Line Determination of Thickness and Sidewall Etch Angle of Surface Micromachined Thin Films
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
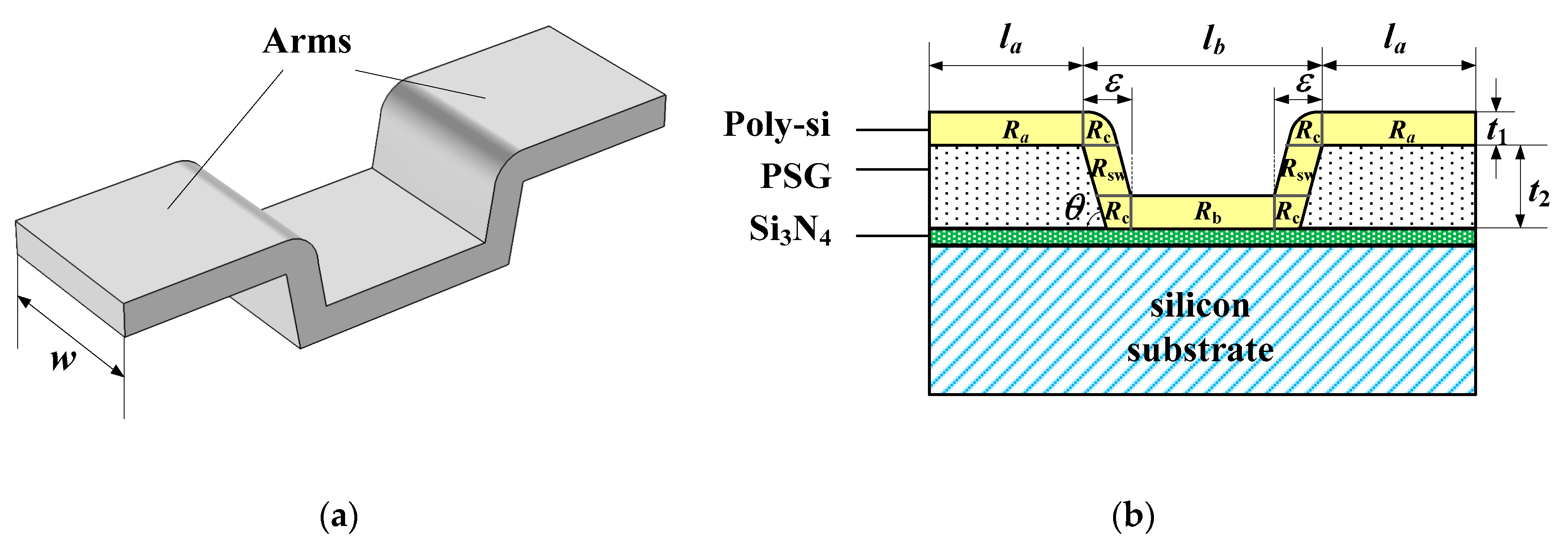
2.1. Resistance of the Step Structure
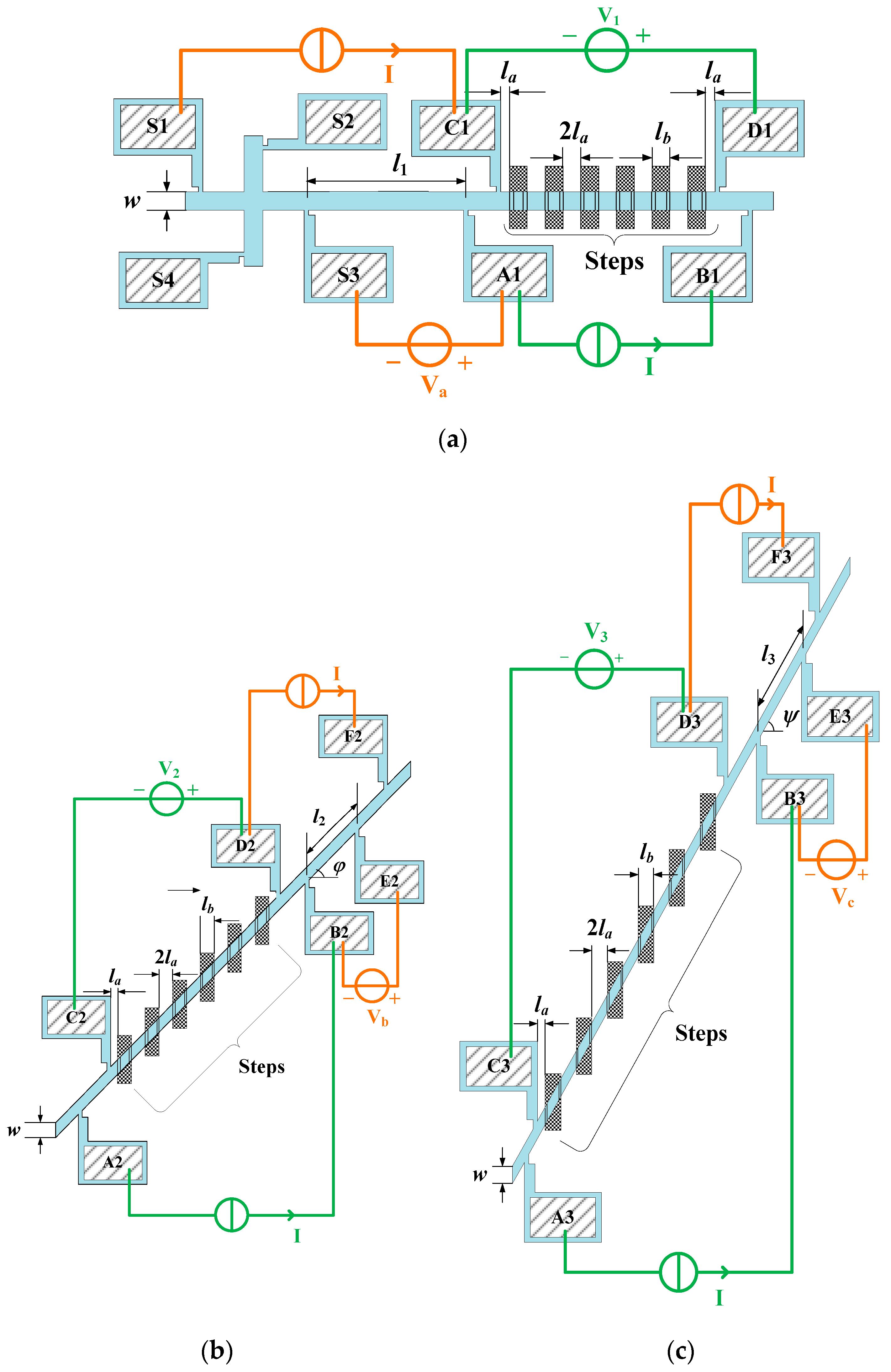
2.2. Test Structure and Extraction Model
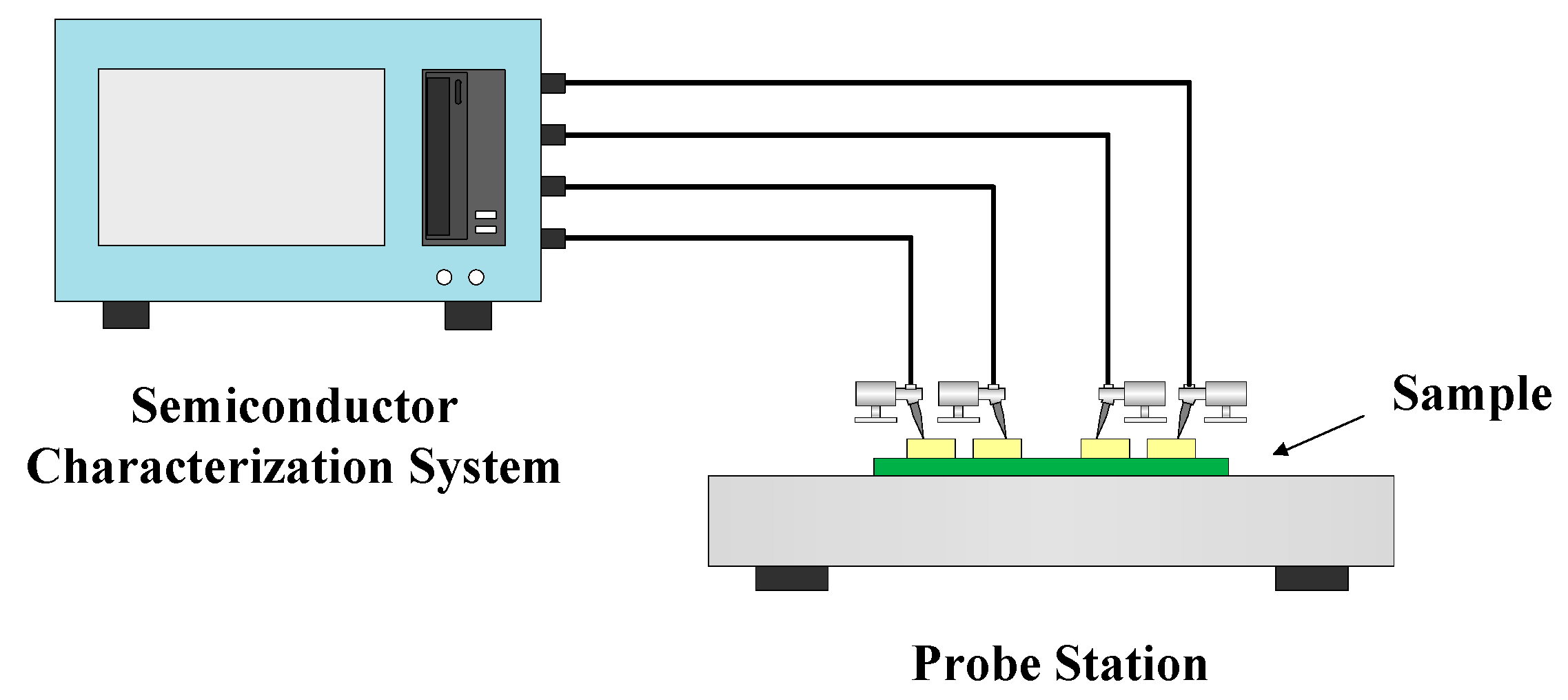
2.3. Fabrication Process and Experimental Setup
3. Results
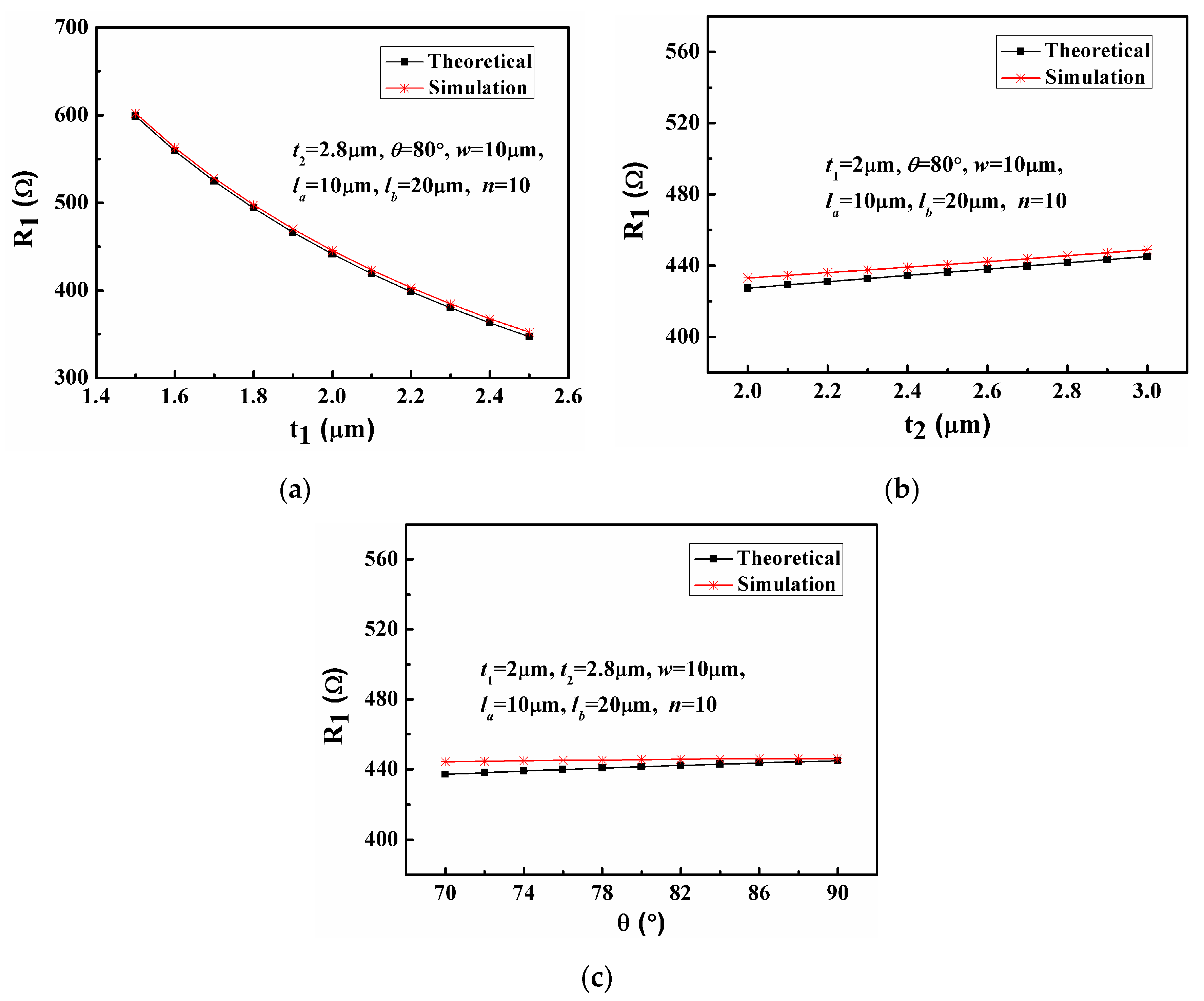
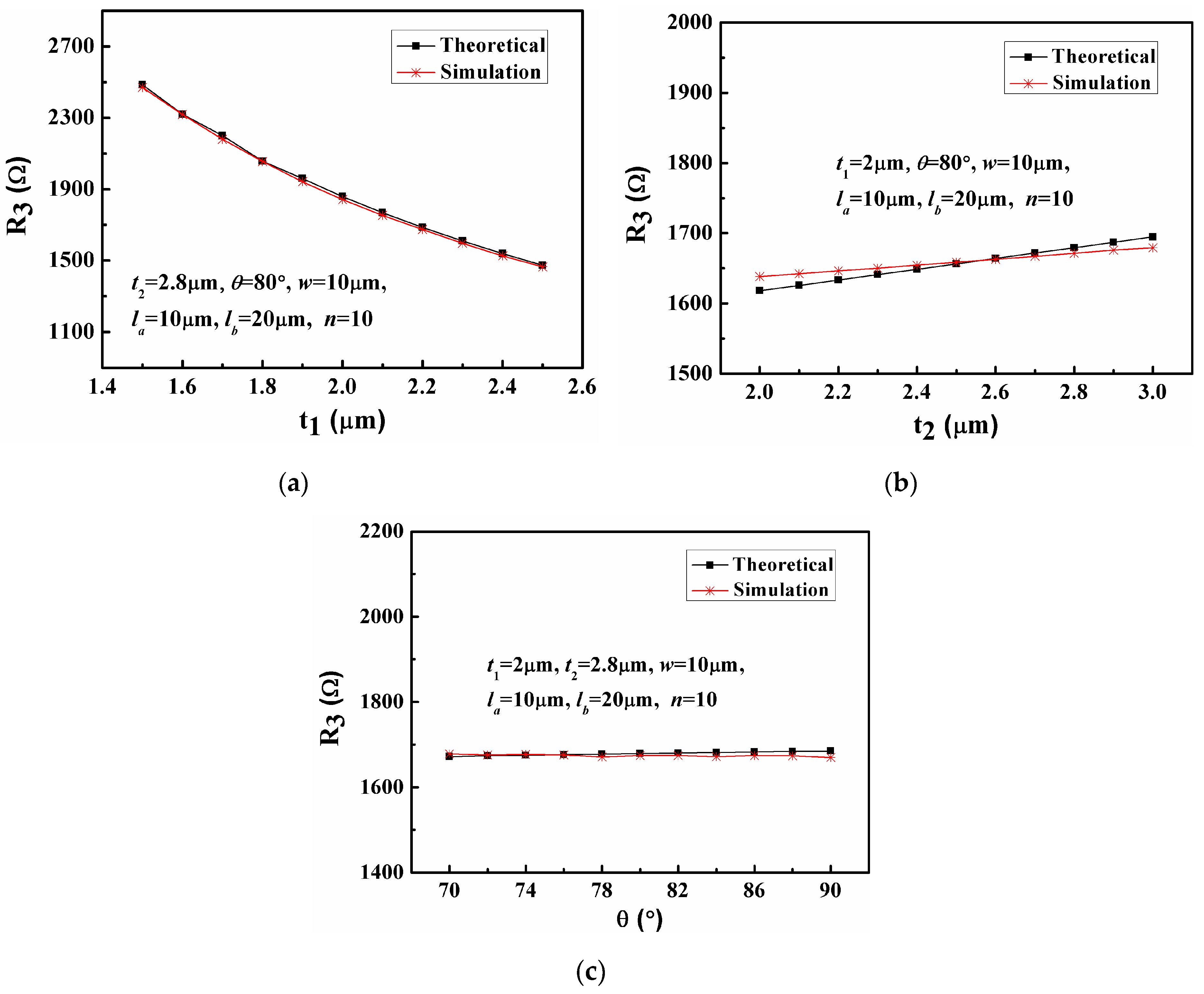
3.1. Simulation Results
3.2. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, C. Foundations of MEMS, 1st ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2006; p. 6. [Google Scholar]
- Hansen, S.T.; Ergun, A.S.; Liou, W.; Auld, B.A.; Khuri-Yakub, B.T. Wideband micromachined capacitive microphones with radio frequency detection. J. Acoust. Soc. Am. 2004, 116, 828–842. [Google Scholar] [CrossRef]
- Blanc, J.P.; Belleville, M.; Mieyeville, F.; Bono, H. Automatic evaluation of sensors geometrical parameters. In Proceedings of the Society of Photo-Optical Instrumentation Engineers (SPIE), Paris, France, 30 March–1 April 1999; pp. 94–102. [Google Scholar]
- Nguyen, C.T.C.; Howe, R.T. An integrated CMOS micromechanical resonator high-Q oscillator. IEEE J. Solid-State Circuits 1999, 34, 440–456. [Google Scholar] [CrossRef]
- Osterberg, P.M.; Senturia, S.D. M-TEST: A test chip for MEMS material property measurement using electrostatically actuated test structures. J. Microelectromech. Syst. 1997, 6, 107–118. [Google Scholar] [CrossRef]
- Ilic, B.; Krylov, S.; Craighead, H.G. Young’s modulus and density measurements of thin atomic layer deposited films using resonant nanomechanics. J. Appl. Phys. 2010, 108, 044317. [Google Scholar] [CrossRef]
- Liu, H.Y.; Wang, L. Measurements of thermal conductivity and the coefficient of thermal expansion for polysilicon thin films by using double-clamped beams. J. Micromech. Microeng. 2018, 28, 015010. [Google Scholar] [CrossRef]
- Jain, A.; Goodson, K.E. Measurement of the thermal conductivity and heat capacity of freestanding shape memory thin films using the 3 method. J. Heat Trans. 2008, 130, 102402. [Google Scholar] [CrossRef]
- Bennett, J.M.; Dancy, J.H. Stylus profiling instrument for measuring statistical properties of smooth optical surfaces. Appl. Opt. 1981, 20, 1785–1802. [Google Scholar] [CrossRef] [PubMed]
- Raley, N.F.; Van Duzer, T. Simple, nondestructive silicon membrane thickness measurement using a scanning electron microscope. J. Appl. Phys. 1985, 58, 280–286. [Google Scholar] [CrossRef]
- Henck, S.A. In situ real-time ellipsometry for film thickness measurement and control. J. Vac. Sci. Technol. A 1992, 10, 934–938. [Google Scholar] [CrossRef]
- Lockyer, C. A new interferometric method for measuring the thickness of thin films. J. Sci. Instrum. 1967, 44, 393–394. [Google Scholar] [CrossRef]
- de Groot, P.J.; de Lega, X.C. Transparent film profiling and analysis by interference microscopy. In Proceedings of the Interferometry XIV: Applications, San Diego, CA, USA, 10–14 August 2008; Volume 7064. [Google Scholar] [CrossRef]
- Dong, J.T.; Lu, R.S. Sensitivity analysis of thin-film thickness measurement by vertical scanning white-light interferometry. Appl. Opt. 2012, 51, 5668–5675. [Google Scholar] [CrossRef] [PubMed]
- Kuehnhold, P.; Nolvi, A.; Tereschenko, S. Transparent layer thickness measurement using low-coherence interference microscopy. In Proceedings of the Optical Measurement Systems for Industrial Inspection IX, Munich, Germany, 21–25 June 2015; Volume 9525. [Google Scholar]
- Kim, M.G.; Pahk, H.J. Fast and reliable measurement of thin film thickness profile based on wavelet transform in spectrally resolved white-light interferometry. Int. J. Precis. Eng. Manuf. 2018, 19, 213–219. [Google Scholar] [CrossRef]
- Lindner, M.; Schmid, M. Thickness measurement methods for physical vapor deposited aluminum coatings in packaging applications: A review. Coatings 2017, 7, 9. [Google Scholar] [CrossRef]
- Shaporin, A.; Streit, P.; Specht, H.; Mehner, J.; Dötzel, W. Novel test structures for characterization of microsystems parameters at wafer level. In Proceedings of the Reliability, Packaging, Testing, and Characterization of MEMS/MOEMS and Nanodevices VIII, San Diego, CA, USA, 24–29 January 2009; Volume 7206. [Google Scholar] [CrossRef]
- Chee, J.L.; Clark, J.V. The effect of noise on capacitive measurements of MEMS geometries. In Proceedings of the Society for Experimental Mechanics Series Conference, Indianapolis, IN, USA, 7–10 June 2010; pp. 43–51. [Google Scholar] [CrossRef]
- Gupta, R.K. Electronically probed measurements of MEMS geometries. J. Microelectromech. Syst. 2000, 9, 380–389. [Google Scholar] [CrossRef]
- Gennat, M.; Meinig, M.; Shaporin, A.; Kurth, S.; Rembe, C.; Tibken, B. Determination of parameters with uncertainties for quality control in MEMS fabrication. J. Microelectromech. Syst. 2013, 22, 613–624. [Google Scholar] [CrossRef]
- Wille, H.; Burte, E.; Ryssel, H. Simulation of the step coverage for chemical vapor deposited silicon dioxide. J. Appl. Phys. 1992, 71, 3532–3537. [Google Scholar] [CrossRef]
- Hagedorn, F.B.; Hall, P.M. Right-angle bends in thin strip conductors. J. Appl. Phys. 1963, 34, 128–133. [Google Scholar] [CrossRef]
- Hall, P.M. Resistance calculations for thin film patterns. Thin Solid Films 1968, 1, 277–295. [Google Scholar] [CrossRef]
- Hall, P.M. Resistance calculations for thin film rectangles. Thin Solid Films 1997, 300, 256–264. [Google Scholar] [CrossRef]
- Enderling, S.; Smith, C.L.S.; Dicks, M.H.; Stevenson, J.T.M.; Mitkova, M.; Kozicki, M.N.; Walton, A.J. Sheet resistance measurement of non-standard cleanroom materials using suspended Greek cross test structures. IEEE Trans. Semicond. Manuf. 2006, 19, 2–9. [Google Scholar] [CrossRef]
- Vernsel, W. Analysis of the Greek cross, a Van der Pauw structure with finite contacts. Solid State Electron. 1979, 22, 911–914. [Google Scholar] [CrossRef]
- Buehler, M.G.; Grant, S.D.; Thurber, W.R. Bridge and Van der Pauw sheet resistors for characterizing the line width of conducting layers. J. Electrochem. Soc. 1978, 125, 650–654. [Google Scholar] [CrossRef]
- Cowen, A.; Hardy, B.; Mahadevan, R.; Wilcenski, S. PolyMUMPs Design Handbook: Revision 13.0; MEMSCAP Inc.: Durham, NC, USA, 2012. [Google Scholar]



| Samples | Parameters | Four-Probe Bridges | SEM | Error |
|---|---|---|---|---|
| Sample 1a | RS | 12.26 Ω/sq | - | - |
| w | 10.121 µm | - | - | |
| t1 | 2.083 µm | 1.995 μm | 4.41% | |
| t2 | 2.128 µm | 2.003 µm | 6.22% | |
| θ | 77.64° | 80.77° | 3.88% | |
| Sample 2a | RS | 11.97 Ω/sq | - | - |
| w | 10.081 µm | - | - | |
| t1 | 2.096 µm | 1.997 µm | 4.96% | |
| t2 | 2.144 µm | 2.005 µm | 6.91% | |
| θ | 77.04° | 80.35° | 4.12% | |
| Sample 3a | RS | 12.01 Ω/sq | - | - |
| w | 15.132 µm | - | - | |
| t1 | 2.069 µm | 1.993 µm | 3.83% | |
| t2 | 2.153 µm | 2.002 µm | 7.52% | |
| θ | 77.58° | 80.17° | 3.23% | |
| Sample 4a | RS | 12.33 Ω/sq | - | - |
| w | 15.111 µm | - | - | |
| t1 | 2.081 µm | 2.001 µm | 3.99% | |
| t2 | 2.131 µm | 2.003 µm | 6.37% | |
| θ | 78.36° | 80.44° | 2.59% | |
| Sample 5a | RS | 11.85 Ω/sq | - | - |
| w | 20.106 µm | - | - | |
| t1 | 2.073 µm | 2.001 µm | 3.58% | |
| t2 | 2.152 µm | 2.008 µm | 7.17% | |
| θ | 76.92° | 79.89° | 3.72% |
| Samples | Parameters | Four-Probe Bridges | SEM | Error |
|---|---|---|---|---|
| Sample 1b | RS | 22.07 Ω/sq | - | - |
| w | 10.074 µm | - | - | |
| t1 | 1.626 µm | 1.512 µm | 7.54% | |
| t2 | 2.887 µm | 2.773 µm | 4.12% | |
| θ | 76.03° | 80.22° | 5.22% | |
| Sample 2b | RS | 21.75 Ω/sq | - | - |
| w | 10.134 µm | - | - | |
| t1 | 1.624 µm | 1.518 µm | 6.98% | |
| t2 | 2.910 µm | 2.776 µm | 4.82% | |
| θ | 75.82° | 80.64° | 5.98% | |
| Sample 3b | RS | 22.17 Ω/sq | - | - |
| w | 15.290 µm | - | - | |
| t1 | 1.594 µm | 1.510 µm | 5.59% | |
| t2 | 2.893 µm | 2.773 µm | 4.33% | |
| θ | 75.29° | 80.96° | 7.01% | |
| Sample 4b | RS | 21.89 Ω/sq | - | - |
| w | 15.108 µm | - | - | |
| t1 | 1.607 µm | 1.515 µm | 6.07% | |
| t2 | 2.891 µm | 2.778 µm | 4.07% | |
| θ | 77.56° | 81.03° | 4.28% | |
| Sample 5b | RS | 21.93 Ω/sq | - | - |
| w | 20.090 µm | - | - | |
| t1 | 1.619 µm | 1.511 µm | 7.18% | |
| t2 | 2.881 µm | 2.773 µm | 3.90% | |
| θ | 76.15° | 80.88° | 5.85% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhang, Z.; Chen, J. Four-Probe Bridges for In-Line Determination of Thickness and Sidewall Etch Angle of Surface Micromachined Thin Films. Appl. Sci. 2018, 8, 2424. https://doi.org/10.3390/app8122424
Liu H, Zhang Z, Chen J. Four-Probe Bridges for In-Line Determination of Thickness and Sidewall Etch Angle of Surface Micromachined Thin Films. Applied Sciences. 2018; 8(12):2424. https://doi.org/10.3390/app8122424
Chicago/Turabian StyleLiu, Haiyun, Zhen Zhang, and Jiaqi Chen. 2018. "Four-Probe Bridges for In-Line Determination of Thickness and Sidewall Etch Angle of Surface Micromachined Thin Films" Applied Sciences 8, no. 12: 2424. https://doi.org/10.3390/app8122424
APA StyleLiu, H., Zhang, Z., & Chen, J. (2018). Four-Probe Bridges for In-Line Determination of Thickness and Sidewall Etch Angle of Surface Micromachined Thin Films. Applied Sciences, 8(12), 2424. https://doi.org/10.3390/app8122424





