Towards GW-Scale Isolated Attosecond Pulse Far beyond Carbon K-Edge Driven by Mid-Infrared Waveform Synthesizer
Abstract
:1. Introduction
2. Results and Discussion
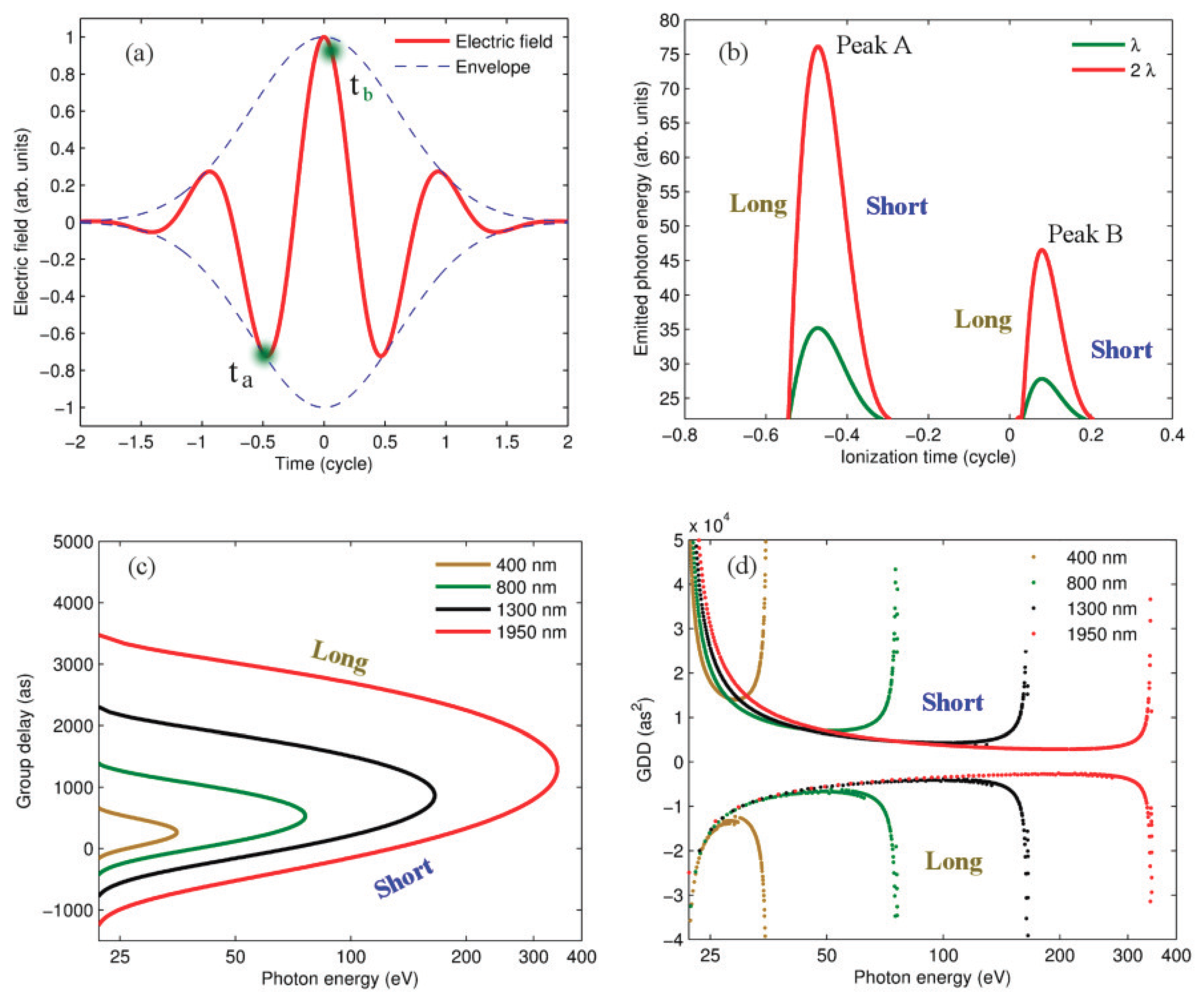
2.1. Advantages of an MIR Waveform Synthesizer for Generating an Isolated Attosecond Pulse
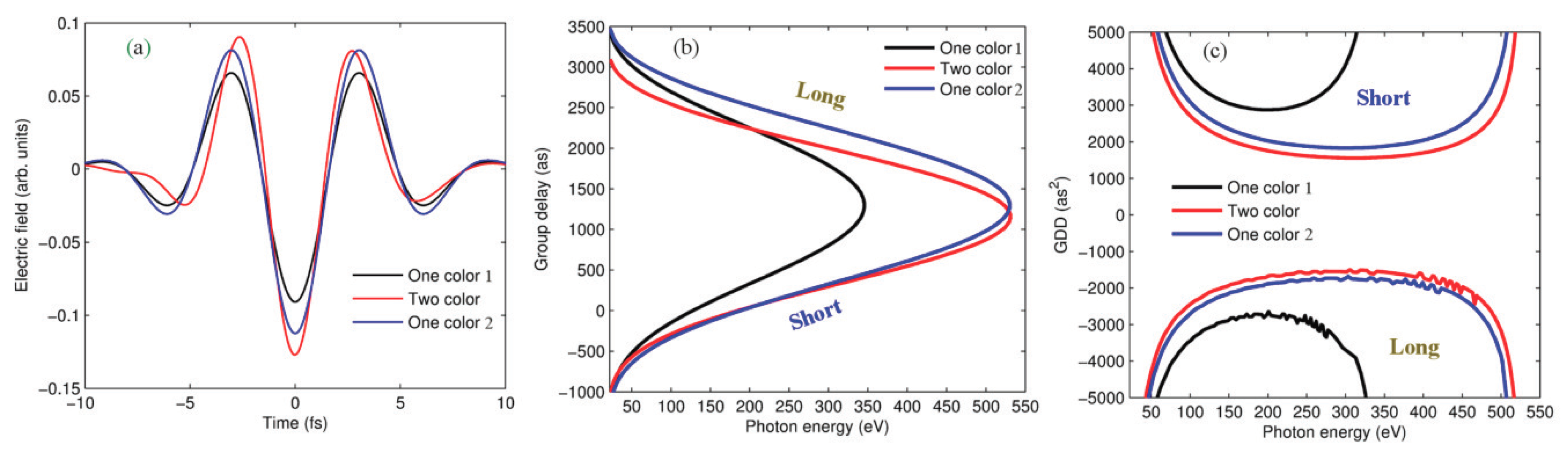
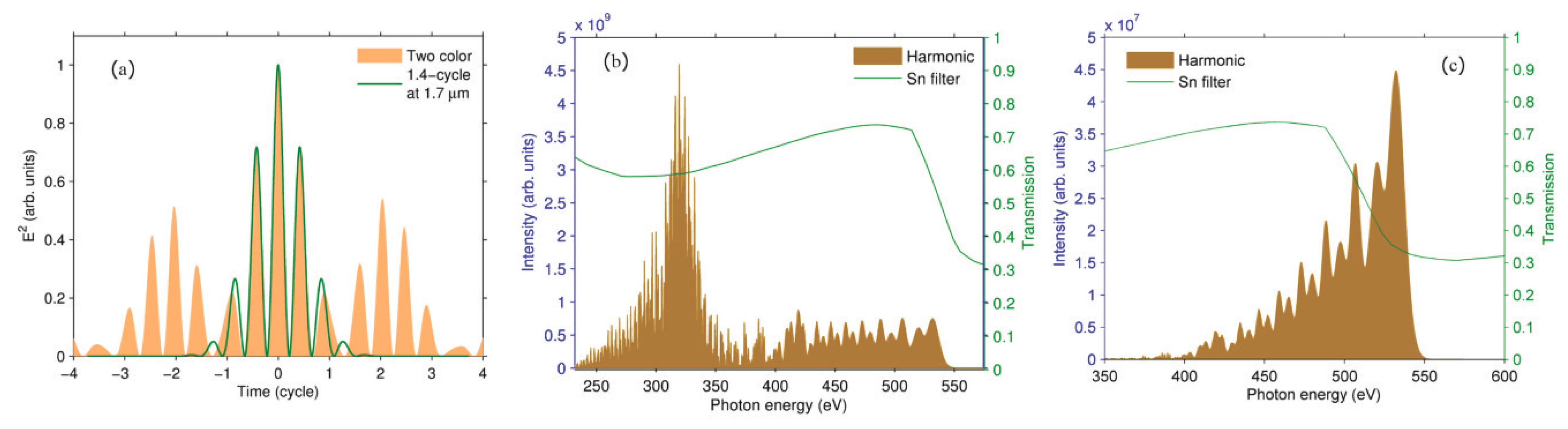
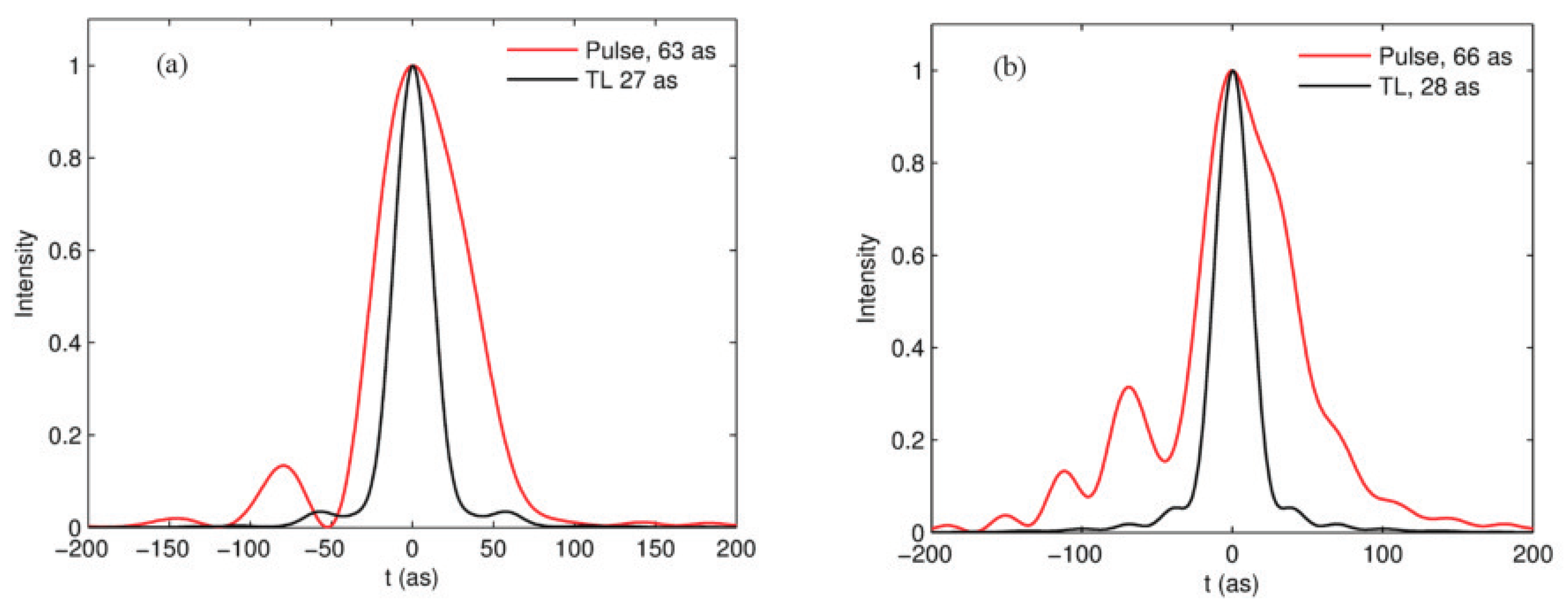
2.2. Generation of Water Window IAPs from an MIR Waveform Synthesizer
2.2.1. Simulation Method
2.2.2. Simulation Results
3. Design for a TW-Scale MIR Waveform Synthesizer for Generating Water Window IAP
3.1. TW-Class MIR Laser Source Based on DC-OPA
3.2. Stabilizing the Delay Jitter and Phase Jitter in the Synthesizer
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Li, J.; Ren, X.; Yin, Y.; Zhao, K.; Chew, A.; Cheng, Y.; Cunningham, E.; Wang, Y.; Hu, S.; Wu, Y.; et al. 53-attosecond X-ray pulses reach the carbon K-edge. Nat. Commun. 2017, 8, 186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gaumnitz, T.; Jain, A.; Pertot, Y.; Huppert, M.; Jordan, I.; Aardana-Lamas, F.; Jakob Wörner, H. Streaking of 43-attosecond soft-X-ray pulses generated by a passively CEP-stable mid-infrared driver. Opt. Express 2017, 25, 27506–27518. [Google Scholar] [CrossRef]
- Goulielmakis, E.; Loh, Z.-H.; Wirth, A.; Santra, R.; Rohringer, N.; Yakovlev, V.S.; Zherebtsov, S.; Pfeifer, T.; Azzeer, A.M.; Kling, M.F.; et al. Real-time observation of valence electron motion. Nature 2010, 466, 739–743. [Google Scholar] [CrossRef]
- He, L.; Zhang, Q.; Lan, P.; Cao, W.; Zhu, X.; Zhai, C.; Wang, F.; Shi, W.; Li, M.; Bian, X.; et al. Monitoring ultrafast vibrational dynamics of isotopic molecules with frequency modulation of high-order harmonics. Nat. Commun. 2018, 9, 1108. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Lan, P.; Le, A.T.; Wang, B.; Wang, B.; Zhu, X.; Lu, P.; Lin, C.D. Real-time observation of molecular spinning with angular high-harmonic spectroscopy. Phys. Rev. Lett. 2018, 121, 163201. [Google Scholar] [CrossRef]
- Sommer, A.; Bothschafter, E.M.; Sato, S.A.; Jakubeit, C.; Latka, T.; Razskazovskaya, O.; Fattahi, H.; Jobst, M.; Schweinberger, W.; Shirvanyan, V.; et al. Attosecond nonlinear polarization and light-matter energy transfer in solids. Nature 2016, 534, 86–90. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Kienberger, R.; Spielmann, C.; Reider, G.A.; Milosevic, N.; Brabec, T.; Corkum, P.; Heinzmann, U.; Drescher, M.; Krausz, F. Attosecond metrology. Nature 2001, 414, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Heyl, C.M.; Arnold, C.L.; Couairon, A.; L’Huillier, A. Introduction to macroscopic power scaling principles for high-order harmonic generation. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 013001. [Google Scholar] [CrossRef]
- Spielmann, C.; Burnett, N.H.; Sartania, S.; Koppitsch, R.; Schnürer, M.; Kan, C.; Lenzner, M.; Wobrauschek, P.; Krausz, F. Generation of Coherent X-rays in the Water Window Using 5-Femtosecond Laser Pulses. Science 1997, 278, 661–664. [Google Scholar] [CrossRef]
- Seres, C.; Seres, J.; Krausz, F.; Spielmann, C. Generation of Coherent Soft-X-ray Radiation Extending Far beyond the Titanium L Edge. Phys. Rev. Lett. 2004, 92, 163002. [Google Scholar] [CrossRef]
- Ishii, N.; Kaneshima, K.; Kitano, K.; Kanai, T.; Watanabe, S.; Itatani, J. Sub-two-cycle, Carrier-envelope phase-dependent high harmonic generation in the water window using few-cycle infrared pulses. Nat. Commun. 2014, 5, 3331. [Google Scholar] [CrossRef] [PubMed]
- Silva, F.; Teichmann, S.M.; Cousin, S.L.; Hemmer, M.; Biegert, J. Spatiotemporal isolation of attosecond soft X-ray pulses in the water window. Nat. Commun. 2015, 6, 6611. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takahashi, E.J.; Kanai, T.; Ishikawa, K.L.; Nabekawa, Y.; Midorikawa, K. Coherent water window x ray by phase-matched high-order harmonic generation in neutral media. Phys. Rev. Lett. 2008, 101, 253901. [Google Scholar] [CrossRef]
- Takahashi, E.J.; Kanai, T.; Midorikawa, K. High-order harmonic generation by an ultrafast infrared pulse- Efficient generation of a coherent water window X-ray. Appl. Phys. B 2010, 100, 29–41. [Google Scholar] [CrossRef]
- Brizuela, F.; Heyl, C.M.; Rudawski, P.; Kroon, D.; Rading, L.; Dahlström, J.M.; Mauritsson, J.; Johnsson, P.; Arnold, C.L.; L’Huillier, A. Efficient high-order harmonic generation boosted by below-threshold harmonics. Sci. Rep. 2013, 3, 1410. [Google Scholar] [CrossRef] [Green Version]
- Seres, J.; Yakovlev, V.S.; Seres, E.; Streli, C.; Wobrauschek, P.; Spielmann, C.; Krausz, F. Coherent superposition of laser-driven soft-X-ray harmonics from successive sources. Nat. Phys. 2007, 3, 878–883. [Google Scholar] [CrossRef]
- Serrat, C.; Roca, D.; Seres, J. Coherent amplification of attosecond light pulses in the water-window spectral region. Opt. Express 2015, 23, 4867–4872. [Google Scholar] [CrossRef]
- Serrat, C.; Roca, D.; Budesca, J.M.; Seres, J.; Seres, E.; Aurand, B.; Hoffmann, A.; Namba, S.; Kuehl, T.; Spielmann, C. Avalanche of stimulated forward scattering in high harmonic generation. Opt. Express 2016, 24, 8028–8044. [Google Scholar] [CrossRef]
- Bredtmann, T.; Chelkowski, S.; Bandrauk, A.D.; Ivanov, M. XUV lasing during strong-field-assisted transient absorption in molecules. Phys. Rev. A 2016. [Google Scholar] [CrossRef]
- Takahashi, E.; Nabekawa, Y.; Otsuka, T.; Obara, M.; Midorikawa, K. Generation of highly coherent submicrojoule soft x rays by high-order harmonics. Phys. Rev. A 2002. [Google Scholar] [CrossRef]
- Takahashi, E.; Tosa, V.; Nabekawa, Y.; Midorikawa, K. Experimental and theoretical analyses of a correlation between pump-pulse propagation and harmonic yield in a long-interaction medium. Phys. Rev. A 2003, 68, 023808. [Google Scholar] [CrossRef]
- Doumy, G.; Wheeler, J.; Roedig, C.; Chirla, R.; Agostini, P.; DiMauro, L.F. Attosecond synchronization of high-order harmonics from midinfrared drivers. Phys. Rev. Lett. 2009, 102, 093002. [Google Scholar] [CrossRef] [PubMed]
- Chang, Z.; Corkum, P.B.; Leone, S.R. Attosecond optics and technology: Progress to date and future prospects. J. Opt. Soc. Am. B 2016, 33, 1081–1097. [Google Scholar] [CrossRef]
- Trallero-Herrero, C.; Kajumba, N.; Bandulet, H.-C.; Comtois, D.; Légaré, F.; Giguère, M.; Kieffer, J.-C.; Corkum, P.B.; Villeneuve, D.M. Wavelength Scaling of High Harmonic Generation Efficiency. Phys. Rev. Lett. 2009, 103, 073902. [Google Scholar] [CrossRef] [Green Version]
- Cousin, S.L.; Palo, N.D.; Buades, B.; Teichmann, S.M.; Reduzzi, M.; Devetta, M.; Kheifets, A.; Sansone, G.; Biegert, J. Attosecond streaking in the water window: A new regime of attosecond pulse characterization. Phys. Rev. X 2017, 7, 041030. [Google Scholar] [CrossRef]
- Schiessl, K.; Ishikawa, K.L.; Persson, E.; Burgdörfer, J. Quantum path interference in the wavelength dependence of high-harmonic generation. Phys. Rev. Lett. 2007, 99, 253903. [Google Scholar] [CrossRef]
- Zhang, J.; Mak, K.F.; Nag, N.; Seidel, M.; Bauer, D. Dirk Sutter, Vladimir Pervak, Ferenc Krausz and Oleg Pronin, Multi-mW, few-cycle mid-infrared continuum spanning from 500 to 2250 cm−1. Light Sci. Appl. 2017. [Google Scholar] [CrossRef]
- Kaneshima, K.; Ishii, N.; Takeuchi, K.; Itatani, J. Generation of carrier-envelope phase-stable mid-infrared pulses via dual-wavelength optical parametric amplification. Opt. Express 2016, 24, 8660–8665. [Google Scholar] [CrossRef]
- Sanchez, D.; Hemmer, M.; Baudisch, M.; Cousin, S.L.; Zawilski, K.; Schunemann, P.; Chalus, O.; Simon-boisson, C.; Biegert, J. 7 μm, ultrafast, sub-millijoule-level mid-infrared optical parametric chirped pulse amplifier pumped at 2 μm. Optica 2016, 3, 147–150. [Google Scholar] [CrossRef]
- Henke, B.L.; Gullikson, E.M.; Davis, J.C. X-ray interactions: Photoabsorption, scattering, transmission and reflection E= 50-30,000 eV, Z = 1-92. At. Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Jin, C.; Wang, G.; Wei, H.; Le, A.-T.; Lin, C.D. Waveforms for optimal sub-keV high-order harmonics with synthesized two- or three-colour laser fields. Nat. Commun. 2014, 5, 4003. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, E.J.; Lan, P.; Mücke, O.D.; Nabekawa, Y.; Midorikawa, K. Infrared two-color multicycle laser field synthesis for generating an intense attosecond pulse. Phys. Rev. Lett. 2010, 104, 233901. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, E.J.; Lan, P.; Mücke, O.D.; Nabekawa, Y.; Midorikawa, K. Attosecond nonlinear optics using gigawatt-scale isolated attosecond pulses. Nat. Commun. 2013, 4, 2691. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lan, P.; Takahashi, E.J.; Midorikawa, K. Isolated-attosecond-pulse generation with infrared double optical gating. Phys. Rev. A 2011, 83, 063839. [Google Scholar] [CrossRef]
- Takahashi, E.J.; Lan, P.; Mücke, O.D.; Nabekawa, Y. Midorikawa, K. Nonlinear attosecond metrology by intense isolated attosecond pulses. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 8800112. [Google Scholar] [CrossRef]
- Krauss, G.; Lohss, S.; Hanke, T.; Sell, A.; Eggert, S. Rupert Huber and Alfred Leitenstorfer, Synthesis of a single cycle of light with compact erbium-doped fibre technology. Nat. Photonics 2009, 4, 33–36. [Google Scholar] [CrossRef]
- Chia, S.-H.; Cirmi, G.; Fang, S.; Rossi, G.M.; Mücke, O.D.; Kärtner, F.X. Two-octave-spanning dispersion-controlled precision optics for sub-optical-cycle waveform synthesizers. Optica 2014, 1, 315–322. [Google Scholar] [CrossRef]
- Huang, S.-W.; Cirmi, G.; Moses, J.; Hong, K.-H.; Bhardwaj, S.; Birge, J.R.; Chen, L.-J.; Li, E.; Eggleton, B.J.; Cerullo, G.; et al. High-energy pulse synthesis with sub-cycle waveform control for strong-field physics. Nat. Photonics 2011, 5, 475–479. [Google Scholar] [CrossRef] [Green Version]
- Xue, B.; Takahashi, E.J.; Fu, Y.; Midorikawa, K. Intense attosecond soft X-ray pulse by a high-energy three-channel waveform synthesizer. Opt. Soc. Am. Tech. Dig. 2017. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong-field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Zeng, Z.; Zou, P.; Zhang, L.; Li, X.; Liu, P.; Li, R.; Xu, Z. Dynamic chirp control and pulse compression for attosecond high-order harmonic emission. Phys. Rev. Lett. 2009, 103, 043904. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.; Zheng, Y.; Cheng, Y.; Li, R.; Xu, Z. Attosecond pulse generation driven by a synthesized laser field with two pulses of controlled related phase. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 074004. [Google Scholar] [CrossRef]
- Kohler, M.C.; Keitel, C.H.; Hatsagortsyan, K.Z. Attochirp-free high-order harmonic generation. Opt. Express 2011, 19, 4411–4420. [Google Scholar] [CrossRef] [Green Version]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2131. [Google Scholar] [CrossRef] [PubMed]
- Balcou, P.; Salières, P.; L’Huillier, A.; Lewenstein, M. Generalized phase-matching conditions for high harmonics: The role of field-gradient forces. Phys. Rev. A 1997, 55, 3204–3210. [Google Scholar] [CrossRef]
- Ammosov, M.V.; Delone, N.B.; Krainov, V.P. Tunnel ionization of complex atoms and of atomic ions in an altemating electromagnetic field. Sov. Phys. JETP 1986, 64, 1191–1194. [Google Scholar] [CrossRef]
- Priori, E.; Cerullo, G.; Nisoli, M.; Stagira, S.; Silvestri, S.D.; Villoresi, P.; Poletto, L.; Ceccherini, P.; Altucci, C.; Bruzzese, R.; et al. Nonadiabatic three-dimensional model of high-order harmonic generation in the few-optical-cycle regime. Phys. Rev. A 2000, 61, 063801. [Google Scholar] [CrossRef]
- Lan, P.; Lu, P.; Li, Q.; Li, F.; Hong, W.; Zhang, Q. Macroscopic effects for quantum control of broadband isolated attosecond pulse generation with a two-color field. Phys. Rev. A 2009, 79, 043413. [Google Scholar] [CrossRef]
- Xiong, H.; Xu, H.; Fu, Y.; Yao, J.; Zeng, B.; Chu, W.; Cheng, Y.; Xu, Z.; Takahashi, E.J.; Midorikawa, K.; et al. Generation of a coherent x ray in the water window region at 1 kHz repetition rate using a mid-infrared pump source. Opt. Lett. 2009, 34, 1747–1749. [Google Scholar] [CrossRef] [PubMed]
- Stein, G.J.; Keathley, P.D.; Krogen, P.; Liang, H.; Siqueira, J.P.; Chang, C.-L.; Lai, C.-J.; Hong, K.-H.; Laurent, G.M.; Kärtner, F.X. Water-window soft X-ray high-harmonic generation up to the nitrogen K-edge driven by a kHz, 2.1 μm OPCPA source. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 155601. [Google Scholar] [CrossRef]
- Fu, Y.; Midorikawa, K.; Takahashi, E.J. Towards a petawatt-class fewcycle infrared laser system via dual-chirped optical parametric amplification. Sci. Rep. 2018, 8, 7692. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Takahashi, E.J.; Mücke, O.D.; Lu, P.; Midorikawa, K. Dual-chirped optical parametric amplification for generating few hundred mJ infrared pulses. Opt. Express 2011, 9, 7190–7212. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Takahashi, E.J.; Midorikawa, K. High-energy infrared femtosecond pulses generated by dual-chirped optical parametric amplification. Opt. Lett. 2015, 40, 5082–5085. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Takahashi, E.J.; Zhang, Q.; Lu, P.; Midorikawa, K. Optimization and characterization of dual-chirped optical parametric amplification. J. Opt. 2015, 17, 124001. [Google Scholar] [CrossRef]
- Fu, Y.; Takahashi, E.J.; Midorikawa, K. Energy Scaling of Infrared Femtosecond Pulses by Dual-Chirped Optical Parametric Amplification. IEEE Photonics J. 2017, 9, 1503108. [Google Scholar] [CrossRef]
- Fu, Y.; Xue, B.; Midorikawa, K.; Takahashi, E.J. TW-scale mid-infrared pulses near 3.3 μm directly generated by dual-chirped optical parametric amplification. Appl. Phys. Lett. 2018, 112, 241105. [Google Scholar] [CrossRef]
- Takahashi, E.J.; Fu, Y.; Midorikawa, K. Carrier-envelope phase stabilization of a 16 TW, 10 Hz Ti:sapphire laser. Opt. Lett. 2015, 40, 4835–4838. [Google Scholar] [CrossRef]
- Ishii, N.; Kaneshima, K.; Kitano, K.; Kanai, T.; Watanabe, S.; Itatani, J. Sub-two-cycle, carrier-envelope phase-stable, intense optical pulses at 1.6 μm from a BiB3O6 optical parametric chirped-pulse amplifier. Opt. Lett. 2012, 37, 4182–4184. [Google Scholar] [CrossRef]
- Yin, Y.; Li, J.; Ren, X.; Zhao, K.; Wu, Y.; Cunningham, E.; Chang, Z. High-efficiency optical parametric chirped-pulse amplifier in BiB3O6 for generation of 3 mJ, two-cycle, carrier-envelope-phase-stable pulses at 1.7 μm. Opt. Lett. 2016, 41, 1142–1145. [Google Scholar] [CrossRef]
- Mücke, O.D.; Fang, S.; Cirmi, G.; Rossi, G.M.; Chia, S.-H.; Ye, H.; Yang, Y.; Mainz, R.; Manzoni, C.; Farinello, P.; et al. Toward Waveform Nonlinear Optics Using Multimillijoule Sub-Cycle Waveform Synthesizers. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 8700712. [Google Scholar] [CrossRef]
- Mainz, R.; Rossi, G.M.; Cirmi, G.; Yang, Y.; Mücke, O.D.; Kärtner, F.X. High-dynamic-range arrival time control for flexible, accurate and precise parametric sub-cycle waveform synthesis. Opt. Express 2017, 25, 3052–3068. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Takahashi, E.J.; Midorikawa, K. Indirect high-bandwidth stabilization of carrier envelope phase of a high-energy, low-repetition rate laser. Opt. Express 2016, 24, 13276–13287. [Google Scholar] [CrossRef] [PubMed]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Yuan, H.; Midorikawa, K.; Lan, P.; Takahashi, E.J. Towards GW-Scale Isolated Attosecond Pulse Far beyond Carbon K-Edge Driven by Mid-Infrared Waveform Synthesizer. Appl. Sci. 2018, 8, 2451. https://doi.org/10.3390/app8122451
Fu Y, Yuan H, Midorikawa K, Lan P, Takahashi EJ. Towards GW-Scale Isolated Attosecond Pulse Far beyond Carbon K-Edge Driven by Mid-Infrared Waveform Synthesizer. Applied Sciences. 2018; 8(12):2451. https://doi.org/10.3390/app8122451
Chicago/Turabian StyleFu, Yuxi, Hua Yuan, Katsumi Midorikawa, Pengfei Lan, and Eiji J. Takahashi. 2018. "Towards GW-Scale Isolated Attosecond Pulse Far beyond Carbon K-Edge Driven by Mid-Infrared Waveform Synthesizer" Applied Sciences 8, no. 12: 2451. https://doi.org/10.3390/app8122451
APA StyleFu, Y., Yuan, H., Midorikawa, K., Lan, P., & Takahashi, E. J. (2018). Towards GW-Scale Isolated Attosecond Pulse Far beyond Carbon K-Edge Driven by Mid-Infrared Waveform Synthesizer. Applied Sciences, 8(12), 2451. https://doi.org/10.3390/app8122451




