An Interdisciplinary Approach to the Nanomanipulation of SiO₂ Nanoparticles: Design, Fabrication and Feasibility

Abstract

Although some recent developments in nanotechnology made the prospects of a direct mechanical manipulation of micro- or nano-objects quite realistic, there are still several concerns and difficulties that affect such an endeavor. This is probably due to the large base of knowledge that is necessary to approach the problem of handling a nano-object by means of a nano- or micro-device. Therefore, any progress in this field is possible only by means of an integrated and interdisciplinary approach, which takes into account different aspects of the phenomenon. During the actual pioneering phase, there is a certain convenience in handling nano-objects that: (a) have peculiar known characteristics; (b) are easily recognizable, and (c) are interesting to the scientific community. This paper presents the interdisciplinary activities that were necessary to set up an experiment where specifically synthesized SiO₂ particles came in contact with the tips of specifically-designed and -fabricated nanomanipulators. SiO₂ mesoporous nanoparticles (KCC-1), having a peculiar dendritic structure, have been selected as a suitable nano-object because of the possibility to easily modulate their morphology. The expected contact force has been also calculated by means of Finite Element Analysis (FEA) electro-mechanical simulations.

1. Introduction

The rapid development of nanotechnologies has made it possible to create innovative materials and devices applicable in many new technologies [1,2]. Considering devices at the micro-scale, some new original multi-D.o.F. (Degree of Freedom) multi-hinge devices appeared in the literature, such as, for example, multi-axis MEMS (Micro-Electro-Mechanical Systems) gyroscopes [3], micro-mechanisms [4], and 3 D.o.F. micro-robots [5,6,7,8], which take advantage of the appearance of new micro-hinges [9,10,11] and microgrippers [12,13,14,15,16,17,18,19,20,21,22].

However, further miniaturization to the nano-scale is still possible, although there are still several severe concerns [23,24], and therefore, the study of the action of grasping a nanoparticle by means of a nano-gripper remains difficult under many points of view.

Since, at the nanometric scale, materials behave quite differently from the bulk, understanding the size and shape dependence of physical properties in nanoparticles is a fundamental step towards the design, fabrication, and assembly of materials and devices with predictable behavior. In particular, the mechanical properties of nanoparticles may be of fundamental importance in controlling their performances in specific applications. Mechanical characterization of nanoparticles presents several challenges, it being difficult to prepare isolated nanoparticles on a substrate and to locate one individual nanoparticle. It is even more challenging to apply the required low loads on the nanoparticles, to measure the small deformations produced and to interpret the experimental data. Nano-indentation and Atomic Force Microscopy (AFM) are two common tools used for the mechanical characterization at the nanoscale level [25,26,27,28].

Actually, the contacts between nano-gripper jaws and nanoparticles, with possible mechanical characterization of the nanoparticles, is still a rather unexplored field. Some techniques have been applied by means of AFM [29,30,31] or nano-indenters [32].

This investigation presents the feasibility study of a nano-gripper to be used for the mechanical characterization of isolated nanoparticles. Firstly, the synthesis procedure and the morphological characterization by Scanning Electron Microscope (SEM) and Brunauer–Emmett–Teller (BET) method of silica nanoparticles KCC-1 will be presented. Then, the design and fabrication of a nano-gripper will be described, together with some crucial issues that make the process rather difficult and complicated. The contact of the nano-gripper jaws and the KCC-1 nanoparticles is documented by means of SEM imaging. Finally, a series of simulations based on finite element analysis will assess the force-to-voltage relations that govern the comb drives, which provide actuation to the microsystem.

2. Synthesis and Characterization of the Nanoparticles

2.1. Properties and Applications

Silica nanoparticles KCC-1 have a unique spherical morphology described as fibrous, nanoflowers, radial wrinkle, or dendritic structure, characterized by a high surface area with a large pore volume and narrow pore size distribution.

Nanofibers are organized along the center-radial direction with gradually-decreasing material density and gradually increasing pore size from particle interior to surface. That peculiar morphology and the high surface area are responsible for the exceptional performances when applied in many fields ranging from catalysis to biomedical applications. In addition, the silica KCC-1 exhibits thermal and hydrothermal stability and relatively low cytotoxicity. KCC-1, as the catalyst support, increases the dispersion of metals, giving superior activity and stability [33]. In the biomedical field, the structural KCC-1 features drive the adsorption and release of large guest molecules and macromolecules (protein, DNA) [34]. KCC-1 has been exploited also in the field of sensoring as a multifunction organic/inorganic hybrid material, by the immobilization of the Rhodamine-based receptor (RB-Si), exhibiting high efficiency for ${\mathrm{Hg}}^{2+}$ detection [35].

The silica KCC-1 exhibits excellent physical and chemical properties, very important for practical applications. The features of dendritic nanofibers mainly determine some of these properties. Indeed, by regulating the length, thickness, and density of fibers, particle size and pore size can be adjusted. The evaluation of the particle resistance to mechanical stress or manipulation appears very important, in order to preserve the KCC-1 properties across time. As an example, in the catalytic processes, it is important to avoid the breaking of the nanofibers, leading to catalyst deactivation. As a consequence, the dependence of mechanical stability from the density and thickness of the external fiber layer should be studied. Some authors reported an indirect mechanical stability evaluation by High-Resolution Transmission Electron Microscopy (HRTEM), where comparing particles before and after compression stress up to 216 MPa pressure showed that the fibrous morphology of KCC-1 remained unaffected [36]. To the best of our knowledge, the mechanical resistance toward compression or manipulation of KCC-1 has not yet been sufficiently tested.

2.2. Synthesis and Experimental Methods

Silica mesoporous nanoparticles with a lamellar structure, KCC-1, were prepared by a protocol obtained by literature procedures [37,38] with a few modifications. In detail, 30.0 mL of cyclohexane, 1.5 mL of 1-penthanol, and 2.50 g of TEOS (Tetraethyl Orthosilicate) were mixed in a flask, obtaining an organic mixture. In a second flask, 1.00 g of CPB (Cetylpyridinium Bromide) was dissolved in water heating under stirring until complete dissolution. Then, 0.60 g of urea were added to the CPB solution at room temperature, obtaining an aqueous solution. Finally, the organic mixture was dropwise added to the aqueous solution under stirring. After vigorous stirring for 1 h at room temperature, the mixture was heated in a Teflon-lined hydrothermal reactor at 120 ${}^{\circ }$C for 4 h. Then, the solid product was separated by centrifugation, washed with ethanol, dried in air at 120 ${}^{\circ }$C, and finally calcined at 550 ${}^{\circ }$C for 4 h in air.

N₂ adsorption–desorption isotherms were obtained at −196 ${}^{\circ }$C using a Micromeritics Gemini V apparatus. The surface area was calculated by the Brunauer–Emmett–Teller (BET) method in the equilibrium pressure interval 0.03 < P/P${}^{\circ }$ < 0.3. The pore size distribution was obtained from the adsorption branch using the Barrett–Joyner–Halenda (BJH) method, and the total pore volume was calculated from the maximum adsorption point at P/P${}^{\circ }$ = 0.99. Prior to the N₂ adsorption, the sample was heated in flowing He at 200 ${}^{\circ }$C for 1 h.

Observations in electron microscopy were performed with two different instruments. Low magnification images were acquired by means of SEM HITACHI S2500 with a secondary electrons detector, acceleration voltage = 25 kV, and work distance = 9 mm. Samples were sputtered by carbon before introduction in the vacuum chamber. High resolution images were acquired by means of a FEG-SEM (Field Emission Gun-Scanning Electron Microscope), SUPRA${}^{\mathrm{TM}}$ 35, Carl Zeiss SMT (Oberkochen, Germany), using an in-lens electron detector operating at 10.00 kV and a working distance = 5 mm. Samples were sputtered with gold before observation.

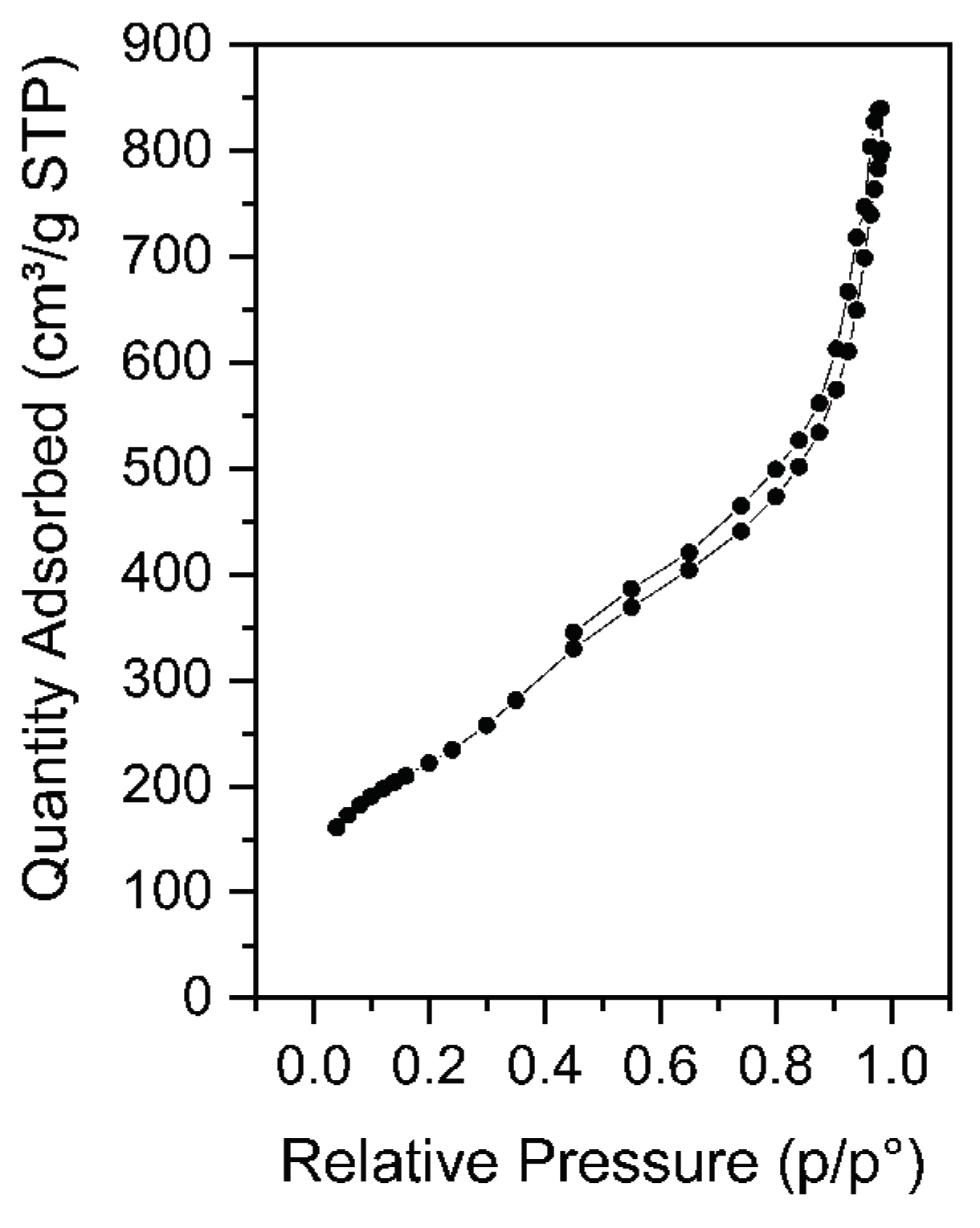
2.3. Morphological Characterization

Figure 1a represents a bunch of particles, while Figure 1b depicts more details of the particle surface at a greater magnification.

The low magnification SEM image of the synthesized silica KCC-1 nanoparticles showed a spherical morphology with particles sizes of about 600–700 nm (Figure 1a). The high magnification FEG-SEM image, Figure 1b, highlights the well-developed wrinkle morphology and high porosity characteristics of KCC-1.

The BET N₂ adsorption and desorption isotherms (Figure 2) showed hysteresis the characteristics of a mesoporous material, with a high surface area of 520 m² g${}^{-1}$ and a total pore volume of 1.7 cm${}^3$ g${}^{-1}$.

3. Design and Fabrication of the Nanomanipulator

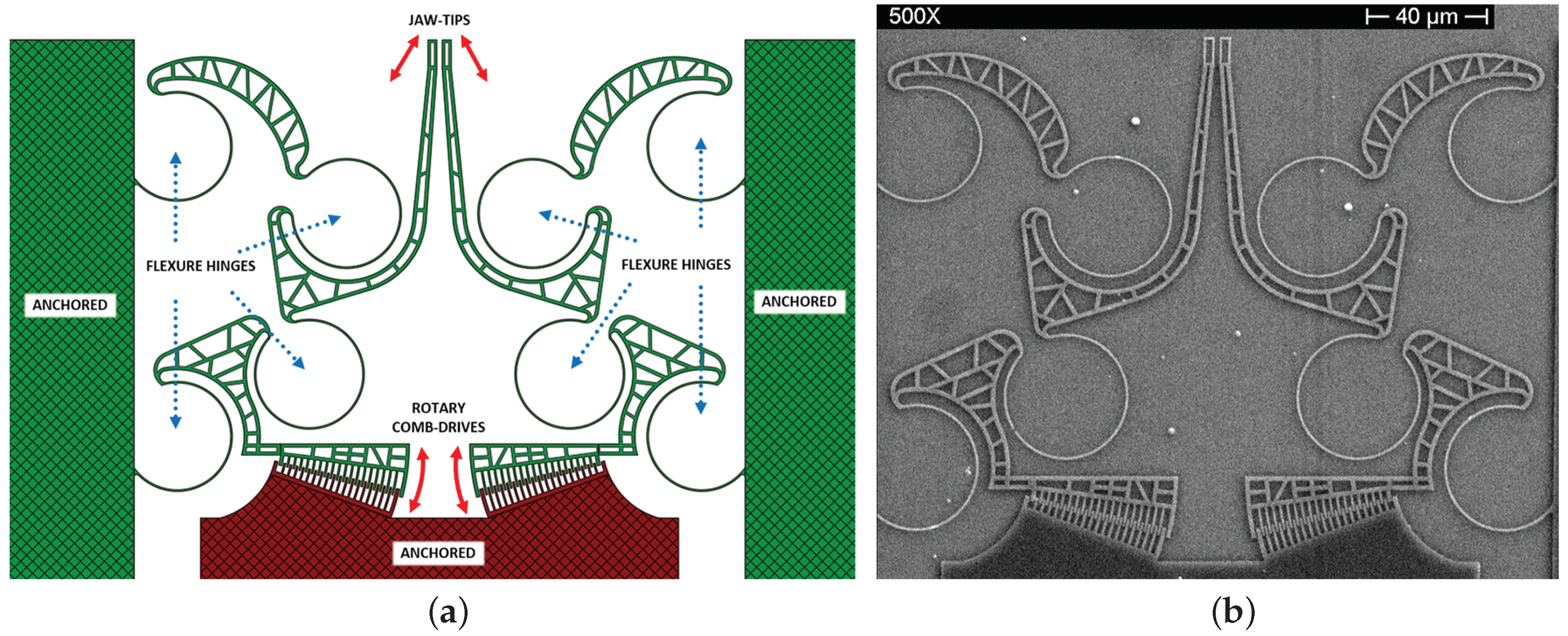
3.1. Design

A nano-gripper has been designed by using the fundamental concepts of compliant mechanisms and nanotechnology. Based on a previously-developed design [23,39], a four-bar linkage was used as the Pseudo-Rigid Body Model (PRBM), and from this, a compliant structure was obtained, as depicted in Figure 3. The idea consists of designing an ordinary mechanism by using classical kinematic synthesis (see for example [40]) and then using the rigid-body replacement method as described in a recent investigation [41]. By using this method, it is possible to design a large variety of gripping devices. For example, the one illustrated in Figure 3 belongs to the normally closed type. The advantage of using a four-bar linkage as a PRBM consists of the fact that the designer has full control of the position of the instantaneous rotation center of the coupler link (namely, the link that is attached to the one nano-gripper jaw). As is known, this result can be easily achieved by adjusting the positions of the two revolute pairs that are adjacent to the frame link, with respect to the position of the two mobile revolute joints.

3.2. Fabrication

Standard MEMS micromachining fabrication techniques are usually required in order to obtain this kind of microscaled and nanoscaled electro-mechanical device [42]. In this work, we relied, in particular, on surface micromachining: according to this method, a complex system can be fabricated as a superimposition, on a chosen substrate, of various thin/thick films of different materials, whose geometries can be defined through lithography ad wet/dry etching techniques [43].

Standard silicon-on-insulator stacks were not used. The fabrication procedure, with glass as the substrate, was carried out as follows:

• The smallest geometric dimension of the system was the width of the comb-drive fingers (600 nm); in order to reach it, a sub-micrometric lithographic resolution is required: the geometries definition was carried out using Electron Beam Lithography (EBL) on an e-resist polymeric film [44].
• Highly versatile materials, suitable for low-cost and low-energy fabricated systems, such as hydrogenated amorphous silicon (a-Si:H) and Indium Tin Oxide (ITO), were investigated for the device mainframe: the main goal was to achieve a system that can be biologically compatible and, at the same time, monolithically integrable even on flexible and polymeric substrates [45,46,47,48,49,50,51]. Dry etching methods, such as sputter-etching and Reactive Ion Etching (RIE), for the structural layer patterning were adopted, using a metal as a masking layer, such as chromium or aluminum.
• An intermediate sacrificial layer between the substrate and the structural layer must be considered: its selective removal after completing the mainframe patterning phase assures the achievement of a structure partially suspended from the substrate. The wet etching procedure offers both isotropic and selective removal of a determined material; furthermore, “etch holes: in the mainframe were specifically designed as under-etching promoters for the rigid suspended body of the system.

Figure 4 shows ${30}^{\circ }$ tilted SEM images (a) of a gripping device sample between the process of structure patterning and the releasing phase, with an enlargement (b) of the jaw-tips. The displayed device has n-doped a-Si:H (hydrogenated amorphous silicon), deposited by Plasma-Enhanced Chemical Vapor Deposition (PECVD), as the structural layer.

4. Tip-to-Particle Contact Tests

At the end of each fabrication process, the device geometry is transferred to the chip by means of electron beam lithography. The geometry is copied on nine different positions, and therefore, nine device samples are available. As explained in the previous Section 3.2, the device is still attached to the bottom layer and appears as in Figure 5. This circumstance is quite convenient for preliminary studies, because the presence of a bottom layer makes the deposition of particles in contact with the device easier.

KCC-1 nanoparticles have been deposited on the chip surface by the following steps: (a) dispersing the particles in ethanol by means of ultrasound; (b) placing a drop of KCC-1 dispersion by micropipette in correspondence with the device; (c) pouring drops of solutions in correspondence with the devices; (d) waiting for the ethanol to evaporate at room temperature. The adopted KCC-1 particles dispersion has been optimized in a trial and error bases up to the concentration of 0.01 g L${}^{-1}$.

Only a limited number of different concentrations of KCC-1 particles in solutions have been tested, because of the difficulties in achieving a large number of good samples. Figure 6 shows how a single particle fits approximately one third of the available tips window, which corresponds to a ratio of 2 μm (jaws-tip window) to 600 nm (particle approximated diameter).

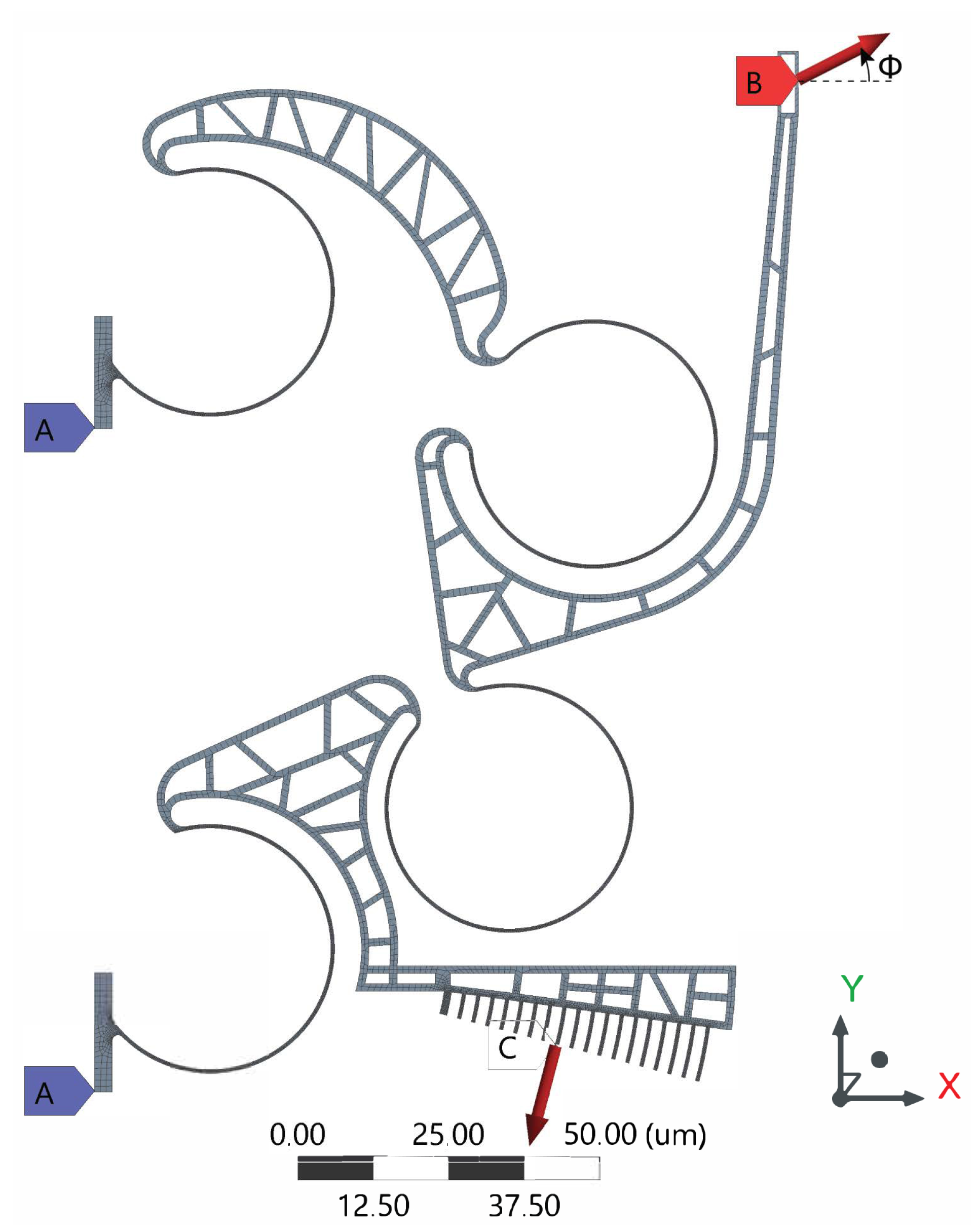
5. Feasibility Study Based on FEA Simulation

To simulate the possible interactions between the jaw and the environment and to evaluate the kinetostatic performance of the nanogripper, finite element simulations have been performed with the ANSYS ^© Ver. 18 (Canonsburg, PA, USA) software [52]. The nonlinearity due to large deflections and the isotropic material formulation were considered in the analysis (polycrystalline silicon with Young’s modulus equal to 164 GPa and Poisson’s ratio equal to 0.22 [53]). Figure 7 shows the mesh composed of 21,935 nodes and 17,343 elements, refined in the flexible beams and in the comb-drive fingers.

The simulation setup is also illustrated in Figure 7. Two fixed supports were introduced at the flexures end-sections (labeled A), where the structure was anchored to the frame.

An external force was applied to the tip considering four different directions. With reference to Figure 7, the application point is highlighted by the label B, while the four different directions correspond to the angles $\varphi =0$, $\varphi =\pi /2$, $\varphi =\pi$, and $\varphi =3\pi /2$. For each direction, four magnitudes have been considered: $F=0$ μN, $F=0.01$ μN, $F=0.05$ μN, and $F=0.1$ μN.

To model the actuator action, a force was applied to each one of the 19 fingers, with the line of action perpendicular to the finger free-end section (labeled C) and magnitude equal to $F_C={ϵ}_0{ϵ}_{r}h{V}^2/g$ [54]. In the previous relation, ${ϵ}_0$ is the vacuum permittivity ($8.8541\times {10}^{-12}$ Fm${}^{-1}$), ${ϵ}_r$ is the air relative permittivity (1.00058), h is the thickness of the finger (600 nm), g is the radial distance between the movable and fixed finger (600 nm), and V is the applied voltage. For each force at the tip, the simulations ran from a value of the applied tension equal to 1 V to the maximum tension value corresponding to the stroke of the rotary comb-drive (5 deg). In any case, the maximum voltage did not exceed 25 V.

The simulation results, corresponding to the tip force directions of $\varphi =0$, $\varphi =\pi$, $\varphi =\pi /2$, and $\varphi =3\pi /2$ are reported in Figure 8, Figure 9, Figure 10 and Figure 11, respectively. The results include displacements and rotations of the tip, rotations of the floating part of the comb-drive, and maximum values of the maximum principal stress.

Generally, it can be noted that in the case of $F=0$, the tip displacement, with negative components along the x- and y-axes, increases its magnitude as the actuation force (applied tension) increases. However, the application of the tip force significantly affects the kinetostatic behavior of the system.

In fact, considering the case $\varphi =0$, the force is opposite the displacement x-component. With reference to Figure 8, it can be noted that as the magnitude of F increases:

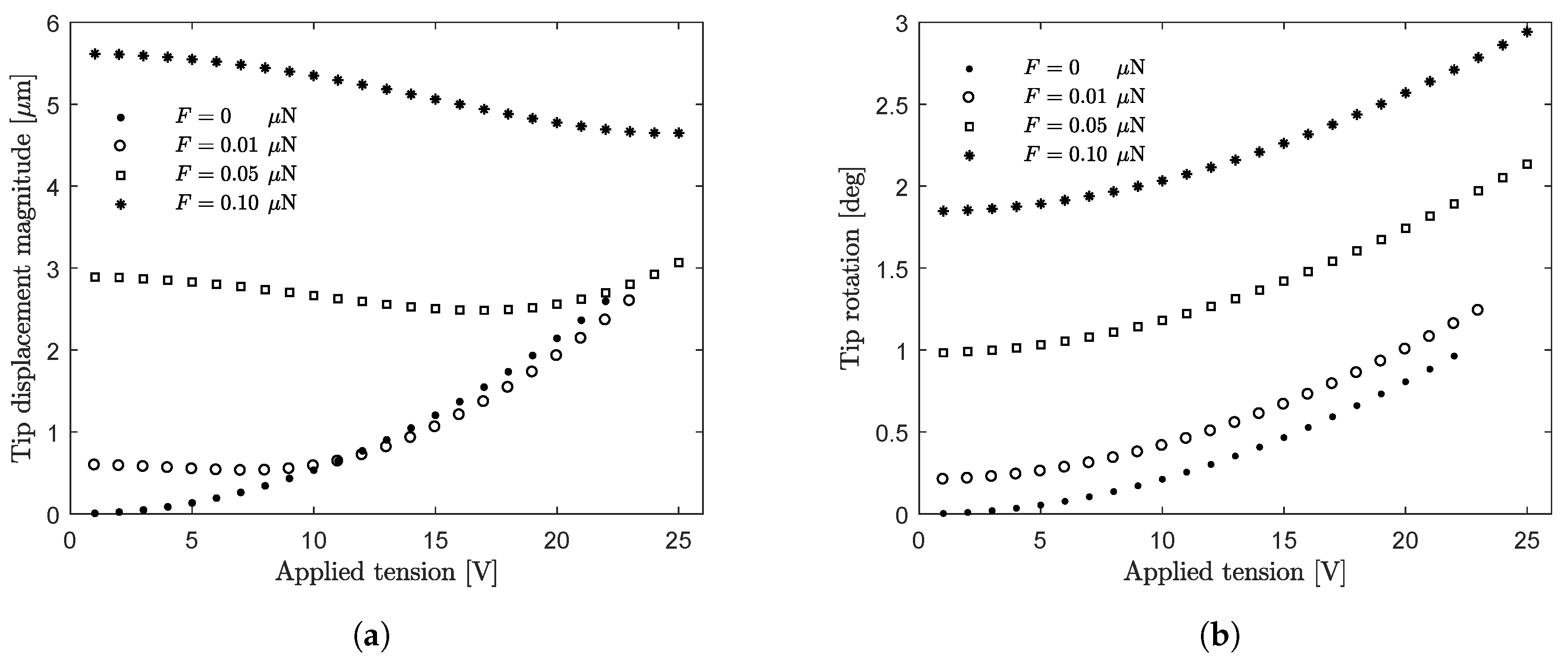
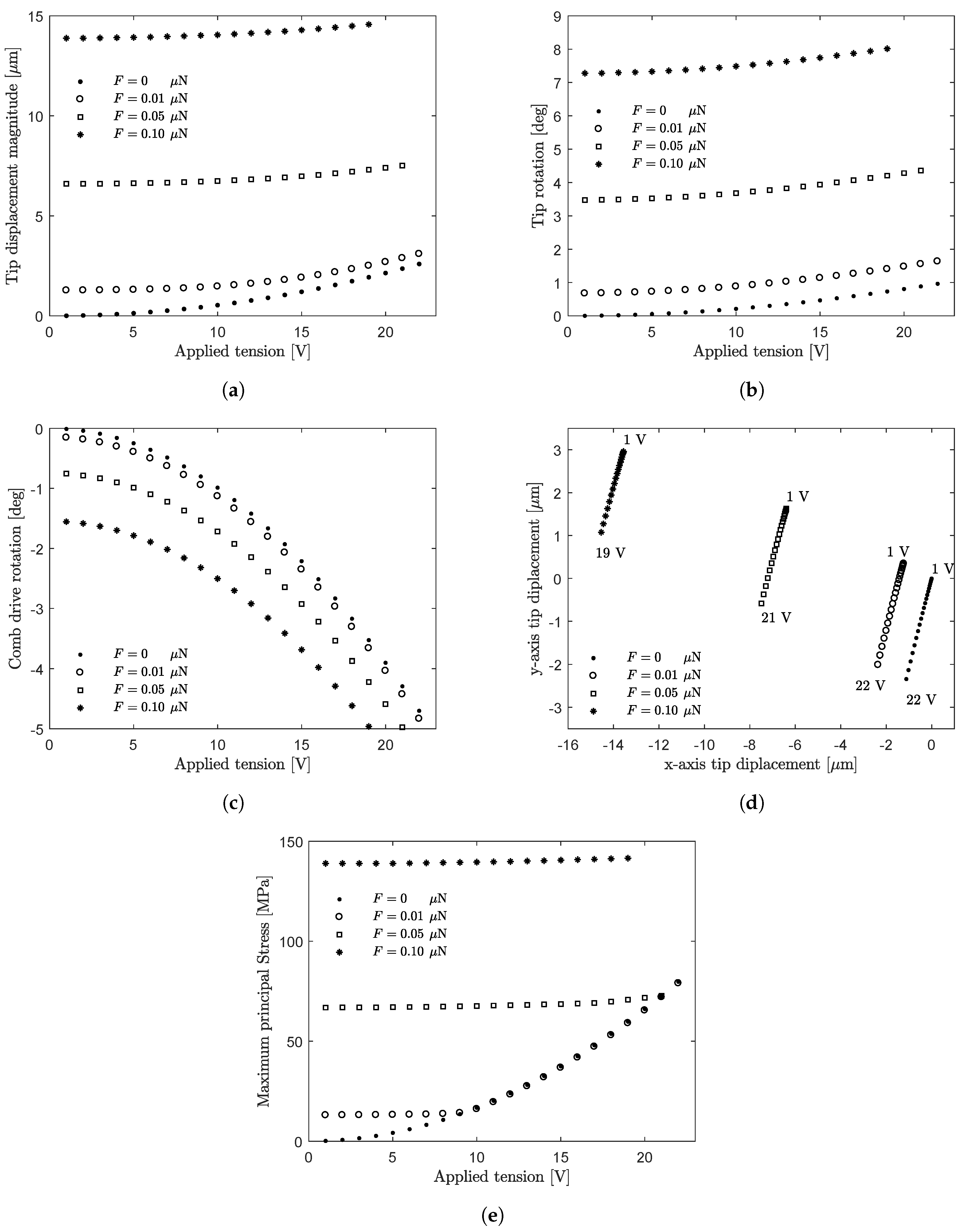
• the tip displacement magnitude increases (Figure 8a); only for the lowest value of the force ($F=0.01$ μN) and for high tension values (>20 V), the tip displacement magnitude is close to the case $F=0$;
• the tip rotation (magnitude) increases (Figure 8b);
• the applied tension required to achieve the maximum rotation of the comb-drive increases (from 22 V for $F=0$ to 25 V for $F=0.01$ μN; Figure 8c);
• the tip displacement shifts increasingly along the positive direction of the x-axis (Figure 8d);
• the maximum principal stress increases for all the applied tension values only for the highest value of the force magnitude ($F=0.01$ μN). The force magnitudes $F=0.05$ μN and $F=0.01$ μN give the predominant contribution to the MPSuntil the applied tension does not exceed about 20 V and 9 V, respectively (Figure 8e).

In the case $\varphi =\pi /2$, the force F is opposite the displacement y-component (Figure 9). As the magnitude of F increases:

• the tip displacement magnitude increases (Figure 9a); however, with respect to the case $\varphi =0$ (Figure 8a), it is also affected by high values of the applied tension;
• the tip rotation increases (Figure 9b);
• the applied tension required to achieve the maximum rotation of the comb-drive increases (from 22 V for $F=0$ to 25 V for $F=0.10$ μN, Figure 9c);
• the tip displacement shifts increasingly along the negative direction of the x-axis (Figure 9d);
• the maximum principal stress generally increases, but depends on the applied tension values (Figure 9e).

In the case $\varphi =\pi$, the force F has the same direction of the displacement x-component (Figure 10). As the magnitude of F increases:

• the tip displacement magnitude increases (Figure 10a);
• the tip rotation increases (Figure 10b);
• the applied tension required to achieve the maximum rotation of the comb-drive decreases (from 22 V for $F=0$ to 19 V for $F=0.10$ μN, Figure 10c);
• the tip displacement shifts increasingly along the negative direction of the $x$-axis (Figure 10d);
• the maximum principal stress increases (for $F=0.10$ μN and for $F=0.05$ μN). The force magnitude $F=0.01$ μN gives the predominant contribution to the MPS until the applied tension does not exceed about 8 V (Figure 10e).

In the case $\varphi =3\pi /2$, the force F has the same direction of the displacement y-component (Figure 11). As the magnitude of F increases:

• the tip displacement magnitude increases (Figure 11a);
• the tip rotation (magnitude) increases (Figure 11b);
• the applied tension required to achieve the maximum rotation of the comb-drive decreases (from 22 V for $F=0$ to 15 V for $F=0.10$ μN, Figure 11c);
• the tip displacement shifts increasingly along the positive direction of the x-axis (Figure 11d);
• the maximum principal stress increases (Figure 11e).

The results of the simulations performed show that the possible interactions between the gripper jaw and the environment, modeled as a set of forces applied at the tip, affect the tip pose and, through the deformation of the gripper compliant structure, the rotation of the comb-drive actuator. As a consequence, the required voltage to reach the end of the stroke position depends on the tip force magnitude and direction. For all the considered load conditions, the maximum principal stress value is below 150 MPa, less than the yield strength of silicon, i.e., 7 GPa [55].

6. Conclusions

This paper has shown that the ambitious project of direct contact manipulation of nanoparticles is quite reasonable and that the key to success for this endeavor is the interdisciplinary approach. Thanks to different competencies, the research group was able to assess the feasibility of a nano-gripper for grasping KCC-1 particles. Both the nano-gripper and the particles have been independently synthesized and fabricated by the group. Furthermore, thanks to electronic microscopy, some images have been obtained to assess the feasibility of the microsystem. Finally, FEA simulation was also used to assess actuation in operating conditions.