Comparative Analysis of Current Control Techniques to Support Virtual Inertia Applications †
Abstract
:1. Introduction
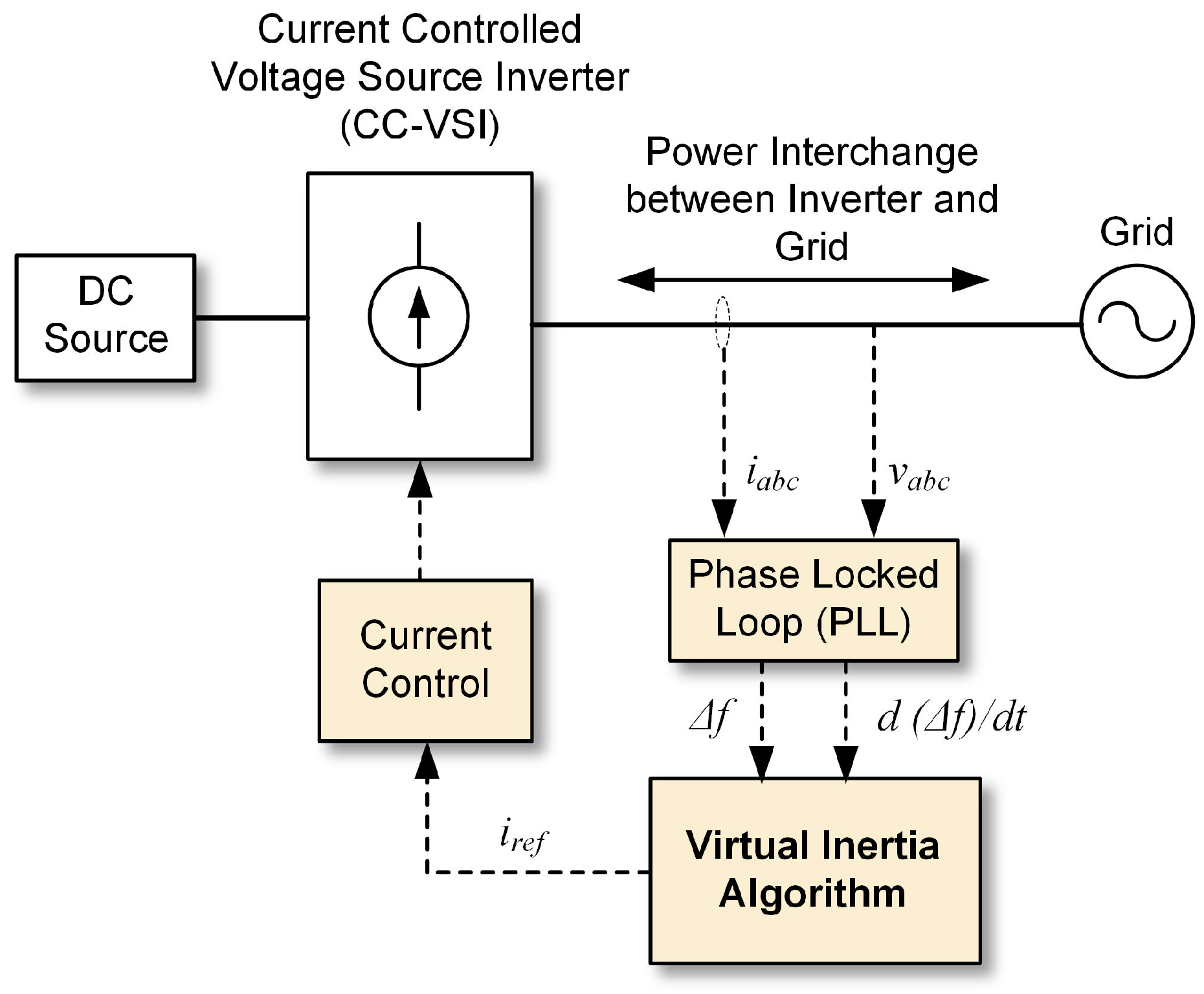
2. Virtual Inertia and Current Control Techniques
2.1. Concept of Virtual Inertia
2.2. Proportional-Integral Controller
2.3. Proportional-Resonant Controller
2.4. Hysteresis Controller
2.5. Model Predictive Controller
2.6. Supplementary Adaptive Dynamic Programming Controller
3. Design of Current Controllers
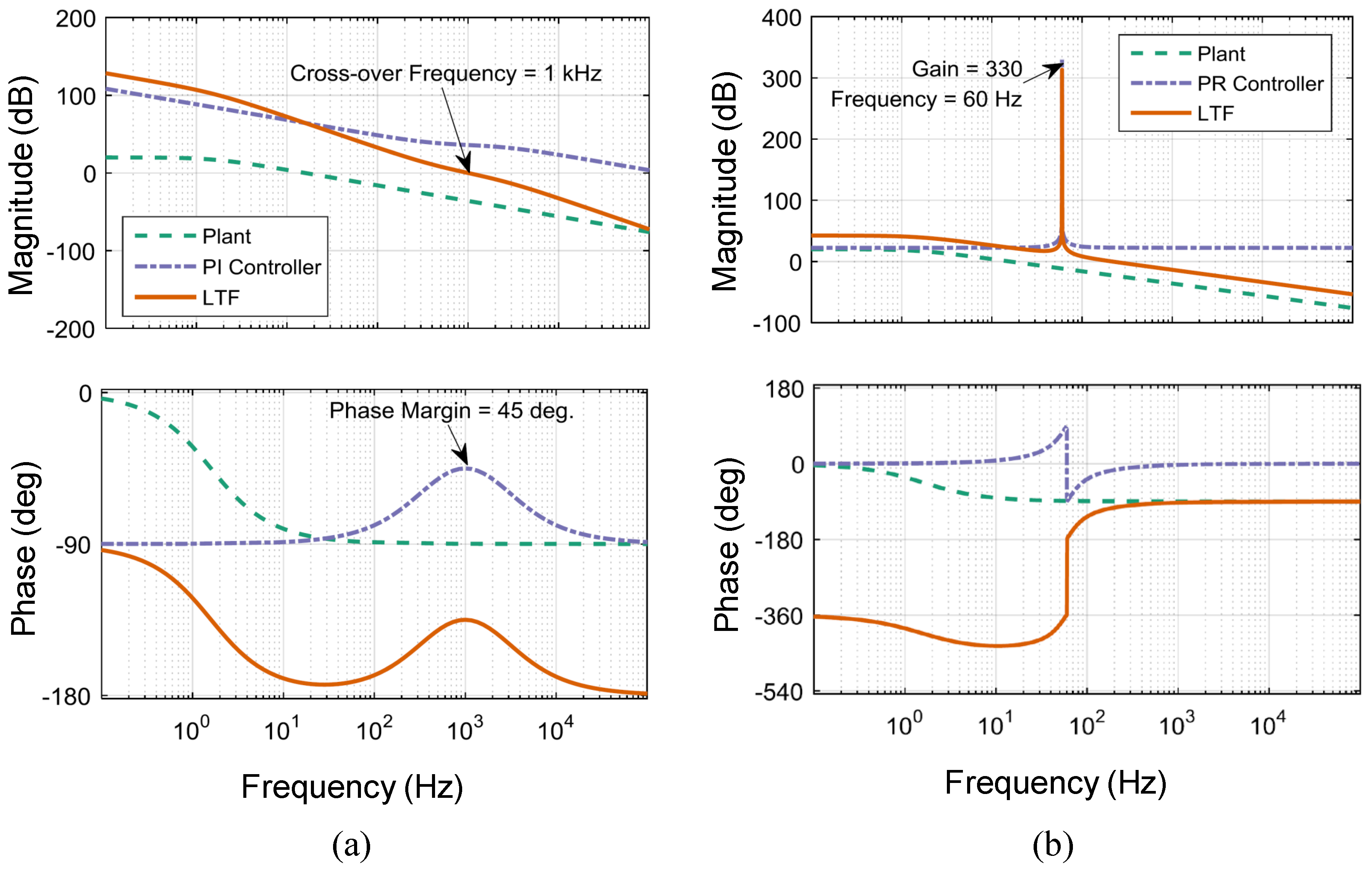
3.1. PI (Proportional-Integral) Controller Design
3.2. PR (Proportional-Resonant) Controller
3.3. Hysteresis Controller Design
3.4. Model Predictive Controller Design
3.5. Supplementary ADP (Adaptive Dynamic Programming) Controller Design
4. Simulation Results and Comparative Analysis
4.1. PI Controller Simulation Results
4.2. PR Controller Simulation Results
4.3. Hysteresis Controller Simulation Results
4.4. Model Predictive Controller Simulation Results
4.5. Supplementary ADP Controller Simulation Results
4.6. Transient Response Comparison
4.7. Harmonic Contents Comparison
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADP | Adaptive dynamic programming |
| CC-VSI | Current-controlled voltage source inverter |
| DSP | Digital signal processors |
| ESS | Energy storage system |
| FCS-MPC | Finite control set model predictive control |
| FPGA | Field programmable gate array |
| MLP | Multi-layer perceptron |
| MPC | Model predictive control |
| PI | Proportional integral |
| PLL | Phase-locked loop |
| PR | Proportional resonant |
| NERC | North American Electric Reliability Corporation |
| PI | Proportional-integral |
| PV | Photovoltaic |
| RES | Renewable energy system |
| ROCOF | Rate of change of frequency |
References
- Kroposki, B.; Mather, B. Rise of Distributed Power: Integrating Solar Energy into the Grid [Guest Editorial]. IEEE Power Energy Mag. 2015, 13, 14–18. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. Distributed power system virtual inertia implemented by grid-connected power converters. IEEE Trans. Power Electron. 2018, 33, 8488–8499. [Google Scholar] [CrossRef]
- Tielens, P.; Van Hertem, D. Grid inertia and frequency control in power systems with high penetration of renewables. In Proceedings of the Young Researchers Symposium in Electrical Power Engineering, Delft, The Netherlands, 16–17 April 2012. [Google Scholar]
- Tamrakar, U.; Galipeau, D.; Tonkoski, R.; Tamrakar, I. Improving transient stability of photovoltaic-hydro microgrids using virtual synchronous machines. In Proceedings of the IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Shrestha, D.; Tamrakar, U.; Malla, N.; Ni, Z.; Tonkoski, R. Reduction of energy consumption of virtual synchronous machine using supplementary adaptive dynamic programming. In Proceedings of the IEEE International Conference on Electro Information Technology (EIT), Grand Forks, ND, USA, 19–21 May 2016; pp. 690–694. [Google Scholar] [CrossRef]
- Beck, H.P.; Hesse, R. Virtual synchronous machine. In Proceedings of the International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007. [Google Scholar]
- Alipoor, J.; Miura, Y.; Ise, T. Power System Stabilization Using Virtual Synchronous Generator With Alternating Moment of Inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Zhang, W.; Cantarellas, A.M.; Rocabert, J.; Luna, A.; Rodriguez, P. Synchronous Power Controller With Flexible Droop Characteristics for Renewable Power Generation Systems. IEEE Trans. Sustain. Energy 2016, 7, 1572–1582. [Google Scholar] [CrossRef]
- Tamrakar, U.; Tonkoski, R.; Ni, Z.; Hansen, T.M.; Tamrakar, I. Current control techniques for applications in virtual synchronous machines. In Proceedings of the IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016. [Google Scholar] [CrossRef]
- Kassakian, J.G.; Jahns, T.M. Evolving and Emerging Applications of Power Electronics in Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 47–58. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model Predictive Control: A Review of Its Applications in Power Electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef] [Green Version]
- Malla, N.; Shrestha, D.; Ni, Z.; Tonkoski, R. Supplementary control for virtual synchronous machine based on adaptive dynamic programming. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 1998–2005. [Google Scholar] [CrossRef]
- Malla, N.; Tamrakar, U.; Shrestha, D.; Ni, Z.; Tonkoski, R. Online learning control for harmonics reduction based on current controlled voltage source power inverters. IEEE/CAA J. Autom. Sin. 2017, 4, 447–457. [Google Scholar] [CrossRef]
- Sakimoto, K.; Miura, Y.; Ise, T. Stabilization of a power system with a distributed generator by a Virtual Synchronous Generator function. In Proceedings of the 8th International Conference on Power Electronics—ECCE Asia, Jeju, South Korea, 30 May–3 June 2011; pp. 1498–1505. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A. Virtual synchronous machines—Classification of implementations and analysis of equivalence to droop controllers for microgrids. In Proceedings of the 2013 IEEE Grenoble PowerTech (POWERTECH), Grenoble, France, 16–20 June 2013; pp. 1–7. [Google Scholar]
- Bevrani, H.; Ise, T.; Miura, Y. Virtual synchronous generators: A survey and new perspectives. Int. J. Electr. Power Energy Syst. 2014, 54, 244–254. [Google Scholar] [CrossRef]
- Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.; Hansen, T.; Tonkoski, R. Virtual inertia: Current trends and future directions. Appl. Sci. 2017, 7, 654. [Google Scholar] [CrossRef]
- Cha, H.; Vu, T.K.; Kim, J.E. Design and control of Proportional-Resonant controller based Photovoltaic power conditioning system. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), San Jose, CA, USA, 20–24 September 2009; pp. 2198–2205. [Google Scholar]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Li, Y.W.; Blaabjerg, F.; Wang, X. Active harmonic filtering using current-controlled, grid-connected DG units with closed-loop power control. IEEE Trans. Power Electron. 2014, 29, 642–653. [Google Scholar]
- Zhong, Q.C.; Hornik, T. Control of Power Inverters in Renewable Energy and Smart Grid Integration; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 97. [Google Scholar]
- Dannehl, J.; Wessels, C.; Fuchs, F.W. Limitations of voltage-oriented PI current control of grid-connected PWM rectifiers with LCL filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar] [CrossRef]
- Vasquez, J.C.; Guerrero, J.M.; Savaghebi, M.; Eloy-Garcia, J.; Teodorescu, R. Modeling, analysis, and design of stationary-reference-frame droop-controlled parallel three-phase voltage source inverters. IEEE Trans. Ind. Electron. 2013, 60, 1271–1280. [Google Scholar] [CrossRef]
- Timbus, A.V.; Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. Adaptive resonant controller for grid-connected converters in distributed power generation systems. In Proceedings of the 21st Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Dallas, TX, USA, 19–23 March 2006. [Google Scholar] [CrossRef]
- Sato, Y.; Ishizuka, T.; Nezu, K.; Kataoka, T. A new control strategy for voltage-type PWM rectifiers to realize zero steady-state control error in input current. IEEE Trans. Ind. Appl. 1998, 34, 480–486. [Google Scholar] [CrossRef]
- Davoodnezhad, R.; Holmes, D.; McGrath, B. A fully digital hysteresis current controller for current regulation of grid connected PV inverters. In Proceedings of the 2014 IEEE 5th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Galway, Ireland, 24–27 June 2014; pp. 1–8. [Google Scholar]
- Wu, F.; Zhang, L.; Wu, Q. Simple unipolar maximum switching frequency limited hysteresis current control for grid-connected inverter. IET Power Electron. 2014, 7, 933–945. [Google Scholar] [CrossRef]
- Suul, J.A.; Ljokelsoy, K.; Midtsund, T.; Undeland, T. Synchronous Reference Frame Hysteresis Current Control for Grid Converter Applications. IEEE Trans. Ind. Appl. 2011, 47, 2183–2194. [Google Scholar] [CrossRef]
- Davoodnezhad, R.; Holmes, D.G.; McGrath, B.P. A novel three-level hysteresis current regulation strategy for three-phase three-level inverters. IEEE Trans. Power Electron. 2014, 29, 6100–6109. [Google Scholar] [CrossRef]
- Wu, F.; Feng, F.; Luo, L.; Duan, J.; Sun, L. Sampling period online adjusting-based hysteresis current control without band with constant switching frequency. IEEE Trans. Ind. Electron. 2015, 62, 270–277. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, H.; Wang, T.; Li, L.; Dorrell, D.G.; Lu, D.D.C. Field-oriented control based on hysteresis band current controller for a permanent magnet synchronous motor driven by a direct matrix converter. IET Power Electron. 2018, 11, 1277–1285. [Google Scholar] [CrossRef]
- Tamrakar, I.; Shilpakar, L.; Fernandes, B.; Nilsen, R. Voltage and frequency control of parallel operated synchronous generator and induction generator with STATCOM in micro hydro scheme. IET Gener. Trans. Distrib. 2007, 1, 743–750. [Google Scholar] [CrossRef]
- Bolognani, S.; Bolognani, S.; Peretti, L.; Zigliotto, M. Design and Implementation of Model Predictive Control for Electrical Motor Drives. IEEE Trans. Ind. Electron. 2009, 56, 1925–1936. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kazmierkowski, M.P.; Espinoza, J.R.; Zanchetta, P.; Abu-Rub, H.; Young, H.A.; Rojas, C.A. State of the Art of Finite Control Set Model Predictive Control in Power Electronics. IEEE Trans. Ind. Inf. 2013, 9, 1003–1016. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, Y.; Qu, C. Model Predictive Control and Direct Power Control for PWM Rectifiers With Active Power Ripple Minimization. IEEE Trans. Ind. Appl. 2016, 52, 4909–4918. [Google Scholar] [CrossRef]
- Rodriguez, J.; Pontt, J.; Silva, C.A.; Correa, P.; Lezana, P.; Cortés, P.; Ammann, U. Predictive current control of a voltage source inverter. IEEE Trans. Ind. Electron. 2007, 54, 495–503. [Google Scholar] [CrossRef]
- Cortes, P.; Kazmierkowski, M.P.; Kennel, R.M.; Quevedo, D.E.; Rodriguez, J. Predictive Control in Power Electronics and Drives. IEEE Trans. Ind. Electron. 2008, 55, 4312–4324. [Google Scholar] [CrossRef]
- Aguilera, R.P.; Lezana, P.; Quevedo, D.E. Finite-Control-Set Model Predictive Control With Improved Steady-State Performance. IEEE Trans. Ind. Inf. 2013, 9, 658–667. [Google Scholar] [CrossRef]
- Kouro, S.; Cortes, P.; Vargas, R.; Ammann, U.; Rodriguez, J. Model Predictive Control—A Simple and Powerful Method to Control Power Converters. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Drobnic, K.; Nemec, M.; Nedeljkovic, D.; Ambrozic, V. Predictive Direct Control Applied to AC Drives and Active Power Filter. IEEE Trans. Ind. Electron. 2009, 56, 1884–1893. [Google Scholar] [CrossRef]
- Young, H.A.; Perez, M.A.; Rodriguez, J. Analysis of Finite-Control-Set Model Predictive Current Control With Model Parameter Mismatch in a Three-Phase Inverter. IEEE Trans. Ind. Electron. 2016, 63, 3100–3107. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Lewis, F.; Liu, D. (Eds.) Reinforcement Learning and Approximate Dynamic Programming for Feedback Control; Wiley-IEEE Press: Piscataway, NJ, USA, 2013. [Google Scholar]
- Si, J.; Barto, A.G.; Powell, W.B.; Wunsch, D.C. (Eds.) Handbook of Learning and Approximate Dynamic Programming; Wiley-IEEE Press: Piscataway, NJ, USA, 2004. [Google Scholar]
- He, H.; Ni, Z.; Fu, J. A Three-Network Architecture for On-Line Learning and Optimization based on Adaptive Dynamic Programming. Neurocomputing 2012, 78, 3–13. [Google Scholar] [CrossRef]
- Guo, W.; Liu, F.; Si, J.; He, D.; Harley, R.; Mei, S. Approximate dynamic programming based supplementary reactive power control for DFIG wind farm to enhance power system stability. Neurocomputing 2015, 170, 417–427. [Google Scholar] [CrossRef]
- Zhang, H.G.; Zhang, X.; Yan-Hong, L.; Jun, Y. An overview of research on adaptive dynamic programming. Acta Autom. Sin. 2013, 39, 303–311. [Google Scholar] [CrossRef]
- Si, J.; Wang, Y.T. Online learning control by association and reinforcement. IEEE Trans. Neural Netw. 2001, 12, 264–276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, C.; Si, J.; Xie, X. Direct heuristic dynamic programming for damping oscillations in a large power system. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2008, 38, 1008–1013. [Google Scholar]
- Ulbig, A.; Borsche, T.S.; Andersson, G. Impact of low rotational inertia on power system stability and operation. IFAC Proc. Vol. 2014, 47, 7290–7297. [Google Scholar] [CrossRef]
- IEEE Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems; IEEE Std 519-1992; IEEE: Piscataway, NJ, USA, 2014.












| Parameters | Values |
|---|---|
| DC Voltage () | 400 V |
| Grid Frequency (f) | 60 Hz |
| Grid Voltage () | 208 V (L-L) |
| Grid Impedance () | |
| Switching Frequency (PI, PR, and ADP) () | 10 kHz |
| Switch Dead-time () | 2 s |
| Filter Inductance (L) | 10 mH |
| Filter Resistance (r) | 0.1 |
| Filter Capacitance (C) | 3.3 F |
| Controller | THD | Overshoot | Response Time (s) | Switching/Cycle |
|---|---|---|---|---|
| PI | 2.30% | 40.5% | 492 | 333 |
| PR | 1.02% | 8.2% | 462 | 333 |
| Hysteresis | 1.60% | 1.0% | 447 | 669 |
| MPC | 1.35% | 0.9% | 238 | 935 |
| ADP | 1.68% | 26.1% | 465 | 333 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamrakar, U.; Shrestha, D.; Malla, N.; Ni, Z.; Hansen, T.M.; Tamrakar, I.; Tonkoski, R. Comparative Analysis of Current Control Techniques to Support Virtual Inertia Applications. Appl. Sci. 2018, 8, 2695. https://doi.org/10.3390/app8122695
Tamrakar U, Shrestha D, Malla N, Ni Z, Hansen TM, Tamrakar I, Tonkoski R. Comparative Analysis of Current Control Techniques to Support Virtual Inertia Applications. Applied Sciences. 2018; 8(12):2695. https://doi.org/10.3390/app8122695
Chicago/Turabian StyleTamrakar, Ujjwol, Dipesh Shrestha, Naresh Malla, Zhen Ni, Timothy M. Hansen, Indraman Tamrakar, and Reinaldo Tonkoski. 2018. "Comparative Analysis of Current Control Techniques to Support Virtual Inertia Applications" Applied Sciences 8, no. 12: 2695. https://doi.org/10.3390/app8122695
APA StyleTamrakar, U., Shrestha, D., Malla, N., Ni, Z., Hansen, T. M., Tamrakar, I., & Tonkoski, R. (2018). Comparative Analysis of Current Control Techniques to Support Virtual Inertia Applications. Applied Sciences, 8(12), 2695. https://doi.org/10.3390/app8122695





