1. Introduction
Artificial turf has become an increasingly prominent type of playing surface for many sports due to its versatility for all-year-round and multi-sport use [
1]. Whilst natural turf remains the star quality for many sports, the advantages of artificial surfaces over natural pitches means their use, especially at the grassroots level, is increasing [
2]. The Fédération Internationale de Football Association (FIFA) have described the latest 3G surfaces as “the best alternative to natural grass” due to their resistance to weather and ability to sustain more intensive use [
3]. All these factors led the English football association to commit to an investment of £230 million for new 3G pitches by 2020 [
4].
Third generation (3G) artificial surfaces contain a number of polymer materials that exhibit various strain rate and temperature dependant behaviours [
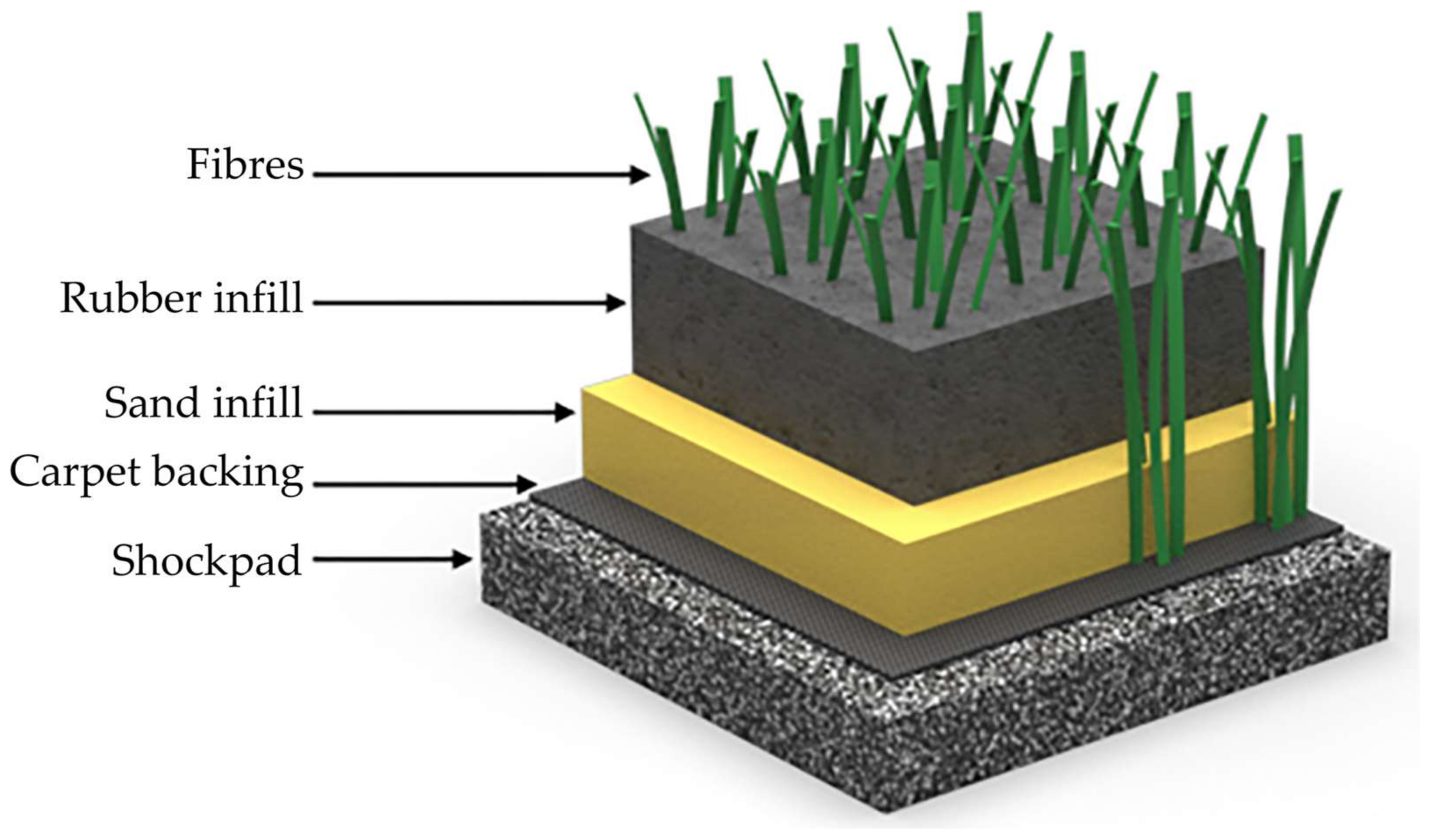
5]. The surface is constructed in a layered format [
6] consisting of a lower layer of an elastomeric mat called a shockpad, used to absorb the impact forces of boot-surface interactions and thereby reduce the stress upon the athletes (
Figure 1). On top of this lies the carpet consisting of a bed of polymer fibres arranged in tufts and stitched into a canvas backing. The carpet is filled with two separate infill layers: a stabilising layer to provide support to the fibres and weigh the carpet down and a performance layer to fill the carpet fibres and provide an interface for ball and player interactions. The stabilising layer is typically created using sand whilst the performance layer can consist of a variety of different polymer or organic materials however styrene butadiene rubber (SBR) granules are the most common choice.
The main design requirement of the shockpad layer is to absorb some of the impact forces applied from player interactions such as running foot strikes. They must also allow for drainage and be durable to withstand cold temperatures and repeated freeze-thaw cycles [
7]. Elastomers are a popular choice as they have favourable shock absorption properties and can deform to large strains without permanent deformation. These properties result from the chemical structure of elastomers being made up of long randomly oriented molecular chains that align when stretched and restore when the load is released. The term elastomer, a combination of elastic and polymer is often used interchangeably with rubber [
8]. Rubber is a popular choice of elastomer for engineering applications due to its flexibility, extensibility, resiliency and durability [
9]. Shockpads are typically constructed to be cellular, a move that enhances energy absorption properties and allows drainage through the system [
10]. The presence of air voids also allows larger strains to be reached under compression [
11]. Elastomer foams can be found in many sports products, a common example being in sports footwear acting as shock absorbers [
12]. A key difference between these foams however is their construction method. Whilst most elastomeric foams are formed with the use of a blowing agent, shockpads are typically formed using recycled rubber compounds bound together with adhesive with the voids in the structure formed by the spaces between solid rubber particles [
6].
The behaviour of shockpads under compression has been analysed previously. Both Anderson [
13] and Allgeuer et al. [
14] identified three key stages: air void compression, transition and rubber compression. The air void compression phase is associated with an initial low stiffness, high deflection response. A transition phase then provides an increase in the stiffness as the void ratio is reduced and the shockpad turns into a two phase system of rubber and binder. A final phase is realised when rubber-on-rubber contact is made resulting in a substantial increase in stiffness due to the compression of the rubber.
The modelling of sports surfaces has been attempted before with examples of running tracks, vinyl flooring and rubber treadmill belts all investigated [
15,
16,
17,
18]. Anderson [
13] created a mechanical model to describe the three regions in shockpad compression using a non-linear damped model consisting of a linear spring and damper in parallel, similar in nature to a hyperelastic Bergstrom-Boyce model [
19]. Mehravar et al. [
20] used a finite element (FE) model to simulate the loading of an elastomeric shockpad using an Arruda-Boyce hyperelastic material model. Compression data was used to fit the coefficients of the model and a power equation created to describe the frequency dependency of the strain energy density function. The simulation was able to accurately fit the loading response under compression for frequencies in the range 0.9–10 Hz. However, the model was restricted to describing the loading behaviour with the viscoelastic unloading response not considered. The purpose of this study was to mechanically characterise the behaviour of two elastomeric shockpads and to find suitable material models to describe both loading and unloading behaviours. The mechanical behaviour of the rubber shockpads were characterised through calculation of the stress-strain properties obtained from testing using the FIFA standard Advanced Artificial Athlete (AAA, FIFA, 2015).
4. Results
The microfoam material model showed good overall agreement with the experimental data for both the Berleburger and Holywell shockpads and all drop heights (
Figure 8). The FE simulations met the accuracy criteria for both shockpads and all drop heights, except for the Berleburger 15 mm drop height where the strain RMSE was slightly above the threshold at 18% (
Table 3).
The FE simulations under-estimated shock absorption for the Berleburger shockpad by a consistent 3–4% across drop heights, corresponding to an over-estimation in peak force. Agreement was better for the Holywell shockpad with the difference within 2% throughout. The FE simulations over-estimated vertical deformation for the Berleburger shockpad, by up to 0.3 mm, while agreement was again better for the Holywell shockpad with the difference being no more than 0.2 mm throughout. In all cases if shock absorption was under-estimated then vertical deformation was over-estimated and vice versa, suggesting that for both shockpads the overall loading stiffness response was better estimated than the two loading extreme measures of shock absorption and vertical deformation. The FE simulations over-estimated energy restitution by up to 8% suggesting that more energy was returned to the impactor than was observed experimentally. These differences were larger than those for shock absorption and vertical deformation which was not unexpected given that both the loading and unloading phases contributed to this variable [
20]. Interestingly, for both shockpads, the difference in energy restitution decreased with decreasing drop height; from 6 to 8% for the 55 mm drop height to only 0–1% for the 15 mm drop height. This trend suggests that the loading–unloading response is accurately captured by the simulations for low strains, but less so for higher strains that reach the hyperelastic region of the stress-strain curve (
Figure 5). For low strains, the compression and recovery are dominated by air voids, while for higher strains the compression and recovery includes not only air voids but also the rubber shreds/granules. This poorer performance may, therefore, represent a limitation of using a microfoam model to estimate compression and recovery of a granular/shredded rubber held together by a polyurethane binder (
Table 1).
Strain RMSEs were also larger than those for shock absorption and vertical deformation, on average similar between shockpads, but showed no consistent trend with drop height. For the Berleburger shockpad the strain RMSE increased with decreasing drop height (from 6 to 18%) and appeared linked to an increasing offset in the unloading curves between the experimental data and simulation output. In contrast, for the Holywell shockpad the strain RMSE decreased with decreasing drop height (from 14% to 6%) and appeared to be linked to the simulation output exhibiting undulations during the loading phase that, as noted above, were not present in the experimental data for this shockpad, with the undulations being of greater magnitude for the higher drop heights (
Figure 8).
Although some of these differences will be due to inaccuracies in the material models and FE simulations, there will also be a contribution related to uncertainties in the experimental data itself. These include: inconsistency in the shockpad thicknesses (
Table 1) due to construction method and granular nature; errors introduced through numerical integration of the accelerometer data to generate the velocity and displacement data [
20]; and in the use of this calculated velocity data to identify the instant of impact and impact conditions.
5. Discussion
Microfoam models provided a good fit to the experimental shockpad data, particularly for the Berleburger shockpad. Although the Holywell shockpad exhibited more traditional hyper-elastic and viscoelastic behaviour, the microfoam model performed better overall than a more traditional hyper-elastic and viscoelastic Bergstrom-Boyce model. Further work is needed to understand the reasons for the differences in loading response for the two shockpads. Using the AAA test device to experimentally capture the stress-strain behaviour of the two shockpads under high strain rates was successful in helping to define these material models. Although the predictive capabilities of the two models have not been addressed, the ability of the models to fit not only to the impact drop height on which they were based, but also to lower energy impact drop heights, has been demonstrated. In reality, shockpads are exposed to a wide range of impact energies and a model that can estimate the response over this full range through a single set of measurements is relevant in optimising the design of 3G turf surface systems.
The AAA test can be very limited in terms of output if only considering the shock absorption and vertical deformation values as standalone measures of surface characteristics. Extracting the raw data from each of the drops allowed for a deeper analysis to be completed. Calculation of the corresponding stress and strain not only provided more information about the whole material response but also a way to use the data for material model calibration. This proved key in creating material models for both shockpads as using data recorded at slower strain rates, such as in the study by Mehvarar et al. [
20], did not yield a material model that could successfully be used within AAA simulations.
The three regions of shockpad deformation, as described in the literature [
13,
14], were observed in the experimental stress-strain response at higher drop heights. An initial period of low stiffness and high deflection was followed by a transition region and finally an increase in stiffness at higher strains as the air was squeezed out of the system and rubber-on-rubber contact ensued. At lower drop heights this was less evident and the response was more linear in nature as the shockpad did not experience sufficient strain to enter the second or third stages of compressive behaviour. Interestingly, the loading response for the Berleburger shockpad showed undulations in the loading curve from the AAA impact that was not seen in either the unloading, or in the Holywell shockpad.
Repeatability between drops of the same height remained high as the shockpads remained in their elastic region even at the highest drop heights. Thus, a single drop could be used to represent the shockpad response. The Berleburger shockpad was stiffer and had higher peak accelerations associated with all impacts at different heights when compared to the Holywell shockpad. This may be due to the reduced thickness of the Berleburger shockpad, resulting in the mass and impact foot having a shorter deceleration distance. The strains for each shockpad remained similar despite the difference in thickness, suggesting that thickening of the Berleburger shockpad may lead to better shock absorbing properties.
Calibration of the material models to the experimental data was a multi-step process (
Figure 7). The microfoam material model proved to be the more accurate as it allowed for the cellular characteristics of the shockpads to be captured. Relative density is an important characteristic for cellular materials as it expresses the density of the cellular material in relation to the dense solid [
24]. The model was able to incorporate the relative density of the shockpads and thus make a distinction between the density of the solid compared to that of the cellular material. As this value could be estimated for both the shockpads, the variable could be fixed whilst optimizing for the remaining model coefficients.
The FE simulation was deemed accurate if the mean error across all comparative measures was less than 10%, with no individual error greater than 15% (
Table 3). These values were chosen for a number of reasons but principally due to the experimental values used in the error assessment also being subject to errors. There was an uncertainty associated with the shockpad thickness values due to their construction method and granular nature (standard deviation from 15 thickness measurements was 0.1 mm for the Berleburger and 0.9 mm for the Holywell;
Table 1). This has the potential to influence the experimental strain calculations and the outputs from the simulation. The AAA test uses an accelerometer embedded within the 20 kg drop mass to determine the shock absorption, vertical deformation and energy restitution, and in this study the accelerometer output was also used to determine the experimental stress–strain response of the shockpad. The main errors that result from use of the accelerometer are in numerical integration of the acceleration data to determine velocity and displacement, and in determining the instant and conditions at impact. Some measures of these uncertainties can be inferred from the FIFA Quality Concept [
21]. In particular, these standards only require vertical deformation to be reported to the nearest 0.5 mm, corresponding to an uncertainty of 7–20% for the experimental values in this study (
Table 3). In addition, the standards specify a range for the required impact velocity of 1.02 to 1.04 m/s (for the 55 mm drop height). A sensitivity analysis conducted on the FE simulation, where the impact velocity was increased over this range, found a 1% reduction in shock absorption (corresponding to a 2% error in the FE simulation value) and no detectable change in vertical deformation, energy restitution or contact time. The second main reason for the chosen error values relates to the levels of accuracy reported in a previous study that simulated the AAA drop test onto athletic track materials [
15,
16]. This previous study used a less extensive error analysis than performed here, however, comparable errors of up to 8% in shock absorption were reported and deemed acceptable for the simulated response.
Validation of the material model was completed by running FE simulations for different drop heights and comparing the results to the experimental data. The results showed a good match to the stress-strain response for the lower drop heights. This result is somewhat unsurprising given that the lower drop heights tended to follow the same loading—unloading curve as the higher impacts. The energy restitution was poorly estimated for the higher drop heights due to the rebound velocity being much higher in the FE simulation than that of the experimental data. This suggests more energy needs to be taken out of the system. Attempts to further adjust the material models to allow for more energy to be absorbed caused the maximum force to drop and the vertical deformation to increase beyond the 15% error margin. Therefore, optimisation of all parameters requires a compromise to be made between making the models stiff enough to stop excessive deformation, but also compliant enough to absorb the impact forces and dissipate the impact energy.
More accurate deformation responses for the shockpads under the lower drop heights could have been achieved through calibration of the models to the stress–strain data for these drop heights. Calibration to the 55 mm drop height allowed for all three phases of shockpad response to be captured. Lower drop heights, particularly under 35 mm, were linear in nature and therefore were unlikely to be successful in estimating the shockpad response for higher drop heights. When considering the intended future application of this modelling work, i.e., to model the whole 3G turf surface system under human loading conditions, the stress at the shockpad level will be more variable than for the controlled conditions of this study. Therefore, having a model that can fit the shockpad response for a range of drop heights becomes much more desirable. While the 55 mm drop height (designed to emulate the impact of heel strike running on 3G turf) is likely to represent the maximum stress conditions the shockpad would be exposed to [
26].
The FIFA test measurements of shock absorption, energy restitution and vertical deformation allow for easy evaluation of the models and comparison of the shockpad responses. However, they are reliant on only a few discrete values taken from the impact data. Using only these values it would be easy to miss any differences in the loading curves between the two shockpads. Therefore, creating a simulation capable of reproducing acceptable values only for the FIFA test criteria may not result in an accurate representation of the full shockpad response. Inclusion of strain RMSE as an assessment criterion was important in giving a measure of how well the simulation captured this full response.