Abstract
Advances in nanofabrication technologies have enabled the study of acoustic wave phenomena in the technologically relevant GHz–THz range. First steps towards applying concepts from topology in nanophononics were made with the proposal of a new topological acoustic resonator, based on the concept of band inversion. In topology, the Su–Schrieffer–Heeger (SSH) model is the paradigm that accounts for the topological properties of many one-dimensional structures. Both the classical Fabry–Perot resonator and the reported topological resonators are based on Distributed Bragg Reflectors (DBRs). A clear and detailed relation between the two systems, however, is still lacking. Here, we show how a parallelism between the standard DBR-based acoustic Fabry–Perot type cavity and the SSH model of polyacetylene can be established. We discuss the existence of surface modes in acoustic DBRs and interface modes in concatenated DBRs and show that these modes are equivalent to Fabry–Perot type cavity modes. Although it is not possible to assign topological invariants to both acoustic bands enclosing the considered minigap in the nanophononic Fabry–Perot case, the existence of the confined mode in a Fabry–Perot cavity can nevertheless be interpreted in terms of the symmetry inversion of the Bloch modes at the Brillouin zone edge.
1. Introduction
Optical semiconductor microcavities are widely used in nanophotonic applications. Based on the concept of a Fabry–Perot resonator, the metallic mirrors are replaced by distributed Bragg reflectors (DBRs), where two materials with contrasting indices of refraction are arranged in a periodic stack. A widely used material combination for optical DBRs is GaAs/AlAs and their alloys [1], which have been extensively studied in electronics, optoelectronics, optics, and more recently in phononics [2]. Other applications of GaAs/AlAs also include solar cells, lasers, and, in general, any application requiring optical cavities working in the near-infrared transparency band of GaAs. Optical semiconductor cavities have been widely applied to the study of nonlinear optical effects, polariton physics [3,4,5,6] and in the development of single photon sources for quantum optical technologies [7,8].
The nanophononic equivalent of a Fabry–Perot resonator can be constructed by enclosing a resonant spacer between two acoustic DBRs, which present a periodic modulation of the acoustic impedance [9,10,11]. Similar to optical DBRs, these resonant structures can control the propagation of acoustic phonons in the technologically relevant GHz–THz range by making use of minigaps in their band structure at the center and the edge of the Brillouin zone. The properties that determine the behavior of a nanophononic DBR-based device are the thickness () of the layers, the mass density () and the speed of sound (). The mass density and the speed of sound are usually condensed into a single parameter, the acoustic impedance () [11,12]. Acoustic cavities have been used to study fundamental phenomena such as the confinement of acoustic phonons [10,13,14], their lifetimes [15] to control phonon propagation dynamics [10], and as efficient coherent phonon generators [13,16,17]. By coupling several acoustic resonators, it is furthermore possible to generate effective phononic potentials and to study, e.g., Bloch oscillations of acoustic phonons [12,18,19]. From a more applied point of view, acoustic DBRs and cavities have been useful to demonstrate the enhancement of magnetic measurements [20], the control of emission of quantum-dot based lasers [21], and the amplification and stimulated emission of acoustic waves [16,22,23]. In a nutshell, the Fabry–Perot resonator demonstrated to be a versatile and useful structure in nanophononics. Alternative proposals to confine a nanophononic mode have been explored by adapting concepts previously applied in optics such as adiabatic cavities, Tamm resonators and topological cavities [24,25]. It was recently realized that an optimized optical cavity in the near infrared is at the same time an optimized acoustic cavity in the 20 GHz range [11]. This concept was extended into GaAs/AlAs micropillars showing unprecedented quality factors at room temperature and high vacuum optomechanical couplings [2,26]. The possibility of simultaneously confining light and sound make the GaAs/AlAs microstructures a very attractive platform for optomechanics and optoelectronics where interactions with phonons can be used as an additional engineering tool.
In a previous work [27], we introduced the concept of topological invariants to nanophononics and experimentally implemented a nanophononic system supporting a robust topological interface state at 350 GHz. The confined nanophononic state was constructed through band inversion, i.e., by concatenating two semiconductor superlattices with inverted spatial mode symmetries at the Brillouin zone center. This led to the generation of robust interface states between two topologically different superlattices. To induce the exchange of spatial mode symmetries, i.e., the band inversion, we changed the thickness ratio between the two materials forming the individual DBRs. The existence of the resulting interface state was purely determined by the Zak phases, i.e., the one-dimensional analog of the geometric Berry phases, associated to the band structures of the constituent superlattices [28,29,30,31].
The thicknesses of the material layers constituting the heterostructure are the usual parameter space to tune the acoustic, optical and electronic properties in nanodevices. In this work, we study another set of parameters to control the symmetries of the Bloch modes: the composition of the materials forming the layers of the individual DBRs. We establish similarities and differences with the Su–Schrieffer–Heeger model, the standing paradigm of one-dimensional topological systems. We study the role of the composition () in a AlxGa1−xAs/Al1−xGaxAs superlattice and how to directly map an acoustic Fabry–Perot type structure to a polyacetylene chain described by the Su–Schrieffer–Heeger (SSH) model [32,33]. For the sake of clarity, in the rest of the article, we focus only on the mechanical response of the multilayers. The same analogies, however, also hold in the optical domain.
2. Interface Modes through Material Composition Tuning
The concept of inverted band structures is of paramount importance in the context of topological interface modes. In two-dimensional materials, the concept of inverted band structures usually refers to systems where the conduction and valence band symmetries are inverted [34]. In the context of this work, we denote that two one-dimensional systems present inverted bands when: (1) they have a common band gap; and (2) the modes at the Brillouin zone edge present opposite spatial symmetries. The concatenation of two superlattices with an inverted band gap typically leads to the formation of a confined mode at the interface. The presence of this interface state is unaffected by any perturbation which does not affect the topological invariants associated to the underlying lattices. In the case of a periodic one-dimensional system, the most commonly considered topological invariant is the Zak phase [28,29,30,35]. In a previous work [27], using the relative layer thickness ratio in a GaAs/AlAs superlattice, a band inversion [36] was achieved for the second minigap. By changing the thickness ratio, a band inversion can, however, only be achieved for the second and higher order minigaps [37]. In contrast, the first minigap at the Brillouin zone edge remains open for any thickness ratio, and thus a band inversion cannot be implemented in the same manner. We will show how to implement the band inversion principle around the first minigap through material composition tuning and how this strategy enables us to establish a link between Fabry–Perot resonators and a one-dimensional topological model.
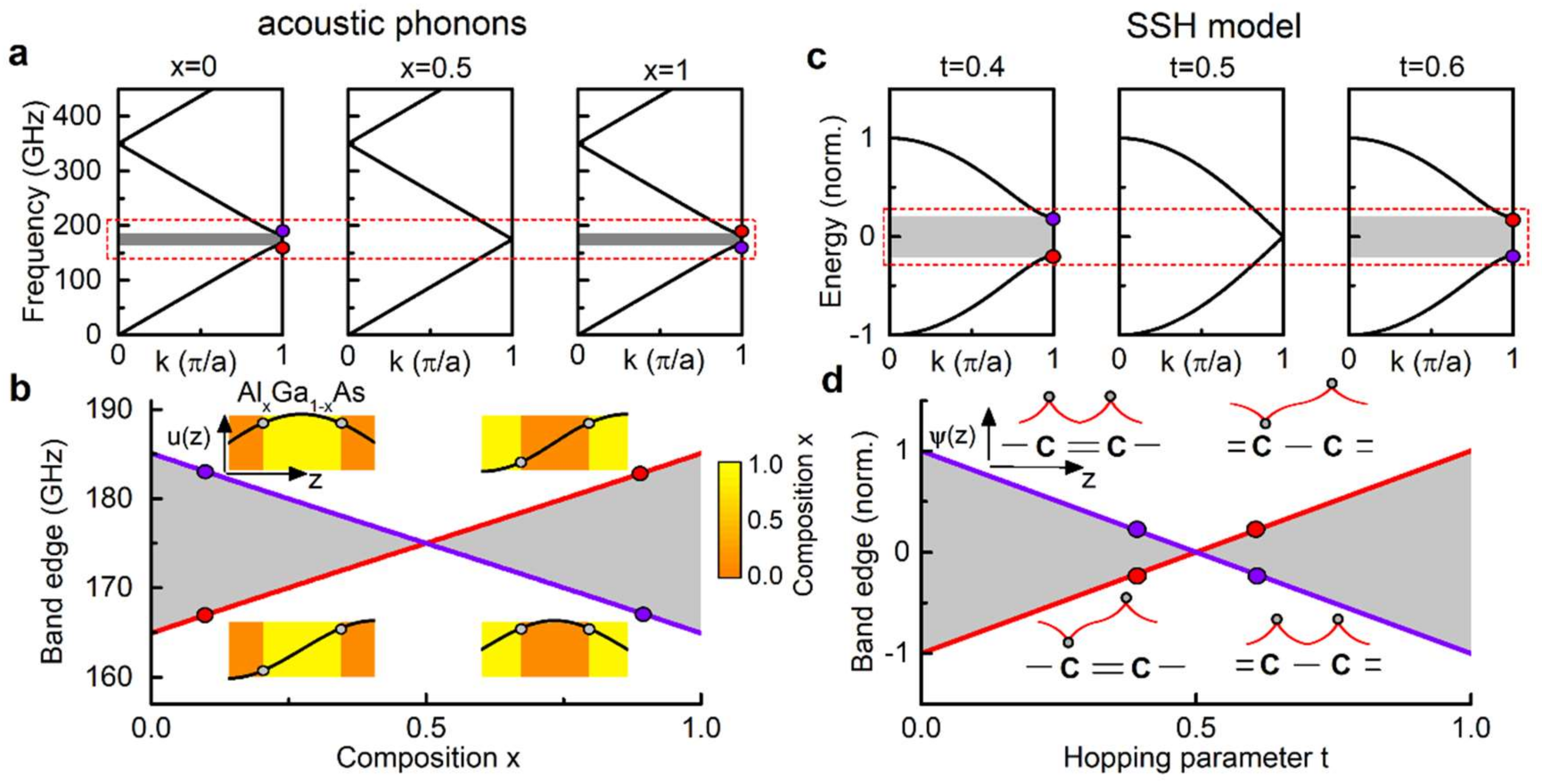
The Su–Schrieffer–Heeger (SSH) model [32,33,38] is one of the paradigms in one-dimensional topology. It describes an electron in the potential of a carbon chain with alternating single and double chemical bonds, i.e., a polyacetylene molecule. The order of the single and double bonds leads to two energetically degenerate isomers. In the tight binding approximation, the periodic potential gives rise to a simple band structure, as shown in Figure 1c. Let us denote the strength of a single bond as t and that of a double bond as . For the case (left panel), we observe an open minigap at the Brillouin zone edge. For (right panel) the weak and strong coupling terms are exchanged with respect to giving rise to exactly the same band structure. For the particular case , however, all hopping terms become identical and the minigap closes (central panel). By looking at the symmetries of the corresponding electronic wave function at the band edges bounding the minigap (shown in the insets of panel d), it becomes evident that an inversion of the symmetries occurs when crossing the point . We denote (anti-)symmetric electron wave functions with a violet (red) dot. By varying the value of continuously, we trace out the evolution of the spectral width of the electronic minigap as shown in Figure 1d. The violet and red lines indicate the normalized energies of the two band edges enclosing the minigap. In grey, the span of the minigap is indicated.
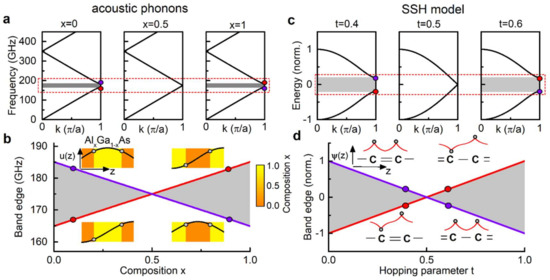
Figure 1.
Band inversion principle shown for the nanophononic superlattice case (left) and the SSH model (right). (a,c) The band structure diagram for the nanophononic and polyacetylene cases. Three conditions are illustrated: open minigap, closed minigap, and reopened minigap with the symmetries of the band edge modes inverted. The symmetries of the Bloch modes are indicated with violet (symmetric) and red (antisymmetric) dots, respectively; (b,d) The span of the minigap as a function of the material composition (left) or SSH hopping parameter (right). The symmetries of the Bloch edge modes are inverted when crossing the value 0.5, i.e., equal material for all layers or equal hopping strength for all bonds, respectively. The insets in the bottom panels indicate the acoustic field distribution (left) and the electronic wavefunction (right) corresponding to the Bloch modes at the Brillouin zone edge. Note that the symmetries of the modes are exchanged between the upper and lower edge when crossing the topological phase transition at a value of .
We now establish a direct relationship between the elements of an acoustic superlattice and the electronic potential of a polyacetylene molecule. Note that the chemical bonds are mirror planes of the infinite carbon chain, whereas the centers of the material layers are mirror planes of the infinite acoustic superlattice. The carbon atoms can thus be associated to acoustic interfaces and the bonds to material layers. Interestingly, if the atoms were associated to acoustic layers, this correspondence between mirror planes would be broken. In the following, we explore to which extent this mapping can account for the behavior of a nanophononic systems by relying on conclusions drawn from the SSH model.
A method to realize the band inversion principle for the first minigap at the Brillouin zone edge is depicted in Figure 1a,b. We consider DBRs for longitudinal acoustic phonons, which are constituted by alternating layers of materials A and B with acoustic impedances and ( mass density and speed of sound). At a design frequency , the total acoustic path length of each layer is set to a quarter of a phonon wavelength , i.e., the thicknesses of the layers obey . For GaAs (AlAs), () and () resulting in (). A phase of is thus accumulated by a phonon at frequency traversing both layers of the unit cell. Consequently, all band gaps of the DBR are centered at integer multiples of . For the sake of clarity, we consider that materials A and B are AlxGa1−xAs and Al1−xGaxAs where parametrizes the composition.
Let us analyze the band inversion in this system. In Figure 1a, we show three band structures for different values of , obtained by a transfer matrix method. First, for the first minigap is open, presenting a symmetric (anti-symmetric) Bloch mode at the upper (lower) band edge. As before, we denote (anti-)symmetric modes with a violet (red) dot. Second, for , the minigap is closed and thus no symmetries can be assigned to the degenerate edge modes. Note that this case represents a homogeneous material and the folding of the dispersion relation in the Brillouin zone is merely an arbitrary choice. Third, for , we observe the same bandstructure as in the first case, but the spatial symmetries of the band edge modes are inverted. By varying the value of continuously, we trace out the evolution of the spectral width of the first acoustic minigap, as shown in Figure 1b. The violet and red lines indicate the frequencies of the two band edges enclosing the considered gap. In grey, the span of the minigap is indicated. For our particular case, according to Refs. [27,28,29,35,39], the Zak phase corresponding to the lowest band is unequivocally related to the order of mode symmetries at the band edge.
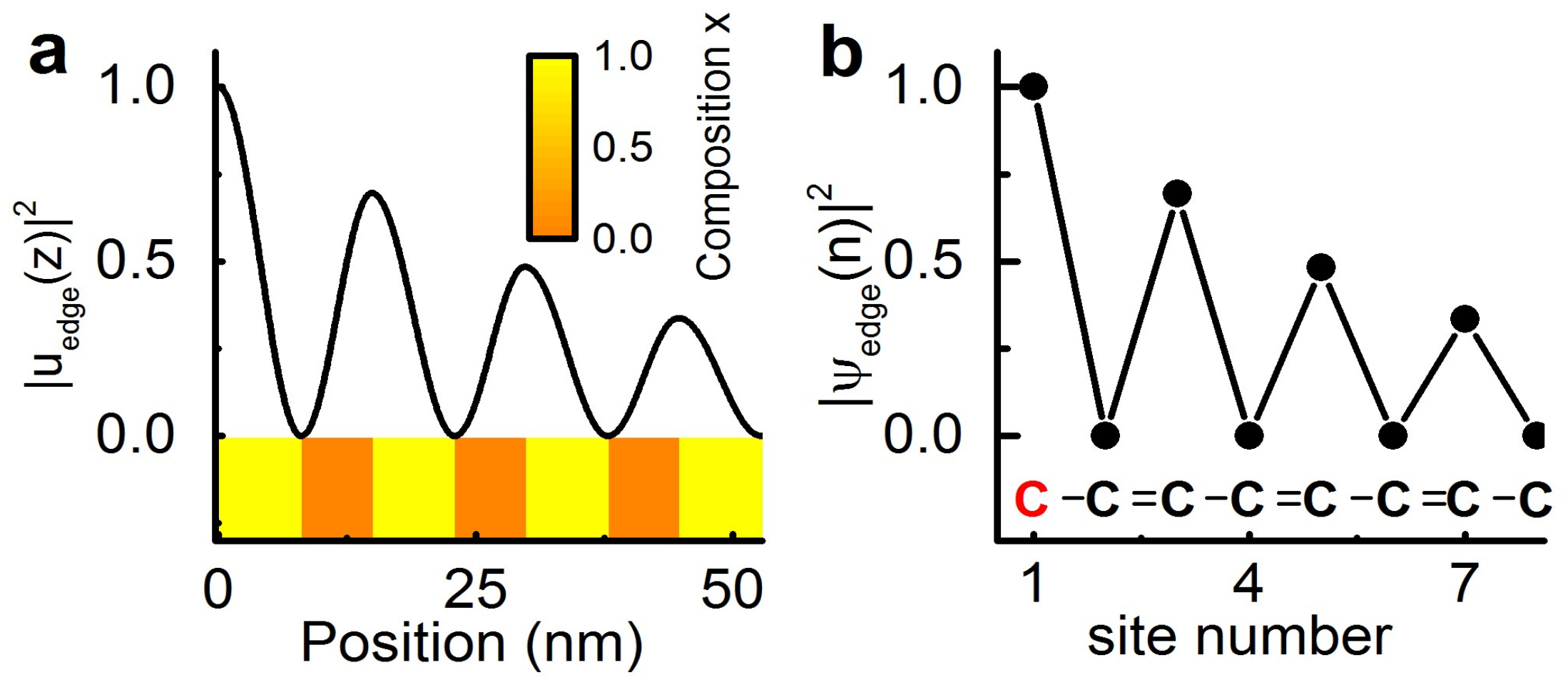
The SSH model predicts the appearance of an edge mode in the center of the minigap when the last bond in a terminated carbon chain is of the weaker (single bond) type. The electronic density distribution of this edge mode is shown in Figure 2b together with an illustration of the corresponding semi-infinite carbon chain. In Figure 2a, we show the nanophononic equivalent of this situation: a AlAs layer terminating a DBR. In this case, a surface mode appears, with a frequency at the center of the first acoustic minigap. The acoustic displacement corresponding to this confined mode is shown in the same figure. Note that for the DBR the standard zero-stress condition is applied at the left boundary. This accounts for the fact that high frequency phonons do not propagate in air and are hence completely reflected. The analogy to the edge mode in the SSH model is evident. Maxima of the mechanical displacement (the electronic wavefunction) are observed at every other interface (on every other carbon atom) and both modes decay evanescently away from the surface (the end of the carbon chain).
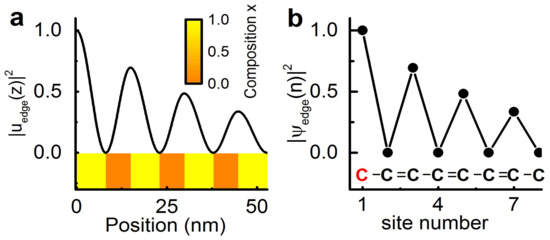
Figure 2.
Edge mode observed in a semi-infinite system in the case of: a nanophononic GaAs/AlAs superlattice (a); and a polyacetylene molecule (b). This mode only exists when the last bond in the chain is the weaker among the two types: in the acoustic case it corresponds to finishing the chain with an AlAs layer, in the case of the polyacetylene it corresponds to a single (weak hopping) bond at the end of the chain.
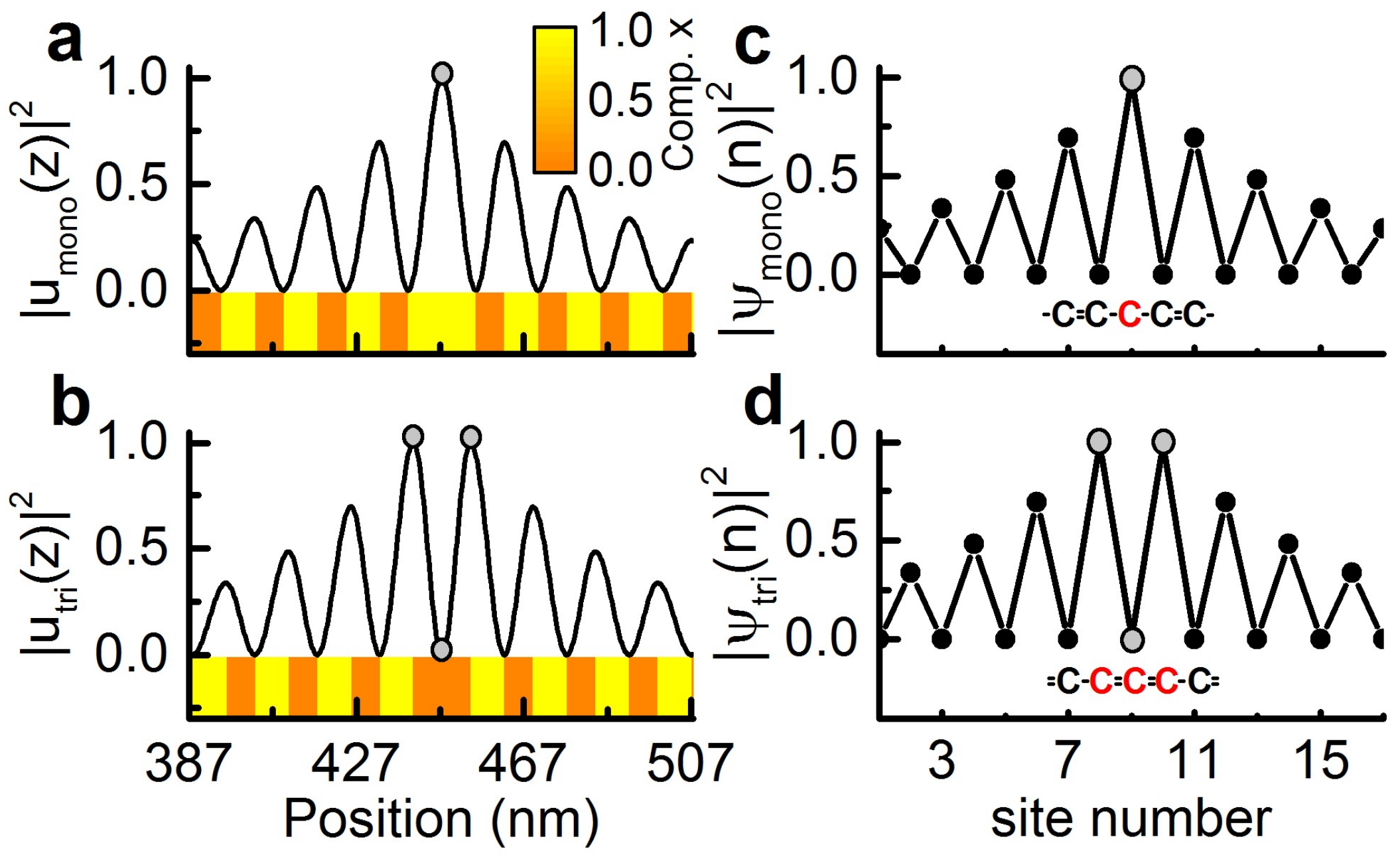
Perhaps one of the most important predictions of the SSH model is the generation of an interface mode when two carbon chains with inverted bands are concatenated. This interface mode appears at the center of the minigap as shown in Figure 3c,d. Two possible ways exist to connect two semi-infinite carbon chains: either by adding an additional single (weak hopping) bond, or a double (strong hopping) bond. The strength of the additional bond determines whether the confined state will be monomer-like (with a single maximum) or a trimer-like state (with two maxima).
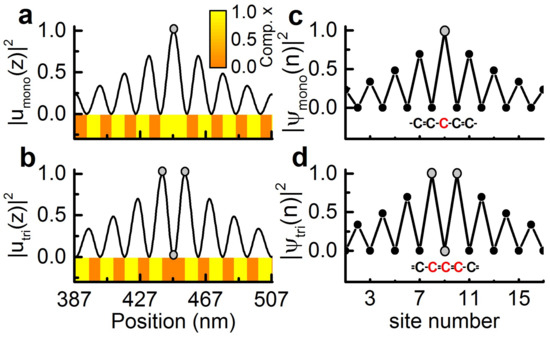
Figure 3.
Interface mode resulting from the concatenation of two semi-infinite systems with different topological phases: (a,b) the nanophononic case; and (c,d) the polyacetylene–SSH model. There are two possibilities to connect the two semi-infinite systems with different topological phases: (a,c) the monomer case, in which the two chains are connected with a single bond, i.e., a weak hopping link; and (c,d) the trimer case, i.e., when the two chains are connect with a double bond, resulting in a strong hopping link.
In Figure 3c, we show the representation of these two concatenated carbon chains with an additional weak link and the corresponding electronic density confined around the central atom. Following this construction principle, two acoustic superlattices with inverted bands can be concatenated by a weak link (i.e., an AlAs layer) as well. This generates the interface mode shown in Figure 3a. As predicted by the SSH model, the acoustic mode appears at the center of the first acoustic minigap. The resulting nanophononic structure presents two identical layers at the interface forming a spacer. Therefore, the system can be effectively decomposed into a resonant spacer enclosed by two identical DBRs, resulting in the widely used Fabry–Perot resonator. By using the composition as a design parameter inducing a topological phase transition, Fabry–Perot resonators can hence be explained in terms of symmetry considerations, in particular the inversion of the Bloch mode symmetries at the Brillouin zone edge. In Figure 3b, we show the nanophononic case resulting in a trimer like confined state. Here, the two DBRs are connected by an additional GaAs layer generating a GaAs spacer. The GaAs spacer generates an anti-guiding mode, i.e., a mode with maxima of the field at the interfaces of the DBRs, contrary to what happens with an AlAs spacer that presents minima at these interfaces. The equivalent trimer state in the framework of the SSH model is shown in Figure 3d.
At high phononic frequencies, usually only modes around the Brillouin zone center are accessible through Raman scattering and pump probe experiments. A confined mode at the edge of the Brillouin zone, as the one presented in Figure 3, could be experimentally measured in resonant Raman scattering or in resonant pump probe coherent phonon generation experiments. In these cases, the excitation laser should be resonant with the excitonic transition of the acoustic spacer, as described in Refs. [13,40].
3. Discussion and Conclusions
The possibility using nanophononic cavities as a suitable platform to study topological phenomena is in fact an interesting perspective of this work. Two parameters are usually used to engineer the performance of acoustic phonon devices, the thickness of the layers and the material composition of these heterostructures. In this work, we showed how it is possible to predict the confinement characteristics of a standard Fabry–Perot resonator from topological considerations based on the SSH model. Although main predictions such as the existence of edge and interface modes are confirmed, the strict assignment of Zak phases to the bands enclosing the considered minigap is not possible in the phononic case. In particular, the band bounding the first minigap from above is not isolated, i.e., the second acoustic minigap is closed for a superlattice.
In a previous work [27], it was demonstrated that the band inversion principle can be implemented in nanophononic systems by changing the thickness of the composing materials. Using this technique, it is however only possible to induce a band inversion for the second and higher order minigaps since the first minigap (at the Brillouin zone edge) is open for any thickness ratio, such that the symmetries of the Bloch modes at the minigap edges cannot be swapped by a band inversion.
In contrast, we showed in this work that, by tuning the composition of the materials, while keeping the acoustic length of each layer fixed at the specific value of , it is indeed possible to close and reopen the first minigap with exchanged Bloch mode symmetries. Depending on the chosen way to concatenate two DBRs, it is furthermore possible to form the equivalent of a monomer and the trimer states predicted by the SSH model, which correspond to the modes of a Fabry–Perot resonator with either a high-index or low-index spacer.
Acknowledgments
The authors acknowledge funding through the ERC Starting Grant No. 715939 Nanophennec; a public grant overseen by the French National Research Agency (ANR) as part of the ”Investissements d’Avenir” program (Labex NanoSaclay, reference: ANR-10-LABX-0035); and the “Initiative de Recherche stratégique” of the Université Paris-Saclay through the IQUPS project.
Author Contributions
M.E. and N.D.L.K. contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results
References
- Adachi, S. GaAs, AlAs, and AlxGa1−xAs: Material parameters for use in research and device applications. J. Appl. Phys. 1985, 58, R1. [Google Scholar] [CrossRef]
- Anguiano, S.; Bruchhausen, A.E.; Jusserand, B.; Favero, I.; Lamberti, F.R.; Lanco, L.; Sagnes, I.; Lemaître, A.; Lanzillotti-Kimura, N.D.; Senellart, P.; et al. Micropillar Resonators for Optomechanics in the Extremely High 19–95-GHz Frequency Range. Phys. Rev. Lett. 2017, 118, 263901. [Google Scholar] [CrossRef] [PubMed]
- Bajoni, D.; Senellart, P.; Wertz, E.; Sagnes, I.; Miard, A.; Lemaître, A.; Bloch, J. Polariton Laser Using Single Micropillar GaAs−GaAlAs Semiconductor Cavities. Phys. Rev. Lett. 2008, 100, 47401. [Google Scholar] [CrossRef] [PubMed]
- Galbiati, M.; Ferrier, L.; Solnyshkov, D.; Tanese, D.; Wertz, E.; Amo, A.; Abbarchi, M.; Senellart, P.; Sagnes, I.; Lemaître, A.; et al. Polariton Condensation in Photonic Molecules. Phys. Rev. Lett. 2012, 108, 126403. [Google Scholar] [CrossRef] [PubMed]
- Jacqmin, T.; Carusotto, I.; Sagnes, I.; Abbarchi, M.; Solnyshkov, D.D.; Malpuech, G.; Galopin, E.; Lemaître, A.; Bloch, J.; Amo, A. Direct Observation of Dirac Cones and a Flatband in a Honeycomb Lattice for Polaritons. Phys. Rev. Lett. 2014, 112, 116402. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.S.; Gerace, D.; Carusotto, I.; Sanvitto, D.; Galopin, E.; Lemaître, A.; Sagnes, I.; Bloch, J.; Amo, A. Acoustic Black Hole in a Stationary Hydrodynamic Flow of Microcavity Polaritons. Phys. Rev. Lett. 2015, 114, 36402. [Google Scholar] [CrossRef] [PubMed]
- Somaschi, N.; Giesz, V.; Santis, L.D.; Loredo, J.C.; Almeida, M.P.; Hornecker, G.; Portalupi, S.L.; Grange, T.; Antón, C.; Demory, J.; et al. Near-optimal single-photon sources in the solid state. Nat. Photonics 2016, 10, 340–345. [Google Scholar] [CrossRef]
- Giesz, V.; Somaschi, N.; Hornecker, G.; Grange, T.; Reznychenko, B.; de Santis, L.; Demory, J.; Gomez, C.; Sagnes, I.; Lemaître, A.; et al. Coherent manipulation of a solid-state artificial atom with few photons. Nat. Commun. 2016, 7, 11986. [Google Scholar] [CrossRef] [PubMed]
- Trigo, M.; Bruchhausen, A.; Fainstein, A.; Jusserand, B.; Thierry-Mieg, V. Confinement of Acoustical Vibrations in a Semiconductor Planar Phonon Cavity. Phys. Rev. Lett. 2002, 89, 227402. [Google Scholar] [CrossRef] [PubMed]
- Huynh, A.; Lanzillotti-Kimura, N.; Jusserand, B.; Perrin, B.; Fainstein, A.; Pascual-Winter, M.; Peronne, E.; Lemaître, A. Subterahertz Phonon Dynamics in Acoustic Nanocavities. Phys. Rev. Lett. 2006, 97, 115502. [Google Scholar] [CrossRef] [PubMed]
- Fainstein, A.; Lanzillotti-Kimura, N.D.; Jusserand, B.; Perrin, B. Strong Optical-Mechanical Coupling in a Vertical GaAs/AlAs Microcavity for Subterahertz Phonons and Near-Infrared Light. Phys. Rev. Lett. 2013, 110, 37403. [Google Scholar] [CrossRef] [PubMed]
- Lanzillotti-Kimura, N.; Fainstein, A.; Balseiro, C.; Jusserand, B. Phonon engineering with acoustic nanocavities: Theoretical considerations on phonon molecules, band structures, and acoustic Bloch oscillations. Phys. Rev. B 2007, 75, 24301. [Google Scholar] [CrossRef]
- Winter, M.F.P.; Rozas, G.; Fainstein, A.; Jusserand, B.; Perrin, B.; Huynh, A.; Vaccaro, P.O.; Saravanan, S. Selective Optical Generation of Coherent Acoustic Nanocavity Modes. Phys. Rev. Lett. 2007, 98, 265501. [Google Scholar] [CrossRef] [PubMed]
- Villafañe, V.; Soubelet, P.; Bruchhausen, A.E.; Lanzillotti-Kimura, N.D.; Jusserand, B.; Lemaître, A.; Fainstein, A. Slow light and slow acoustic phonons in optophononic resonators. Phys. Rev. B 2016, 94, 205308. [Google Scholar] [CrossRef]
- Rozas, G.; Winter, M.; Jusserand, B.; Fainstein, A.; Perrin, B.; Semenova, E.; Lemaître, A. Lifetime of THz Acoustic Nanocavity Modes. Phys. Rev. Lett. 2009, 102, 15502. [Google Scholar] [CrossRef] [PubMed]
- Lanzillotti-Kimura, N.; Fainstein, A.; Perrin, B.; Jusserand, B.; Soukiassian, A.; Xi, X.; Schlom, D. Enhancement and Inhibition of Coherent Phonon Emission of a Ni Film in a BaTiO3/SrTiO3 Cavity. Phys. Rev. Lett. 2010, 104, 187402. [Google Scholar] [CrossRef] [PubMed]
- Lanzillotti-Kimura, N.D.; Fainstein, A.; Jusserand, B. Towards GHz–THz cavity optomechanics in DBR-based semiconductor resonators. Ultrasonics 2015, 56, 80–89. [Google Scholar] [CrossRef] [PubMed]
- Kimura, N.D.L.; Fainstein, A.; Jusserand, B. Phonon Bloch oscillations inacoustic-cavity structures. Phys. Rev. B 2005, 71, 41305. [Google Scholar] [CrossRef]
- Lanzillotti-Kimura, N.D.; Fainstein, A.; Perrin, B.; Jusserand, B.; Mauguin, O.; Largeau, L.; Lemaître, A. Bloch Oscillations of THz Acoustic Phonons in Coupled Nanocavity Structures. Phys. Rev. Lett. 2010, 104, 197402. [Google Scholar] [CrossRef] [PubMed]
- Jäger, J.V.; Scherbakov, A.V.; Glavin, B.A.; Salasyuk, A.S.; Campion, R.P.; Rushforth, A.W.; Yakovlev, D.R.; Akimov, A.V.; Bayer, M. Resonant driving of magnetization precession in a ferromagnetic layer by coherent monochromatic phonons. Phys. Rev. B 2015, 92, 20404. [Google Scholar] [CrossRef]
- Brüggemann, C.; Akimov, A.V.; Scherbakov, A.V.; Bombeck, M.; Schneider, C.; Höfling, S.; Forchel, A.; Yakovlev, D.R.; Bayer, M. Laser mode feeding by shaking quantum dots in a planar microcavity. Nat. Photonics 2012, 6, 30–34. [Google Scholar] [CrossRef]
- Beardsley, R.P.; Akimov, A.V.; Henini, M.; Kent, A.J. Coherent Terahertz Sound Amplification and Spectral Line Narrowing in a Stark Ladder Superlattice. Phys. Rev. Lett. 2010, 104, 85501. [Google Scholar] [CrossRef] [PubMed]
- Maryam, W.; Akimov, A.V.; Campion, R.P.; Kent, A.J. Dynamics of a vertical cavity quantum cascade phonon laser structure. Nat. Commun. 2013, 4, 2184. [Google Scholar] [CrossRef] [PubMed]
- Villafañe, V.; Bruchhausen, A.E.; Jusserand, B.; Senellart, P.; Lemaître, A.; Fainstein, A. Confinement of gigahertz sound and light in Tamm plasmon resonators. Phys. Rev. B 2015, 92, 165308. [Google Scholar] [CrossRef]
- Lamberti, F.R.; Esmann, M.; Lemaître, A.; Carbonell, C.G.; Krebs, O.; Favero, I.; Jusserand, B.; Senellart, P.; Lanco, L.; Lanzillotti-Kimura, N.D. Nanomechanical resonators based on adiabatic periodicity-breaking in a superlattice. Appl. Phys. Lett. 2017, 111, 173107. [Google Scholar] [CrossRef]
- Lamberti, F.R.; Yao, Q.; Lanco, L.; Nguyen, D.T.; Esmann, M.; Fainstein, A.; Sesin, P.; Anguiano, S.; Villafañe, V.; Bruchhausen, A.; et al. Optomechanical properties of GaAs/AlAs micropillar resonators operating in the 18 GHz range. Opt. Express 2017, 25, 24437–24447. [Google Scholar] [CrossRef] [PubMed]
- Esmann, M.; Lamberti, F.R.; Senellart, P.; Favero, I.; Krebs, O.; Lanco, L.; Carbonell, C.G.; Lemaitre, A.; Lanzillotti-Kimura, N.D. Topological nanophononic states by band inversion. arxiv, 2018; arXiv:1802.08870. [Google Scholar]
- Xiao, M.; Ma, G.; Yang, Z.; Sheng, P.; Zhang, Z.Q.; Chan, C.T. Geometric phase and band inversion in periodic acoustic systems. Nat. Phys. 2015, 11, 240–244. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, Z.Q.; Chan, C.T. Surface Impedance and Bulk Band Geometric Phases in One-Dimensional Systems. Phys. Rev. X 2014, 4, 21017. [Google Scholar] [CrossRef]
- Rhim, J.-M.; Behrends, J.; Bardarson, J.H. Bulk-boundary correspondence from the inter-cellular Zak phase. Phys. Rev. B 2017, 95, 35421. [Google Scholar] [CrossRef]
- Amo, A.; Lemaître, A.; Galopin, E.; Sagnes, I.; Bloch, J.; Gratiet, L.L.; St-Jean, P.; Ozawa, T.; Goblot, V. Lasing in topological edge states of a one-dimensional lattice. Nat. Photonics 2017, 11, 651–656. [Google Scholar]
- Heeger, A.J. Nobel Lecture: Semiconducting and metallic polymers:The fourth generation of polymeric materials. Rev. Mod. Phys. 2001, 73, 681. [Google Scholar] [CrossRef]
- Su, W.; Schrieffer, J.R.; Heeger, A.J. Solitons in Polyacetylene. Phys. Rev. Lett. 1979, 42, 1698. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.-C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef] [PubMed]
- Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 1989, 62, 2747. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.-G.; Geng, Z.-G.; Zhu, X.-F. Topologically protected bound states in one-dimensional Floquet acoustic waveguide systems. J. Appl. Phys. 2018, 123, 91716. [Google Scholar] [CrossRef]
- Jusserand, B.; Cardona, M. Light Scatt. Solids V; Springer: Berlin/Heidelberg, Germany, 1989; pp. 49–152. [Google Scholar]
- Su, W.-P.; Schrieffer, J.R.; Heeger, A.J. Soliton excitations in polyacetylene. Phys. Rev. B 1980, 22, 2099. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 1984, 392, 45–57. [Google Scholar] [CrossRef]
- Lanzillotti-Kimura, N.D.; Fainstein, A.; Jusserand, B.; Lemaître, A. Resonant Raman scattering of nanocavity-confined acoustic phonons. Phys. Rev. B 2009, 79, 35404. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).