Energy Management Strategy for the Hybrid Energy Storage System of Pure Electric Vehicle Considering Traffic Information
Abstract
1. Introduction
2. Parameters and Model
3. Adaptive Rule Based Controller
3.1. Offline Optimization of Dynamic Programming
3.2. Formulation of Adaptive Rule Based Controller
4. Comprehensive Controller Considering Traffic Information
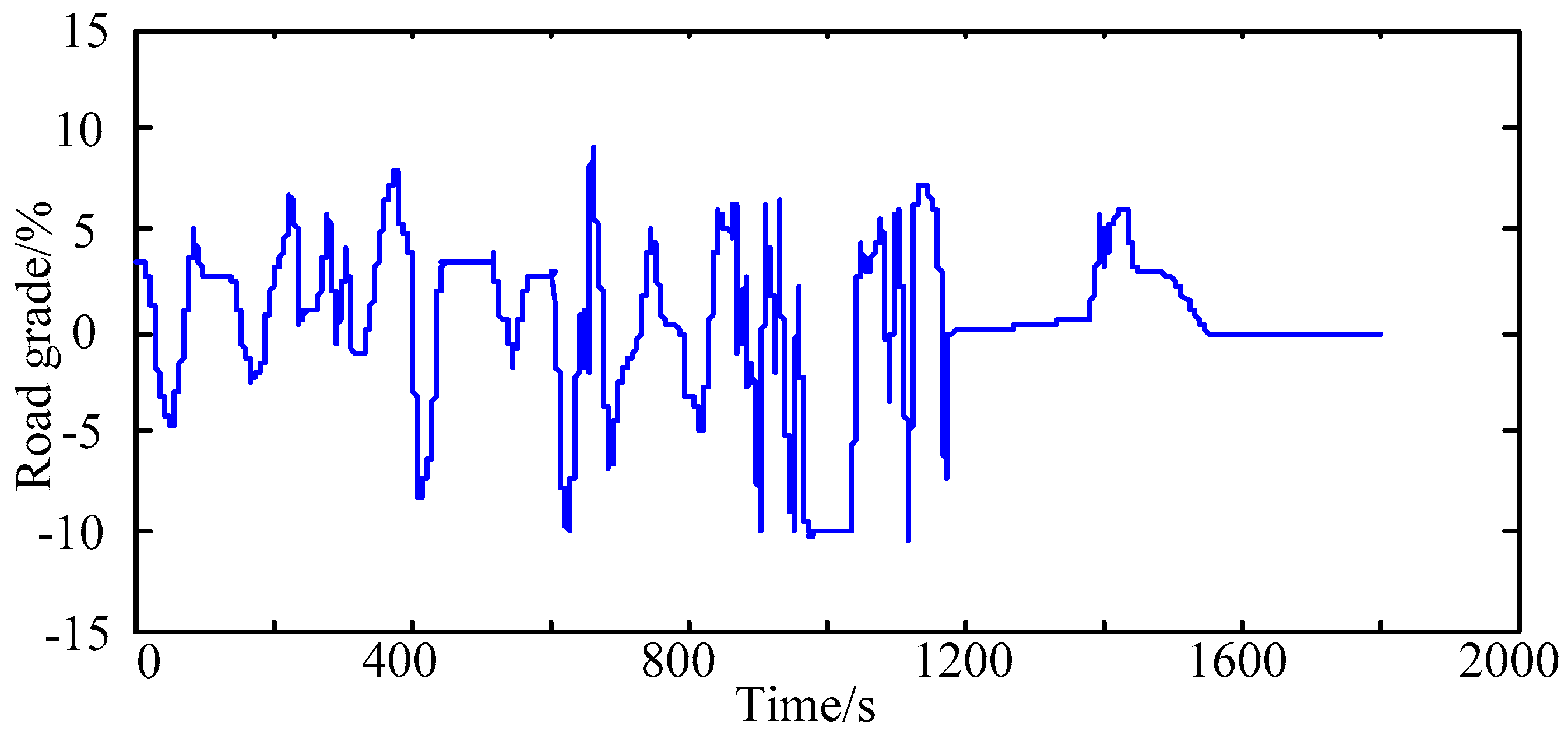
4.1. Access to the Traffic Condition and the Road Grade
4.2. Future Trend Prediction of Vehicle Speed
- ①
- The combined driving cycle, including MANHATTAN, NYCC, UDDS, NEDC, WVUINTER, and HWFET, is selected as the sample driving cycle, as shown in Figure 6. These six driving cycles cover urban, suburban, and expressway condition.
- ②
- The sampling period is 1 s and the driving cycle between the two sampling points is a driving cycle block. The average accelerated speed, the standard deviation of the vehicle speed, and the difference between the initial speed and the last speed of a driving cycle block are selected as the characteristic parameters of the driving cycles [32]. The characteristic parameters of 10 s are calculated at each sampling point.
- ③
- ④
- After obtaining the cluster centers, the distance, , from various characteristic parameters to the th cluster center can be computed by Equation (11). If & , the state of the vehicle speed is the type of speed descending, and the state of the vehicle speed belongs to the speed stabling when & . If & , the vehicle speed is considered to be a speed rising.
4.3. Optimization of Instantaneous Power Allocation
5. Results
6. Conclusions
- (1)
- A general law exists in the optimal power allocation of HESS under various types of driving cycles, and the controllers based on the law can achieve good economic performance of HESS.
- (2)
- Considering traffic information in a controller is beneficial to the performance promotion of HESS.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jordán, J.; Palanca, J.; Val, E.D.; Julian, V.; Botti, V. A Multi-Agent System for the Dynamic Emplacement of Electric Vehicle Charging Stations. Appl. Sci. 2018, 8, 313. [Google Scholar] [CrossRef]
- Gong, H.; Zou, Y.; Yang, Q.; Fan, J.; Sun, F. Generation of a driving cycle for battery electric vehicles: A case study of Beijing. Energy 2018, 150, 901–912. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, W.; Wei, S.; Lin, H.; Jia, Z. An Improved Energy Management Strategy for Hybrid Energy Storage System in Light Rail Vehicles. Energies 2018, 11, 423. [Google Scholar] [CrossRef]
- Fu, Z.M.; Wang, B.; Zhou, P.G. An improved logic threshold approach of energy management for a power-split hybrid electric vehicle. In Proceedings of the International Conference on Advanced Mechatronic Systems, Zhengzhou, China, 29 August–2 September 2018; pp. 244–248. [Google Scholar]
- Xiang, C.; Wang, Y.; Hu, S.; Wang, W. A New Topology and Control Strategy for a Hybrid Battery-Ultracapacitor Energy Storage System. Energies 2014, 7, 2874–2896. [Google Scholar] [CrossRef]
- Wu, J.; Peng, J.; He, H.; Luo, J. Comparative Analysis on the Rule-based Control Strategy of Two Typical Hybrid Electric Vehicle Powertrain. Energy Procedia 2016, 104, 384–389. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Zhao, Y.; Yang, L.; Chen, W. A Fuzzy-Logic Power Management Strategy Based on Markov Random Prediction for Hybrid Energy Storage Systems. Energies 2016, 9, 25. [Google Scholar] [CrossRef]
- Ferreira, A.A.; Pomilio, J.A.; Spiazzi, G.; Silva, L.D.A. Energy Management Fuzzy Logic Supervisory for Electric Vehicle Power Supplies System. IEEE Trans. Power Electron. 2008, 23, 107–115. [Google Scholar] [CrossRef]
- Jaafar, A.; Akli, C.R.; Sareni, B.; Roboam, X.; Jeunesse, A. Sizing and Energy Management of a Hybrid Locomotive Based on Flywheel and Accumulators. IEEE Trans. Veh. Technol. 2009, 58, 3947–3958. [Google Scholar] [CrossRef]
- Song, Z.; Hofmann, H.; Li, J.; Hou, J.; Han, X.; Ouyang, M. Energy management strategies comparison for electric vehicles with hybrid energy storage system. Appl. Energy 2014, 134, 321–331. [Google Scholar] [CrossRef]
- Santucci, A.; Sorniotti, A.; Lekakou, C. Power split strategies for hybrid energy storage systems for vehicular applications. J. Power Sources 2014, 258, 395–407. [Google Scholar] [CrossRef]
- Chen, B.C.; Wu, Y.Y.; Tsai, H.C. Design and analysis of power management strategy for range extended electric vehicle using dynamic programming. Appl. Energy 2014, 113, 1764–1774. [Google Scholar] [CrossRef]
- Chen, S.Y.; Hung, Y.H.; Wu, C.H.; Huang, S.T. Optimal energy management of a hybrid electric powertrain system using improved particle swarm optimization. Appl. Energy 2015, 160, 132–145. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Cao, J.; Lund, H.; Kaiser, M.J. Particle swarm optimization-based optimal power management of plug-in hybrid electric vehicles considering uncertain driving conditions. Energy 2016, 96, 197–208. [Google Scholar] [CrossRef]
- Xiao, R.; Liu, B.; Shen, J.; Guo, N.; Yan, W.; Chen, Z. Comparisons of Energy Management Methods for a Parallel Plug-In Hybrid Electric Vehicle between the Convex Optimization and Dynamic Programming. Appl. Sci. 2018, 8, 218. [Google Scholar] [CrossRef]
- Hu, X.; Moura, S.J.; Murgovski, N.; Bo, E.; Cao, D. Integrated Optimization of Battery Sizing, Charging, and Power Management in Plug-In Hybrid Electric Vehicles. IEEE Trans. Control. Syst. Technol. 2016, 24, 1036–1043. [Google Scholar] [CrossRef]
- Godina, R.; Rodrigues, E.M.G.; Pouresmaeil, E.; Matias, J.C.O.; Catalão, J.P.S. Model Predictive Control Home Energy Management and Optimization Strategy with Demand Response. Appl. Sci. 2018, 8, 408. [Google Scholar] [CrossRef]
- Zhou, F.; Xiao, F.; Chang, C.; Shao, Y.; Song, C. Adaptive Model Predictive Control-Based Energy Management for Semi-Active Hybrid Energy Storage Systems on Electric Vehicles. Energies 2017, 10, 1063. [Google Scholar] [CrossRef]
- Zhang, S.; Xiong, R.; Sun, F. Model predictive control for power management in a plug-in hybrid electric vehicle with a hybrid energy storage system. Appl. Energy 2017, 185, 1654–1662. [Google Scholar] [CrossRef]
- Lei, Z.; Qin, D.; Liu, Y.; Peng, Z.; Lu, L. Dynamic energy management for a novel hybrid electric system based on driving pattern recognition. Appl. Math. Model. 2017, 45, 940–954. [Google Scholar] [CrossRef]
- Salmasi, F.R. Control Strategies for Hybrid Electric Vehicles: Evolution, Classification, Comparison, and Future Trends. IEEE Trans. Veh. Technol. 2007, 56, 2393–2404. [Google Scholar] [CrossRef]
- He, H.; Guo, J.; Sun, C. Road Grade Prediction for Predictive Energy Management in Hybrid Electric Vehicles ☆. Energy Procedia 2017, 105, 2438–2444. [Google Scholar] [CrossRef]
- Hovgard, M.; Jonsson, O.; Murgovski, N.; Sanfridson, M.; Fredriksson, J. Cooperative energy management of electrified vehicles on hilly roads. Control. Eng. Pract. 2018, 73, 66–78. [Google Scholar] [CrossRef]
- Bouwman, K.R.; Pham, T.H.; Wilkins, S.; Hofman, T. Predictive Energy Management Strategy Including Traffic Flow Data for Hybrid Electric Vehicles. IFAC-PapersOnLine 2017, 50, 10046–10051. [Google Scholar] [CrossRef]
- Song, Z.; Hofmann, H.; Li, J.; Han, X.; Zhang, X.; Ouyang, M. A comparison study of different semi-active hybrid energy storage system topologies for electric vehicles. J. Power Sources 2015, 274, 400–411. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, F.; Yu, H. Research on LiFePO4 battery life model based on driving cycle. Automobile Eng. 2015, 8, 881–885. [Google Scholar]
- Luo, Y.; Liu, X.; Liang, W. Design of hybrid energy storage system for electric vehicles to extend the life of lithium ion batteries. J. South China Univ. Technol. 2016, 44, 51–59. [Google Scholar]
- Song, Z.; Hofmann, H.; Li, J.; Han, X.; Ouyang, M. Optimization for a hybrid energy storage system in electric vehicles using dynamic programing approach. Appl. Energy 2015, 139, 151–162. [Google Scholar] [CrossRef]
- Introduction to Geographic Information Systems. Available online: https://www.mheducation.com/highered/product/introduction-geographic-information-systems-chang/M0078095131.html (accessed on 8 July 2018).
- Research on highway route design system. Available online: http://www.cqvip.com/qk/93913x/201128/39195995.html (accessed on 8 July 2018).
- Ding, F.; Wang, W.D.; Xiang, C.L.; He, W.; Qi, Y.L. Speed prediction and energy management for hybrid electric vehicles based on driving recognition. Automob. Eng. 2017, 39, 1223–1231. [Google Scholar]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]













| Parameter | Value |
|---|---|
| Total weight/kg | 1900 |
| Curb weight/kg | 1500 |
| Front section/m2 | 2.3 |
| Aerodynamic drag factor | 0.29 |
| Rolling resistance | 0.012 |
| Wheel radius/m | 0.307 |
| Motor rated power/kW | 80 |
| Motor peak power/kW | 105 |
| Motor voltage class/V | ≤360 |
| Index | Value |
|---|---|
| Nominal capacity/Ah | 20 |
| Nominal voltage/V | 3.2 |
| Internal resistance/mΩ | ≤6 |
| Weight/g | 514 ± 10 |
| Charge voltage/V | 3.65 ± 0.05 |
| Discharge termination voltage/V | 2.0 |
| Operating temperature/°C | −20 ~ 60 |
| Driving Cycle | Average Positive Power/kW | Threshold in Region 2/kW | Fitting Curves in Region 3 |
|---|---|---|---|
| UKBUS6 | 3.360 | 3.291 | f(x) = 0.7647x − 3.040 |
| MANHATTAN | 6.172 | 5.132 | f(x) = 0.7850x − 4.366 |
| NYCC | 7.121 | 6.673 | f(x) = 0.7855x − 5.905 |
| UDDS | 10.202 | 6.486 | f(x) = 0.7772x − 6.187 |
| New York Bus | 11.000 | 8.070 | f(x) = 0.7767x − 7.065 |
| INDIAHWY | 11.669 | 10.85 | f(x) = 0.7892x − 8.444 |
| EUDC_LOW | 11.770 | 13.68 | f(x) = 0.7872x − 11.15 |
| HWFET | 14.251 | 18.67 | f(x) = 0.7628x − 14.53 |
| Operating Condition | Switch Condition | Power Allocation |
|---|---|---|
| Driving: battery and UC | Pmin < Pdem and SOCuc,min < SOCuc | Puc = aPdem + b Pbat = Pdem − Puc |
| Driving: battery | Pmin ≤ Pdem and SOCuc ≤ SOCuc,min | Pbat = Pdem Puc = 0 |
| Driving: battery | 0 ≤ Pdem ≤ Pmin | Pbat = Pdem Puc = 0 |
| Braking: UC | Pdem < 0 and SOCuc < SOCuc,max | Puc = Pdem Pbat = 0 |
| Braking: neither of them | Pdem < 0 and SOCuc,max ≤ SOCuc | Pbat = 0 Puc = 0 |
| Cluster Centers | |||
|---|---|---|---|
| Average accelerated speed | −0.65394301496 | −0.00551733775 | 0.51745111141 |
| Standard deviation of vehicle speed | 7.78720463753 | 1.10825192133 | 6.05417011930 |
| Speed difference | −22.1134815365 | −0.1531105304 | 17.3566038619 |
| Input and Output | Actual Domain | Fuzzy Domain | Membership Function | Fuzzy Subset Levels |
|---|---|---|---|---|
| 0 ~ 70 | 0 ~ 1 | Gauss type/Bilateral Gauss | 3 | |
| −3 ~ 3 | −3 ~ 3 | Triangle | 7 | |
| −10 ~ 10 | −1 ~ 1 | Triangle | 7 | |
| −0.2 ~ 0.2 | −0.2 ~ 0.2 | Gauss type/Bilateral Gauss | 7 |
| Operating Conditions | Switch Requirement | Power Allocation |
|---|---|---|
| Battery discharges alone | Pmin ≤ Pdem & SOCuc ≤ SOCuc,min | Pbat = Pdem, Puc = 0 |
| Battery discharges alone | 0 ≤ Pdem < Pmin & SOCuc,tag ≤ SOCuc | Pbat = Pdem, Puc = 0 |
| Battery and UC discharge | Pmin ≤ Pdem & SOCuc,min < SOCuc | Pbat = Pmin, Puc = Pdem-Pmin |
| Battery discharges and UC charges | 0 ≤ Pdem < Pmin & SOCuc < SOCuc,tag | Pbat = Pdem + Pch, Puc = −Pch |
| UC absorbs braking energy | Pdem < 0 & SOCuc < SOCuc,max | Pbat = 0, Puc = Pdem |
| Neither of them absorbs the braking energy | Pdem < 0 & SOCuc,max ≤ SOCuc | Pbat = 0, Puc = 0 |
| Controllers\Battery Index | Battery Life Loss | ||
|---|---|---|---|
| TRBC 3 | 0.9 | 0.7788 | 1.4028 × 10−4 |
| ARBC 4 | 0.9 | 0.7831 | 1.3501 × 10−4 |
| CC 5 | 0.9 | 0.7853 | 1.3106 × 10−4 |
| Battery index\Controllers | TRBC | ARBC | CC |
|---|---|---|---|
| Battery using times | 13,074 | 10,933 | 9564 |
| Average power of battery/kW | 9.31 | 9.05 | 8.87 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Jiang, X.; Jia, M.; Zheng, Y. Energy Management Strategy for the Hybrid Energy Storage System of Pure Electric Vehicle Considering Traffic Information. Appl. Sci. 2018, 8, 1266. https://doi.org/10.3390/app8081266
Hu J, Jiang X, Jia M, Zheng Y. Energy Management Strategy for the Hybrid Energy Storage System of Pure Electric Vehicle Considering Traffic Information. Applied Sciences. 2018; 8(8):1266. https://doi.org/10.3390/app8081266
Chicago/Turabian StyleHu, Jianjun, Xingyue Jiang, Meixia Jia, and Yong Zheng. 2018. "Energy Management Strategy for the Hybrid Energy Storage System of Pure Electric Vehicle Considering Traffic Information" Applied Sciences 8, no. 8: 1266. https://doi.org/10.3390/app8081266
APA StyleHu, J., Jiang, X., Jia, M., & Zheng, Y. (2018). Energy Management Strategy for the Hybrid Energy Storage System of Pure Electric Vehicle Considering Traffic Information. Applied Sciences, 8(8), 1266. https://doi.org/10.3390/app8081266





