Dual-Band Light Absorption Enhancement in Hyperbolic Rectangular Array
Abstract
:1. Introduction
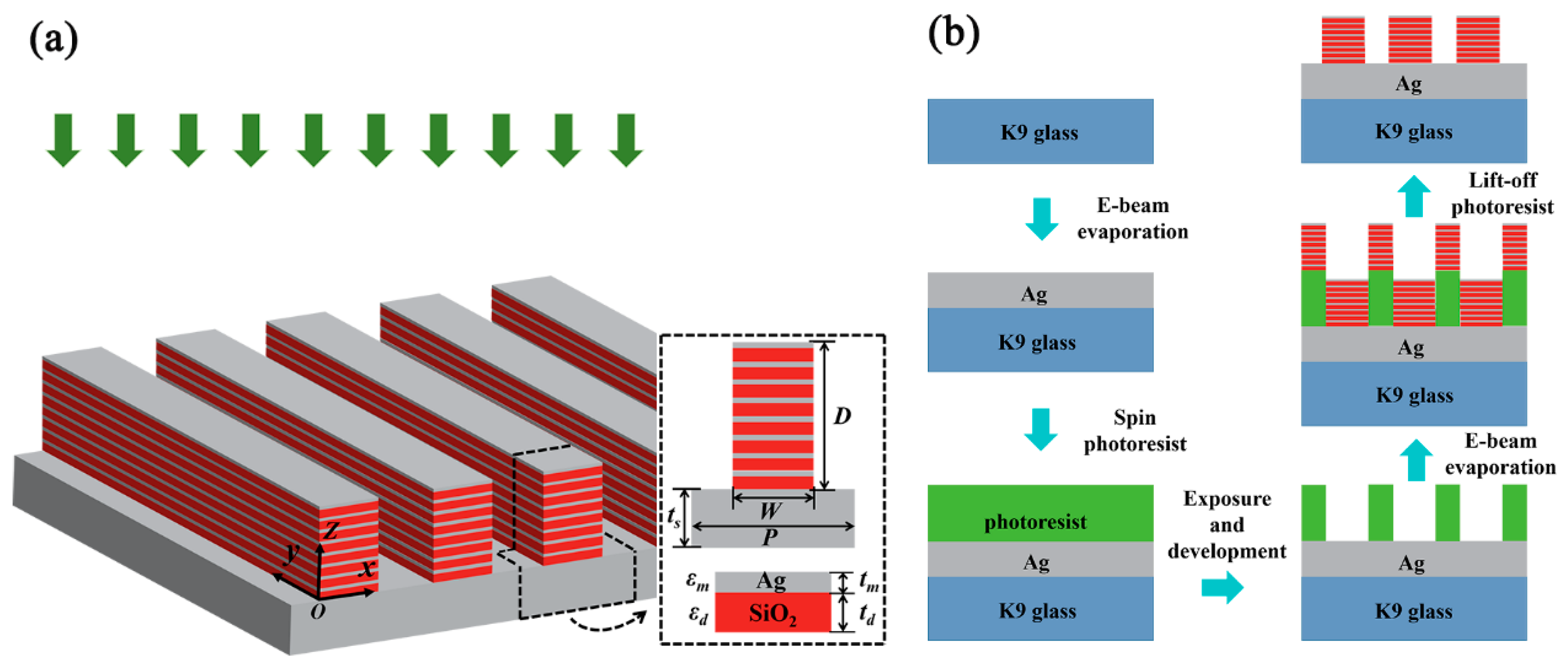
2. Design Principles
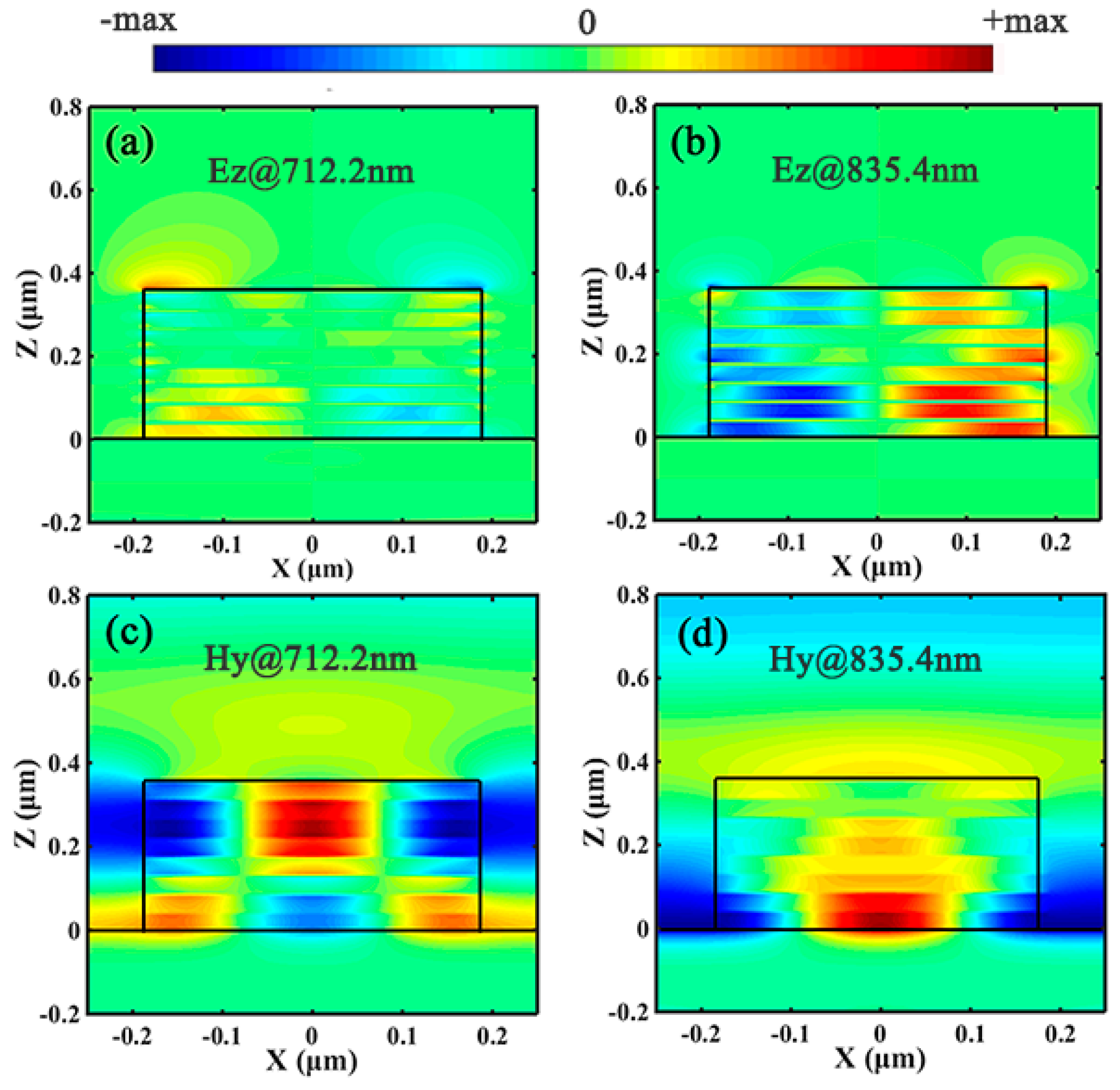
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Noginov, M.A.; Barnakov, Y.A.; Zhu, G.; Tumkur, T.; Li, H.; Narimanov, E.E. Bulk photonic metamaterial with hyperbolic dispersion. Appl. Phys. Lett. 2009, 94, 151105. [Google Scholar] [CrossRef] [Green Version]
- Naik, G.V.; Liu, J.J.; Kildishev, A.V.; Shalaev, V.M.; Boltasseva, A. Demonstration of Al:ZnO as a plasmonic component for near-infrared metamaterials. Proc. Natl. Acad. Sci. USA 2012, 109, 8834–8838. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Yao, J.; Rho, J.; Yin, X.; Zhang, X. Experimental realization of three-dimensional indefinite cavities at the nanoscale with anomalous scaling laws. Nat. Photonics 2012, 6, 450–454. [Google Scholar] [CrossRef]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948–967. [Google Scholar] [CrossRef]
- Ishii, S.; Kildishev, A.V.; Narimanov, E.; Shalaev, V.M.; Drachev, V.P. Sub-wavelength interference pattern from volume plasmon polaritons in a hyperbolic medium. Laser Photonics Rev. 2013, 7, 265–271. [Google Scholar] [CrossRef]
- Yao, J.; Liu, Z.W.; Liu, Y.M.; Wang, Y.; Sun, C.; Bartal, G.; Stacy, A.M.; Zhang, X. Optical negative refraction in bulk metamaterials of nanowires. Science 2008, 321, 930. [Google Scholar] [CrossRef]
- Hoffman, A.J.; Alekseyev, L.; Howard, S.S.; Franz, K.J.; Wasserman, D.; Podolskiy, V.A.; Narimanov, E.E.; Sivco, D.L.; Gmachl, C. Negative refraction in semiconductor metamaterials. Nat. Mater. 2007, 6, 946–950. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Cortes, C.L.; Molesky, S.; Jacob, Z. Broadband super-planckian thermal emission from hyperbolic metamaterials. Appl. Phys. Lett. 2012, 101, 559–588. [Google Scholar] [CrossRef]
- Kabashin, A.V.; Evans, P.; Pastkovsky, S.; Hendren, W.; Wurtz, G.A.; Atkinson, R.; Pollard, R.; Podolskiy, V.A.; Zayats, A.V. Plasmonic nanorod metamaterials for biosensing. Nat. Mater. 2009, 8, 867–871. [Google Scholar] [CrossRef]
- Sreekanth, K.V.; Alapan, Y.; ElKabbash, M.; Ilker, E.; Hinczewski, M.; Gurkan, U.A.; De Luca, A.; Strangi, G. Extreme sensitivity biosensing platform based on hyperbolic metamaterials. Nat. Mater. 2016, 15, 621–627. [Google Scholar] [CrossRef] [Green Version]
- Shen, K.C.; Ku, C.T.; Hsieh, C.; Kuo, H.C.; Cheng, Y.J.; Tsai, D.P. Deep-ultraviolet hyperbolic metacavity laser. Adv. Mater. 2018, 30, 1706918. [Google Scholar] [CrossRef]
- Zhukovsky, S.V.; Kidwai, O.; Sipe, J.E. Physical nature of volume plasmon polaritons in hyperbolic metamaterials. Opt. Express 2013, 21, 14982–14987. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Long, C.; Li, J.; Zhu, H.; Chen, L.; Guan, J.; Li, X. Ultra-wideband microwave absorber by connecting multiple absorption bands of two different-sized hyperbolic metamaterial waveguide arrays. Sci. Rep. 2015, 5, 15367. [Google Scholar] [CrossRef]
- Ning, R.; Liu, S.; Zhang, H.; Bian, B.; Kong, X. A wide-angle broadband absorber in graphene-based hyperbolic metamaterials. Eur. Phys. J. Appl. Phys. 2014, 68, 20401. [Google Scholar] [CrossRef]
- Yin, X.; Chen, L.; Li, X. Ultra-broadband super light absorber based on multi-sized tapered hyperbolic metamaterial waveguide arrays. J. Lightwave Technol. 2015, 33, 3704–3710. [Google Scholar] [CrossRef]
- Zhou, X.; Yin, X.; Zhang, T.; Chen, L.; Li, X. Ultrabroad terahertz bandpass filter by hyperbolic metamaterial waveguide. Opt. Express 2015, 23, 11657–11664. [Google Scholar] [CrossRef] [PubMed]
- Desouky, M.; Mahmoud, A.M.; Swillam, M.A. Silicon based mid-IR super absorber using hyperbolic metamaterial. Sci. Rep. 2018, 8, 2036. [Google Scholar] [CrossRef] [Green Version]
- Riley, C.T.; Smalley, J.S.T.; Brodie, J.R.J.; Fainman, Y.; Sirbuly, D.J.; Liu, Z.W. Near-perfect broadband absorption from hyperbolic metamaterial nanoparticles. Proc. Natl. Acad. Sci. USA 2017, 114, 1264–1268. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zhang, Z.M.; Quan, X.; Cheng, P. A perfect absorber design using a natural hyperbolic material for harvesting solar energy. Sol. Energy 2018, 159, 329–336. [Google Scholar] [CrossRef]
- Ning, R.; Liu, S.; Zhang, H.; Jiao, Z. Dual-gated tunable absorption in graphene-based hyperbolic metamaterial. AIP Adv. 2015, 5, 067106. [Google Scholar] [CrossRef] [Green Version]
- Ning, R.; Liu, S.; Zhang, H.; Bian, B.; Kong, X. Tunable absorption in graphene-based hyperbolic metamaterials for mid-infrared range. Phys. B Condens. Matter 2015, 457, 144–148. [Google Scholar] [CrossRef]
- Fu, S.M.; Zhong, Y.K.; Ju, N.P.; Tu, M.H.; Chen, B.R.; Lin, A. Broadband polarization-insensitive metamaterial perfect absorbers using topology optimization. IEEE Photonics J. 2016, 8, 1–11. [Google Scholar] [CrossRef]
- Wu, D.; Liu, C.; Liu, Y.; Xu, Z.; Yu, Z.; Yu, L.; Chen, L.; Ma, R.; Zhang, J.; Ye, H. Numerical study of a wide-angle polarization independent ultra-broadband efficient selective metamaterial absorber for near-ideal solar thermal energy conversion. RSC Adv. 2018, 8, 21054–21064. [Google Scholar] [CrossRef]
- Zhou, J.; Kaplan, A.F.; Chen, L.; Guo, L.J. Experiment and theory of the broadband absorption by a tapered hyperbolic metamaterial array. ACS Photonics 2014, 1, 618–624. [Google Scholar] [CrossRef]
- He, S.; Ding, F.; Mo, L.; Bao, F. Light absorber with an ultra-broad flat band based on multi-sized slow-wave hyperbolic metamaterial thin-films. Prog. Electromagn. Res. 2014, 147, 69–79. [Google Scholar] [CrossRef]
- Liu, J.; Naik, G.V.; Ishii, S.; Devault, C.; Boltasseva, A.; Shalaev, V.M.; Narimanov, E. Optical absorption of hyperbolic metamaterial with stochastic surfaces. Opt. Express 2014, 22, 8893–8901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, G.; Wu, F.; Zheng, M.; Chen, C.; Zhou, X.; Diao, C.; Liu, F.; Du, G.; Xue, C.; Jiang, H.; et al. Perfect optical absorbers in a wide range of incidence by photonic heterostructures containing layered hyperbolic metamaterials. Opt. Express 2019, 27, 5326–5336. [Google Scholar] [CrossRef]
- Dao, T.D.; Chen, K.; Ishii, S.; Ohi, A.; Nabatame, T.; Kitajima, M.; Nagao, T. Infrared perfect absorbers fabricated by colloidal mask etching of Al-Al2O3-Al trilayers. ACS Photonics 2015, 2, 964–970. [Google Scholar] [CrossRef]
- Jung, J.Y.; Lee, J.; Choi, D.G.; Choi, J.H.; Jeong, J.H.; Lee, E.S.; Neikirk, D.P. Wavelength-selective infrared metasurface absorber for multispectral thermal detection. IEEE Photon. J. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Chen, T.; Zhao, R.; Wang, B.X. Theoretical investigation of a simple design of triple-band terahertz metamaterial absorber for high-Q sensing. Appl. Sci. 2019, 9, 1410. [Google Scholar] [CrossRef]
- Rakic, A.D.; Djurisic, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef]
- Mazulquim, D.B.; Lee, K.J.; Yoon, J.W.; Muniz, L.V.; Borges, B.H.; Neto, L.G.; Magnusson, R. Efficient band-pass color filters enabled by resonant modes and plasmons near the Rayleigh anomaly. Opt. Express 2014, 22, 30843–30851. [Google Scholar] [CrossRef] [PubMed]
- Qian, Q.; Sun, T.; Yan, Y.; Wang, C.H. Large-area wide-incident-angle metasurface perfect absorber in total visible band based on coupled mie resonances. Adv. Opt. Mater. 2017, 5, 1700064. [Google Scholar] [CrossRef]
- Zhang, R.Z.; Zhang, Z.M. Validity of effective medium theory in multilayered hyperbolic materials. J. Quant. Spectr. Radiat. Transf. 2017, 197, 132–140. [Google Scholar] [CrossRef]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef]
- Cong, J.; Zhou, Z.; Yun, B.; Lv, L.; Yao, H.; Fu, Y.; Ren, N. Broadband visible-light absorber via hybridization of propagating surface plasmon. Opt. Lett. 2016, 41, 1965–1968. [Google Scholar] [CrossRef]
- Cui, Y.; Fung, K.H.; Xu, J.; Ma, H.; Jin, Y.; He, S.; Fang, N.X. Ultra-broadband light absorption by a sawtooth anisotropic metamaterial slab. Nano Lett. 2012, 12, 1443–1447. [Google Scholar] [CrossRef] [PubMed]
- Mesch, M.; Metzger, B.; Hentschel, M.; Giessen, H. Nonlinear plasmonic sensing. Nano Lett. 2016, 16, 3155–3159. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Sarkar, S.; Joseph, J. High sensitivity guided-mode resonance optical sensor employing phase detection. Sci. Rep. 2017, 7, 7607. [Google Scholar] [CrossRef]
- Misiakos, K.; Raptis, I.; Makarona, E.; Botsialas, A.; Salapatas, A.; Oikonomou, P.; Psarouli, A.; Petrou, P.S.; Kakabakos, S.E.; Tukkiniemi, K.; et al. All-silicon monolithic Mach-Zehnder interferometer as a refractive index and biochemical sensor. Opt. Express 2014, 22, 26809–26819. [Google Scholar]
- Foreman, M.R.; Swaim, J.D.; Vollmer, F. Whispering gallery mode sensors. Adv. Opt. Photonics 2015, 7, 168–240. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Sang, T.; Li, J.; Zhou, J.; Wang, B.; Wang, Y. High-sensitive transmission type of gas sensor based on guided-mode resonance in coupled gratings. J. Mod. Opt. 2018, 65, 1601–1608. [Google Scholar] [CrossRef]
- Ku, Y.F.; Li, H.Y.; Hsieh, W.H.; Chau, L.K.; Chang, G.E. Enhanced sensitivity in injection-molded guided-mode-resonance sensors via low-index cavity layers. Opt. Express 2015, 23, 14850–14859. [Google Scholar] [CrossRef]
- Szeghalmi, A.; Kley, E.B.; Knez, M. Theoretical and experimental analysis of the sensitivity of guided mode resonance sensors. J. Phys. Chem. C 2010, 114, 21150–21157. [Google Scholar] [CrossRef]
- Long, Y.; Li, Y.; Shen, L.; Liang, W.; Deng, H.; Xu, H. Dually guided-mode-resonant graphene perfect absorbers with narrow bandwidth for sensors. J. Phys. D Appl. Phys. 2016, 49, 32LT01. [Google Scholar] [CrossRef]
- Lu, X.Y.; Zhang, L.X.; Zhang, T.Y. Nanoslit-microcavity-based narrow band absorber for sensing applications. Opt. Express 2015, 23, 20715–20720. [Google Scholar] [CrossRef]
- Li, Y.; An, B.; Jiang, S.; Gao, J.; Chen, Y.; Pan, S. Plasmonic induced triple-band absorber for sensor application. Opt. Express 2015, 23, 17607–17612. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, H.; Sang, T.; Wang, L.; Yin, X.; Wang, J.; Wang, Y. Dual-Band Light Absorption Enhancement in Hyperbolic Rectangular Array. Appl. Sci. 2019, 9, 2011. https://doi.org/10.3390/app9102011
Qi H, Sang T, Wang L, Yin X, Wang J, Wang Y. Dual-Band Light Absorption Enhancement in Hyperbolic Rectangular Array. Applied Sciences. 2019; 9(10):2011. https://doi.org/10.3390/app9102011
Chicago/Turabian StyleQi, Honglong, Tian Sang, La Wang, Xin Yin, Jicheng Wang, and Yueke Wang. 2019. "Dual-Band Light Absorption Enhancement in Hyperbolic Rectangular Array" Applied Sciences 9, no. 10: 2011. https://doi.org/10.3390/app9102011
APA StyleQi, H., Sang, T., Wang, L., Yin, X., Wang, J., & Wang, Y. (2019). Dual-Band Light Absorption Enhancement in Hyperbolic Rectangular Array. Applied Sciences, 9(10), 2011. https://doi.org/10.3390/app9102011






