A Robot Learning Method with Physiological Interface for Teleoperation Systems
Abstract
:1. Introduction
2. Equipment
2.1. MYO Armband
2.2. Touch X
2.3. Baxter Robot
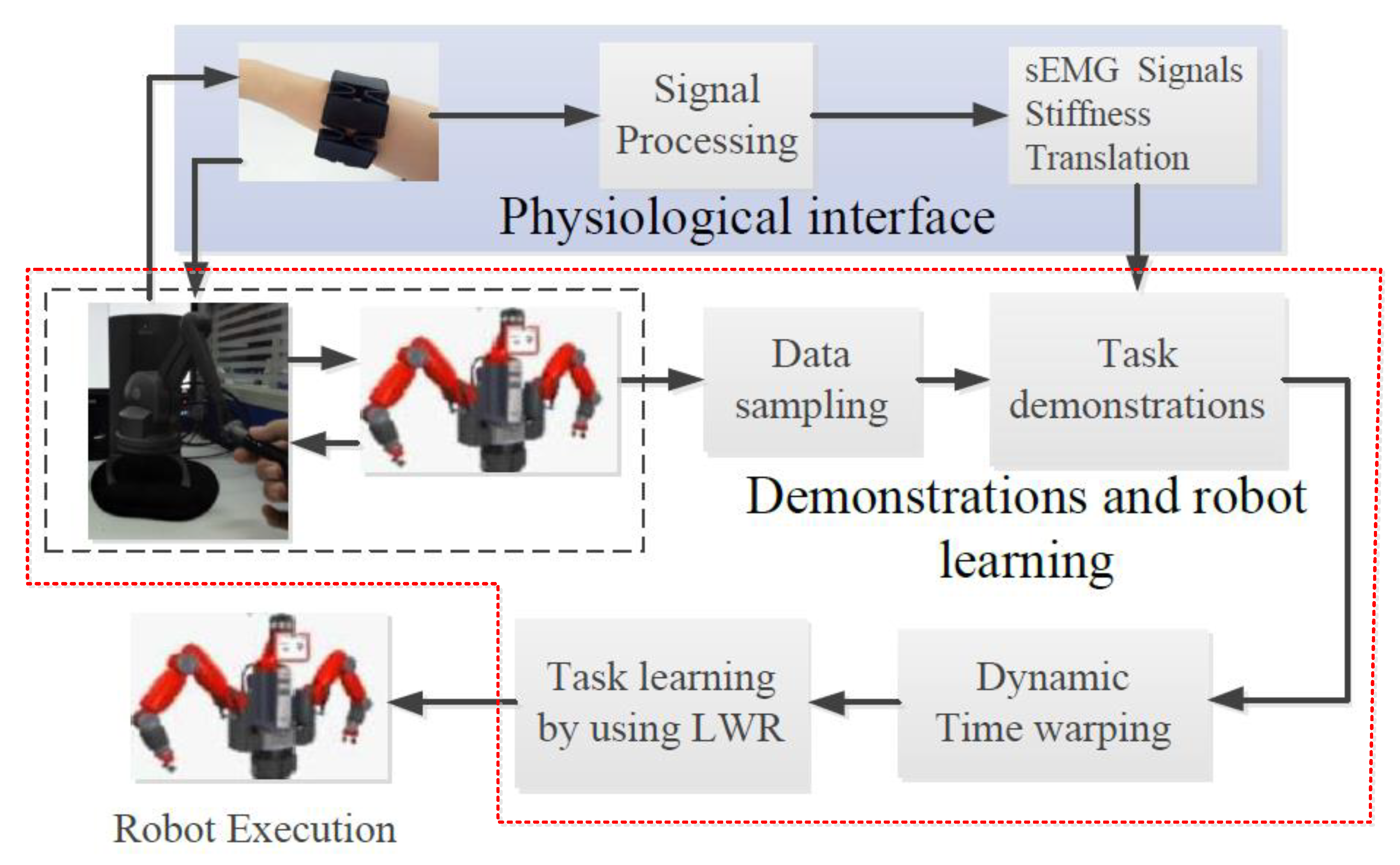
3. Method
- Physiological interface module. Physiological interface module consists of sEMG signal processing unit and sEMG-signals-stiffness translation unit. In this module, raw sEMG signal is collected by the MYO armband. The human stiffness can be obtained through the sEMG-signals-stiffness unit.
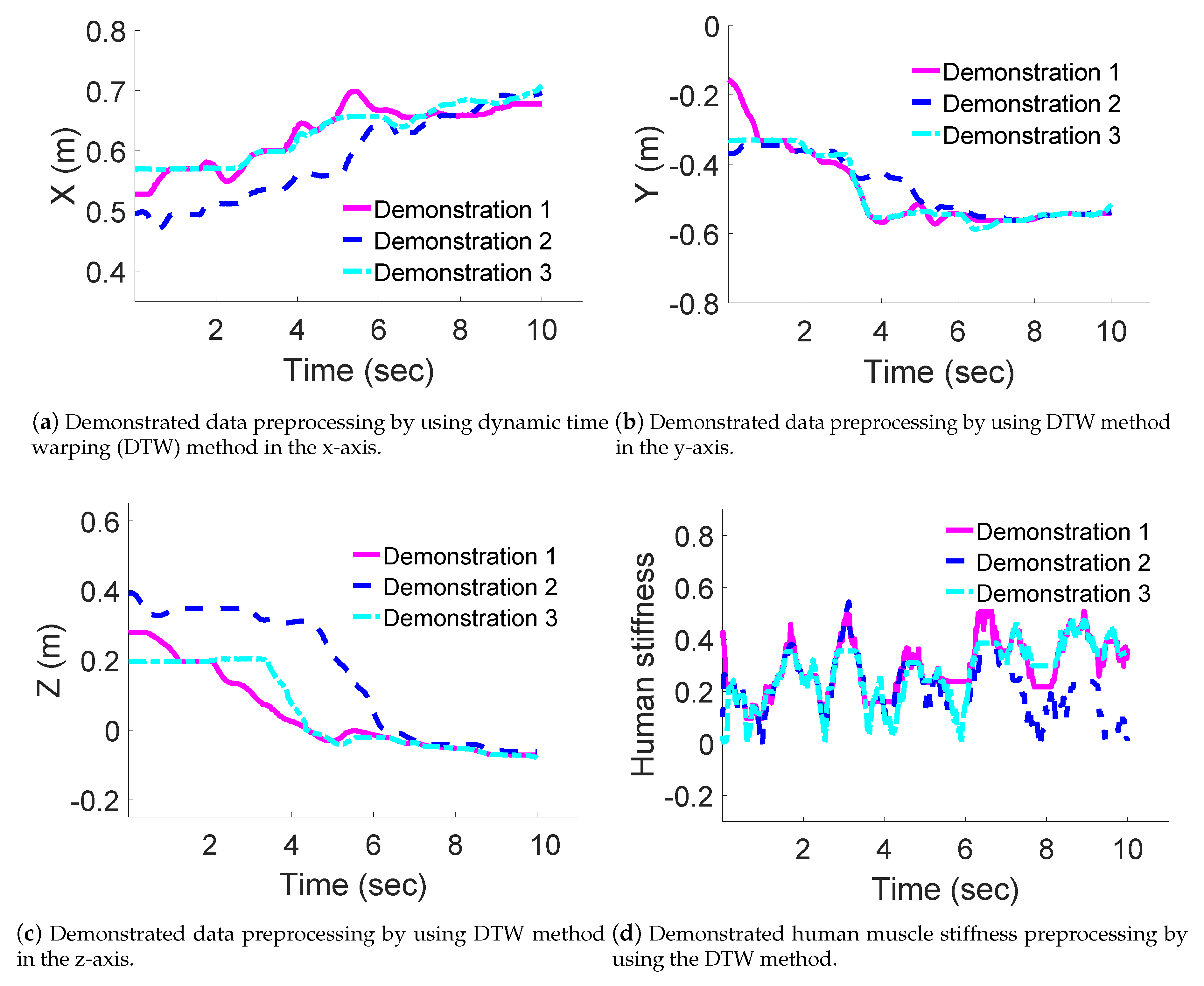
- Demonstrations and robot learning module. This module is the main part of the proposed frame. The data processing unit is used to process task trajectories from the remote Baxter robot. The collected data contains task trajectories and human stiffness. The collected task trajectories and collected stiffness are ready for the demonstration and learning process. DTW unit is used to align the demonstration data in a united time scale. The robot learning model is mainly used to obtain a generative model according to the demonstrated information related to the collected task trajectories and collected muscle stiffness.
- Robot execution module. This module is mainly used to enable the remote Baxter robot to execute the task according to the learned task trajectories and learned muscle stiffness.
3.1. Physiological Interface Design
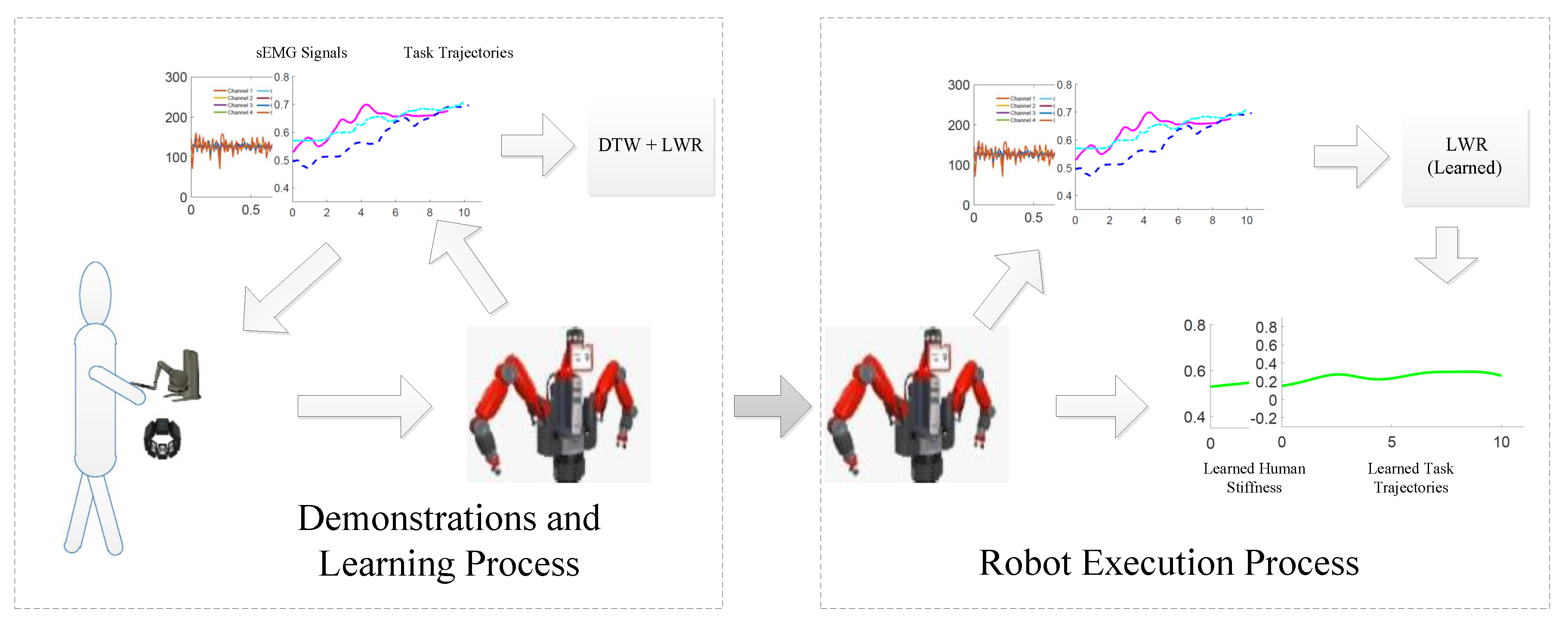
3.2. Task Demonstrations
3.2.1. Data Constitution
3.2.2. Data Preprocessing
3.3. Learning Algorithm
4. Results and Discussion
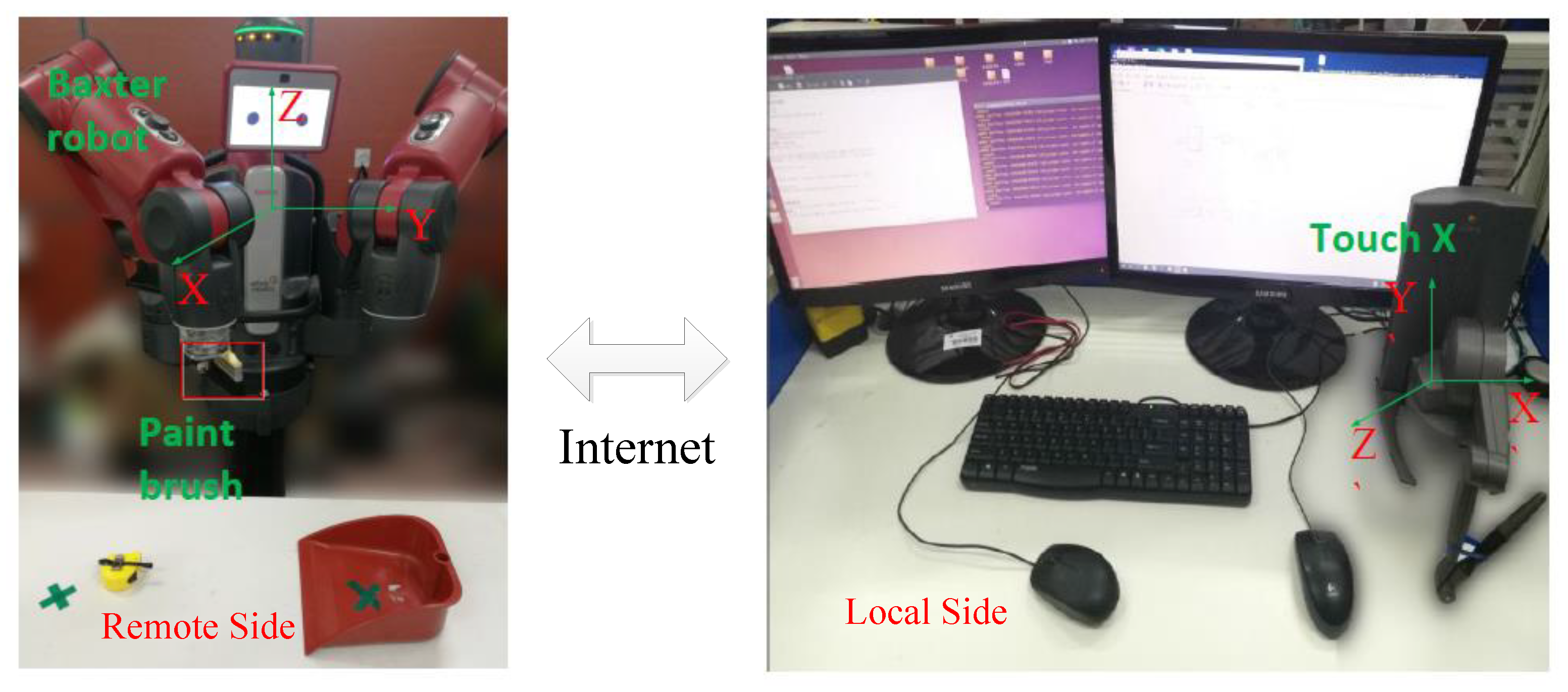
4.1. Experimental Setup
- Hardware equipment. The experiment hardware equipment consist of the Touch X, the Baxter robot, and the MYO armband with eight channels. The left panel of Figure 5, exhibits that a red garbage bucket and a yellow tapeline (as garbage) are placed on the testbed. A paint brush is installed in the right arm of the Baxter robot.
- Software environment. MATLAB software and Visual Studio 2013 (VS 2013, Microsoft, US) operate on Windows 7 in the master computer. Robot operating system (ROS) runs on the Ubuntu system in the remote computer. The master computer communicates with the remote computer through the User Datagram Protocol (UDP).
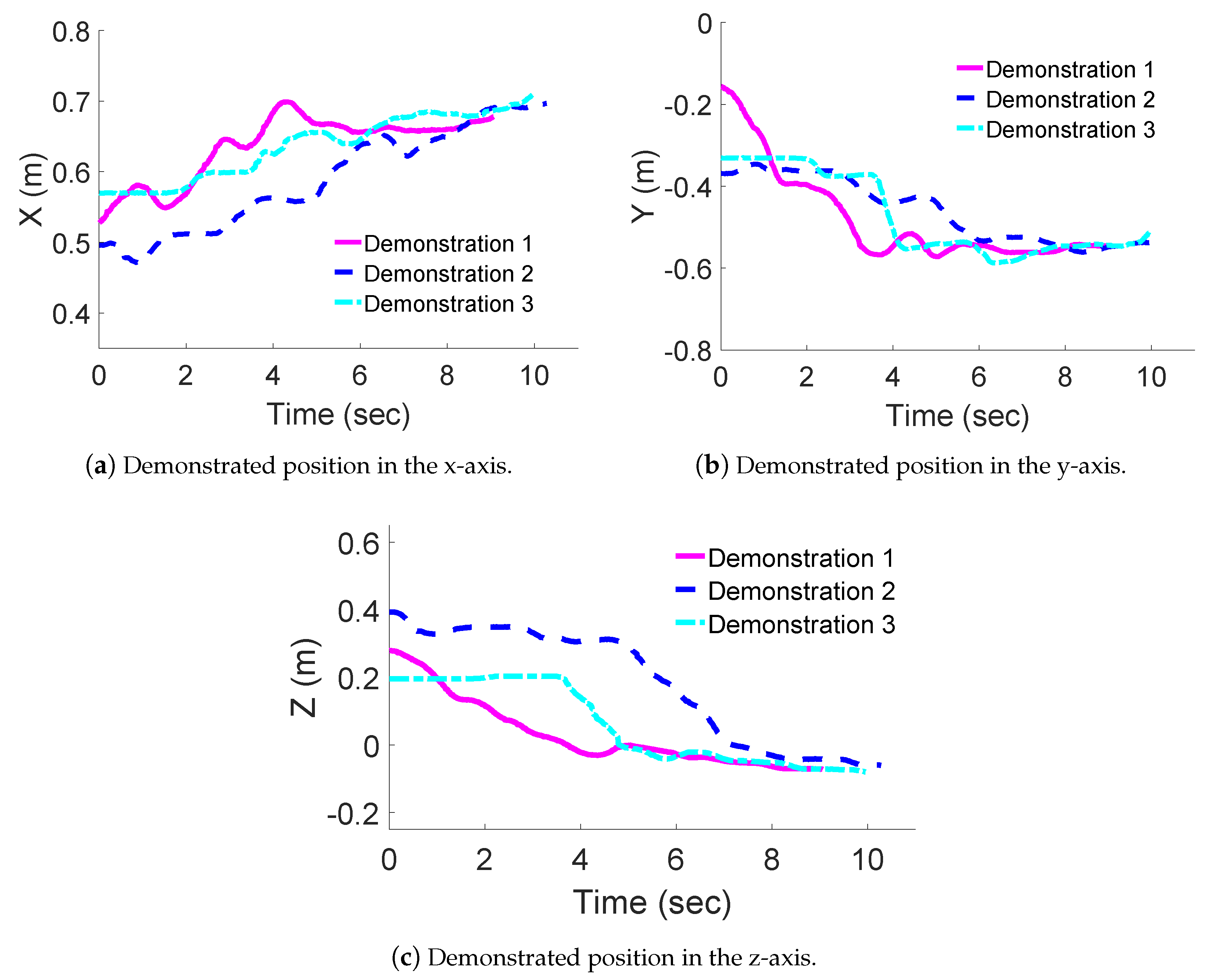
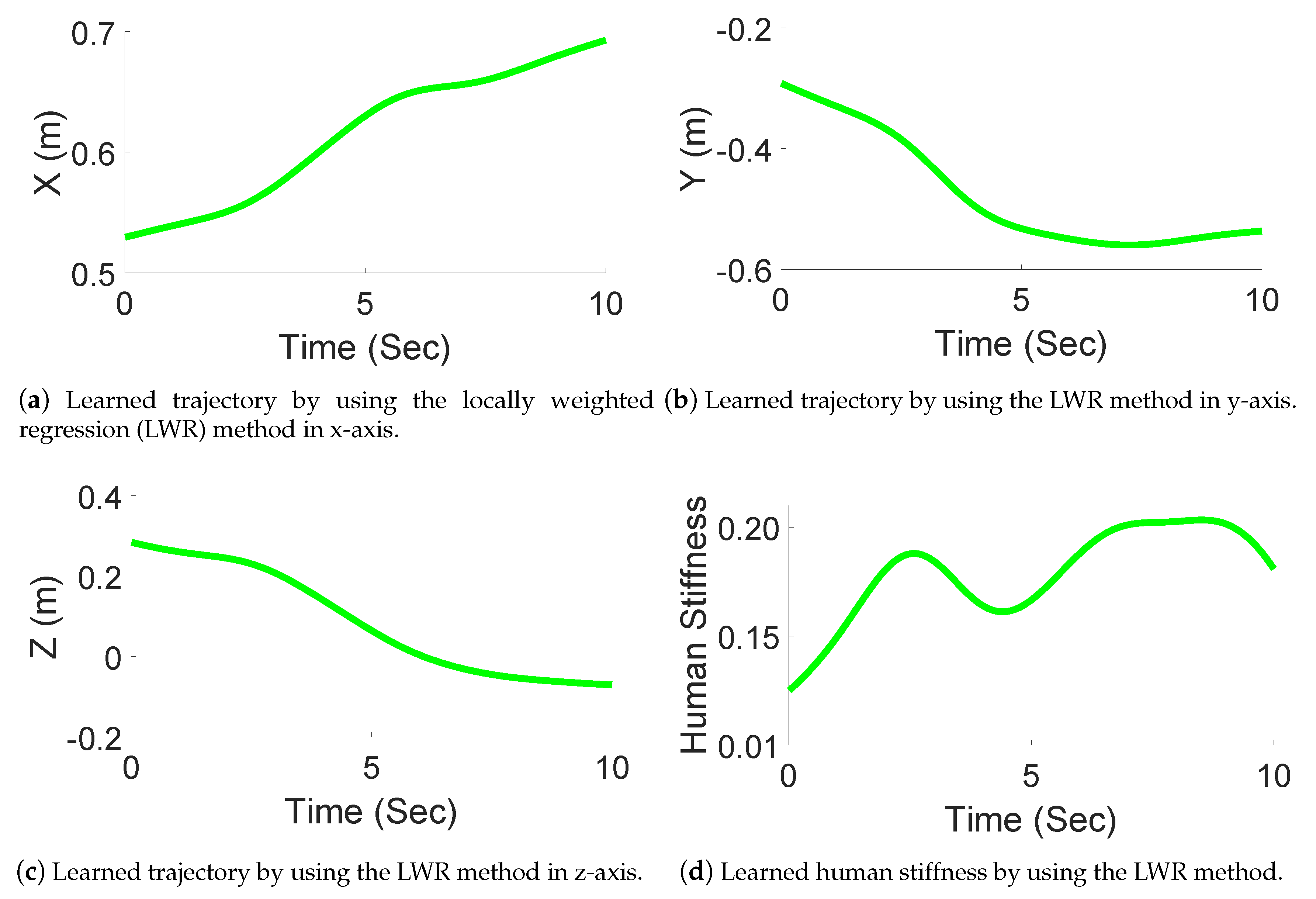
4.2. Results
4.3. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Raw sEMG signal. | |
| u | Sum of sEMG signal. |
| Moving average filter. | |
| Envelope of sEMG signal. | |
| Indicator of the muscle activation. | |
| Muscle stiffness. | |
| O | Demonstration data. |
| P | Collected task trajectories. |
| Input with related to LWR. | |
| Output with related to LWR. | |
| Weights of the . | |
| Log likelihood for the probability with related to LWR. | |
| Maximum of . | |
| W | Diagonal weight matrix of . |
| Nonlinear model with related to LWR. |
References
- Kalam, A.A.E.; Ferreira, A.; Kratz, F. Bilateral teleoperation system using qos and secure communication networks for telemedicine applications. IEEE Syst. J. 2016, 10, 709–720. [Google Scholar] [CrossRef]
- Falleni, S.; Filippeschi, A.; Ruffaldi, E.; Avizzano, C.A. Teleoperated multi-modal robotic interface for telemedicine: A case study on remote auscultation. In Proceedings of the 2017 26th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN), Lisbon, Portugal, 28 August–1 September 2017; pp. 476–482. [Google Scholar]
- Sharifi, M.; Behzadipour, S.; Salarieh, H. Nonlinear bilateral adaptive impedance control with applications in telesurgery and telerehabilitation. J. Dyn. Syst. Meas. Control. 2016, 138, 111010. [Google Scholar] [CrossRef]
- Milstein, A.; Ganel, T.; Berman, S.; Nisky, I. The scaling of the gripper affects the action and perception in teleoperated grasping via a robot-assisted minimally invasive surgery system. IEEE Trans. Hum. Mach. Syst. 2018. [Google Scholar] [CrossRef]
- Gregory, J.; Fink, J.; Stump, E.; Twigg, J.; Rogers, J.; Baran, D.; Fung, N.; Young, S. Application of multi-robot systems to disaster-relief scenarios with limited communication. In Field and Service Robotics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 639–653. [Google Scholar]
- Gancet, J.; Urbina, D.; Letier, P.; Ilzokvitz, M.; Weiss, P.; Gauch, F.; Antonelli, G.; Indiveri, G.; Casalino, G.; Birk, A.; et al. Dexrov: Dexterous undersea inspection and maintenance in presence of communication latencies. IFAC-PapersOnLine 2015, 48, 218–223. [Google Scholar] [CrossRef]
- Artigas, J.; Hirzinger, G. A brief history of dlrs space telerobotics and force feedback teleoperation. Acta Polytech. Hung. 2016, 13, 239–249. [Google Scholar]
- Taylor, R.H.; Menciassi, A.; Fichtinger, G.; Fiorini, P.; Dario, P. Medical robotics and computer-integrated surgery. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1657–1684. [Google Scholar]
- Manupati, V.; Krishnan, M.G.; Varela, M.L.R.; Machado, J. Telefacturing based distributed manufacturing environment for optimal manufacturing service by enhancing the interoperability in the hubs. J. Eng. 2017, 2017, 9305989. [Google Scholar] [CrossRef]
- Bennett, M.; Williams, T.; Thames, D.; Scheutz, M. Differences in interaction patterns and perception for teleoperated and autonomous humanoid robots. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6589–6594. [Google Scholar]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. Hitchhiking Robots: A Collaborative Approach for Efficient Multi-Robot Navigation in Indoor Environments. Sensors 2017, 17, 1878. [Google Scholar] [CrossRef] [PubMed]
- Sheridan, T.B. Human–robot interaction: status and challenges. Hum. Fact. 2016, 58, 525–532. [Google Scholar] [CrossRef] [PubMed]
- Ramos, J.; Wang, A.; Kim, S. Robot-human balance state transfer during full-body humanoid teleoperation using divergent component of motion dynamics. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1587–1592. [Google Scholar]
- Cheng, L.; Tavakoli, M. Switched-impedance control of surgical robots in teleoperated beating-heart surgery. J. Med. Robot. Res. 2018, 2018, 1841003. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, Y.; Guo, L. Force reflecting control for bilateral teleoperation system under time-varying delays. IEEE Trans. Ind. Inform. 2018, 15, 1162–1172. [Google Scholar] [CrossRef]
- Zeestraten, M.J.; Havoutis, I.; Calinon, S. Programming by demonstration for shared control with an application in teleoperation. IEEE Robot. Autom. Lett. 2018, 3, 1848–1855. [Google Scholar] [CrossRef]
- Janabi-Sharifi, F.; Hassanzadeh, I. Experimental analysis of mobile-robot teleoperation via shared impedance control. IEEE Trans. Syst. Man Cybern. Part (Cybern.) 2011, 41, 591–606. [Google Scholar] [CrossRef]
- Corredor, J.; Sofrony, J.; Peer, A. Decision-making model for adaptive impedance control of teleoperation systems. IEEE Trans. Haptics 2017, 10, 5–16. [Google Scholar] [CrossRef]
- Li, M.; Ishii, M.; Taylor, R.H. Spatial motion constraints using virtual fixtures generated by anatomy. IEEE Trans. Robot. 2007, 23, 4–19. [Google Scholar] [CrossRef]
- Ni, D.; Song, A.; Li, H. Haptic assisted teleoperation based on virtual fixture and dynamic modelling. Sens. Mater. 2017, 29, 1367–1381. [Google Scholar]
- Yang, C.; Wang, X.; Li, Z.; Li, Y.; Su, C.-Y. Teleoperation control based on combination of wave variable and neural networks. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2125–2136. [Google Scholar] [CrossRef]
- Yang, C.; Luo, J.; Pan, Y.; Liu, Z.; Su, C.-Y. Personalized variable gain control with tremor attenuation for robot teleoperation. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1759–1770. [Google Scholar] [CrossRef]
- Schaal, S. Learning from demonstration. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1997; pp. 1040–1046. [Google Scholar]
- Lin, H.-C.; Tang, T.; Fan, Y.; Zhao, Y.; Tomizuka, M.; Chen, W. Robot learning from human demonstration with remote lead through teaching. In Proceedings of the 2016 European Control Conference (ECC), Alborg, Denmark, 29 June–1 July 2016; pp. 388–394. [Google Scholar]
- Tanwani, A.K.; Calinon, S. A generative model for intention recognition and manipulation assistance in teleoperation. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 43–50. [Google Scholar]
- Havoutis, I.; Calinon, S. Learning assistive teleoperation behaviors from demonstration. In Proceedings of the 2016 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Lausanne, Switzerland, 23–27 October 2016; pp. 258–263. [Google Scholar]
- Havoutis, I.; Calinon, S. Learning from demonstration for semi-autonomous teleoperation. Auton. Robot. 2018, 43, 713–726. [Google Scholar] [CrossRef] [Green Version]
- Huang, R.; Cheng, H.; Guo, H.; Chen, Q.; Lin, X. Hierarchical interactive learning for a human-powered augmentation lower exoskeleton. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 257–263. [Google Scholar]
- Peternel, L.; Oztop, E.; Babic, J. A shared control method for online human-in-the-loop robot learning based on locally weighted regression. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 3900–3906. [Google Scholar]
- Peternel, L.; Petric, T.; Babic, J. Human-in-the-loop approach for teaching robot assembly tasks using impedance control interface. In Proceedings of the 2015 IEEE International Conference onRobotics and Automation (ICRA), Seattle, WA, USA, 25–30 May 2015; pp. 1497–1502. [Google Scholar]
- Pervez, A.; Ali, A.; Ryu, J.-H.; Lee, D. Novel learning from demonstration approach for repetitive teleoperation tasks. In Proceedings of the 2017 IEEEWorld Haptics Conference (WHC), Munich, Germany, 6–9 June 2017; pp. 60–65. [Google Scholar]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Hoshino, Y.; Peng, C.C. Path smoothing techniques in robot navigation: State-of-the-art, current and future challenges. Sensors 2018, 18, 3170. [Google Scholar] [CrossRef]
- Mao, Y.; Jin, X.; Dutta, G.G.; Scholz, J.P.; Agrawal, S.K. Human movement training with a cable driven arm exoskeleton (CAREX). IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 84–92. [Google Scholar] [CrossRef]
- Meattini, R.; Benatti, S.; Scarcia, U.; Gregorio, D.D.; Benini, L.; Melchiorri, C. An sEMG-based human-robot interface for robotic hands using machine learning and synergies. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 1149–1158. [Google Scholar] [CrossRef]
- Pilarski, P.M.; Dawson, M.R.; Degris, T.; Carey, J.P.; Sutton, R.S. Dynamic switching and real-time machine learning for improved human control of assistive biomedical robots. In Proceedings of the 2012 4th IEEE RAS and EMBS International Conference onBiomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; pp. 296–302. [Google Scholar]
- Antuvan, C.W.; Ison, M.; Artemiadis, P. Embedded human control of robots using myoelectric interfaces. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 820–827. [Google Scholar] [CrossRef] [PubMed]
- Ohkubo, H.; Shimono, T. Motion control of mobile robot by using myoelectric signals based on functionally different effective muscle theory. In Proceedings of the 2013 IEEE International Conference onMechatronics (ICM), Vicenza, Italy, 27 February–1 March 2013; pp. 786–791. [Google Scholar]
- Park, K.-H.; Suk, H.-I.; Lee, S.-W. Position-independent decoding of movement intention for proportional myoelectric interfaces. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 928–939. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Luo, J.; Liu, C.; Li, M.; Dai, S. Haptics Electromyogrphy Perception and Learning Enhanced Intelligence for Teleoperated Robot. IEEE Trans. Autom. Sci. Eng. 2018, PP, 1–10. [Google Scholar] [CrossRef]
- Sansanayuth, T.; Nilkhamhang, I.; Tungpimolrat, K. Teleoperation with inverse dynamics control for phantom omni haptic device. In Proceedings of the 2012 SICE Annual Conference (SICE), Akita, Japan, 20–23 August 2012; pp. 2121–2126. [Google Scholar]
- Silva, A.J.; Ramirez, O.A.D.; Vega, V.P.; Oliver, J.P.O. Phantom omni haptic device: Kinematic and manipulability. In Proceedings of the 2009 Electronics, Robotics and Automotive Mechanics Conference, CERMA’09, Cuernavaca, Morelos, Mexico, 22–25 September 2009; pp. 193–198. [Google Scholar]
- Ju, Z.; Yang, C.; Ma, H. Kinematics modelling and experimental verification of baxter robot. In Proceedings of the 2014 33rd ChineseControl Conference (CCC), Nanjing, China, 28–30 July 2014; pp. 8518–8523. [Google Scholar]
- Han, J.; Ding, Q.; Xiong, A.; Zhao, X. A state-space EMG model for the estimation of continuous joint movements. IEEE Trans. Ind. Electron. 2015, 62, 4267–4275. [Google Scholar] [CrossRef]
- Lloyd, D.G.; Besier, T.F. An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. J. Biomech. 2003, 36, 765–776. [Google Scholar] [CrossRef]
- Wllmer, M.; Al-Hames, M.; Eyben, F.; Schuller, B.; Rigoll, G. A multidimensional dynamic time warping algorithm for efficient multimodal fusion of asynchronous data streams. Neurocomputing 2009, 73, 366–380. [Google Scholar] [CrossRef]
- Sun, Y.; Qian, H.; Xu, Y. Robot learns chinese calligraphy from demonstrations. In Proceedings of the 2014 IEEE/RSJ International Conference onIntelligent Robots and Systems (IROS 2014), Chicago, IL, USA, 14–18 September 2014; pp. 4408–4413. [Google Scholar]
- Wang, J.; Yu, L.C.; Lai, K.R.; Zhang, X. Locally weighted linear regression for cross lingual valence-arousal prediction of affective words. Neurocomputing 2016, 1943, 271–278. [Google Scholar] [CrossRef]
- Luo, J.; Yang, C.; Wang, N.; Wang, M. Enhanced teleoperation performance using hybrid control and virtual fixture. Int. J. Syst. Sci. 2019, 50, 451–462. [Google Scholar] [CrossRef]




| Variable | X | Y | Z | Stiffness |
|---|---|---|---|---|
| Error | 0.0130 (m) | 0.0018 (m) | 0.0346 (m) | 0.0124 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Yang, C.; Su, H.; Liu, C. A Robot Learning Method with Physiological Interface for Teleoperation Systems. Appl. Sci. 2019, 9, 2099. https://doi.org/10.3390/app9102099
Luo J, Yang C, Su H, Liu C. A Robot Learning Method with Physiological Interface for Teleoperation Systems. Applied Sciences. 2019; 9(10):2099. https://doi.org/10.3390/app9102099
Chicago/Turabian StyleLuo, Jing, Chenguang Yang, Hang Su, and Chao Liu. 2019. "A Robot Learning Method with Physiological Interface for Teleoperation Systems" Applied Sciences 9, no. 10: 2099. https://doi.org/10.3390/app9102099
APA StyleLuo, J., Yang, C., Su, H., & Liu, C. (2019). A Robot Learning Method with Physiological Interface for Teleoperation Systems. Applied Sciences, 9(10), 2099. https://doi.org/10.3390/app9102099








