Evaluation of Calf Muscle Reflex Control in the ‘Ankle Strategy’ during Upright Standing Push-Recovery
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
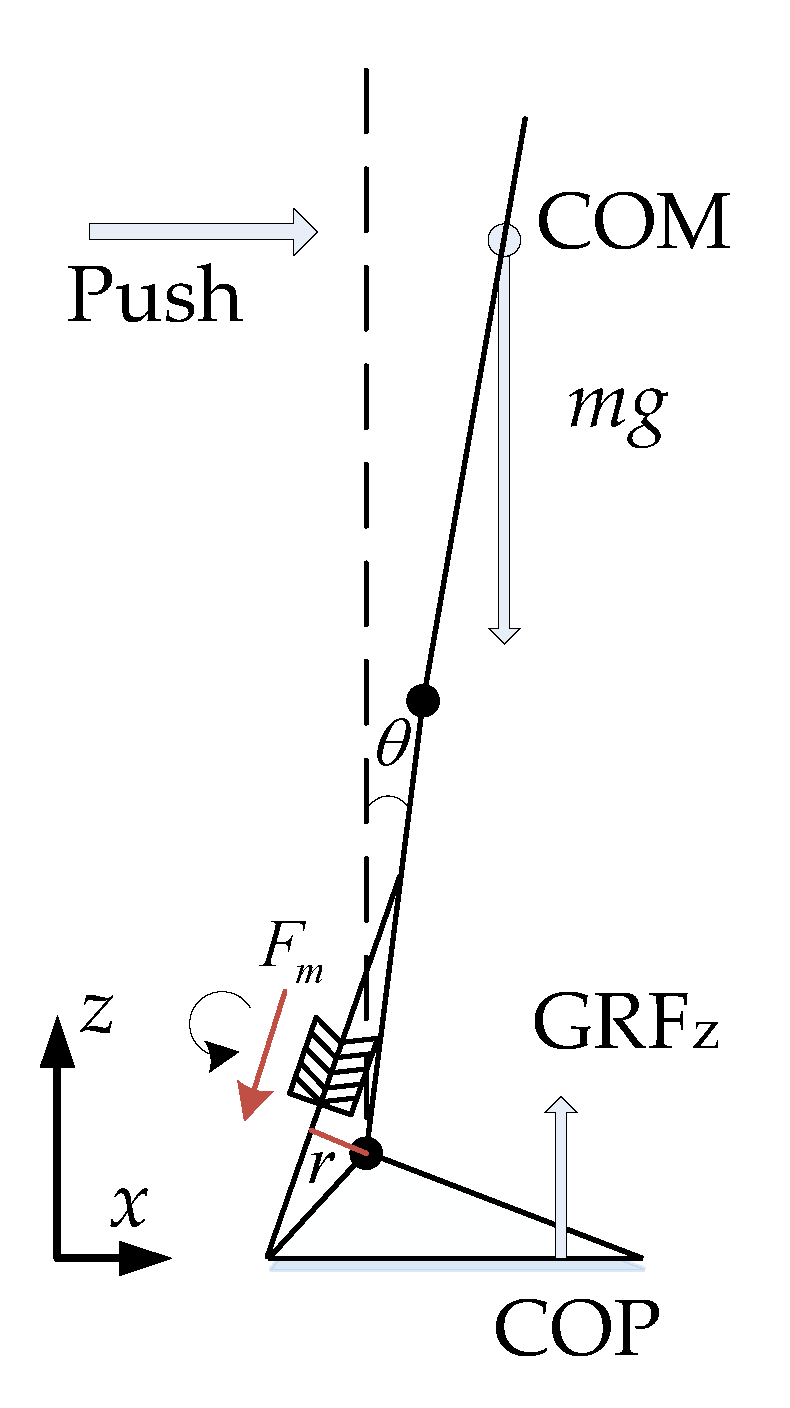
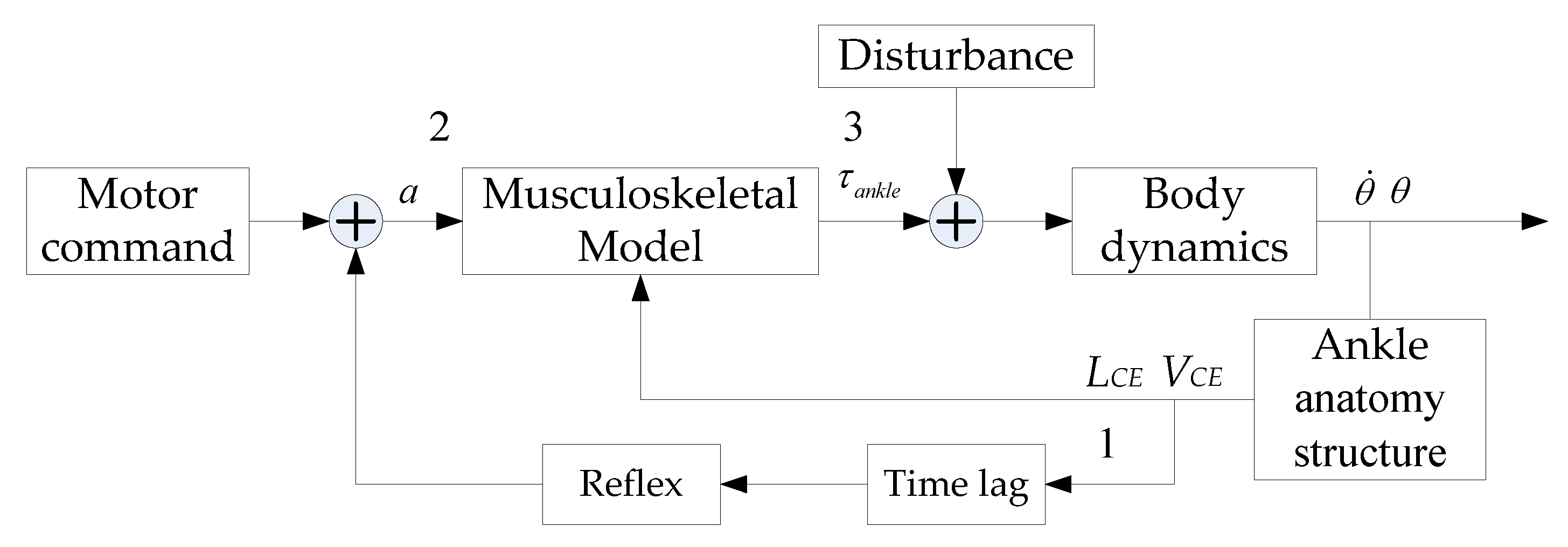
2.1. Calf Muscle Reflex Model and Parameter Calculation
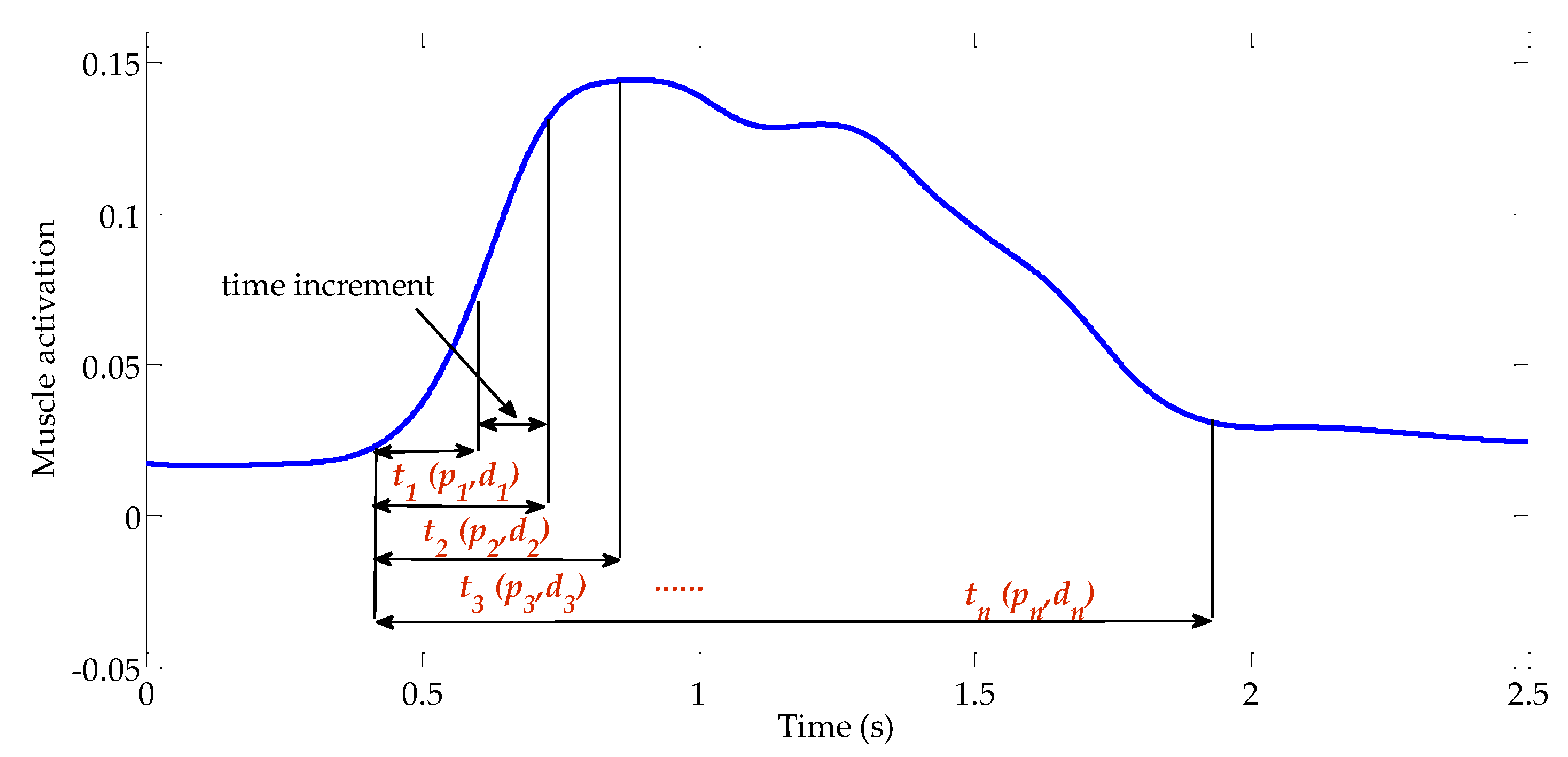
2.2. Muscle Activation Calculation
2.3. Hill-Type-Based Muscular Model
2.4. Experimental Setup and Data Process
2.5. Data Synchronization
3. Experimental Results
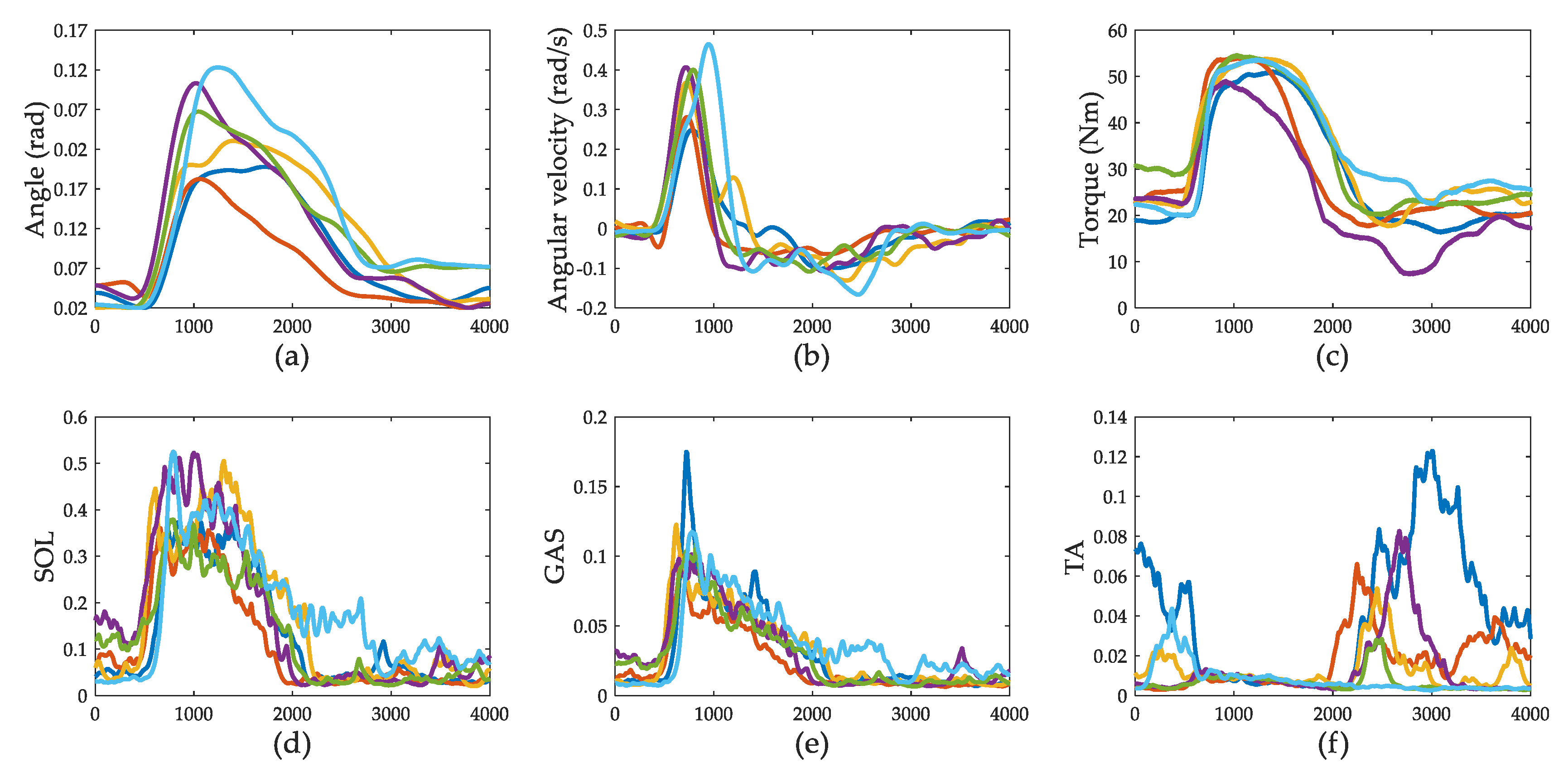
3.1. Push-Recovery Movement
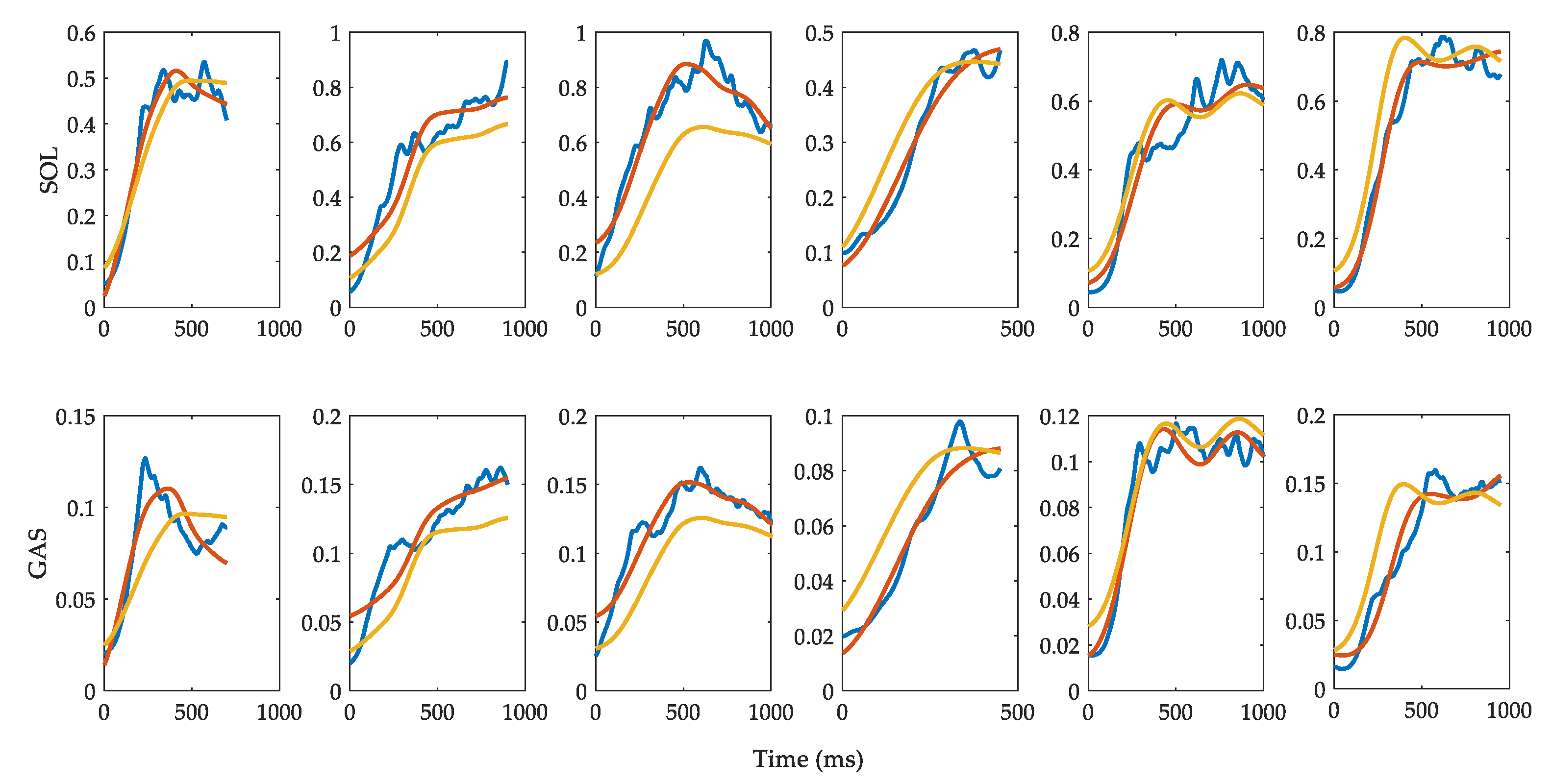
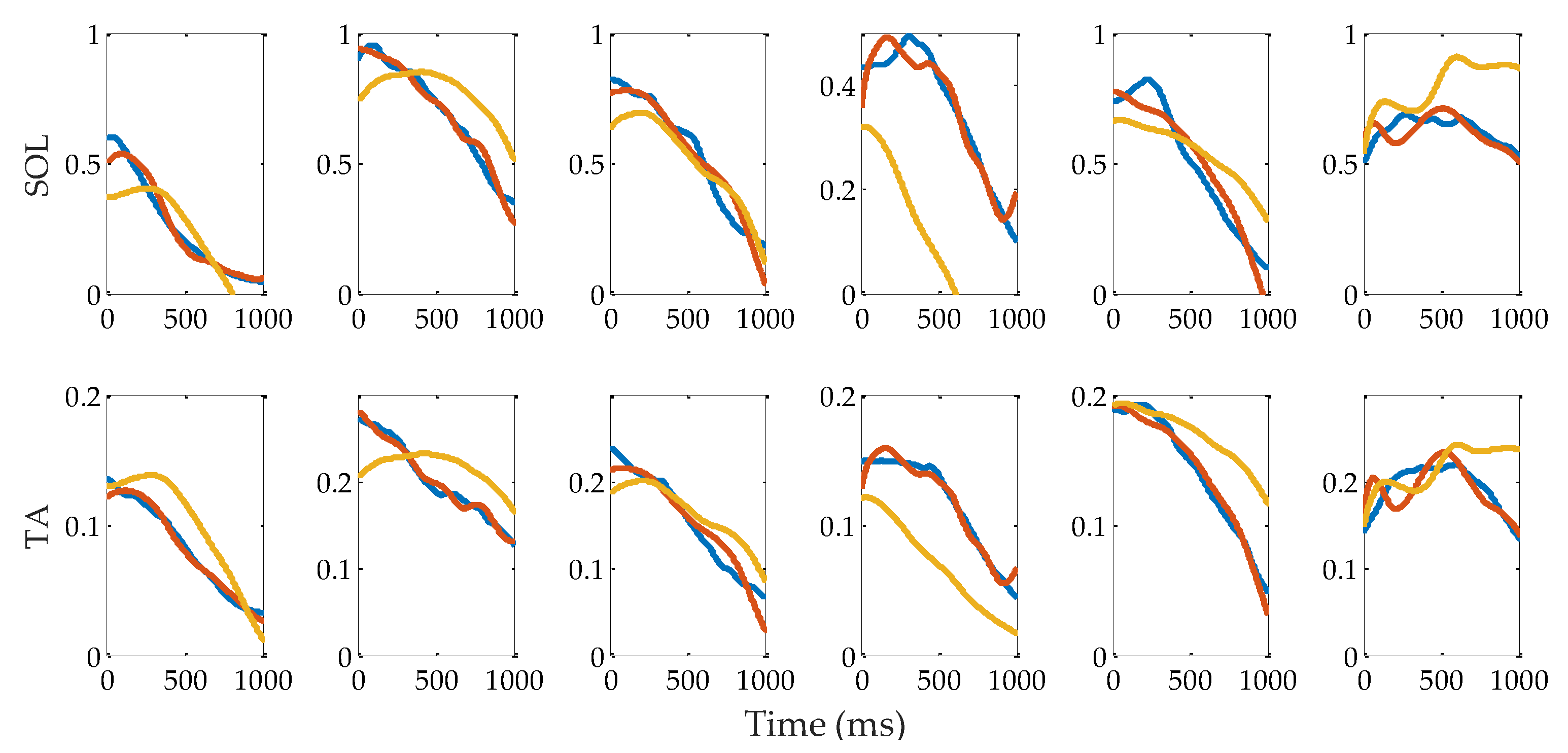
3.2. Muscle Activation
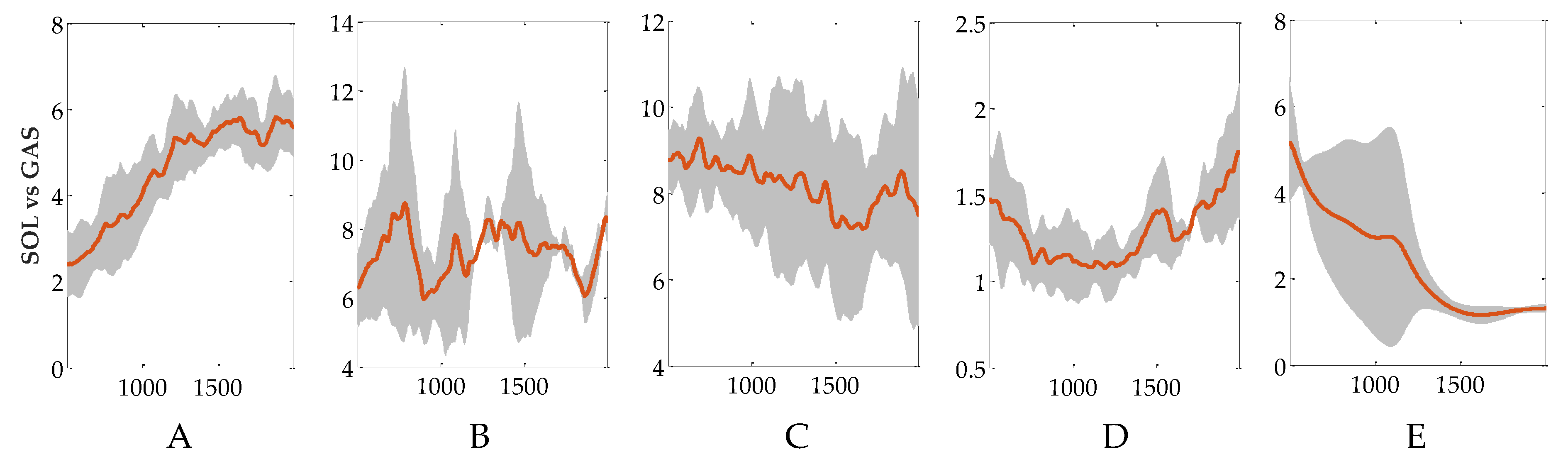
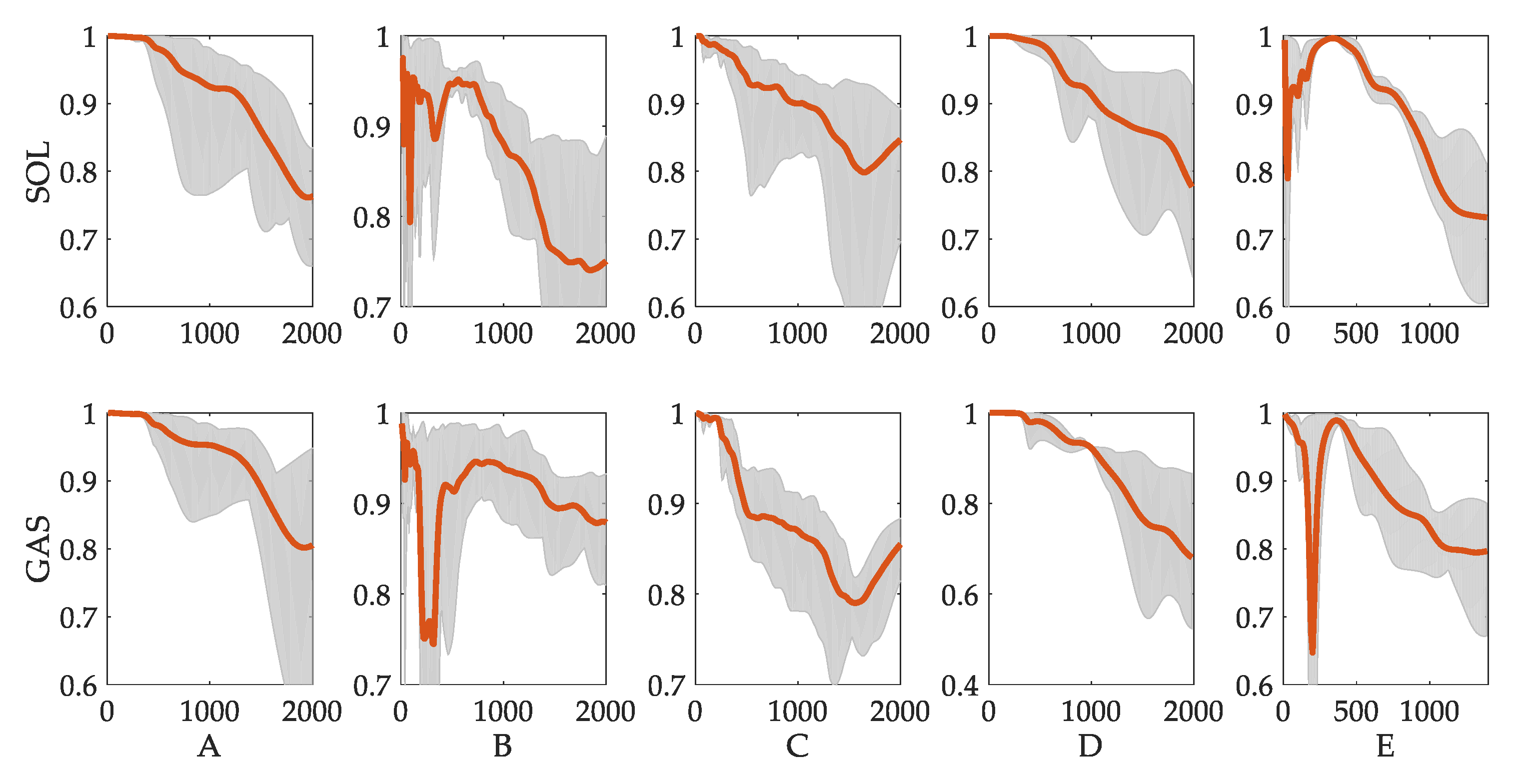
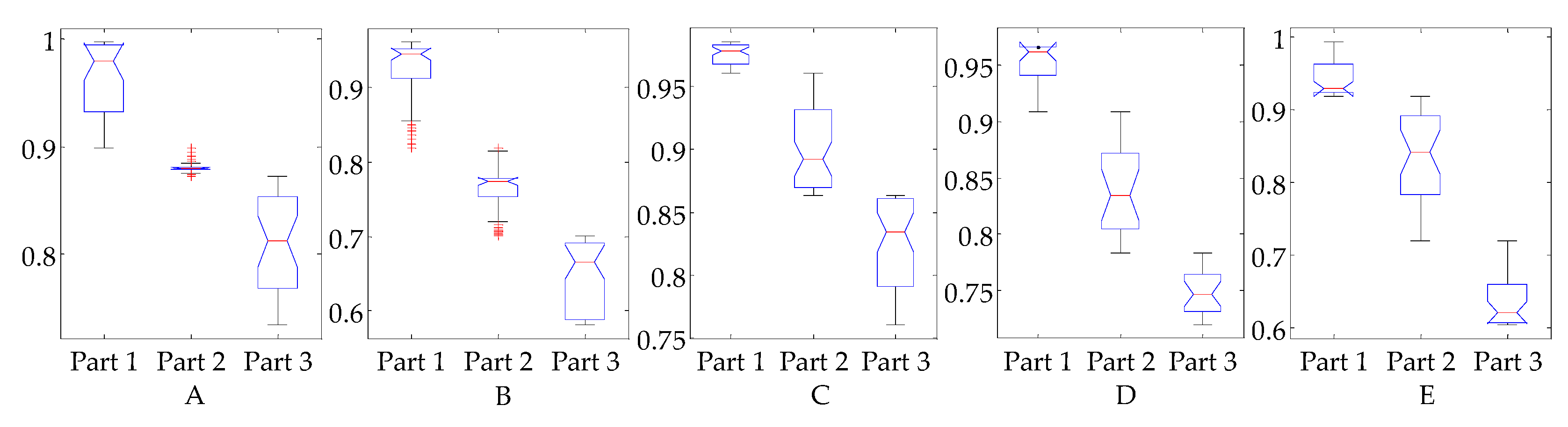
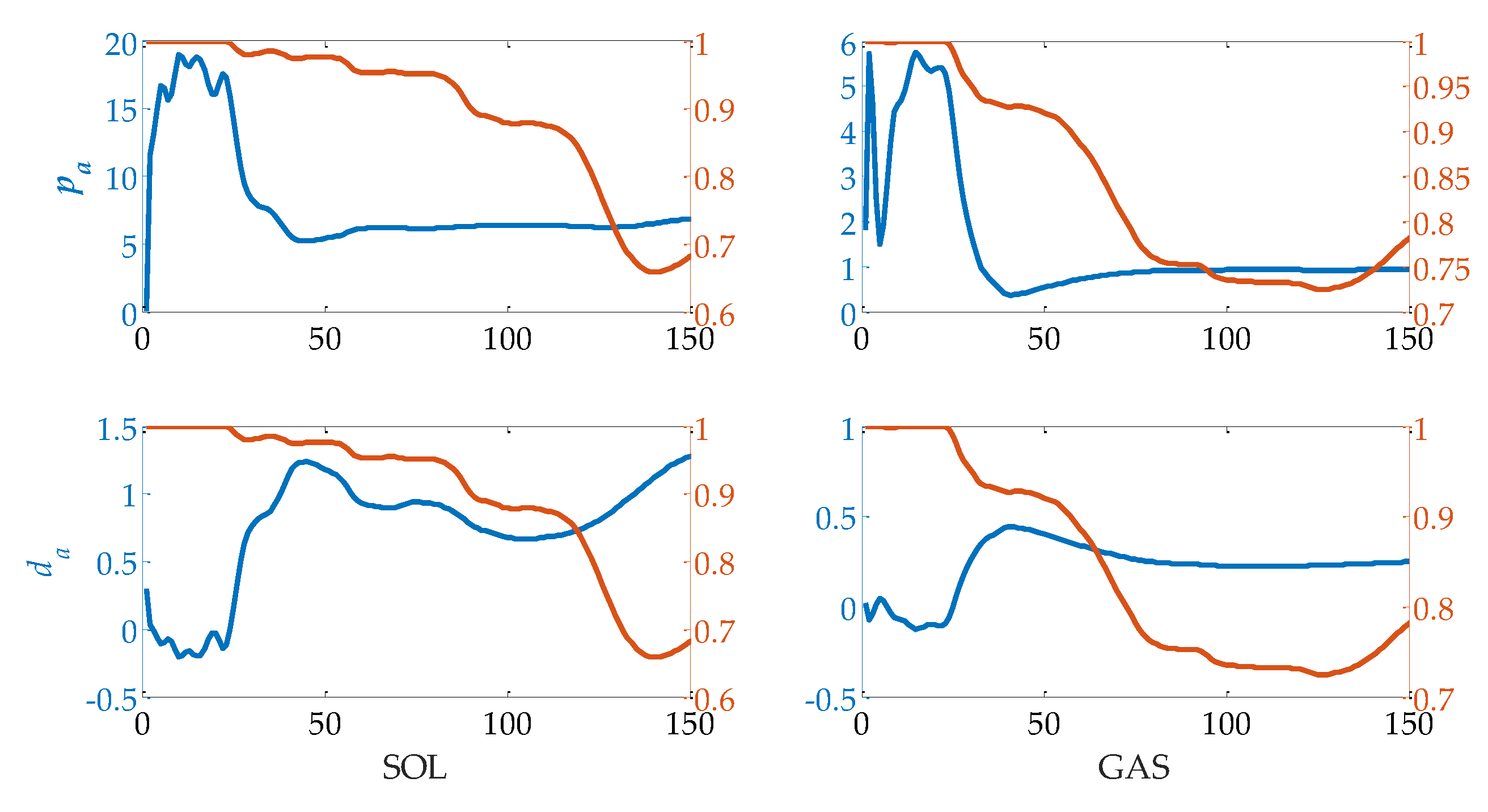
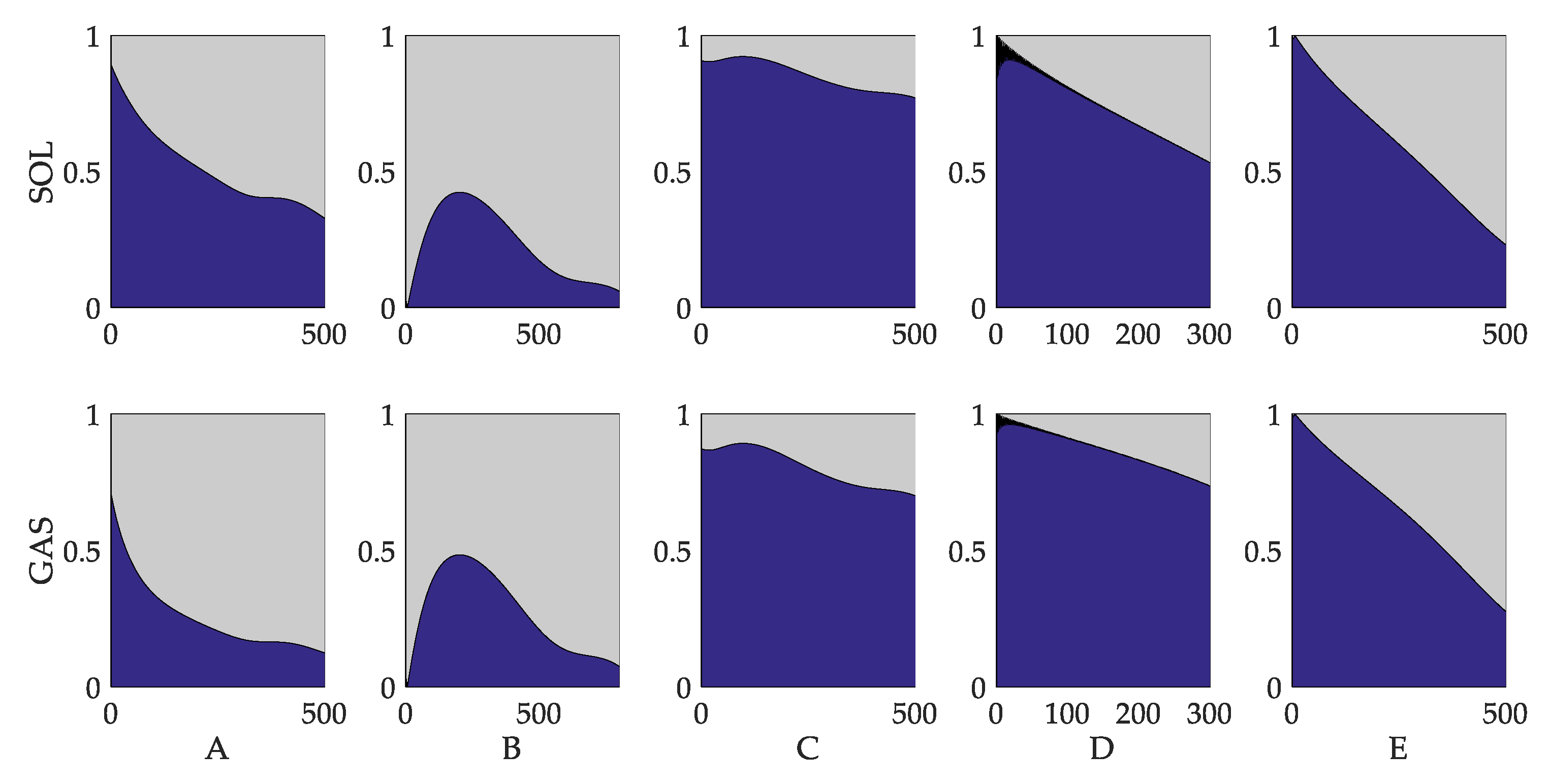
3.3. Evaluation of Reflex Control Model
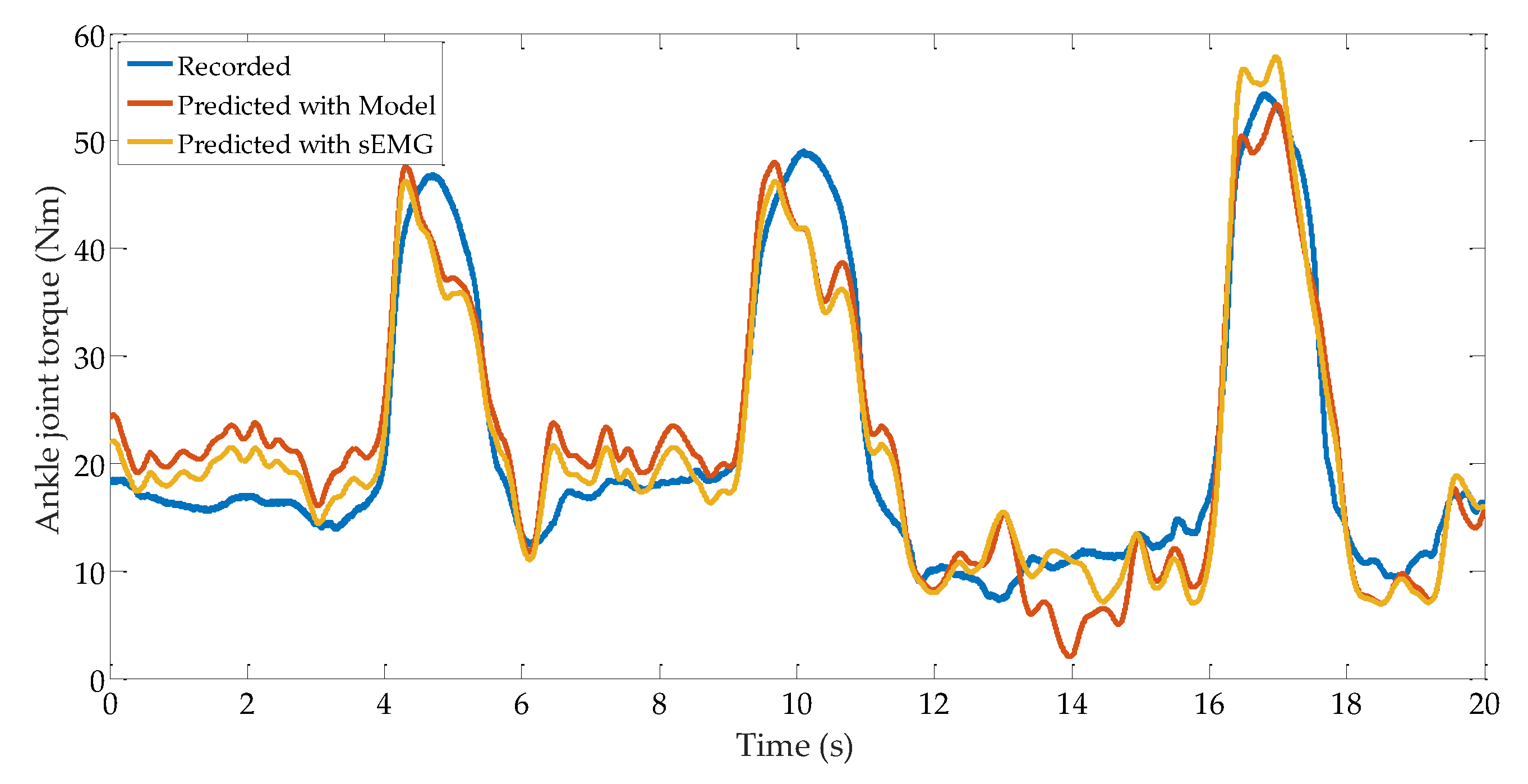
3.4. Ankle Joint Torque Prediction Results
4. Discussion
4.1. Comparison with Currently Existing Studies
4.2. The Role of Ankle Joint Reflex Control
4.3. Implementation of the Proposed Method
4.4. Selection of sEMG Low-Pass Cutoff Frequency
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, C.; Ganesh, G.; Haddadin, S.; Parusel, S.; Albu-Schaeffer, A.; Burdet, E. Human-like adaptation of force and impedance in stable and unstable interactions. IEEE Trans. Robot. 2011, 27, 918–930. [Google Scholar] [CrossRef]
- Collins, S.H.; Wiggin, M.B.; Sawicki, G.S. Reducing the energy cost of human walking using an unpowered exoskeleton. Nature 2015, 522, 212–215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mooney, L.M.; Herr, H.M. Biomechanical walking mechanisms underlying the metabolic reduction caused by an autonomous exoskeleton. J. Neuroeng. Rehabil. 2016, 13, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Rajasekaran, V.; Aranda, J.; Casals, A.; Pons, J.L. An adaptive control strategy for postural stability using a wearable robot. Robot. Auton. Syst. 2015, 73, 16–23. [Google Scholar] [CrossRef] [Green Version]
- Hogen, N. Impedance control: An approach to manipulation. J. Dyn. Syst.-Trans. ASME 1985, 107, 17. [Google Scholar] [CrossRef]
- Sentis, L.; Khatib, O. A whole-body control framework for humanoids operating in human environments. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–18 May 2006; pp. 2641–2648. [Google Scholar] [CrossRef]
- McMahon, T.A. Muscles, Reflexes, and Locomotion; Princeton University Press: Princeton, NJ, USA, 1984; pp. 139–161. ISBN 0-691-08322-3. [Google Scholar]
- Fitzpatrick, R.C.; Gorman, R.B.; Burke, D.; Gandevia, S.C. Postural proprioceptive reflexes in standing human subjects: Bandwidth of response and transmission characteristics. J. Physiol. 1992, 458, 69–83. [Google Scholar] [CrossRef]
- Masani, K.; Popovic, M.R.; Nakazawa, K.; Kouzaki, M.; Nozaki, D. Importance of body sway velocity information in controlling ankle extensor activities during quiet stance. J. Neurophysiol. 2003, 90, 3774–3782. [Google Scholar] [CrossRef]
- Finley, J.M.; Dhaher, Y.Y.; Perreault, E.J. Contributions of feed-forward and feedback strategies at the human ankle during control of unstable loads. Exp. Brain Res. 2012, 217, 53–66. [Google Scholar] [CrossRef] [PubMed]
- Peterka, R.J. Sensorimotor integration in human postural control. J. Neurophysiol. 2002, 88, 1097–1118. [Google Scholar] [CrossRef]
- Insperger, T.; Milton, J.; Stépán, G. Acceleration feedback improves balancing against reflex delay. J. R. Soc. Interface. 2013, 10, 20120763. [Google Scholar] [CrossRef] [PubMed]
- Prochazka, A.; Gillard, D.; Bennett, D.J. Positive force feedback control of muscles. J. Neurophysiol. 1997, 77, 3226–3236. [Google Scholar] [CrossRef] [PubMed]
- Prochazka, A.; Gillard, D.; Bennett, D.J. Implications of positive feedback in the control of movement. J. Neurophysiol. 1997, 77, 3237–3251. [Google Scholar] [CrossRef] [PubMed]
- Pfeifer, S.; Vallery, H.; Hardegger, M.; Riener, R.; Perreault, E.J. Model-based estimation of knee stiffness. IEEE Trans. Bio-Med. Eng. 2012, 59, 2604–2612. [Google Scholar] [CrossRef] [PubMed]
- Misgeld, B.J.; Zhang, T.; Lüken, M.J.; Leonhardt, S. Model-based estimation of ankle joint stiffness. Sensors 2017, 17, 713. [Google Scholar] [CrossRef] [PubMed]
- Clancy, E.A.; Liu, L.; Liu, P.; Moyer, D.V.Z. Identification of constant-posture EMG-torque relationship about the elbow using nonlinear dynamic models. IEEE Trans. Bio-Med. Eng. 2012, 59, 205–212. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Zeng, C.; Liang, P.; Li, Z.; Li, R.; Su, C.Y. Interface design of a physical human–robot interaction system for human impedance adaptive skill transfer. IEEE Trans. Autom. Sci. Eng. 2018, 15, 329–340. [Google Scholar] [CrossRef]
- Ajoudani, A.; Tsagarakis, N.; Bicchi, A. Tele-impedance: Teleoperation with impedance regulation using a body–machine interface. Int. J. Robot. Res. 2012, 31, 1642–1656. [Google Scholar] [CrossRef]
- Ju, Z.; Liu, H. Human hand motion analysis with multisensory information. IEEE-ASME Trans. Mech. 2014, 19, 456–466. [Google Scholar] [CrossRef]
- Lee, H.; Krebs, H.I.; Hogan, N. Multivariable dynamic ankle mechanical impedance with active muscles. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 971–981. [Google Scholar] [CrossRef]
- Hashemi, J.; Morin, E.; Mousavi, P.; Hashtrudi-Zaad, K. Surface EMG force modeling with joint angle based calibration. J. Electromyogr. Kinesiol. 2013, 23, 416–424. [Google Scholar] [CrossRef]
- Artemiadis, P.K.; Kyriakopoulos, K.J. A switching regime model for the EMG-based control of a robot arm. IEEE Trans. Syst. Man Cybern. B 2001, 41, 53–63. [Google Scholar] [CrossRef]
- Hill, A.V. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. Ser. B-Biol. Sci. 1938, 126, 136–195. [Google Scholar] [CrossRef] [Green Version]
- Zajac, F.E. Muscle and tendon: Properties, models, scaling, and application to biomechanics and motor control. Crit. Rev. Biomed. Eng. 1989, 17, 359–411. [Google Scholar]
- Durandau, G.; Farina, D.; Sartori, M. Robust real-time musculoskeletal modeling driven by electromyograms. IEEE Trans. Bio-Med. Eng. 2018, 65, 556–564. [Google Scholar] [CrossRef]
- Lockhart, D.B.; Ting, L.H. Optimal sensorimotor transformations for balance. Nat. Neurosci. 2007, 10, 1329–1336. [Google Scholar] [CrossRef]
- Geyer, H.; Herr, H. A muscle-reflex model that encodes principles of legged mechanics produces human walking dynamics and muscle activities. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 263–273. [Google Scholar] [CrossRef]
- Nitish, T.; Geyer, H. Toward balance recovery with leg prostheses using neuromuscular model control. IEEE Trans. Bio-Med. Eng. 2016, 63, 904–913. [Google Scholar] [CrossRef]
- Batts, Z.; Song, S.; Geyer, H. Toward a virtual neuromuscular control for robust walking in bipedal robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 6318–6323. [Google Scholar]
- Winter, D.A.; Patla, A.E.; Prince, F.; Ishac, M.; Gielo-Perczak, K. Stiffness control of balance in quiet standing. J. Neurophysiol. 1998, 80, 1211–1221. [Google Scholar] [CrossRef]
- Vette, A.H.; Masani, K.; Nakazawa, K.; Popovic, M.R. Neural-mechanical feedback control scheme generates physiological ankle torque fluctuation during quiet stance. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 86–95. [Google Scholar] [CrossRef]
- Emmens, A.R.; van Asseldonk, E.H.; van der Kooij, H. Effects of a powered ankle-foot orthosis on perturbed standing balance. J. Neuroeng. Rehabil. 2018, 15, 50–62. [Google Scholar] [CrossRef]
- Cafolla, D.; Marco, C. Design and simulation of humanoid spine. New Trends Mech. Mach. Sci. 2015, 24, 585–593. [Google Scholar] [CrossRef]
- Cafolla, D.; Chen, I.M.; Ceccarelli, M. An experimental characterization of human torso motion. Front. Mech. Eng. 2015, 10, 311–325. [Google Scholar] [CrossRef]
- Fitzpatrick, R.; Burke, D.; Gandevia, S.C. Loop gain of reflexes controlling human standing measured with the use of postural and vestibular disturbances. J. Neurophysiol. 1996, 76, 3994–4008. [Google Scholar] [CrossRef] [PubMed]
- Blum, K.P.; D’Incamps, B.L.; Zytnicki, D.; Ting, L.H. Force encoding in muscle spindles during stretch of passive muscle. PLoS Comput. Biol. 2017, 13, e1005767. [Google Scholar] [CrossRef]
- Maganaris, C.N. Force-length characteristics of the in vivo human gastrocnemius muscle. Clin. Anat. 2003, 16, 215–223. [Google Scholar] [CrossRef]
- Buchanan, T.S.; Lloyd, D.G.; Manal, K.; Besier, T.F. Estimation of muscle forces and joint moments using a forward-inverse dynamics model. Med. Sci. Sports Exerc. 2005, 37, 1911–1916. [Google Scholar] [CrossRef]
- OpenSim Documentation—Musculoskeletal Models. Available online: https://simtk-confluence.stanford.edu/display/OpenSim/Musculoskeletal+Models#MusculoskeletalModels-OpenSimCoreModels (accessed on 10 May 2018).
- Roberts, T.J. The integrated function of muscles and tendons during locomotion. Comp. Biochem. Phys. A 2002, 133, 1087–1099. [Google Scholar] [CrossRef]
- Hansen, N. The CMA evolution strategy: A tutorial. arXiv 2016, arXiv:1604.00772. [Google Scholar]
- Hogan, N. Adaptive control of mechanical impedance by coactivation of antagonist muscles. IEEE Trans. Autom. Control 1984, 29, 681–690. [Google Scholar] [CrossRef]
- Kearney, R.E.; Stein, R.B.; Parameswaran, L. Identification of intrinsic and reflex contributions to human ankle stiffness dynamics. IEEE Trans. Bio-Med. Eng. 1997, 44, 493–504. [Google Scholar] [CrossRef]
- Vlutters, M.; Boonstra, T.A.; Schouten, A.C.; van der Kooij, H. Direct measurement of the intrinsic ankle stiffness during standing. J. Biomech. 2015, 48, 1258–1263. [Google Scholar] [CrossRef] [PubMed]
- Potvin, J.R.; Brown, S.H.M. Less is more: High pass filtering, to remove up to 99% of the surface EMG signal power, improves EMG-based biceps brachii muscle force estimates. J. Electromyogr. Kinesiol. 2004, 14, 389–399. [Google Scholar] [CrossRef] [PubMed]


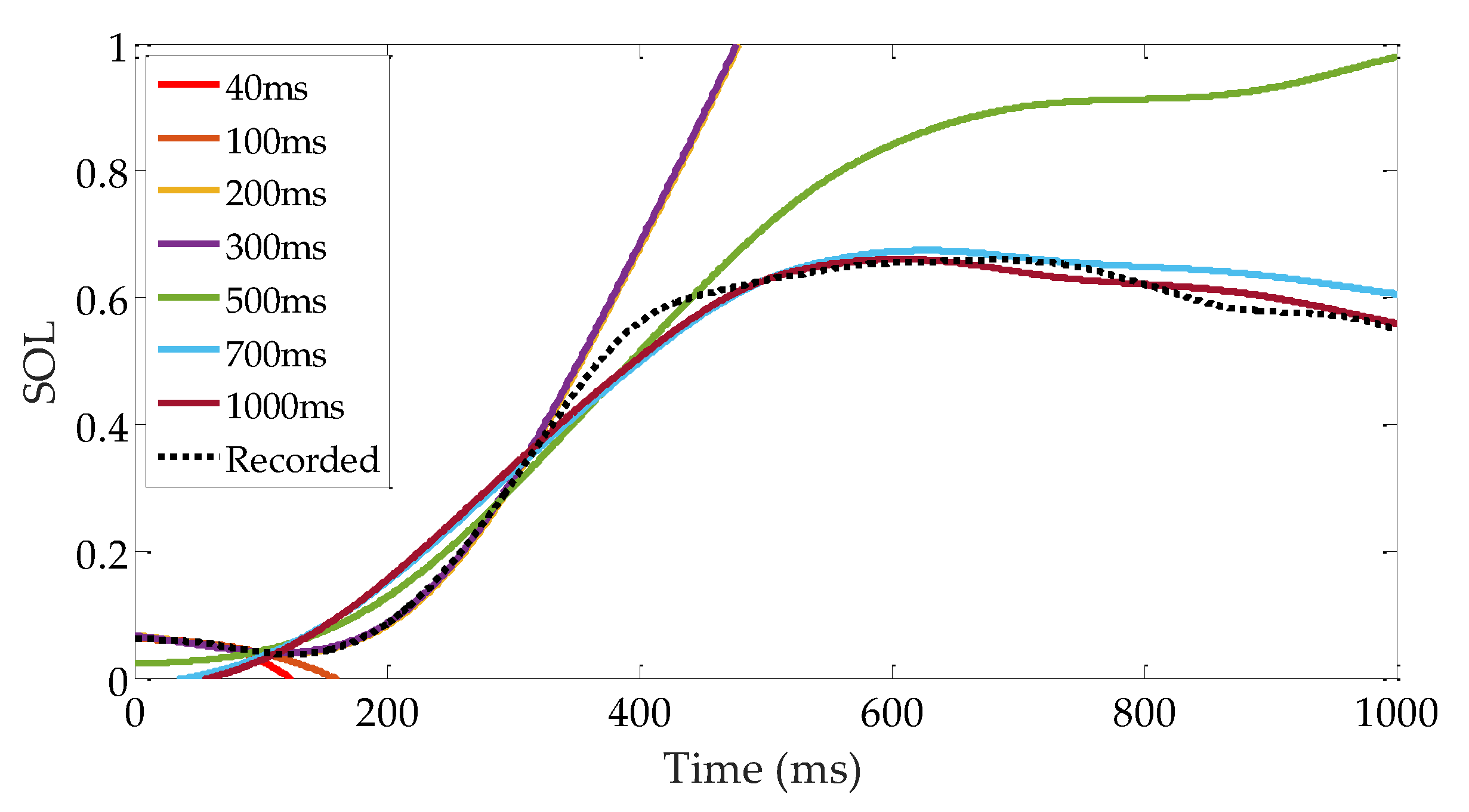

| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| pa of SOL | 6.20 | 6.12 | 5.34 | 6.90 | 6.85 | 6.82 |
| da of SOL | 0.91 | 0.50 | 1.02 | 0.19 | 0.24 | 0.29 |
| VAF 1 of SOL | 0.94/0.96 | 0.92/0.93 | 0.78/0.95 | 0.91/0.95 | 0.83/0.95 | 0.88/0.92 |
| RMSE 2 of SOL | 0.03/0.02 | 0.11/0.06 | 0.13/0.04 | 0.08/0.01 | 0.10/0.05 | 0.09/0.05 |
| pa of GAS | 0.84 | 1.06 | 0.85 | 1.31 | 1.08 | 1.31 |
| da of GAS | 0.28 | 0.03 | 0.14 | 0.05 | 0.11 | 0.07 |
| VAF of GAS | 0.77/0.94 | 0.94/0.96 | 0.88/0.93 | 0.97/0.97 | 0.96/0.97 | 0.90/0.95 |
| RMSE of GAS | 0.02/0.005 | 0.04/0.01 | 0.03/0.01 | 0.01/0.002 | 0.02/0.01 | 0.02/0.01 |
| A | B | C | D | E | |
|---|---|---|---|---|---|
| pa of SOL | 6.37 ± 0.61 | 2.43 ± 0.37 | 3.59 ± 0.81 | 2.44 ± 0.51 | 14.51 ± 3.70 |
| da of SOL | 0.52 ± 0.36 | 1.92 ± 0.52 | 0.28 ± 0.14 | 0.36 ± 0.28 | 0.81 ± 0.63 |
| VAF 1 | 88.2/94.8 | 89.0/91.6 | 88.2/90.4 | 89.4/94.2 | 90.4/92.2 |
| pa of GAS | 1.08 ± 0.21 | 1.90 ± 0.70 | 4.06 ± 1.01 | 4.65 ± 1.30 | 8.36 ± 2.78 |
| da of GAS | 0.11 ± 0.09 | 0.20 ± 0.08 | 0.31 ± 0.18 | 1.09 ± 0.49 | 0.66 ± 0.34 |
| VAF | 90.4/95.7 | 90.3/92.3 | 87.2/91.3 | 88.3/92.1 | 87.3/91.5 |
| B | C | D | E | |
|---|---|---|---|---|
| A | 0.001, 0.002 1 | 0.018, 0.865 | 0.001, 0.561 | 0.038, 0.265 |
| B | 0.094, 0.002 | 0.955, 0.005 | 0.008, 0.131 | |
| C | 0.109, 0.630 | 0.014, 0.279 | ||
| D | 0.009, 0.368 |
| A | B | C | D | E | |
|---|---|---|---|---|---|
| pa of SOL 1 | 16.84 ± 7.51(<0.01) | 8.88 ± 9.356(<0.01) | 3.75 ± 1.02(0.826) | 2.00 ± 1.07(0.03) | 9.61 ± 4.70(0.03) |
| pd of SOL | −1.13 ± 3.71(<0.01) | 0.70 ± 0.82(0.031) | 0.73 ± 0.60(0.017) | 0.56 ± 0.43(0.17) | 0.93 ± 1.06(0.03) |
| VAF | 64.9/90.4(<0.01) | 67.0/77.0(<0.01) | 77.6/88.1(0.185) | 59.3/83.2(<0.01) | 73.7/88.7(0.23) |
| pa of GAS | 2.97 ± 1.79(0.108) | 0.67 ± 0.52(0.021) | 6.46 ± 1.94(0.087) | 1.88 ± 1.05(<0.01) | 6.11 ± 2.50(0.397) |
| pd of GAS | −0.13 ± 0.98(<0.01) | 0.18 ± 0.09(0.428) | 0.33 ± 0.30(0.029) | 1.11 ± 1.40(0.43) | 0.35 ± 0.48(0.09) |
| VAF | 67.5/93.0(<0.01) | 76.9/82.7(0.027) | 90.0/95.3(0.045) | 60.1/80.1(<0.01) | 79.3/86.4(0.47) |
| Muscle | FMAX (N) | θp (°) | LCE0 (cm) | VCE0 (cm/s) |
|---|---|---|---|---|
| SOL | 4572.3 | 28.3 | 4.78 | 50 |
| GAS | 2225.7 | 12 | 5.78 | 60 |
| TA 1 | 1148.9 | 9.6 | 6.04 | 60 |
| 10Hz | 7Hz | 6Hz | 5Hz | 4Hz | 3Hz | 2Hz | 1Hz | |
|---|---|---|---|---|---|---|---|---|
| pa | 4.06 | 4.35 | 4.48 | 4.66 | 4.93 | 5.35 | 5.84 | 5.33 |
| da | 0.38 | 0.42 | 0.44 | 0.46 | 0.48 | 0.48 | 0.39 | 0.19 |
| VAF | 0.74 | 0.84 | 0.86 | 0.88 | 0.91 | 0.95 | 0.98 | 0.98 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, M.; Xu, X.; Tang, B.; Xiang, K.; Ju, Z. Evaluation of Calf Muscle Reflex Control in the ‘Ankle Strategy’ during Upright Standing Push-Recovery. Appl. Sci. 2019, 9, 2085. https://doi.org/10.3390/app9102085
Pang M, Xu X, Tang B, Xiang K, Ju Z. Evaluation of Calf Muscle Reflex Control in the ‘Ankle Strategy’ during Upright Standing Push-Recovery. Applied Sciences. 2019; 9(10):2085. https://doi.org/10.3390/app9102085
Chicago/Turabian StylePang, Muye, Xiangui Xu, Biwei Tang, Kui Xiang, and Zhaojie Ju. 2019. "Evaluation of Calf Muscle Reflex Control in the ‘Ankle Strategy’ during Upright Standing Push-Recovery" Applied Sciences 9, no. 10: 2085. https://doi.org/10.3390/app9102085
APA StylePang, M., Xu, X., Tang, B., Xiang, K., & Ju, Z. (2019). Evaluation of Calf Muscle Reflex Control in the ‘Ankle Strategy’ during Upright Standing Push-Recovery. Applied Sciences, 9(10), 2085. https://doi.org/10.3390/app9102085





