Design of Terminal Sliding Mode Controllers for Disturbed Non-Linear Systems Described by Matrix Differential Equations of the Second and First Orders
Abstract
:1. Introduction
1.1. Motivation
1.2. Related Work
1.3. Contribution
1.4. Organization of the Paper
2. Systems Description
2.1. Matrix Second-Order System
2.2. Matrix First-Order System
3. Controller Design
3.1. TSMC for Matrix Second-Order System
3.2. TSMC for Matrix First-Order System
4. Illustrative Examples
4.1. RLC Circuit
4.2. RC Circuit
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Skruch, P. Feedback stabilization of a class of nonlinear second-order systems. Nonlinear Dyn. 2010, 59, 681–692. [Google Scholar] [CrossRef]
- Spong, M.; Vidyasagar, M. Robot Dynamics and Control; John Willey & Sons: New York, NY, USA, 2009. [Google Scholar]
- Skruch, P. An educational tool for teaching vehicle electronic system architecture. Int. J. Electr. Eng. Educ. 2011, 48, 174–183. [Google Scholar] [CrossRef]
- Skruch, P.; Panek, M.; Kowalczyk, B. Model-based testing in embedded automotive systems. In Model-Based Testing for Embedded Systems; Zander-Nowicka, J., Schieferdecker, I., Mosterman, P., Eds.; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2011; pp. 293–308. [Google Scholar]
- Długosz, M. Aggregation of state variables in an RC model. Build. Serv. Eng. Res. Technol. 2018, 39, 66–80. [Google Scholar] [CrossRef]
- Długosz, M.; Skruch, P. The application of fractional-order models for thermal process modelling inside buildings. J. Build. Phys. 2016, 39, 440–451. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K.; Gawin, E.; Mitkowski, W. Modeling heat distribution with the use of a non-integer order, state space model. Int. J. Appl. Math. Comput. Sci. 2016, 26, 749–756. [Google Scholar] [CrossRef] [Green Version]
- Moon, F. Chaotic Vibrations: An Introduction for Applied Scientists and Engineers; John Willey & Sons: New York, NY, USA, 2004. [Google Scholar]
- Buscarino, A.; Fortuna, L.; Frasca, M.; Sciuto, G. Chua’s circuit synchronization with diffusive coupling: New results. Int. J. Bifurc. Chaos 2009, 19, 3103–3107. [Google Scholar] [CrossRef]
- Buscarino, A.; Corradino, C.; Fortuna, L.; Frasca, M.; Sprott, J. Nonideal behavior of analog multipliers for chaos generation. IEEE Trans. Circuits Syst. II. Express Briefs 2016, 63, 396–400. [Google Scholar] [CrossRef]
- Edward, C.; Spurgeon, S. Sliding Mode Control: Theory and Appliations; Taylor and Francis: London, UK, 1998. [Google Scholar]
- Liu, J.; Wang, X. Advanced Sliding Mode Control for Mechanical Systems; Springer: Heidelberg, Germany; Dordrecht, The Netherlands; London, UK; New York, NY, USA, 2011. [Google Scholar]
- Pisano, A.; Usai, E. Sliding mode control: A survey with application in math. Math. Comput. Simul. 2011, 81, 954–979. [Google Scholar] [CrossRef]
- Dlugosz, M. Optimization problems of power transmission in automation and robotic. Prz. Elektrotech. 2011, 87, 238–242. [Google Scholar]
- Bandyopadhyay, B.; Deepak, F.; Kim, K. Sliding Mode Control Using Novel Sliding Surfaces; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Liu, J.; Sun, F. A novel dynamic terminal sliding mode control of uncertain nonlinear systems. J. Control Theory Appl. 2007, 5, 189–193. [Google Scholar] [CrossRef]
- Man, Z.; Yu, X. Terminal sliding mode control of MIMO linear systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 1065–1070. [Google Scholar]
- Skruch, P.; Dlugosz, M.; Mitkowski, W. Mathematical methods for verification of microprocessor-based PID controllers for improving their reliability. Eksploat. I Niezawodn. Maint. Reliab. 2015, 17, 327–333. [Google Scholar] [CrossRef]
- Mobayen, S.; Majd, V.; Sojoodi, M. An LMI-based composite nonlinear feedback terminal sliding-mode controller design for disturbed MIMO systems. Math. Comput. Simul. 2012, 85, 1–10. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Zheng, J. Nonsingular terminal sliding mode control of uncertain multivariable systems. In Proceedings of the 2006 International Workshop on Variable Structure Systems, Alghero, Italy, 5–7 June 2006; pp. 196–201. [Google Scholar]
- Hong, Y.; Yang, G.; Cheng, D.; Spurgeon, S. A new approach to terminal sliding mode control design. Asian J. Control 2005, 7, 177–181. [Google Scholar] [CrossRef]
- Zhihong, M.; Paplinski, A.; Wu, H. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators. IEEE Trans. Autom. Control 1994, 39, 2464–2469. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Tang, Y. Terminal sliding mode control for rigid robots. Automatica 1998, 34, 51–56. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Mezghani, N.; Romdhane, B.; Damak, T. Terminal sliding mode feedback linearization control. Int. J. Sci. Tech. Autom. Control Comput. Eng. 2010, 4, 1174–1187. [Google Scholar]
- Wu, Y.; Yu, X.; Man, Z. Terminal slidingmodecontrol design for uncertain dynamic systems. Syst. Control Lett. 1998, 34, 281–287. [Google Scholar] [CrossRef]
- Xiang, W.; Huangpu, Y. Second-order terminal sliding mode controller for a class of chaotic systems with unmatched uncertainties. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3241–3247. [Google Scholar] [CrossRef]
- Li, J.; Yu, F.; Zhang, J.; Feng, J.; Zhao, H. The rapid development of a vehicle electronic control system and its application to an antilock braking system based on hardware-in-the-loop simulation. J. Automob. Eng. 2002, 216, 95–105. [Google Scholar] [CrossRef]
- Chen, F.; Hou, R.; Jiang, B.; Tao, G. Study on fast terminal sliding mode control for a helicopter via quantum information technique and nonlinear fault observer. Int. J. Innov. Comput. Inf. Control 2013, 9, 3437–3447. [Google Scholar]
- Yang, L.; Yang, J. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems. Int. J. Robust Nonlinear Control 2011, 21, 1865–1879. [Google Scholar] [CrossRef]
- Yu, X.; Zhihong, M. Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 261–264. [Google Scholar]
- Tao, C.; Taur, J. Adaptive fuzzy terminal sliding mode controller for linear systems with mismatched time-varying uncertainties. IEEE Trans. Syst. Man, Cybern. Part B Cybern. 2004, 34, 255–262. [Google Scholar] [CrossRef]
- Mon, Y. Terminal sliding mode fuzzy-PDC control for nonlinear systems. Int. J. Sci. Technol. Res. 2013, 2, 218–221. [Google Scholar]
- Mitkowski, W.; Skruch, P. Fractional-order models of the supercapacitors in the form of RC lader networks. Bull. Pol. Acad. Sci. Tech. Sci. 2013, 61, 100–106. [Google Scholar]
- Wang, Y.; Luo, G.; Gu, L.; Li, X. Fractional-order nonsingular terminal sliding mode control of hydraulic manipulators using time delay estimation. J. Vib. Control 2016, 22, 3998–4011. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Zheng, Z. Second-order terminal sliding mode control of input-delay systems. Asian J. Control 2006, 8, 12–20. [Google Scholar] [CrossRef]
- Rasvan, V. Stability and sliding modes for a class of nonlinear time delay systems. Math. Bohem. 2011, 136, 155–164. [Google Scholar]
- Xi, Z.; Hesketh, T. On discrete time terminal sliding mode control for nonlinear systems with uncertainty. In Proceedings of the 2010 Americal Control Conferenece, Baltimore, MD, USA, 30 June–2 July 2010; pp. 980–984. [Google Scholar]
- Zhuang, K.; Su, H.; Zhang, K.; Chu, J. Adaptive terminal sliding mode control for high-order nonlinear dynamic systems. J. Zhejiang Univ.-SCIENCE A 2003, 4, 58–63. [Google Scholar] [CrossRef]
- Skruch, P. A terminal sliding mode control of disturbed nonlinear second-order dynamical systems. J. Comput. Nonlinear Dyn. 2016, 11, 054501. [Google Scholar] [CrossRef]
- Skruch, P.; Dlugosz, M. A linear dynamic feedback controller for non-linear systems described by matrix differential equations of the second and first orders (accepted for publication). Meas. Control 2019, 1–9. [Google Scholar] [CrossRef]
- Alekseev, V.; Tikhomirov, V.; Fomin, S. Optimal Control; Consultants Bureau: New York, NY, USA, 1987. [Google Scholar]
- Boltyanskii, V. Mathematical Methods of Optimal Control; Holt Rinehart & Winston: New York, NY, USA, 1971. [Google Scholar]
- Ioffe, A.; Tikhomirov, V. Theory of Extremal Problems; North-Holland: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Moulay, E.; Peruquetti, W. Finite time stability and stabilization of a class of continuous systems. J. Math. Anal. Appl. 2006, 323, 1430–1443. [Google Scholar] [CrossRef] [Green Version]
- Buscarino, A.; Famoso, C.; Fortuna, L.; Frasca, M. Passive and active vibrations allow self-organization in large-scale electromechanical systems. Int. J. Bifurc. Chaos 2016, 26, 1–10. [Google Scholar] [CrossRef]

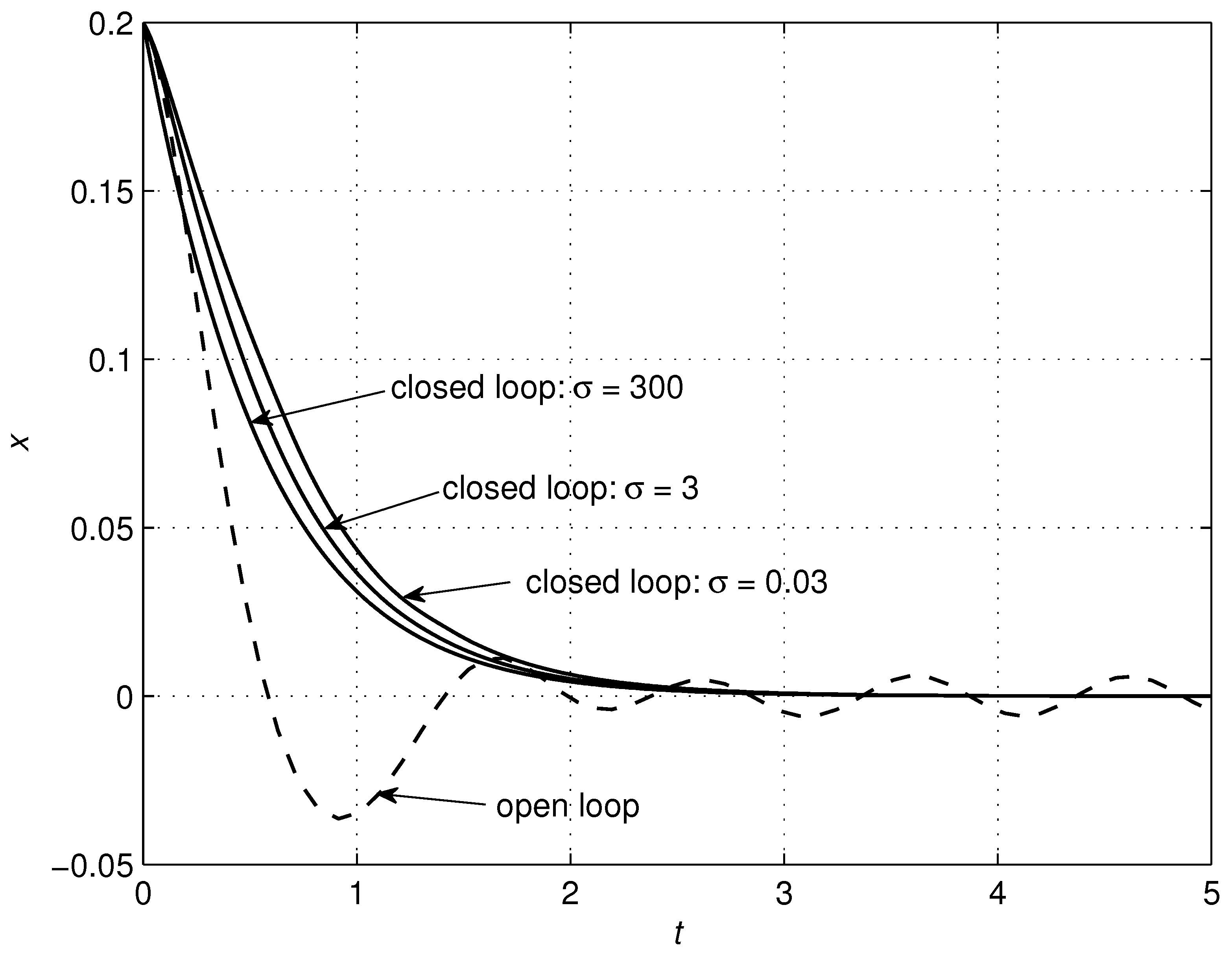
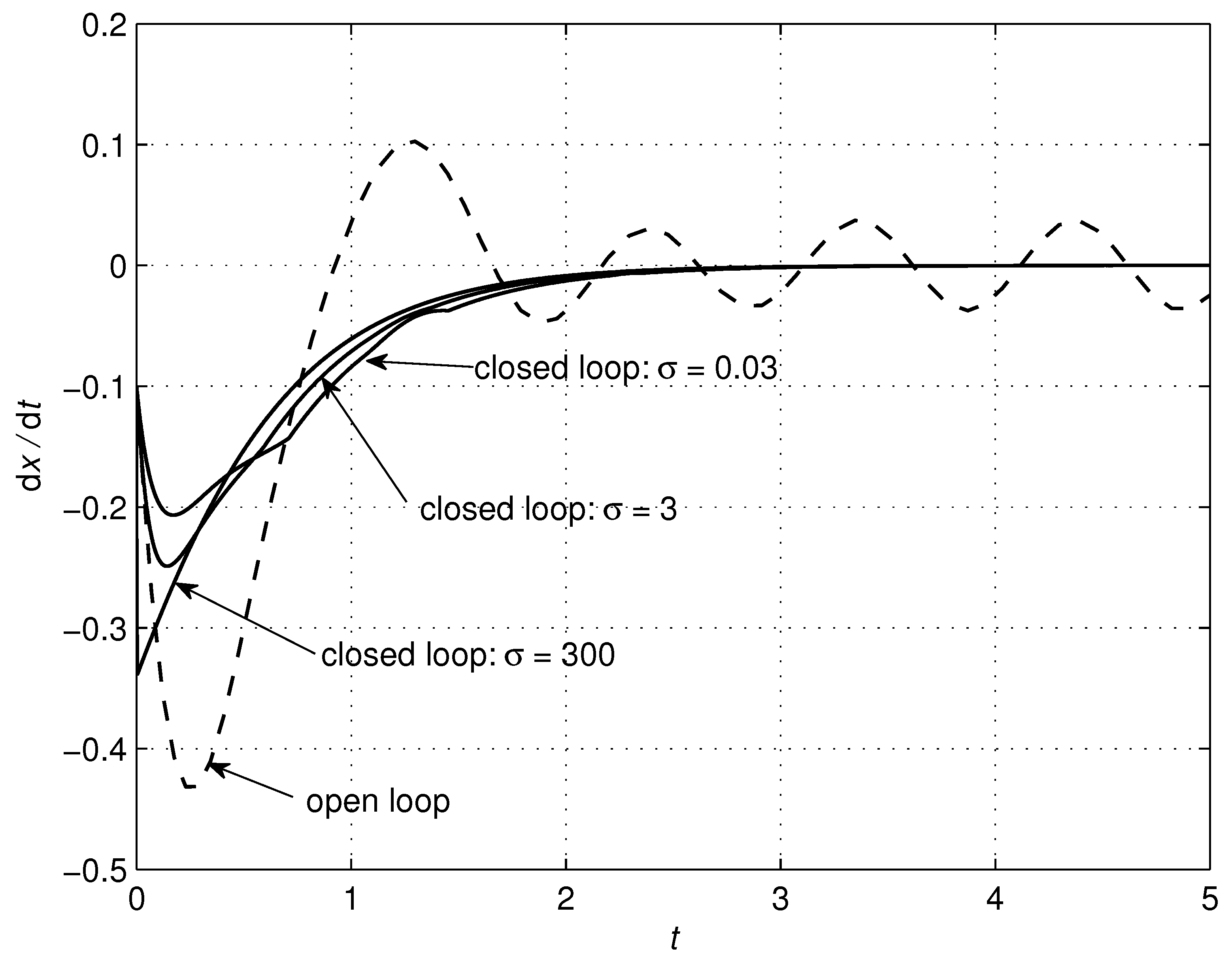
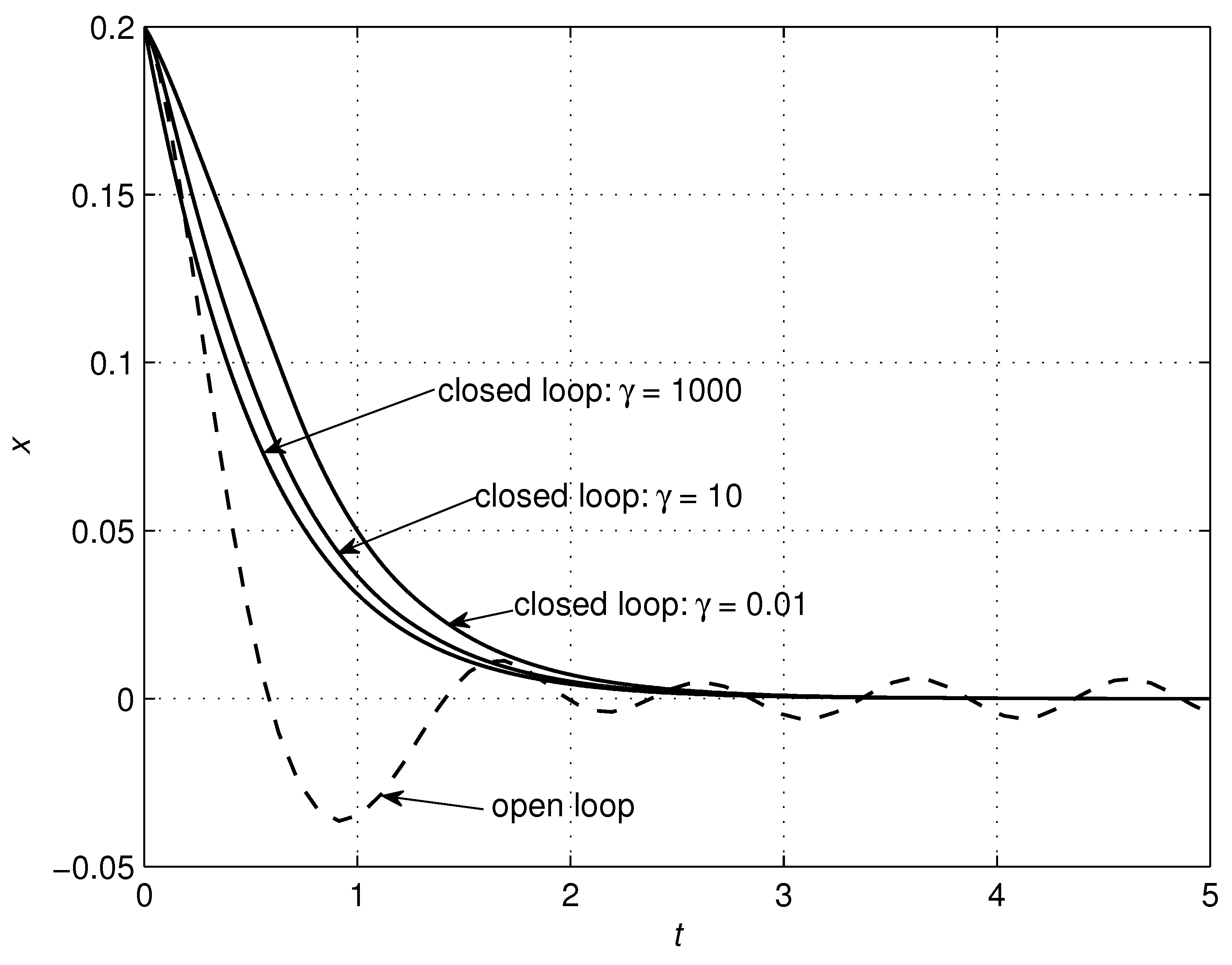
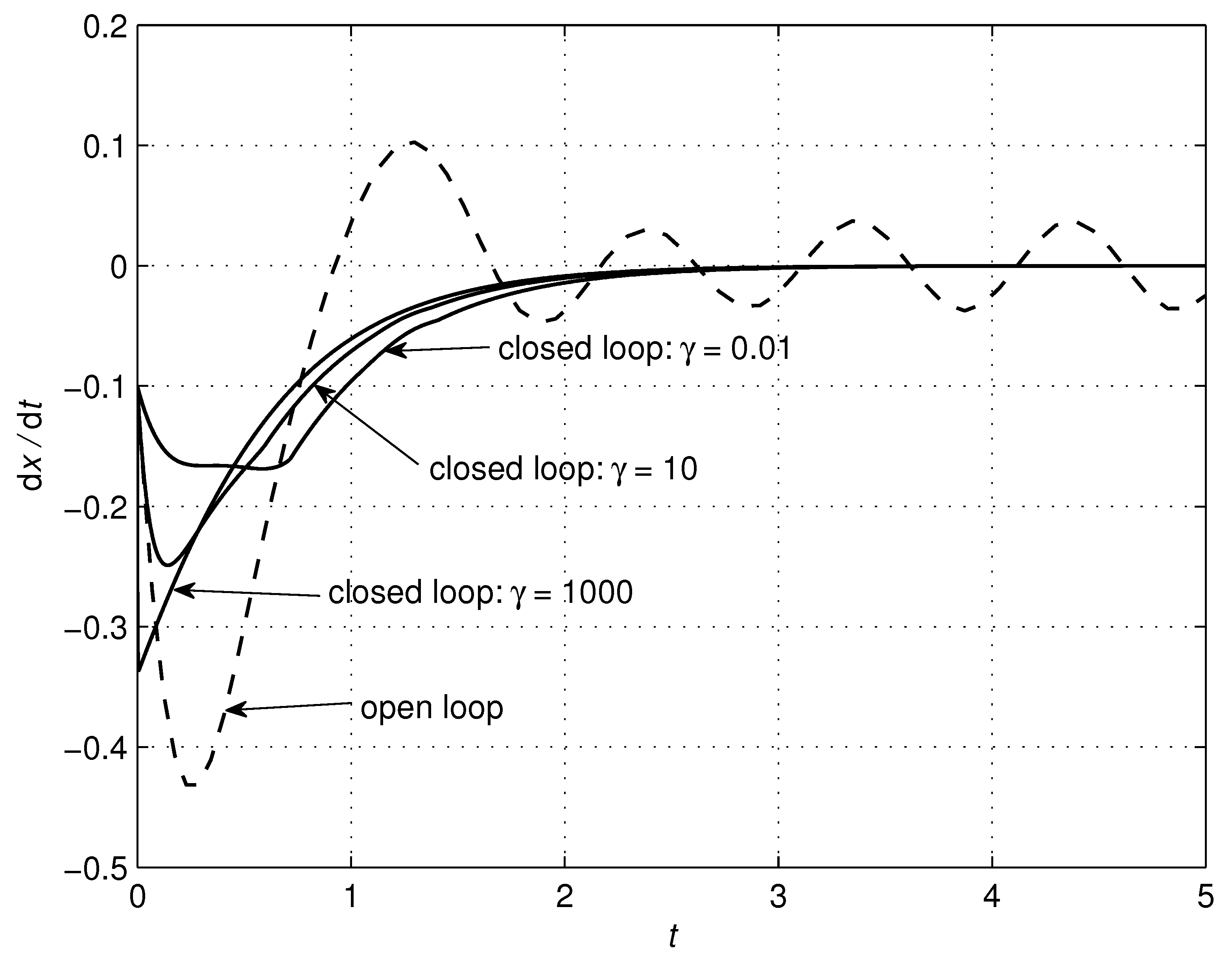
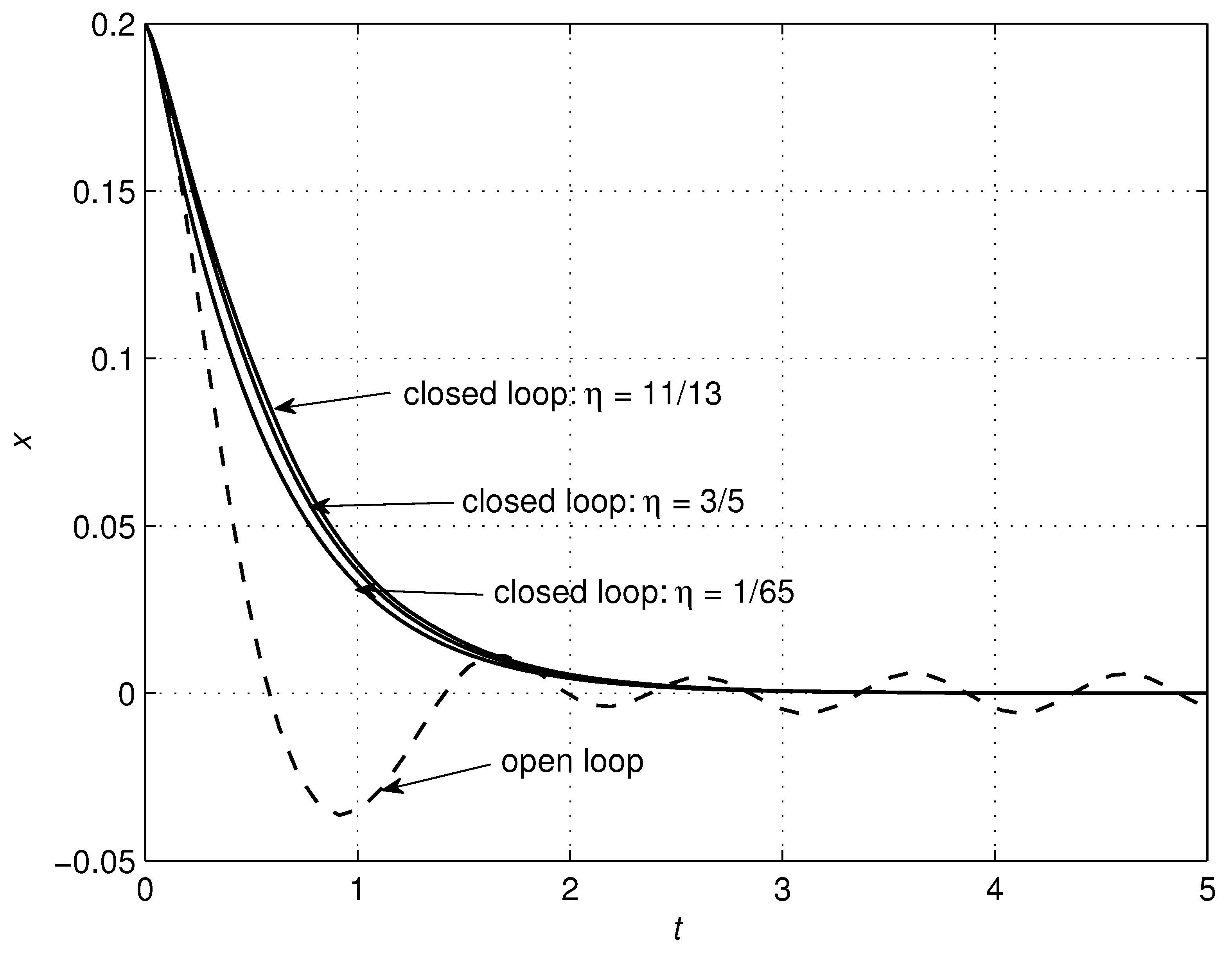
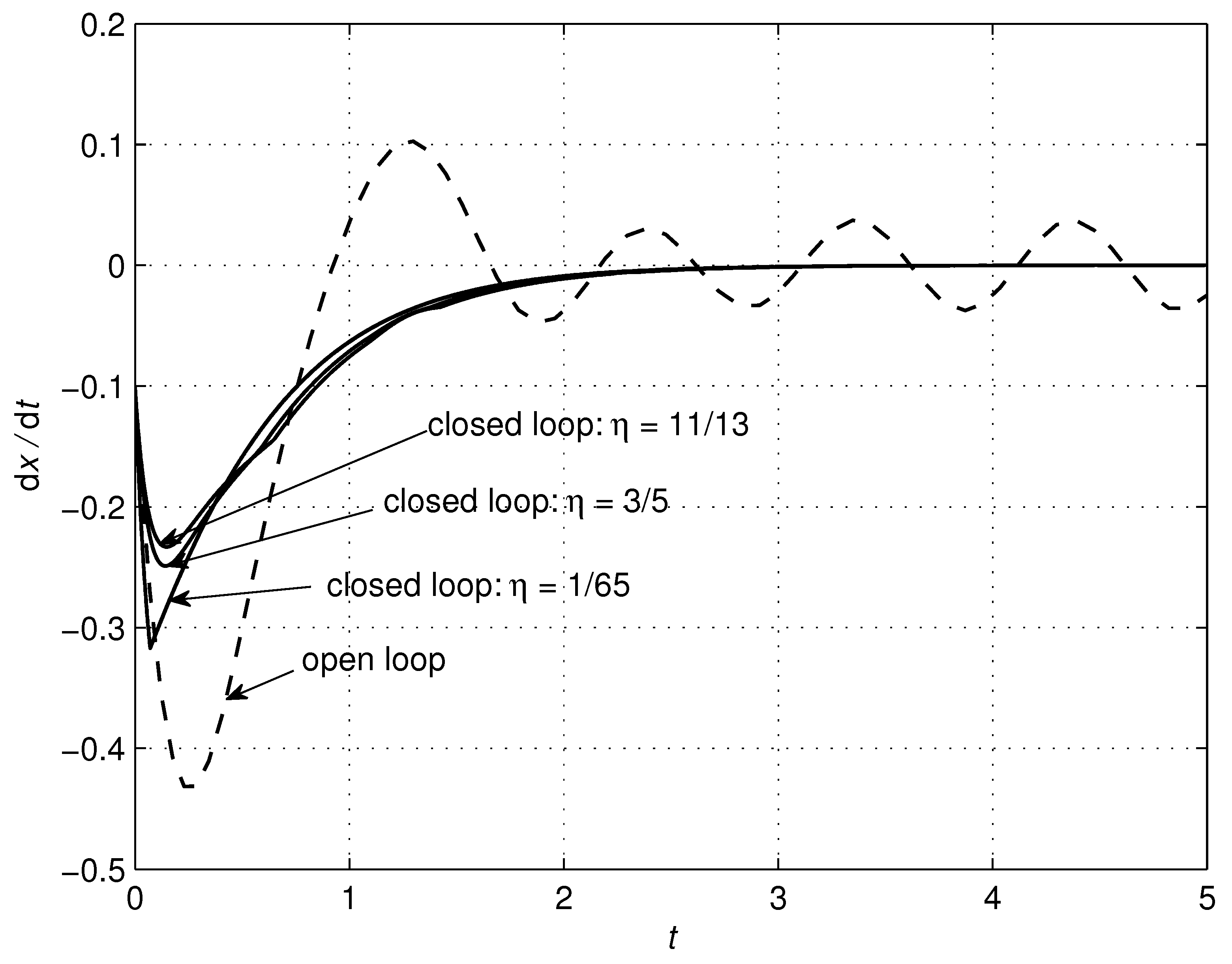
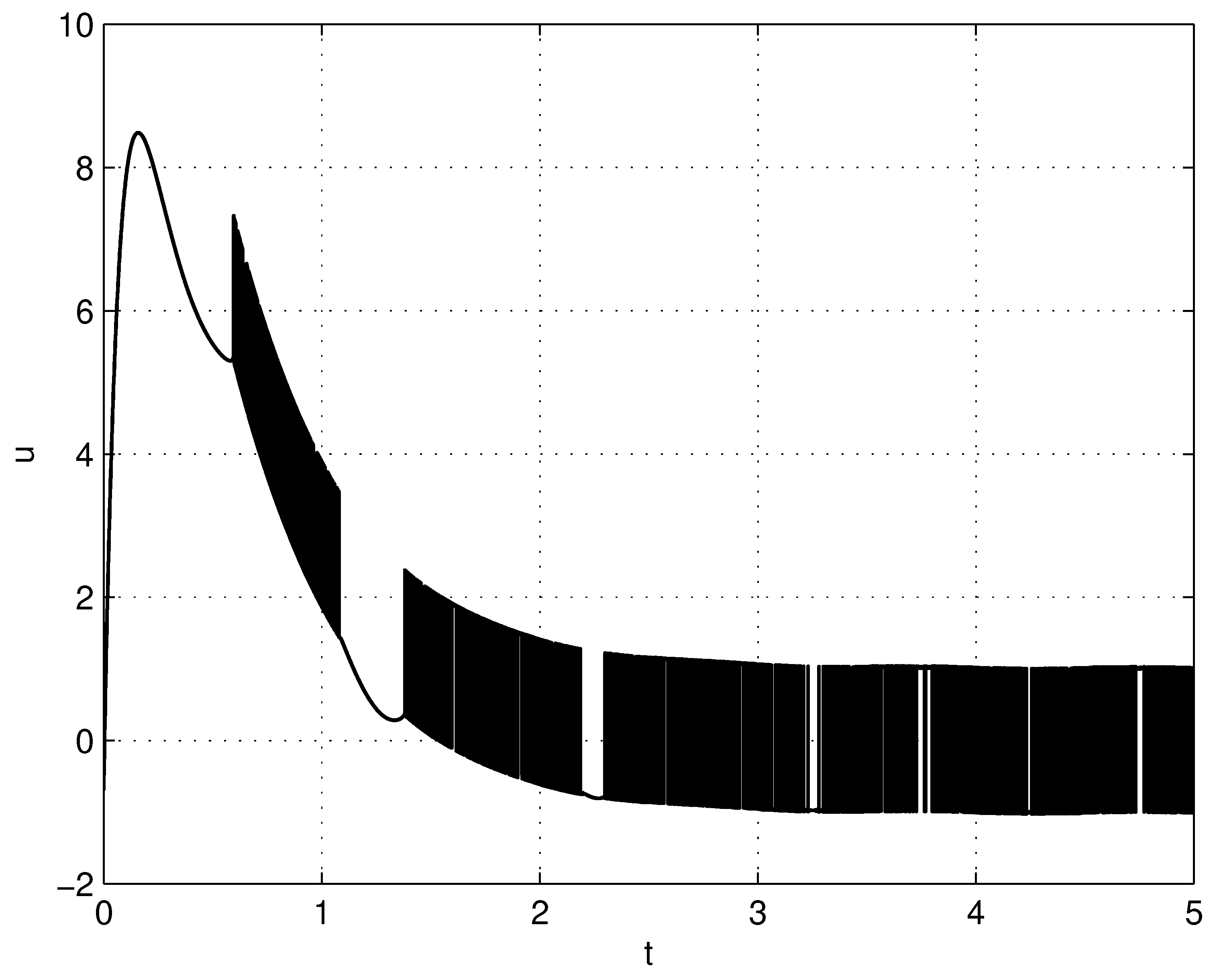

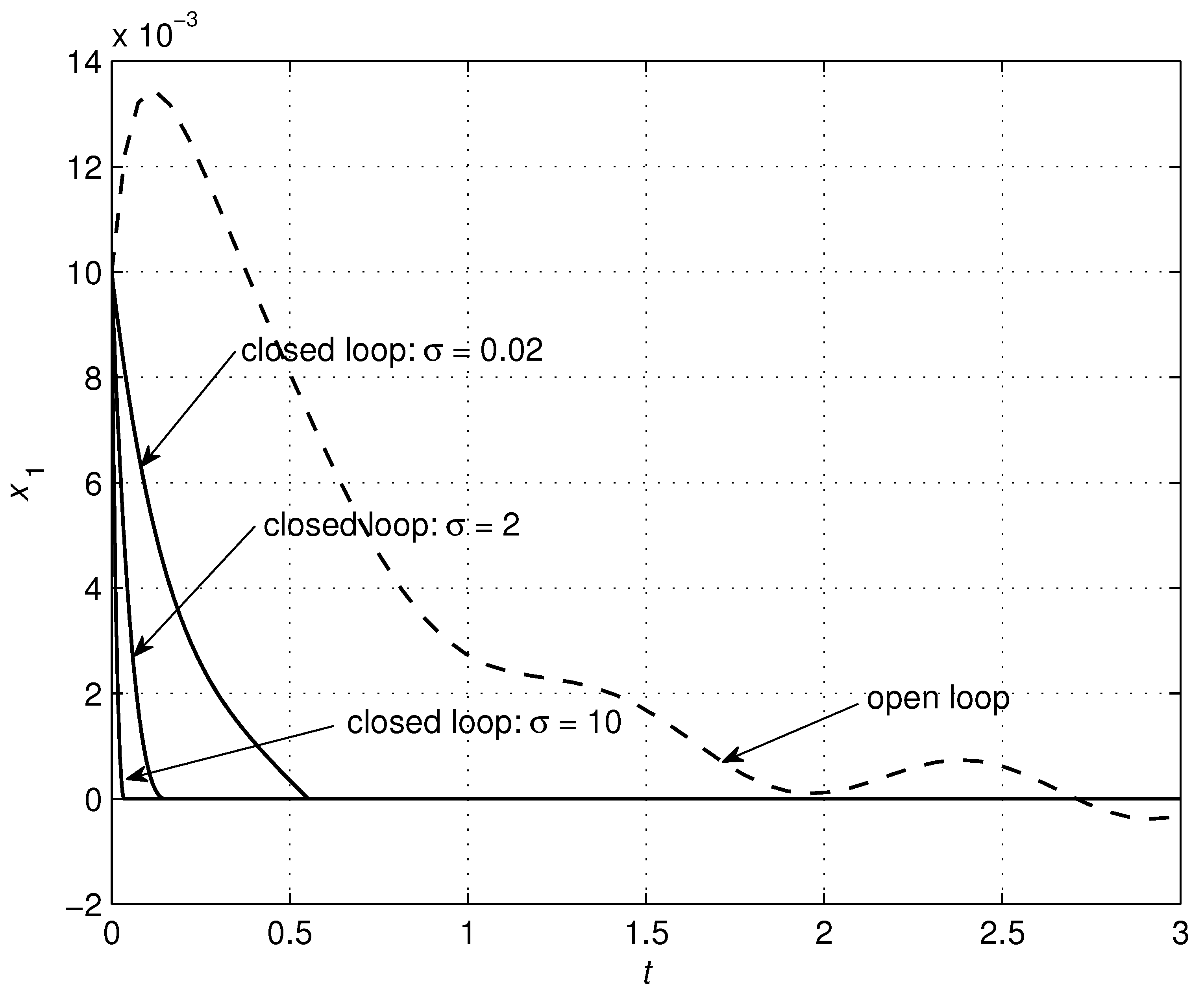
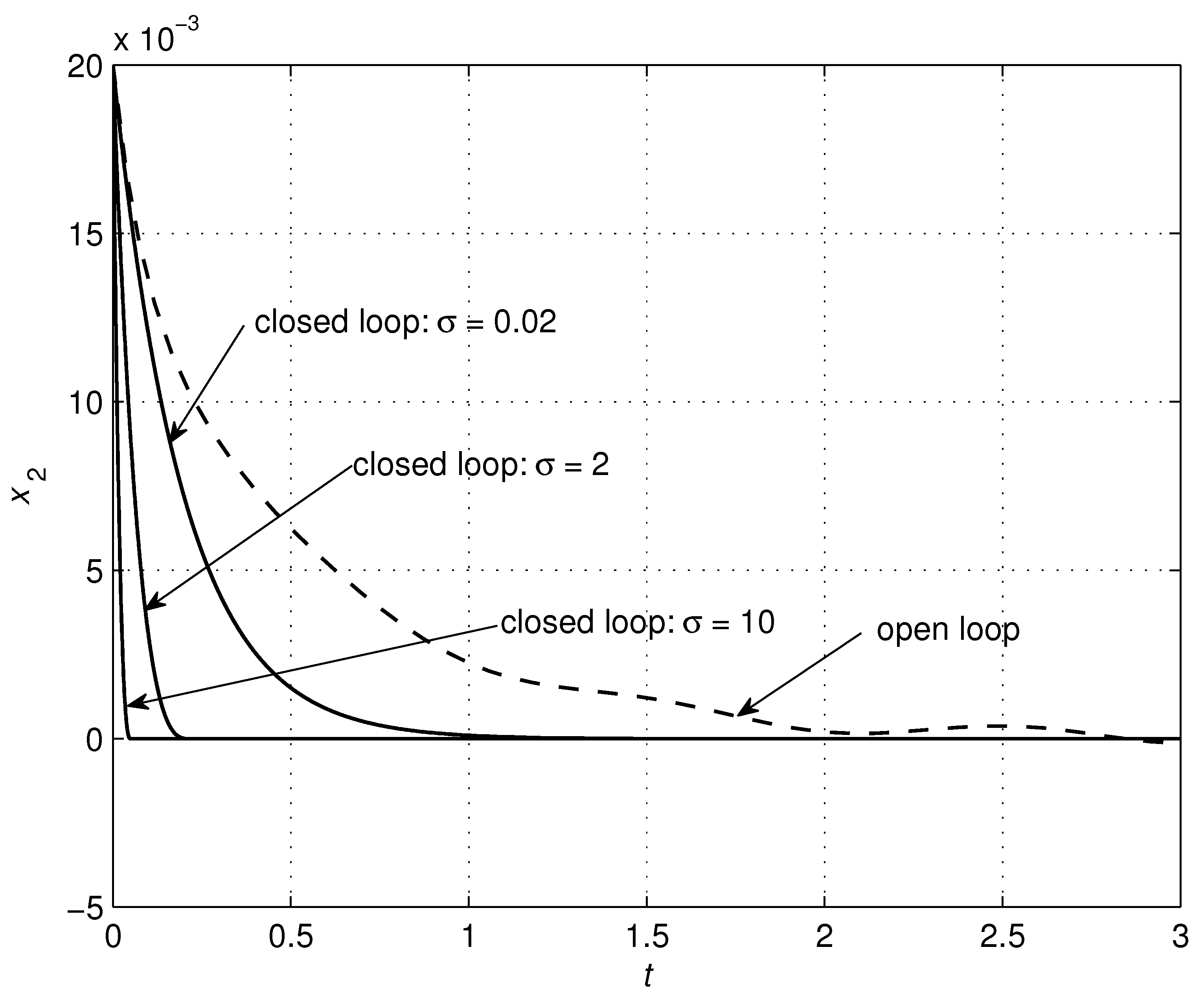
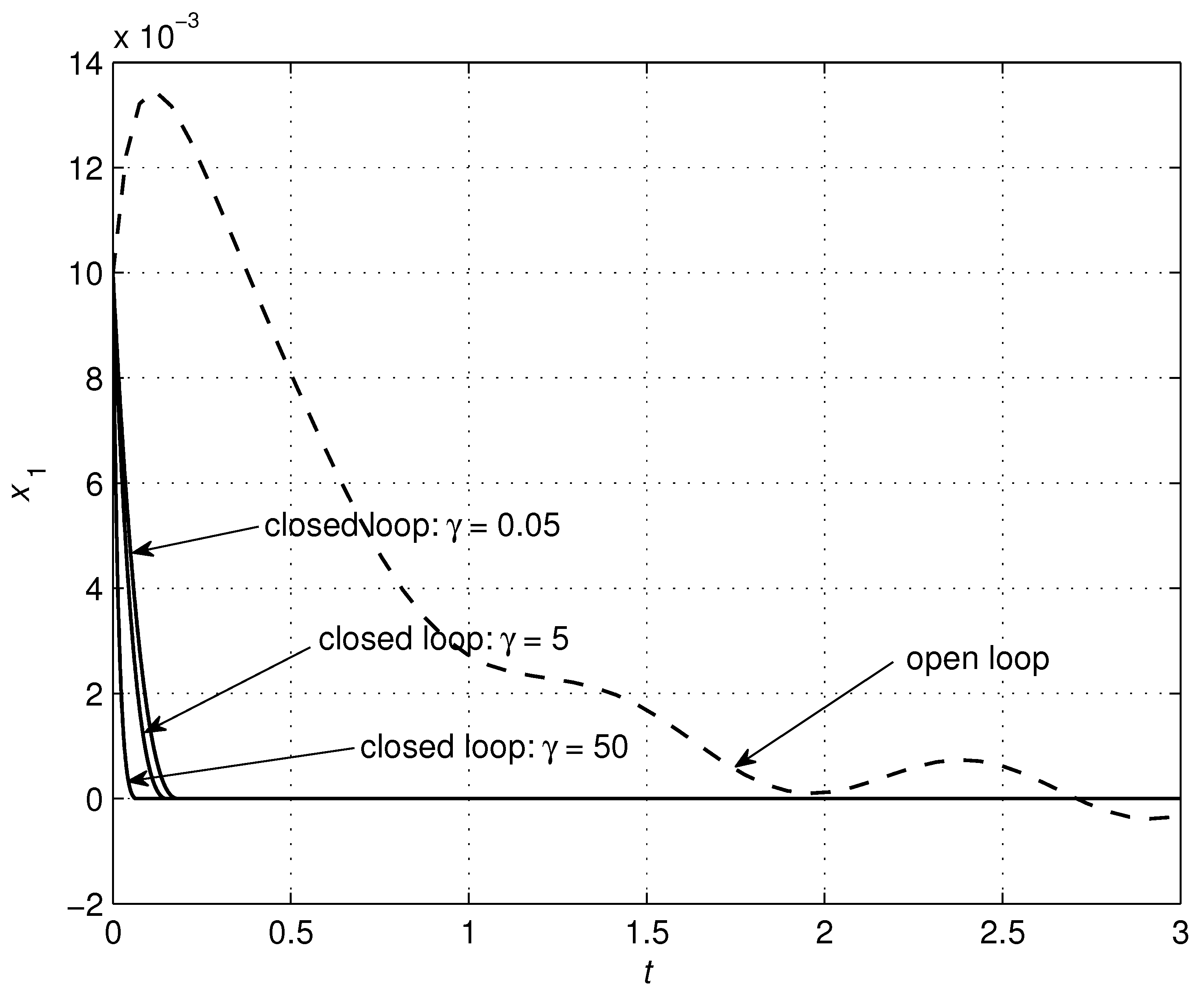
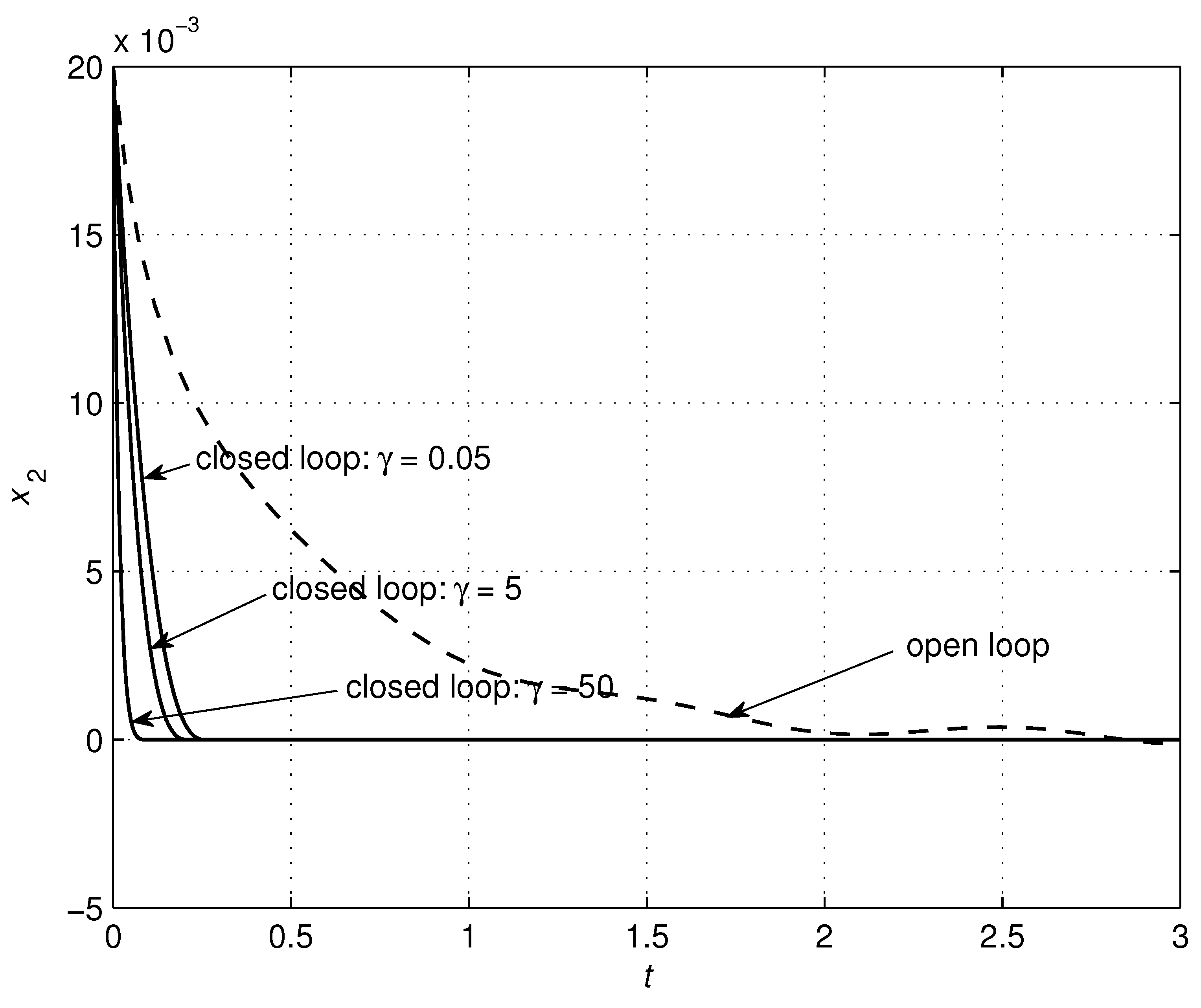
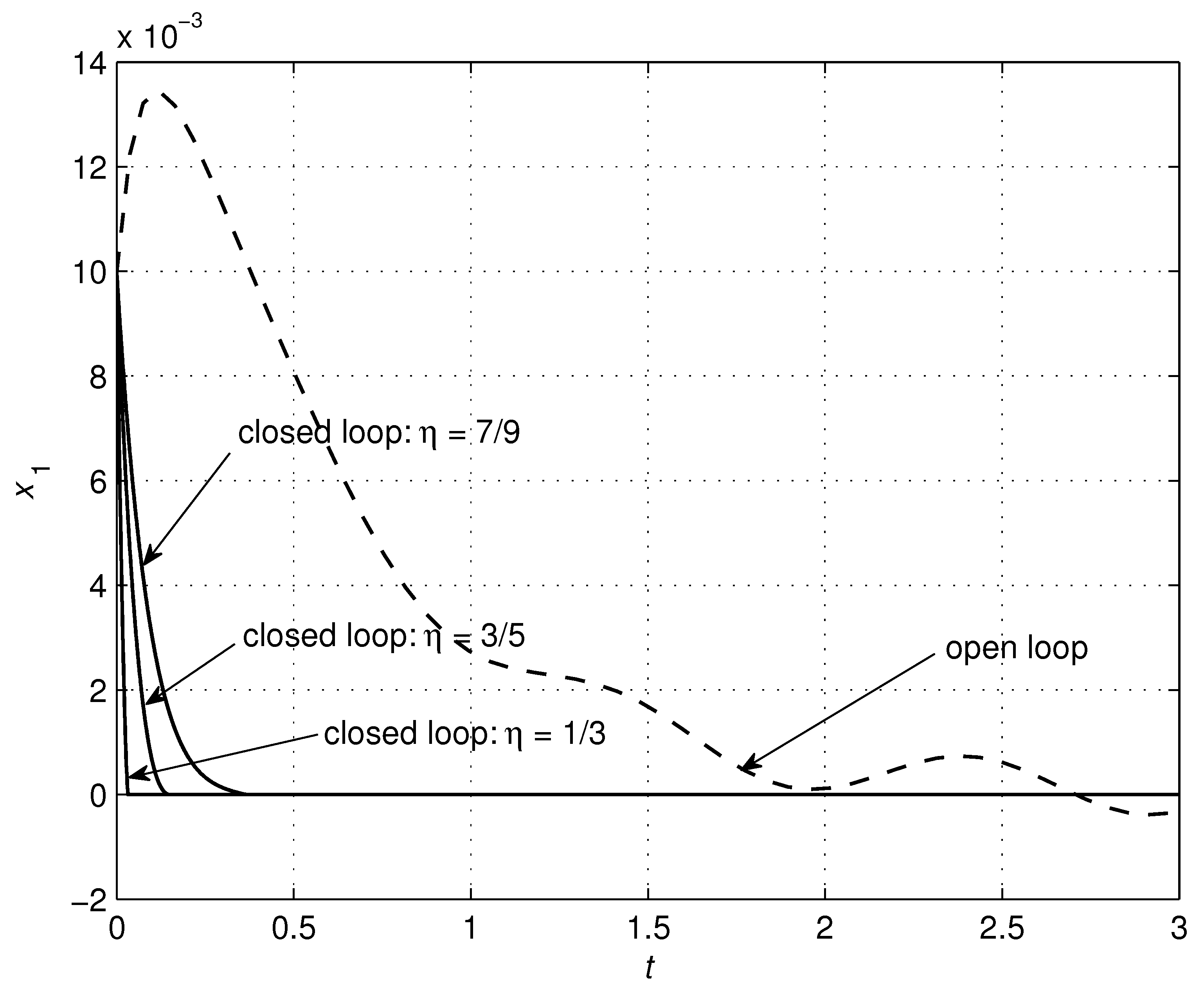
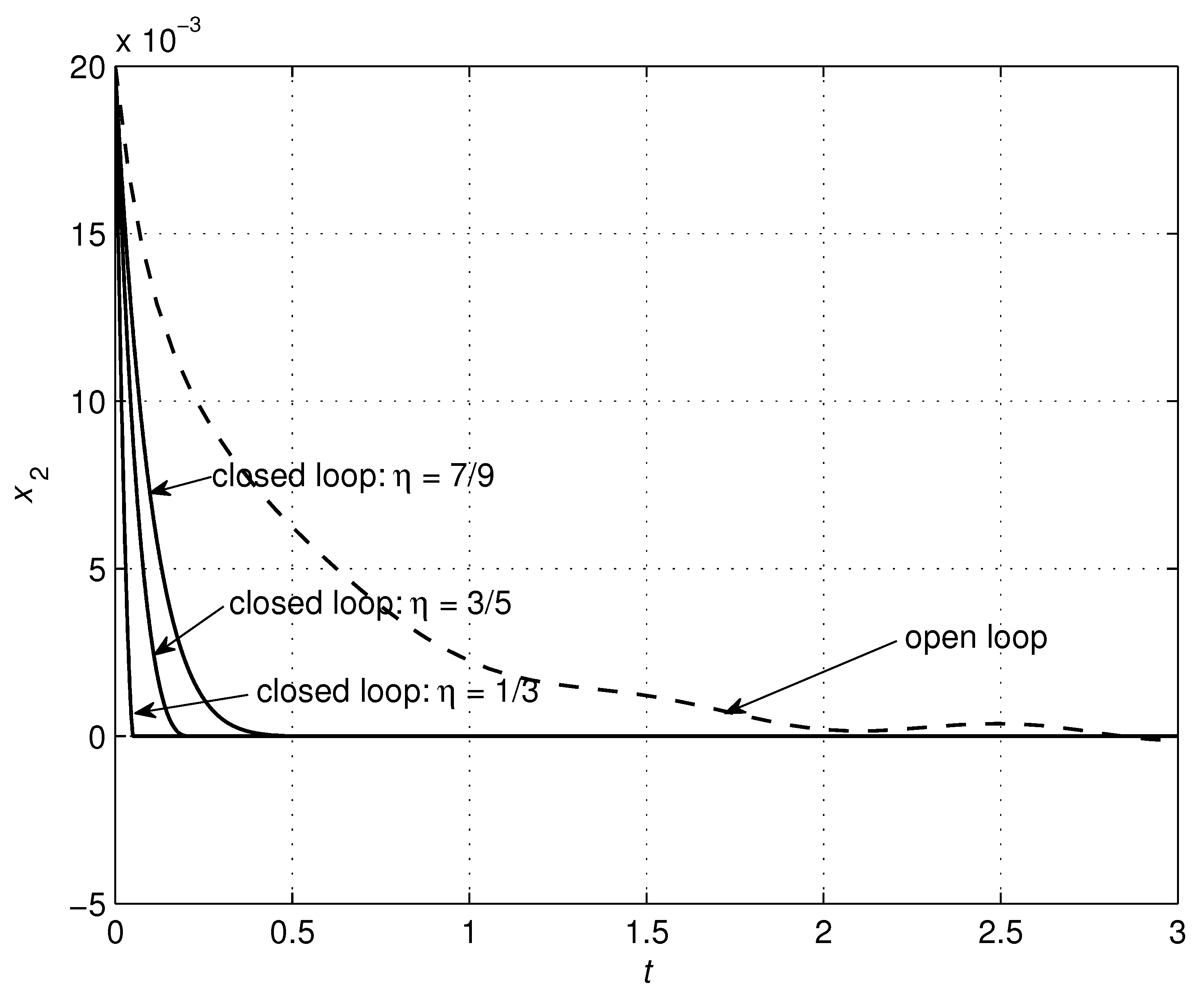
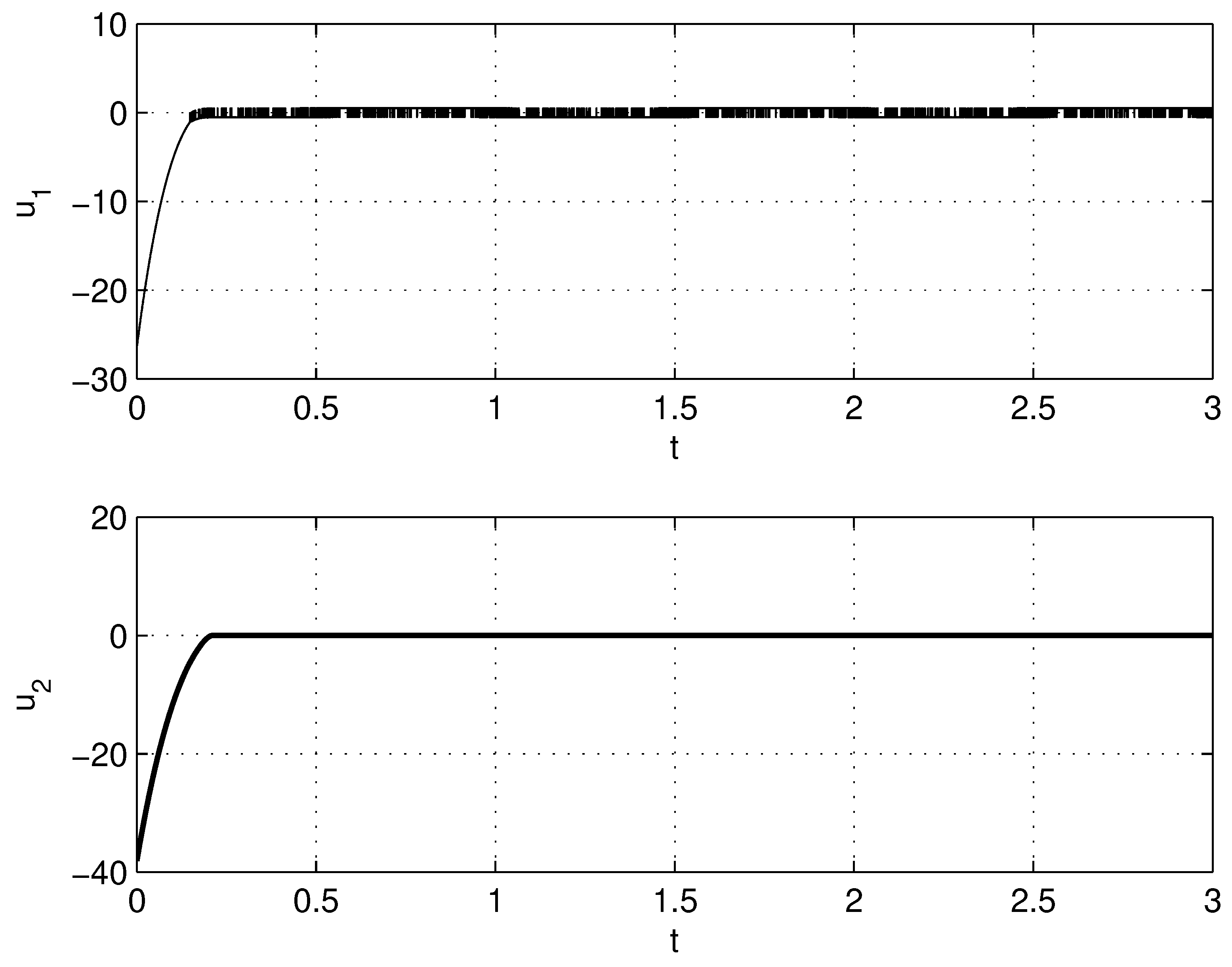
| RLC Circuit | Controller | ||||
|---|---|---|---|---|---|
| Parameter | Value | Unit | Parameter | Value | Unit |
| 0 | |||||
| P | 2 | ||||
| L | 5 | Q | |||
| 10 | |||||
| − | |||||
| 3 | |||||
| Parameter | Value | Unit |
|---|---|---|
| 100 | ||
| 200 | ||
| Parameter | Value | Unit |
|---|---|---|
| 5 | ||
| − | ||
| 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skruch, P.; Długosz, M. Design of Terminal Sliding Mode Controllers for Disturbed Non-Linear Systems Described by Matrix Differential Equations of the Second and First Orders. Appl. Sci. 2019, 9, 2325. https://doi.org/10.3390/app9112325
Skruch P, Długosz M. Design of Terminal Sliding Mode Controllers for Disturbed Non-Linear Systems Described by Matrix Differential Equations of the Second and First Orders. Applied Sciences. 2019; 9(11):2325. https://doi.org/10.3390/app9112325
Chicago/Turabian StyleSkruch, Paweł, and Marek Długosz. 2019. "Design of Terminal Sliding Mode Controllers for Disturbed Non-Linear Systems Described by Matrix Differential Equations of the Second and First Orders" Applied Sciences 9, no. 11: 2325. https://doi.org/10.3390/app9112325





