Novel Design and Lateral Stability Tracking Control of a Four-Wheeled Rollator

Featured Application

A rollator is an integrated functional application used clinically to empower and assist natural human mobility for the elderly or disabled users. In this paper, an integrated system of four-wheeled rollator is designed by introducing a novel mechanical design theory and a lateral stability tracking control is performed to validate the control feasibility of the four-wheeled rollator, providing an optimized procedure for further development of rollators.

Abstract

Design and control of smart rollators have attracted increasing research interests in the past decades. To meet the requirements of the elderly or disabled users, this paper proposes a novel design and tracking control scheme for empowering and assisting natural human mobility with a four-wheeled rollator. Firstly, by integrating the advantages of Kano Model Analysis and the Theory of Inventive Problem Solving (TRIZ), we introduce a novel Kano-TRIZ industrial design method to design and optimize its mechanical structure. The demand and quality characteristics of the clinical rollator are analyzed according to the Kano model. The Quality Function Deployment (QFD) and TRIZ are adopted to integrate industrial product innovations and optimize the function configuration. Furthermore, a lateral stability controller based on Model Predictive Control (MPC) scheme is introduced to achieve good tracking control performance with the lateral deviation and the heading angle deviation. Finally, the feasibility of the design and control method is verified with a simulation study. The simulation results indicate that the proposed algorithm keeps the lateral position error in a reasonable range. In the co-simulation of ADAMS-MATLAB, the trajectory of the rollator is smooth with constrained position error within 0.1 m, the turning angle and speed can achieve stable tracking control within 5 s and the heading angle is accurate and the speed is stable. A compared experiment with MPC and SMC show that MPC controller has faster response, higher tracking accuracy and smoother trajectory on the novel designed rollator. With the increasing demand for rollators in the global market, the methodology proposed in this paper will attract more research and industry interests.

1. Introduction

With the aging population, the physiological changes of organs and its consequent loss of function lead to the increased physical disability, which limits human mobility of the elderly. This has been one of the main reasons for the loneliness, and it affects the mental health of the elderly [1,2,3]. A four-wheeled rollator is a tool that assists human with motor dysfunction to walk. As a life partner for the elderly, the four-wheeled rollator creates a relative old-age lifestyle by empowering and assisting natural human mobility [4] and improves the quality of life in later life, allowing older people with motion system limitation to go out with the assistance from the four-wheeled rollator, which is beneficial to the physical and mental health of users.

In recent years, the research in the design and control of smart rollators has attracted many interests [5,6,7,8]. However, most of the research in the literature adopt questionnaires, interviews, observations and other methods to obtain user needs [9], without analyzing the type and importance of the requirements. They directly designed the mechanical structure according to the original demand. Functions of the design and the requirement that needs to be solved are still not satisfied. The solving the problem invention theory (TRIZ) [10,11,12] has been successfully applied in several domains such as aeronautics, car industry, and electronics, etc. It is known as using the TRIZ problem model to describe the design problem and then using TRIZ tool to solve the described problem. TRIZ is capable of modeling and converting the simulation solution into the practical solution of the industry domain. Kano model is a non-linear relationship between customer satisfaction and product objective quality. By integrating the advantages of Kano Model Analysis and TRIZ, the Kano-TRIZ design theory [13,14] presents an effective methodology to study and to provide design principles of the four-wheeled rollator, which take account of the physical and mental characteristics of the elderly. Quality Function Deployment (QFD) is a user-driven quality function configuration method. However, in the research of rollator design [15,16,17,18,19], the popularity of TRIZ to solve the problems of four-wheeled rollator design is still relatively limited, basically in the germination stage.

Except for the mechanical design of the four-wheeled rollator, its mobility is also of vital of importance for its market feasibility. The lateral motion stability control of four-wheeled rollator is the main challenge in terms of safety, especially for the elderly lacking motion ability. Hence it is necessary to develop a stable controller to validate the feasibility of motion control of the rollator. Since the longitudinal movement of the four-wheeled rollator can be controlled by handbrake and human traction, this paper focuses on its lateral motion stability. The purpose of the lateral stability control of the four-wheel rollator is to design an advanced controller to achieve the smooth trajectory tracking control of the rollator. According to the literature, the lateral control approaches of the rollators mainly include proportional-integral-derivative (PID) control, fuzzy adaptive control, sliding mode variable structure control, neural network control, etc. Wu et al. [20] proposed a parameter self-tuning fuzzy PID control method to effectively reduce the yaw rate and slip rate. Based on the rollator model and steering system model, Han et al. [21] designed a neural network PID controller with good real-time and robustness. In order to overcome the problems of nonlinearity, parameter uncertainty, and time-varying external disturbance, ref. [22] proposed an adaptive fuzzy sliding mode control strategy to achieve adaptive control. The performance in terms of smooth is considered in [23], a fuzzy control algorithm based on iterative genetic algorithm is proposed. Ref. [24] proposed a trajectory optimization algorithm to formulate the lateral vehicle guidance task along a reference trajectory, which is with optimized efficiency. Ref. [25] proposed a two-layer model predictive control controller to optimize the required longitudinal force and yaw moment adjustments and to achieve the minimized error of the steady state tracking objective. A combined control algorithm was designed in [26] by taking the yaw rate and the centroid slip angle error as input variables and using the braking torque as the steering angle of the control objectives. In [27], a novel fusion feed-forward neural network controller for task decomposition was proposed to realize the lateral control of autonomous vehicles. In [28], a robust output feedback vehicle lateral motion control strategy considering network-induced delay and tire force saturation was proposed to overcome the uncertainty of tire turning stiffness and external disturbance.

In this paper, we introduce a QFD model and Kano-TRIZ industrial design method to design a novel four-wheeled rollator and adopt a model predictive control algorithm to achieve the lateral trajectory tracking control of the rollator. A simulation was conducted to validate its feasibility in terms of the trajectory tracking error of the proposed design and control methodology.

The remainder of this paper is structured as follows: Section 2 describes the novel rollator design with Kano-Triz theory; Section 3 discusses the kinematic and dynamic model of the designed rollator and introduces lateral stability tracking control for its controller development; simulation and validation is performed and the corresponding results and discussions are drawn in Section 4. The conclusion and future work are presented in Section 5.

2. Novel Rollator Mechanical Design with Kano-TRIZ

This chapter focuses on the development of a four-wheeled elderly rollator application based on the new Kano-TRIZ industrial design approach. The main idea is to analyze the characteristics of the target users and the problems of using rollators for elderly people in daily life. The Kano model is applied to construct the demand function. Further, the QFD method is used to optimize the technical features, and the TRIZ industrial design method is utilized to design the function of a rollator to meet the characteristics of the elderly user. By taking account of the motion system, material weight, human weight and ground counterforce, the optimized functional diagram design of the four-wheeled rollator is shown in Figure 1.

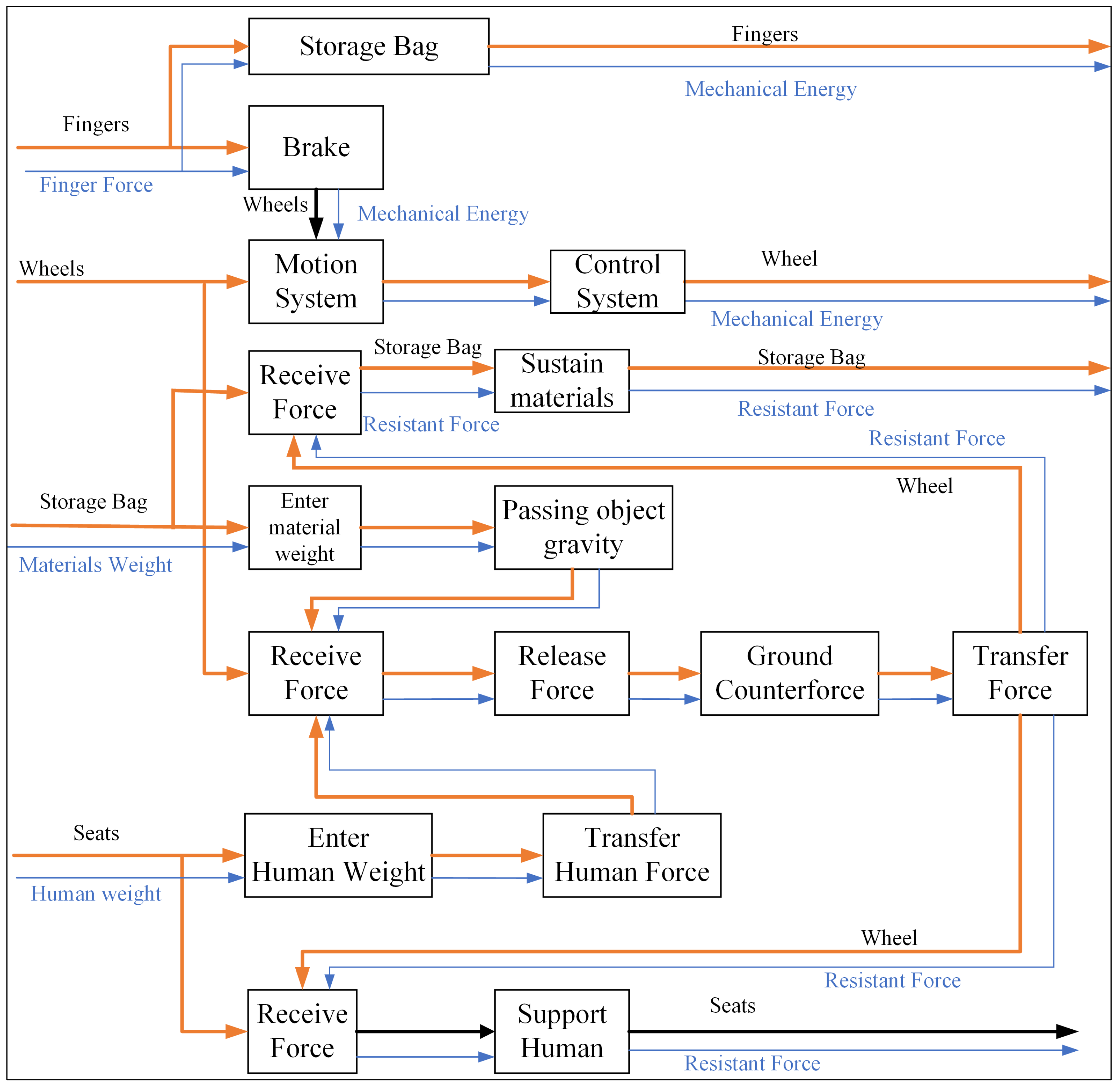
2.1. Functional Mechanical Design

The main functions of the four-wheeled elderly rollator are assisted walking, rest, storage and safety control. Similar to the functions of bicycle operation, this rollator is divided into three sub-functions: adjusting the height, moving forward and stopping the movement. The function diagram for the rollator mechanical design shown in Figure 1.

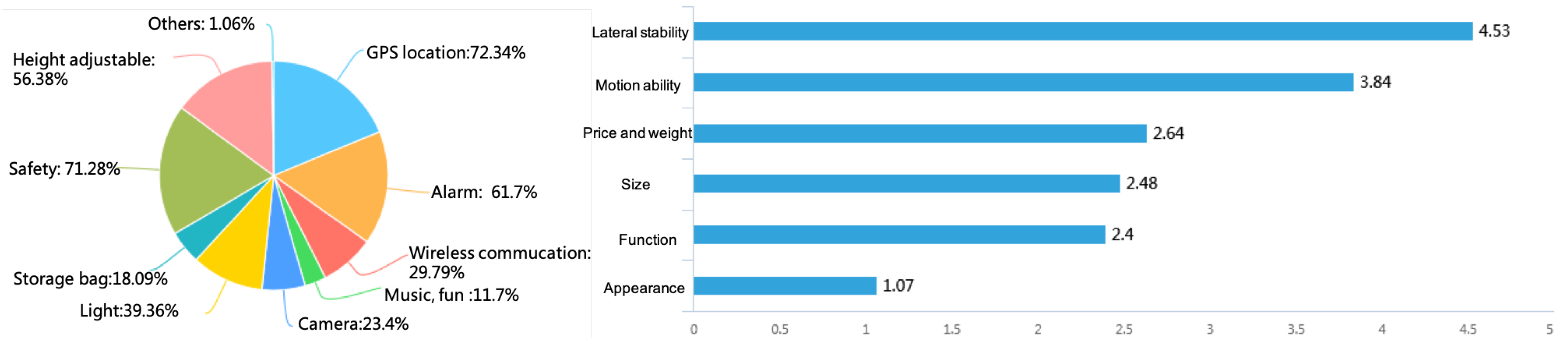
2.2. Kano Model Analysis

Firstly, the questionnaires of the demand for the products to analyze the needs of the target users is conducted after product analysis. A sorting rule of the questionnaires is chosen as:

The average composite score of the sorting questions is automatically calculated according to the ranking of all the candidates’ options. It reflects the comprehensive ranking of the options. The higher the score is, the higher the overall ranking will be. The calculation method is to calculate the option average comprehensive score and its weight is determined by where the options are arranged. For example, if there are 3 candidates to participate in sorting, the rank has a weight of 3 in the first position, the second position has a weight of 2, and the third position has a weight of 1. If a topic is filled in 12 times, option A is selected and ranked in the first position 2 times, while the second position is 4 times and the third position is 6 times. The average comprehensive score of option $A=(2\times 3+4\times 2+6\times 1)/12=1.67$ points.

It is should be noticed that the score here is related to the number of options. For example, there are 3 options for sorting and the first score is 3 points. If there are 30 options, the first score is 30 points, and this score won’t be affected. If the sorting option is a multiple-choice question that refers to the previous question, the first score in that row is the number of options for the multiple-choice question.

The survey method is adopted and a conclusion of the questionnaires is made and shown in Figure 2. Then we compared all the collected Kano attribute questionnaires with the Kano model analysis table, and obtain the Kano category membership of demand indicators in questionnaires filled out by each user. The corresponding analysis principle diagram of TRIZ solving problem is shown in Figure 3. TRIZ tools for electronic data processing allow building a specific idea and database. A criterion proposed in the literature is adapted to allow automatic update of the Knowledge Base [29,30].

TRIZ theory is a creative method to solve the inherent contradictions of products, which can produce breakthrough innovations and fundamentally eliminate the problems of navigation design for elderly rollators. The designer ignores the type and importance of the demand and directly designs the product according to the original requirements, which leads to some of the functions are not what the user is currently demanding. The Kano model can be used to classify users’ needs and determine the relative importance. The QFD evaluation is used to convert customer requirements into effective product demand after the Kano analysis. Therefore, the process of using TRIZ-KANO-DQF industrial design new method is shown in Figure 3:

• TRIZ translates specific product technical features into technical features that engineering designers can understand;
• The Kano model is used to analyze the function demand after the survey of user requirements;
• The QFD evaluation method with the design of the quality house (HOQ) is carried out to transform the user’s requirements to product demand.

Figure 4 exhibits the specific process of the four-wheeled rollator. In the original manuscript, the roundness combined with the block shape makes the user feel more energetic, but it lacks diplomatic feeling. Then an improved manuscript that combining the lines and block shape is designed. This manuscript gives a steady feeling but it makes the user feel heavy with fatigue. We finally decided to combine the line style, and strengthen the structural performance of the bottom, making users feel that the product is stable and reliable.

2.3. Structural Details of Modeling, Structure and Materials

With the increase of age, the physical function of the elderly continues to deteriorate, resulting in a weakened memory and cognitive disability. From the Kano questionnaires, the product with simple and intuitive feelings is more suitable for elderly users. Therefore, the simple geometric shape is used as the modeling foundation, and the common object design form in daily life is applied, which can meet the needs of safety and reliability. The seat adjuster is designed to meet the needs of different users while planning a simple replacement structure for the tire. The frame is mainly made of aluminum alloy. The handle is in direct contact with the user for a long time, which requires the soft material and air permeability, so we select the permeability rubber. The seat and storage bag materials are made of nylon fabric, for weight, durable and easy to install.

3. Lateral Stability Tracking Control of Designed Rollator

Because of the high safety requirement of rollator for the elderly, it is necessary to design the lateral motion control of the auxiliary driving system [31]. In this chapter, a tracking controller of the four-wheel rollator is carried out by the model prediction algorithm in term of the trajectory error.

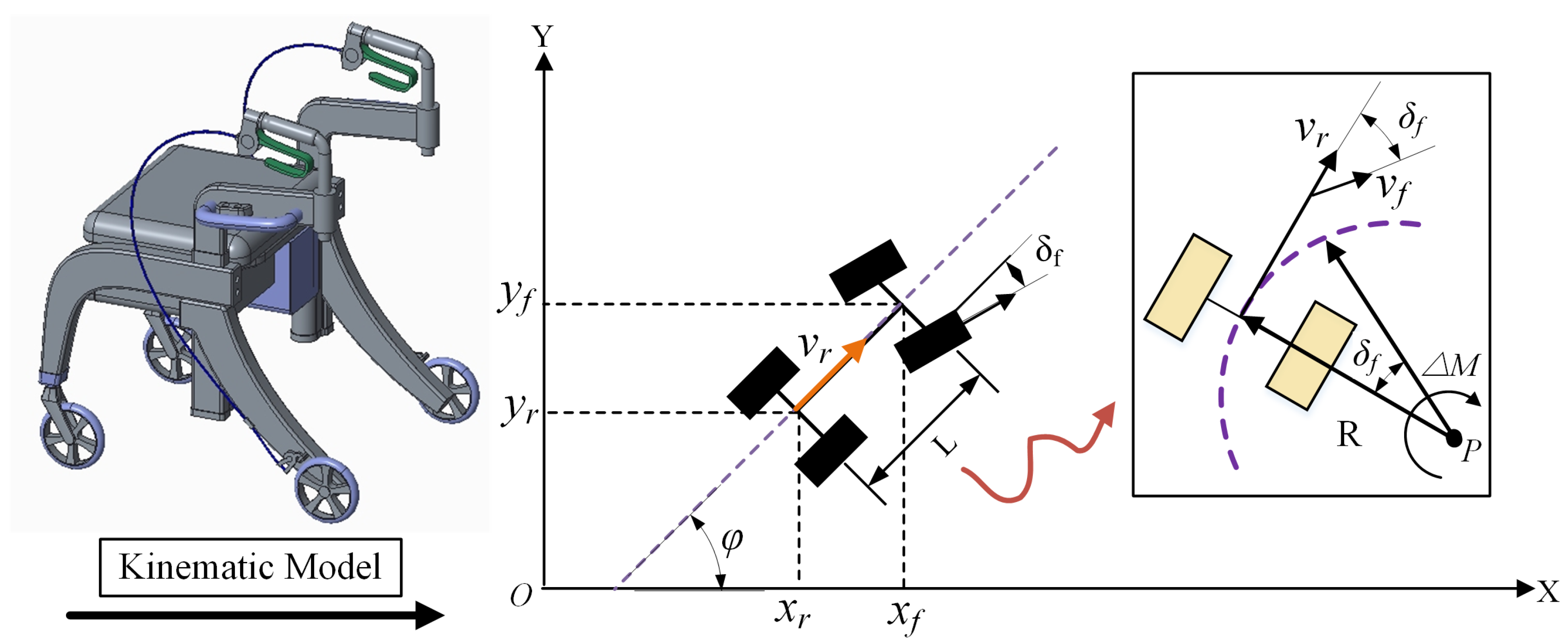
3.1. Rollator Kinematic Model

Figure 5 exhibits the kinematic model of the rollator. $\left(X_r,Y_r\right)$ and $\left(X_f,Y_f\right)$ are the center coordinates of the rear axis and the front axis, respectively. $\phi$ is the yaw angle, ${\delta }_f$ the steering angle of front wheels, $v_r$ the velocity of the rear axle center, $v_f$ the velocity of front axle center, L is the wheel track, R is the radius, P is the center of rotation, M is the center of the rear axis, and N is the center of the front axis.

Assuming that the steering radius and the radius of road curvature are the same in the steering process, the velocity of the rear axis $v_r$ can be described as:

$$v_r={\dot{X}}_{r}cos\phi +{\dot{Y}}_{r}sin\phi$$

(1)

The kinematic model of the rollator is presented as:

$$\begin{array}{c}{\dot{X}}_{f}sin\left(\phi +{\delta }_f\right)-{\dot{Y}}_{f}cos\left(\phi +{\delta }_f\right)=0\hfill \\ {\dot{X}}_{r}cos\phi -{\dot{Y}}_{r}sin\phi =0\hfill \end{array}$$

(2)

According to Equation (2), we can define:

$$\begin{array}{cc}\hfill {\dot{X}}_r& =v_{r}cos\phi \hfill \\ \hfill {\dot{Y}}_r& =v_{r}sin\phi \hfill \end{array}$$

(3)

where $v_r$ is the robot speed, $\left(X_r,Y_r\right)$ and $\left(X_r,Y_r\right)$ are the coordinate of rear-wheel and front-wheel, respectively, and $\phi$ and ${\delta }_f$ are the course angle and turning angle of front-wheel, respectively. From the mathematical relationship between the front and rear wheels, the following can be obtained as:

$$\begin{array}{cc}\hfill X_f& =X_r+Lcos\phi \hfill \\ \hfill Y_f& =Y_r+Lsin\phi \hfill \end{array}$$

(4)

Furthermore, the angle rate $\omega$ is obtained as:

$$\omega =\frac{v_{r}tan{\delta }_f}{L}$$

(5)

where L is the wheel base of front and rear wheels.

Therefore, the kinematic model of rollator could be written as:

$$\left[\begin{array}{c}{\dot{X}}_r\\ {\dot{Y}}_r\\ \dot{\phi }\end{array}\right]=\left[\begin{array}{c}cos\phi \\ sin\phi \\ 0\end{array}\right]v_r+\left[\begin{array}{c}0\hfill \\ 0\hfill \\ 1\hfill \end{array}\right]\omega$$

(6)

where ${\xi }_s={\left[X_r,Y_r,\phi \right]}^T$ is the system state and $u_S={\left[v_r,\omega \right]}^T$ is the control value.

3.2. Rollator Dynamic Model and Tire Model

Figure 6 demonstrates the dynamic model and tire model of the rollator.

In order to insure the high safety requirement of the elderly rollator, we design longitudinal motion, lateral motion and transverse motion, separately [32,33,34]. According to the Newton’s laws, the dynamic model can be described as:

$$\begin{array}{cc}\hfill m\ddot{x}& =m\dot{y}{\omega }_c+F_{a1}cos{\delta }_f+F_{a2}cos{\delta }_f+F_{a3}+F_{a4}\hfill \\ \hfill m\ddot{y}& =-m\dot{x}{\omega }_c+F_{b1}cos{\delta }_f+F_{b2}cos{\delta }_f+F_{b3}+F_{b4}\hfill \\ \hfill I_z\ddot{\phi }& =A\left(F_{b1}cos{\delta }_f+F_{b2}cos{\delta }_f\right)-B\left(F_{b3}+F_{b4}\right)+M\left(-F_{a1}cos{\delta }_f+F_{a2}cos{\delta }_f-F_{a3}+F_{a4}\right)\hfill \end{array}$$

(7)

where $F_{a1}$, $F_{a2}$, $F_{a3}$ and $F_{a4}$ are the wheel force of left front, right front, left rear and right front respectively in X-axis. $F_{b1}$, $F_{b2}$, $F_{b3}$ and $F_{b4}$ are the wheel force of left front, right front, left rear and right front respectively in Y-axis. $I_Z$ is the rotational inertia and ${\omega }_c$ the center yaw velocity.

Assuming that the lateral force of the tire during the regular tire movement is proportional, there are:

$$\begin{array}{c}{F}_{b1}={\psi }_{\delta F}{\mathsf{\Gamma }}_{\delta F}\hfill \\ F_{b2}={\psi }_{\delta R}{\mathsf{\Gamma }}_{\delta R}\hfill \\ {\psi }_{\delta F}=\beta +\frac{M{\omega }_r}{v_x}-{\delta }_f\hfill \\ {\psi }_{\delta R}=\beta +\frac{M{\omega }_r}{v_x}\hfill \end{array}$$

(8)

where ${\psi }_{\delta F}$ and ${\psi }_{\delta R}$ are tire cornering angle of front-wheel and rear-wheel, respectively. ${\mathsf{\Gamma }}_{\delta F}$ and ${\mathsf{\Gamma }}_{\delta B}$ of front-wheel and rear-wheel, respectively. $\beta$ is the slip angle.

Slip ratio is the key issue of the tire in maintaining stable motion. In Figure 6, the tire model can be presented as:

$$\begin{array}{c}J\dot{\omega }=R{F}_x-R{F}_{\omega }-T_b\hfill \\ M\dot{v}=-F_x-\mu F_v\hfill \end{array}$$

(9)

where R is the rolling radius, v is rollator speed, $T_b$ is the braking torque, $F_x$ is the friction, $F_v$ is the air resistance, $F_{\omega }$ is the rolling resistance, $F_z$ is the ground reaction force, M is the rollator quality and J is the rotational inertia At the same time, the slip rate S and the friction $F_x$ can be defined as:

$$\begin{array}{c}S=\frac{v-\omega R}{v}\hfill \\ F_x=\mu F_z\hfill \end{array}$$

(10)

where $\mu$ is the adhesion coefficient.

We assume that the system state is $x_1=\frac{v}{R},x_2=\omega$ and $x_3=S$, then the tire function can be transformed as:

$$\begin{array}{cc}\hfill {\dot{x}}_1& =-\frac{F_v+F_Z\mu }{MR}\hfill \\ \hfill {\dot{x}}_2& =\frac{F_{z}R\mu -F_{w}R-T_b}{J}\hfill \\ \hfill {\dot{x}}_3& =\frac{1}{v}\left[\frac{(S-1)\left(F_v+F_z+\mu F_z\right)}{M}+\frac{F_z{R}^2\left(T_b-\mu \right)}{J}\right]\hfill \end{array}$$

(11)

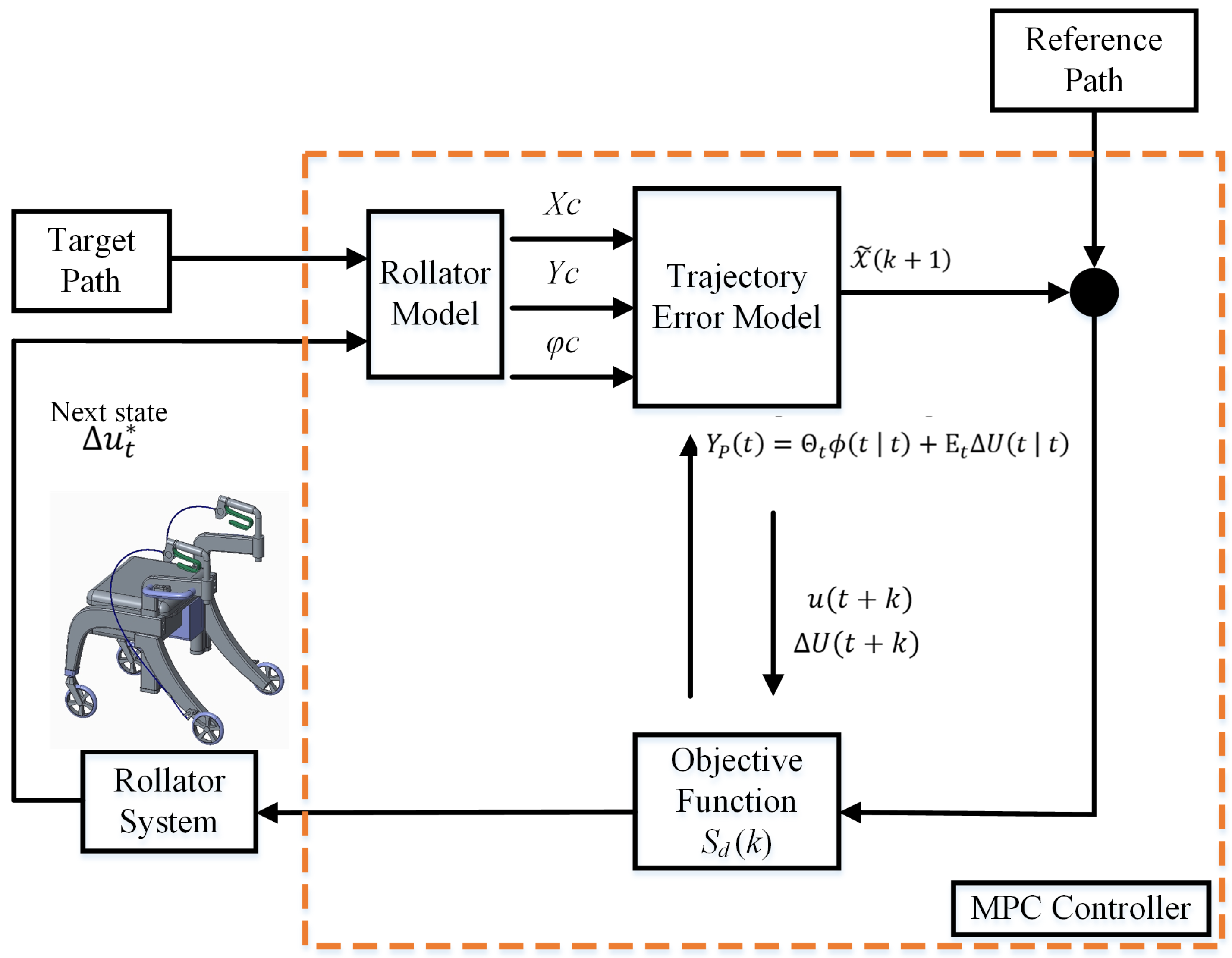
3.3. Lateral Controller Development

Figure 7 exhibits the MPC controller structure for lateral trajectory tracking. MPC scheme is mainly composed of a trajectory error function, system constraint and optimization objective function [35]. The error equation is the mathematical description of the tracking control system and the basis of the control algorithm. System constraints include rollator actuator constraints, control smooth constraints and stability constraints. The design of the objective function is based on the stability and rapidity of trajectory tracking.

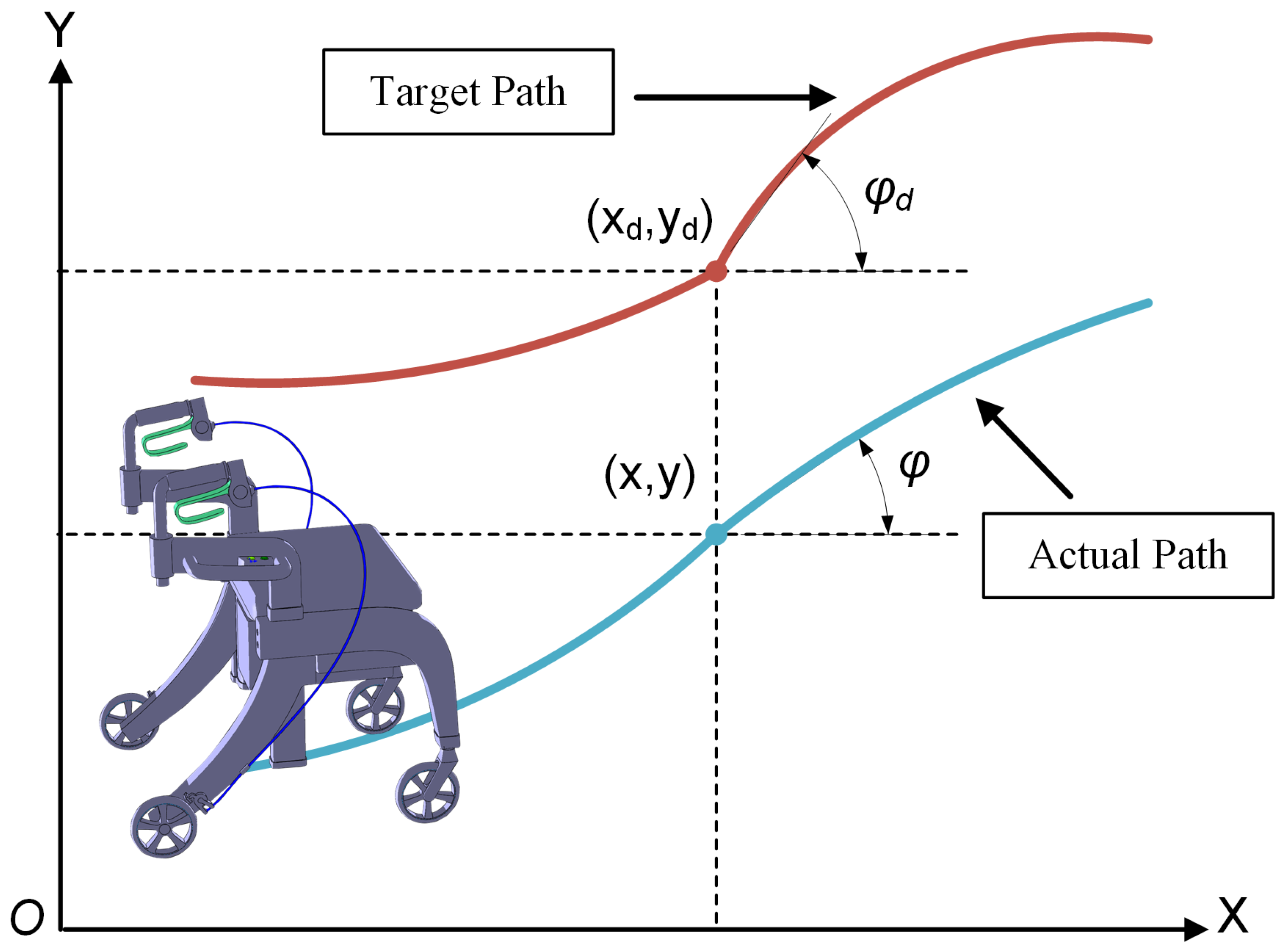
3.3.1. Trajectory Error Function

According to the kinematic model in Equation (6) and tracking error model in Figure 8, we can obtain the relationship as:

$$\left[\begin{array}{c}{\dot{X}}_r\\ {\dot{Y}}_r\\ \dot{\phi }\end{array}\right]=\left[\begin{array}{c}cos\phi \\ sin\phi \\ tan\delta /L\end{array}\right]v_r$$

(12)

where $(x,y)$ is the center coordinate, $\phi$ is yaw angle, and v is the velocity. Then the rollator control system can be seen as input variable $u(v,\delta )$ and state variable $\chi (x,y,\phi )$:

$$\dot{\mathcal{X}}=\mathcal{W}(\mathcal{X},u)$$

(13)

To facilitate the MPC controller [36], we define the expected equation of motion trajectory as:

$${\dot{\chi }}_d=\mathcal{W}\left({\mathcal{X}}_d,u_d\right)$$

(14)

where expected state variable is ${\chi }_d={\left[x_d,y_d,{\phi }_d\right]}^T$ and the expected input variable is $u_d=\left[v_d,{\delta }_d\right]$. We transform the Equation (13) according to the Taylor formulation and ignore the high-order term, then:

$$\dot{x}=w\left(x_d,u_d\right)+{\left.\frac{\partial \mathcal{W}(x,u)}{\partial x}\right|}_{\genfrac{}{}{0pt}{}{x=x_d}{u=u_d}}\left(x-x_d\right)+{\left.\frac{\partial w(x,u)}{\partial u}\right|}_{\genfrac{}{}{0pt}{}{x=x_d}{u=u_d}}\left(u-u_d\right)$$

(15)

Therefore, we can get the lateral error function according to Equations (14) and (15).

$$\begin{array}{cc}\hfill {\dot{x}}_e& =\left(\dot{x}-{\dot{x}}_d\right)=-v_{d}sin{\phi }_d\left(x-x_d\right)+cos{\phi }_d\left(v-v_d\right)\hfill \\ \hfill {\dot{y}}_e& =\left(\dot{y}-{\dot{y}}_d\right)=v_{d}cos{\phi }_d\left(y-y_d\right)+sin{\phi }_d\left(v-v_d\right)\hfill \\ \hfill {\dot{\phi }}_e& =\left(\dot{\phi }-{\dot{\phi }}_d\right)=\frac{tan{\delta }_d}{L}\left(v-v_d\right)+\frac{v_d}{L{cos}^2{\delta }_d}\left(\delta -{\delta }_d\right)\hfill \end{array}$$

(16)

Furthermore, to discretize the error function, we can obtain the model as follow

$$\tilde{\mathcal{X}}(k+1)={\mathcal{H}}_{k,t}\tilde{\mathcal{X}}\left(k\right)+{\mathcal{K}}_{k,t}\tilde{u}\left(k\right)$$

(17)

Among them, ${\mathcal{H}}_{k,t}=\left[\begin{array}{ccc}1& 0& -v_{d}Tsin{\phi }_d\\ 0& 1& v_{d}Tcos{\phi }_d\\ 0& 0& 1\end{array}\right],{\mathcal{K}}_{k,t}=\left[\begin{array}{cc}Tcos{\phi }_d& 0\\ Tsin{\phi }_d& 0\\ \frac{tan{\delta }_d}{L}T& \frac{v_d}{L{cos}^2{\delta }_d}T\end{array}\right]$ and T is the sampling time.

3.3.2. Objective Function Design

The objective function requires that elderly rollator can track the desired trajectory safely and quickly, so it is necessary to optimize the state error and control variable. We set the objective function as follows:

$$\mathcal{S}\left(k\right)=\sum _{j=1}^N{\tilde{X}}^T(k+j|k)\mathcal{L}(k+j)+{\tilde{u}}^T(k+j-1)\mathcal{M}\tilde{u}(k+j-1)$$

(18)

where $\mathcal{L}$ and $\mathcal{M}$ are weighting factors.

As can be seen form the objective function, ${\sum }_{j=1}^N{\tilde{\mathcal{X}}}^T(k+j|k)\mathcal{L}\tilde{\mathcal{X}}(k+j)$ reflects the ability of the control system to follow the desired trajectory, and ${\tilde{u}}^T(k+j-1)\mathcal{M}\tilde{u}(k+j-1)$ represents the constraints of control variables. The objective function can be transformed into the standard quadratic form, but the control increment cannot be controlled. Therefore, we design an improved objective function using relaxation factors as follows:

$${\mathcal{S}}_d\left(k\right)=\sum _{i=1}^{N_P}{∥Y(k+i|t)-Y_{\mathrm{ref}}(k+i|t)∥}_{\mathcal{L}}^2+\sum _{i=1}^{N_e-1}{\parallel \Delta U(k+i|t)\parallel }_{\mathcal{L}}^2+\sigma {\psi }^2$$

(19)

Among them, $N_P$ is the prediction horizon, $N_e$ is the control horizon, $\sigma$ is the weight coefficient, and $\psi$ is the weighting factor. Then, we can transform the trajectory error model as:

$$\varphi \left(k\right|t)={[\tilde{X}\left(k\right|t),\tilde{u}(k-1|t)]}^T$$

(20)

The state function can be described as:

$$\begin{array}{c}\varphi (k+1|t)={\tilde{\mathcal{H}}}_{k,t}\left(k\right|t)+{\tilde{\mathcal{F}}}_{k,t}\Delta U\left(k\right|t)\hfill \\ Y\left(k\right|t)={\tilde{z}}_{k,t}\varphi \left(k\right|t)\hfill \end{array}$$

(21)

where ${\tilde{\mathcal{H}}}_{k,t}=\left[\begin{array}{cc}{\mathcal{H}}_{k,t}& {\mathcal{K}}_{k,t}\\ 0_{m\times n}& I_m\end{array}\right]$, ${\tilde{\mathcal{K}}}_{k,t}={\left[{\mathcal{X}}_{k,t},I_m\right]}^T$, n is the state degree and m is the control variable degree. To simplify the calculation, we assume

$$\begin{array}{c}{\mathcal{H}}_{k,t}={\mathcal{H}}_{t,t}\hfill \\ {\mathcal{X}}_{k,t}={\mathcal{X}}_{t,t}\hfill \end{array}$$

(22)

where $k=1,2,\cdots ,t+N-1$. Based on the above analysis, the model prediction output can be obtained as follows:

$$Y_P\left(t\right)={\mathsf{\Theta }}_t\varphi \left(t\right|t)+{\mathrm{E}}_t\Delta U\left(t\right|t)$$

(23)

which subjects to $Y_P\left(t\right)=\left[\begin{array}{c}Y(t+1|t)\\ Y(t+2|t)\\ \cdots \\ \gamma \left(t+N_c|t\right)\\ \cdots \\ \gamma \left(t+N_P|t\right)\end{array}\right]$, ${\mathsf{\Theta }}_t=\left[\begin{array}{c}{\tilde{\mathcal{Z}}}_{t,t}{\tilde{\mathcal{H}}}_{t,t}\\ {\tilde{Z}}_{t,t}{\tilde{\mathcal{F}}}_{t,t}^2\\ \cdots \\ {\tilde{\mathcal{Z}}}_{t,t}{\tilde{\mathcal{F}}}_{t,t}^{N_c}\\ \cdots \\ {\tilde{Z}}_{t,t}{\tilde{\mathcal{F}}}_{t,t}^{N_P}\end{array}\right]$, $\Delta U=\left[\begin{array}{c}\Delta u\left(t\right|t)\\ \Delta u(t+1|t)\\ \cdots \\ \Delta u\left(t+N_c|t\right)\end{array}\right]$, and ${\mathrm{E}}_t=\left[\begin{array}{cccc}{\tilde{\mathcal{Z}}}_{t,t}{\tilde{\mathcal{H}}}_{t,t}& 0& 0& 0\\ {\tilde{Z}}_{t,t}{\tilde{\mathcal{F}}}_{t,t}{\tilde{\mathcal{K}}}_{t,t}& {\tilde{\mathcal{Z}}}_{t,t}{\tilde{\mathcal{K}}}_{t,t}& 0& 0\\ \cdots & \cdots & \ddots & \cdots \\ {\tilde{Z}}_{t,t}{\tilde{\mathcal{H}}}_{t,t}^{N_c-1}{\tilde{\mathcal{K}}}_{t,t}& {\tilde{Z}}_{t,t}{\tilde{\mathcal{H}}}_{t,t}^{N_c-2}{\tilde{\mathcal{K}}}_{t,t}& \cdots & {\tilde{\mathcal{Z}}}_{t,t}{\tilde{\mathcal{K}}}_{t,t}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{\mathcal{Z}}}_{t,t}{\tilde{\mathcal{H}}}_{t,t}^{N_P-1}{\tilde{\mathcal{K}}}_{t,t}& {\tilde{\mathcal{Z}}}_{t,t}{\tilde{\mathcal{H}}}_{t,t}^{N_P-2}{\tilde{\mathcal{K}}}_{t,t}& \cdots & {\tilde{Z}}_{t,t}{\tilde{\mathcal{H}}}_{t,t}^{N_P-N_c-1}{\tilde{\mathcal{K}}}_{t,t}\end{array}\right]$.

3.3.3. Control Constraint Design

In the previous section, an improved optimization function is designed for the trajectory tracking error model. Considering the safety and stability of the rollator, it is necessary to restrict the control limit and control increment, as following:

$$\begin{array}{c}{u}_{min}(t+k)\le u(t+k)\le u_{max}(t+k)\hfill \\ \Delta U_{min}(t+k)\le \Delta U(t+k)\le \Delta U_{max}(t+k)\hfill \end{array}$$

(24)

where $k=1,2,\cdots ,t+N_c-1$. To transform the Equation (24), we can get

$$u(t+k)=u(t+k-1)+\Delta U(t+k)$$

(25)

Define the following vectors: $U_{\lambda }=1_{N_c}\otimes u(k-1)$ and $H=I_m\otimes \left[\begin{array}{ccccc}1& 0& \cdots & \cdots & 0\\ 1& 1& 0& \cdots & 0\\ 1& 1& 1& \ddots & 0\\ ⋮& ⋮& \ddots & \ddots & 0\\ 1& 1& \cdots & 1& 1\end{array}\right]$.

The optimization objective function can be represented as

$$\delta [\varphi \left(t\right),u\left(t\right),\Delta U\left(t\right)]={\mathcal{F}}_t{\left[\Delta U{\left(t\right)}^T,\psi \right]}^T+{\left[\Delta U{\left(t\right)}^T,\psi \right]}^T{\mathcal{D}}_t{\left[\Delta U{\left(t\right)}^T,\psi \right]}^T$$

(26)

$\mathrm{where}|{\mathcal{F}}_t=\left[2e_t^T\mathcal{L}{\mathrm{E}}_t,0\right]\mathrm{and}{\mathcal{D}}_t=\left[\begin{array}{cc}{\mathrm{E}}_t^T\mathcal{L}{\mathrm{E}}_t+\mathcal{M}& 0\\ 0& \sigma \end{array}\right]$. Therefore, the prediction horizon error can be obtained:

$$\begin{array}{c}{e}_t={\mathsf{\Theta }}_t\varphi \left(t\right|t)-Y_{\mathrm{ref}}\left(t\right)\hfill \\ Y_{\mathrm{ref}}\left(t\right)={\left[Y_{\mathrm{ref}}(t+1|t),\cdots ,Y_{\mathrm{ref}}\left(t+N_P|t\right)\right]}^T\hfill \end{array}$$

(27)

When the model predictive control completes the optimization objective function each time, the control input increment of the system in the control horizon is:

$$\Delta U_t^{*}={\left[\Delta u_t^{*},\Delta u_{t+1}^{*},\cdots ,\Delta u_{t+N_c-1}^{*}\right]}^T$$

(28)

Finally, the first element of the control increment (Equation (28)) is applied to the control system as the actual control input increment

$$u\left(t\right)=u(t-1)+\Delta u_t^{*}$$

(29)

In order to achieve the ability of stability and smoothness for tracking performance, we define the constraint condition of control variable as

$$\begin{array}{c}\left[\begin{array}{c}-0.3\\ -25\end{array}\right]\le u\le \left[\begin{array}{c}0.3\\ 25\end{array}\right]\\ \left[\begin{array}{c}-0.02\\ -0.04\end{array}\right]\le \Delta U\le \left[\begin{array}{c}0.02\hfill \\ 0.04\hfill \end{array}\right]\end{array}$$

(30)

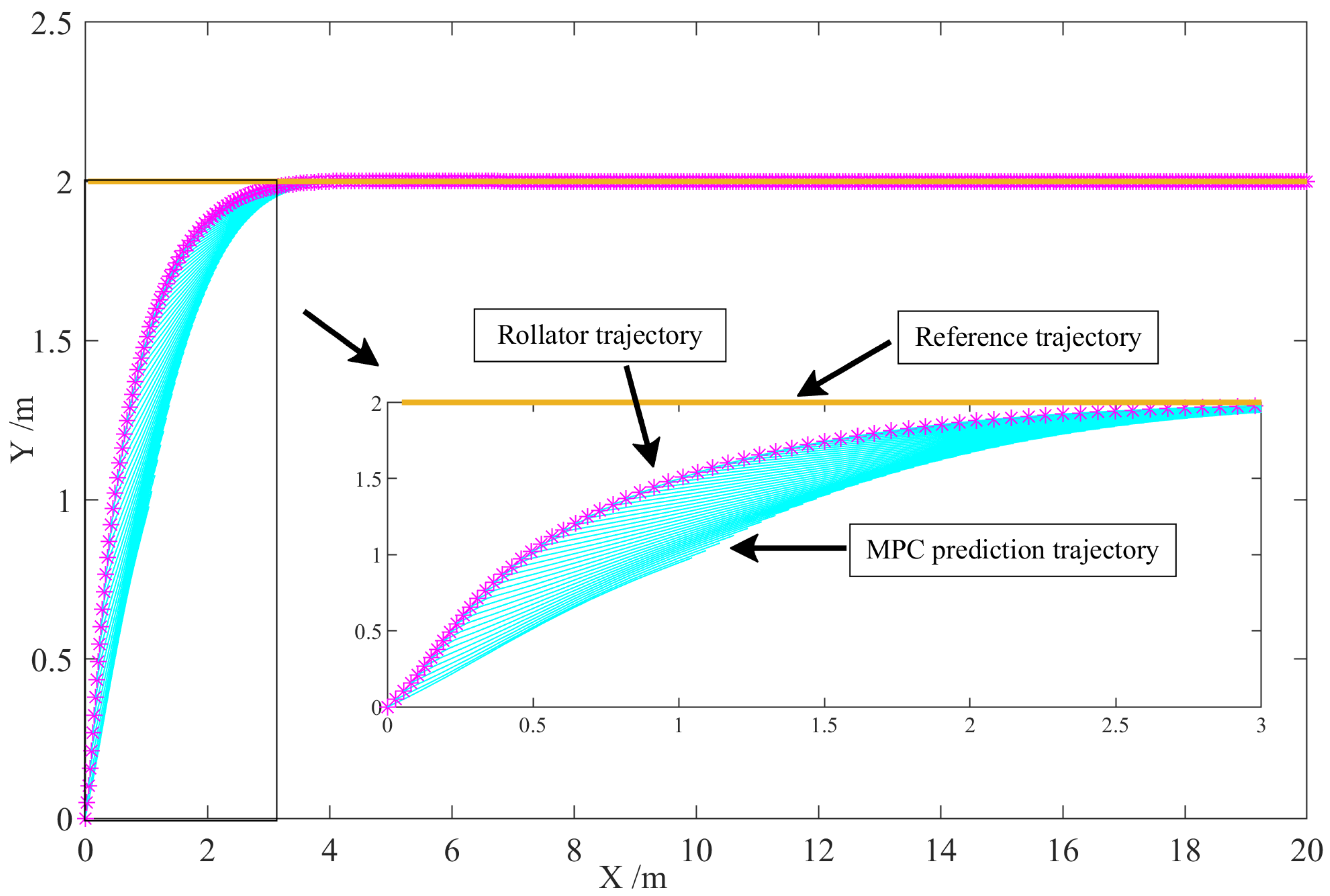
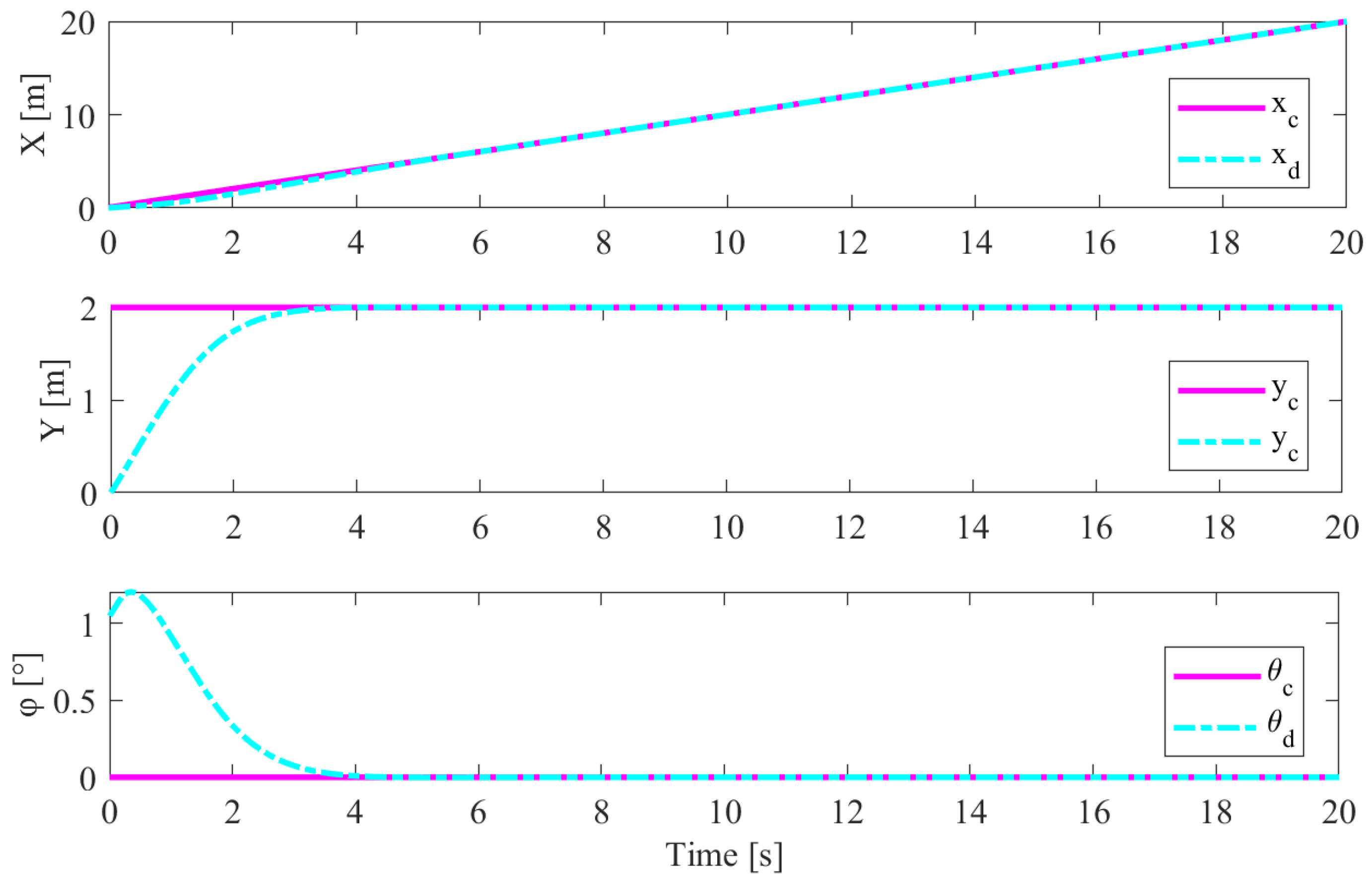
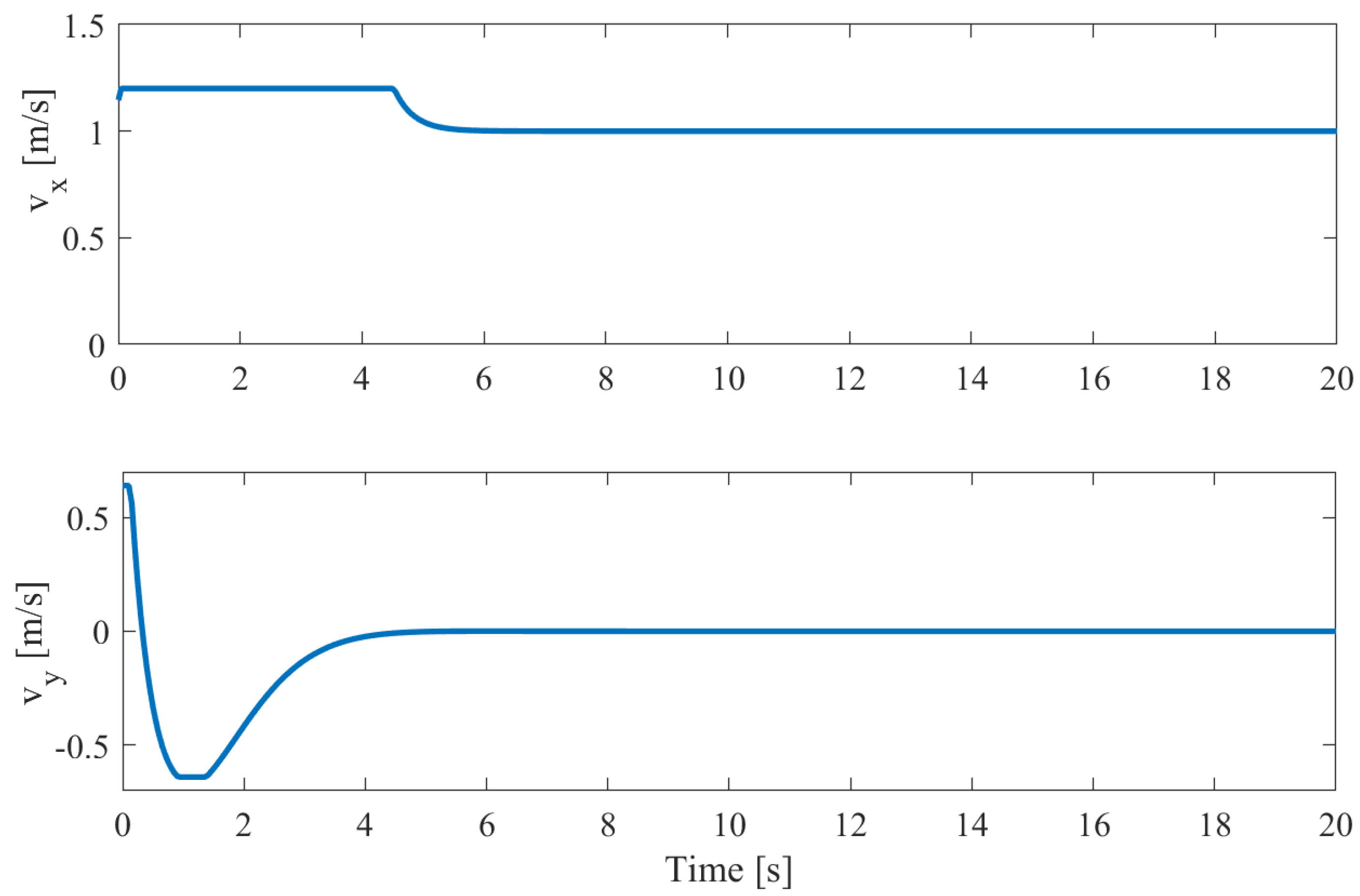
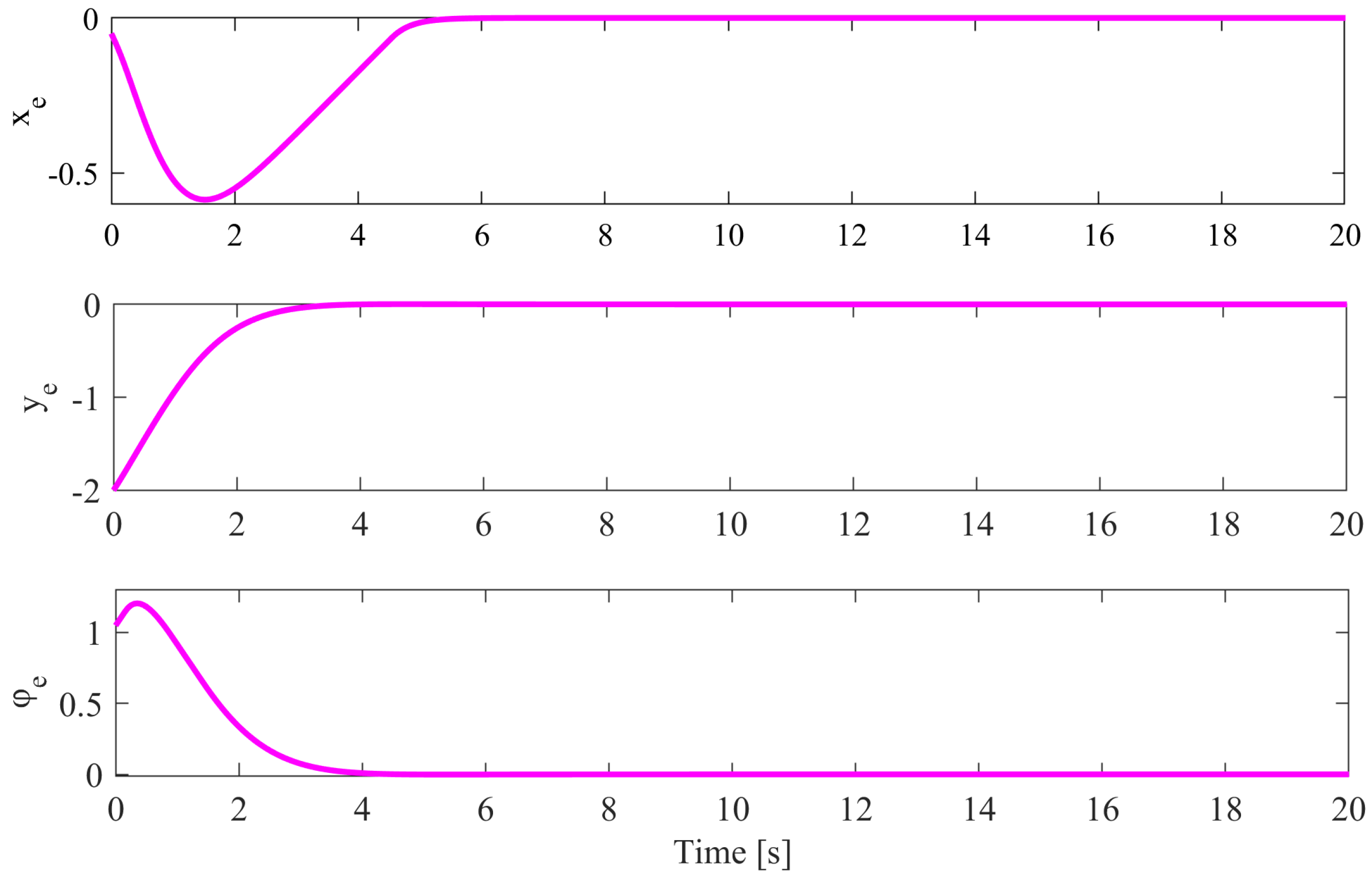
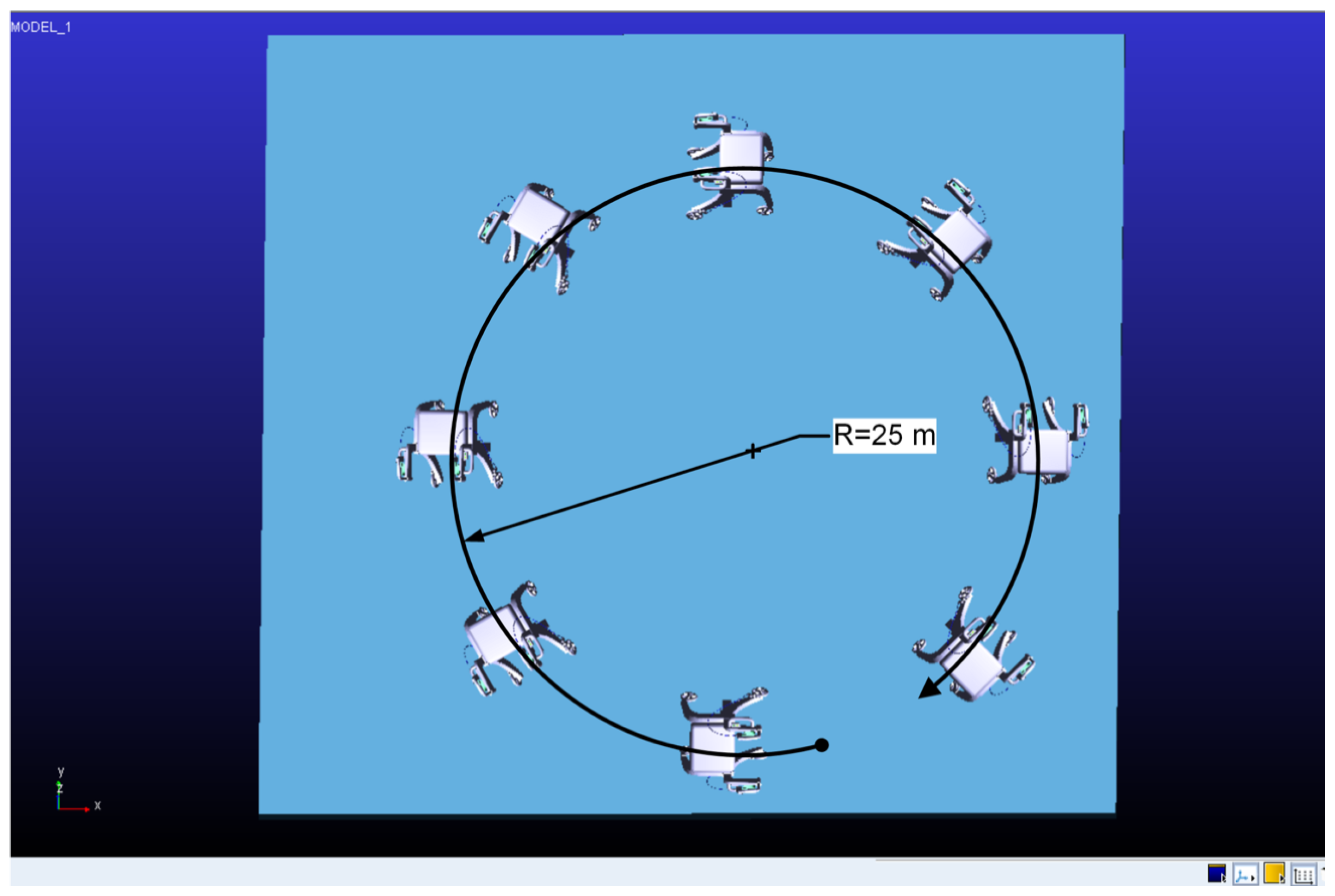
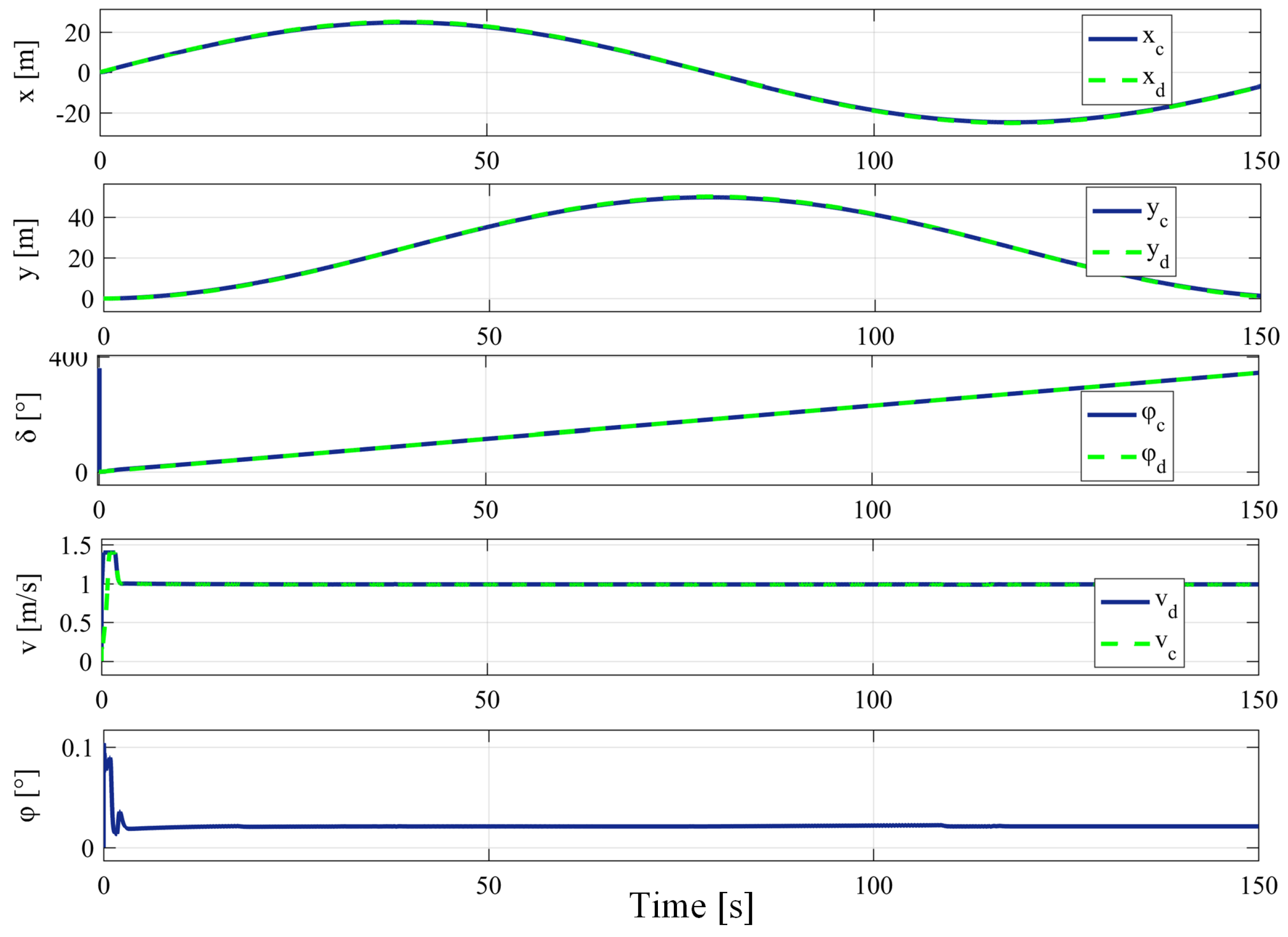
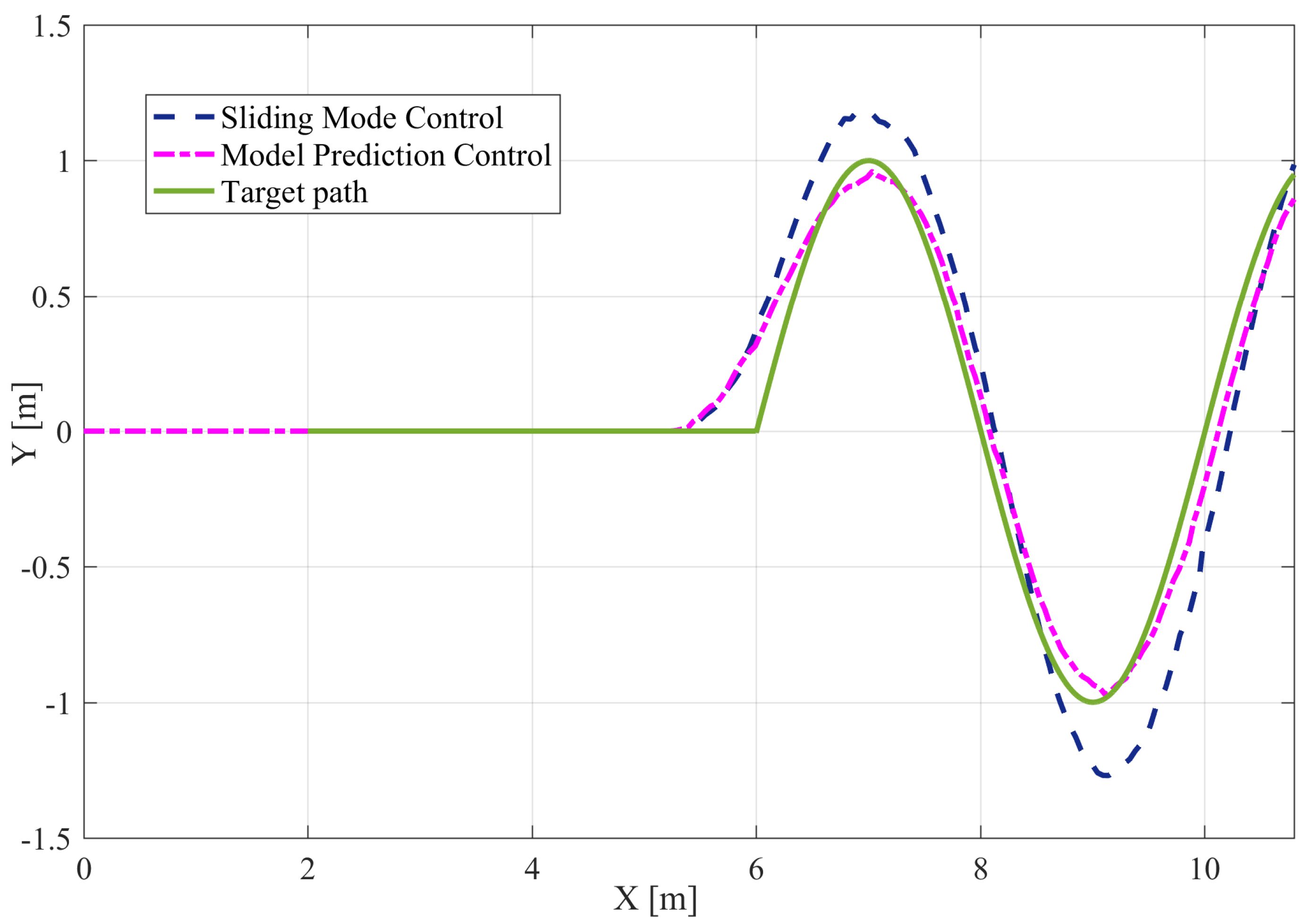
4. Results and Discussion

In order to verify the lateral stability control of the MPC algorithm proposed in the previous chapter, simulation experiments are performed using ADAMS-MATLAB.

We set up two different experiments, including tracking a desired line with MPC algorithm and following a sinusoid with MPC and SMC.

The initial condition of the simulation is set as follows: the rollator starts from the coordinate origin and tracks the expected curve $y=2$ with the desired longitudinal velocity $v=1$ m/s. The sampling time is 50 ms and the simulation time is 20 s. The simulation process includes areference trajectory generation, variable initialization, system matrix definition and controller design. The simulation results are shown in Figure 9, Figure 10, Figure 11 and Figure 12.

Figure 9, Figure 10, Figure 11 and Figure 12 present the trajectory control performance of the elderly rollator based on the model prediction controller. The reference trajectory is a straight line as shown in Figure 9. The four-wheeled rollator is moved at a uniform speed of 1 m/s. The tracking performance of longitudinal position, lateral position and yaw angle to follow the desired trajectories are shown in Figure 10 based on the MPC control method. Figure 11 shows the longitudinal speed and lateral speed. Figure 12 demonstrates the longitudinal error, lateral error and leading angle error. It can be seen from Figure 9, Figure 10, Figure 11 and Figure 12 that the rollator can quickly track the reference trajectory at 0–4 s as well as at 4–20 s. The curve is smooth and the fluctuation is small. The position control is within the constraint range, and the yaw angle is within the constraint range in particular. Therefore, the MPC algorithm proposed in this rollator system can be used to improve the stability of elderly rollator.

In order to demonstrate how the controller response and the accuracy of thealgorithm, the co-simulation of rollator for ADAMS-MATLAB are carried out. The reference path is a circle shape with a radius of 25 m, and Figure 13 and Figure 14 show the control effect of the rollator based on the MPC algorithm to track the circular trajectory. Figure 13 shows the tracking performance, and Figure 14 exhibits the longitudinal position, lateral position, angle relationship, speed change and heading angle of the rollator. It can be seen from the co-simulation results that the proposed MPC strategy can track the reference path well, and the rollator responds smoothly with position error within 0.1 m. The turning angle and speed can achieve stable tracking control within 5 s. There are no fluctuations in lateral position and longitudinal position. In addition, the heading angle is accurate and the speed is stable. Thus, the MPC algorithm can be used to improve the efficiency of the rollator system.

To further illustrate the effectiveness of the proposed algorithm, a contrastive experiment of trajectory tracking is designed. The reference trajectory is set to a 5 m straight line and then a sinusoidal curve. The model predictive control algorithm and the sliding mode control algorithm are used for simulation respectively. The comparison results are shown in Figure 15. It can be concluded that both MPC and SMC can track the reference path well in a straight direction, but the MPC algorithm has a better effect in tracking the reference curve than SMC control in sinusoidal curve section. The deviation error of MPC control is almost zero, while the SMC is 0.3 m. Obviously, the MPC controller has faster response, higher tracking accuracy and smoother trajectory, meeting the travel requirements of the elderly rollator.

Since the four-wheeled rollator is an integrated functional application for empowering and assisting human mobility for the elderly or disabled users. The design must consider the practical demand of the elderly or disabled users. As the conclusion of the questionnaires, functions of the rollator, such as height adjustable, safety, GPS location, and wireless communication, etc., has been reorganized. A Kano model analysis is conducted and the TRIZ theory is utilized to redesign a novel rollator for meeting the requirements of the elderly. Compared to the designed rollator in the state of art [3,37,38,39], the novel rollator is more suitable for elderly users, featured with a simple geometric shape, the adjustable seat, and suitable materials, etc.

Furthermore, safety [40,41] and reliability are also important factors for the rollator. Uncertain human-robot interactions [42,43,44,45] cannot be avoided during the usage of the rollator. However, there are few studies achieving lateral stability control of the systems of the rollator using MPC. Hence, we validate the novel designed rollator with the lateral stability tracking control, which is a main challenge of the commercial rollator. Hence, we try to design the lateral stability of an active control system for the elderly walker. In this paper, we have presented an MPC based path-tracking controller to improve the safety of elderly rollator. The simulation results indicate that the proposed algorithm keeps the lateral position error in a reasonable range. In the co-simulation of ADAMS-MATLAB, the trajectory of the rollator is smooth with constrained position error within 0.1 m, the turning angle and speed can achieve stable tracking control within 5 s and the heading angle is accurate and the speed is stable. In addition, a compared experiment with MPC and SMC show that MPC controller has faster response, higher tracking accuracy and smoother trajectory on the novel designed rollator. Thus, the novel designed rollator can be available in practical life. The research on the rollator focuses on the novel design and balance control of the novel rollator, while the main issue in this paper is to design the stability system of the novel designed elderly rollator for practical engineering.

The characteristics of the novel rollator are with high security, low-speed stability and reliability. Adopting the MPC algorithm in the actual engineering application of rollator system is to meets the requirements of the low-speed stability of the elderly rollator. At the same time, MPC has the advantages of higher tracking accuracy, lower position error, and robustness, which meet the requirements of high security.

5. Conclusions and Future Work

To facilitate the development of the elderly or disabled users, this paper presents a novel design and tracking control scheme for empowering and assisting natural human mobility with a four-wheeled rollator. The main contributions of this paper are listed as follows:

• An integrated system of four-wheeled rollator is designed to meet the requirements of the elderly by introducing a novel mechanical design theory that integrates the advantages of Kano Model Analysis with the Theory of Inventive Problem Solving (TRIZ).
• A lateral stability tracking control approach based on an MPC scheme is performed to validate the control feasibility of the novel designed four-wheeled rollator, which is introduced to achieve the high safety requirements of the elderly walker.

The contributions of this paper mentioned above provides an optimized procedure for further development of rollators. At present, the rollator designed for the elderly is being industrialized in China and European, providing convenience for the users to travel safely. For future works, extensive experiments will be performed to verify the effectiveness of the proposed MPC approach on the actual rollator system. We will consider more challenging problems (e.g., dead-zone and time-delay) [46,47,48,49] in our proposed control framework. The system stability and tracking accuracy might not be guaranteed under these situations. It will mainly focus on the improvement of the intelligent level of the rollator for walking aids.