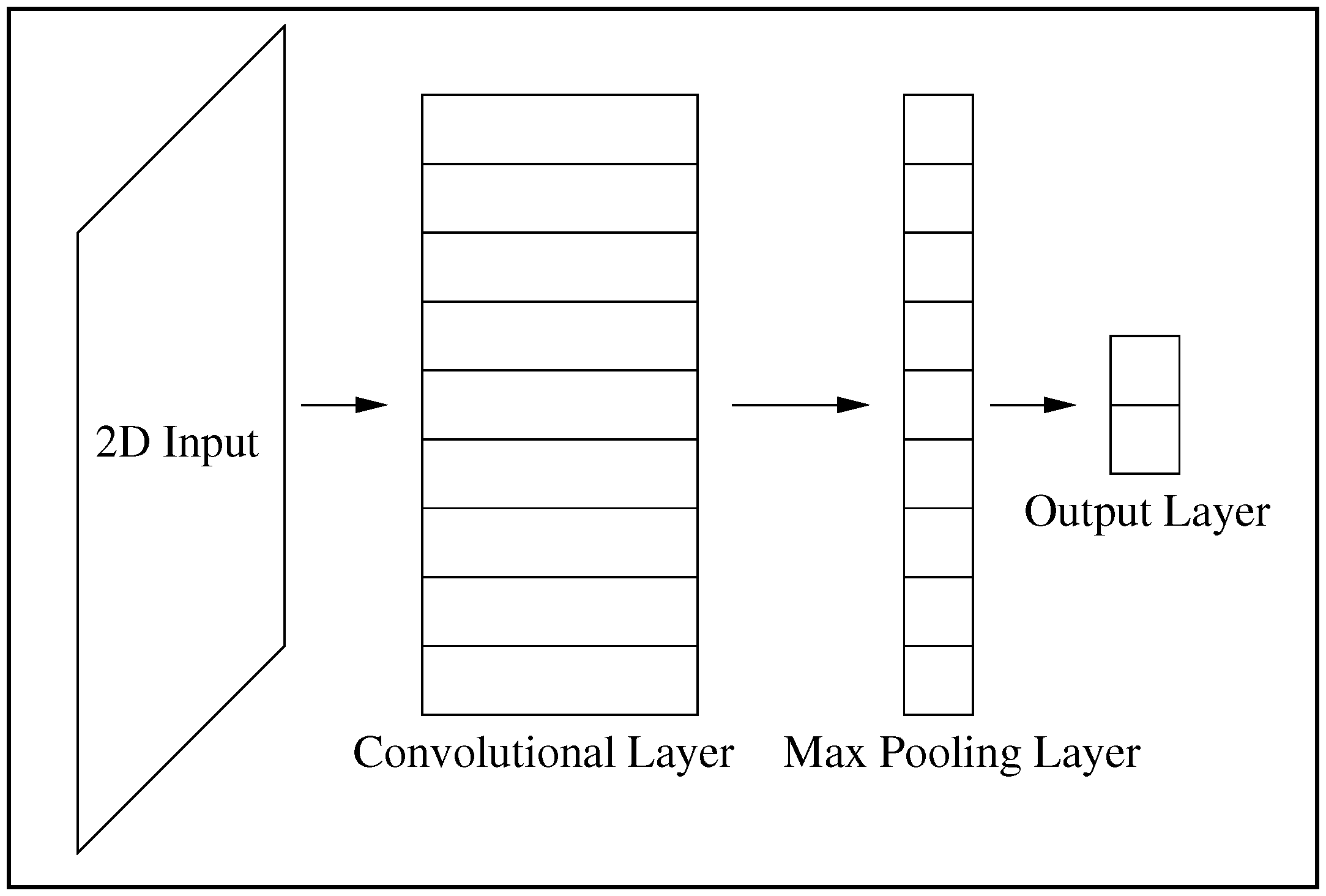
Figure 1.
The Convolutional Neural Networks (CNN) architecture used in this work. From left to right are shown a two-dimensional input layer, a convolutional layer, a max-pooling layer, and an output layer which is fully connected.
Figure 1.
The Convolutional Neural Networks (CNN) architecture used in this work. From left to right are shown a two-dimensional input layer, a convolutional layer, a max-pooling layer, and an output layer which is fully connected.
Figure 2.
Representation of text by a matrix of real numbers. A word is represented on the horizontal axis by word embeddings, while vertically several words are expressed.
Figure 2.
Representation of text by a matrix of real numbers. A word is represented on the horizontal axis by word embeddings, while vertically several words are expressed.
Figure 3.
Wide convolution: The number of columns of the kernel is equal to the number of columns of the text matrix. The result of convolution (showed after the arrow) is a vector.
Figure 3.
Wide convolution: The number of columns of the kernel is equal to the number of columns of the text matrix. The result of convolution (showed after the arrow) is a vector.
Figure 4.
The max-pool operator: The maximal value of each vector in the left is selected and concatenated in a new layer denoted as the “Max-pooling” layer (right most vector).
Figure 4.
The max-pool operator: The maximal value of each vector in the left is selected and concatenated in a new layer denoted as the “Max-pooling” layer (right most vector).
Figure 5.
A Discretized Interpretable Multi Layer Perceptron (DIMLP) network that potentially creates a discriminative hyperplane in . The activation function of the hidden neuron is a step function, while for the output neuron it is a sigmoid.
Figure 5.
A Discretized Interpretable Multi Layer Perceptron (DIMLP) network that potentially creates a discriminative hyperplane in . The activation function of the hidden neuron is a step function, while for the output neuron it is a sigmoid.
Figure 6.
Flow of data in the interpretable CNN (see the text for more details).
Figure 6.
Flow of data in the interpretable CNN (see the text for more details).
Figure 7.
N-grams determined from and the following “tweet” (in the testing set): “it is just too bad the film’s story does not live up to its style”. On the vertical axis are represented the n-grams classified according to their linear contribution. Negative values are against the final classification, while positive values are in its favor. The sum of the n-grams linear contributions is 0.435.
Figure 7.
N-grams determined from and the following “tweet” (in the testing set): “it is just too bad the film’s story does not live up to its style”. On the vertical axis are represented the n-grams classified according to their linear contribution. Negative values are against the final classification, while positive values are in its favor. The sum of the n-grams linear contributions is 0.435.
Figure 8.
N-grams determined from and the following “tweet”: “a zippy 96 min of mediocre special effects, hoary dialogue, fluxing accents, and—worst of all—silly-looking morlocks”. The sum of the n-grams linear contributions is 0.302.
Figure 8.
N-grams determined from and the following “tweet”: “a zippy 96 min of mediocre special effects, hoary dialogue, fluxing accents, and—worst of all—silly-looking morlocks”. The sum of the n-grams linear contributions is 0.302.
Figure 9.
N-grams determined from and the following “tweet”: “so mind-numbingly awful that you hope britney won’t do it one more time, as far as movies are concerned”. The sum of the n-grams linear contributions is 0.211.
Figure 9.
N-grams determined from and the following “tweet”: “so mind-numbingly awful that you hope britney won’t do it one more time, as far as movies are concerned”. The sum of the n-grams linear contributions is 0.211.
Figure 10.
N-grams determined from and the following “tweet”: “the tuxedo wasn’t just bad; it was, as my friend david cross would call it, hungry-man portions of bad.” The sum of the n-grams linear contributions is 0.283.
Figure 10.
N-grams determined from and the following “tweet”: “the tuxedo wasn’t just bad; it was, as my friend david cross would call it, hungry-man portions of bad.” The sum of the n-grams linear contributions is 0.283.
Figure 11.
N-grams determined from and the following “tweet”: “it has a subtle way of getting under your skin and sticking with you long after it’s over”. The sum of the n-grams linear contributions is 0.260.
Figure 11.
N-grams determined from and the following “tweet”: “it has a subtle way of getting under your skin and sticking with you long after it’s over”. The sum of the n-grams linear contributions is 0.260.
Figure 12.
N-grams determined from and the following “tweet”: “though the controversial korean filmmaker’s latest effort is not for all tastes, it offers gorgeous imagery, effective performances, and an increasingly unsettling sense of foreboding.” The sum of the n-grams linear contributions is 0.251.
Figure 12.
N-grams determined from and the following “tweet”: “though the controversial korean filmmaker’s latest effort is not for all tastes, it offers gorgeous imagery, effective performances, and an increasingly unsettling sense of foreboding.” The sum of the n-grams linear contributions is 0.251.
Figure 13.
N-grams determined from and the following “tweet”: “thoughtful, provocative and entertaining”. The sum of the n-grams linear contributions is 0.398.
Figure 13.
N-grams determined from and the following “tweet”: “thoughtful, provocative and entertaining”. The sum of the n-grams linear contributions is 0.398.
Figure 14.
N-grams determined from and the following “tweet”: “it’s a beautifully accomplished lyrical meditation on a bunch of despondent and vulnerable characters living in the renown chelsea hotel . . .”. The sum of the n-grams linear contributions is 0.355.
Figure 14.
N-grams determined from and the following “tweet”: “it’s a beautifully accomplished lyrical meditation on a bunch of despondent and vulnerable characters living in the renown chelsea hotel . . .”. The sum of the n-grams linear contributions is 0.355.
Figure 15.
N-grams determined from and the following “tweet” (in the testing set): “some movies are like a tasty hors-d’oeuvre; this one is a feast”. It is correctly classified by the rule, but wrongly classified by the network.
Figure 15.
N-grams determined from and the following “tweet” (in the testing set): “some movies are like a tasty hors-d’oeuvre; this one is a feast”. It is correctly classified by the rule, but wrongly classified by the network.
Table 1.
CNN architecture. Symbols for each layer are specified in the second row and sizes in the last.
Table 1.
CNN architecture. Symbols for each layer are specified in the second row and sizes in the last.
| Input | Convolution | Max-Pooling Layer | Output |
|---|
| I | | M | O |
| 59 × 300 | 1 × 300 × 40 2 × 300 × 40 3 × 300 × 40 | 120 | 2 |
Table 2.
Interpretable CNN architecture with symbols and sizes.
Table 2.
Interpretable CNN architecture with symbols and sizes.
| Input | Conv. | Max-Pooling Layer | DIMLP Hid. Layer | Output |
|---|
| I | C = (C1, C2, C3) | M | H | O |
| 59 × 300 | 1 × 300 × 40 2 × 300 × 40 3 × 300 × 40 | 120 | 120 | 2 |
Table 3.
Average results based on cross-validation. The models are CNNs and interpretable CNN approximations with varying numbers of stairs in the staircase activation function. Standard deviations are given between parentheses.
Table 3.
Average results based on cross-validation. The models are CNNs and interpretable CNN approximations with varying numbers of stairs in the staircase activation function. Standard deviations are given between parentheses.
| | Tr. Acc. | Tst. Acc. | Fid. | Rul. Acc. (1) | Rul. Acc. (2) | #Rul. | #Ant. |
|---|
| CNN | 82.1 (1.3) | 74.1 (1.1) | – | – | – | – | – |
| CNN () | 82.1 (1.3) | 74.1 (1.1) | 95.3 (0.6) | 73.7 (1.0) | 75.1 (1.0) | 651.7 (53.1) | 5368.9 (379.3) |
| CNN () | 82.2 (1.4) | 74.1 (1.0) | 95.8 (0.4) | 73.7 (1.0) | 74.9 (1.0) | 573.8 (49.0) | 5040.7 (354.0) |
| CNN () | 82.1 (1.4) | 74.1 (1.1) | 95.6 (0.8) | 73.6 (1.0) | 75.0 (0.9) | 566.1 (28.0) | 4980.7 (364.5) |
Table 4.
Average results obtained by Decision Trees (DTs) trained to learn datasets with CNN targets, instead of true labels. Columns from left to right represent average results on: Training accuracy; predictive accuracy; fidelity on the training set; fidelity on the testing set; number of extracted rules; and number of antecedents in the rules. In the rows, the parameter controlling the size of the trees varies.
Table 4.
Average results obtained by Decision Trees (DTs) trained to learn datasets with CNN targets, instead of true labels. Columns from left to right represent average results on: Training accuracy; predictive accuracy; fidelity on the training set; fidelity on the testing set; number of extracted rules; and number of antecedents in the rules. In the rows, the parameter controlling the size of the trees varies.
| | Tr. Acc. | Tst. Acc. | Tr. Fid. | Tst Fid. | #Rul. | #Ant. |
|---|
| DT | 82.1 (1.3) | 57.5 (1.4) | 100.0 (0.0) | 60.9 (0.8) | 797.9 (16.9) | 10,354.3 (704.6) |
| DT | 78.6 (1.1) | 57.9 (0.9) | 94.3 (0.2) | 61.0 (1.0) | 615.7 (6.4) | 7134.4 (304.6) |
| DT | 75.6 (0.8) | 58.4 (1.3) | 89.1 (0.2) | 61.4 (1.3) | 456.8 (7.4) | 4863.7 (149.3) |
| DT | 73.3 (0.7) | 58.5 (1.4) | 85.4 (0.4) | 61.6 (0.8) | 362.2 (5.6) | 3666.2 (116.4) |
| DT | 71.9 (0.6) | 58.5 (1.5) | 82.9 (0.3) | 61.5 (2.2) | 299.5 (4.5) | 2904.5 (86.4) |
| DT | 70.6 (0.6) | 58.6 (1.6) | 81.1 (0.4) | 61.4 (1.8) | 253.9 (3.5) | 2363.1 (71.6) |
| DT | 69.8 (0.6) | 59.3 (1.0) | 79.8 (0.4) | 62.1 (1.8) | 222.7 (4.4) | 2015.9 (52.1) |
| DT | 69.0 (1.0)) | 59.3 (1.6) | 78.5 (0.4) | 62.5 (1.5) | 194.4 (4.2) | 1707.9 (64.1) |
| DT | 68.5 (0.7) | 59.7 (1.8) | 77.4 (0.3) | 62.3 (1.4) | 173.9 (3.8) | 1482.8 (42.4) |
| DT | 67.6 (0.6) | 59.6 (1.1) | 75.9 (0.4) | 62.7 (1.2) | 143.8 (2.7) | 1168.4 (31.5) |
Table 5.
Average results obtained by the rules generated from Decision Trees that replace the fully connected layer of CNNs. Columns from left to right represent average results on: Training accuracy; testing accuracy; number of extracted rules; number of antecedents in the rules. In the rows, the parameter controlling the size of the trees varies.
Table 5.
Average results obtained by the rules generated from Decision Trees that replace the fully connected layer of CNNs. Columns from left to right represent average results on: Training accuracy; testing accuracy; number of extracted rules; number of antecedents in the rules. In the rows, the parameter controlling the size of the trees varies.
| | Tr. Acc. | Tst. Acc. | #Rul. | #Ant. |
|---|
| DT | 100.0 (0.0) | 66.0 (1.6) | 943.2 (23.6) | 11,160.8 (367.7) |
| DT | 93.4 (0.2) | 66.8 (1.4) | 640.0 (16.3) | 6710.8 (191.2) |
| DT | 89.0 (0.3) | 67.0 (1.4) | 450.4 (9.3) | 4414.5 (97.7) |
| DT | 86.5 (0.4) | 67.6 (1.1) | 342.6 (5.6) | 3198.0 (60.5) |
| DT | 84.8 (0.4) | 68.0 (1.0) | 276.8 (7.4) | 2483.2 (69.9) |
| DT | 83.6 (0.4) | 67.9 (1.3) | 234.6 (4.7) | 2043.1 (38.4) |
| DT | 82.7 (0.4) | 68.6 (0.9) | 201.8 (4.2) | 1704.5 (38.1) |
| DT | 82.0 (0.5) | 68.3 (1.1) | 178.0 (3.5) | 1468.0 (40.1) |
| DT | 81.3 (0.5) | 68.3 (1.2) | 159.1 (3.5) | 1281.6 (29.0) |
Table 6.
Average results obtained by Support Vector Machines (SVMs). Each row illustrates the accuracy results with respect to the C parameter.
Table 6.
Average results obtained by Support Vector Machines (SVMs). Each row illustrates the accuracy results with respect to the C parameter.
| | Tr. Acc. | Tst. Acc. |
|---|
| SVM | 75.1 (0.1) | 70.5 (1.4) |
| SVM | 77.1 (0.2) | 70.6 (1.3) |
| SVM | 81.6 (0.2) | 70.2 (0.8) |
| SVM | 83.6 (0.3) | 69.9 (1.0) |
| SVM | 88.6 (0.2) | 68.1 (0.9) |
| SVM | 90.7 (0.2) | 67.5 (0.9) |
Table 7.
ANOVA comparison between CNNs and SVMs providing the better average predictive accuracy (equal to 70.6%).
Table 7.
ANOVA comparison between CNNs and SVMs providing the better average predictive accuracy (equal to 70.6%).
| | CNN Rul. Acc. (Average) | CNN Rul. Acc. (Median) | p-Value |
|---|
| CNN () and SVM () | 73.7 | 73.8 | |
| CNN () and SVM () | 73.7 | 73.6 | |
| CNN () and SVM () | 73.6 | 73.9 | |
Table 8.
ANOVA comparison between CNNs and SVMs providing the second better average predictive accuracy (equal to 70.5%).
Table 8.
ANOVA comparison between CNNs and SVMs providing the second better average predictive accuracy (equal to 70.5%).
| | p-Value |
|---|
| CNN () and SVM () | |
| CNN () and SVM () | |
| CNN () and SVM () | |