1. Introduction
Implant-supported fixed partial dental prosthesis is a popular treatment option for partially edentulous patients. The mean implant failure rate of fixed partial dentures in partially edentulous patients was reported to be 6% in both the maxilla and mandible (range: 1.9–12.5%) [
1,
2]. Conditions that contribute to restoration failure include cracking, chipping fracture, bulk fracture, excessive wear of the opposing tooth surface, excessive roughening of the ceramic surface, and unacceptable esthetics. Anusavice [
3] defined restoration success as intact prosthesis survival with acceptable surface quality, anatomic contour, function, and esthetic. In clinical settings, delivering an implant prosthesis is challenging when the implant tilts during implantation, which may stem from anatomic limitation, unique treatment design (such as all-on-4), or other iatrogenic factors. Delivery methods of implant crowns mainly divide into the following: Cement-retained and screw-retained implant prosthesis. The implant abutment is always milled or custom-made to fit the insertion pathway.
Fixing a single implant prosthesis on a tilted implant fixture over the posterior area is often a challenging task due to limited insertion pathway, short interdental space, and difficult interproximal hygiene maintenance. After properly milling the implant abutment, one must put into consideration the ceramic materials used, prosthesis thickness, and repairing method after implant prosthesis failed in the future. The advantages of screw-retained implant prosthesis are easy retrieval, better tissue response, and capable of installing when interocclusal space is limited. On the other hand, delivering a cement-retained implant is easier than delivering a screw-retained implant. However, the clinician should evaluate the retention and resistance of the crown meticulously and clean excess cement after delivery.
Based on the method of fabrication, implant abutments can be classified into prefabricated and custom-made abutments. Prefabricated abutments are often used in the esthetic zones owing to difficulty in achieving a good emergence profile, and the margin of the abutment requires milling because it remains supragingival. The milling of prefabricated implant abutment is typically performed using high-speed handpiece and diamond dental burs [
4,
5]. The total occlusal convergence (TOC) [
6], which is the convergence angle between two opposing axial walls, is one of the critical factors for the success of ceramic crowns. Low values of TOC [
7,
8], range 2° to 5°, are difficult for crown delivery and result in an increasing cement hydraulic pressure. High values of TOC [
9], over 24°, are difficult to obtain proper retention of the crown in long-term follow-up. Owing to advances in software and hardware for the open computer numerical control (CNC) system development, computer-aided design (CAD) and computer-aided manufacture (CAM) have increased interoperability and dimension control when milling the implant abutment [
10]. Designing abutment using software and milling metal/zirconia material have gained great popularity in clinical dentistry. These abutments have allowed the dentists to create individual emergence profile and provide an ideal structure and crown path insertion. After manual or machine milling, the morphology of the implant abutment can be adjusted, and the prosthesis is always set on an asymmetrical convergent angle of the axial surfaces which lead to different occlusal areas.
Zirconia is a crystalline form of zirconium dioxide; it has excellent mechanical properties similar to metal and with color close to natural teeth. The best properties for medical use are exhibited by zirconia stabilizing with Y
2O
3—also known as tetragonal zirconia polycrystal (TZP) [
11]. A high flexure strength (900–1200 MPa) and compression resistance (2000 MPa) [
12] render it suitable for use in clinical dentistry [
13]. Monolithic zirconia crowns have gained popularity since 2010 [
14,
15,
16], primarily for reducing the major clinical complications that resulted from the fracture of porcelain veneers and zirconia frameworks [
17]. Lawn et al. [
18] mentioned that failure mode, materials, flaw state, layer thickness, and cement may affect the fracture resistance of ceramic crowns. Deng et al. [
19] showed that fully dense zirconia (Y-TZP) has the highest critical load (100–1000 N) at low thicknesses (0.1–1.0 mm) when comparing different ceramic specimens. Hamburger et al. [
20] showed that the fracture risk of ceramic materials has a positive correlation to layer thickness. Weigl et al. [
21] showed that 0.5 mm thick monolithic crowns possessed sufficient strength to endure physiological performance, regardless of the type of cementation. Lan et al. [
22] showed that the mean fracture loading cycles of a 0.5-mm zirconia specimen is 8480 ± 2009. He recommended the use of an implant prosthesis of monolithic zirconia crown with a thickness of 0.8 mm during clinical practice. Additionally, Kelly [
23] suggested a more relevant approach using the finite element method (FEM) to solve for stress as a function of load. Anatomically, axial loading posterior teeth with the implant prosthesis can vary from 42 to 412 N [
24], and Raadsheer et al. [
25] found that maximum voluntary occlusal force was 545.7 N in men and 383.6 N in women in natural dentition. On the other hand, Lan et al. [
22] used 300 N to simulate the bite force of implant prosthesis of molar area. During maximum intercuspation (MICP), loading force would spread among all contacted teeth. Therefore, we anticipated that maximal voluntary occlusal force should not approach the value Raadsheer has presented.
As discussed above, the fracture resistance of monolithic zirconia specimens is primarily affected by the thickness [
22], and researchers have attempted to determine the correlation between the different convergent occlusal area of implant abutment and breaking test of zirconia specimens after lead bearing. Therefore, the purpose of this study is to compare the fracture resistance and stress distribution of zirconia specimens on four different occlusal convergence implant abutments. The hypothesis is that more occlusal convergence of implant abutment would lead to less fracture resistance of monolithic zirconia crowns.
2. Materials and Methods
2.1. Specimens Preparation
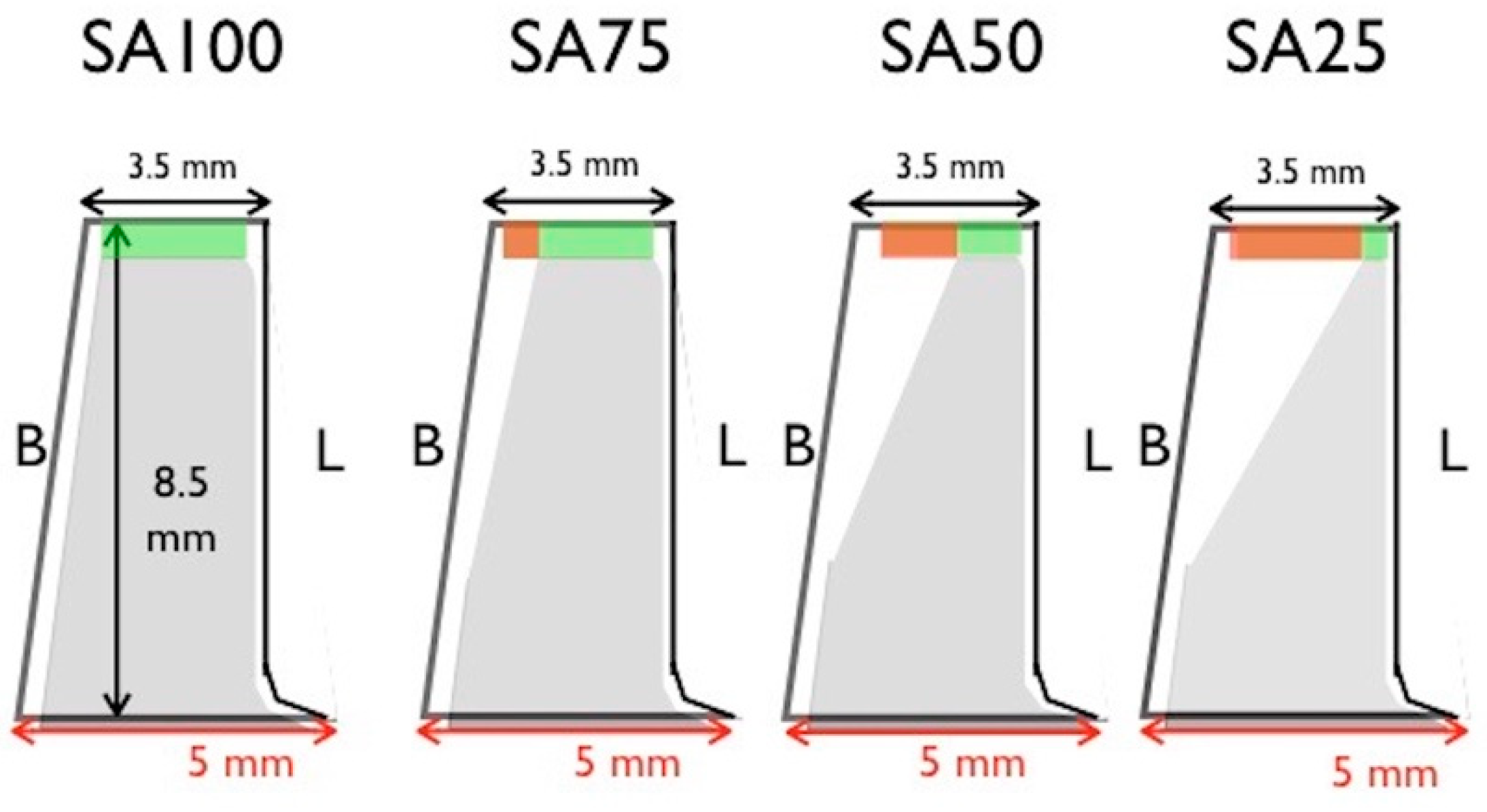
Figure 1 shows four implant abutments [occlusal surface area (SA) SA100, SA75, SA50, and SA25] in the molar area that were prepared to receive monolithic zirconia specimens. SA50 implies that the total occlusal surface contact area is half of SA100. The removed occlusal surface area (A) was calculated using the equation:
where r is the radius of the circle; θ is the central angle measured in radians.
The specimen holder and the operating program of the test machine were adjusted to simulate the human masticatory cycle. The specimen holder had three parts: A precise adapter for the test machine, a heat-treated steel rod with a tapered tip to accommodate the specimen, and a spring to simulate cyclic occlusal contact and position control. The spring was checked before and after tests to verify the slope of strain and stress by Hooke’s law [
26], as it should remain constant throughout tests. The G power analysis [
27] was used to estimate the required sample size; assuming four test groups, an effect size of 0.56, the probability of an α error of 0.05, and power of 0.95. The sample size was set to have 15 per group. Overall, 60 complete zirconia specimens were designed using the computer-aided design/computer-aided manufacturing (CAD/CAM) technique to match the implant abutment design. The specimens were designed by the DentalCAD software (Exocad 2016, Exocad GmbH, Darmstadt, Germany). All specimens were milled from one commercial block of Y-TZP zirconia V (made in made in Bad Sackingen, Germany) using the same open CNC system milling machine (ARDENTA CNC MILL, CS100-5A, ARIX, Tainan, Taiwan) and were densely sintered at 1450 °C for 2 h.
2.2. Cyclic Loading Test
Figure 2 is the schematic representation of four implant abutment designs. The specimens were retained on the implant dies by friction and could only be removed by crown remover. The stability of the prosthesis was enhanced by the anti-rotation surface design of the dental implant abutment. The dimension of SA100 specimen was designed to fit the implant abutment with thickness of 0.5 mm over occlusal surface, diameter of 5 mm at base, and diameter of 3.5 mm at top. The reduction began 2 mm from the bottom to preserve retentive property, and tapered up to the desired occlusal surface area. Reduced volume was replaced with zirconia. Fifteen specimens in each group were tested vertically at 5 Hz and 300 N in a servo-hydraulic testing machine (Instron M8810, Instron Ltd. Norwood, MA, USA) until the specimen fractured or the test machine automatically stopped after 30,000 cyclic counts. To ensure that a consistent force was exerted on the specimen, the computer program had a 2-stage control to emulate the masticatory cycle of human jaw. The first stage, which simulated natural occlusal displacement, was position control. This stage ensured constant stroke distance between the load cell and specimen. The second stage was load control. This stage ensured a consistent force exerted by the load cell to the specimen remained constant throughout the test cycle.
The indentation stress-strain relation is well defined by the classic Hertzian theory for ideally elastic, homogeneous bulk materials with Young’s modulus E and Poisson’s ratio ν. The linear form of the Hertzian solution [
28,
29] is expressed as:
where
a is the radius of the contact area,
r is the radius of indent and
d the depth, F is the loading, and
P is the maximum contact pressure.
2.3. Finite Element Method
The dental implant abutment models were constructed using the CAD software (SolidWorks 2010, SolidWizard Corporation, Concord., MA, USA). Four finite element (FE) models with the different occlusal surface areas covered by zirconia specimens were constructed to simulate the posterior molar region. ANSYS was the FEM software used in this study (ANSYS Workbench 11, Canonsburg, PA, USA). The Young’s modulus and Poisson ratio of Ti-6Al-4V [
30] were 110 GPa and 0.33, respectively. The Young’s modulus and Poisson ratio of zirconia [
31] were 220 GPa and 0.3, respectively.
The materials used in the models were assumed to be isotropic, homogeneous, and linearly elastic. The average tetrahedral element size was 1 mm in length and the 3D FE model of SA100 model was meshed in the 115484 elements and 147842 nodes by convergence test. The 10-node tetrahedral element could provide six degrees of freedom (DOF), including three translations and three rotations on a node. Hence, total number of the DOF in the FEM was related to real nodal numbers. The boundary constrain of the bottom of the holder base would restrict the DOF of the implant-prosthesis complex of any rotational or translational movement. The mesh convergence test of element sensitivity was performed in this study before FEM. The convergence criterion was set to 5% to identify a reliable numerical result of the FEM.
The contact analysis in the contact area must be assumed that contact and target elements were paired to analyze surface interaction between two solid models under loading. Furthermore, the coefficient of friction must also be applied in the contact area. However, in this study, our main goal was to test the fracture resistance of different zirconia crown and implant abutment designs. Therefore, the sliding effect between the zirconia crown and implant abutment was considered negligible. For contact connection between the zirconia crown and implant abutment, we defined the finite element analysis (FEA) as a non-separating connection without any frictional effect. Hence, the contact analysis with frictional effect was not included in this study. Vertical loading of 300 N was applied on the occlusal surface of the specimens, and a 4-directional oblique force of 300 N at 10 degrees was applied to the marginal ridge of the specimens. The maximum von Mises (EQV) stress values were measured for specimens in different loading directions and implant prosthesis and abutment designs.
2.4. Statistical Analysis and Microstructural Observation
Data were normally distributed (P > 0.05) and there was no homogeneity of variance among groups of tests (P > 0.05). Data were compared using the Krukal-Wallis test, and the Spearman correlation was determined using a statistical program (SPSS Statistics for Windows, v20; IBM Corp, Armonk, NY, USA). Using scanning electron microscope imaging (JSM-6360; JEOL, Tokyo, Japan), the microscopic conditions of the specimens were examined.
4. Discussion
Lan et al. [
22] found that the fracture resistance of zirconia specimens have positive correlation with prosthesis thickness, and the mean cyclic number of broken specimens on 0.5 mm thickness was 8480 ± 2009. This study demonstrated breakage in 11 of 15 specimens (73%) and a similar cyclic number of broken specimens for 0.5 mm (SA100) zirconia specimens (
Table 1). In addition, the breakage percentage of SA75 specimens (6/15) showed no statistical significance (P > 0.05) compared to SA50 specimens (5/15). On the other hand, only one SA25 zirconia specimen (1/15) broke during 300 N vertical loading. The results supported the speculation that the implant abutment occlusal surface area affects the fracture resistance of the zirconia crown, although only a moderately strong correlation was found (
r = 0.475). The FEM showed the lowest peak stress value for SA25 specimen in all loading types, hence, we speculated that the implant abutment occlusal area has an inverse proportion to fracture resistance of the zirconia specimens (
Figure 1 and
Figure 2). Under oblique loading, the peak value of the crown from the lingual side was lower than that from the buccal and distal side. This difference was attributed to the contact area of the prosthesis because the radius of the contact area from the lingual side was greater than other surfaces (
Figure 5 bottom row). Moreover, the radius of the contact area negatively affecting the stress under constant loading is clarified by the Hertzian theory [
28,
29]. On the other hand, the oblique buccal loading and oblique distal loading showed similar peak stress, which may be attributed to the same contact area between the indenter and zirconia crown (
Figure 6 top and bottom row).
Cyclic loadings could cause an accumulation of deformation and decrease the load resistance of the tested materials. Static loadings were loads with a very low rate of change to maximum stresses on specimens. Studart et al. [
32] showed the cyclic fatigue behavior of zirconia at loads between 50 and 200 N and indicated that zirconia can tolerate the severe cyclic loading in the molar area. On the other hand, static FEM analysis was shown the maximum stress value and stress distribution from an applied load 250 N on the specimens. For brittle materials, Choi and Salem [
33] mentioned the prediction of cyclic fatigue lifetime from static lifetime by using the ratio of static to cyclic fatigue life. These results demonstrated the similar failure trend between static and cyclic fatigue for brittle materials, and the fracture of brittle materials would be induced immediately when the maximum stress was higher than the flexural strength. In addition, in this present study, the cyclic experimental tests showed the positive correlation between the percentage of broken specimens over total specimens with the peak stress value of FEA corresponding to four types of abutment designs (
r = 0.391). Moreover, both cyclic experimental tests and static FEM analysis were shown the same results that the SA25 specimens had the lowest stress values and higher fracture resistance under 300 N loading. The results hence rejected the hypothesis described in the introduction. Alammari et al. [
34] reported that an increase of TOC (from 12 to 20 degree) did not affect marginal and internal fit but resulted in higher load to fracture values of ceramic crowns. A similar finding was reported by Corazza et al. [
35], who compared the influence of 6°, 12°, and 20° TOC on the fracture load of yttria partially stabilized zirconia veneered with feldspathic porcelain. The 20° TOC had the best outcome. On the other hand, it could be reasonably speculated that the SA25 specimen allowed for greater implant body tilting. Asymmetric abutment milling with different occlusal convergence was inevitable in clinical practice and also needs to put in consideration of proper crown morphology to avoid food deposition, which relied heavily on accurate standard abutment milling and CAD/CAM custom abutment design.
Milling typically increased the sharp angle and surface roughness. The sharp angle without a fitting contact surface with ceramic could easily increase the stress concentration between zirconia and the implant abutment. Therefore, using zirconia to match the abutment occlusal surface can increase the fracture resistance and ensure a proper fitting contact surface; however, if the surface is not finished or polished properly to decrease the improper contact surface, stress would concentrate on the sharp edges between the zirconia and abutment. The breakage of one SA25 zirconia specimen after 8000 cycles under 300 N loading was attributed to the tiny sharp contact point between zirconia and the abutment despite a meticulous inspection before testing.
Implant abutment milling or adjustment was a frequent practice in clinical dentistry. The success of implant restoration and its long-term survival depended on several factors. First, a well-designed treatment plan would put implant installation and restoration into consideration before the operation. Second, the dentists need to confirm whether the implant requires tilting using the abutment design based on the biomechanical and biomaterial aspects. Third, the zirconia crown used should be fully densified and sufficiently sintered for strength and longevity. Fourth, accurate interdental space calculation, meticulous execution of the procedure, and routine follow-up are required to achieve excellent results.