A Theoretical Solution for Pile-Supported Embankment with a Conical Pile-Head
Abstract
:1. Introduction
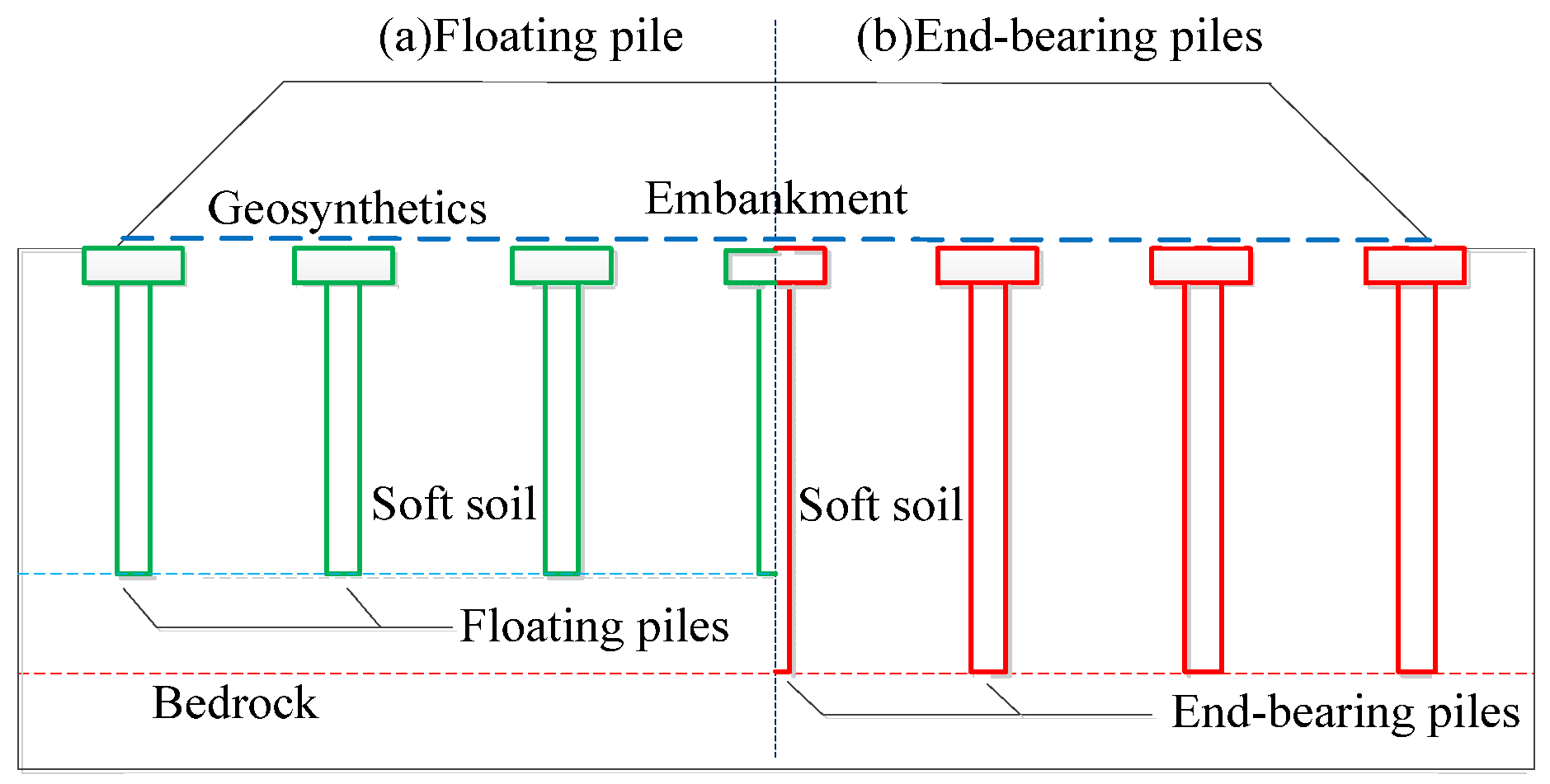
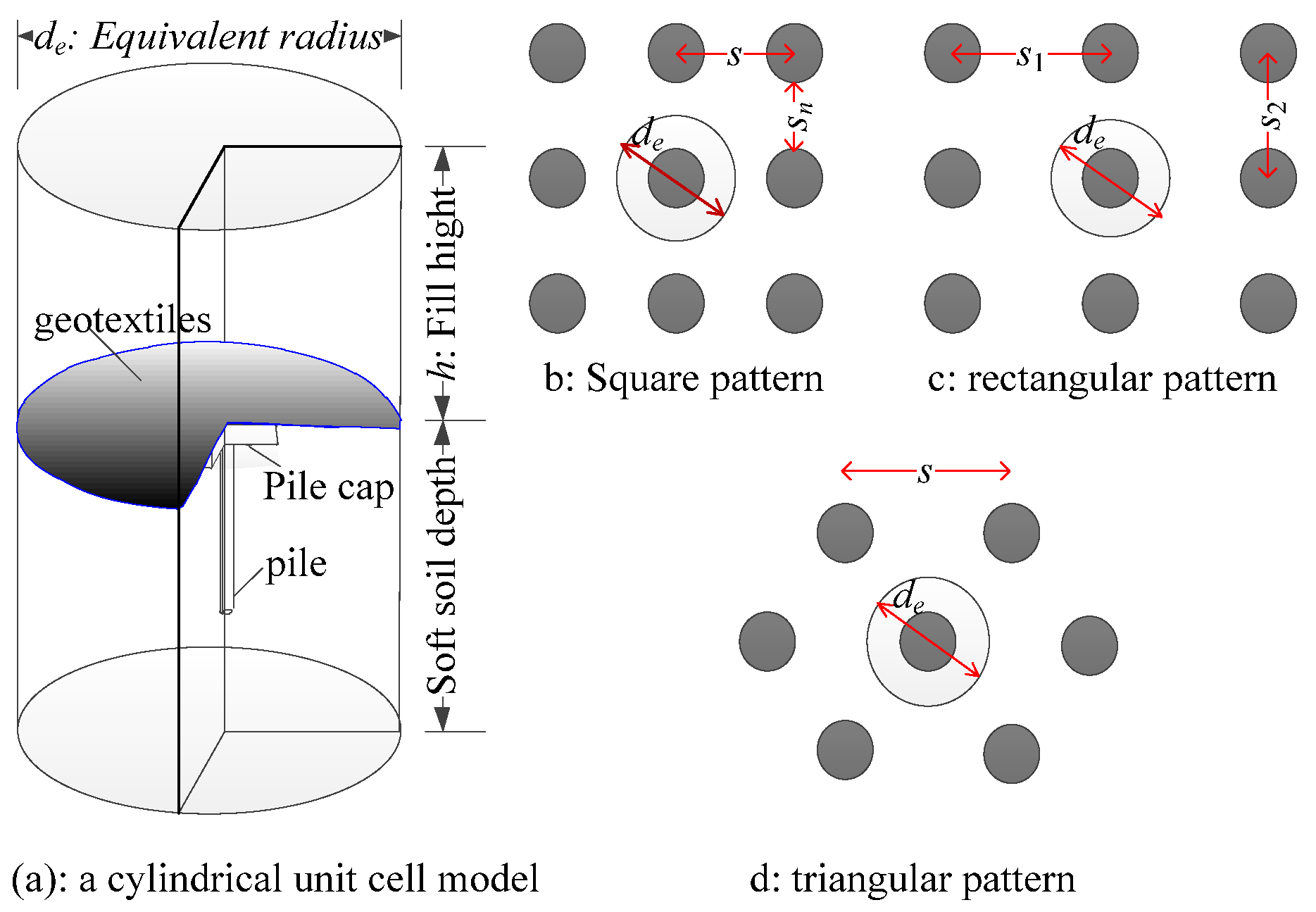
2. Theoretical Model
2.1. Soil Arching in the Embankment
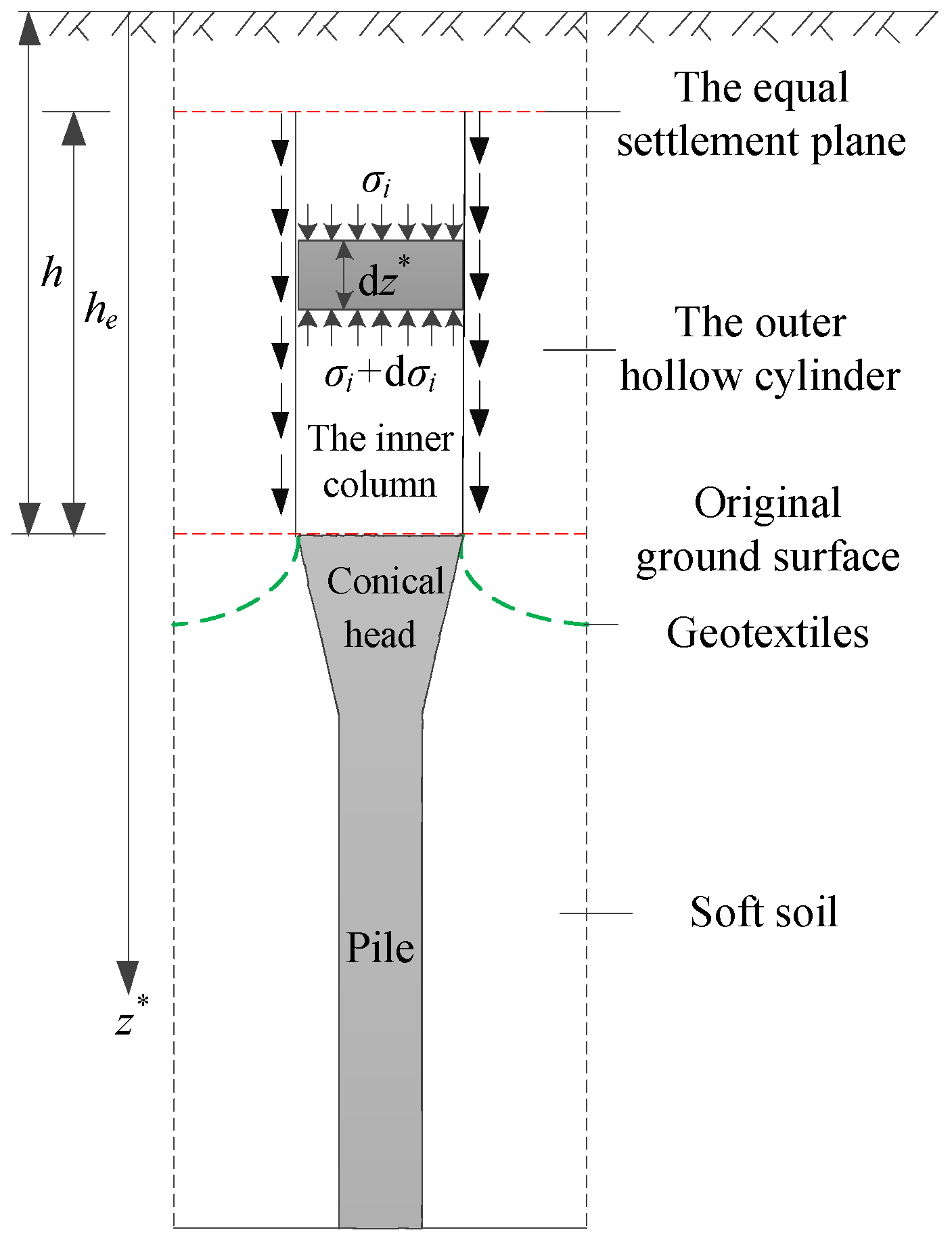
2.2. Load Transfers between Pile and Soil
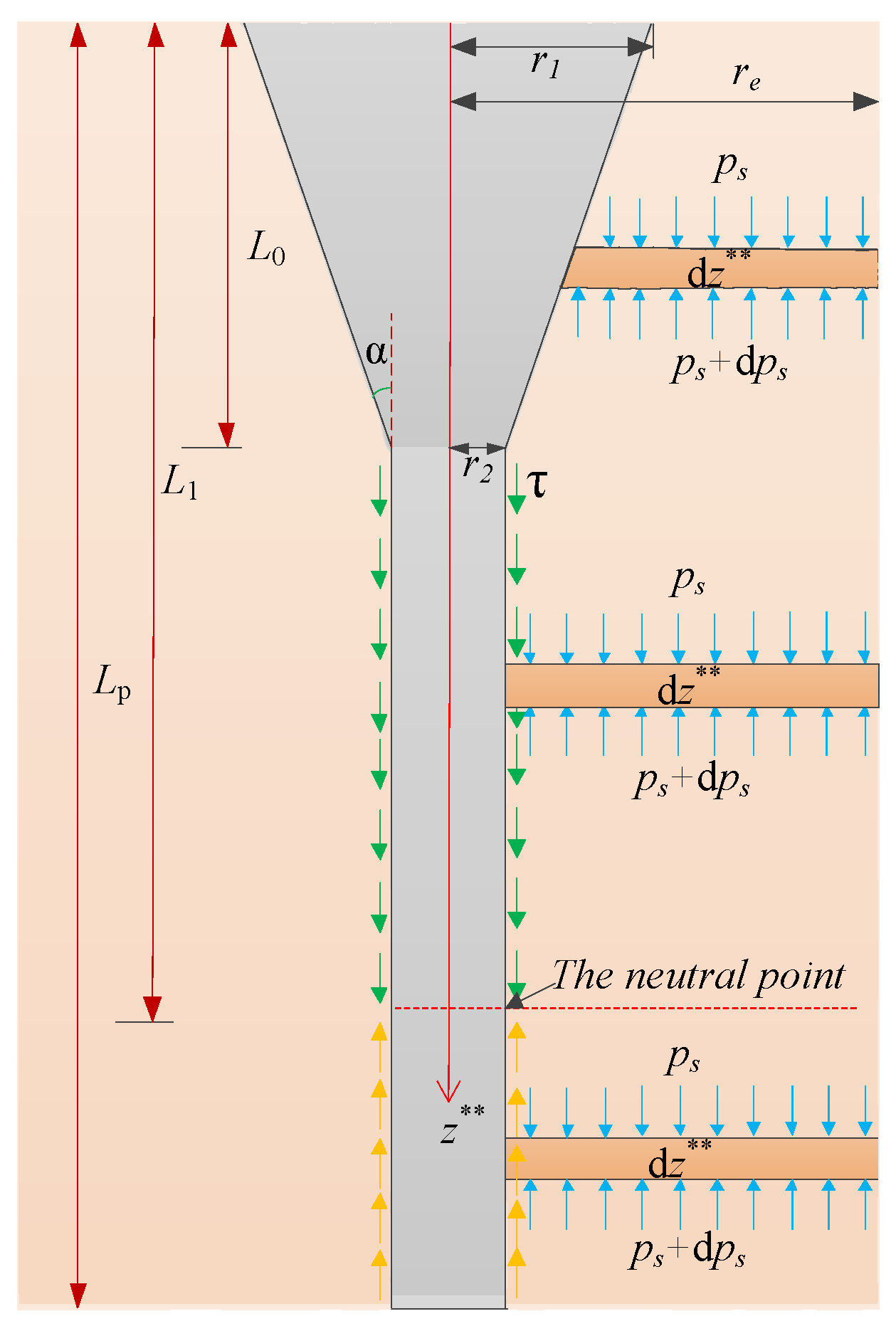
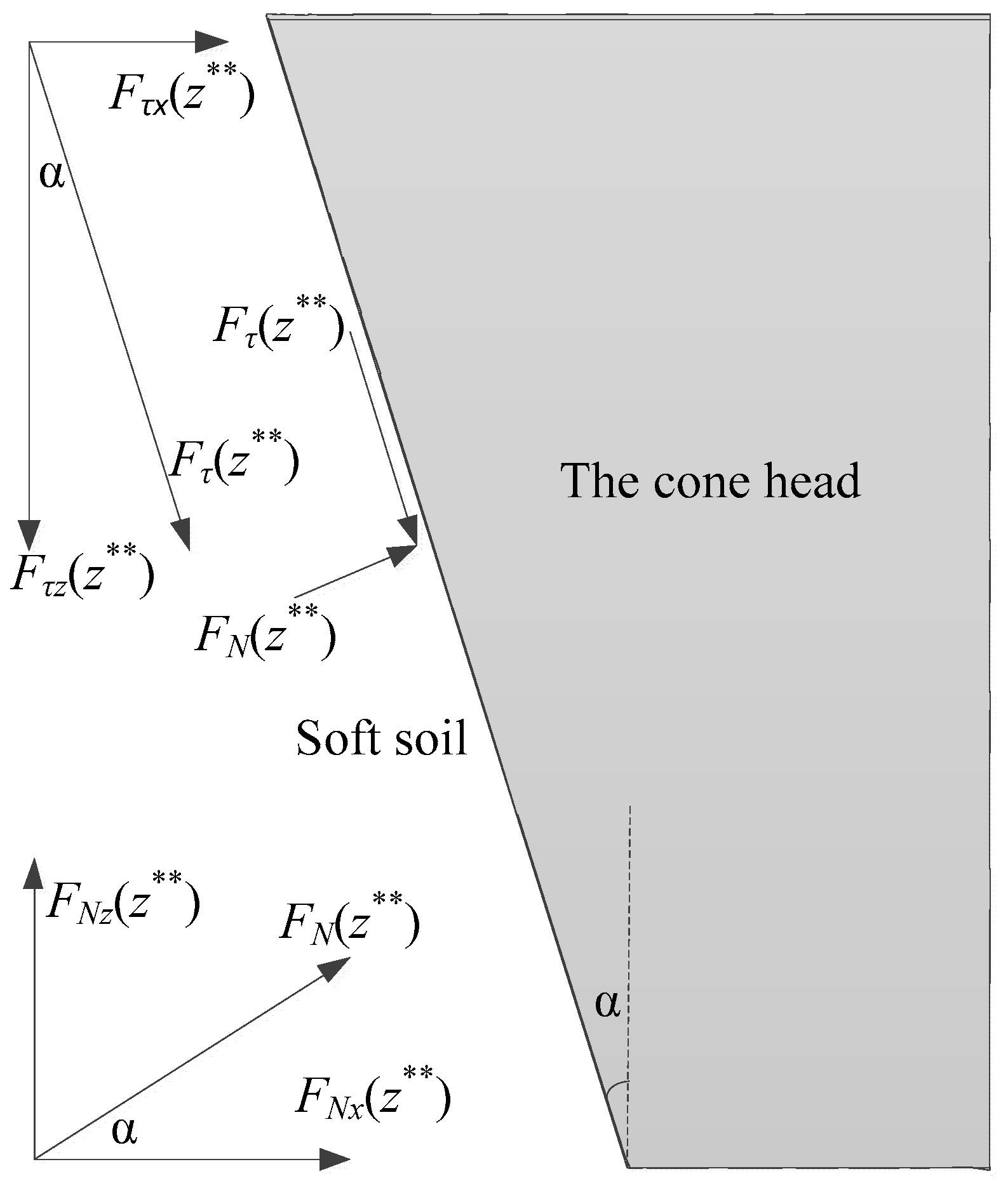
2.2.1. The zone of the conical head
2.2.2. The Negative Friction Zone
2.2.3. The Positive Friction Zone
2.3. Pile toe displacement
2.4. Solution
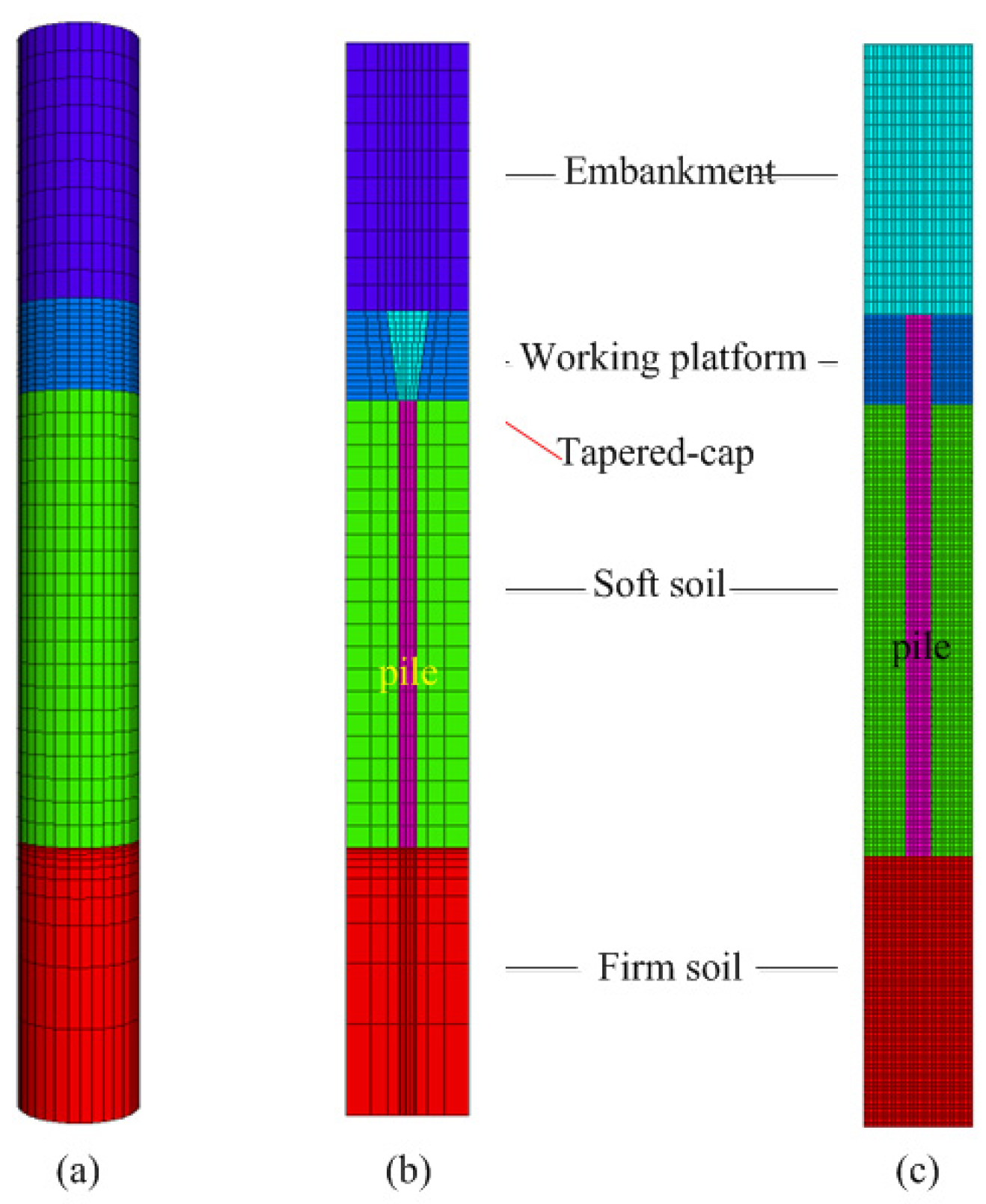
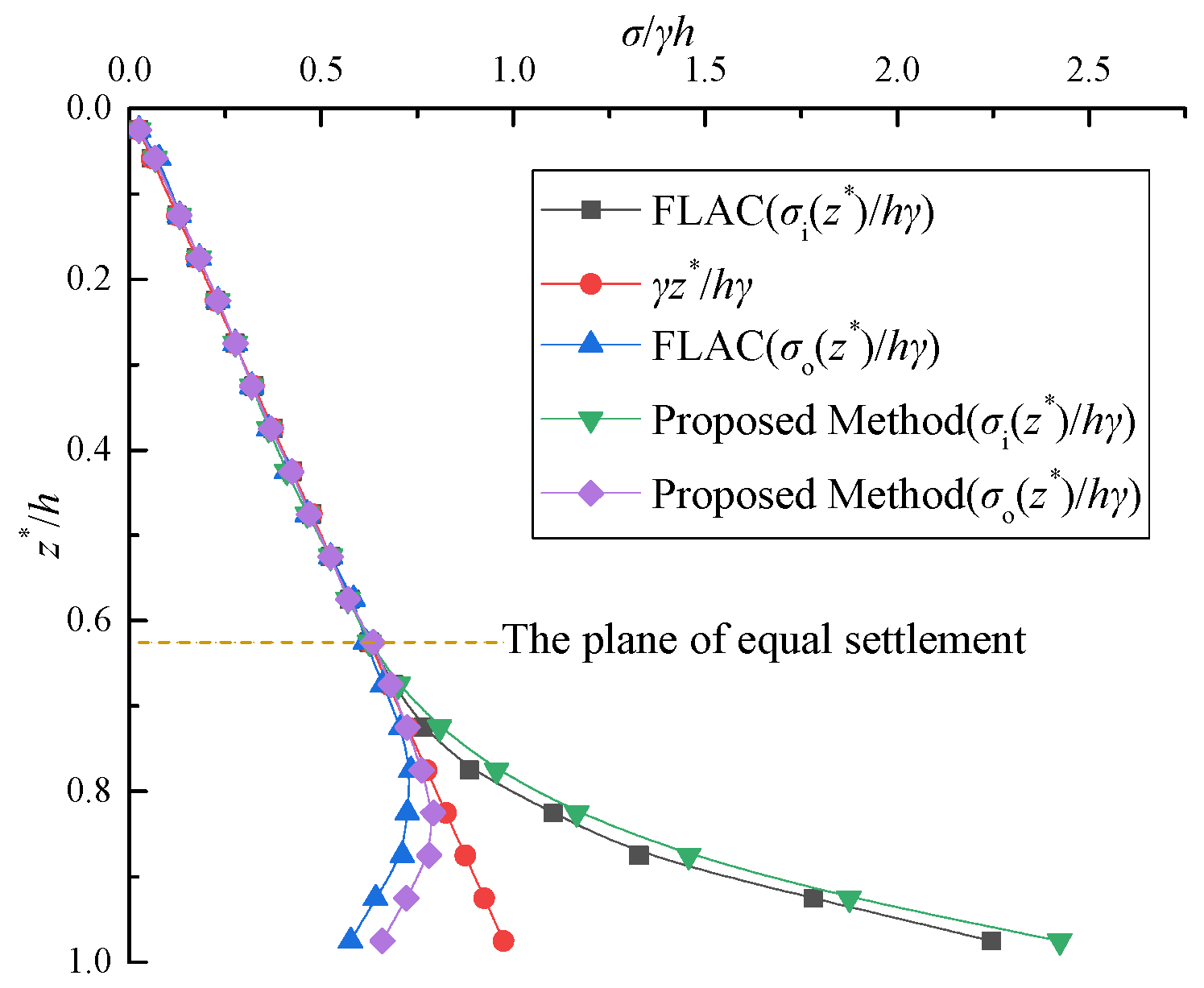
3. Validation
3.1. Validation 1
3.2. Validation 2
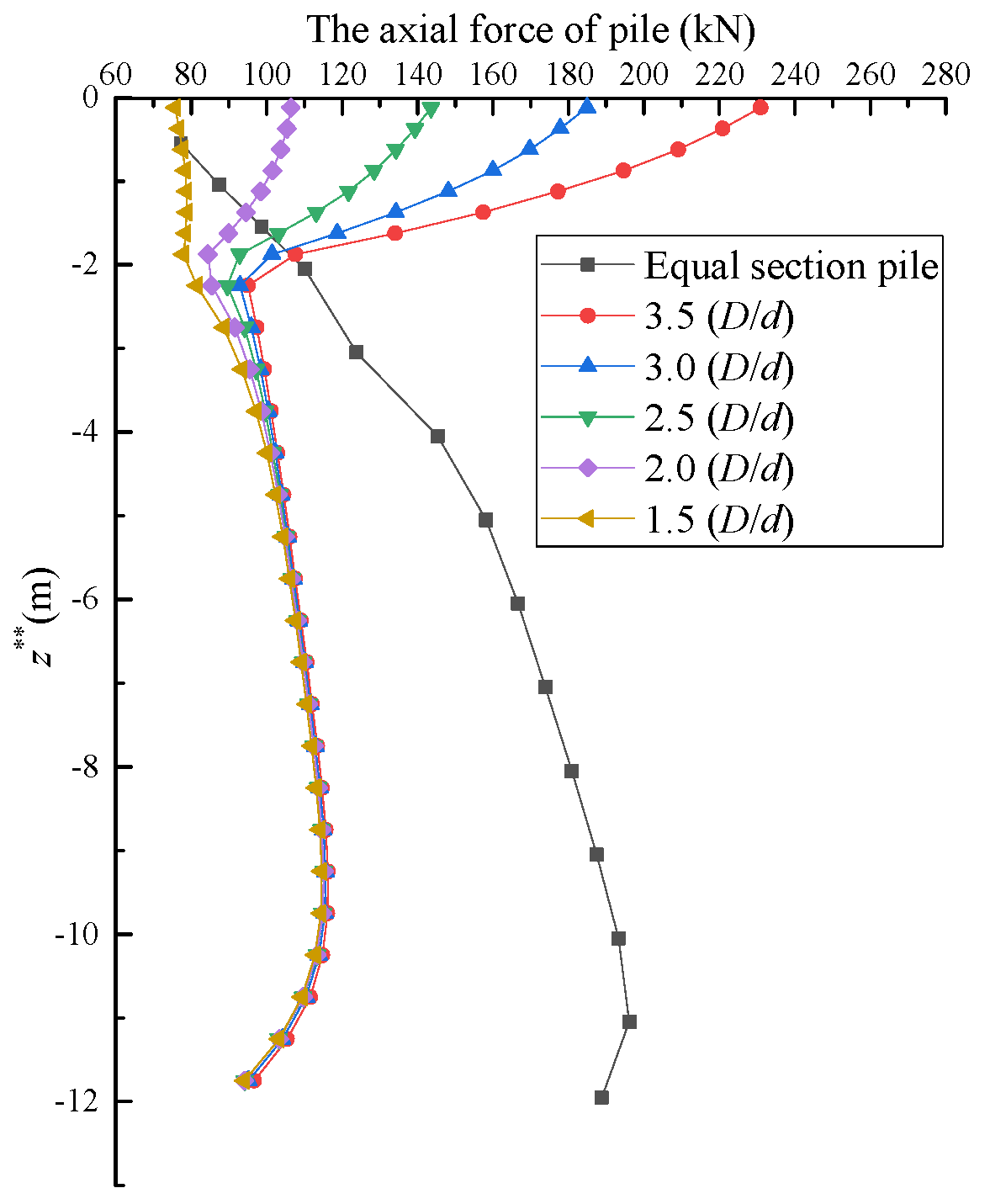
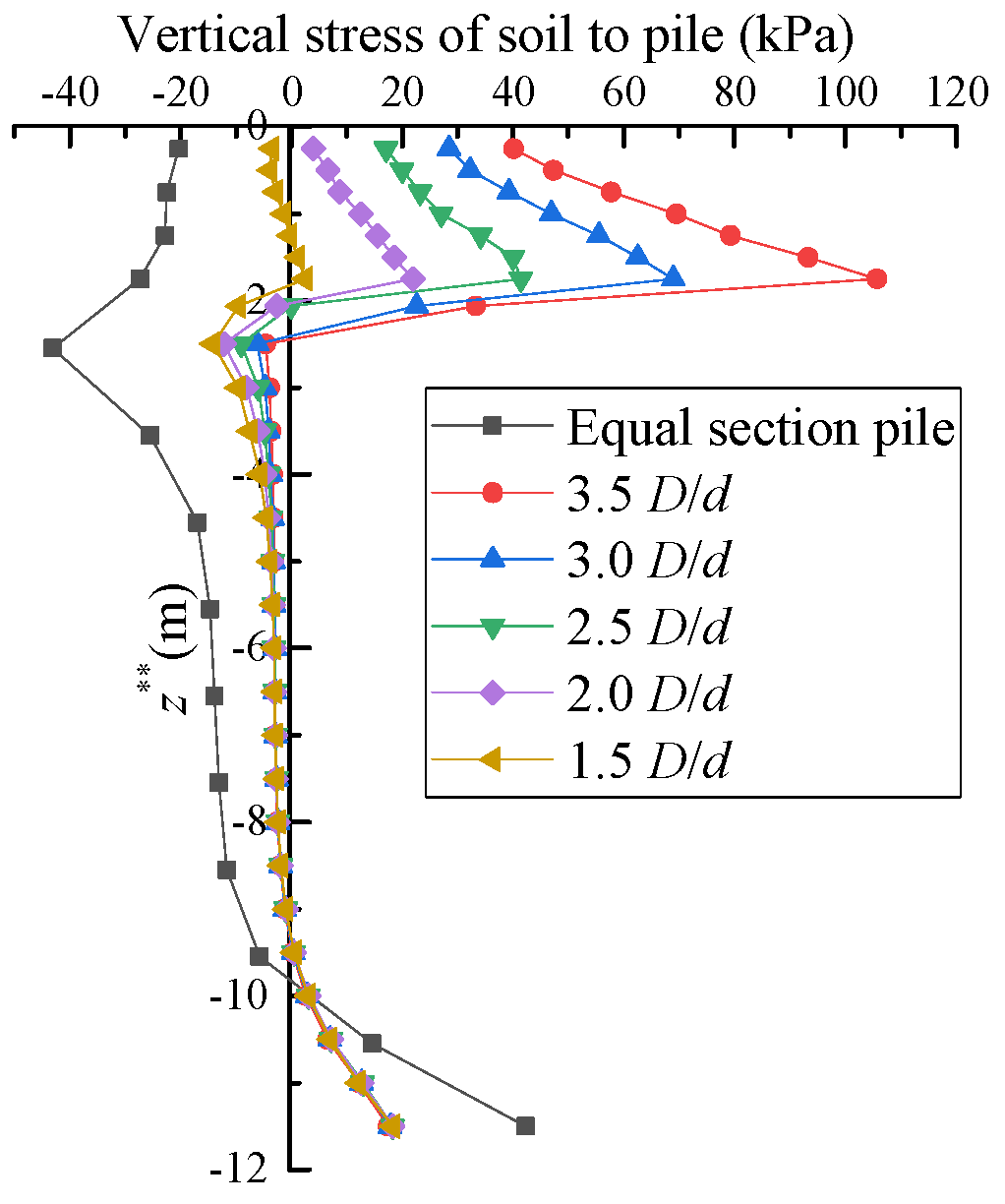
4. Parametric Studies
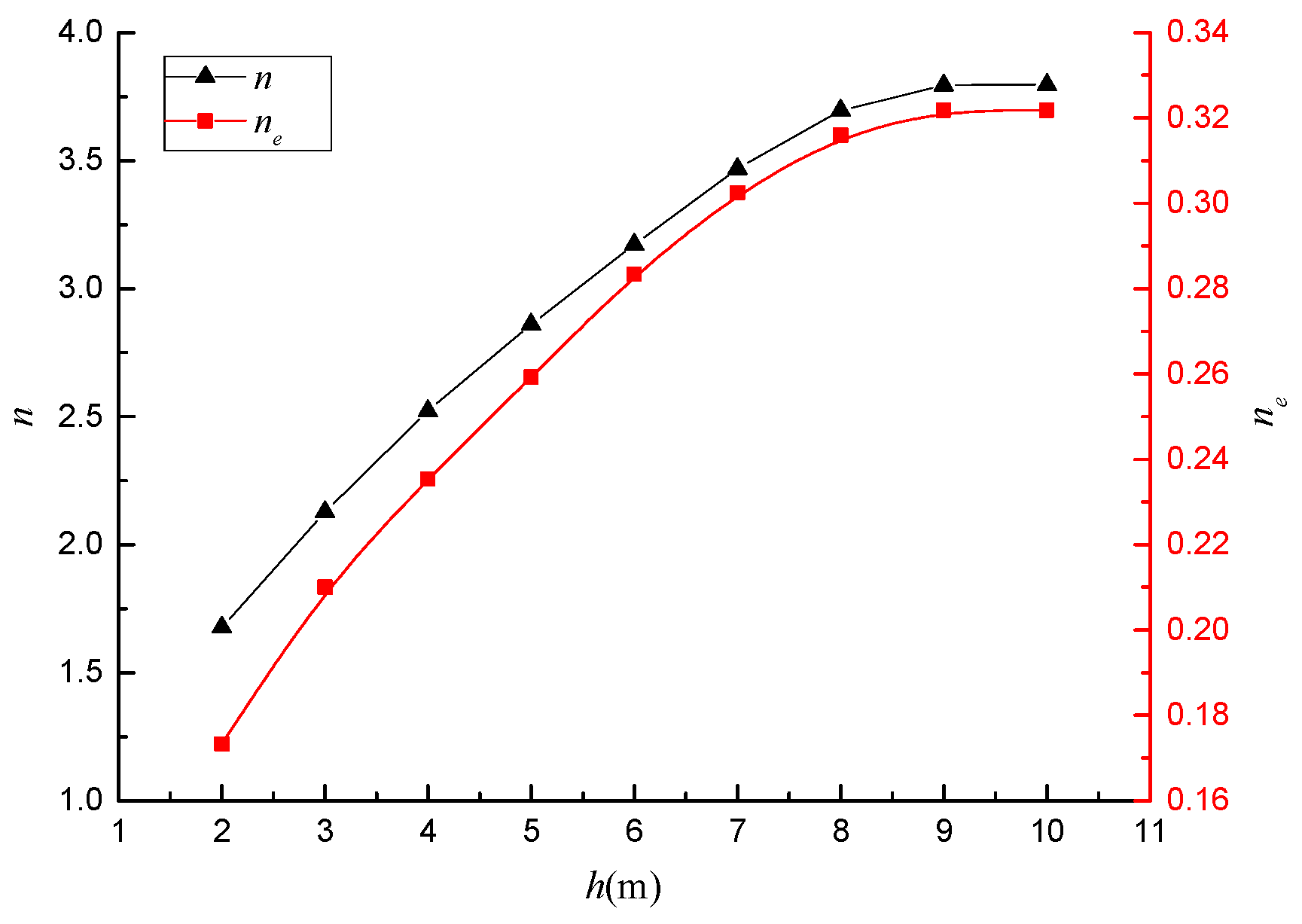
4.1. Effect of the Embankment Height (h)
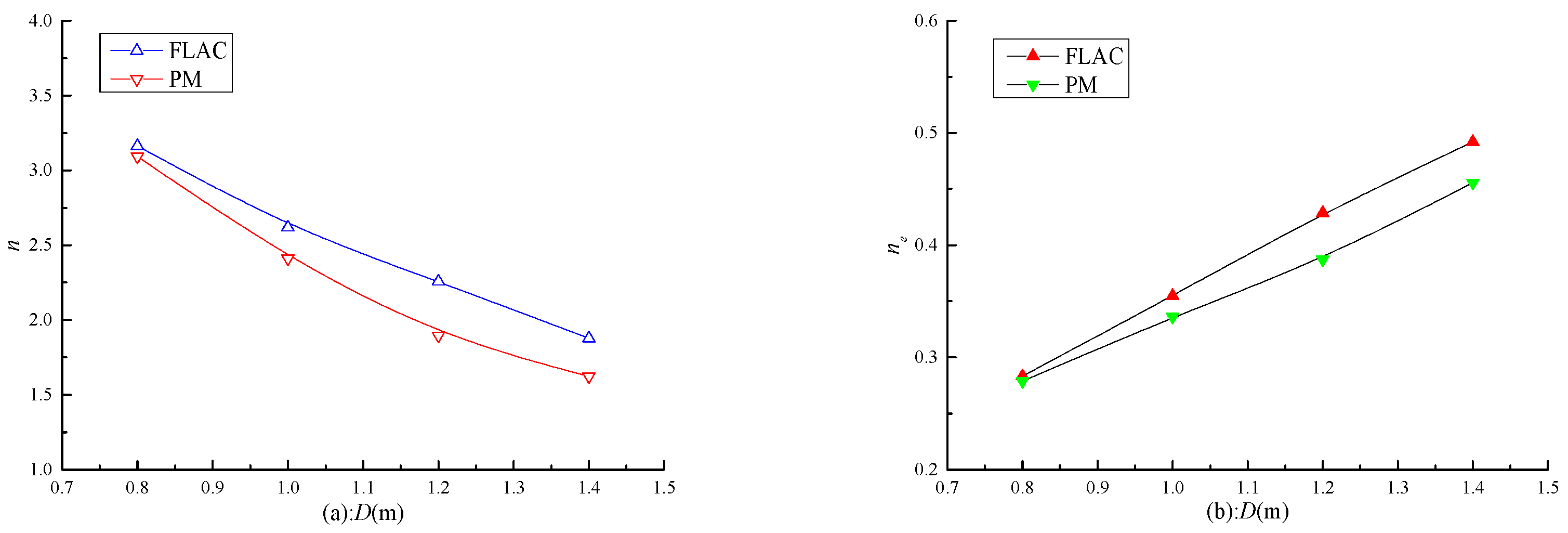
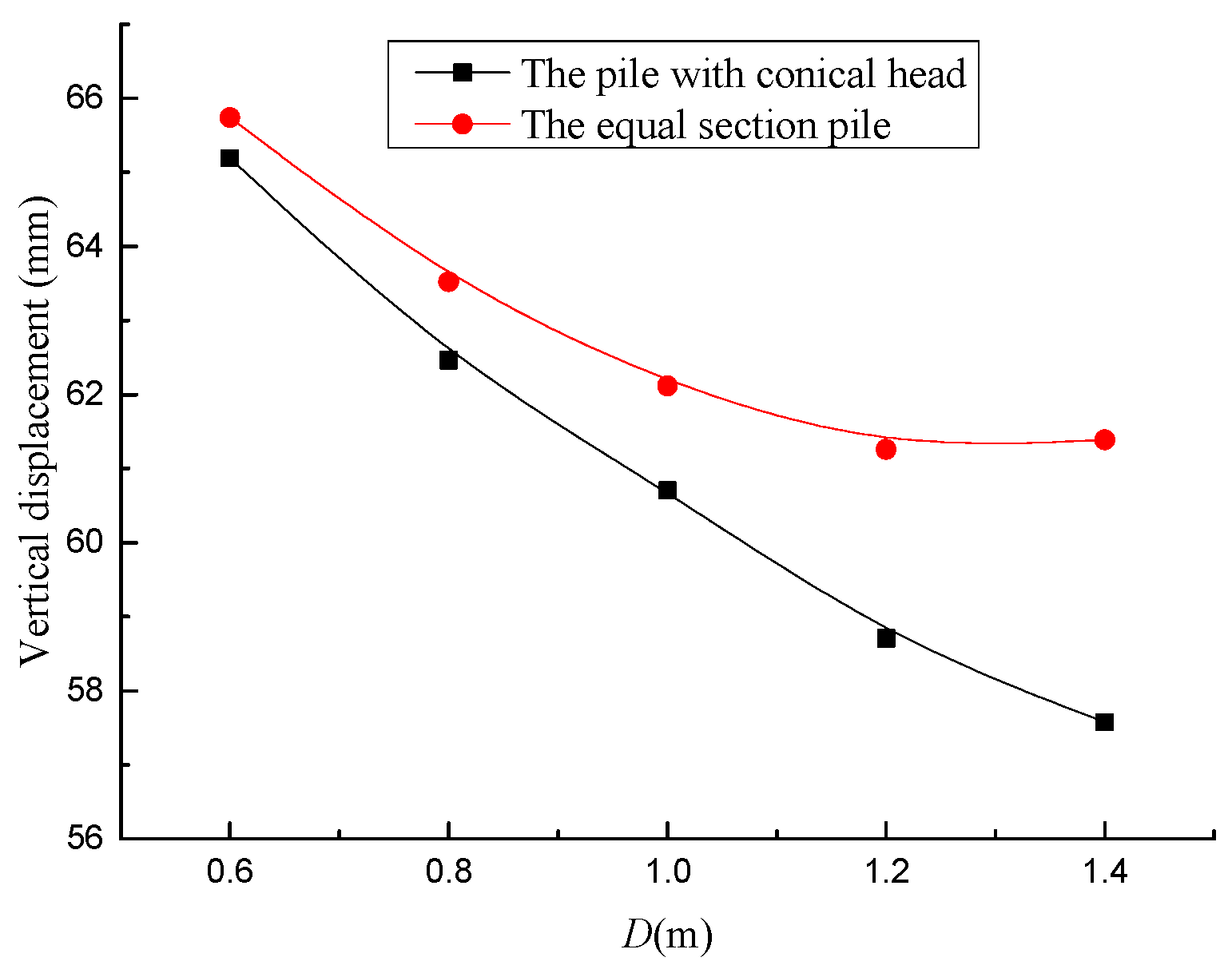
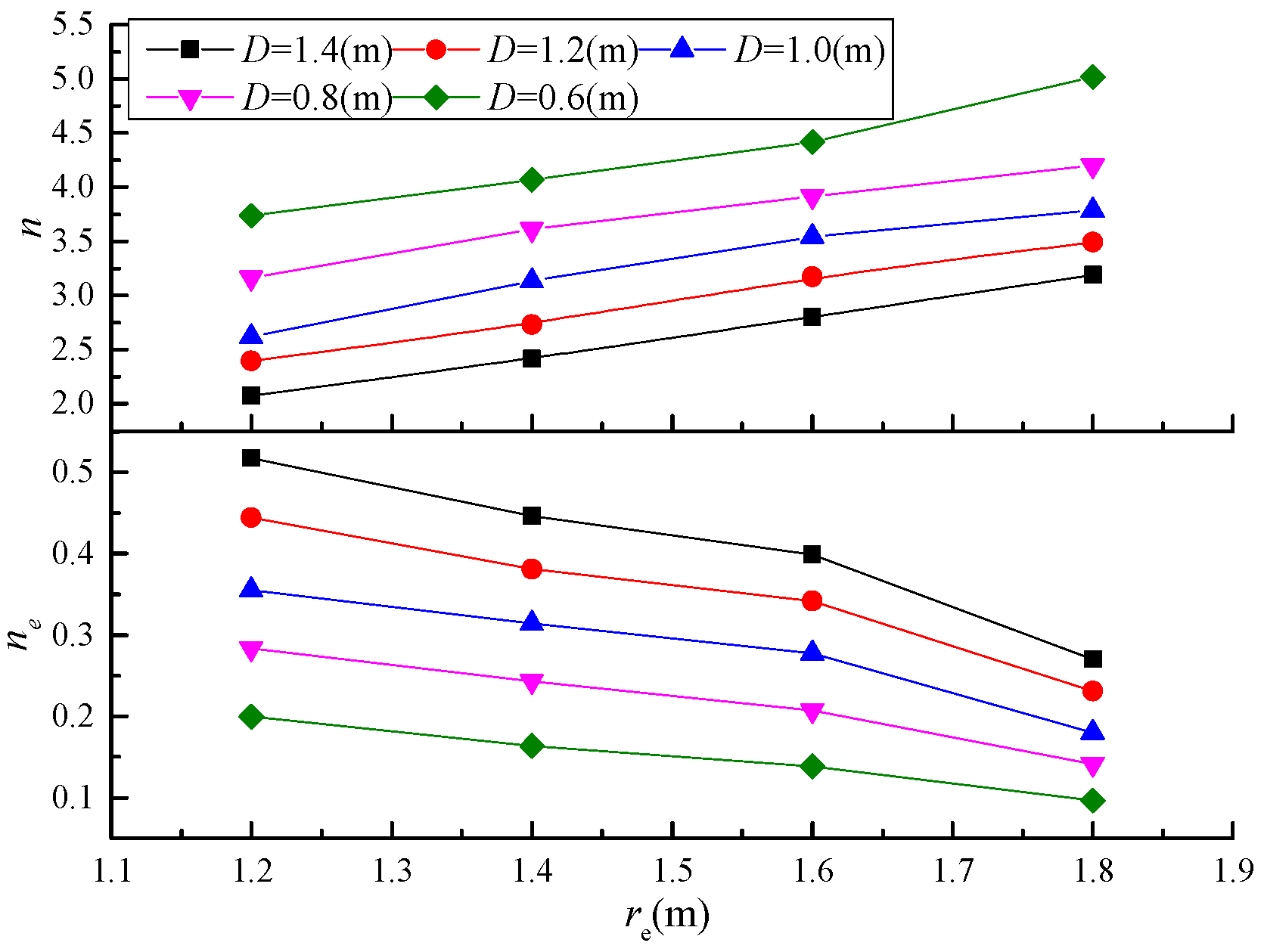
4.2. Effect of the Maximum Diameter of the Conical Head (D)
4.3. Effect of the Effective Reinforcement Radius of the Pile(re)
5. Conclusions
- The conical head converts a portion of the vertical load into a horizontal load and transmits it into the uppermost crust or artificial working platform, which helps to elevate the position of the neutral point and reduce the settlement of the embankment;
- When the height of the embankment is greater than that of the plane of equal settlement, increasing the height of the embankment has little benefit to the load sharing ratio;
- Not all of the fill load above the plane of equal settlement is transmitted to the pile through the soil arch but is assigned to the pile and soil according to the load sharing ratio.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- King, D.J.; Bouazza, A.; Gniel, J.R.; Rowe, R.K.; Bui, H.H. Serviceability design for geosynthetic reinforced column supported embankments. Geotext. Geomembr. 2017, 45, 261–279. [Google Scholar] [CrossRef]
- Briançon, L.; Simon, B.; Auray, G. Pile-supported embankment over soft soil for a high-speed line. Geosynth. Int. 2017, 24, 293–305. [Google Scholar] [CrossRef]
- Yu, Y.; Bathurst, R.J.; Damians, I.P. Modified unit cell approach for modelling geosynthetic-reinforced column-supported embankments. Geotext. Geomembr. 2016, 44, 332–343. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, G.; Liu, X.; Buzzi, O. Arching in geogrid-reinforced pile-supported embankments over silty clay of medium compressibility: Field data and analytical solution. Geotext. Geomembr. 2016, 77, 11–25. [Google Scholar] [CrossRef]
- Zhou, W.-H.; Lok, T.M.-H.; Zhao, L.-S.; Mei, G.-X.; Li, X.-B. Analytical solutions to the axisymmetric consolidation of a multi-layer soil system under surcharge combined with vacuum preloading. Geotext. Geomembr. 2017, 45, 487–498. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, S.; Zhao, H.; Deng, Y. Performance of Geosynthetic-Reinforced and Pile-Supported Embankment with Consideration of Soil Arching. J. Eng. Mech. 2018, 144, 06018005. [Google Scholar] [CrossRef]
- Pham, H.V.; Dias, D. 3D Numerical Modeling of a Piled Embankment under Cyclic Loading. Int. J. Geomech. 2019, 19, 04019010. [Google Scholar] [CrossRef]
- Van Eekelen, S.J.M.; Bezuijen, A.; Van Tol, A.F. An analytical model for arching in piled embankments. Geotext. Geomembr. 2013, 39, 78–102. [Google Scholar] [CrossRef]
- Lu, W.; Miao, L. A simplified 2-D evaluation method of the arching effect for geosynthetic-reinforced and pile-supported embankments. Comput. Geotech. 2015, 65, 97–103. [Google Scholar] [CrossRef]
- Gallant, A.P.; Shatnawi, E.; Farouz, E.; Jones, T. A Case Study of Settlement and Load Transfer at Depth Beneath Column-Supported Embankments in IFCEE 2018; American society of Civil Engineers: Orlando, FL, USA, 2018. [Google Scholar] [CrossRef]
- Robinsky, E.I.; Mnorrison, C.F. Sand displacement and complaction around model friction piles. Can. Geotech. J. 1964, 1, 81–93. [Google Scholar] [CrossRef]
- Zil’Berberg, S.D.; Sherstnev, A.D. Construction of compaction tapered pile foundations (from the experience of the “Vladspetsstroi” trust). Soil Mech. Found. Eng. 1990, 27, 96–101. [Google Scholar] [CrossRef]
- Ladanyi, B.; Guichaoua, A. Bearing capacity and settlement of shaped piles in permafrost. In Proceedings of the Eleventh International Conference on Soil Mechanics and Foundation Engineering, San Francisco, CA, USA, 12–16 August 1985; pp. 1421–1427. [Google Scholar]
- Sawaguchi, M. Model tests in relation to a method to reduce negative skin friction by tapering a pile. Soils Found. 1982, 22, 130–133. [Google Scholar] [CrossRef]
- Dias, D. Numerical modelling of a Pile-Supported Embankment using variable inertia piles. Struct. Eng. Mech. 2017, 61, 245–253. [Google Scholar] [CrossRef]
- Lai, H.-J.; Zheng, J.-J.; Zhang, R.-J.; Cui, M.-J. Classification and characteristics of soil arching structures in pile-supported embankments. Comput. Geotech. 2018, 98, 153–171. [Google Scholar] [CrossRef]
- Collin, J.G.; Watson, C.H.; Han, J. Column-supported embankment solves time constraint for new road construction. ASCE Geotech. Spec. Publ. 2005, 131, 1–10. [Google Scholar]
- Carlsson, B. Reinforced Soil, Principles for Calculation; Terratema AB: Link-öping, Terranova, Sweden, 1987. [Google Scholar]
- Guido, V.A.; Knueppel, J.D.; Sweeney, M.A. Plate loading test on geogrid reinforced earth slabs. In Proceedings of the Geosynthetics’87 Conference, New Orleans, LA, USA, 24–25 February 1987; pp. 216–225. [Google Scholar]
- Rogbeck, Y.; Gustavsson, S.; Södergren, I.; Lindquist, D. Reinforced piled embankments in Sweden e design aspects. In Proceedings of the Sixth International Conference on Geosynthetics, Atlanta, GA, USA, 25–29 March 1998; pp. 755–764. [Google Scholar]
- Van Eekelen, S.J.M.; Bezuijen, A.; Van Tol, A.F. An analytical model for arching in piled embankments. Geotext. Geomembr. 2013, 39, 78–102. [Google Scholar] [CrossRef]
- Hewlett, W.J.; Randolph, M.F. Analysis of piled embankments. Ground Eng. 1988, 21, 12–18. [Google Scholar]
- Chen, R.P.; Chen, Y.M.; Han, J.; Xu, Z.Z. A theoretical solution for pile-supported embankments on soft soils under one-dimensional compression. Can. Geotech. J. 2008, 45, 611–623. [Google Scholar] [CrossRef]
- Iii, M.K. The anatomy of soil arching. Geotext. Geomembr. 1994, 13, 317–329. [Google Scholar]
- Russell, D.; Pierpoint, N. An assessment of design methods for piled embankments. Ground Eng. 1997, 30, 39–44. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1943. [Google Scholar]
- Balaam, N.P.; Poulos, H.G.; Brown, P.T. Settlement analysis of soft clays reinforced with granular piles. In Proceedings of the 5th Asian Regional Conf., Bangkok, Thailand, 2–4 July 1997; Volume 1, pp. 81–92. [Google Scholar]
- Alamgir, M.; Miura, N.; Poorooshasb, H.B.; Madhav, M.R. Deformation analysis of soft ground reinforced by columnar inclusions. Comput. Geotech. 1996, 18, 267–290. [Google Scholar] [CrossRef]
- Zhao, L.-S.; Zhou, W.-H.; Yuen, K.-V. A simplified axisymmetric model for column supported embankment systems. Comput. Geotech. 2017, 92, 96–107. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, C.; Gao, Y.; Kodikara, J. Effect of 2D spatial variability on slope reliability: a simplified FORM analysis. Geosci. Front. 2018, 9, 1631–1638. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, C.; Gao, Y.; Kodikara, J. Reliability-based design for geotechnical engineering: An inverse FORM approach for practice. Comput. Geotech. 2019, 111, 22–29. [Google Scholar] [CrossRef]
- Zhang, F.; Gao, Y.F.; Wu, Y.X.; Zhang, N. Upper-bound solutions for face stability of circular tunnels in undrained clays. Geotechnique 2018, 68, 76–85. [Google Scholar] [CrossRef]
- Randolph, M.F. Analysis of deformation of vertical loaded piles. J. Geotech. Geoenvironmental Eng. 1978, 104, 1465–1488. [Google Scholar]
- Giroud, J.P.; Bonaparte, R.; Beech, J.F.; Gross, B.A. Design of Soil Layer-Geosynthetic Systems Overlying. Geotext. Geomembr. 1990, 9, 11–50. [Google Scholar] [CrossRef]
- Chen, Y.M.; Xu, D.P. FLAC/FLAC3D Foundation and Engineering Examples; China Water Power Press: Beijing, China, 2013. [Google Scholar]
- Cao, W.P.; Chen, R.P.; Chen, Y.M. Experimental investigation on soil arching in piled reinforced embankments. Chin. J. Geotech. Eng. 2007, 29, 436–441. [Google Scholar]
- Zhuang, Y.; Wang, K.Y. Finite-Element Analysis on the Effect of Subsoil in Reinforced Piled Embankments and Comparison with Theoretical Method Predictions. Int. J. Geomech. 2016, 16, 04016011. [Google Scholar] [CrossRef]
- Girout, R.; Blanc, M.; Thorel, L.; Dias, D. Geosynthetic reinforcement of pile-supported embankments. Geosynth. Int. 2018, 25, 1–13. [Google Scholar] [CrossRef]
- Eskişar, T.; Otani, J.; Hironaka, J. Visualization of soil arching on reinforced embankment with rigid pile foundation using X-ray CT. Geotext. Geomembr. 2012, 32, 44–54. [Google Scholar] [CrossRef]

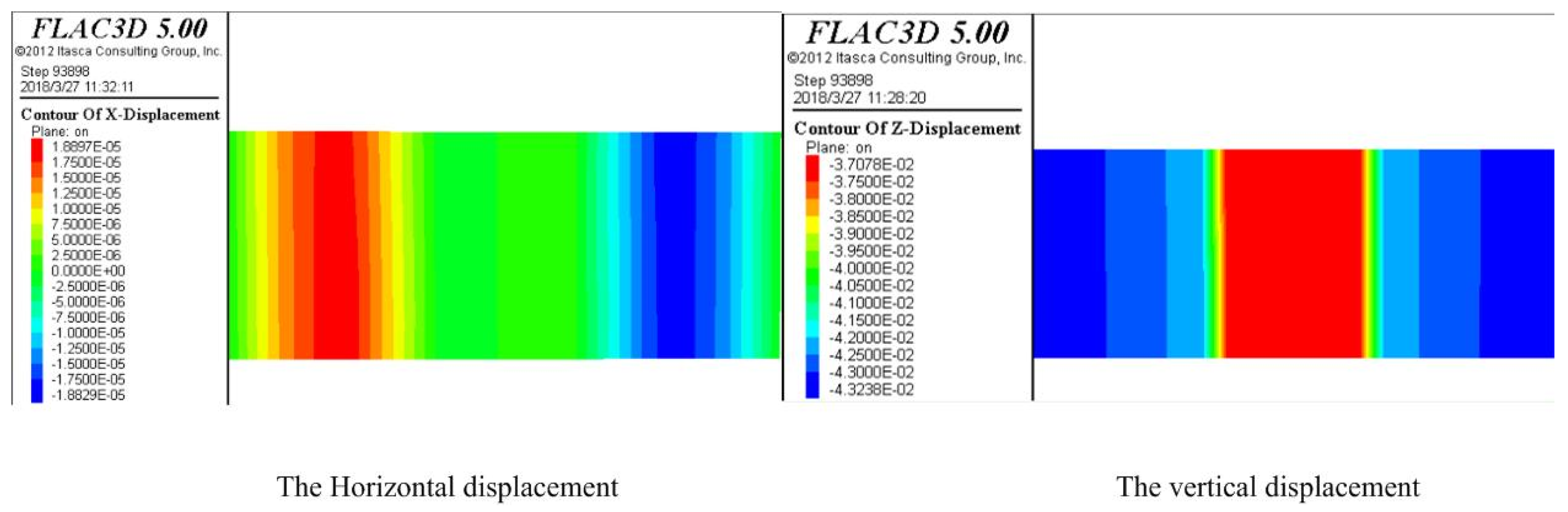

| Items | Embankment | Soft Soil | Firm Soil | Working Platform | Pile |
|---|---|---|---|---|---|
| Height (m) | 6 | 10 | 6 | 2 | 12 |
| Young’s modulus (MPa) | 30 | 7 | 48 | 15 | 30000 |
| Poisson’s ratio | 0.25 | 0.25 | 0.35 | 0.25 | 0.15 |
| Cohesion (kPa) | 0 | 15 | 30 | 10 | - |
| Friction angle (°) | 30 | 9 | 22 | 35 | - |
| Density (kg/m3) | 2000 | 1750 | 1750 | 2000 | 2500 |
| Items | Embankment | Soft Soil | Firm Soil | Cap | Pile |
|---|---|---|---|---|---|
| Height (m) | 4 | 25 | 6 | 0.35 | 20 |
| Friction angle (°) | 30 | ||||
| Effective friction angle (°) | 9 | 22 | |||
| Cohesion (kPa) | 0 | ||||
| Effective Cohesion (kPa) | 15 | 30 | |||
| Young’s modulus (MPa) | 30 | 35 | 35 | ||
| Constrained modulus (MPa) | 2.2 | 15 | |||
| Poisson’s ratio | 0.25 | 0.35 | 0.35 | 0.15 | 0.15 |
| Density (kg/m3) | 2000 | 2500 | 2500 | ||
| Saturated unit weight (kN/m3) | 17.5 | 18 | |||
| Pile spacing (m) | 1 | 2.5 | |||
| Diameter (m) | 1.13 | 0.4 |
| Pile Diameter (m) | Pile Volume (m3) | Settlement (mm) | Percentage of Material Consumption | |||
|---|---|---|---|---|---|---|
| D | d | Pile with the Conical Head | Equal Section Pile | Pile with the Conical Head | Equal Section Pile | |
| 0.6 | 0.4 | 1.65 | 3.39 | 65.19 | 65.74 | 51.30% |
| 0.8 | 0.4 | 1.84 | 6.03 | 62.46 | 63.52 | 69.40% |
| 1 | 0.4 | 2.07 | 9.42 | 60.71 | 62.12 | 78% |
| 1.2 | 0.4 | 2.34 | 13.6 | 58.71 | 61.23 | 82.70% |
| 1.4 | 0.4 | 2.66 | 18.5 | 56.37 | 61.39 | 85.60% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Zhao, M.; Zhou, S.; Xu, Z. A Theoretical Solution for Pile-Supported Embankment with a Conical Pile-Head. Appl. Sci. 2019, 9, 2658. https://doi.org/10.3390/app9132658
Zhang C, Zhao M, Zhou S, Xu Z. A Theoretical Solution for Pile-Supported Embankment with a Conical Pile-Head. Applied Sciences. 2019; 9(13):2658. https://doi.org/10.3390/app9132658
Chicago/Turabian StyleZhang, Chengfu, Minghua Zhao, Shuai Zhou, and Zeyu Xu. 2019. "A Theoretical Solution for Pile-Supported Embankment with a Conical Pile-Head" Applied Sciences 9, no. 13: 2658. https://doi.org/10.3390/app9132658
APA StyleZhang, C., Zhao, M., Zhou, S., & Xu, Z. (2019). A Theoretical Solution for Pile-Supported Embankment with a Conical Pile-Head. Applied Sciences, 9(13), 2658. https://doi.org/10.3390/app9132658




