Modeling of Fatigue-Strength Development in Cold-Emulsion Asphalt Mixtures Using Maturity Method

Abstract

Emulsion asphalts are cost-effective, environmentally friendly, and sustainable alternatives to hot-mix asphalts. Laboratory curing protocols currently used to simulate field curing of emulsion asphalts have been observed to offer conflicting predictions. This study employed the maturity method to account for the combined effects of temperature and time on fatigue-strength development in emulsion asphalts. An emulsion asphalt, composed of 55% reclaimed asphalt pavement, 45% virgin aggregates, 6.2% bitumen emulsion, and 4% pre-mix water was designed following the Asphalt Institute procedure. A total of 168 specimens from the mix were variously cured at 5 °C, 25 °C, 40 °C, and 50 °C for time intervals of 1, 3, 5, 7, 14, 21, and 28 days, before being tested for fatigue-strengths on the four-point bending test jig. It was observed that fatigue-strengths increased with an increase in cure temperature but decreased with an increase in cure duration. A parabolic hyperbolic fatigue-maturity model was developed from results of specimens cured at 5 °C, 25 °C, and 40 °C and validated with results from specimens cured at 50 °C. A strong correlation was observed between predicted fatigue-maturity and laboratory-determined fatigue-strengths at test strain levels between 125 µm/m and 200 µm/m. The study concluded that the laboratory characterization of emulsion asphalts should consider the curing history of the mix.

1. Introduction

1.1. Background

Flexible roads, around the globe, are predominantly paved with hot-mix asphalt (HMA). Production of hot-mix asphalts involves batching of virgin stone aggregates with penetration grade bitumen at elevated temperatures. The batching process consumes huge amounts of energy and generates toxic fumes from the oxidation of bitumen. Sustainable construction practices demand that materials for road construction purposes be obtained from environmentally friendly and sustainable sources [1]. This calls for exploration of construction materials and technologies that exert less pressure on sources of virgin aggregates and fossil fuel. Cold-mix asphalts (CMA) are alternative asphaltic materials that utilize emulsified or foamed bitumen binders in place of penetration grade bitumen. Compared to hot-mix asphalts, cold-mix asphalts are more energy efficient, cheaper, and environmentally friendly [2,3,4]. Since they are laid at ambient temperatures, they are well suited for small works, as well as works in remote places, where hot-mix asphalt batching plants may not be accessible. Incorporation of marginal aggregates, such as reclaimed asphalt pavement and demolition wastes, into cold-mix asphalts, will further reduce costs of disposal to landfills and the cost of sourcing bitumen and virgin aggregates [5,6,7,8].

In spite of the numerous positive attributes of cold-mix asphalts, characterization of their engineering properties remains a chief hindrance to their acceptance as suitable alternatives to hot-mix asphalts [9]. Whereas hot-mix asphalts attain their ultimate engineering properties immediately after batching and compaction, foamed and emulsion bitumen asphalts require time for the foaming, or emulsification water, to evaporate before bitumen can coalesce and bind the aggregates. Due to the presence of water in their matrices, cold-mix asphalts behave more like improved granular materials in the early stages of their lives but eventually attain properties similar to those of hot-mix asphalts once all the foaming, or emulsification water, is lost through evaporation [10,11]. The ultimate engineering properties of cold-mix asphalts are attained after months, or even years, of field curing. To characterize cold-mix asphalts using methods traditionally developed for hot-mix asphalts, agencies, and institutions have proposed accelerated laboratory curing protocols to simulate field curing and strength development in cold-mix asphalt.

The literature is replete with laboratory curing protocols utilized, across the globe, to simulate field curing of cold-mix asphalt. Generally, curing temperatures ranging between 5 °C and 60 °C and curing durations ranging between 3 and 28 days are widely used [12]. Curing at 60 °C for 3 days, a protocol proposed by Bowering [13], and curing at 40 °C for 3 days, a protocol proposed by Ruckel et al. [14], are the most popular of the laboratory curing protocols. Prediction discrepancies among laboratory curing protocols is a major impediment to the adequate characterization of cold-mix asphalt. Curing at 60 °C for 3 days, for instance, has been used to variously represent early life curing [15], curing during construction [16,17], field cure of between 23 and 200 days [16,18], and 1 year of field cure [19]. Similarly, curing at 40 °C for 3 days has been used to variously simulate 1 month of field cure [14] and 6 months of field cure [20,21]. Besides these prediction discrepancies, the curing protocols in existence are region-specific and may, therefore, not allow for universal comparison of results on cold-mix asphalt behavior [9,22,23]. Furthermore, it has been noted that cold-mix asphalts cured at higher temperatures attain superior engineering qualities than those cured at lower temperatures [10,24,25]. These inconsistencies render the existing laboratory curing protocols quite unreliable in the prediction of field performance of cold-mix asphalt.

Harmonization of laboratory curing protocols has been identified in the recent past as a priority research area for cold-mix asphalts [12,23]. The numerous protocols need to be brought to concurrence through the adoption of characterization procedures that consider the combined effects of cure temperature and cure duration. Determination of cold-mix asphalt properties at the end of the curing period, as is done in most of the existing protocols, ignores the dependence of strength gain in cold-mix asphalts on both cure temperature and cure duration [10,26]. The maturity method, a concept borrowed from concrete technology, has recently been used to study stiffness development in both emulsion and foamed asphalt mixtures [27,28,29]. Asphalt stiffness, resistance to rutting and resistance to fatigue cracking are key inputs in the mechanistic-empirical asphalt pavement design process [30,31,32,33,34]. Fatigue characterization of cold-mix asphalt mixtures is a subject of current research in the field of pavement materials. Extensive literature review done at the beginning of the project on “Characterization of Advanced Cold Recycling Bitumen Pavement Solutions” (CoRePaSol) noted that fatigue phenomenon in cold-emulsion asphalt mixtures, especially those incorporating reclaimed asphalt pavement, has received limited attention from researchers [35]. It is imperative, therefore, that an approach that takes into consideration the combined effects of cure temperature and cure duration on fatigue-strength development in cold-emulsion reclaimed asphalt pavement mixtures be explored.

This research, therefore, endeavored to develop a fatigue-strength prediction model using the maturity method and asphalt fatigue-strength results obtained from four-point bending (4PB) fatigue tests. Hyperbolic maturity functions, previously used to study stiffness in cold-asphalt mixtures [27,28,29], were modified and used to study temperature and time effects on fatigue-strength development in a cold-emulsion asphalt mix incorporating reclaimed asphalt pavement. The maturity function developed in this study will allow fatigue strengths of cold-mix asphalts cured under the different existing curing protocols to be compared, provided their curing histories are known. This will, in turn, build confidence in the use of cold-mix asphalts as feasible alternatives to hot-mix asphalt.

1.2. The Maturity Method

The maturity method is a concept applied in concrete technology to account for the combined effects of cure time and cure temperature on strength development of cement concrete [36]. The method is attributed to Nurse [37], who used it to study accelerated steam curing of commercial concrete. The method has, over the years, been used to estimate the minimum waiting times before removal of formwork from concrete structural elements, opening of concrete pavement sections to traffic, sawing of joints in concrete structural elements, and post-tensioning of concrete structural elements [38]. In the recent past, the maturity method has been used to model the combined effects of cure temperature and cure time on stiffness development in cold-mix asphalts [27,28,39]. Strength development of cold-mix asphalts is closely related to that of conventional cement concrete. Whereas the conventional cement concrete requires hydration water for strength development, cold-mix asphalts need to lose emulsification, or foaming, water for the base bitumen binder to come into contact with the aggregates. In both instances, strength development is temperature and time-dependent [40]. The maturity approach reckons that samples of concrete from the same batch will, at the same maturity, have approximately the same strength regardless of the cure temperature and cure time combinations. The strength-maturity function of a given batch of concrete is developed from strength values of specimens cured for varied time intervals at three isothermal temperatures.

1.2.1. Maturity Functions

The Nurse–Saul and the Arrhenius maturity functions are two models that are popularly used to compute maturity indices of concrete [41]. Nurse–Saul maturity function computes the maturity index of a concrete sample as the product of its cure temperature and the cure duration [42]. Despite its simplicity in application, Nurse–Saul maturity function has the limitation of assuming concrete maturity to be a linear function of temperature. Previous research has proved that the maturity temperature relationship is more exponential than it is linear [43]. The Nurse–Saul maturity function is given by Equation (1).

$$\mathrm{M}={\displaystyle \sum _{\mathrm{o}}^{\mathrm{t}}}(\mathrm{T}-{\mathrm{T}}_{\mathrm{o}})\times \Delta \mathrm{t}$$

(1)

where,

• $\mathrm{M}$ = Maturity index at age t, (°C·hours or °C·days)
• $\mathrm{T}$ = Average concrete temperature during the time interval $\Delta \mathrm{t}$ (°C)
• ${\mathrm{T}}_{\mathrm{o}}$ = Datum temperature, the temperature below which no curing occurs (°C)
• $\mathrm{t}$ = Elapsed time (hours or days)
• $\Delta \mathrm{t}$ = Time interval (hours or days)

The Arrhenius maturity function, Equation (2), was proposed by Freiesleben and Pedersen [44], to address the non-linear relationship between the rate of initial strength gain and cure temperature in concrete strength-age functions [45].

$${\mathrm{t}}_{\mathrm{e}}={\displaystyle \sum _0^{\mathrm{t}}}\left\{{\mathrm{e}}^{\frac{-\mathrm{E}}{\mathrm{R}}\left(\frac{1}{273+\mathrm{T}}-\frac{1}{273+{\mathrm{T}}_{\mathrm{r}}}\right)}\right\}\times \Delta \mathrm{t}$$

(2)

where,

• ${\mathrm{t}}_{\mathrm{e}}$ = The equivalent age at the reference curing temperature (hours or days)
• E = The apparent activation energy, characterizing temperature sensitivity of the mix (J/mol)
• $\mathrm{R}$ = The universal gas constant, 8.314 (J/mol-K)
• $\mathrm{T}$ = The average temperature of the concrete during interval Δt, (°C)
• ${\mathrm{T}}_{\mathrm{r}}$ = The reference temperature (20 °C in Europe and 23 °C in North America)
• $\Delta \mathrm{t}$ = Time interval (hours or days)

The equivalent age represents the curing period, at a chosen reference temperature, that would yield concrete maturity equivalent to that which would be attained by curing at the actual concrete temperature.

1.2.2. Effects of Temperature on Concrete Strength Development

The apparent activation energy, denoted as E in Equation (2), defines the dependence of the rate of concrete strength development on the cure temperature. Noting the challenge associated with accurate determination of the activation energy for the equivalent age function, Carino and Tank [46], proposed its replacement with the rate constant, k, which is given by the initial slope of the strength versus cure duration plots for concrete samples cured at isothermal temperature conditions. The simplified exponential relationship, Equation (3), describes the variation of the rate constant with cure temperature.

$$\mathrm{k}={\mathrm{A}}_{\mathrm{o}}{\mathrm{e}}^{\mathrm{BT}}$$

(3)

where,

• $\mathrm{k}$ = Rate constant, the initial slope of strength versus duration curve (1/days)
• ${\mathrm{A}}_{\mathrm{o}}$ = The value of the rate constant at 0 °C (1/days)
• $\mathrm{B}$ = The temperature sensitivity factor, (1/°C)
• $\mathrm{T}$ = Concrete temperature (°C)

In Equation (3), the temperature sensitivity factor, B, indicates the effects of the cure temperature on the rate constant and, by extension, the effect of temperature on the rate of strength gain at variable cure temperature conditions. The temperature sensitivity factor for a particular batch of concrete is determined by fitting the simplified exponential function, Equation (3), to the plot of the rate constant versus the cure temperatures. Replacement of the activation energy with the rate constant in the Arrhenius maturity function, Equation (2), yielded the simplified exponential maturity function presented as Equation (4).

$${\mathrm{t}}_{\mathrm{e}}={\displaystyle \sum _0^{\mathrm{t}}}\propto \times \Delta \mathrm{t}$$

(4)

where,

• ${\mathrm{t}}_{\mathrm{e}}$ = The equivalent age at the reference temperature (hours or days)
• $\propto$ = Age conversion factor, given as ${\mathrm{e}}^{\mathrm{B}(\mathrm{T}-{\mathrm{T}}_{\mathrm{r}})}$
• $\mathrm{B}$ = The temperature sensitivity factor, (1/°C)
• $\mathrm{T}$ = Average concrete temperature during time interval, $\Delta \mathrm{t}$ (°C)
• ${\mathrm{T}}_{\mathrm{r}}$ = The reference temperature, (20 °C in Europe and 23 °C in North America)
• $\Delta \mathrm{t}$ = Time interval (hours or days)

The age conversion factor in Equation (4) defines the temperature sensitivity of the maturity function [46]. In a study of stiffness development in a foamed bitumen asphalt, Kuna et al. [47], observed that at the same equivalent age, foamed bitumen asphalt samples cured variously at 5 °C, 20 °C, and 40 °C had different stiffness values. This observation defies the traditional definition of maturity, which anticipates concrete with the same equivalent age to have the same stiffness values regardless of the cure histories. To address this shortcoming in the equivalent age method, Kuna et al. [47] proposed the modification of Equation (4) by the introduction of cure temperature into it. This modification was guided by an observation that the ultimate stiffness of the foamed bitumen asphalt had an almost linear relationship with the cure temperature. The modification yielded a new maturity index given by Equation (5).

$$\mathrm{M}={\displaystyle \sum _0^{\mathrm{t}}}\propto \times \Delta \mathrm{t}\times \mathrm{T}$$

(5)

where,

• $\mathrm{M}$ = Maturity index at age t (°C·hours or °C·days)
• $\propto$ = Age conversion factor, given as ${\mathrm{e}}^{\mathrm{B}(\mathrm{T}-{\mathrm{T}}_{\mathrm{r}})}$
• $\mathrm{B}$ = The temperature sensitivity factor, (1/°C)
• $\mathrm{T}$ = Average concrete temperature during time interval, $\Delta \mathrm{t}$ (°C)
• ${\mathrm{T}}_{\mathrm{r}}$ = The reference temperature, (20 °C in Europe and 23 °C in North America)
• $\Delta \mathrm{t}$ = Time interval (hours or days)

1.2.3. Strength-Maturity Relationships

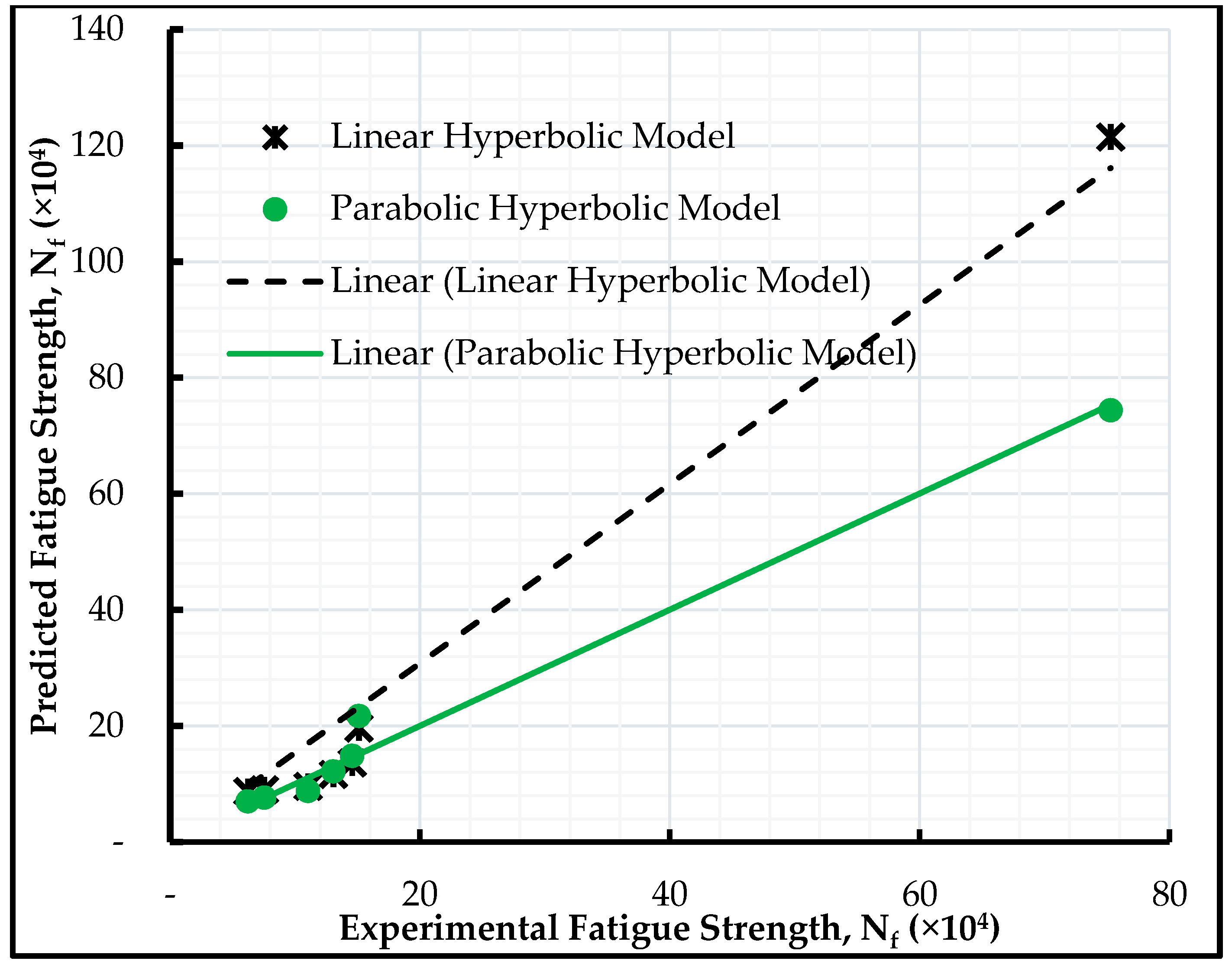
The relationship between concrete strength development and maturity has been described using logarithmic [48], linear hyperbolic [49], parabolic hyperbolic [50], and exponential maturity functions [51]. Recent studies on foamed and emulsion bitumen asphalts have found out that linear hyperbolic and parabolic hyperbolic maturity functions offer the best prediction of stiffness development in cold-mix asphalts [28,39]. The linear hyperbolic and parabolic hyperbolic maturity functions are given by Equations (6) and (7), respectively.

$$\mathrm{S}={\mathrm{S}}_{\mathrm{u}}\frac{\mathrm{k}(\mathrm{M}-{\mathrm{M}}_{\mathrm{o}})}{1+\mathrm{k}(\mathrm{M}-{\mathrm{M}}_{\mathrm{o}})}$$

(6)

$$\mathrm{S}={\mathrm{S}}_{\mathrm{u}}\frac{\sqrt{\mathrm{k}(\mathrm{M}-{\mathrm{M}}_{\mathrm{o}})}}{1+\sqrt{\mathrm{k}(\mathrm{M}-{\mathrm{M}}_{\mathrm{o}})}}$$

(7)

where,

• $\mathrm{S}$ = Strength at age $\mathrm{t}$
• ${\mathrm{S}}_{\mathrm{u}}$ = Limiting strength at infinite age
• $\mathrm{k}$ = Rate constant, initial slope of strength-maturity curve (1/days)
• ${\mathrm{M}}_{\mathrm{o}}$ = Maturity index at the start of strength development, at age ${\mathrm{t}}_{\mathrm{o}}$ (°C·hours or °C·days)
• $\mathrm{M}$ = Maturity index at age t (°C·hours or °C·days)

1.2.4. Development of Fatigue Maturity Functions for Cold-Mix Asphalts

The study presented in this paper modified the hyperbolic strength-maturity functions, Equations (6) and (7), to yield fatigue-maturity functions presented as Equations (8) and (9), respectively. The modifications reflect the inverse relationship between stiffness and fatigue resistance in asphalt mixtures [52,53]. In the modification, stiffness development of the cold-mix asphalt was assumed to start immediately after compaction, so that Mo = 0 at a datum temperature of 0 °C.

$$\mathrm{F}={\mathrm{F}}_{\mathrm{u}}\frac{\mathrm{kM}}{1+\mathrm{kM}}$$

(8)

$$\mathrm{F}={\mathrm{F}}_{\mathrm{u}}\frac{\sqrt{\mathrm{kM}}}{1+\sqrt{\mathrm{kM}}}$$

(9)

where,

• ${\mathrm{N}}_{\mathrm{f}}$ = Fatigue strength at age $\mathrm{t}$
• ${\mathrm{N}}_{\mathrm{fu}}$ = Limiting fatigue-strength at infinite age
• $\mathrm{F}$ = Modified fatigue strength at age $\mathrm{t}$, given by $({{\mathrm{N}}_{\mathrm{f}}}^{-1})$
• ${\mathrm{F}}_{\mathrm{u}}$ = Modified limiting fatigue strength at infinite age, given by $({{\mathrm{N}}_{\mathrm{fu}}}^{-1})$
• $\mathrm{k}$ = Rate constant, the initial slope of the strength-maturity curve (1/days)
• M = Maturity index (°C·Days)

Interpretation of results from the modeling exercise should always keep in mind that, inasmuch as they exhibit positive growth with time, Equations (8) and (9) technically represent a reduction in fatigue strength with time. Previous studies have shown that at isothermal curing conditions, the hyperbolic maturity functions, Equations (8) and (9) can be modified to provide a good fit for strength-age plots [47]. Maturity, M, in Equations (8) and (9) was substituted with chronological time, t, to yield modified fatigue-age functions presented as Equations (10) and (11).

$$\mathrm{F}={\mathrm{F}}_{\mathrm{u}}\frac{\mathrm{kt}}{1+\mathrm{kt}}$$

(10)

$$\mathrm{F}={\mathrm{F}}_{\mathrm{u}}\frac{\sqrt{\mathrm{kt}}}{1+\sqrt{\mathrm{kt}}}$$

(11)

In Equations (10) and (11), t denotes the cure duration in days while the rest of the symbols remain as defined for Equations (8) and (9). The actual fatigue-age functions, Equations (12) and (13), were obtained by substituting natural logarithmic values of N_f and N_fu in Equations (10) and (11) and by making N_f the subject of the Equations. Expression of fatigue-strength in natural logarithmic form is based on the assumption of logarithmic linearity between asphalt fatigue-strength and load strain levels [54].

$${\mathrm{N}}_{\mathrm{f}}={{\mathrm{N}}_{\mathrm{fu}}}^{\left(\frac{1+\mathrm{kt}}{\mathrm{kt}}\right)}$$

(12)

$${\mathrm{N}}_{\mathrm{f}}={{\mathrm{N}}_{\mathrm{fu}}}^{\left(\frac{1+\sqrt{\mathrm{kt}}}{\sqrt{\mathrm{kt}}}\right)}$$

(13)

2. Materials and Methods

2.1. Materials

The cold-emulsion asphalt mix used in this study was composed of a blend of reclaimed asphalt pavement (RAP) and virgin aggregates bound with a slow-setting cationic bitumen emulsion. Reclaimed asphalt pavement was obtained as slabs from a road undergoing rehabilitation in Nairobi, Kenya. The slabs were processed into four aggregate fractions of nominal sizes 0/6 mm, 6/10 mm, 10/14 mm, and 14/20 mm. The virgin aggregates of nominal size 0/6 mm were obtained from Katani Quarries, located in Machakos County of Kenya. X-ray fluorescent analysis conducted on both virgin and reclaimed asphalt pavement aggregates revealed a siliceous mineralogy with SiO₂ constituting 65.497% of reclaimed asphalt pavement aggregates and 62.503% of the virgin aggregates, respectively. Siliceous rocks have a net negative surface charge, which is compatible with positively charged cationic bitumen emulsions [55,56]. The cationic bitumen emulsion, K_3-65, complying with BS EN 13808 [57], was obtained from COLAS East Africa Ltd., situated in Nairobi, Kenya. Residual bitumen was recovered from the reclaimed asphalt pavement using the Rotary Evaporator Method, conducted in accordance with BS EN 12697-3 [58]. Base bitumen was recovered from the cationic bitumen emulsion by Evaporation Method, following procedures set out in BS EN 13074-2 [59]. Bitumen recovered from both reclaimed asphalt pavement and the cationic bitumen emulsion were subjected to Needle Penetration and Softening Point (Ring and Ball) tests following procedures set out in BS EN 1426 [60] and BS EN 1427 [61], respectively. Properties of bitumen recovered from bitumen emulsion and the reclaimed asphalt pavement are presented in

Table 1. Properties of Bitumen Recovered from Emulsion and Reclaimed Asphalt Pavement.

Material Description	Softening Point (°C)	Needle Penetration (mm)	Percentage in Total Mix (%)
Bitumen Emulsion	54.5	88.25	65
Reclaimed Asphalt Pavement	63.4	16.3	4.1

.

This study adopted the Asphalt Institute procedure, detailed in MS 19 [62], to design a cold-emulsion asphalt mix of gradation 0/20 mm, suitable for surfacing of low to medium traffic volume roads [4,7]. Individual aggregate fractions were graded following procedures set out in BS 812: Part 103 [63] and iteratively blended to fit within Transport and Road Research Laboratories (TRRL) gradation envelope recommended by the Asphalt Institute for cold-emulsion asphalts [62]. The final design mix was composed of 45% 0/6 mm virgin aggregates, 15% 0/6 mm reclaimed asphalt pavement aggregates, 10% 6/10 mm reclaimed asphalt pavement aggregates, 15% 10/14 mm reclaimed asphalt pavement aggregates, and 15% 14/20 mm reclaimed asphalt pavement aggregates, as percentages by mass of the total dry aggregates. Figure 1 depicts the gradation of the design aggregates blend.

The design pre-mix water and bitumen emulsion constituted 4% and 6.2% by mass of the dry aggregates, respectively. Besides contributing to the workability of the cold-emulsion asphalt mix, pre-mix water aid in activating surface charges in the aggregates, and thus serves to accelerate breaking of the bitumen emulsion.

2.2. Specimen Preparation

Based on the design mix presented in Section 2.1, 42 cold-emulsion asphalt slabs measuring 400 mm × 300 mm × 80 mm were produced in the laboratory following procedures set out in BS EN 12697-33 [64]. This research made use of electro-mechanically operated Dynapave Rolling Wheel Compactor, supplied by Industrial Process Controls Ltd., Italy to compact the cold-mix asphalt slabs. Upon completion of compaction, slabs were kept in their molds for 24 h at ambient temperatures before being de-molded and cured for a further 24 h at 40 °C. Since the specimens were still fragile, only the sides of the molds were struck off, while the asphalt slabs went into the curing chambers with the base plates. To minimize aggregate chipping and excessive dust generation during sawing, the slabs were thereafter conditioned at 5 °C for 24 h in a fridge. At the end of the preliminary curing period, prismatic specimens measuring 400 ± 5 mm by 63.5 ± 5 mm by 50.8 ± 5 mm, were obtained from the slabs by sawing in the direction of compaction with a diamond masonry saw. For dimensional stability, 6 mm were sawn off from the sides as well as the top and bottom faces of the slabs. Each slab produced 4 prismatic asphalt beams.

The resulting 168 asphalt beams were divided into four sets, of 42 asphalt specimens each, which were variously cured at 5 °C, 25 °C, 40 °C, and 50 °C in temperature-controlled chambers, with what was the upper side during compaction facing up. The cure temperatures were chosen to give a range below the softening point temperature of the base bitumen of the emulsion. This was informed by findings of previous studies, that curing of cold-mix asphalts at temperatures below the softening point of the base bitumen results in minimal bitumen aging [28,32,39,65,66,67,68]. Specimens were drawn from each curing chamber at intervals of 1, 3, 5, 7, 14, 21, and 28 days and tested for fatigue strength.

2.3. Fatigue Testing and Data Analysis

Fatigue tests on the cold-emulsion reclaimed asphalt pavement beams was conducted in accordance with procedures set out in BS EN 12697-24 (E) Annex D [69]. Flexural tests were conducted on a four-point bending (4PB) test jig enclosed in a universal testing machine, Dynapave UTM 30, developed and supplied by Industrial Process Controls Ltd., Italy. The test setup is composed of a loading frame, an environmental chamber, a control panel, a hydraulic power supply unit and a personal computer equipped with automated control and data acquisition system (CDAS) that collects and stores information in American Standard Code for Information Interchange (ASCII), Comma Separated Variable (CSV) format. Six specimens for each cure duration, within each cure temperature, were tested in controlled-strain set up at 5 °C, 10 Hz, and strain levels spread at intervals of 25 µm/m between 125 µm/m and 250 µm/m. Upon completion of each test, data collected and stored by the control and data acquisition system (CDAS) was exported and saved in notepad form. Figure 2 depicts the setup of equipment used in the four-point bending fatigue test.

For purposes of data analysis, fatigue test results were imported from notepad to excel as semicolon delimited data. The number of load cycles to failure, N_f, at a particular strain level was determined by plotting the complex stiffness modulus, E*, against the number of load applications, N, for each of the 168 tested specimens. A third-order polynomial equation was fitted to the data to obtain the number of load cycles, N_f, at which the stiffness of the specimen had reduced to 50% of the initial value. Typically, a material under cyclic loading accumulates damage and experiences a reduction in stiffness as the test progresses. According to BS EN 12697-24 (E) Annex D [69], the initial value of complex stiffness modulus is taken as that of the 100th cycle, to allow the specimen to “bed-in” in the loading jig. Figure 3 shows how the stiffness of an asphalt specimen evolves during a flexural fatigue test. In Figure 3, E*₁₀₀ denotes initial complex stiffness modulus of the specimen measured at the 100th load cycle, E*_f denotes the complex stiffness modulus at failure and N_f denotes the number of load cycles at failure.

Upon completion of fatigue tests for each cure duration, within each cure temperature, the number of load cycles to failure were plotted against the test strain levels and fitted to Equation (14) using linear regression approach. Equation (14) was proposed by Monismith et al. [70] as a suitable predictive model for asphalt fatigue strength at a loading frequency of 10 Hz in controlled-strain test mode. Based on Miner’s law of cumulative pavement damage, Equation (14) assumes logarithmic linearity between the test strains and the number of load applications to failure [54]. This linearity has been found to hold best at temperatures below 5 °C, when asphalt behaves in an almost linear-elastic manner

$$\ln ({\mathrm{N}}_{\mathrm{f}})=\mathrm{a}+\mathrm{b}\ln (\mathsf{Ɛ})$$

(14)

where,

• N_f = Number of load cycles to failure
• Ɛ = Strain levels in (µm/m)
• a = Intercept of the regression curve
• b = Slope of the regression curve.

2.4. Prediction of Fatigue-Strength Development in Emulsion Asphalt

The combined effects of cure temperature and cure duration on fatigue-strength development in the cold-emulsion reclaimed asphalt pavement mixture was studied using the maturity method. Fatigue-strength evolution with time in the cold-emulsion asphalt mix was tracked using Equation (14). This study evaluated both linear hyperbolic fatigue-maturity function, Equation (8), and the parabolic hyperbolic fatigue-maturity function, Equation (9). Model coefficients, k and F_u, for Equations (8) and (9), were obtained from fatigue strengths of cold-emulsion asphalt specimens cured at 5 °C, 25 °C, and 40 °C, and validated with fatigue-strength results of specimens cured at 50 °C. Keeping in mind that asphalt fatigue test results are sensitive to test strain levels, the models were replicated at each of the six strain levels adopted in the four-point bending (4PB), test to establish the range of their validity.

3. Results and Discussions

3.1. Fatigue-Age Relationships

Fatigue strength, in terms of number of load cycles to failure, N_f, was determined for each of the cold-emulsion reclaimed asphalt pavement specimens as described in Section 2.3 and the results plotted in Figure 4, Figure 5 and Figure 6 for specimens cured at 5 °C, 25 °C, and 40 °C, respectively. Results for specimens cured at 50 °C were reserved for model validation purposes. As can be seen in Figure 4, Figure 5 and Figure 6, the number of load cycles to failure are expressed in terms of natural logarithms.

To study the combined effects of cure temperature and cure duration on fatigue strength development of the cold-emulsion reclaimed asphalt pavement mixture, fatigue strengths at each of the 6 test strain levels in Figure 4, Figure 5 and Figure 6 for specimens cured at 5 °C, 25 °C, and 40 °C, respectively, were plotted against the cure duration, as shown in Figure 7. Evolution of fatigue-strength was observed by fitting a general logarithmic curve to the data. Although it does not provide the best fit to the fatigue-age data, a logarithmic plot has been found to give a good indication of strength trends in cold-mix asphalts [28].

It can be observed, in Figure 7, that fatigue strength in the cold-emulsion reclaimed asphalt pavement mixture generally decreased with increase in cure duration. This observation implies that as curing proceeds, the cold-emulsion asphalt mixture experiences continued reduction in its ability to resist flexure and a corresponding increase in its sensitivity to change in load strain levels. This behavior is attributed to a continued increase in asphalt stiffness, as emulsification and pre-mix water is progressively lost by the specimens through evaporation. An increase in asphalt stiffness is associated with increased brittleness, the property responsible for low fatigue resistance. It can also be noted that specimens cured at higher temperatures consistently achieved higher fatigue strengths than their counterparts cured at lower temperatures. An increase in cure temperature is expected to enhance adhesion of the binder film to the aggregate surfaces, leading to an increase in fatigue resistance and a reduction in sensitivity to change in load strain levels.

It is evident from Figure 7 that specifying a curing protocol solely on the basis of cure temperature and duration will not suffice in the prediction of strength development in a cold-mix asphalt. The continued decrease, with time, of fatigue-strength of the cold-emulsion reclaimed asphalt pavement mixture will have some implications on the design of cold-emulsion asphalt pavements to resist fatigue cracking. There is a need for a model that predicts the ultimate fatigue strength of the cold-emulsion asphalt mix, for the avoidance of overestimation of fatigue performance during design. These observations lend credence to the choice of maturity method as an option to account for the combined effects of time and temperature on fatigue strength development of the cold-emulsion reclaimed asphalt pavement mixture.

3.2. Prediction of Fatigue-Strength Development in Emulsion Asphalt.

The modified linear hyperbolic and parabolic hyperbolic maturity functions, Equations (8) and (9), were used to predict strength development in the cold-emulsion reclaimed asphalt pavement mixture. The models were replicated in the six strain levels to establish their range of validity. The phenomenological method of asphalt fatigue analysis assumes logarithmic linearity between the number of load cycles to failure, N_f, and the load-strain levels, Ɛ. In the strict sense of the word, this does not always hold at very low and very high strain levels. At very low strain levels, asphalts approach fatigue endurance limit while at high strain levels, their linear elastic limits are exceeded. A strain level ranging between the two extremes should thus be established for the fatigue data to make sense.

3.2.1. Modified Fatigue-Age Relationships

The maturity method anticipates positive strength development, over time, in both cement concrete and cold-mix asphalt concrete. As can be observed in Figure 7, fatigue-strength of the cold-emulsion asphalt mix decreases with an increase in cure time. The fatigue-age functions, given as Equations (12) and (13), suggest that at t = 0, the cold-emulsion asphalt mix would have infinite fatigue resistance. To allow for the computation of the rate constant, k, fatigue strengths depicted in Figure 7 were modified, as described in Section 1.2.4, to reflect an apparent positive fatigue strength growth. The modified fatigue strength results for the cold-emulsion reclaimed asphalt pavement mixture are as given in

Table 2. Modified fatigue strengths for emulsion reclaimed asphalts cured at 5 °C.

Strain Level, ln (Ɛ)	Modified Fatigue Strengths, {1/ln(Nf)} × 10−3
	1 Day’s Cure	3 Days’ Cure	5 Days’ Cure	7 Days’ Cure	14 Days’ Cure	21 Days’ Cure	28 Days’ Cure
4.8	76.4	77.2	83.1	95.3	85.8	92.2	103.1
5.0	84.6	85.0	91.3	100.8	92.4	99.9	113.0
5.2	93.1	92.8	99.5	105.9	99.0	107.5	123.1
5.3	102.0	100.9	108.0	110.8	105.4	115.0	133.4
5.4	111.3	109.2	116.7	115.5	111.9	122.6	144.0
5.5	121.2	118.0	125.9	120.1	118.3	130.4	155.0

,

Table 3. Modified fatigue strengths for emulsion reclaimed asphalts cured at 25 °C.

Strain Level, ln (Ɛ)	Modified Fatigue Strengths, {1/ln(Nf)} × 10−3
	1 Day’s Cure	3 Days’ Cure	5 Days’ Cure	7 Days’ Cure	14 Days’ Cure	21 Days’ Cure	28 Days’ Cure
4.8	75.8	73.0	78.3	84.5	94.4	91.6	95.2
5.0	82.8	81.3	86.3	94.1	100.3	99.2	102.8
5.2	90.0	89.9	94.4	104.0	105.9	106.7	110.3
5.3	97.2	99.0	102.9	114.4	111.3	114.2	117.7
5.4	104.6	108.7	111.7	125.5	116.5	121.7	125.2
5.5	112.2	119.2	120.9	137.5	121.6	129.4	132.7

and

Table 4. Modified fatigue strengths for emulsion reclaimed asphalts cured at 40 °C.

Strain Level, ln (Ɛ)	Modified Fatigue Strengths, {1/ln(Nf)} × 10−3
	1 Day’s Cure	3 Days’ Cure	5 Days’ Cure	7 Days’ Cure	14 Days’ Cure	21 Days’ Cure	28 Days’ Cure
4.8	75.7	74.0	84.0	81.9	81.7	78.3	92.2
5.0	82.6	82.2	89.9	90.4	89.2	88.2	97.2
5.2	89.5	90.6	95.6	99.0	96.6	98.8	101.9
5.3	96.5	99.5	101.1	108.0	104.1	110.2	106.3
5.4	103.6	108.9	106.5	117.3	111.8	122.8	110.5
5.5	110.9	119.0	111.9	127.2	119.6	136.7	114.6

for specimens cured at 5 °C, 25 °C, and 40 °C, respectively.

The tabulated data were used to derive model coefficients for Equations (8) and (9). In deriving the various model coefficients, the results should be interpreted keeping in mind that they represent the inverse of the actual fatigue strength data. In essence, modified fatigue strength describes the loss of fatigue strength with time by the cold-emulsion reclaimed asphalt pavement mixture

3.2.2. Rate Constants for Modified Fatigue-Age Relationships

The rate constants, k, together with the modified limiting fatigue-strength values, F_u, were determined for each cure temperature by fitting modified fatigue data in Table 2, Table 3 and Table 4 to modified fatigue-age functions, Equations (10) and (11), respectively. The parameters, k and F_u, were computed by non-linear least squares curve fitting technique using “Solver”, a data analysis tool embedded in Microsoft Office Excel spreadsheets application. For illustration purposes, computation of k and F_u for cold-emulsion asphalt specimens cured at 5 °C and tested at 125 µm/m are presented in

Table A1. F_u and k Values for Specimens Cured at 5 °C and Tested at 125 µm/m.

Cure Duration (Days)	Number of Load Cycles to Failure (Nf)	ln(Nf)	1/Ln(Nf)	1/ln(Nf) × 10−3	Linear Hyperbolic Model
					kt	Predictions	Squared Residuals
1	481,330	13.084	0.07643	76.427	3.329	72.141	18.377
3	418,823	12.945	0.07725	77.249	9.986	85.274	64.409
5	167,825	12.031	0.08312	83.121	16.643	88.496	28.897
7	36,083	10.494	0.09530	95.296	23.300	89.953	28.549
14	115,985	11.661	0.08575	85.754	46.600	91.843	37.071
21	51,075	10.841	0.09224	92.242	69.900	92.491	0.062
28	16,343	9.702	0.10308	103.076	93.200	92.818	105.234
						∑	282.60
				k	3.33
				Fu	93.81

of Appendix A. Values of k and F_u obtained for all the strain levels and cure temperatures are recorded in

Table 5. Fatigue-age parameters for a linear hyperbolic model for emulsion reclaimed asphalt.

Strain Level, Ɛ (µm/m)	5 °C Cure		25 °C Cure		40 °C Cure
	k (1/day)	Fu (×10−3)	k (1/day)	Fu (×10−3)	k (1/day)	Fu (×10−3)
125	3.33	93.81	3.36	90.63	7.23	83.93
150	3.79	101.30	3.74	98.30	7.58	91.44
175	4.38	108.67	4.15	105.97	7.85	99.06
200	5.16	116.02	4.62	113.78	8.02	106.90
225	6.27	123.43	5.16	121.78	8.08	115.09
250	7.95	130.96	5.79	130.10	8.00	123.73

and

Table 6. Fatigue-age parameters for a parabolic hyperbolic model for emulsion reclaimed asphalt.

Strain Level, Ɛ (µm/m)	5 °C Cure		25 °C Cure		40 °C Cure
	k (1/day)	Fu (×10−3)	k (1/day)	Fu (×10−3)	k (1/day)	Fu (×10−3)
125	5.57	103.06	4.89	100.57	27.13	87.80
150	6.81	110.58	6.42	107.63	31.25	95.32
175	8.50	117.84	8.49	114.62	35.04	102.96
200	10.95	124.91	11.39	121.64	38.19	110.88
225	14.72	131.87	15.65	128.77	40.32	119.19
250	20.82	138.83	21.93	136.16	41.09	128.03

for linear hyperbolic and parabolic hyperbolic models, respectively.

It can be observed in Table 5 and Table 6 that, at each test strain level, the rate constants for the cold-emulsion reclaimed asphalt pavement mixture generally increase with an increase in cure temperature. The modified limiting fatigue strength values, on the other hand, decrease with an increase in cure temperature. The trend displayed by the rate constants implies that, at early curing periods, specimens cured at higher temperatures experience a more rapid drop in their fatigue strength than their counterparts cured at lower temperatures. This behavior is attributed to a more rapid moisture loss by specimens cured at higher temperatures than those cured at lower temperatures. The modified limiting fatigue values indicate that specimens cured at higher temperatures eventually attain higher fatigue strength values than those cured at lower temperatures. This behavior is attributed to enhanced adhesion between aggregates and the binder brought about by increased curing temperatures.

3.2.3. Temperature Sensitivity Factors for Modified Fatigue-Age Relationships

The rate constants recorded in Table 5 and Table 6 were fitted to the cure temperatures (5 °C, 25 °C, and 40 °C) using the simplified Arrhenius function, Equation (3), to obtain slopes and intercepts of the Arrhenius function. The temperature sensitivity factors, B, for both linear hyperbolic and parabolic hyperbolic models were recorded in

Table 7. Temperature sensitivity factors emulsion reclaimed asphalt pavement mixture.

Strain Level, Ɛ (µm/m)	Linear Hyperbolic Model		Parabolic Hyperbolic Model
	Ao	B	Ao	B
125	0.975	0.0477	0.975	0.0411
150	0.975	0.0532	0.975	0.0484
175	0.975	0.0584	0.975	0.0559
200	0.975	0.0630	0.975	0.0633
225	0.975	0.0363	0.975	0.0707
250	0.975	0.0384	0.975	0.0784

. A_o is the rate constant at 0 °C, while B is the temperature sensitivity factor of the cold-emulsion reclaimed asphalt pavement mixture under variable temperature curing.

There is a general increase in the temperature sensitivity factors with strain levels, in Table 7, implying that fatigue strength of the cold-emulsion reclaimed asphalt pavement mixture diminishes under variable temperature curing as the loading strains increase. This is a reflection of the conventional fatigue test, in which, the number of load cycles to failure decreases logarithmically with an increase in load strain levels. At high test strain levels, specimens experience a rapid reduction in stiffness leading to early failure.

3.2.4. Equivalent Modified Fatigue Ages

The equivalent modified fatigue ages for the three cure temperatures of 5 °C, 25 °C, and 40 °C and cure durations of 1, 3, 5, 7, 14, 21, and 28 days were computed using Equation (4) and values of temperature sensitivity factors recorded in Table 7. A reference temperature, T_r = 20 °C, was used in the computation of the age conversion factors for the linear hyperbolic and parabolic hyperbolic models. The age conversion factors are presented in

Table 8. Age conversion factors for linear hyperbolic and parabolic hyperbolic models.

Strain Level, Ɛ (µm/m)	5 °C Cure		25 °C Cure		40 °C Cure
	Linear Hyperbolic	Parabolic Hyperbolic	Linear Hyperbolic	Parabolic Hyperbolic	Linear Hyperbolic	Parabolic Hyperbolic
125	2.044	1.852	0.788	0.814	0.385	0.440
150	2.222	2.068	0.766	0.785	0.345	0.380
175	2.401	2.313	0.747	0.756	0.311	0.327
200	2.574	2.585	0.730	0.729	0.283	0.282
225	1.725	2.889	0.834	0.702	0.483	0.243
250	1.780	3.242	0.825	0.676	0.464	0.208

, while the equivalent modified fatigue ages at the various cure durations are presented in

Table A2. Equivalent modified fatigue ages for linear hyperbolic model.

Temperature	Cure Duration	Tested at 125 µm/m	Tested at 150 µm/m	Tested at 175 µm/m	Tested at 200 µm/m	Tested at 225 µm/m	Tested at 250 µm/m
Cure at 5 °C	1	2.0	2.2	2.4	2.6	1.7	1.8
	3	6.1	6.7	7.2	7.7	5.2	5.3
	5	10.2	11.1	12.0	12.9	8.6	8.9
	7	14.3	15.6	16.8	18.0	12.1	12.5
	14	28.6	31.1	33.6	36.0	24.1	24.9
	21	42.9	46.7	50.4	54.1	36.2	37.4
	28	57.2	62.2	67.2	72.1	48.3	49.8
Cure at 25 °C	1	0.8	0.8	0.7	0.7	0.8	0.8
	3	2.4	2.3	2.2	2.2	2.5	2.5
	5	3.9	3.8	3.7	3.6	4.2	4.1
	7	5.5	5.4	5.2	5.1	5.8	5.8
	14	11.0	10.7	10.5	10.2	11.7	11.6
	21	16.5	16.1	15.7	15.3	17.5	17.3
	28	22.1	21.5	20.9	20.4	23.3	23.1
Cure at 40 °C	1	0.4	0.3	0.3	0.3	0.5	0.5
	3	1.2	1.0	0.9	0.9	1.5	1.4
	5	1.9	1.7	1.6	1.4	2.4	2.3
	7	2.7	2.4	2.2	2.0	3.4	3.2
	14	5.4	4.8	4.4	4.0	6.8	6.5
	21	8.1	7.2	6.5	6.0	10.2	9.7
	28	10.8	9.7	8.7	7.9	13.5	13.0

of Appendix B and

Table A3. Equivalent modified fatigue ages for parabolic hyperbolic model.

Temperature	Cure Duration	Tested at 125 µm/m	Tested at 150 µm/m	Tested at 175 µm/m	Tested at 200 µm/m	Tested at 225 µm/m	Tested at 250 µm/m
Cure at 5 °C	1	1.9	2.1	2.3	2.6	2.9	3.2
	3	5.6	6.2	6.9	7.8	8.7	9.7
	5	9.3	10.3	11.6	12.9	14.4	16.2
	7	13.0	14.5	16.2	18.1	20.2	22.7
	14	25.9	29.0	32.4	36.2	40.4	45.4
	21	38.9	43.4	48.6	54.3	60.7	68.1
	28	51.9	57.9	64.8	72.4	80.9	90.8
Cure at 25 °C	1	0.8	0.8	0.8	0.7	0.7	0.7
	3	2.4	2.4	2.3	2.2	2.1	2.0
	5	4.1	3.9	3.8	3.6	3.5	3.4
	7	5.7	5.5	5.3	5.1	4.9	4.7
	14	11.4	11.0	10.6	10.2	9.8	9.5
	21	17.1	16.5	15.9	15.3	14.7	14.2
	28	22.8	22.0	21.2	20.4	19.7	18.9
Cure at 40 °C	1	0.4	0.4	0.3	0.3	0.2	0.2
	3	1.3	1.1	1.0	0.8	0.7	0.6
	5	2.2	1.9	1.6	1.4	1.2	1.0
	7	3.1	2.7	2.3	2.0	1.7	1.5
	14	6.2	5.3	4.6	3.9	3.4	2.9
	21	9.2	8.0	6.9	5.9	5.1	4.4
	28	12.3	10.6	9.2	7.9	6.8	5.8

of Appendix C, for linear hyperbolic and parabolic hyperbolic models respectively.

3.2.5. Modified Fatigue Maturity Functions

Modified fatigue maturity of the cold-emulsion reclaimed asphalt pavement mix at cure intervals of 1, 3, 5, 7, 14, 21, and 28 days was calculated using Equation (5) and the Equivalent ages tabulated in Table A2 of Appendix B and Table A3 of Appendix C. As explained in Section 1.2.2, the chronological age in the Nurse–Saul maturity function was replaced with the equivalent age in the computation of maturity. The fit parameters, k and F_u, of the linear hyperbolic and parabolic hyperbolic fatigue maturity functions presented as Equations (8) and (9) were obtained by fitting the modified fatigue strength values to the computed maturity values using non-linear least squares curve fitting techniques and recorded in

Table 9. Modified fatigue-maturity parameters for linear and parabolic hyperbolic models.

Strain Level, Ɛ (µm/m)	Linear Hyperbolic Model		Parabolic Hyperbolic Model
	k (1/day)	Fu (×10−3)	k (1/day)	Fu (×10−3)
125	0.35	88.67	0.91	94.30
150	0.36	96.48	0.93	102.73
175	0.39	104.23	1.01	110.92
200	0.43	112.03	1.17	118.91
225	0.67	118.62	1.44	126.76
250	0.74	126.91	1.90	134.62

.

3.2.6. Actual Fatigue-Maturity Functions

The modified fatigue maturity parameters obtained in Table 9 were based on a modification of the “actual fatigue” to allow for the computation of the rate constant from the initial slopes of fatigue-age functions. The reciprocal linear hyperbolic model, Equation (15) and the reciprocal parabolic hyperbolic model, Equation (16), were obtained by making N_f the subject in Equations (8) and (9), respectively. The desired coefficients, k and N_fu, of the actual fatigue-maturity functions were obtained by fitting actual fatigue strengths, N_f, to the computed maturity values using non-linear least squares curve fitting techniques.

$${\mathrm{N}}_{\mathrm{f}}={{\mathrm{N}}_{\mathrm{fu}}}^{\left(\frac{1+\mathrm{kM}}{\mathrm{kM}}\right)}$$

(15)

$${\mathrm{N}}_{\mathrm{f}}={{\mathrm{N}}_{\mathrm{fu}}}^{\left(\frac{1+\sqrt{\mathrm{kM}}}{\sqrt{\mathrm{kM}}}\right)}$$

(16)

According to the maturity concept, Equations (15) and (16) can be used to predict fatigue-strengths of the cold-emulsion reclaimed asphalt pavement mixture at any other combination of cure temperatures and cure durations.

Table 10. Actual fatigue-maturity parameters for linear and parabolic hyperbolic models.

Strain Level, Ɛ (µm/m)	Linear Hyperbolic Model		Parabolic Hyperbolic Model
	k (1/day)	Nfu (×10−3)	k (1/day)	Nfu (×10−3)
125	0.35	79,050.35	0.91	40,320.75
150	0.36	31,718.35	0.93	16,891.44
175	0.39	14,675.67	1.01	8228.80
200	0.43	7524.19	1.17	4491.14
225	0.67	4585.38	1.44	2667.23
250	0.74	2642.76	1.90	1682.90

gives model coefficients applicable to each of the six strain levels used to determine fatigue behavior of the cold-emulsion reclaimed asphalt pavement mixture in the four-point bending fatigue test.

3.2.7. Validation of the Actual Fatigue-Maturity Models

The models presented as Equations (15) and (16) were developed using fatigue data of specimens of cold-emulsion reclaimed asphalt mix cured at 5 °C, 25 °C, and 40 °C. To validate these models, an independent set of fatigue data from specimens cured at 50 °C for up to 28 days was used. The coefficients in Table 10 were used in Equations (15) and (16) to predict fatigue strength values of the cold-emulsion reclaimed asphalt pavement mix at a cure temperature of 50 °C. Results of load cycles to failure for the specimens cured at 50 °C were determined using procedures set out in Section 2.3 and plotted alongside the predicted values as shown in Figure 8.

It can be observed in Figure 8 that both the linear hyperbolic and parabolic hyperbolic maturity functions give good prediction early-life and the limiting fatigue values but fail to accurately capture fatigue strengths in the intermediate cure durations. When visually inspected, both the linear hyperbolic and parabolic hyperbolic models in Figure 8 appear to almost coincide at test strain levels between 125 µm/m and 200 µm/m. To ascertain the accuracy of the prediction offered by each of these functions, the predicted fatigue strength values were plotted against the experimental fatigue values for all test strain levels. Figure 9 depicts such a plot, for specimens tested at 125 µm/m.

It can be observed in Figure 9 that, there was a rapid drop in fatigue strength of the cold-emulsion asphalt between the first and third day of cure. This is attributed to the rapid evaporation in this period, as reflected in the rate constants presented in Section 3.2.2. Coefficients of determination of the fit between predicted and experimental fatigue strengths were determined at the 6 test strain levels and recorded in

Table 11. Model coefficients of determination at various test strain levels.

Strain Level, Ɛ (µm/m)	Linear Hyperbolic Model	Parabolic Hyperbolic Model
125	0.9755	0.9854
150	0.9116	0.9823
175	0.8078	0.9235
200	0.6799	0.8202
225	0.4495	0.4515
250	0.3817	0.3932

.

The coefficients of determination, R², were used to assess the accuracy with which the linear hyperbolic and the parabolic hyperbolic models predicted fatigue strength development in the cold-emulsion reclaimed asphalt pavement mixture. It can be deduced from Table 11 that the proposed models offered reasonable predictions for cold-mix asphalt fatigue strengths up to a strain level of 175 µm/m for the linear hyperbolic model and up to a strain level of 200 µm/m for the parabolic hyperbolic model. Generally, the parabolic hyperbolic model offered a better correlation to the experimental data than the linear hyperbolic model at all strain levels. The reduction in the predictive accuracy of the models at load strain levels beyond 200 µm/m can be explained by the manner in which asphalt mixtures behave under loads. At low strain levels, asphalt behaves in an almost linear elastic manner but tends to visco-elastic behavior as loads increase. This inevitably leads to high variability in results at higher load strain levels than in lower load strain levels.

4. Conclusions

The combined effects of cure temperature and cure duration on fatigue strength, N_f, of a cold-emulsion reclaimed asphalt pavement mixture was studied through the maturity method. A parabolic hyperbolic maturity model predicted fatigue strength of the cold-emulsion asphalt mixture with coefficients of determination, R², above 0.8 for strain levels ranging between 125 µm/m and 200 µm/m. From these findings, it is concluded that there is a strong correlation between cold-mix asphalt fatigue maturity and its fatigue strength.

• It is recommended that laboratory fatigue characterization of cold-emulsion asphalt mixtures considers both cure time and cure temperature.
• This study recommends the use of the developed parabolic hyperbolic strength prediction model to predict cold-emulsion asphalt fatigue for pavement design purposes
• Design for fatigue resistance in cold-emulsion asphalt mixtures should be based on the predicted limiting fatigue strength values, for the avoidance of over estimation of fatigue performance at the design stage.