Seismic Performance of Reinforced Concrete Short Columns Subjected to Freeze–Thaw Cycles
Abstract
1. Introduction
2. Experimental Program
2.1. Test Specimens
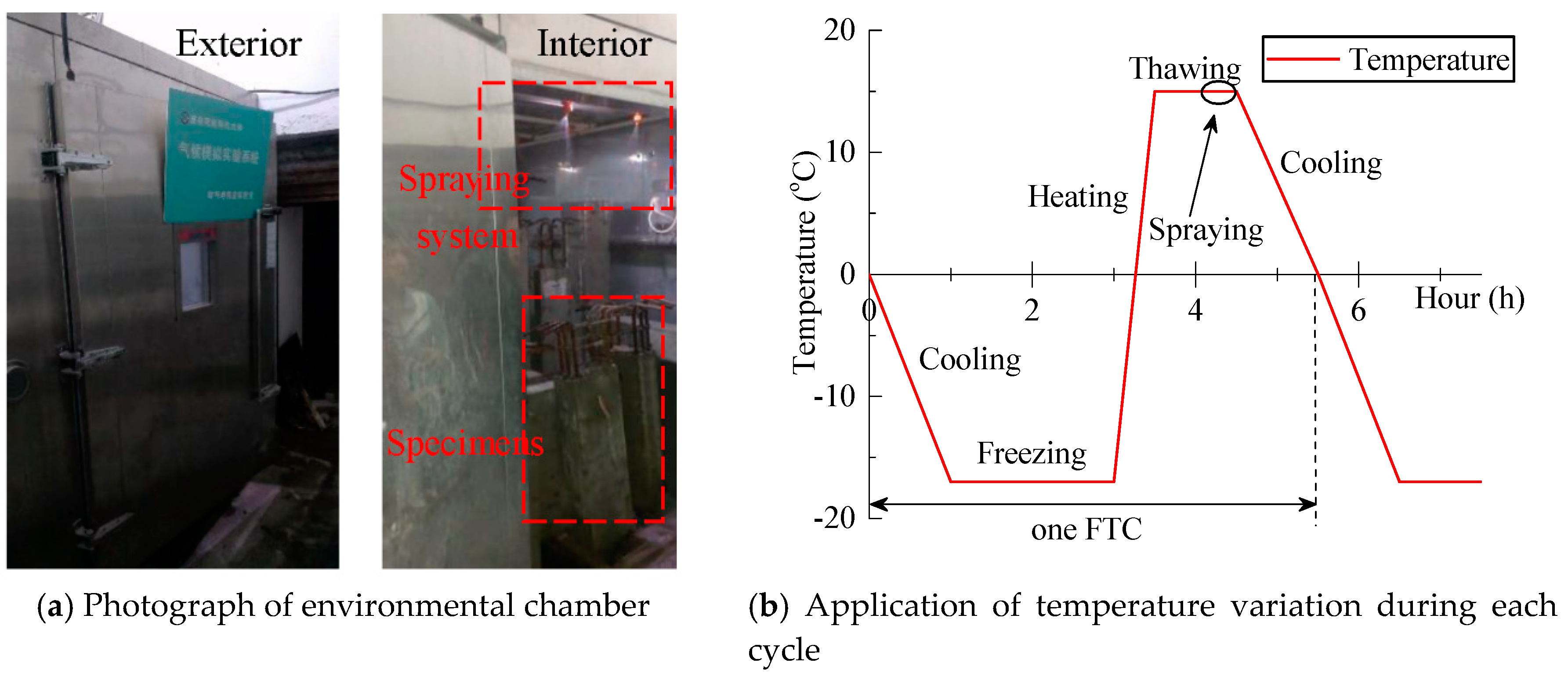
2.2. Details of FTCs
2.3. Material Properties
2.4. Crack Patterns of Specimens after FTCs
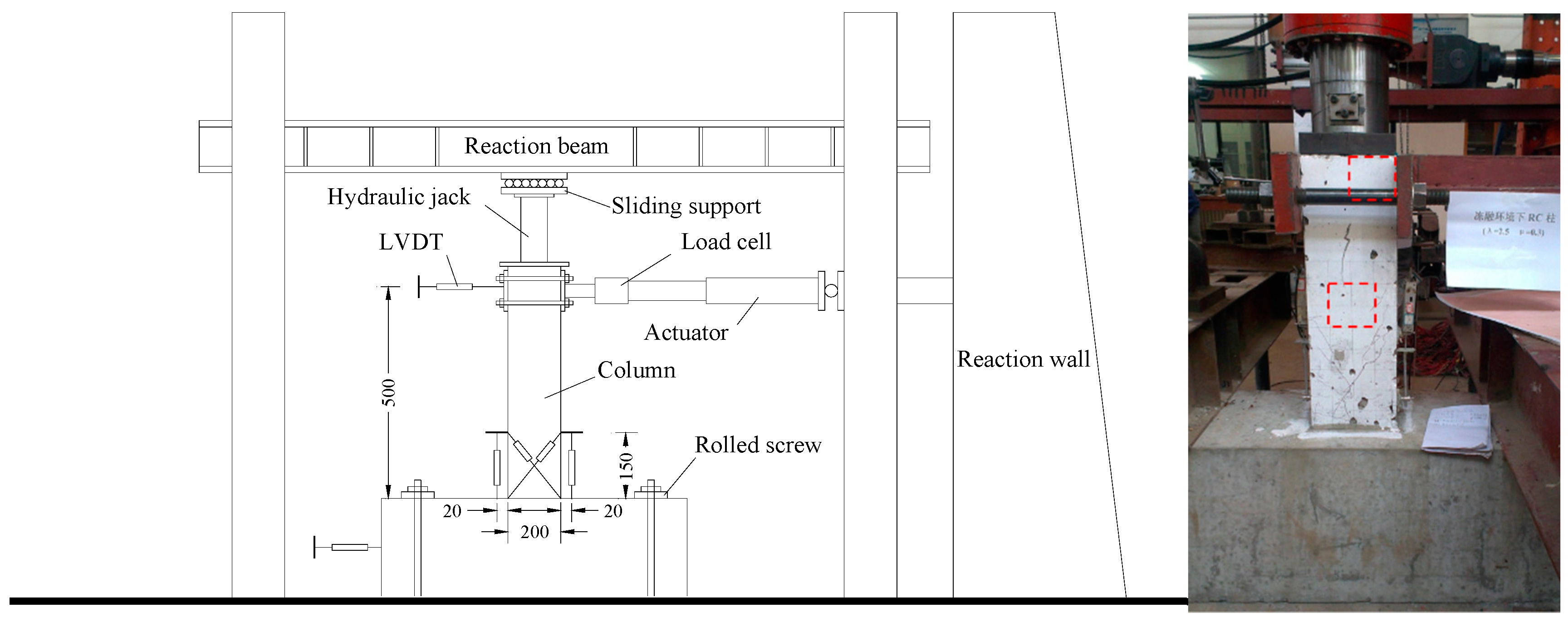
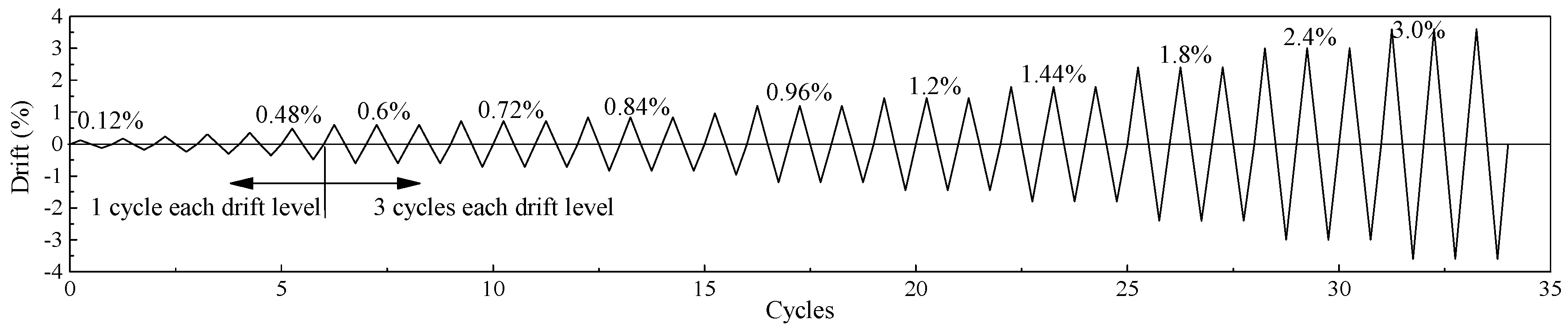
2.5. Pseudo-Static Test Setup and Loading Procedure
3. Test Results and Analysis
3.1. Damage Process and Failure Pattern
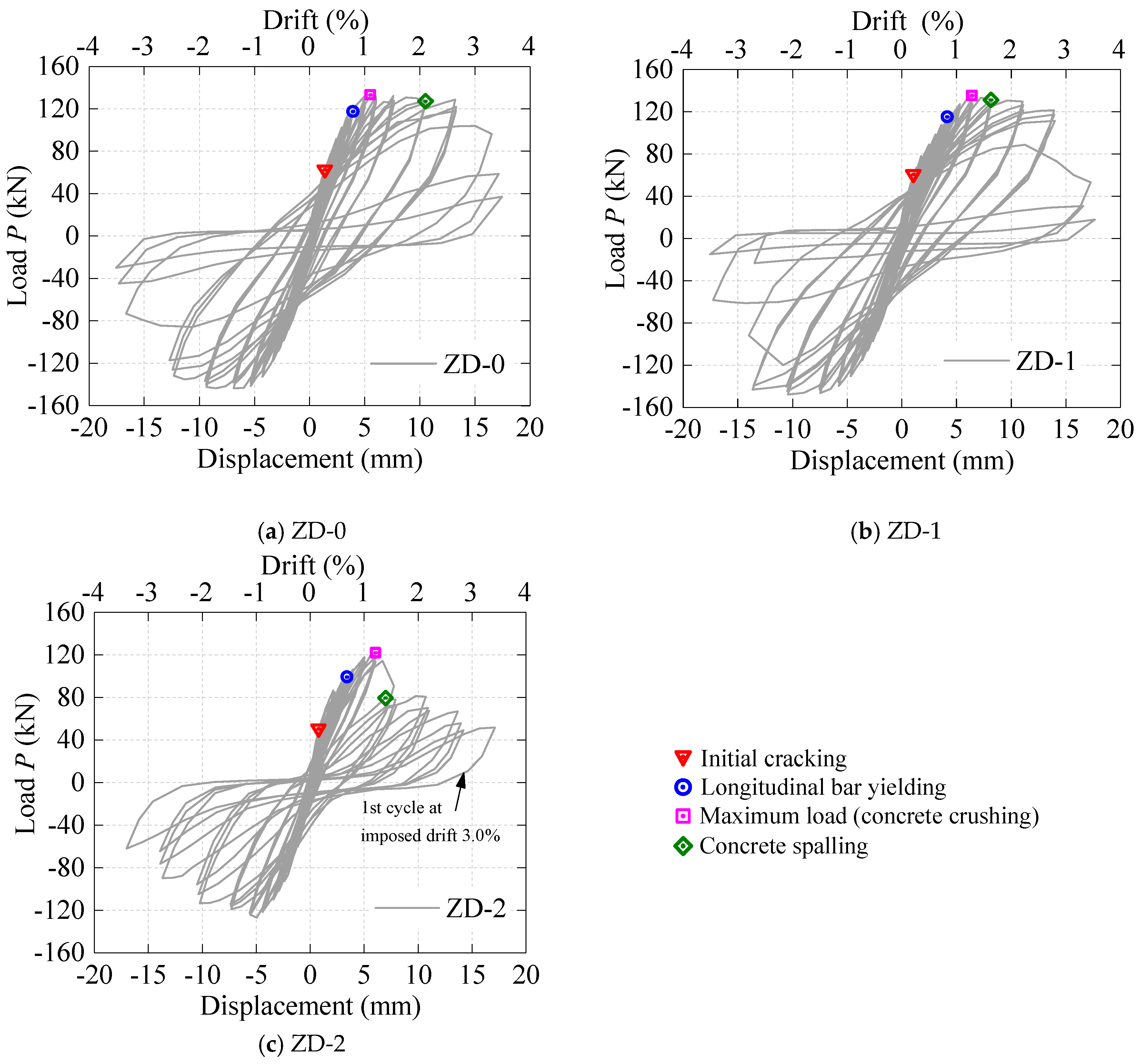
3.2. Hysteretic Behavior
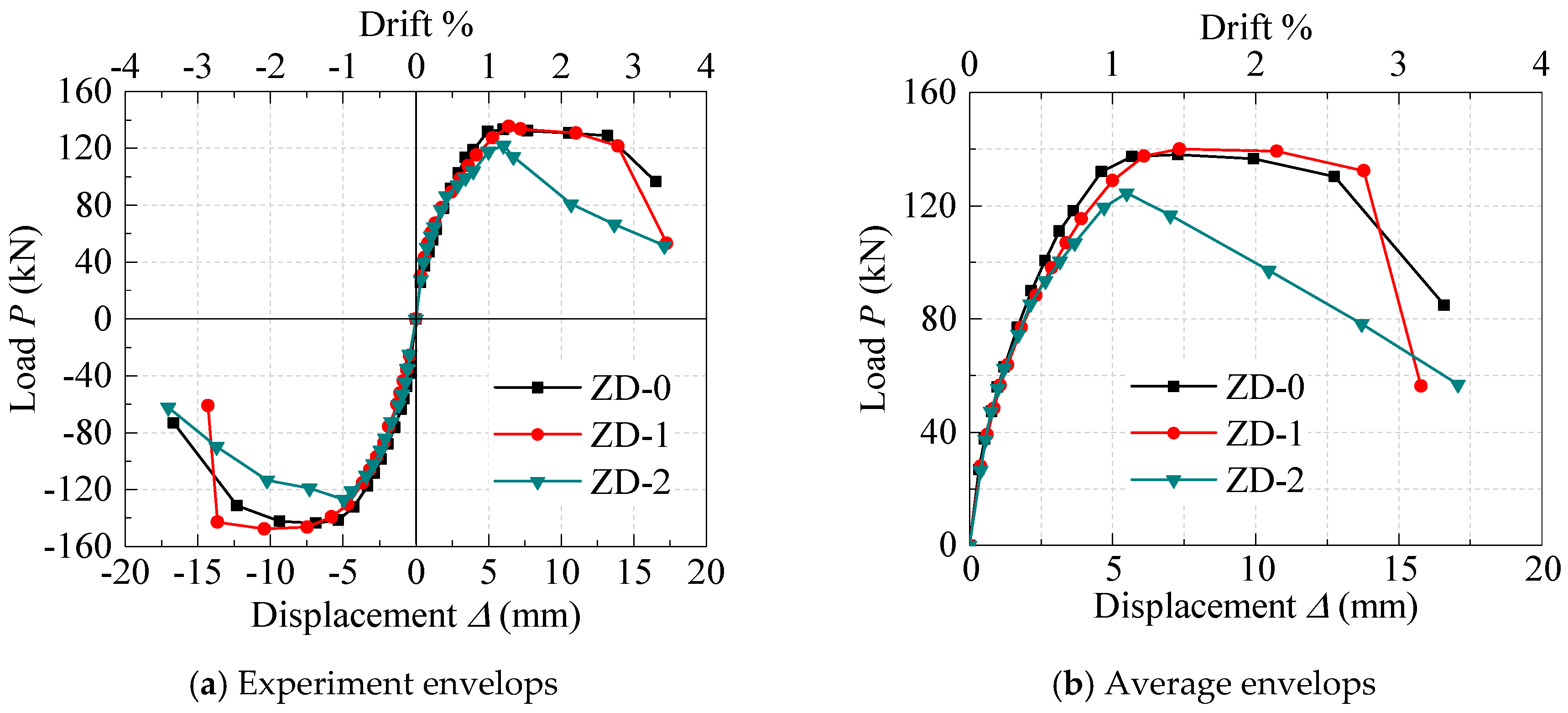
3.3. Skeleton Curves and Characteristic Values
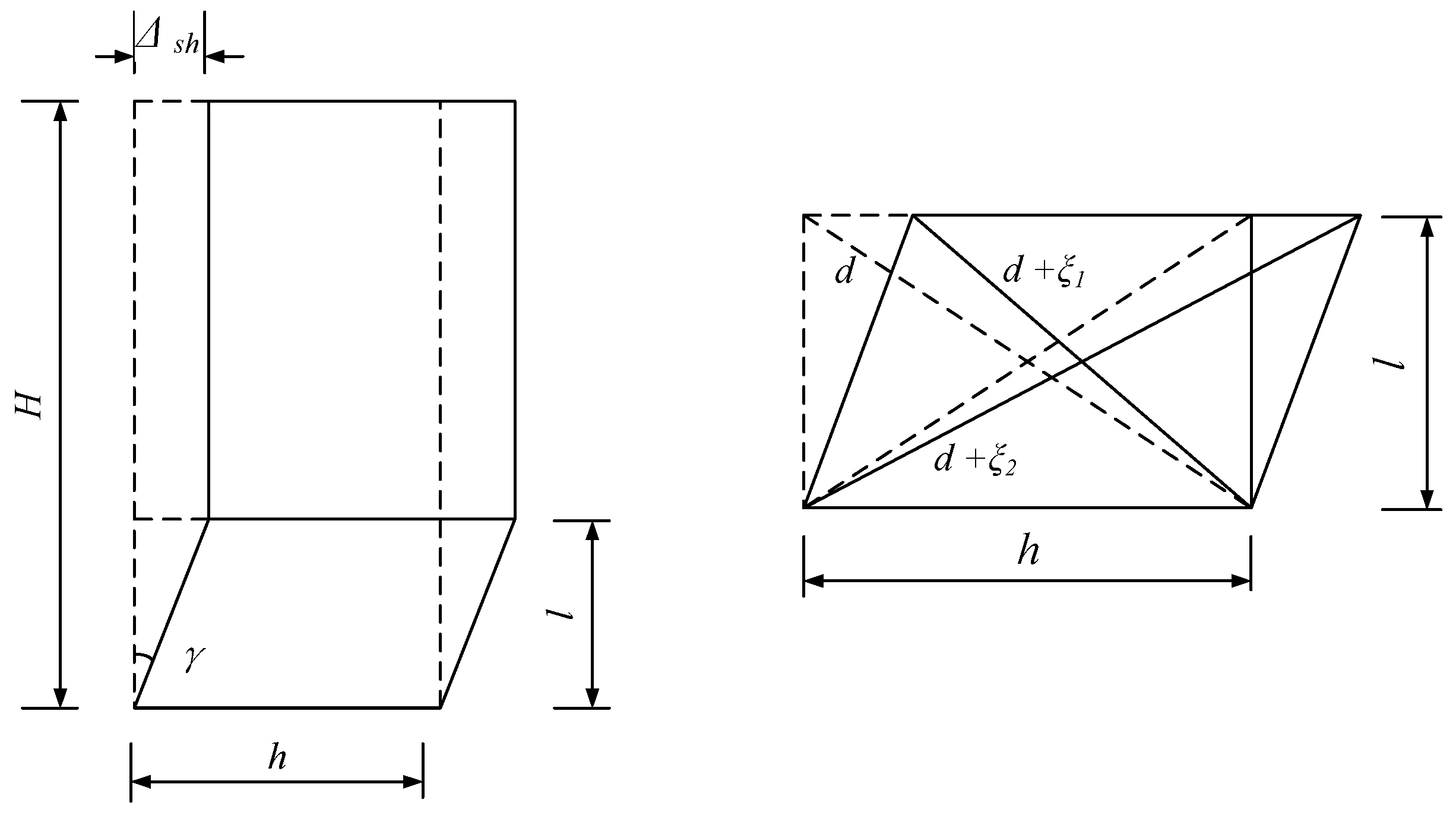
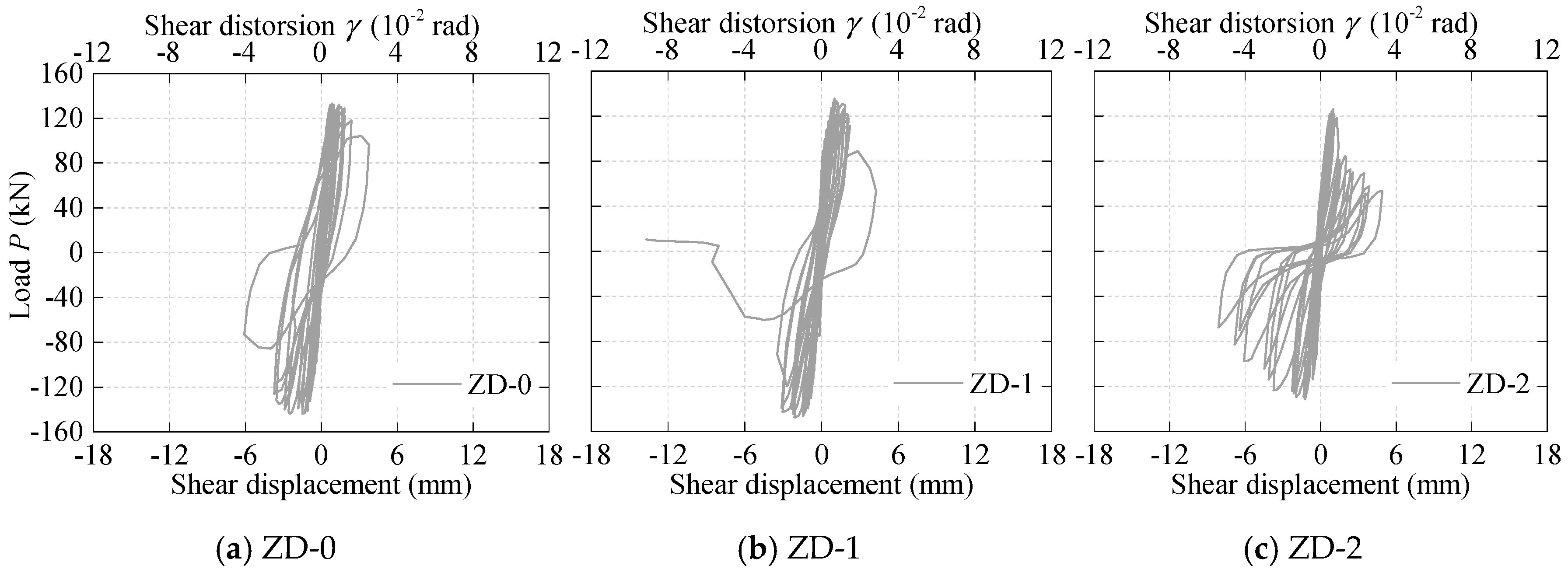
3.4. Shear Deformation
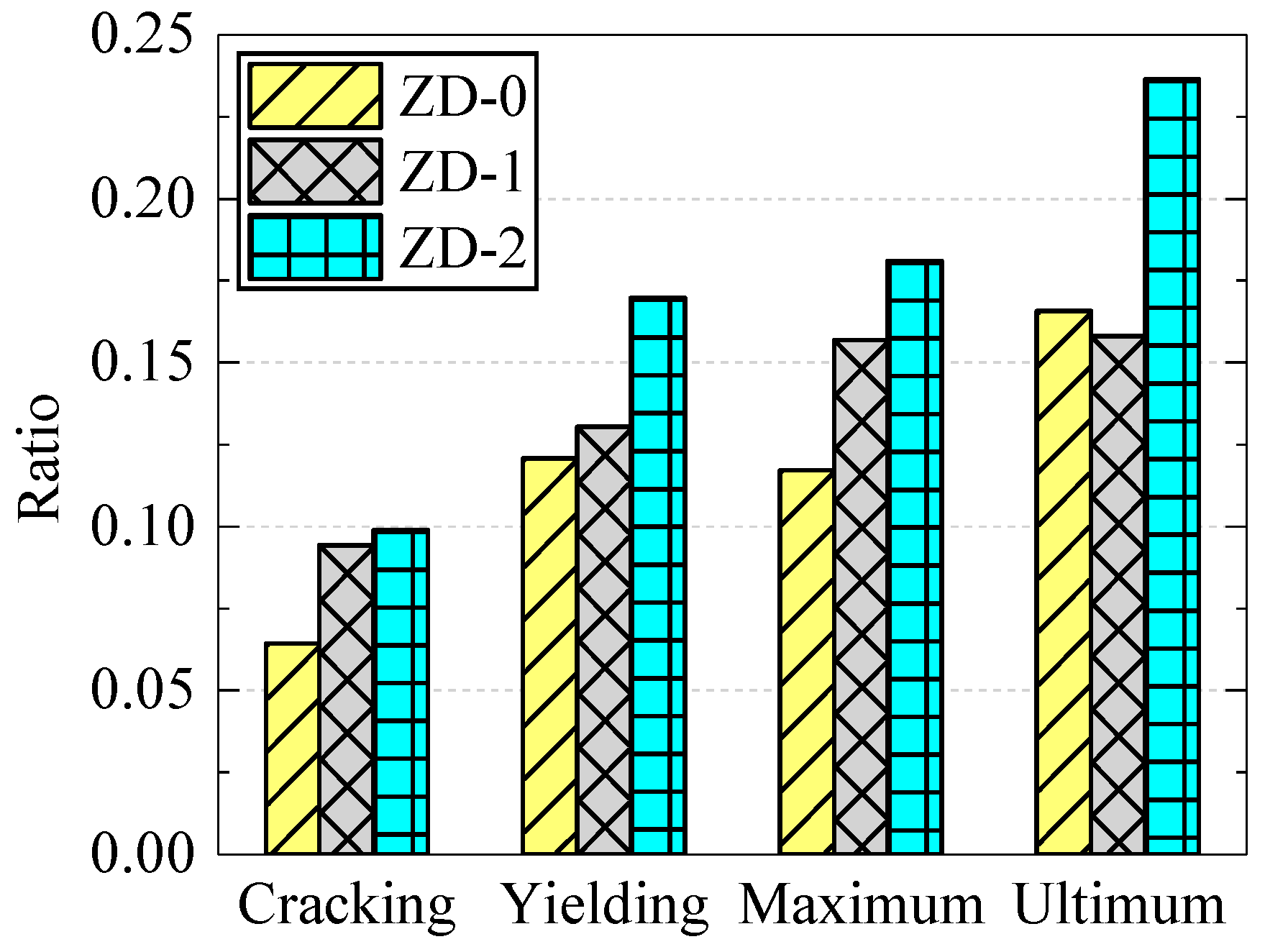
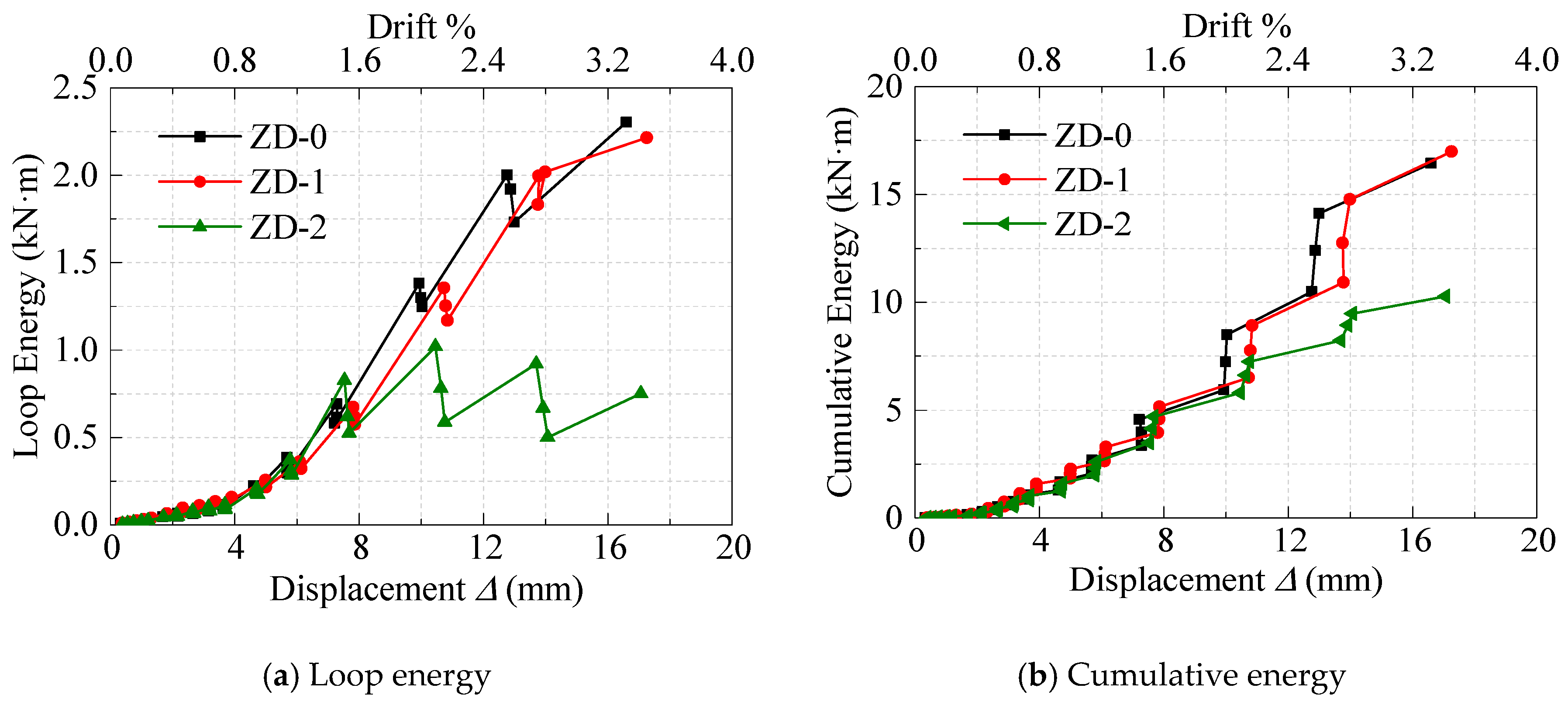
3.5. Energy Dissipation and Damping Ratio
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sato, K.; Satow, K.; Yamaguchi, H.; Araki, N. A survey of frost damages on concrete structures and building in the northeastern part of China. J. Eng. Heilongjiang 1995, 3, 67–69. (In Chinese) [Google Scholar]
- Li, J.Y.; Xu, W.Y.; Cao, J.G.; Lin, L.; Guan, Y.S. Study on the mechanism of concrete destruction under frost action. J. Hydraul. Eng. 1999, 1, 41–49. (In Chinese) [Google Scholar]
- Powers, T.C. A working hypothesis for further studies of frost resistance. J. ACI 1945, 16, 245–272. [Google Scholar]
- Powers, T.C. The air requirement of frost-resistant concrete. Proc. Highw. Res. Board 1949, 29, 184–202. [Google Scholar]
- Scherer, G.W. Crystallization in pores. Cem. Concr. Res. 1999, 29, 1347–1358. [Google Scholar] [CrossRef]
- Shih, T.S.; Lee, G.C.; Chang, K.C. Effect of freezing cycles on bond strength of concrete. J. Struct. Eng. 1988, 114, 717–726. [Google Scholar] [CrossRef]
- Shang, H.S.; Song, Y.P. Experimental study of strength and deformation of plain concrete under biaxial compression after freezing and thawing cycles. Cem. Concr. Res. 2006, 36, 1857–1864. [Google Scholar] [CrossRef]
- Petersen, L.; Lohaus, L.; Polak, M.A. Influence of freezing-and-thawing damage on behavior of reinforcement concrete elements. ACI Mater. J. 2007, 4, 369–378. [Google Scholar]
- Duan, A.; Jin, W.; Qian, J. Effect of freeze–thaw cycles on the stress–strain curves of unconfined and confined concrete. Mater. Struct. 2011, 44, 1309–1324. [Google Scholar] [CrossRef]
- Hanjari, K.Z.; Utgenannt, P.; Lundgren, K. Experimental study of the material and bond properties of frost-damaged concrete. Cem. Concr. Res. 2011, 41, 244–254. [Google Scholar] [CrossRef]
- Suzuki, T.; Ogata, H.; Takada, R.; Aoki, M.; Ohtsu, M. Use of acoustic emission and X-ray computed tomography for damage evaluation of freeze–thawed concrete. Constr. Build. Mater. 2010, 24, 2347–2352. [Google Scholar] [CrossRef]
- Molero, M.; Aparicio, S.; Al-Assadi, G.; Casati, M.J.; Hernández, M.G.; Anaya, J.J. Evaluation of freeze–thaw damage in concrete by ultrasonic imaging. NDT E Int. 2012, 52, 86–94. [Google Scholar] [CrossRef]
- Ranz, J.; Aparicio, S.; Romero, H.; Casati, M.J.; Molero, M.; González, M.G. Monitoring of freeze–thaw cycles in concrete using embedded sensors and ultrasonic imaging. Sensors 2014, 14, 2280–2304. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.D.; Zeng, Q.; Wang, L.; Li, K.F.; Xu, S.L.; Yao, Y. Characterizing frost damages of concrete with flatbed scanner. Constr. Build. Mater. 2016, 102, 872–883. [Google Scholar] [CrossRef]
- Hayashida, H.; Sato, Y.; Ueda, T. Failure behavior of RC beams in relation to the extent and location of frost damage. In Proceedings of the 3rd International Conference on the Durability of Concrete Structures, Belfast, Northern Ireland, 17–19 September 2012; pp. 904–915. [Google Scholar]
- Yang, W.; Zheng, S.S.; Zhang, D.Y.; Sun, L.F.; Gan, C.L. Seismic behaviors of squat reinforced concrete shear walls under freeze-thaw cycles: A pilot experimental study. Eng. Struct. 2016, 124, 49–63. [Google Scholar] [CrossRef]
- Qin, Q.; Zheng, S.S.; Dong, L.G.; Hou, P.J.; Wang, F. Considering Shear Behavior of Beam-Column Connections to Assess the Seismic Performance of RC Frames Subjected to Freeze-Thaw Cycles. J. Earthq. Eng. 2019, 1–26. [Google Scholar] [CrossRef]
- Xu, S.H.; Li, A.B.; Ji, Z.Y.; Wang, Y. Seismic performance of reinforced concrete columns after freeze-thaw cycles. Constr. Build. Mater. 2016, 102, 861–871. [Google Scholar] [CrossRef]
- Qin, Q.; Zheng, S.; Li, L.; Dong, L.; Zhang, Y.; Ding, S. Experimental study and numerical simulation of seismic behavior for RC columns subjected to freeze-thaw cycles. Adv. Mater. Sci. Eng. 2017, 4, 1–13. [Google Scholar] [CrossRef]
- Liu, K.; Yan, J.; Zou, C. A pilot experimental study on seismic behavior of recycled aggregate concrete columns after freeze-thaw cycles. Constr. Build. Mater. 2018, 164, 497–507. [Google Scholar] [CrossRef]
- Sezen, H.; Elwood, K.J.; Whittaker, A.S.; Mosalam, K.M.; Wallace, J.W.; Stanton, J.F. Structural Engineering Reconnaissance of the August 17, 1999, Kocaeli (Izmit), Turkey, Earthquake. PEER Report 2000/09. 2000. Available online: peer.berkeley.edu/publications/peer_reports/reports_2000/0009.pdf (accessed on 30 December 2018).
- Anil, Ö. Strengthening of RC T-section beams with low strength concrete using CFRP composites subjected to cyclic load. Constr. Build. Mater. 2008, 22, 2355–2368. [Google Scholar] [CrossRef]
- Katakalos, K.; Manos, G.; Papakonstantinou, C. Seismic Retrofit of R/C T-Beams with Steel Fiber Polymers under Cyclic Loading Conditions. Buildings 2019, 9, 101. [Google Scholar] [CrossRef]
- Ma, G.; Li, H.; Hwang, H.J. Seismic behavior of low-corroded reinforced concrete short columns in an over 20-year building structure. Soil Dyn. Earthq. Eng. 2018, 106, 90–100. [Google Scholar] [CrossRef]
- Chinese national standard. Code for Design of Concrete Structures; GB 50010-2002; China Architecture and Building Press: Beijing, China, 2002. (In Chinese) [Google Scholar]
- American Society of Civil Engineering (ASCE). Seismic Evaluation and Retrofit of Existing Buildings; ASCE/SEI 41-13; ASCE: Reston, VA, USA, 2014. [Google Scholar]
- Chinese National Standard. Standard for Test Methods of Long-term Performance and Durability of Ordinary Concrete; GB/T50082-2009; China Architecture and Building Press: Beijing, China, 2009. (In Chinese) [Google Scholar]
- Chinese National Standard. Standard for Test Method of Concrete Structures; GB/T 50152-2012; China Architecture and Building Press: Beijing, China, 2012. (In Chinese) [Google Scholar]
- American Society for Testing and Materials (ASTM). Standard Test Method for Resistance of Concrete to Rapid Freezing and Thawing; ASTM C666/ C666M-15; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- Setzer, M.J.; Heine, P.; Kasparek, S.; Palecki, S.; Auberg, R.; Feldrappe, V.; Siebel, E. RILEM TC 176-IDC: Internal damage of concrete due to frost action: Final report. Mater. Struct. 2004, 37, 743–753. [Google Scholar] [CrossRef]
- Gudmundsson, G.; Wallevik, O. Concrete in an aggressive environment. In Proceeding of International RILEM Workshop on Frost Damage in Concrete, 28–30 June 1999. [Google Scholar]
- Fagerlund, G. A Service Life Model for Internal Frost Damage in Concrete; Report TVBM-3119; Lund Institute of Technology: Lund, Sweden, 2004. [Google Scholar]
- Paulay, T.; Priestley, M.N.J. Seismic Design of Reinforced Concrete and Masonry Buildings; John Wiley & Sons, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Fagerlund, G.; Janz, M.; Johannesson, B. Effect of Frost Damage on the Bond Between Reinforcement and Concrete; Report TVBM-9016; Lund Institute of Technology: Lund, Sweden, 1994. [Google Scholar]
- Mahin, S.A.; Bertero, V.V. Problems in establishing and predicting ductility in aseismic design. In Proceedings of the International Symposium on Earthquake Structural Engineering, St. Louis, MO, USA, 19–21 August 1976; pp. 613–628. [Google Scholar]
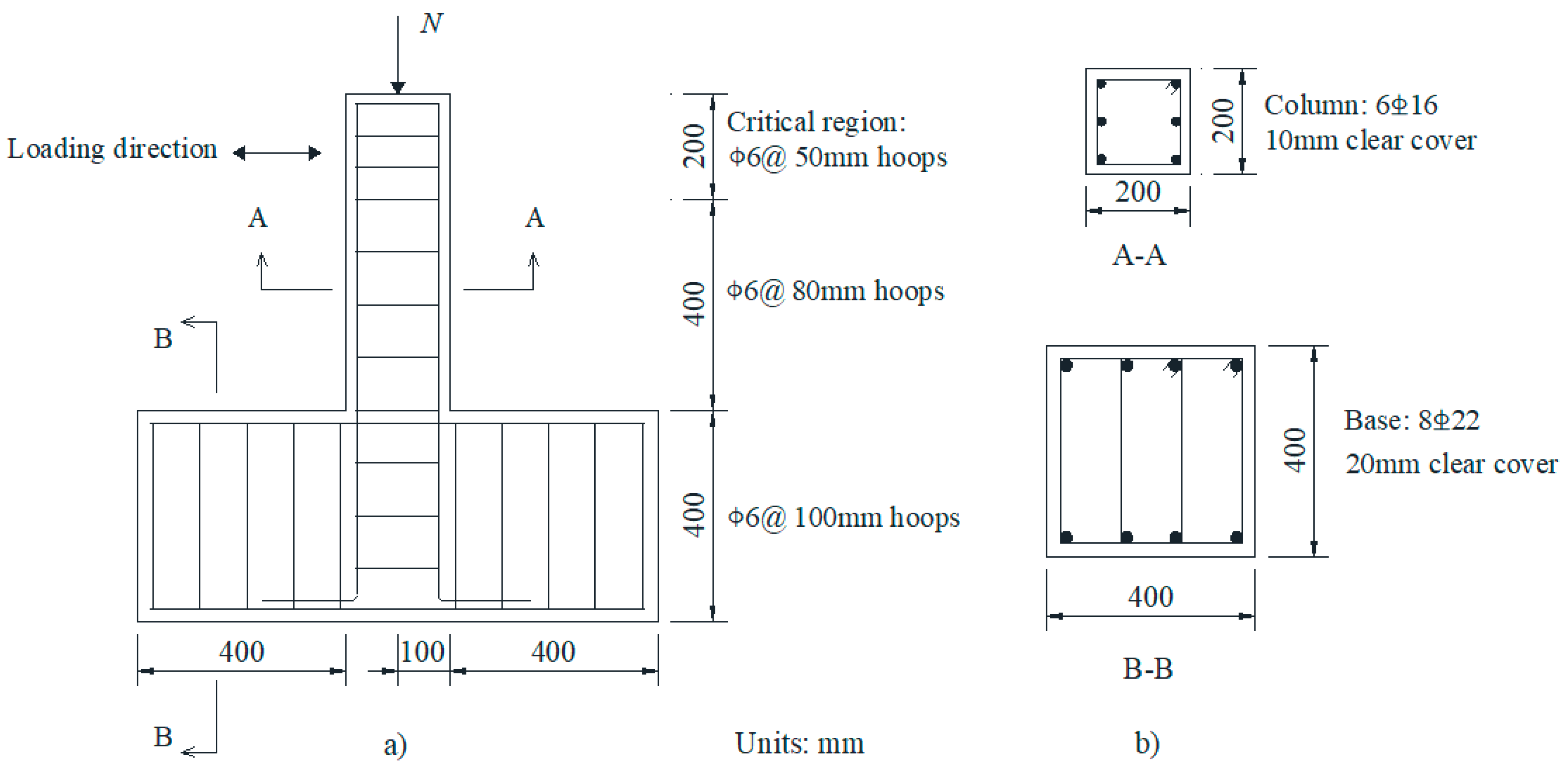




| Specimen | Shear Span Ratio | Concrete Strength Grade | Axial Force N (kN) | ρv | ρl | FTCs |
|---|---|---|---|---|---|---|
| ZD-0 | 2.5 | C50 | 306 | 0.28% | 1.51% | 0 |
| ZD-1 | 2.5 | C50 | 306 | 0.28% | 1.51% | 100 |
| ZD-2 | 2.5 | C50 | 306 | 0.28% | 1.51% | 200 |
| w/c | Water (kg/m3) | Cement (kg/m3) | Sand (kg/m3) | Stone (kg/m3) | fcu,0 (MPa) | fcu,50 (MPa) | fcu,100 (MPa) | fcu,150 (MPa) | fcu,200 (MPa) |
|---|---|---|---|---|---|---|---|---|---|
| 0.42 | 203 | 483 | 688 | 1076 | 56.7 | 54.3 | 51.48 | 47.85 | 43.15 |
| Specimen | Fy (kN) | Δy (%) | Fp(kN) | Δp (%) | Δu (%) | θp | μΔ | ξy | ξp | ξu |
|---|---|---|---|---|---|---|---|---|---|---|
| ZD-0 | 116.87 | 0.71 | 138.01 | 1.46 | 2.77 | 2.06 | 3.91 | 0.02 | 0.06 | 0.10 |
| ZD-1 | 111.81 | 0.82 | 139.97 | 1.47 | 2.83 | 2.01 | 3.40 | 0.03 | 0.05 | 0.09 |
| ZD-2 | 103.05 | 0.67 | 124.45 | 1.10 | 1.79 | 1.12 | 2.65 | 0.02 | 0.04 | 0.08 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zheng, S.; Rong, X.; Dong, L.; Zheng, H. Seismic Performance of Reinforced Concrete Short Columns Subjected to Freeze–Thaw Cycles. Appl. Sci. 2019, 9, 2708. https://doi.org/10.3390/app9132708
Zhang Y, Zheng S, Rong X, Dong L, Zheng H. Seismic Performance of Reinforced Concrete Short Columns Subjected to Freeze–Thaw Cycles. Applied Sciences. 2019; 9(13):2708. https://doi.org/10.3390/app9132708
Chicago/Turabian StyleZhang, Yixin, Shansuo Zheng, Xianliang Rong, Liguo Dong, and Hao Zheng. 2019. "Seismic Performance of Reinforced Concrete Short Columns Subjected to Freeze–Thaw Cycles" Applied Sciences 9, no. 13: 2708. https://doi.org/10.3390/app9132708
APA StyleZhang, Y., Zheng, S., Rong, X., Dong, L., & Zheng, H. (2019). Seismic Performance of Reinforced Concrete Short Columns Subjected to Freeze–Thaw Cycles. Applied Sciences, 9(13), 2708. https://doi.org/10.3390/app9132708




